摘要: 基于反铁磁材料的自旋逻辑器件被认为具有更低的能量损耗、更快的速度和更高的稳定性, 这使得反铁磁材料的超快自旋动力学成为当前自旋电子学研究的热点. 由于反铁磁体具有强的交换耦合和高的共振频率, 将在GHz甚至THz波段得到广泛应用. 本文综述了利用太赫兹(THz)脉冲的磁场分量与反铁磁自旋序之间的相互作用进行探测与操控. 利用THz脉冲时域光谱, 系统研究了反铁磁性稀土正铁氧体(
R FeO
3 )中自旋共振的非热激发及其弛豫动力学. 总结了
R FeO
3 的准铁磁和准反铁磁自旋模式的共振频率, 以及由
R 3+ -Fe
3+ 离子间的相互作用所确定的自旋重取向温区. 不仅可以利用具有时间延迟的THz双脉冲实现DyFeO
3 中自旋极化的相干控制, 利用材料的各向异性以单个THz脉冲也可以实现YFeO
3 中的自旋波相干调控. 在Er
x Y
1- x FeO
3 单晶样品中, 找到了自旋与真空磁子的关联交换耦合的实验证据, 证明了存在以物质-物质相互作用形式的迪克协作耦合. 最后, 讨论了THz波在TmFeO
3 晶体传播过程中诱导的磁极化子.
关键词: 反铁磁 /
自旋共振 /
超快太赫兹光谱 English Abstract Research progress of coherent control of terahertz spin waves and strong coupling in rare-earth orthoferrites Jin Zuan-Ming 1 ,Ruan Shun-Yi 1 ,Li Ju-Geng 1 ,Lin Xian 1 ,Ren Wei 1 ,Cao Shi-Xun 1 ,Ma Guo-Hong 1 ,Yao Jian-Quan 2 1.Department of Physics, Shanghai University, Shanghai 200444, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11604202, 11674213, 61735010, 11774217), the Young Eastern Scholar, China (Grant No. QD2015020), “Chen Guang” Project of the Shanghai Municipal Education Commission of China and the Shanghai Education Development Foundation of China (Grant No. 16CG45), and the Shanghai Rising-Star Program, China (Grant No. 18QA1401700).Received Date: 09 May 2019Accepted Date: 19 June 2019Available Online: 01 August 2019Published Online: 20 August 2019Abstract: Antiferromagnets (AFM) are promising for future spintronic applications due to their advantageous properties. Antiferromagnets produce no stray fields and are insensitive to external magnetic field perturbations. Furthermore, antiferromagnets show intrinsic high terahertz (THz) frequency dynamics. The THz pulses are a direct and general probe of ultrafast spin dynamics in insulating antiferromagnets. In this review article, we discuss the excitation and control of the antiferromagnetic spin resonances in rare-earth orthoferrites (R FeO3 , R indicates Y and rare-earth element) with the THz electromagnetic pulsetime-domain spectroscopy. We believe that this approach is general and can be applied to a broad range of materials with different AFM spin alignments, giving a novel non-contact approach to probing AFM order with ps temporal resolution. We summarize different quasi-ferromagnetic modes (qFM) and quasi-antiferromagnetic modes (qAFM), as well as the spin reorientation transition temperatures of R FeO3 . Coherent control of spin waves at THz frequency promises fruitful applications in ultrafast magnetization control and has received increasing attention. It is demonstrated that not only the delay time between the excitation and control THz pulses arriving DyFeO3 , but also the intrinsic dielectric anisotropy of YFeO3 in the THz range allow the coherent control of both the amplitude and the phase of the excited spin waves. Moreover, we outline the current observation of Dicke cooperativity in magnetic interaction of Erx 1- x 3 , which presents a route to understanding, controlling, and predicting novel phases of condensed matter by using the concepts and tools available in quantum optics. Finally, magnon-polaritonsare demonstrated to play a key role in preparing the THz waves through TmFeO3 .Keywords: antiferromagnet /spin resonance /ultrafast and terahertz spectroscopy 全文HTML --> --> --> 1.引 言 对于反铁磁材料而言, 相邻原子的交替磁矩导致了净磁矩为零, 使得反铁磁体对外界磁场不敏感[1 ,2 ] . 同时, 它同样导致了反铁磁材料中没有漏磁场. 相比于铁磁体, 这些性质能够极大地减小储存1比特信息所需的最小体积. 另一方面, 反铁磁体对外加磁场的不敏感性使得有效操控和探测反铁磁体的自旋态极具挑战性. 克服这个挑战的关键是如何有效地激发反铁磁体中的自旋共振模式以及在皮秒量级的时间尺度上实现磁矢量的超快翻转[3 —5 ] . 基于以上特点, 反铁磁材料在自旋电子学中引起了广泛的兴趣.[6 ] 观测到频率在1.07 THz和0.14 THz的THz辐射. 他们指认高频模式为面外磁模式, 低频模式为面内磁模式[7 ] . 2012年, Nishitani等[8 ] 利用延迟时间可调谐的飞秒激光双脉冲, 实现了面外磁模式的光学相干控制. IFE是一种非线性光学效应, 属于冲击受激Raman散射效应. 2015年, Mikhaylovskiy等[9 ] 研究了通过交换相互作用实现光脉冲电场与自旋的耦合. 通过对铁氧体(具有倾角自旋结构)的自旋共振超快光激发所产生的太赫兹(THz)发射, 实验上证实了各向同性的光磁效应—逆磁折射效应. 根据THz辐射强度可以估算, 能量密度约为1 ${{{\rm{mJ}}} / {{\rm{c}}{{\rm{m}}^{\rm{2}}}}}$ 的激光脉冲可以实现交换相互作用的亚皮秒调制, 相当于一个0.01 T的脉冲有效磁场.[10 ] . 除了利用飞秒激光脉冲诱导反铁磁晶体中的自旋波, 近年来THz电磁脉冲也被广泛地应用于反铁磁材料的自旋动力学, 尤其是自旋模式的共振激发[11 ] . 2011年, Kampfrath等[12 ] 利用强THz脉冲的磁场分量直接激发反铁磁NiO的自旋极化波(面外磁模式), 并通过同步飞秒脉冲的磁光Kerr效应探测该磁模式的进动与弛豫动力学. 此外, 利用时间延迟的双THz脉冲, 实现面外磁模式的相干控制.$R{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ (R 为Y和稀土元素)属于正交晶系, 空间群为Pbnm , 每个单胞中有四个等价的Fe3+ 离子. Fe3+ 与O2- 形成FeO6 八面体, 稀土离子填充在八面体形成的空隙中. 由于晶格畸变, Fe—O—Fe之间的键角小于180°, $R{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 属于倾角反铁磁体. 其独特的磁性能表现为铁的磁矩来自3d电子, 稀土元素的磁矩来自4f电子. 稀土正铁氧体中发现的激光诱导超快自旋重取向和IFE产生的有效磁场实现自旋波调控, 使$R{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 成为凝聚态和材料物理中研究的热点[2 ] . 2010年Suemoto课题组[13 ] 研究了THz辐射实现${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ 单晶准铁磁和准反铁磁模式的选择性激发和相干控制. 2013年, Yamaguchi等[14 ] 利用THz时域光谱研究了${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ 中的自旋重取向相变过程. 近年来关于$R{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 的超快自旋重取向, 以及自旋波的相干控制研究激发了研究兴趣[15 —21 ] . 自旋重取向以及超快磁相变不仅具有重要的学术价值, 同时必将加速超快光磁效应在自旋电子器件中的应用.$R{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 晶体THz自旋波的共振激发以及THz光谱应用于自旋重取向温区的标定. 简述了利用THz脉冲实现自旋波的相干控制. 介绍了上海大学和Rice大学合作在实验上证实了固体中的Dicke协作耦合[22 ] , 并定量给出了${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}{\rm{ - E}}{{\rm{r}}^{{\rm{3 + }}}}$ 对称和反对称的交换耦合常数. 这些常数不仅有助于理解3d-4f的磁耦合, 也是许多化合物中诸如新的磁相变、磁电效应、电磁振子、非线性自旋激发等奇异现象产生的原因. 最后, 介绍了上海大学与荷兰Radboud大学合作, 在TmFeO3 单晶中观测到THz光子与反铁磁共振模式的免交叉现象, 证明了R FeO3 单晶的法布里-珀罗腔可以实现THz光子与反铁磁自旋波模式的强耦合效应, 产生光子与磁振子的杂化元激发-磁极化子.2.基于瞬态Zeeman转矩的磁共振激发 如图1(a) 所示, $R{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 为正交的钙钛矿结构, 用空间群$D_{2h}^{16}{\rm{ - }}pbnm$ 表示[23 ] . 最强的磁相互作用是${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}{\rm{ - F}}{{\rm{e}}^{{\rm{3 + }}}}$ 交换相互作用, 导致在约650 K以下${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的自旋为反铁磁有序. 反对称的Dzyaloshinskir-Moriya(DM)相互作用和磁各向异性产生的综合效应使${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 亚晶格产生了很小的倾斜, 偏离完美的反平行构置, 从而导致一个宏观的磁化矢量M R FeO3 表现出弱铁磁性.图 1 (a) R FeO3 反铁磁晶体晶体结构与自旋结构, 邻近的${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 离子沿着a 轴反平行有序排列; (b) THz激发的准铁磁模式(qFM)和准反铁磁(qAFM)模式Figure1. (a) Lattice and spin structure of R FeO3 , adjacent ${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ ions are antiparallel and ordered along the a axis; (b) THz excitation of qFM mode and qAFM mode.R FeO3 磁结构的描述, 通常采用方向相反的两套铁离子的亚晶格${{{M}}_1}$ 和${{{M}}_{\rm{2}}}$ , 且$\left| {{{{M}}_1}} \right| = \left| {{{{M}}_{\rm{2}}}} \right| = $ ${{{M}}_{\rm{0}}}$ . 分别定义“铁磁矢量”(FM)${{M}} = {{{M}}_1} + {{{M}}_{\rm{2}}}$ 和“反铁磁矢量”(AFM)${{L}} = {{{M}}_1} - {{{M}}_{\rm{2}}}$ . M L [24 ] :[25 ] 和置于微波腔中的铁磁性YIG[26 ] 中表现得十分明显. 对于频率范围为0.1—10 THz的THz电磁辐射, 相应的能量跨度在0.4—40 meV范围. 当THz脉冲入射到晶体中, THz脉冲的磁场分量类似于一个亚皮秒时间尺度的磁脉冲. 宏观上, THz瞬态磁场(${{{H}}_{{\rm{THz}}}}$ )的方向正交于材料的宏观磁化矢量M M ${{T}} \propto {{M}} \times {{{H}}_{{\rm{THz}}}}$ , 这一瞬态转矩T M ${{{H}}_{{\rm{THz}}}}$ 消失后, M M ${{{E}}_{\rm {THz}}} \propto {{\partial {{{M}}^2}} / {\partial {t^2}}}$ , 此电磁波的频率等于磁化矢量的进动频率, 这一过程称为自由感应衰减. 对于反铁磁材料来说, 磁共振模式的频率可以简单表示为${\omega _{{\rm{AF}}}} \approx \gamma \sqrt {{H_{\rm{A}}} \cdot {H_{{\rm{ex}}}}} $ , 其中各向异性场${H_{\rm{A}}}$ < 1 T, 而交换场${H_{{\rm{ex}}}}$ ≈100 T. 相比于铁磁体中的${\omega _{\rm{F}}} \approx \gamma \cdot {H_{\rm{A}}}$ , 两者大小相差了两个数量级.${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 系统中的两类磁子共振模式. 当${{{H}}_{{\rm{THz}}}}$ 垂直于M R FeO3 的准铁磁模式(quasi FM-mode, qFM). 当${{{H}}_{{\rm{THz}}}}$ 平行于M R FeO3 的准反铁磁模式(quasi AFM-mode, qAFM). 图1(b) 给出了THz波磁场分量对R FeO3 中的qFM和qAFM模式的激发示意图. 对于${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的qFM模式, ${{{M}}_1}$ 和${{{M}}_{\rm{2}}}$ 同相位振动, 然而它们之间的夹角保持不变. 因此简化为M a 轴进动. 然而, qAFM模式则表现为M a 轴以 “应切”方式辐射线偏振的自由感应衰减信号.b 切${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ 单晶为例. 样品双面抛光, 厚度为0.72 mm. 在Néel温度(${T_{\rm{N}}}$ = 645 K)以下[27 ] , ${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ 晶体在c 轴方向表现出宏观的弱铁磁性. 图2(a) 和图2(b) 分别是当入射的THz脉冲的电场矢量垂直于a 轴(${{{E}}_{{\rm{THz}}}} \bot a$ , ${{{H}}_{{\rm{THz}}}} \bot c$ )和电场矢量平行于a 轴(${{{E}}_{{\rm{THz}}}}\parallel a$ , ${{{H}}_{{\rm{THz}}}}\parallel c$ )情况下, 透过${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ 单晶后的THz脉冲时域波形. 实验测得THz波形包括两个部分, 一个是在零延迟时间处的宽带THz主脉冲部分, 二是THz主脉冲后指数衰减的长寿命振荡分量. 这部分振荡信号突出显示于图2(a) 和图2(b) 的插图中. qFM和qAFM模式的振荡信号的周期分别为2.63 ps和1.92 ps. 图2(c) 和图2(d) 为振荡分量(时域范围从22—36 ps)的傅里叶变换光谱. 两个共振峰分别位于0.38 THz和0.52 THz, 分别对应于${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ 单晶的qFM(${{{M}}_a}$ , ${{{M}}_b}$ 和${{{L}}_c}$ 的振荡频率)和qAFM(${{{L}}_a}$ , ${{{L}}_b}$ 和${{{M}}_c}$ 的振荡频率)自旋共振模式. 通过改变${{{H}}_{{\rm{THz}}}}$ 与M [28 ] .图 2 (a), (b)分别为激发qFM模式(红色)与qAFM模式(蓝色)时的THz时域透射谱, 插图为振荡部分的放大图; (c), (d)分别为振荡部分的傅里叶变换光谱Figure2. (a), (b) THz time-domain transmission spectrum of qFM mode (red curve) and qAFM mode (blue curve), the insets are enlarged versions of the oscillating sections; (c), (d) Fourier transform spectra of the oscillating parts.表1 总结了${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ [13 ,29 ] , ${\rm{PrFe}}{{\rm{O}}_{\rm{3}}}$ [30 ] , ${\rm{NdFe}}{{\rm{O}}_{\rm{3}}}$ [16 ] ,${\rm{GdFe}}{{\rm{O}}_{\rm{3}}}$ [31 ] ,${\rm{TbFe}}{{\rm{O}}_{\rm{3}}}$ [32 ] , ${\rm{HoFe}}{{\rm{O}}_{\rm{3}}}$ [33 ] , ${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ [14 ] , ${\rm{TmFe}}{{\rm{O}}_{\rm{3}}}$ [32 ] , ${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ [32 ] , ${\rm{SmFe}}{{\rm{O}}_{\rm{3}}}$ [34 ] 等稀土正铁氧体的qFM和qAFM模式的共振频率. 如表2 所列, ${\rm{S}}{{\rm{m}}_x}{\rm{D}}{{\rm{y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_3}$ , ${\rm{S}}{{\rm{m}}_x}{\rm{D}}{{\rm{y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_3}$ , ${\rm{S}}{{\rm{m}}_x}{\rm{D}}{{\rm{y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_3}$ 的qFM频率分别为0.35, 0.39, 0.45 THz, 位于SmFeO3 和DyFeO3 的qFM共振频率的连线上[35 ] . ${\rm{S}}{{\rm{m}}_x}{\rm{D}}{{\rm{y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_3}$ 的qFM共振频率可以写成, $\hbar \omega _{{\rm{FM}}}^{{\rm{S}}{{\rm{m}}_x}{\rm{D}}{{\rm{y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_3}} = x\hbar \omega _{{\rm{FM}}}^{{\rm{SmFe}}{{\rm{O}}_3}} + \left( {{\rm{1}} - x} \right)\hbar \omega _{{\rm{FM}}}^{{\rm{DyFe}}{{\rm{O}}_3}}$ . Liu等[36 ] 的实验结果表明, 通过稀土共掺杂可以有效调节模式的各向异性参数, 从而调谐自旋共振频率. RFeO3 υqFM/THz υqAFM/THz Reference YFeO3 0.299(300K) 0.527(300K) [13 29 ] PrFeO3 0.34(300K) 0.41(300K) [30 ] NdFeO3 0.28(300K) 0.485(290K) [16 ] GdFeO3 0.305(300K) 0.606(300K) [31 ] TbFeO3 0.322(300K) 0.537(300K) [32 ] HoFeO3 0.37(270K) 0.57(270K) [33 ] ErFeO3 0.377(300K) 0.673(300K) [14 ] TmFeO3 0.402(300K) 0.698(300K) [32 ] DyFeO3 0.379(300K) 0.51(300K) [32 ] SmFeO3 0.34(200K) 0.62(200K) [34 ]
表1 RFeO3 的qFM和qAFM模式的自旋共振频率Table1. The qFM and qAFM mode resonance frequencies of rare earth orthoferrite RFeO3 υ qFM /THz DyFeO3 0.2(40K) Sm0.5 Dy0.5 FeO3 0.35(40K) Sm0.6 Dy0.4 FeO3 0.39(40K) Sm0.7 Dy0.3 FeO3 0.45(40K) SmFeO3 0.55(40K)
表2 Smx 1–x FeO3 单晶在40K的qFM模式的自旋共振频率与Sm浓度的关系[35 ] Table2. Resonance frequencies of qFM mode for the single crystals versus Sm concentration at 40 K[34 ] ${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 离子的磁相${\varGamma _4}$ , ${\varGamma _{24}}$ , ${\varGamma _2}$ , ${\varGamma _{12}}$ 和${\varGamma _{\rm{1}}}$ 相, 分别出现于不同的温度. ${\varGamma _{\rm{1}}}$ 相表示在各个方向均表现为无净宏观磁矩, 而${\varGamma _2}$ 相和${\varGamma _4}$ 相分别表示在样品的a 轴和c 轴方向上存在弱的宏观磁化. 第一性原理计算表明, 对于倾角反铁磁结构的R FeO3 , 当稀土元素R 的4f电子不全空或者全满时, 由于稀土离子${R^{{\rm{3 + }}}}$ 和铁离子${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 之间的相互作用(这种相互作用极易受外界温度和磁场的影响), 导致样品内的磁各向异性能发生变化, 从而改变${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的自旋方向, 导致自旋重取向的产生. 一般来说, 在自旋重取向过程中, 由于${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 自旋组态发生了旋转, 宏观磁化矢量M c 轴转变为低温相下平行于晶体的a 轴(旋转了90°), 这是一个二级相变过程. 以${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ 为例, 如图3 所示, 40 K时样品处于${\varGamma _2}$ 相, 从振荡频率分析, THz脉冲激发了qFM模式; 300 K时样品处于${\varGamma _{\rm{4}}}$ , 激发qAFM模式. 温度范围为4.5 —85 K之间时, 晶体处于${\varGamma _2}$ 相; 当温度高于96 K时, 晶体处于${\varGamma _{\rm{4}}}$ 相.图 3 (a), (b) 40 K和300 K时${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ 的THz时域透射谱, 插图为振荡部分的放大图; (c), (d)分别为振荡部分的傅立叶变换光谱, 插图为${\varGamma _2}$ 与${\varGamma _{\rm{4}}}$ 的示意图Figure3. (a), (b) THz time-domain transmission spectra of ${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ at 40 K and 300 K; (c), (d) Fourier transform spectra of the oscillating signals. Insets: schematic diagram of ${\varGamma _2}$ and ${\varGamma _{\rm{4}}}$ .R -Fe之间的相互作用能也就不同, R FeO3 的相变过程及相变温区也不尽相同, 表3 总结了不同稀土正铁氧体的自旋重取向温区, 如${\rm{YbFe}}{{\rm{O}}_{\rm{3}}}$ [37 ] , ${\rm{NdFe}}{{\rm{O}}_{\rm{3}}}$ [16 ] , ${\rm{TbFe}}{{\rm{O}}_{\rm{3}}}$ [38 ] , ${\rm{HoFe}}{{\rm{O}}_{\rm{3}}}$ [33 ] , ${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ [14 ] , ${\rm{TmFe}}{{\rm{O}}_{\rm{3}}}$ [3 ] , ${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ , ${\rm{SmFe}}{{\rm{O}}_{\rm{3}}}$ [34 ] 等. 此外, 如表4 所列, 通过改变稀土元素共掺杂的比例, 也可以有效地调控重取向温区. 在温度诱导的自旋重取向过程中, 有的样品只发生二级相变过程(${\varGamma _{\rm{4}}} \leftrightarrow {\varGamma _{\rm{2}}}$ ), 宏观磁矩只在晶体的ac 面内发生旋转, 如${\rm{NdFe}}{{\rm{O}}_{\rm{3}}}$ [16 ] , ${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ [14 ] , ${\rm{SmFe}}{{\rm{O}}_{\rm{3}}}$ [34 ] , ${\rm{TmFe}}{{\rm{O}}_{\rm{3}}}$ [39 ] , ${\rm{YbFe}}{{\rm{O}}_{\rm{3}}}$ [40 ] 等. 值得注意的是, ${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ 样品发生一级相变(${\varGamma _{\rm{4}}} \leftrightarrow {\varGamma _{\rm{1}}}$ )[41 ] . 由于R FeO3 共振吸收对THz的磁场分量的偏振方向敏感, 如果R 为非磁性金属, 如Y或${\rm{P}}{{\rm{r}}^{{\rm{3 + }}}}$ , 不含4f电子, 则R -Fe之间的相互作用可以忽略, 几乎不会产生温度诱导的Fe离子的自旋重取向过程. 然而, 利用其他外部条件, 如外加磁场可以实现${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ 单晶的自旋重取向过程[42 ] . THz时域光谱为研究磁场调控的${\rm{NdFe}}{{\rm{O}}_{\rm{3}}}$ 自旋重取向磁相变动力学提供了研究方法[43 ] . RFeO3 the spin reorientation Reference YbFeO3 6.85–8.15K [37 ] NdFeO3 110–170K [16 ] TbFeO3 4.2–6.5K [38 ] HoFeO3 37.5(±2.5)–70(±5)K [33 ] ErFeO3 87–96K [14 ] TmFeO3 80–91K [3 ] DyFeO3 48–50K SmFeO3 450–480K [34 ]
表3 稀土正铁氧体的自旋重取向温区总结Table3. The spin reorientation temperature region of rare earth ferrite RFeO3 the spin reorientation temperature region Sm0.3 Dy0.7 FeO3 75–105K Sm0.5 Dy0.5 FeO3 175–220K Sm0.6 Dy0.4 FeO3 235–275K
表4 Smx 1–x FeO3 的自旋重取向温度与Sm浓度的关系Table4. SRT temperatures for the SDFO single crystal family versus Sm concentration3.自旋波的相干控制 相干控制主要有两种途径, 一是采用多束不同频率且具有一定相位关系的激光同时作用在物质上, 形成特定的干涉场, 以控制系统演化的路径及速率. 另一种是利用系统在退相时间内能态间的相位关系, 采用两个或两个以上相同频率且具有一定时间间隔的脉冲, 控制系统的演化. 采用第二种方法, 通过一对具有时间延迟的飞秒脉冲激发ZnTe晶体, 产生两个THz 脉冲序列. 当第二个THz脉冲与第一个THz脉冲相位相同, 此时所激发自旋波的相位也相同, 将相干地加强qFM或qAFM模式; 当第二个THz脉冲与第一个THz脉冲产生的自旋波的相位相反, 此时第二个THz控制脉冲会相干抵消第一个脉冲产生的效应, 实现对自旋波的相干相消. 全THz相干操控技术可以在反铁磁晶体中选择性地激发或湮灭任意模式的自旋波, 从而实现自旋的相干操控.图4(a) —(c) 所示为双THz脉冲激发下得到的THz透过${\rm{DyFe}}{{\rm{O}}_{\rm{3}}}$ 单晶后的时域波形图, 两个THz脉冲的间隔时间为$\Delta t$ . 图4(a) 和图4(b) 分别对应qFM和qAFM模式. 当$\omega \cdot \Delta t/{\text{π}} = 3$ (奇数), 两个自旋波将相干相消, 如图4(a) 和图4(b) 中的黑色曲线所示. 当THz脉冲的电场分量与样品的a 轴呈45°时, 可以同时观察到0.38 THz和0.52 THz两个频率, 表明单个THz脉冲同时激发qFM和qAFM模式. 采用双THz脉冲技术, 改变$\Delta t$ 为qFM模式振荡周期的1.5倍($\Delta t = {\rm{1}}{\rm{.5}}{T_{{\rm{qFM}}}}$ )时, 如图4(c) 中的蓝色曲线, 此时第二个THz脉冲将抑制qFM模式, 同时加强qAFM模式, 如图4(d) 中蓝色曲线所示; 当$\Delta t = {\rm{1}}{\rm{.5}}{T_{{\rm{qAFM}}}}$ 时, qAFM模式被抑制, qFM模式得到加强, 如图4(d) 中红色曲线所示.图 4 (a) THz脉冲激发qFM模式; (b) THz脉冲激发qAFM模式; (c) THz脉冲同时激发qFM和qAFM模式, 当Δt 为qFM(qAFM)振荡周期的1.5倍时, 该自旋进动被有效地抑制; (d)图(c)中振荡部分的傅里叶变换光谱Figure4. (a) THz pulses excite qFM mode; (b) THz pulse excited the qAFM mode; (c) THz pulse excites both qFM mode and qAFM mode, as the interval time is 1.5 times of the qFM (qAFM) oscillation period, the spin precession is suppressed; (d) Fourier transform spectra of the oscillating parts in (c).${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ 晶体本征的介电各向异性, 通过选择THz脉冲和晶体光轴间的夹角$\theta $ , 可实现单THz脉冲在晶体中的相干控制. 图5(a) 为在不同方位角$\theta $ 的情况下, THz波透过${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ 晶体后时域谱上的电场分量. $\theta $ 定义为THz的偏振方向与晶体b 轴间的夹角. $\theta = 0^\circ $ 和$\theta = {\rm{9}}0^\circ $ 分别对应于THz的电场分量沿着b 轴和a 轴. ${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ 晶体的双折射会导致沿着晶体的b 和a 轴的THz脉冲间存在时间延迟. 当$\theta = {\rm{45}}^\circ $ 时, THz脉冲将历经最大的各向异性. 从实验数据得到${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ 晶体的双折射$\Delta n = {n_a} - {n_b} \approx 0.2$ . 图5(b) 为${\rm{YFe}}{{\rm{O}}_{\rm{3}}}$ 晶轴和入射THz脉冲偏振方向间不同夹角时的振荡信号, 实线为通过指数衰减的正弦函数的拟合结果. 实验结果表明, 准铁磁共振信号(0.3 THz)的振幅和相位都强烈依赖于方位角$\theta $ , FID信号的振幅改变了近一半, 相位移动了近$\pi /{\rm{2}}$ .图 5 当$\theta $ = 0°, 45°, 90°时, 透过样品后THz波的电场强度, $\theta $ 的定义如插图所示; (b)振荡部分的放大, 其时域区间为10?25 ps范围内的THz电场, 实线是单指数衰减拟合; (c), (d) qFM模式自旋振荡部分的傅立叶变换得到振幅和相位随方位角$\theta $ 的变化[17 ] Figure5. (a) THz electric fields transmitted through the YFeO3 , as $\theta $ = 0°, 45° and 90°; (b) the oscillating parts of the (a) from 10 ps to 25 ps, the solid line is a single exponential decay fitting; (c) amplitude and (d) phase varies with the angle $\theta $ , by using the Fourier transform of the spin oscillating of qFM mode [17 ] . Reproduced with permission from Ref.[17 ]${{E}}_{{\rm{THz}}}^{{\rm{in}}}$ )以任意方位角入射晶体. 通过各向异性晶体后, 输出的THz脉冲(${{E}}_{{\rm{THz}}}^{{\rm{out}}}$ )由两个正交分量${{{E}}_a}$ 和${{{E}}_b}$ 组成${{E}}_{{\rm{THz}}}^{{\rm{out}}} = {{{E}}_a} + {{{E}}_b}$ . 这两个正交的THz脉冲的磁场分量${{{B}}_{a,b}} = {{{{{E}}_{a,b}}} / c}$ 将各自激发频率都为0.3 THz的FM共振模式. 对于这两个自旋波而言: 1)晶体的各向异性系数${\alpha _{a,b}}$ 决定自旋波的衰减, 导致投影在a 轴和b 轴上的电场分量具有不同的振幅; 2)各向异性的折射率${n_{a,b}}$ 决定了自旋波在a 轴和b 轴上具有不同的相位. 两个子自旋波通过整个晶体过程中, 所积累的不同相位和不同的振幅. 由于干涉, 最终导致磁自由感应衰减信号的振幅加强或削弱, 即实现了相干控制效应. 水平方向上THz场的振幅随方位角度$\theta $ 的依赖关系可以写为$\Delta \alpha = {\alpha _a} - {\alpha _b}$ , $\Delta \varGamma = {\varGamma _a} - {\varGamma _b} = \dfrac{{\omega d}}{c}\Delta n$ 分别是THz脉冲在两个正交分量上的(即两个子自旋波间的)吸收系数差和相位延迟. (3 )式成为新的相干控制方程, $\theta $ 成为一个新的控制参数. 图5(c) 和图5(d) 中, 空心符号分别表示实验测得的FM模式自旋波FID信号的振幅(${{{E}}_{{\rm{FM}}}}$ )和相位随方位角$\theta $ 的依赖关系. 所得信号的相位移动和理论预言的最大值$\Delta \varGamma = - 1.47{\text{π}}$ 符合得很好. 自由感应衰减信号的角度依赖关系表现出的振幅调制因子达到二分之一. 图5(c) 中的实线表示归一化后的相干控制方程(3 )式. 图5(c) 中的虚线表示仅包含折射率的各向异性(设${\alpha _a} = {\alpha _b} = 0$ ), 点线表示仅包含吸收的各向异性(设${n_a} = {n_b}$ ). 可以清晰地区分折射率和吸收系数各自的贡献.4.稀土元素的THz激发跃迁 除了对${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的自旋波激发与相干控制, ${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 离子(${\rm{4}}{{\rm{f}}^{11}}$ )占据了晶体中低对称性的位置. 晶体场将导致${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 离子的能级劈裂, 形成了Kramers双重态, 每一个双重态由一对时间反演态组成. 当在低温下, 施加一个外加的静态磁场${{{H}}_{{\rm{DC}}}}$ , 最低的两个时间反演态之间的跃迁可以解释为离子的电子顺磁共振(EPR). 在经典物理图像中, EPR代表自旋绕${{{H}}_{{\rm{DC}}}}$ 的拉莫进动.图6(a) 描述的是Er3+ 离子在多重效应下的能级图. 自由空间中的Er3+ 离子能级标记为2S+1 LJ , 其中S 和L 分别是总的自旋和轨道量子数, J = L + S 为总的角动量量子数. 由于晶体结构具有低的对称性, 除了Er3+ 离子的Kramers简并, 晶体场效应使有关磁量子数m 的能级退简并. 图中用$\left| {i = {\rm{1}}} \right\rangle,\left| {i = {\rm{2}}} \right\rangle,\left| {i = {\rm{3}}} \right\rangle $ 代表每一个晶体场能级, 它们由一对时间反演态组成. 即使在零磁场下, 由于破坏时间反演对称性的${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}{\rm{ - E}}{{\rm{r}}^{{\rm{3 + }}}}$ 磁交换作用, 他们也将发生交换劈裂成为非简并的. 进一步沿着不同的晶轴施加外磁场${{{H}}_{{\rm{DC}}}}$ , 出现不同的Zeeman劈裂图案.图 6 (a) ErFeO3 中的Er3+ 离子由于多重效应的能级分裂示意图; (b)从0 T到10 T不同磁场下的吸收系数谱, 白色虚线为Fe3+ 的qFM磁振模式; (c)计算得到不同磁场下晶体场的双重态$\left| {i = 1} \right\rangle $ 和$\left| {i = 2} \right\rangle $ [22 ] Figure6. (a) Energy level splitting scheme of ${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ ions due to multiple effects; (b) absorption coefficient spectra at various magnetic fields from 0 T to 10 T, the white dashed line is the ${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ qFM magnon mode; (c) calculated energy levels for the$\left| {i = 1} \right\rangle $ and $\left| {i = {\rm{2}}} \right\rangle $ crystal-field doublets as a function of magnetic field[22 ] .图6(b) 为不同磁场下c 切${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ 的吸收光谱, 实验条件为${{{H}}_{{\rm{THz}}}}\parallel b$ , ${{{H}}_{{\rm{DC}}}}\parallel c$ , T = 30 K. ${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 的吸收谱线可以分成两类. 图6(b) 中标记为“A”的谱线在低的磁场下处于THz系统的可探测带宽之下. 随${{{H}}_{{\rm{DC}}}}$ 的增加而发生蓝移, 在高的外磁场下变得十分清晰. 谱线“A”是${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 离子的EPR, 对应于$\left| {{\rm{1}} - } \right\rangle \to \left| {{\rm{1 + }}} \right\rangle $ 能级跃迁. 在吸收谱上并没有观察到$\left| {{\rm{2}} - } \right\rangle \to \left| {{\rm{2 + }}} \right\rangle $ 的跃迁(图6(c) 中的“B”谱线), 这是由于当前的实验温度30 K, $\left| {i = {\rm{2}}} \right\rangle $ 能级上还没有足够的布居数. 此外, 图6(b) 中标记为1, 2, 3, 4的一组谱线描述的是, 零磁场下位于1.4 THz处的强吸收带在磁场${{{H}}_{{\rm{DC}}}}$ 作用下分裂成多个峰, 如图6(c) 所示. 这一组谱线代表的是两个Kramers双重态之间的晶体场跃迁, 即$\left| {{\rm{1}} - } \right\rangle \to \left| {{\rm{2}} - } \right\rangle $ 跃迁(线1), $\left| {{\rm{1 + }}} \right\rangle \to \left| {{\rm{2}} - } \right\rangle $ 跃迁(线2), $\left| {{\rm{1}} - } \right\rangle \to \left| {{\rm{2 + }}} \right\rangle $ 跃迁(线3), 和$\left| {{\rm{1 + }}} \right\rangle \to \left| {{\rm{2 + }}} \right\rangle $ 跃迁(线4). 此外, 在${{{H}}_{{\rm{DC}}}} = 0$ 时, 中心频率为1.9 THz的晶体场跃迁谱线属于$\left| {i = {\rm{2}}} \right\rangle \to \left| {i = {\rm{3}}} \right\rangle $ 跃迁. 图中, 0.45 THz的吸收谱线(以白色虚线标记)是${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的准FM磁子. 由于极强的磁各向异性, 它在外加磁场的作用下并不发生移动. 除了${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 离子, 在${\rm{TmFe}}{{\rm{O}}_{\rm{3}}}$ [39 ] 和${\rm{PrFe}}{{\rm{O}}_{\rm{3}}}$ 中都观察到了稀土离子由于THz诱导的晶体场跃迁.5.磁相互作用中Dicke协作耦合 N 个二能级原子与单个光场的相互作用是量子光学中研究最广泛的多体问题, Dicke首次分析了其在超辐射背景下的相互作用. 这类系统的一个共同特征是其耦合强度加强了$\sqrt N $ 倍. 美国Rice大学Kono教授和上海大学曹世勋教授团队合作, 发现在${{\rm{Y}}^{{\rm{3 + }}}}$ 掺杂的${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ 单晶样品(${\rm{E}}{{\rm{r}}_x}{{\rm{Y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ )中存在类似于典型的光与物质相互作用的效应. 以物质-物质相互作用形式出现协作耦合加强, 实验结果表明找到了自旋与真空磁子的关联交换耦合的实验证据. 这与在一个光学腔中, 二能级原子系统与真空光场耦合类似.图7 所示, 实验系统研究了Y3+ 掺杂比例、温度、外加磁场依赖的THz吸收光谱. 图7(a) —(k) 所示为不同温度${\rm{E}}{{\rm{r}}_x}{{\rm{Y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 晶体的吸收光谱, 实验构置为${{ H}_{{\rm{THz}}}}\parallel b$ , ${{ H}_{{\rm{DC}}}}\parallel c$ . 可以明显观察到在吸收光谱上, 磁子与EPR的免交叉行为. 当未耦合的磁子和EPR模式的频率相等时, 定义此时外加磁场的大小为零调谐磁场${H_0}$ , 此时的频率为零调谐跃迁频率${\omega _{\rm{0}}}$ . 当磁场为${H_0}$ 时, 光谱中杂化分支间的频率分裂称为拉比劈裂$\varOmega $ (${H_0}$ ), 大小等于磁子-EPR耦合强度$\varLambda $ 的两倍. $\varLambda $ 随温度的降低而增加, 表明Fe3+ -Er3+ 耦合变得更强.图 7 Er3+ 的自旋和Fe3+ 的qFM真空磁子间关联耦合的实验验证 (a)?(k)不同温度和Y3+ 掺杂时的吸收光谱, 图中的虚线用来帮助识别杂化模式; (l)耦合系数Λ 正比于$\sqrt {{\eta _{{\rm{spin}}}}{\omega _{{\rm{FM}}}}} $ , 图为两种机制来决定实验中的${\eta _{{\rm{spin}}}}$ [22 ] Figure7. Experimental evidence for cooperative coupling between paramagnetic ${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ spins and ${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ vacuum magnons: (a)?(k) Absorption spectra measured at various temperatures and ${{\rm{Y}}^{{\rm{3 + }}}}$ doping levels, dashed black lines are guides to the eye for identifying the hybridized modes; (l) the coupling rate Λ is proportionality with$\sqrt {{\eta _{{\rm{spin}}}}{\omega _{{\rm{FM}}}}} $ , the inset shows two types of mechanisms that determine ${\eta _{{\rm{spin}}}}$ in the measurements[22 ] . Reproduced with permission from Ref.[22 ].$\varLambda $ 如何随晶体中${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 自旋密度的变化, 实验中采用的是${{\rm{Y}}^{{\rm{3 + }}}}$ 掺杂的${\rm{E}}{{\rm{r}}_x}{{\rm{Y}}_{1 - x}}{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 体系. 先前的文献已经报道, 通过改变比例系数x , 非磁性的${{\rm{Y}}^{{\rm{3 + }}}}$ 离子能简单地减少${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 的自旋密度, 且并不改变样品的晶体结构和磁结构. 如图7(f) —(h) , (i) —(k) 显示的是x = 0.75(x = 0.5)样品温度依赖的免交叉光谱线, 同样发现$\Lambda $ 随温度的降低而增加的规律. 此外, 比较图7(c) , 7(f) , 7(i) 可见, 当样品温度为20 K, ${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 离子比例高的样品具有更大的$\varLambda $ . 当样品温度为10 K(图7(d) , 7(g) 和7(j) )和5 K(图7(e) , 7(h) 和7(k) ), 都能观察到掺杂浓度的依赖关系具有相同的变化趋势. 值得注意的是, x = 0.5的样品体系在温度为5 K时具有最大的${\varLambda / {{\omega _{\rm{0}}}}}$ =0.18, 此时的材料系统进入超强耦合范畴[44 ,45 ] . 实验发现, Λ 正比于两个量乘积的平方根, 即$\varLambda \propto \sqrt {{\eta _{{\rm{spin}}}}{\omega _{{\rm{FM}}}}} $ , 式中的${\eta _{{\rm{spin}}}}$ 是对EPR产生贡献的${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 净自旋密度(与T , ${H_0}$ 和x 有关), ${\omega _{{\rm{FM}}}}$ 是${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的qFM磁子频率.图7(l) 插图所示, ${\eta _{{\rm{spin}}}}$ 由两种机制所决定. 首先, 低温下的${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 离子可以近似认为是二能级系统, 遵循玻尔兹曼分布. 温度为T 时, 自旋向上($\left| {{\rm{1 + }}} \right\rangle $ )和自旋向下($\left| {{\rm{1}} - } \right\rangle $ )态的热力学分布遵循居里定律, $\dfrac{{\left\langle {{\mu _{{\rm{Er}}}}} \right\rangle }}{{{\mu _{{\rm{sat}}}}}} = {\rm{tanh}}\left( {\dfrac{{ - \Delta E\left( {T,{H_{\rm{0}}}} \right)}}{{2{{\rm{k}}_{\rm{B}}}T}}} \right)$ , 其中$\left\langle {{\mu _{{\rm{Er}}}}} \right\rangle $ 是每个${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 自旋的平均磁矩, ${\mu _{{\rm{sat}}}}$ 是每个${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 自旋的饱和磁矩; 相应于T = 0时的情形, 此时所有的${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 离子占据$\left| {{\rm{1}} - } \right\rangle $ 态; $\Delta E\left( {T,H_0} \right)$ 是$\left| {{\rm{1 + }}} \right\rangle $ 和$\left| {{\rm{1}} - } \right\rangle $ 态之间温度依赖和${H_0}$ 依赖的能级间隔; ${k_{\rm{B}}}$ 为玻尔兹曼常数. 因此, $\left\langle {{\mu _{{\rm{Er}}}}} \right\rangle $ 随温度的下降而单调地增加. 此外, 通过稀释效应(调节比例因子x ), 非磁性的${{\rm{Y}}^{{\rm{3 + }}}}$ 掺杂将降低${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 的自旋密度. 结合这两种机制, 所得的净${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 自旋密度随温度、磁场、掺杂浓度的关系写为${\eta _{{\rm{spin}}}} \equiv x \cdot \dfrac{{\left\langle {{\mu _{{\rm{Er}}}}} \right\rangle }}{{{\mu _{{\rm{sat}}}}}} = x \cdot \tanh \left( { - \dfrac{{\Delta E}}{{{\rm{2}}{k_{\rm{B}}}T}}} \right)$ 为贡献EPR自旋的比例系数, 此外, $n_{{\rm{spin}}}^0 \equiv {2}/{{{V_{\rm{0}}}}}$ 是体积为${V_{\rm{0}}}$ 单胞中总的${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 自旋密度.图7(a) —(k) 所示的光谱曲线, 提取出所有免交叉谱线中可分辨的$\varLambda $ 值. 在图7(l) 给出了$\varLambda $ 与计算得到的$\sqrt {{\eta _{{\rm{spin}}}}{\omega _{{\rm{FM}}}}} $ 的一一对应关系. 如图7(l) 所示, 所有的数据点落在一条穿过原点的直线上. 这一比例行为证实了${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 自旋关联地与${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的真空磁子场耦合.[46 ] 发展了一种微观理论模型, 对于${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 子系统, 遵循Herrmann的处理方法. 哈密顿量${\hat H_{{\rm{Fe}}}}$ 考虑两个子晶格自旋${ S}_{2l - 1}$ 和${ S}_{2l}$ 的对称交换相互作用、反对称交换相互作用和磁各向异性, 其中晶胞指数l = 1,2…${N_{{\rm{uc}}}}$ (${N_{{\rm{uc}}}}$ 是晶胞的总数). 对于${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 子系统, 可以以第l 个晶胞内${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 自旋${{R}}_ {\rm{l}}$ 的拉莫进动来模拟EPR的$\left| {{\rm{1}} - } \right\rangle \to \left| {{\rm{1 + }}} \right\rangle $ 跃迁. EPR的哈密顿量${\hat H_{{\rm{Er}}}} = {\sum\nolimits_{{\rm{l}} = 1}^{{N_{{\rm{UC}}}}} { - \hat { \mu} } _{\rm{1}}} \cdot {\mu _{\rm{0}}}{{{H}}_{{\rm{DC}}}}$ , 其中磁矩表示为各向异性朗德因子g 和${{{R}}_{\rm{1}}}$ 的点积, ${\hat {{\mu}} _{\rm{1}}} = g \cdot {{{R}}_{\rm{1}}}$ ; ${\mu _{\rm{0}}}$ 是真空磁导率. ${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}} - {\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 的耦合哈密顿量写成${J_{\rm{1}}}$ 和${J_{\rm{2}}}$ 是对称交换常数, ${{{D}}_{\rm{1}}}$ 和${{{D}}_{\rm{2}}}$ 为反对称交换常数. 由总的哈密顿量$\hat H = {\hat H_{{\rm{Fe}}}}{\rm{ + }}{\hat H_{{\rm{Er}}}}{\rm{ + }}{\hat H_{{\rm{Fe - Er}}}}$ , 得到${J_{\rm{1}}}{\rm{ = }}{J_{\rm{2}}}{\rm{ = }}J$ , $\gamma $ 是旋磁比, ${J_{{\rm{Fe}}}}$ 是${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 的自旋之间各向同性的交换常数, $\hbar $ 为普朗克常数除以2π. 通过(6 )式拟合$\Lambda $ 的斜率得到交换常数J = 2.95 meV.6.THz磁子-极化子 最近, 莫斯科科技大学的Grishunin、上海大学马国宏以及内梅亨大学的Kimel等人的合作研究表明, 稀土正铁氧体中的时间分辨THz磁共振光谱必须考虑电磁波在材料中的传播效应[47 ] . 以THz波在TmFeO3 中的传播为例, 实验发现当THz波的频率与qAFM模式的自旋共振频率接近时, 磁子-极化子(magnon-polaritons)扮演了一个重要的角色.图8(a) 和(b) 所示, TmFeO3 的温度为40 K, 图中的振荡曲线为THz透射脉冲及其回波之间的THz自由感应衰减信号的时域和频域信号. 红色圆圈为实验结果, 黑色实线为理论计算结果. 图8(c) 和(d) 显示的是TmFeO3 样品薄片在激光辐照下发射的THz脉冲电场的时域谱和频谱. THz透射和发射实验结果都表明, 样品在40 K的自旋动力学表现为略高于和略低于qAFM共振频率两个模式的拍频信号. 通过建立模型描述TmFeO3 的自旋与THz脉冲的相互作用, 理论结果表明这两个频率为磁极化子的上下边带, 如图8(e) 所示.图 8 (a) 透过TmFeO3 晶体的THz时域波形及其(b)傅里叶变换谱; (c) TmFeO3 薄片的THz产生波形及其相应的(d)傅里叶变换谱; (e)自旋共振附近的磁子-极化子色散关系[47 ] Figure8. (a) THz waveforms transmitted through the TmFeO3 sample and (b) its Fourier transforms of the time traces; (c) THz generation in a TmFeO3 slab by a laser pulse and (d) its Fourier spectra shown in (c); (e) the magnon-polariton dispersion in the vicinity of the spin resonance[47 ] . Reproduced with permission from Ref.[47 ]k 垂直于界面. THz脉冲透过一个厚度为d 的样品薄层, 其相对介电常数和磁导率分别是ε 和$\mu (\omega )$ . 在频谱上的耦合波方程写为Ex 为电场时域信号的傅里叶变换, 波矢$k = \dfrac{\omega }{c}\sqrt {\varepsilon \mu \left( \omega \right)} $ . 最终求得透过样品的光谱和入射样品的光谱之比为k 0 是空气中的波矢, k 1 为材料中的波矢, d 是样品的厚度, $E\left( \omega \right)$ 为入射THz脉冲的归一化光谱振幅. 对于材料的磁导率, 用标准Drude-Lorentz形式表示为${\omega _0}$ 为共振频率, $\Delta \omega $ 为吸收线宽, $\Delta \mu $ 为有效振荡强度. 当${\omega _0} = 0.86$ THz, d = 1.5 mm, 其他参数为$\Delta \omega = 8.6{\rm{GHz}}$ , $\Delta \mu = {10^{ - 3}}$ , $\varepsilon = 22 - 0.26i$ , 并将入射的THz脉冲的光谱取逆傅里叶变换代入(9 )式中, 可以得到透过样品的THz脉冲的时域和频域波形, 实验结果表明理论模型与实验结果符合得很好.7.总 结 随着THz光谱技术的不断发展, 基于$R{\rm{Fe}}{{\rm{O}}_{\rm{3}}}$ 晶体的交换相互作用的超快光学调控, 对磁学的基础研究具有重要的意义. 本文主要介绍了THz脉冲的磁场分量实现反铁磁晶体中两类自旋模式的“非热”激发、相干控制、实现自旋重取向的可视化的研究进展. 特别介绍了最近发现固体中稀土铒离子自旋系综与铁离子磁振子间的协同耦合效应表现为真空拉比劈裂特性. ${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 和${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 耦合强度与稀土离子${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ 的浓度依赖关系满足迪克模型. 由此得出的${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 和${\rm{E}}{{\rm{r}}^{{\rm{3+}}}}$ 交换耦合常数为人们更加深刻地理解3d-4f电子的磁耦合导致的新奇效应提供了重要的实验和理论证据. 此外, 介绍了磁子-极化子(magnon-polaritons)对于THz波在TmFeO3 中的传播具有重要的影响. 这两项工作为利用量子光学中的概念去理解和控制凝聚态物质中的新物相提供了新的途径. 



























 图 1 (a) RFeO3反铁磁晶体晶体结构与自旋结构, 邻近的
图 1 (a) RFeO3反铁磁晶体晶体结构与自旋结构, 邻近的























































 图 2 (a), (b)分别为激发qFM模式(红色)与qAFM模式(蓝色)时的THz时域透射谱, 插图为振荡部分的放大图; (c), (d)分别为振荡部分的傅里叶变换光谱
图 2 (a), (b)分别为激发qFM模式(红色)与qAFM模式(蓝色)时的THz时域透射谱, 插图为振荡部分的放大图; (c), (d)分别为振荡部分的傅里叶变换光谱










































































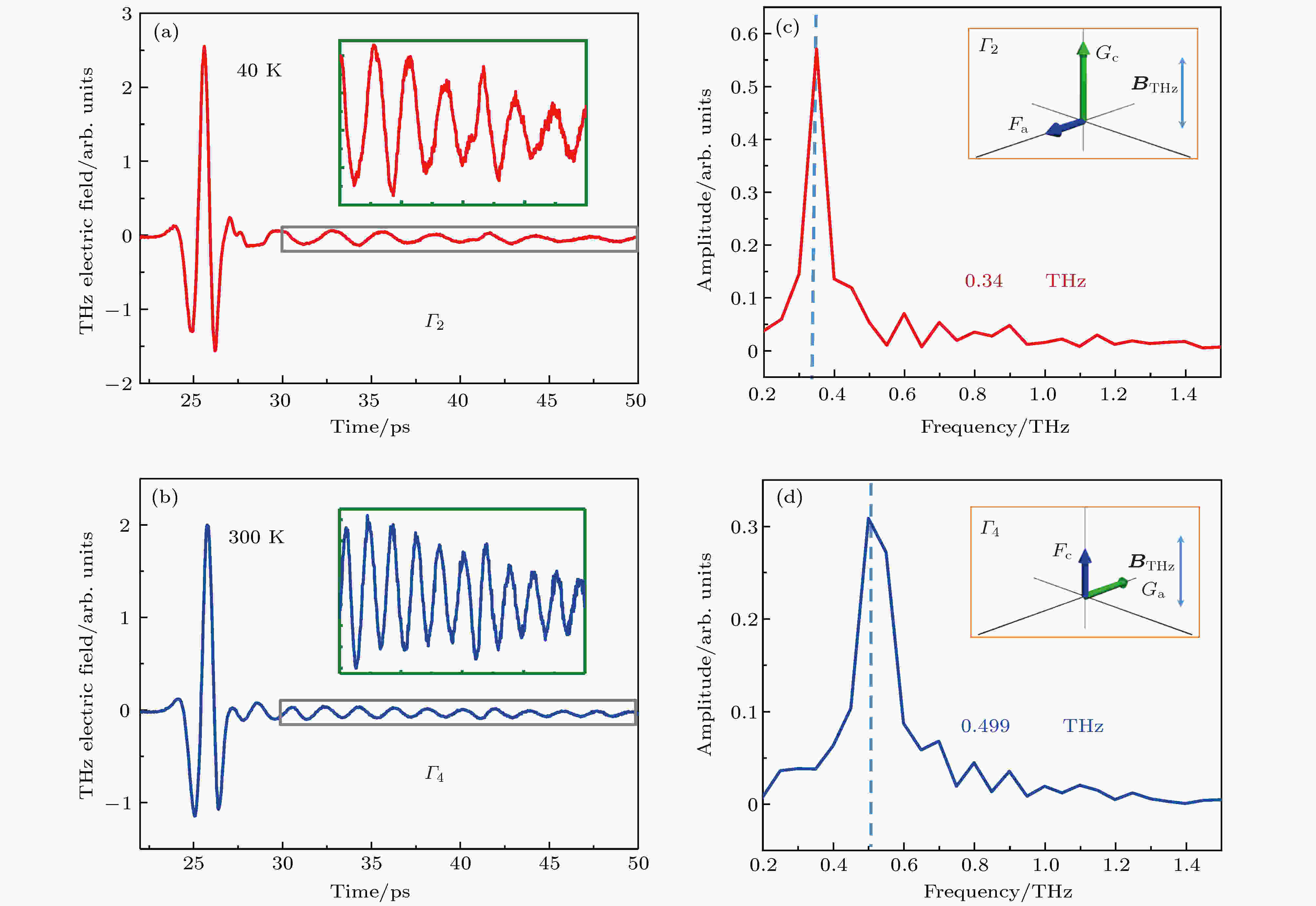 图 3 (a), (b) 40 K和300 K时
图 3 (a), (b) 40 K和300 K时
















































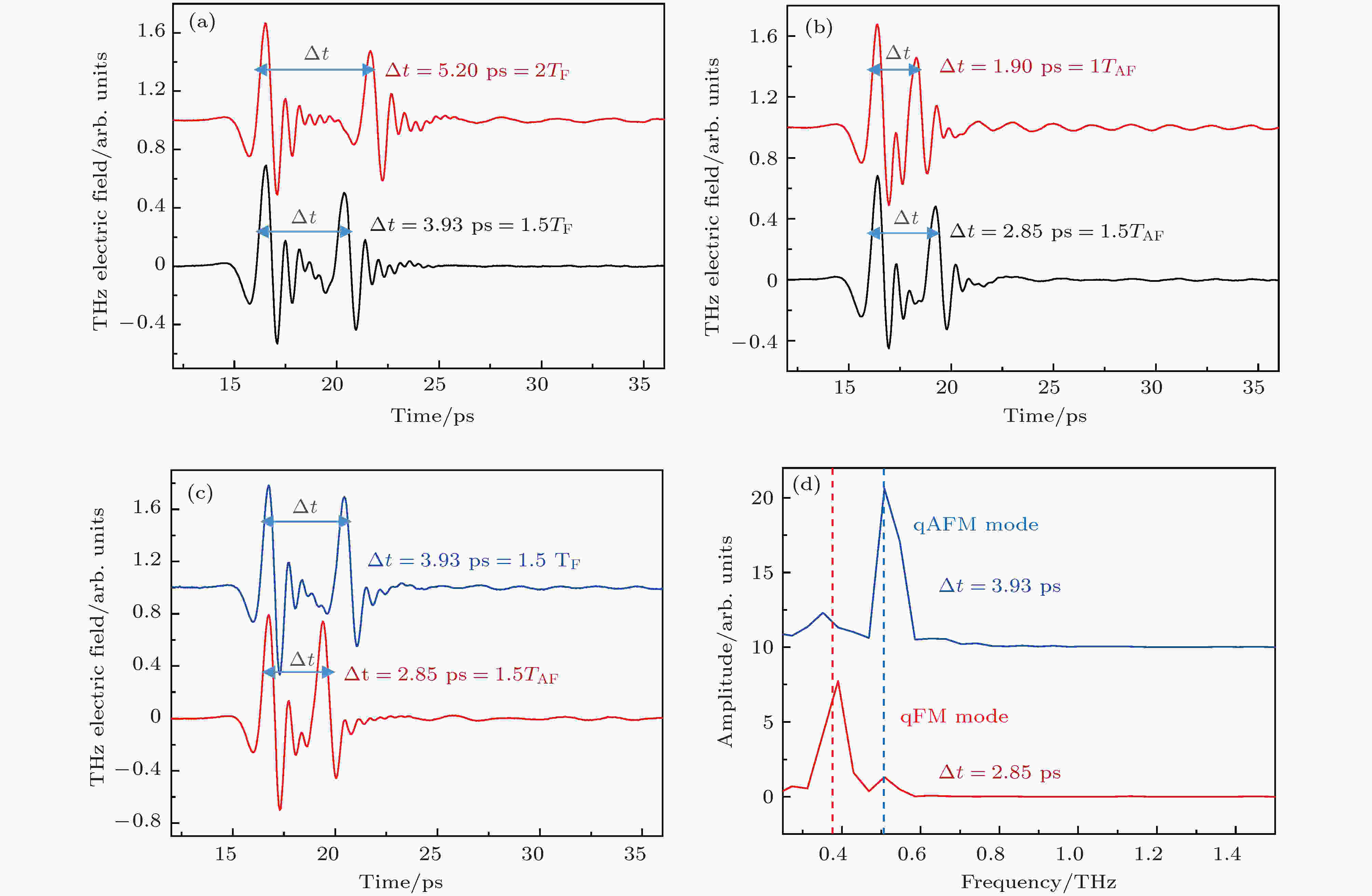 图 4 (a) THz脉冲激发qFM模式; (b) THz脉冲激发qAFM模式; (c) THz脉冲同时激发qFM和qAFM模式, 当Δt为qFM(qAFM)振荡周期的1.5倍时, 该自旋进动被有效地抑制; (d)图(c)中振荡部分的傅里叶变换光谱
图 4 (a) THz脉冲激发qFM模式; (b) THz脉冲激发qAFM模式; (c) THz脉冲同时激发qFM和qAFM模式, 当Δt为qFM(qAFM)振荡周期的1.5倍时, 该自旋进动被有效地抑制; (d)图(c)中振荡部分的傅里叶变换光谱













































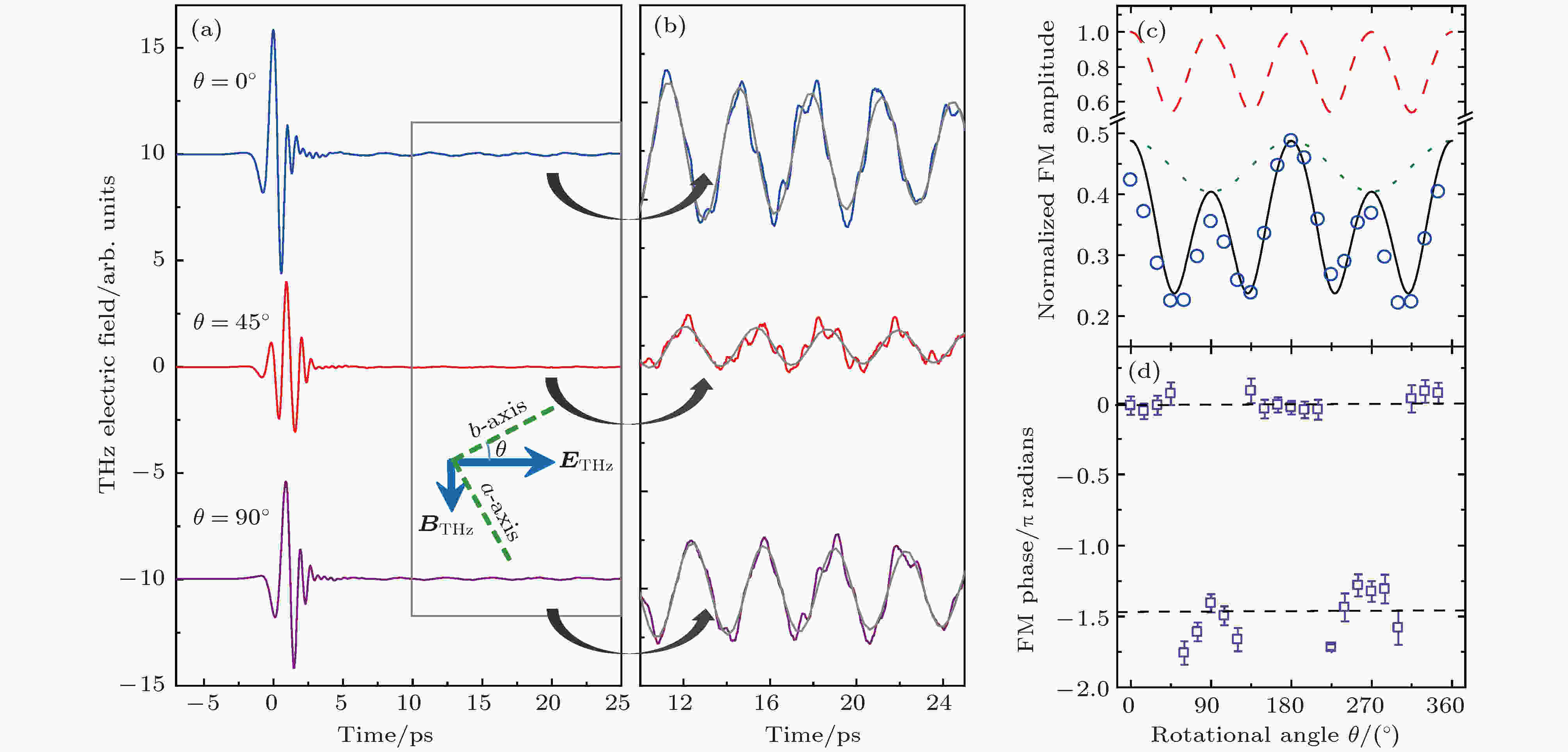 图 5 当
图 5 当












































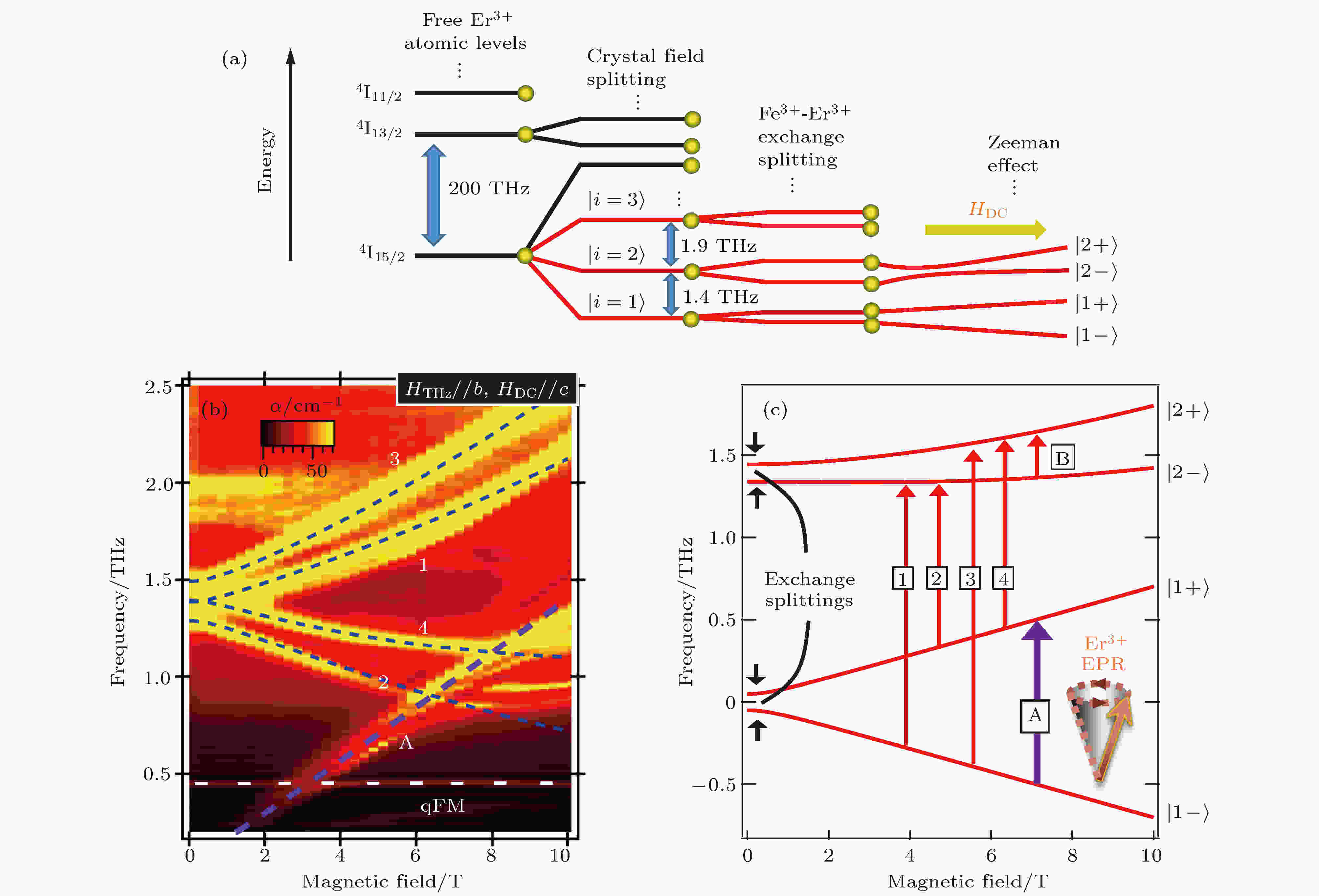 图 6 (a) ErFeO3中的Er3+离子由于多重效应的能级分裂示意图; (b)从0 T到10 T不同磁场下的吸收系数谱, 白色虚线为Fe3+的qFM磁振模式; (c)计算得到不同磁场下晶体场的双重态
图 6 (a) ErFeO3中的Er3+离子由于多重效应的能级分裂示意图; (b)从0 T到10 T不同磁场下的吸收系数谱, 白色虚线为Fe3+的qFM磁振模式; (c)计算得到不同磁场下晶体场的双重态























































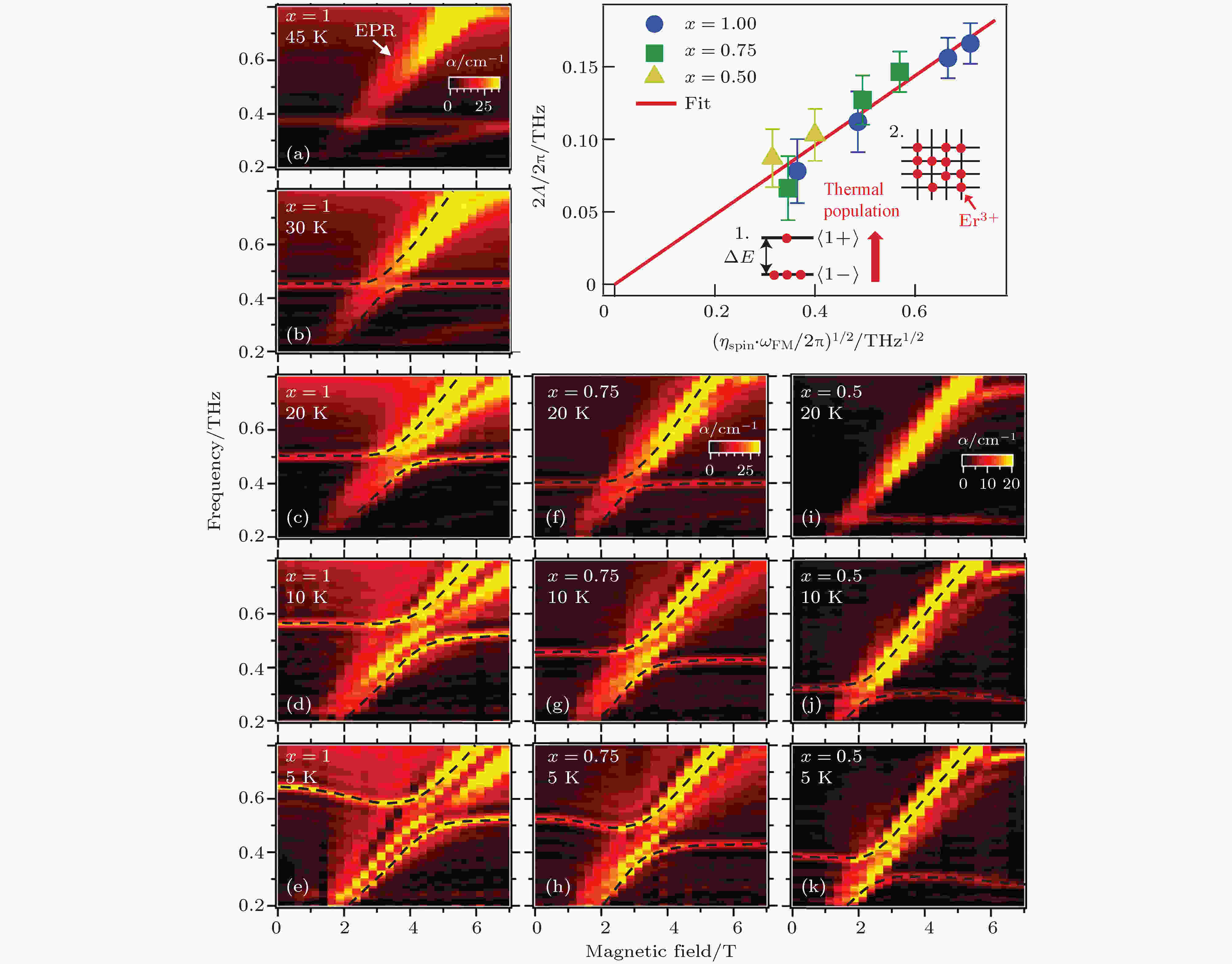 图 7 Er3+的自旋和Fe3+的qFM真空磁子间关联耦合的实验验证 (a)?(k)不同温度和Y3+掺杂时的吸收光谱, 图中的虚线用来帮助识别杂化模式; (l)耦合系数Λ正比于
图 7 Er3+的自旋和Fe3+的qFM真空磁子间关联耦合的实验验证 (a)?(k)不同温度和Y3+掺杂时的吸收光谱, 图中的虚线用来帮助识别杂化模式; (l)耦合系数Λ正比于











































































































































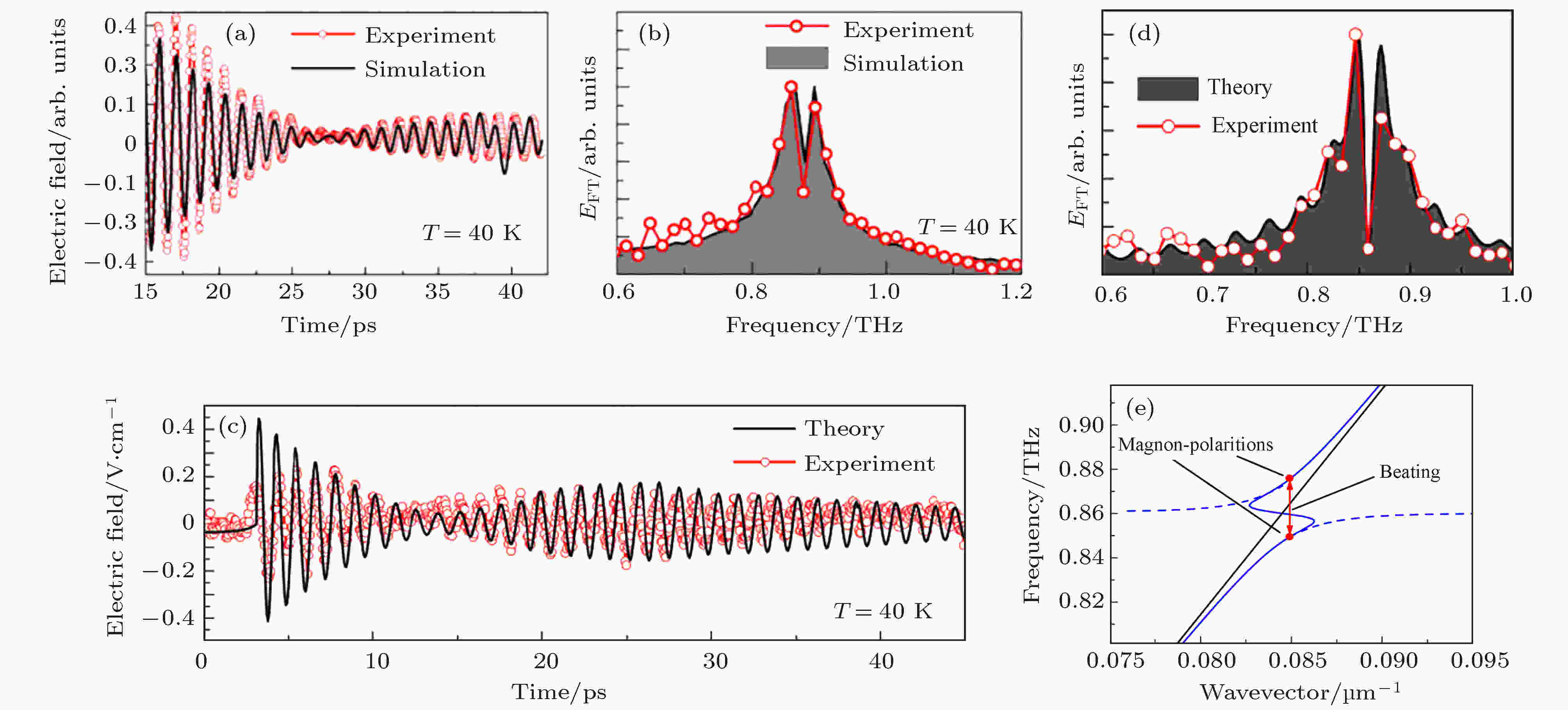 图 8 (a) 透过TmFeO3晶体的THz时域波形及其(b)傅里叶变换谱; (c) TmFeO3薄片的THz产生波形及其相应的(d)傅里叶变换谱; (e)自旋共振附近的磁子-极化子色散关系[47]
图 8 (a) 透过TmFeO3晶体的THz时域波形及其(b)傅里叶变换谱; (c) TmFeO3薄片的THz产生波形及其相应的(d)傅里叶变换谱; (e)自旋共振附近的磁子-极化子色散关系[47]



















