摘要:当直接半导体中存在强的自旋轨道耦合作用, 且材料结构不具备中心反演对称性时, Rashba效应将会出现, 从而使自旋简并的能带分裂为具有相反自旋态的两个子能带. 这两个子能带会偏离布里渊区的对称中心位置, 致使半导体呈现出间接带隙的特征. 金属卤化物钙钛矿兼具强的自旋轨道耦合和结构中心反演不对称性, 在Rashba效应研究中展现出巨大的潜力. 本文围绕钙钛矿中Rashba效应的理论研究与实验证明, Rashba效应对载流子复合的影响以及目前Rashba效应研究中出现的争论, 系统地进行回顾与梳理; 针对钙钛矿中Rashba效应的研究现状, 提出了几个目前亟待解决的问题, 并展望了该领域未来的研究方向.
关键词: 钙钛矿/
Rashba效应/
载流子复合

English Abstract

全文HTML

--> --> -->

金属卤化物钙钛矿是一类性能良好的半导体光电材料, 其三维晶体结构可表示为ABX₃ (图1)^[1,2]. 通常, A位置为甲胺(CH₃NH₃⁺)、铯(Cs⁺)等一价阳离子, B位置为铅(Pb²⁺)、锡(Sn²⁺)等二价金属阳离子, X位置为氯(Cl^–)、溴(Br^–)、碘(I^–)等卤素阴离子. 因其优异的光电性能、低廉丰富的原材料和简单的制备工艺, 近年来, 钙钛矿已成为光伏和发光领域的明星材料^[3—8]. 尤其在光伏领域, 钙钛矿太阳能电池的公证光电转化效率已经超过光伏市场上占主导地位的多晶硅等薄膜太阳能电池的最高效率, 达到24.2%^[9]. 这主要得益于钙钛矿材料高的可见光吸收系数、良好的电荷输运性能以及长的光生载流子寿命^[2,10]. 特别是后者, 相比于其他具有相似带隙宽度和吸收系数的半导体, 钙钛矿中的载流子寿命要长得多^[10—12]. 研究表明, 钙钛矿中的电子-空穴复合速率比采用朗之万(Langevin)复合模型计算的结果低4—5个数量级^[13].
图 1 金属卤化物钙钛矿的晶胞结构^[2]
Figure1. Crystal structure of the metal halide perovskite ^[2].

钙钛矿中载流子的长寿命引起了广泛的研究兴趣, 而关于其背后的物理机制, 该领域内也出现了诸多争议^[14—18]. 早期的研究认为相对较低的缺陷密度是其主要原因^[19,20], 因为它将导致钙钛矿中非辐射复合的显著降低, 从而大幅延长了载流子寿命. 然而, 进一步的研究指出, 在缺陷密度相差5个数量级的样品中, 载流子寿命仅具有一个数量级的差别^[13], 表明钙钛矿中的载流子寿命与缺陷密度的关联性并不高. 另有研究表明, 局域化导致的载流子空间分离是降低其复合速率的主要因素^[16,21]. 然而, 这种解释也有值得商榷的地方, 因为很多材料都具有较大的无序化(例如有机半导体), 但并不都表现出低的载流子复合速率. 同时, 我们注意到光子循环等机制也常被用于解释钙钛矿中载流子的长寿命^[22,23]. 2015年, Zheng等^[24]指出, 导致钙钛矿中载流子的长寿命的主要原因是Rashba效应. 如图2所示, 由于Rashba效应的存在, 钙钛矿的导带底和价带顶在k空间中将会产生一定程度的自旋劈裂, 且由于导带和价带轨道构成的不同, 导带底与价带顶的劈裂程度并不一致. 因此, 劈裂将使钙钛矿中的载流子复合表现出类似间接半导体的特性, 从而降低载流子的复合速率. 另外, 他们还认为由于导带与价带具有相反的自旋螺旋性(spin helicity), 载流子的复合还是自旋禁阻的, 这进一步降低了载流子的复合速率.
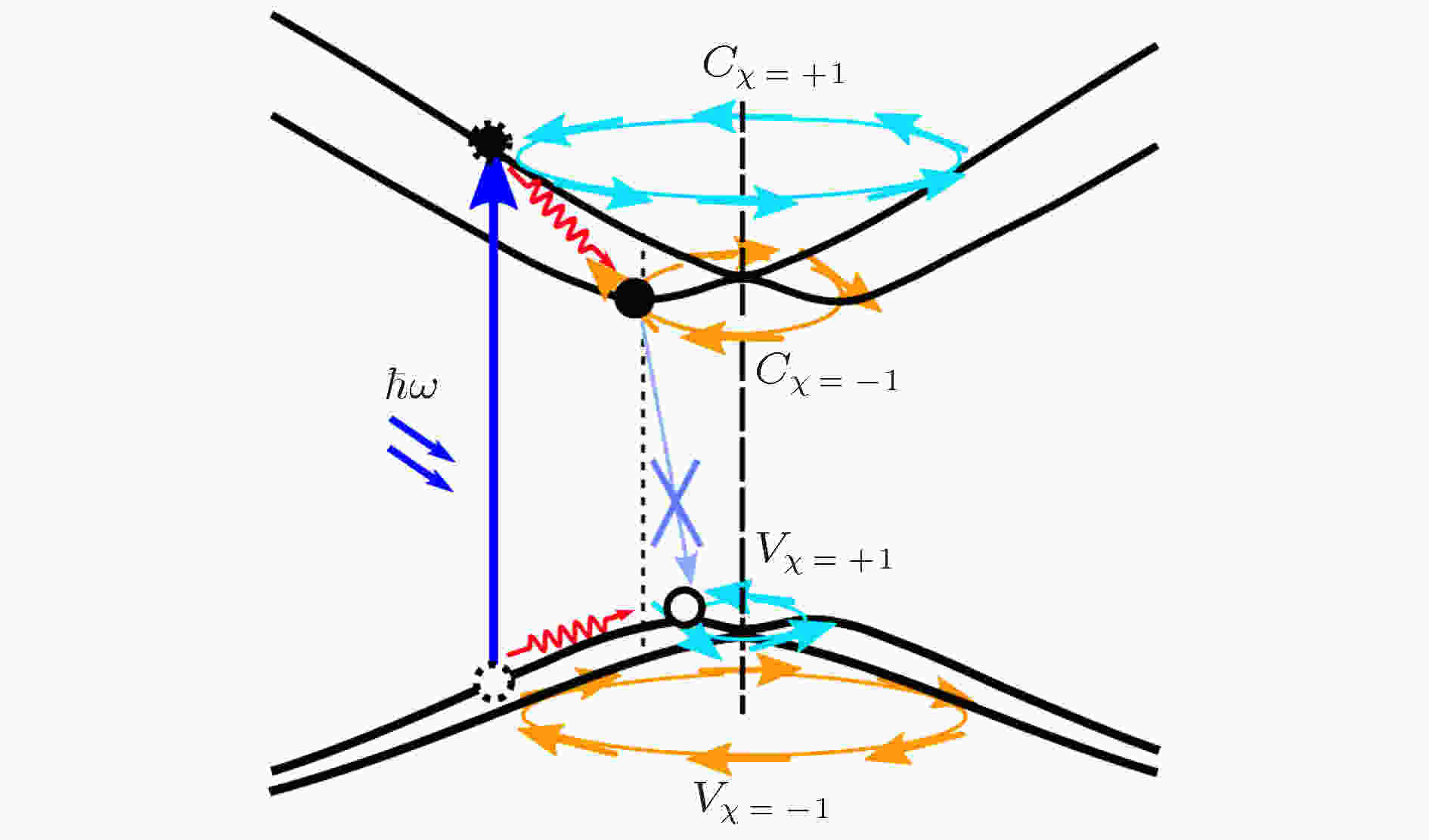图 2 钙钛矿中Rashba效应对载流子复合的影响示意图^[24]
Figure2. Schematic diagram of the impact of Rashba effect on the carriers recombination in perovskite ^[24].

接下来的几年, 针对Rashba效应及其对钙钛矿中载流子寿命的影响, 涌现出了大量研究报道^[25—36]. 综合来看, 目前的研究主要集中在钙钛矿中Rashba效应产生的原因^[25,37]、钙钛矿中Rashba效应的实验验证^[36,38]、不同条件/环境下Rashba效应对载流子复合的影响等几方面^[24,39]. 同时我们也注意到, 针对钙钛矿的Rashba效应, 一些研究者发出了不同的声音, 例如有研究者认为钙钛矿中不存在Rashba效应^[40,41], 或者说至少Rashba效应非常弱^[42]; 也有研究者认为Rashba效应不能对载流子复合产生显著影响^[43,44]等. 因此, 我们认为有必要针对钙钛矿中的Rashba效应及其对载流子复合的影响进行系统地回顾与梳理, 从而为下一步研究工作提供思路. 本文的内容安排如下: 第2节简单介绍钙钛矿中Rashba效应及相关理论研究工作; 第3节介绍Rashba效应的实验验证工作; 第4节回顾有关钙钛矿中Rashba效应对载流子复合影响的工作; 第5节阐述目前存在的一些争议; 最后, 在第6节中提出几点当前亟待解决的问题并对未来的研究进行展望.

1959年, 苏联-美国理论物理学家Emmanuel I. Rashba针对纤锌矿晶体能带的对称性发表了两篇文章^[45,46], 从而拉开了Rashba效应的研究序幕. 通常而言, 半导体的电子和空穴在导带底和价带顶的运动规律可以描述为一个k空间自旋简并的抛物线型能带, E^±(k) = $\hbar^2 { k}^2$/(2m^*)(图3(a)), 其中k是波矢, $ \hbar = h/\left( {2{\text{π}} } \right)$是约化普朗克常数, m^*是电子(或空穴)的有效质量. 然而, 如果半导体缺乏中心反演对称性, 同时又存在较强的自旋轨道耦合作用, 那么Rashba效应将会出现, 从而使自旋简并的能带在k空间中劈裂成两个自旋极化的子能带E^±(k) = $\hbar^2 k^2$/(2m^*) ± α_R|k|, 偏离布里渊区的对称中心位置, 其中的α_R被称作Rashba分裂系数(α_R = 2E_R/k₀), E_R是Rashba劈裂形成的带边与直接带隙之间的能级差, k₀是发生Rashba分裂时能带在k空间的偏移量, 如图3(b)所示^[47]. 应该指出, 除了Rashba效应, 还有一种十分类似的Dresselhaus效应^[48]. Rashba效应与Dresselhaus效应都是强的自旋轨道耦合和中心反演对称性破缺导致的能带在k空间自旋劈裂. 不同之处体现在: 引起Rashba效应的对称性破缺是结构中心反演不对称(structure inversion-asymmetric)^[49], 且分裂子带的自旋构造(spin texture)是螺旋状的(helicity); 而导致Dresselhaus效应的是体中心反演不对称(bulk inversion-asymmetric)^[50], 且分裂子带的自旋构造并不成螺旋状. 对于Dresselhaus效应, 读者可以参考文献[48, 50, 51], 本文我们仅聚焦于Rashba效应.
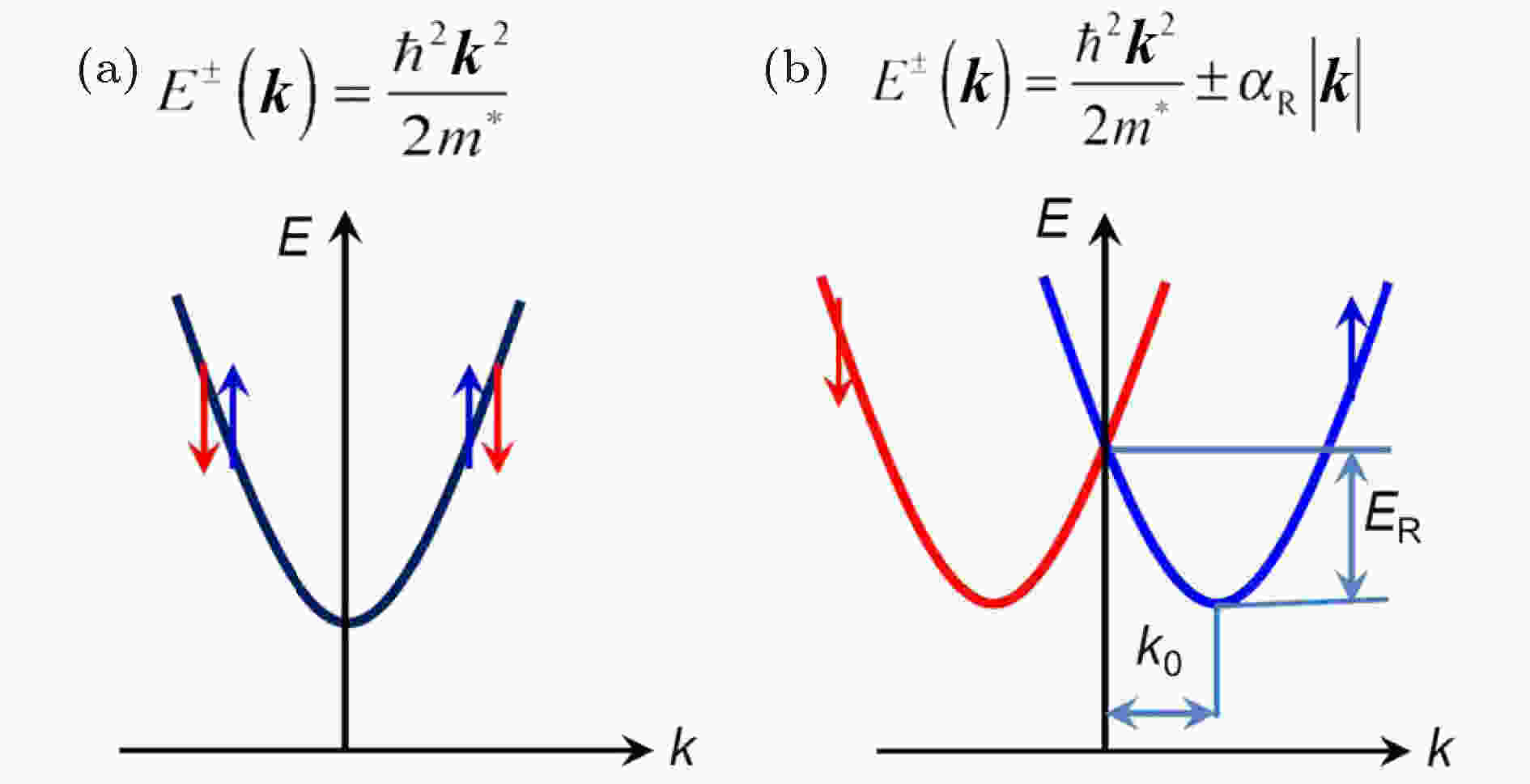图 3 Rashba效应示意图^[47]
Figure3. Schematic diagram of the Rashba effect ^[47].

由于Rashba效应高度依赖晶体的结构对称性和自旋轨道耦合强度, 因此目前已发现的具有较大Rashba效应(α_R为几个eV·?)的材料主要集中在超薄重金属薄膜^[52]、拓扑绝缘体如Bi₂Se₃^[53]以及极性半导体如BiTeI^[54]等. 这些材料的结构都不具备中心反演对称性, 同时都含有原子序数大的元素, 因此自旋轨道耦合很强(自旋轨道耦合强度与原子序数的4次方成正比). 传统的III—V族半导体的Rashba效应很弱, 例如InAlAs/InGaAs界面的Rashba分裂常数α_R只有0.07 eV·?, 其Rashba能级差E_R ≈ 1 meV^[55].
金属卤化物钙钛矿同时具备强的自旋轨道耦合和中心反演非对称性, 被认为是理想的Rashba材料^[56]. 一般认为, 室温下的三维钙钛矿(如MAPbI₃, MA为甲胺)的晶体结构为中心反演对称的四方晶系(或者立方晶系与正交晶系, 依赖于材料组分的构成). 然而, 人们发现实际上钙钛矿晶格并不是严格的中心反演对称结构^[25], 钙钛矿晶格中的铅卤素八面体[BX₆]⁴⁺略微有些扭曲^[57], 且有机阳离子A⁺也具有一定的取向性并处于快速转动的状态^[58,59]. 这些性质使钙钛矿的中心反演对称性遭到了一定程度的破坏. 同时, 由于金属卤化物钙钛矿中存在铅、锡、碘等重元素, 钙钛矿中的自旋轨道耦合作用也非常强. 例如, MAPbI₃中的自旋轨道耦合造成的导带能级位移达到1 eV以上^[1]. 鉴于以上原因, 大量的理论研究预测钙钛矿中存在很强的Rashba效应^[37,57,60].
2013年, Even等^[61]基于密度泛函理论和K·P理论计算MAPb(Sn)I₃的能带时, 发现在四方相的钙钛矿MAPb(Sn)I₃中出现了中心反演对称性破缺, 从而在带边产生了自旋劈裂—具有不同自旋态的能带偏离了钙钛矿k空间的Γ点(图4(a)). 2014年, Kim等^[57]基于紧束缚模型分析和第一性原理计算, 发现由于强的铁电性和自旋轨道耦合, 钙钛矿呈现出三维Rashba材料的性质. 他们的计算表明, 由于导带底为自旋轨道耦合态, 总角动量为J = 1/2 (自旋角动量S = 1/2和轨道角动量L = 1构成的自旋轨道耦合带的角动量为J = 3/2或1/2, 其中J = 1/2的能带能量较低); 而价带顶为纯自旋态, 角动量为J = S = 1/2. 因此Rashba效应引起的导带底和价带顶的角动量螺旋方向正好相反. 另外, 他们发现, 通过改变材料组分或外电场可以调节Rashba效应, 从而使角动量螺旋方向反转(图4(b)). 同年, Stroppa等^[37]基于对称性分析和密度泛函计算, 发现锡基钙钛矿FASnI₃ (FA为甲脒)具有铁电性, 源自具有极性的有机阳离子FA⁺在晶格中的有序排列. 他们发现, 由于FASnI₃中自旋轨道耦合作用较强, 同时材料结构不具备中心反演对称性, Rashba效应和Dresselhaus效应同时存在于材料中. 他们还指出通过控制外电场, 可以调控自旋分裂带中的自旋构造(图4(c)).
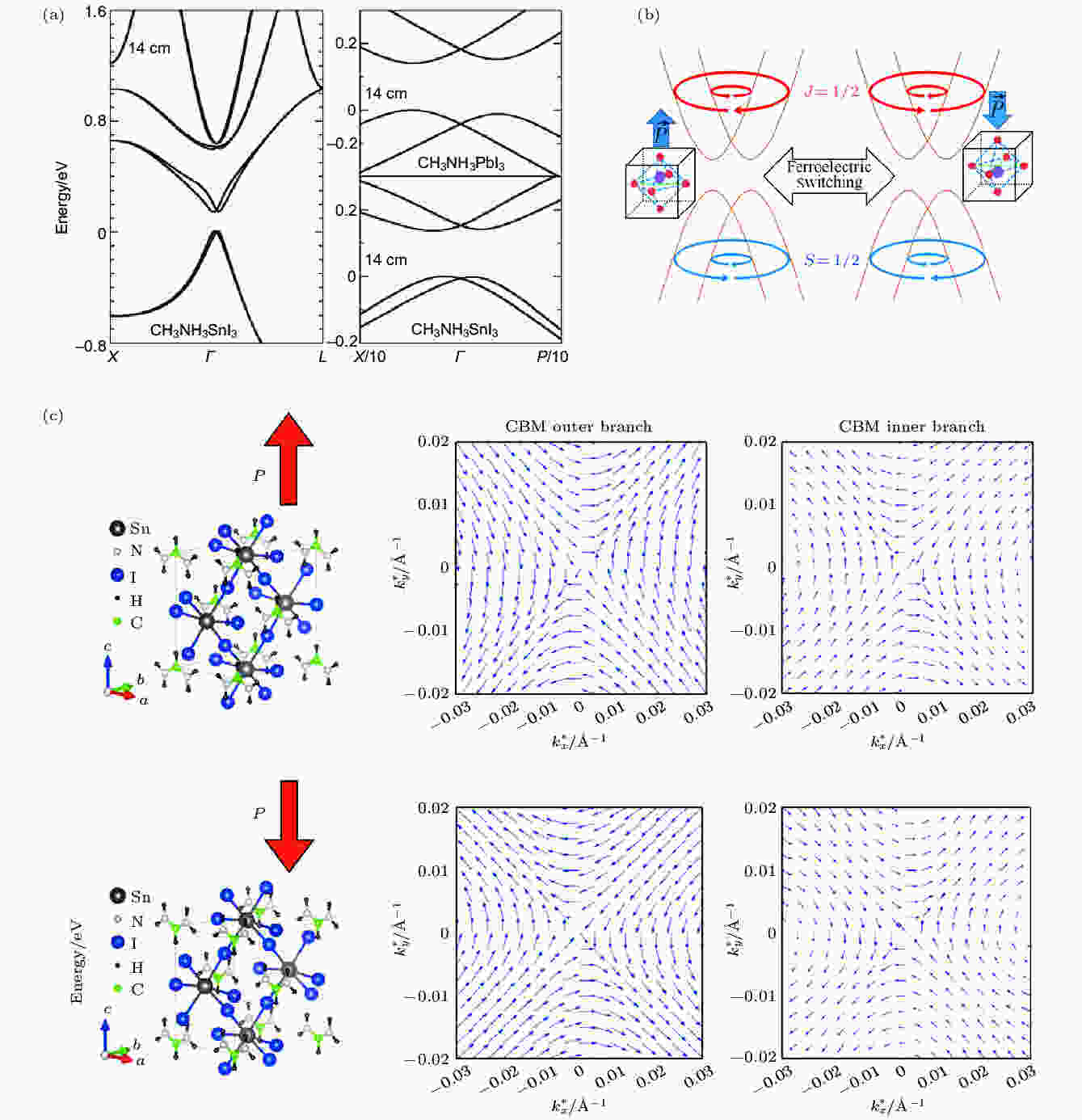图 4 (a)具有不同自旋极化的Rashba分裂子带偏离了k空间的Γ点^[61]; (b)通过调控材料的铁电性改变Rashba分裂子带的自旋螺旋性^[57]; (c)通过控制外电场调控自旋分裂子带中的自旋构造^[37]
Figure4. (a) Rashba-splitting sub-bands with different spin polarization deviate from the Γ point in the k space ^[61]; (b) changing the spin helicity of the Rashba-spliting sub-bands by tuning the ferroelectricity of the material^[57]; (c) tuning the spin texture of the spin-splitting sub-bands by controlling the external electric field ^[37].

也有研究者认为钙钛矿中的Rashba效应是动态的, 而这种动态Rashba效应既可能源自钙钛矿中A位有机阳离子的旋转, 也可能由钙钛矿晶格本身的动态扭曲所导致. 2015年, Motta等^[62]通过范德瓦耳斯修正的密度泛函计算, 发现钙钛矿中的有机阳离子对材料的电子结构起着至关重要的作用. 例如, 当甲胺离子的方向指向$ \left\langle 011 \right\rangle$时, PbI₆八面体构成的笼子将会产生一定程度的扭曲, 从而使钙钛矿成为间接带隙半导体(图5(a)). 他们指出, 分子的转动及其引起的能带结构的动态变化是钙钛矿材料MAPbI₃中载流子复合速率低的主要原因, 同时也是材料光伏效率较高的原因. Etienne等^[58]利用Car-Parrinello分子动力学分析法研究了钙钛矿结构形变的实时变化, 并计算了钙钛矿能带结构随时间的演化. 他们的计算结果表明不管是四方相还是立方相的钙钛矿, 其局部的Rashba效应都是随时间变化的(图5(b)), 而晶格中有机阳离子的动态行为在其中起着关键作用.
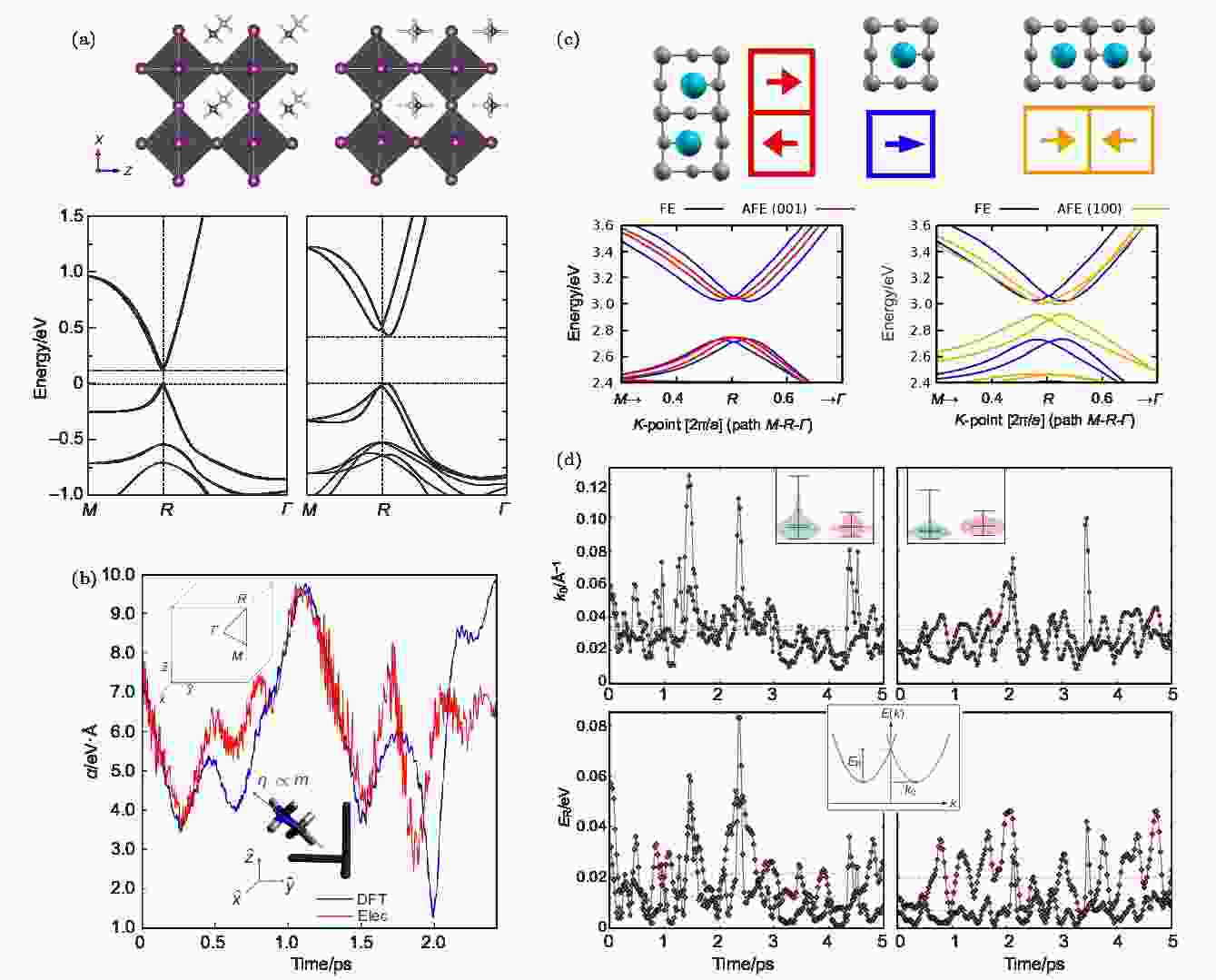图 5 (a)密度泛函计算表明晶格的扭曲致使钙钛矿成为间接带隙半导体^[62]; (b)分子动力学分析指出钙钛矿中的Rashba效应随时间变化^[58]; (c)基于分子动力学和冻结声子分析法的研究表明钙钛矿中动态的Rashba效应源自非简谐结构波动^[63]; (d) ab initio计算分子动力学、密度泛函理论以及准粒子GW理论的综合分析结果表明钙钛矿中动态Rashba效应来源于材料中热无序导致的势能波动^[64]
Figure5. (a) Density functional calculations show that perovskite becomes an indirect semiconductor due to the lattice distortion^[62]; (b) molecular dynamics analysis shows that the Rashba effect in perovskite varies with time^[58]; (c) molecular dynamics and frozen phonon analysis show that the dynamic Rashba effect in perovskite originates from the fluctuation of anharmonic structure^[63]; (d) the combination analysis of ab initio molecular dynamics, density functional theory and quasiparticle GW theory shows that the dynamic Rashba effect in perovskite originates from the potential energy fluctuation caused by thermal disorder in perovskite ^[64].

前面两个工作都认为动态Rashba效应源自有机阳离子的转动. 与之不同, 一些研究者认为钙钛矿中的动态Rashba效应源自晶格本身的非简谐波动. Marronnier等^[63]基于分子动力学和冻结声子分析法研究了Cs掺杂的有机无机杂化钙钛矿, 发现全无机钙钛矿CsPbI₃中存在亚皮秒的非简谐结构波动. 这种快速的结构波动加上强的自旋轨道耦合导致了钙钛矿中动态的Rashba效应(图5(c)). 然而值得一提的是, 尽管他们指出随着晶体结构形变的增大, Rashba效应导致的自旋劈裂愈加明显, 但他们不认为Rashba效应是造成钙钛矿中载流子复合速率慢的原因. 2018年, McKechnie等^[64]基于从头计算(ab initio calculations) 分子动力学、密度泛函理论以及准粒子GW理论, 分析了钙钛矿的Rashba效应, 发现钙钛矿中Rashba分裂的强度和方向依赖于Pb和I的局域不对称性. 而由于热无序导致的势能波动, Rashba效应也相应表现出动态特征(图5(d)). 需要指出的是, 他们发现这种动态Rashba效应在有机无机杂化钙钛矿MAPbI₃和全无机钙钛矿CsPbI₃中表现出相似的性质, 因此推断动态Rashba效应是铅碘钙钛矿的一种基本性质, 而与A位阳离子是否具有极性无关.

虽然大量的理论研究表明钙钛矿中存在很强的Rashba效应, 至今却仅有少数几个工作从实验上研究了钙钛矿中的这一效应. 本节介绍仅有的几个钙钛矿Rashba效应的实验研究工作. 这里不包括那些通过测量载流子寿命来证明钙钛矿Rashba效应的工作, 原因是一方面这部分工作将放在下一节中详细评述, 另一方面也是为了避免循环论证的嫌疑(比如利用Rashba效应来解释载流子复合慢, 而反过来又通过载流子复合慢证明钙钛矿中存在Rashba效应).
晶体结构的扭曲必然造成中心反演对称性的破缺, 所以测量钙钛矿晶体结构的扭曲程度可以验证Rashba效应. Beecher等^[65]利用高能量分辨率的非弹性X射线散射法, 研究了MAPbI₃中的声子色散. 他们本想借此方法分析钙钛矿中是否普遍存在静态结构扭曲, 然而却发现了钙钛矿单晶的另一种结构无序性. 他们发现局域的软非谐振波动(soft anharmonic motion)可以持续到室温或更高的温度, 从而产生在对分布函数(pair distribution function, PDF)中观察到的瞬时局部非中心对称结构(图6(a)), 而声子计算结果表明甲胺的取向与非谐振波动模式强烈耦合(图6(b)). 他们指出, 这种局部对称性破坏是布拉格衍射实验无法观察到的, 但却可以解释材料的超低热传导率和载流子的长寿命. 从PDF中他们估计波动的对称破缺区域的直径在1—3 nm之间.
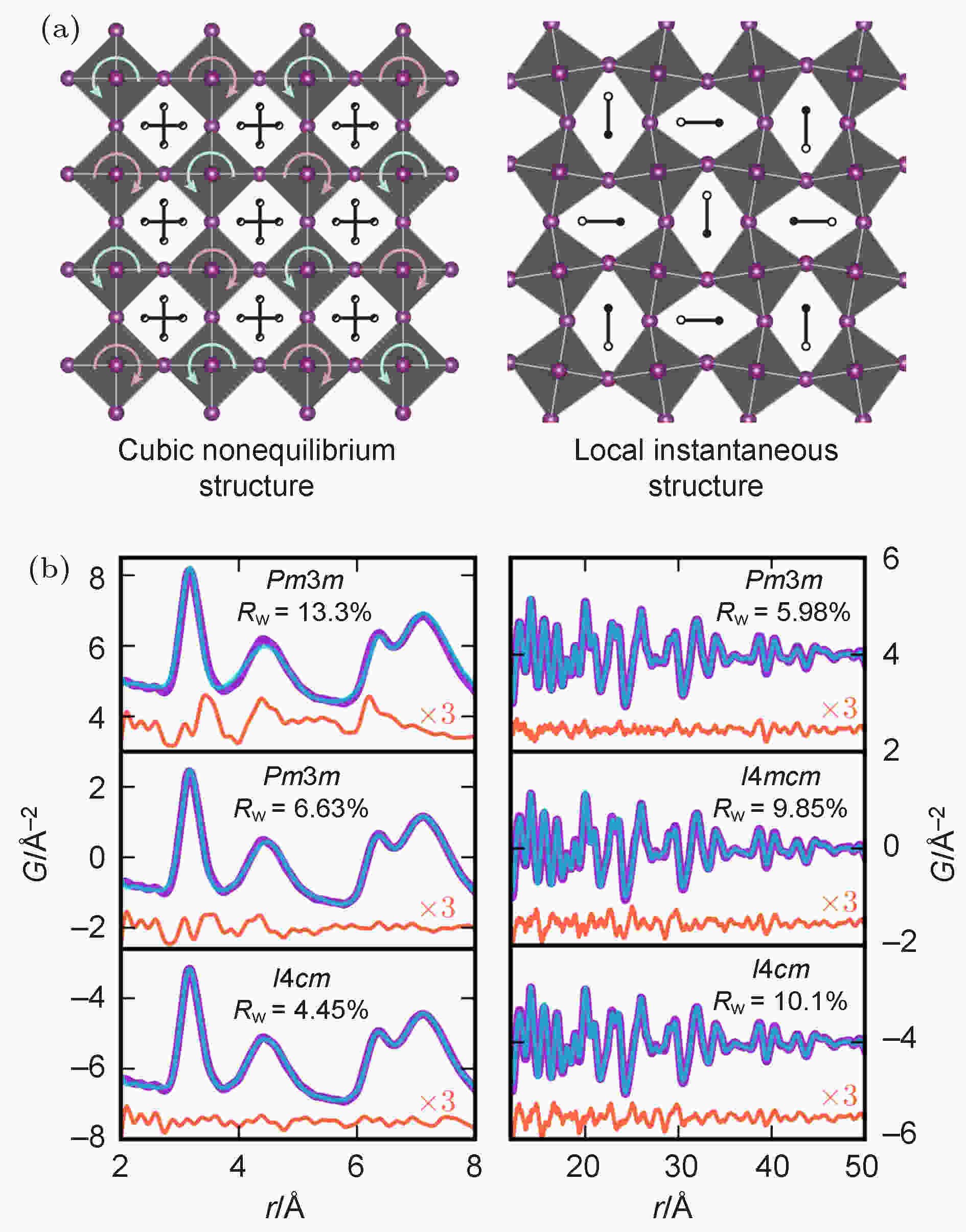图 6 (a)高温下钙钛矿中的局域对称性破缺; (b)甲胺的取向与非谐波模式强烈耦合^[65]
Figure6. (a) Local symmetry breaking in perovskite at high temperature; (b) the orientation of methylammonium is strongly coupled to the non-harmonic mode ^[65].

Niesner等^[36]借助圆偏光生电流效应(circular photogalvanic effect)验证了钙钛矿MAPbI₃单晶中的Rashba效应. 通过测量圆偏光生电流效应与激发光能量的依赖关系, 他们发现产生最强圆偏光生电流效应的激发能量比材料的直接光学带隙更低, 表明自旋极化带隙的能量低于直接带隙(图7(a)). 通过测试圆偏光生电流效应的温度依赖关系, 他们发现随着温度的升高, 四方相的自旋极化带隙与直接带隙的能量差逐渐增大(图7(c)), 圆偏光生电流效应也相应增强(图7(b)), 表明四方相钙钛矿中的Rashba效应随着温度升高而增强. 然而, 在低温下的正交相中他们并没有发现体(bulk) Rashba效应, 变温时的圆偏光生电流效应也没有明显变化(图7(b)), 他们认为这可能是由于不同晶相的低温冻结导致的结果.
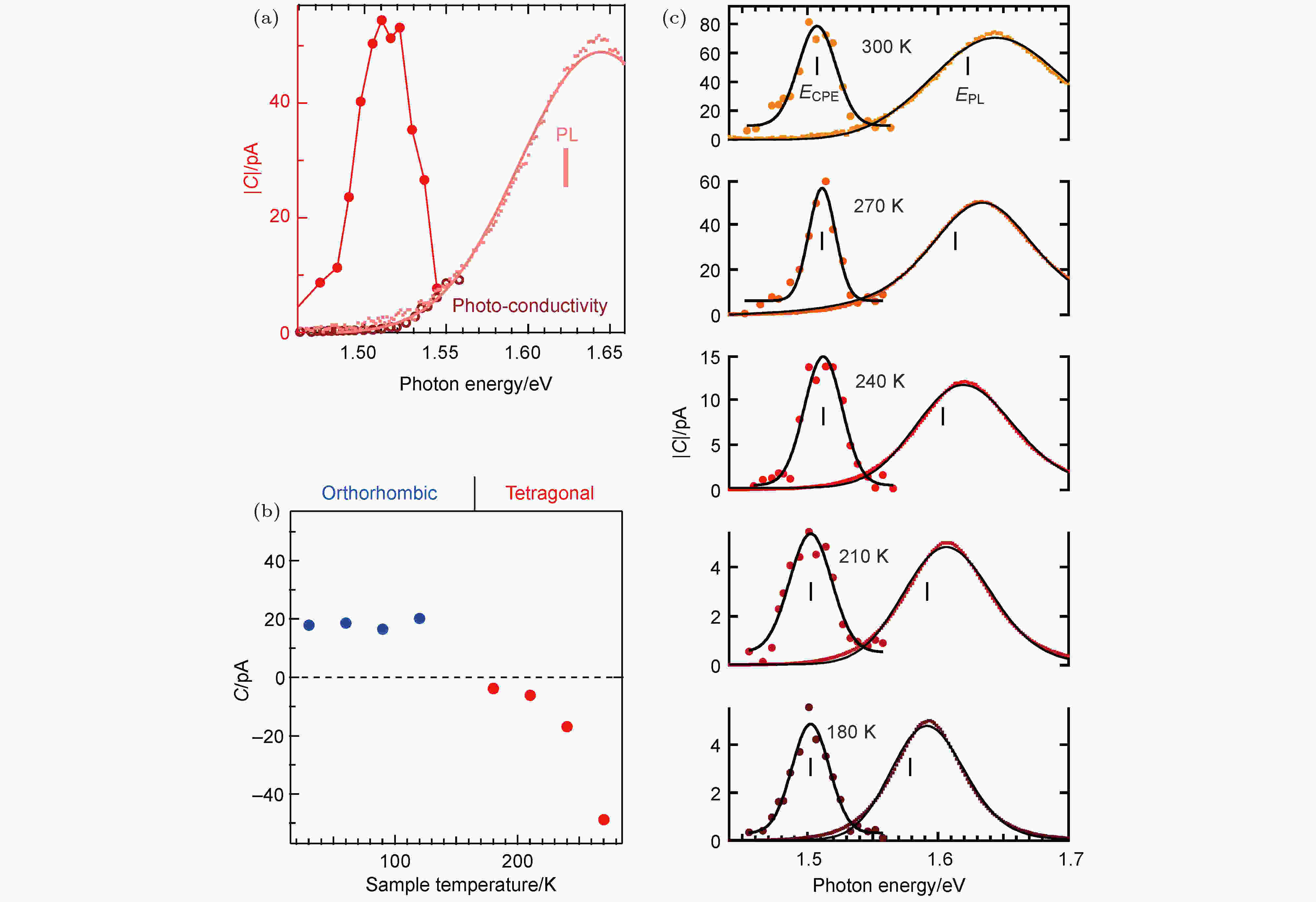图 7 利用圆偏光生电流效应研究钙钛矿中的Rashba效应^[36]
Figure7. Rashba effects in perovskite were studied by measuring the circular photogalvanic effects ^[36].

Hutter等^[66]利用时间分辨微波传导法研究了钙钛矿中的Rashba效应. 时间分辨微波传导法是通过测量样品在暗态和脉冲光照下的微波功率, 取其差值作为该样品的光传导ΔG, 对应材料中的载流子数量(图8(a)). 通过分析光传导ΔG随时间的变化, 可以得到载流子复合的信息. 对于传统的直接带隙半导体(例如GaAs), 通常载流子复合速率随着温度的升高而降低^[67]. 然而Hutter等^[66]的测试结果表明四方相(T > 160 K)的钙钛矿MAPbI₃中的载流子复合速率随着温度的升高而加快, 暗示四方相钙钛矿中的载流子复合是一种非直接带隙间复合(图8(b)). 在时间分辨微波传导测试中, 他们发现只要激发光能量高于间接带隙能量就能产生自由电荷, 而当激发光能量增大到1.7 eV时, 光传导增强到极大值, 对应四方相钙钛矿MAPbI₃的直接带隙(图8(c)). 由于间接带隙的复合需要声子的协助, 所以随着温度的升高(T = 160—300 K), 热能将产生更多的声子促进间接复合, 从而加快载流子复合速率. 他们通过与陷阱辅助复合温度依赖关系的对比分析, 发现导致四方相钙钛矿MAPbI₃这种复合特性的原因即为Rashba效应.
图 8 利用时间分辨微波传导测试研究钙钛矿中的Rashba效应^[66]
Figure8. Studying the Rashba effect in perovskite through time-resolved microwave conductance measurements ^[66].

Isarov等^[29]通过磁光效应研究了CsPbBr₃纳米晶中的Rashba效应. 他们利用线偏光和圆偏光激发样品, 并在低温下测量了磁光效应, 从而探测到了非连续的激子跃迁(图9(a)). 有趣的是, 实验显示自旋极化跃迁的能量劈裂强度与磁场强度呈现出一种非线性的关系, 实验表明在4 T以上, Rashba效应与塞曼效应之间产生了交叉(图9(b)). 他们认为Rashba效应来自Cs离子的运动或纳米晶表面效应引起的晶格畸变. Wang等^[68]通过测试高压下的钙钛矿光电性质研究Rashba效应. 当加在材料上的压力从环境压逐渐升高至325 MPa时, 吸收谱、光致发光(PL)谱以及时间分辨单光子计数(TCSPC)的测试都表明Rashba分裂逐渐减弱(图9(c)), 样品变得更加接近直接带隙的特性, 表现为载流子复合速率增加了五倍. 考虑到压力会导致的Pb原子周围局部电场的减少, 他们的研究结果间接地证明了钙钛矿中存在Rashba效应. 他们还发现, 在高于325 MPa的压力下, MAPbI₃表现出完全直接带隙半导体的性质(图9(c)). Zhai等^[47]则基于电诱导吸收谱等一系列谱学法研究了钙钛矿中的Rashba效应(图9(d)). 他们发现以(C₆H₅C₂H₄NH₃)₂PbI₄ (PEPI)为代表的二维钙钛矿材料中的Rashba分裂非常强, Rashba能级劈裂达到E_R = (40 ± 5) meV, Rashba常数为α_R = (1.6 ± 0.1) eV·?.
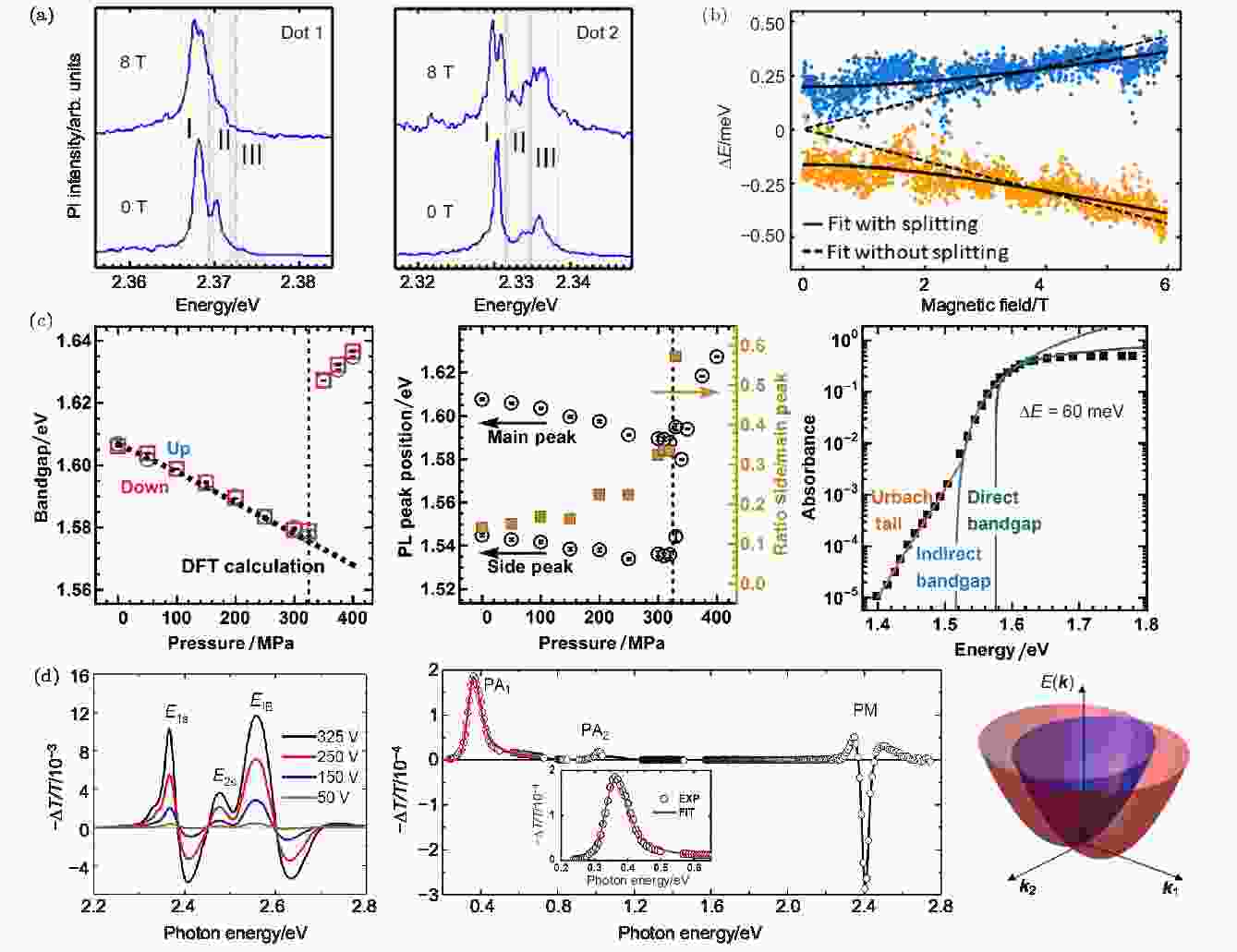图 9 (a), (b)利用磁光效应研究钙钛矿中的Rashba效应^[29]; (c)通过测试高压下的钙钛矿光电性质研究钙钛矿中的Rashba效应^[68]; (d)利用电诱导吸收谱和瞬态光谱测试法研究钙钛矿中的Rashba效应^[47]
Figure9. (a), (b) Studying the Rashba effect in perovskite by measuring the magneto-optical effects ^[29]; (c) studying the Rashba effect in perovskite by measuring the optoelectronic properties of perovskite at high pressure^[68]; (d) studying the Rashba effect in perovskite by measuring the electroabsorption spectra and transient spectroscopy ^[47].

需要指出的是, 目前已报道的工作中, 只有一篇文章是从实验上直接测量了钙钛矿中的Rashba效应. Niesner等^[38]利用角分辨光电子能谱测量了MAPbBr₃单晶的价带色散关系. 他们发现在低温正交相和高温立方相中, 表面布里渊区与体端表面是一致的. 在低温相中, 他们发现了一个半径为0.043 A^–1的环形价带能量极大值, 其中心具有一个大约0.16 eV的能量极小点, 位于价带色散关系的高对称点处(图10(a)). 这些特征强烈地指向了Rashba效应. 为了进一步验证价带劈裂是否源自Rashba效应(即是否与自旋轨道耦合有关), 作者利用圆偏振激光对价带进行了角分辨光电子能谱测量. 他们观察到的强烈的圆二色性(图10(b))证明能带劈裂确实源自自旋轨道耦合, 也即Rashba效应. 他们还发现钙钛矿中的Rashba效应在室温下也存在, 且其强度(α_R = (11 ± 4) eV·?)是目前报道的Rashba效应中最大值之一.
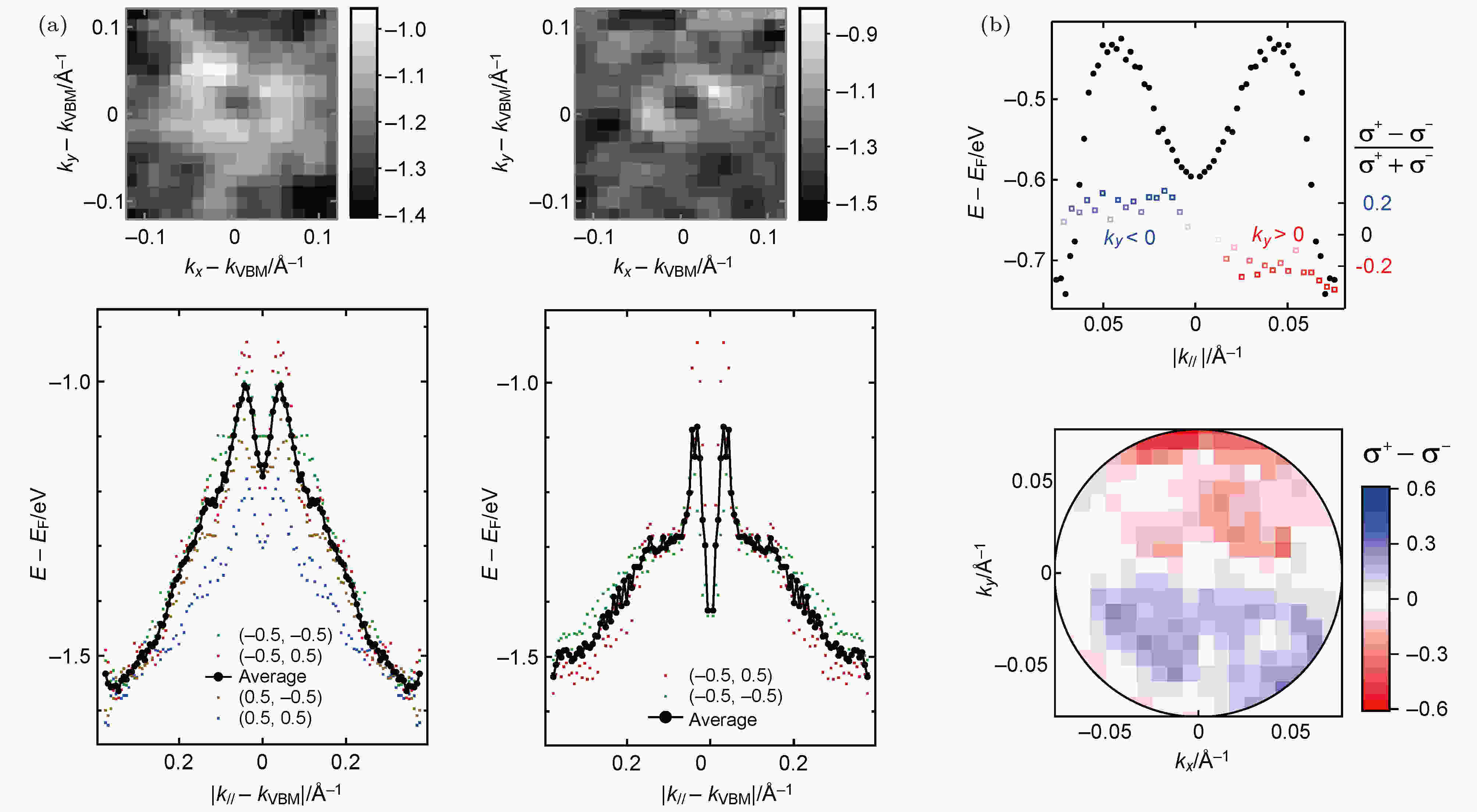图 10 利用角分辨光电子能谱研究钙钛矿中的Rashba效应^[38]
Figure10. Studying the Rashba effect in perovskite by angle-resolved photoelectron spectroscopy measurements ^[38].

除去一些零星的报道, Zheng等^[24]于2015年发表在Nano Letters上的理论工作可看作是第一篇系统研究Rashba效应对钙钛矿中载流子复合影响的论文. 他们基于第一性原理计算和Rashba自旋-轨道耦合模型分析, 发现由于体系中心反演对称性的破缺和重原子的存在, 钙钛矿MAPbI₃中存在较强的Rashba效应, 使导带底和价带顶都产生了一定程度的自旋劈裂(如图2). 他们计算了非弹性声子散射速率, 发现载流子的弛豫时间尺度在飞秒量级(图11(a)). 他们认为有机阳离子对热载流子的快速弛豫起着至关重要的作用. 因此, 光激发后几乎所有的光生载流子都会快速地弛豫到导带底或价带顶, 而由于导带底和价带顶的自旋螺旋性是相反的, 电子与空穴的复合就应该是自旋禁阻的. 另外, 由于导带底和价带顶在k空间的劈裂程度不一致, 电子和空穴的动量也不匹配. 进一步, 他们还发现, 由于Rashba效应的存在, 带边的态密度将大为增加, 致使更多的载流子占据在带边的位置(图11(b)). 考虑到自旋和动量的不匹配, 这一效应将进一步降低载流子的复合速率.
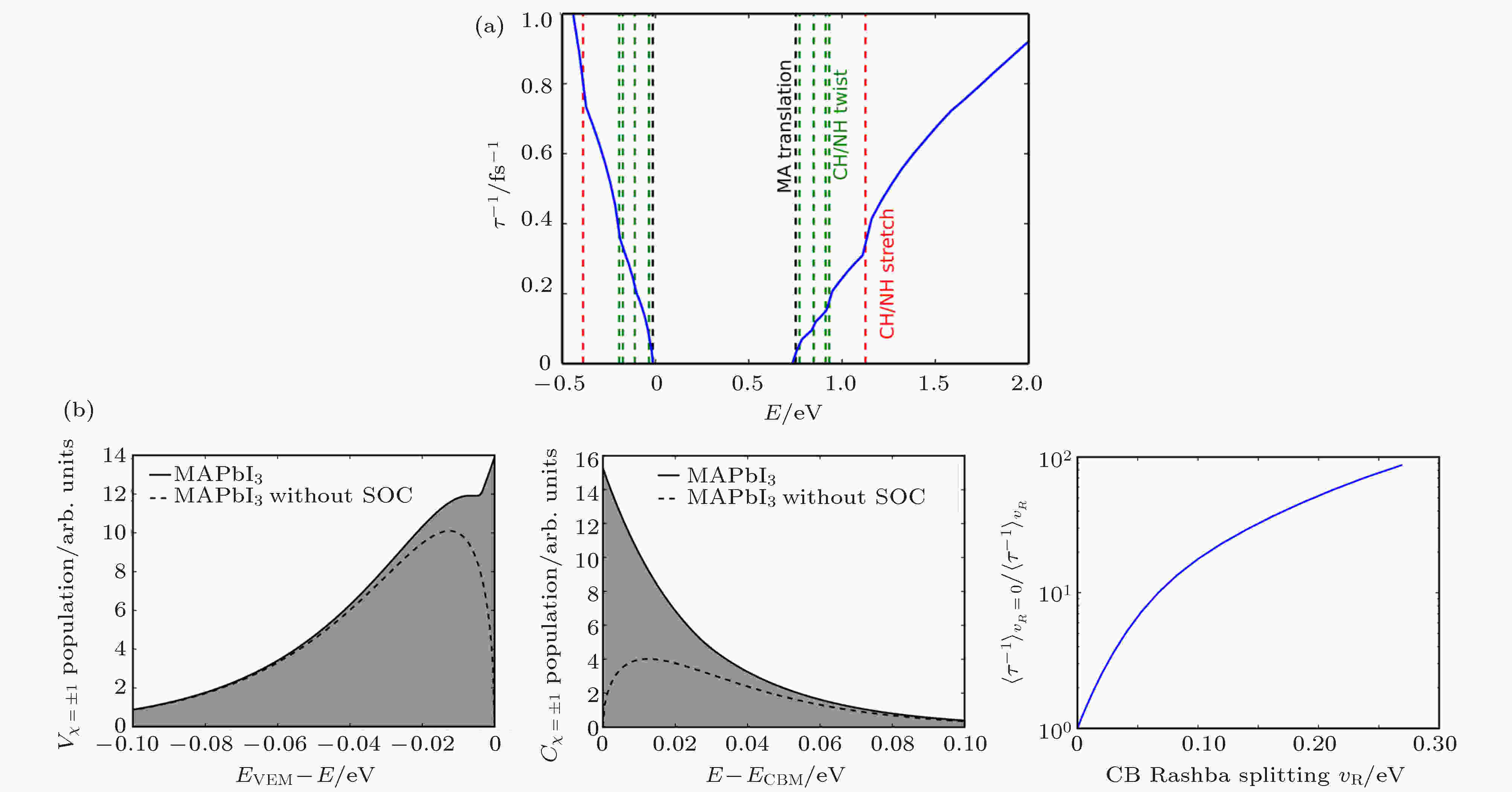图 11 基于第一性原理计算和Rashba自旋-轨道耦合模型的分析研究钙钛矿中Rashba效应对载流子复合的影响^[24]
Figure11. Studying the influence of Rashba effect on carrier recombination based on the first principle calculations and the Rashba spin-orbit coupling model analyses ^[24].

随后, Azarhoosh等^[13]利用准粒子自洽场GW法计算了不同激发密度和温度下, 钙钛矿中光生载流子的辐射复合速率. 他们的计算结果表明, 由于Rashba效应的存在, 钙钛矿MAPbI₃中低的载流子复合速率是材料的内在属性. 在低激发密度下, 材料表现为间接带隙半导体(图12(a)). 而随着激发密度增大或温度升高, 材料中的载流子复合速率逐渐加快, 这与直接带隙半导体(如GaAs等)中载流子复合速率随温度和激发密度的变化关系正好相反(图12(b)). 需要指出的是, 他们的结果表明当激发光强度为一个太阳光强时, 相比于直接带隙, Rashba效应导致的间接带隙使载流子辐射复合速率降低了350倍.
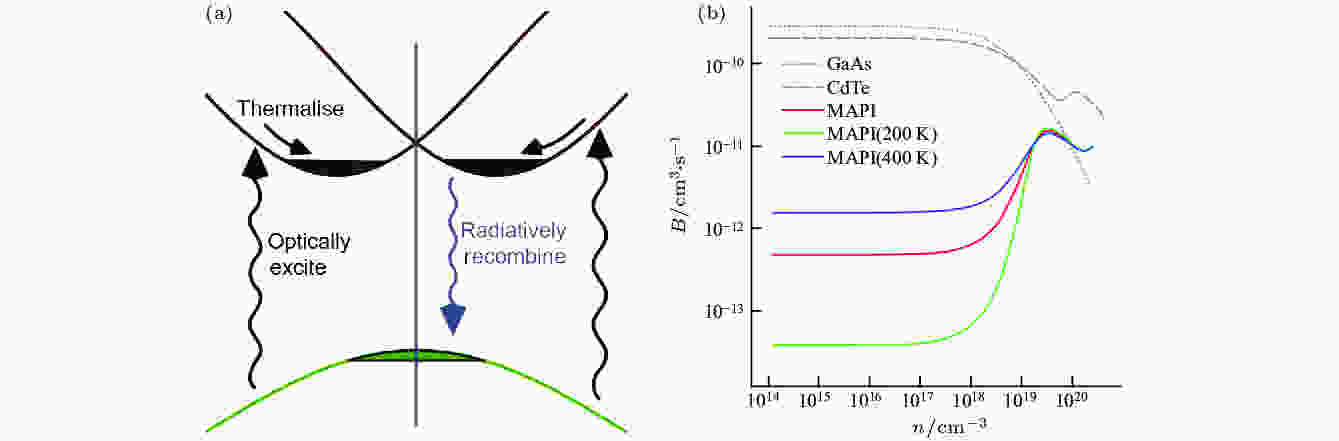图 12 利用准粒子自洽场GW法研究不同激发密度和不同温度下Rashba效应对钙钛矿中光生载流子辐射复合速率的影响^[13]
Figure12. Studying the influence of the Rashba effect on the radiative recombination rates of photo-generated carriers in perovskite under different excitation densities and temperatures by quasiparticle self-consistent field GW method ^[13].

不同于前面的纯理论工作, Li等^[33]从实验上研究了Rashba效应对载流子复合的影响. 他们通过单光子(1PE)和双光子(2PE)激发的瞬态PL谱的测量, 分别研究了单晶样品MAPb(Br_1–xCl_x)₃的体相(bulk)和表面Rashba效应. 选择单晶样品的一个重要原因是与薄膜样品相比, 单晶中的干扰因素更少. 而之所以采用单光子和双光子激发两种方法, 是因为单光子激发通常只能测得样品表面的PL寿命, 而双光子激发可以测量材料内部的PL寿命, 因而可以很好地将单晶表面和内部性质区分开. 图13(a)为单光子激发下的瞬态PL, 每条曲线都可以拟合出两个衰减时间, 较短的τ₁^1PE数值通常在3—6 ns之间, 较长的τ₂^1PE随着Cl的增加而逐渐减小, 作者认为PL寿命缩短的主要因素是表面缺陷. 图13(b)为双光子激发下的瞬态PL, 可知双光子激发的PL寿命τ₂^2PE比单光子激发的PL寿命τ₂^1PE长得多, 同时也与其他文献报道相一致^{[11,12,69,70]}. 通常, 文献中认为PL寿命变长是由材料内部的缺陷减少导致的. 然而, Li等^[33]研究结果表明, 随着Cl浓度的增加, 双光子激发的PL寿命逐渐延长. 考虑到单光子瞬态PL测试结果已经证明单晶表面的缺陷随着Cl的掺入逐渐增加, 故τ₂^2PE的延长并不是由缺陷减少引起的, 而是由于更强的Rashba效应. 他们认为, 由于Rashba效应主要来源于有机阳离子的极性, 而表面有机阳离子更加无序, 内部有机阳离子趋向于有序排列, 所以内部Rashba效应要比表面Rashba效应强得多.
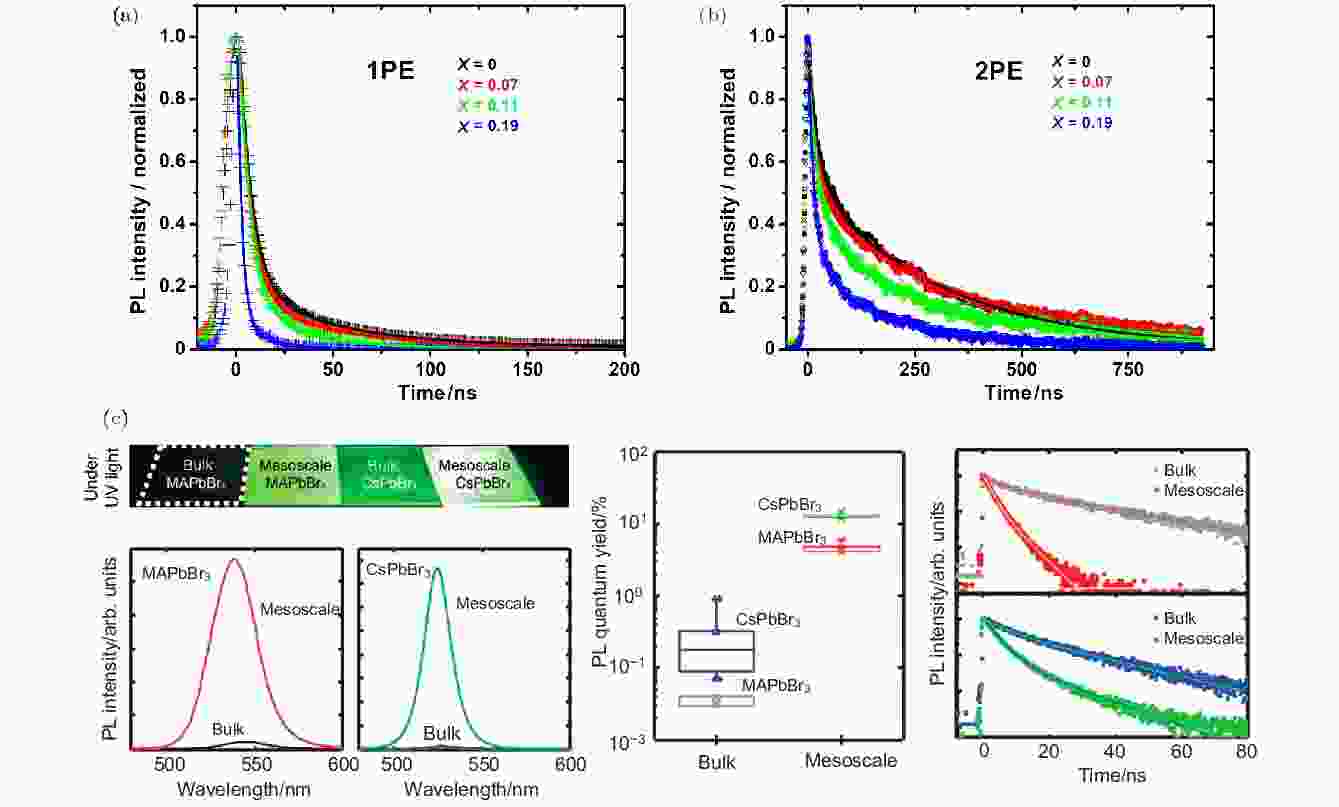图 13 (a), (b)基于1PE和2PE的瞬态光谱测试研究Rashba效应对钙钛矿表面和内部载流子复合速率的影响^[33]; (c)基于瞬态PL研究不同晶粒大小的钙钛矿中Rashba效应对载流子复合的影响^[71]
Figure13. (a), (b) Studying the influences of Rashba effect on the carrier recombination rates on the surface and interior of perovskite by transient spectroscopy measurements based on single-photon (1PE) and two-photon (2PE) excitations ^[33]; (c) studying the impacts of Rashba effect on the carrier recombination in perovskite with different grain size based on transient PL investigation ^[71].

与Li等^[33]不谋而合, Choi等^[71]通过研究不同尺寸钙钛矿晶体的载流子寿命, 也发现体相Rashba效应更强. 他们通过不同的合成手段, 制备了晶粒尺寸不同的两种钙钛矿样品. X射线衍射与形貌表征证实了两种样品晶粒大小的不一致. 他们测试了两种样品的荧光效率和瞬态PL, 发现大晶粒样品的荧光效率更低, 但瞬态PL的时间尺度要大得多(图13(c)). 由此推得, 在大晶粒样品中存在较强的Rashba效应, 而小晶粒尺寸表现为直接带隙的性质. 基于晶体结构分析, 他们发现大晶粒样品呈现四方相, 而小晶粒样品为对称性更高的立方相, 因此他们将大晶粒样品中观察到的较强的Rashba效应归因于更低的晶体结构对称性.
需要指出的是, 体相Rashba效应强于表面Rashba效应这一结论与大多数研究者的观点相反. 由于在界面处存在天然的不对称性, 因此一般认为在表界面处的Rashba效应要远强于材料内部. 而更小的晶粒则意味着更大的比表面积, 因而大多数研究认为其Rashba效应也将更加明显. 我们注意到这与低维钙钛矿的Rashba效应研究结论相一致^[72].
金属卤化物钙钛矿可以分为三维钙钛矿、二维钙钛矿和准二维钙钛矿等. 三维钙钛矿结构通式是ABX₃, 而低维钙钛矿则是在三维钙钛矿中引入大的有机阳离子, 将金属卤素八面体[BX₆]⁴⁺层撑开而形成的有机层与八面体无机层交替排列的钙钛矿. 准二维钙钛矿的结构通式为L₂(SMX₃)_n–1MX₄ (其中L代表大有机阳离子, S代表小有机阳离子, M为金属阳离子, X为卤素阴离子, n为钙钛矿结构中铅卤八面体[BX₆]⁴⁺的层数)^[7].
Chen等^[72]研究了不同n值(n = 1, 2, 3, 4, ∞)的Ruddlesden-Popper相二维钙钛矿单晶中的Rashba效应. 利用瞬态反射谱, 他们分析了载流子寿命随n值的变化(图14(a)). 他们发现当n = 1时, 载流子的寿命最短; 而当n = 2时, 载流子的寿命最长; 当n大于2时, 载流子复合速率随n的增大逐渐变快. 进一步, 他们还测试了样品在室温下的自旋相干时间(图14(b)), 发现当n从1增加到4时, 自旋相干时间逐渐增长, 而当n从4增大到∞时, 自旋寿命却逐渐减短. n = 4时, 样品的自旋相干时间最长, 为7 ps. 他们认为Rashba效应和声子散射的共同作用导致了上述实验现象: 随着层数减小, Rashba效应逐渐增强; 而在n ≤ 4时, 声子散射更加明显, 最终在这两者的共同作用下, 自旋相干寿命呈现出上述趋势.
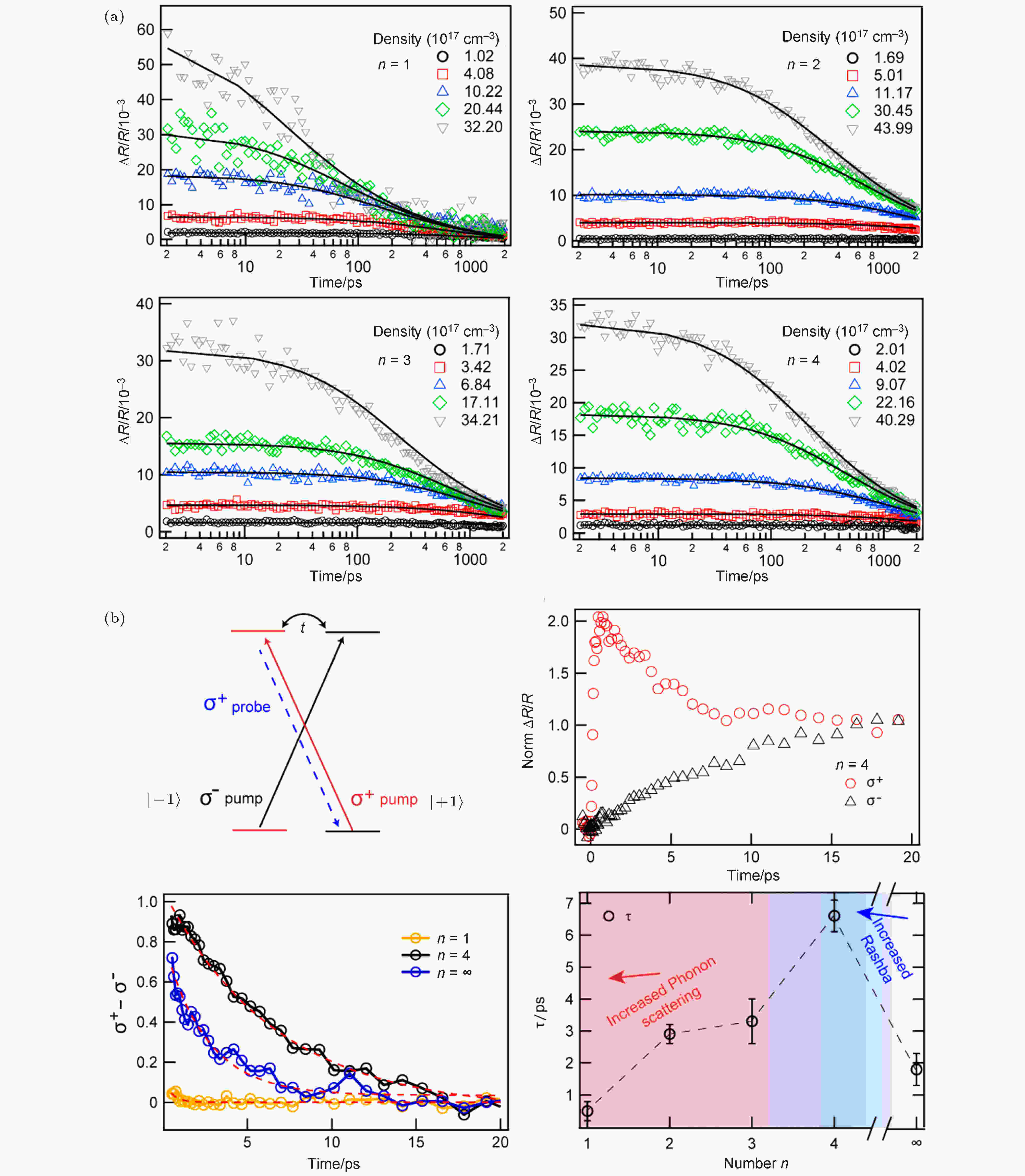图 14 (a)利用瞬态反射谱研究不同n值的二维钙钛矿中Rashba效应对载流子寿命的影响^[72]; (b)利用圆偏振时间分辨光谱研究Rashba效应对钙钛矿中载流子自旋寿命的影响^[72]
Figure14. (a) Studying the influences of Rashba effect on carrier lifetime in two-dimensional perovskite with different n values by using the transient reflection spectroscopy^[72]; (b) studying the influences of Rashba effect on spin lifetime of the carriers in the perovskites by circularly polarized time-resolved spectroscopy ^[72].

同样研究的是不同n值二维钙钛矿中的Rashba效应, Yin等^[73]却得出了不同的结果. 通过密度泛函理论计算和时间分辨激光谱学分析, 他们发现二维钙钛矿中的Rashba效应是由不同的表面末端引起的结构畸变所致. 有意思的是, 他们的理论计算表明, 仅当n = 2时, 导带底和价带顶才发生能级劈裂(图15(a)). 而TCSPC测试结果也表明, n = 2的样品的PL寿命要比n = 1和n = 3的样品要长得多(图15(b)). 如果说n = 2的样品的载流子寿命比n = 1的更长可以解释为n = 1的样品具有强的电声耦合效应, 那么n = 2的载流子寿命比n = 3的也更长就明显地指向了n = 2的样品中更强的Rashba效应了. 结合计算与实验, 他们发现Rashba分裂仅仅发生在无机层数为偶数的低维钙钛矿晶体中.
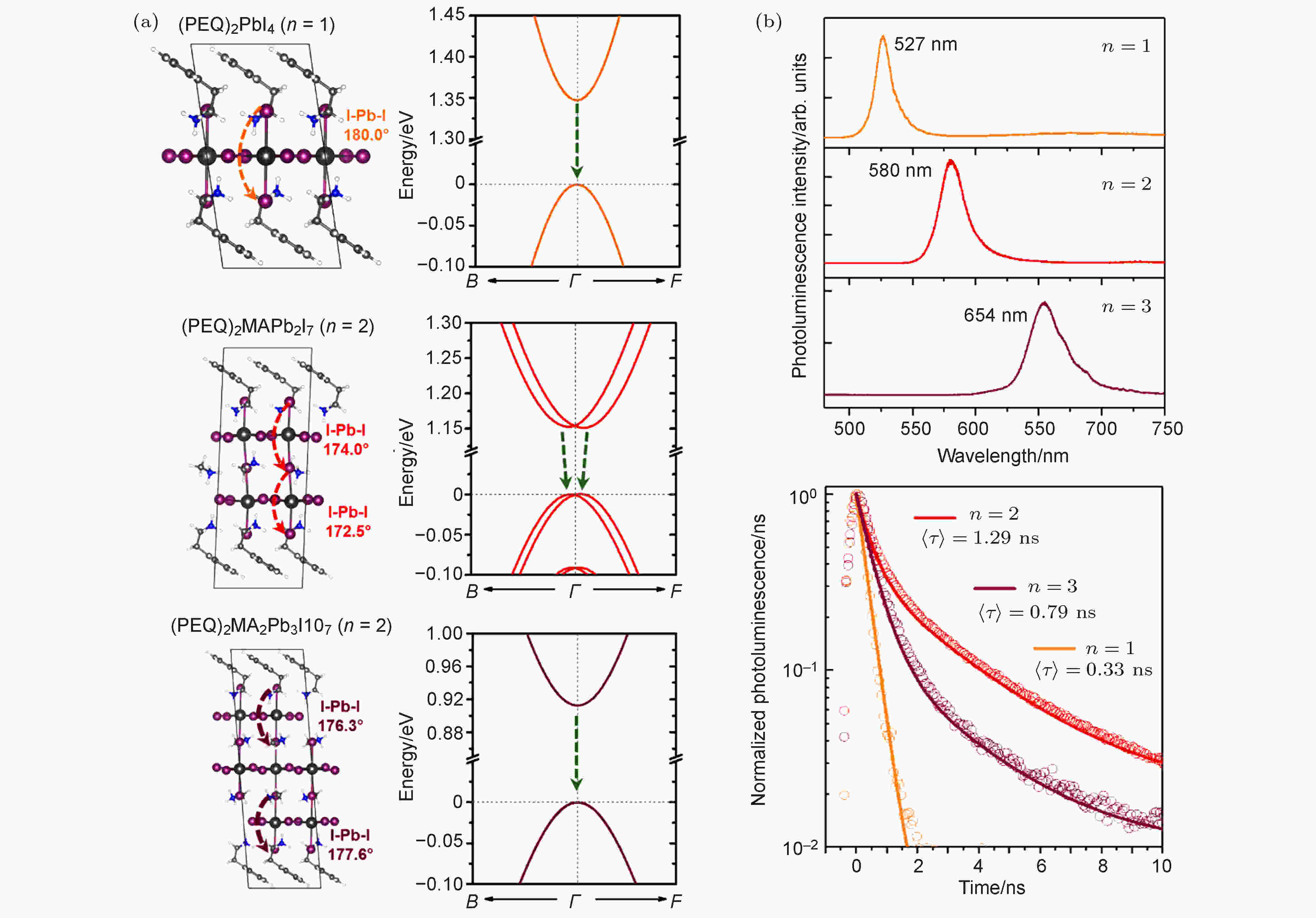图 15 基于密度泛函理论和时间分辨激光谱法研究不同n值的二维钙钛矿中的Rashba效应对载流子寿命的影响^[73]
Figure15. Studying the influences of Rashba effect on carrier lifetime in two-dimensional perovskite with different n values through density functional theory calculations and time-resolved spectroscopy measurements ^[73].

从前文可知, 关于钙钛矿中Rashba效应的来源及其对载流子复合的影响, 该领域内存在诸多争论. 然而, 这些争论都是建立在承认钙钛矿中存在较强的Rashba效应这一共识之下的. 我们注意到, 目前关于钙钛矿中Rashba效应, 还存在一些更为严重的争议, 主要体现在: 1)钙钛矿中是否存在本征的Rashba效应; 2) Rashba效应能否对载流子的复合产生有效的影响.
Rashba效应存在的一个显著特征是材料由直接带隙半导体变成间接带隙半导体. 因而其逆否命题也应成立, 即如果实验结果表明钙钛矿是直接带隙半导体, 那么钙钛矿中不存在Rashba效应(或者说Rashba效应微乎其微). Davies等^[40]的研究表明钙钛矿中载流子的双分子复合是完全的光吸收逆过程, 暗示钙钛矿是纯的直接带隙半导体. 因此, 他们的结论表明钙钛矿中不存在Rashba效应. 在这一工作中, 作者通过精确考虑激子和电子-空穴连续态对吸收的贡献(图16(a)), 从而利用van Roosbroeck-Shockley关系从吸收光谱中获得了双分子复合速率常数(图16(b)). 结果表明, 随着温度的降低, 载流子复合逐渐增强. 因此, 他们认为电子和空穴之间的辐射复合是直接带隙跃迁(图16(c)). 虽然文章中并没有提到Rashba效应, 但文章的结果无疑表明钙钛矿中不存在Rashba效应.
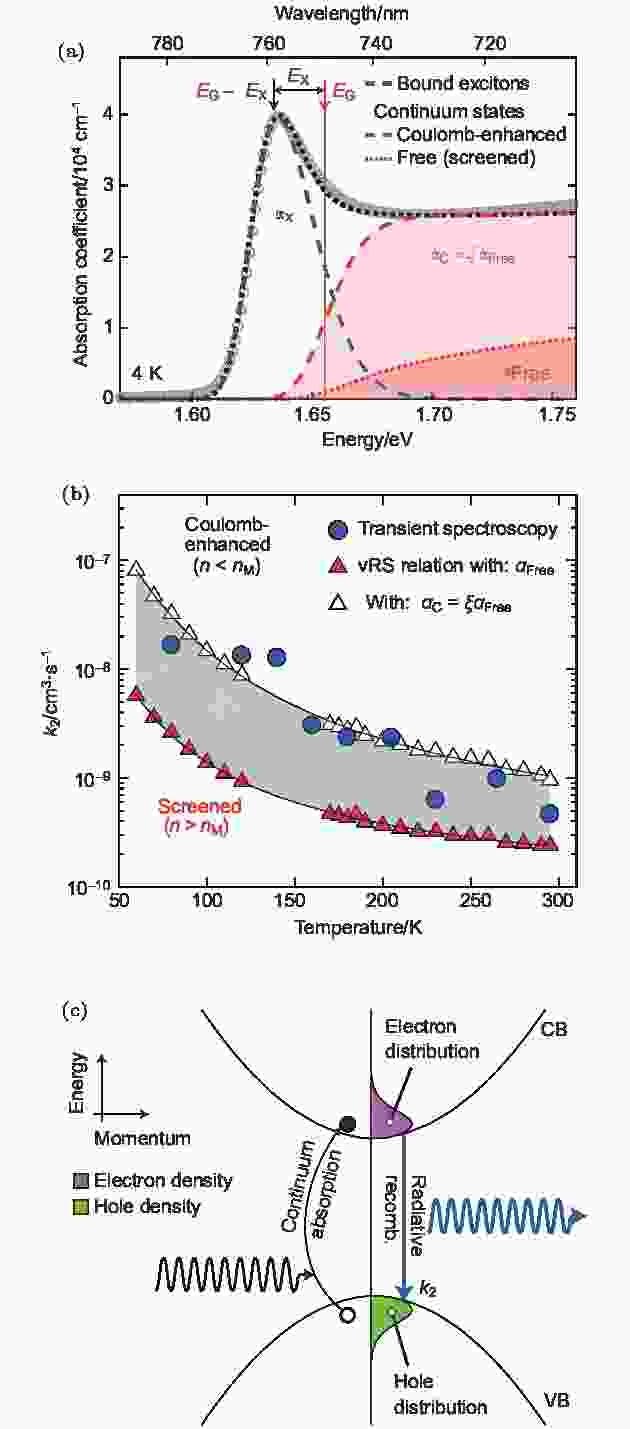图 16 温度依赖的光谱研究表明钙钛矿是直接带隙半导体^[40]
Figure16. Temperature-dependent spectroscopy measurements indicate that the perovskite is a direct bandgap semiconductor ^[40].

无独有偶, Sarritzu等^[41]基于温度依赖的瞬态PL测试, 指出钙钛矿并不表现出Rashba效应导致的间接半导体性质. 他们首先利用对等关系将吸收谱转换成PL谱, 发现其与实验测量的PL重合得非常好(图17(a)), 暗示PL来自于直接带隙的复合. 进一步, 他们测量了样品温度依赖的瞬态PL谱(为了排除其他因素从而精确提取双分子复合速率, 他们只考察激光脉冲过去后一小段时间内的瞬态PL)(图17(b)). 结果显示, 随着温度升高, 钙钛矿的双分子复合速率常数逐渐降低, 正好与Rashba效应相矛盾, 而与GaAs等直接半导体相类似. 因此, 他们认为钙钛矿(MAPbI₃和MAPbBr₃)是直接半导体, 也就不存在Rashba效应.
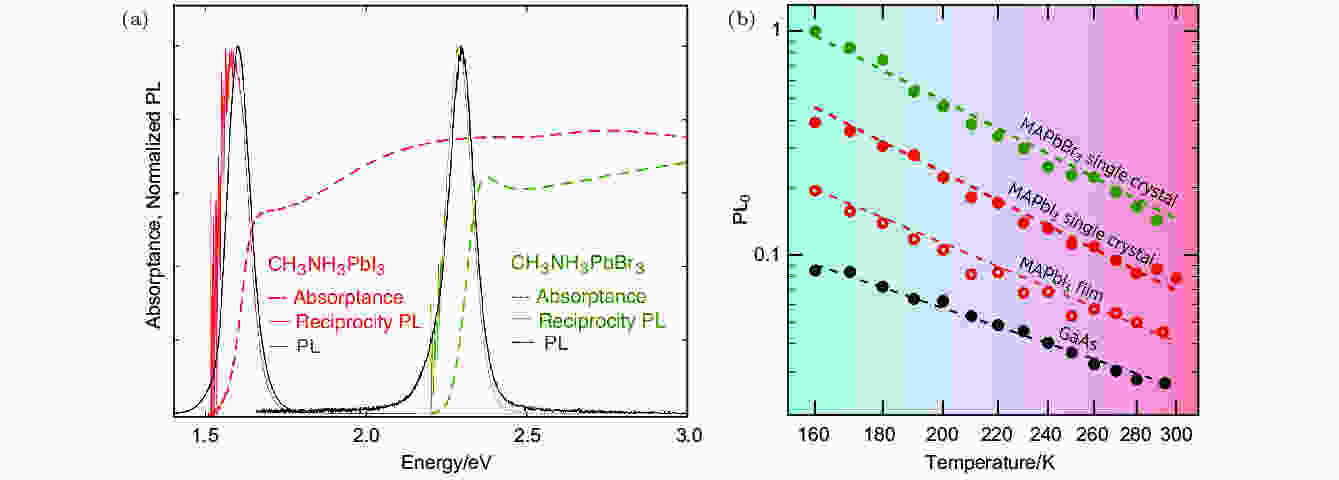图 17 通过吸收-PL谱的对比研究(a)和温度依赖的瞬态PL测试(b)证明钙钛矿是直接带隙半导体^[41]
Figure17. Absorption-PL spectra study (a) and temperature-dependent transient PL measurements (b) show that the perovskite is a direct bandgap semiconductor ^[41].

Rashba效应要求材料结构不具备中心反演对称性. 然而, 有研究表明钙钛矿的晶体结构并不满足这一条件. Frohn等^[42]基于二次谐波旋转各向异性(second harmonic generation rotational anisotropy, SHG-RA)谱的测量, 发现钙钛矿的结构不存在中心反演对称性破缺. 作者测量了四方相MAPbI₃样品的SHG-RA谱(如图18(a)), 发现其属于中心反演对称的I4/mcm空间群. 进一步, 他们通过密度泛函理论的计算, 证明钙钛矿中确实不存在明显的Rashba效应. 仅当考虑有机阳离子MA⁺的旋转时, 才能观察到极其微弱的Rashba效应, 且此时带边色散关系十分接近于抛物线型, 呈现出直接带隙的特征(图18(b)). 而当考虑了与实验不相符的晶格扭曲或原子位移时, 较大的Rashba效应才会出现, 因此他们认为之前的理论计算结果值得商榷. 他们还进一步指出, 钙钛矿中也不存在较大的动态Rashba效应.
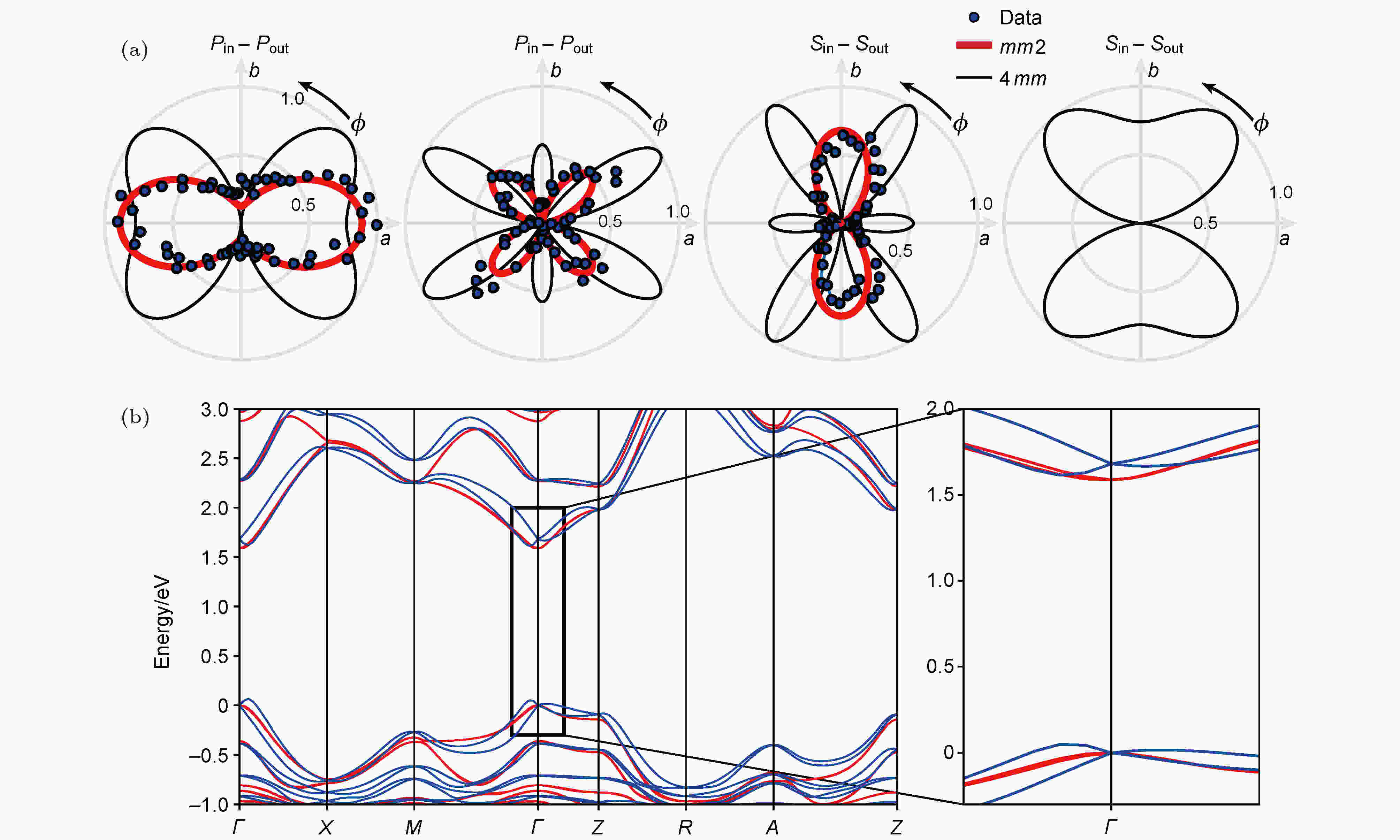图 18 SHG-RA测量(a)和第一性原理计算(b)的结果表明钙钛矿结构具有中心反演对称性^[42]
Figure18. SHG-RA measurements (a) and first principle calculations (b) show that the structure of perovskite is inversion-symmetric ^[42]

另有一些研究者虽然认为钙钛矿中存在Rashba效应, 却不认为Rashba效应对载流子复合具有较大的影响. Zhang等^[44]注意到了Zheng等^[24]提出的Rashba效应影响载流子复合的理论, 即导带底与价带顶的自旋与动量失配导致载流子的复合速率被强烈抑制. 于是, 他们采用第一性原理计算, 并将有机阳离子MA⁺的旋转作为晶格扭曲的来源, 研究了钙钛矿MAPbI₃中的Rashba效应及其对载流子复合的影响^[44]. 然而计算结果显示导带底与价带顶的自旋螺旋性并无区别, 也就不存在Zheng等^[24]所说的自旋禁阻问题(图19(a)).
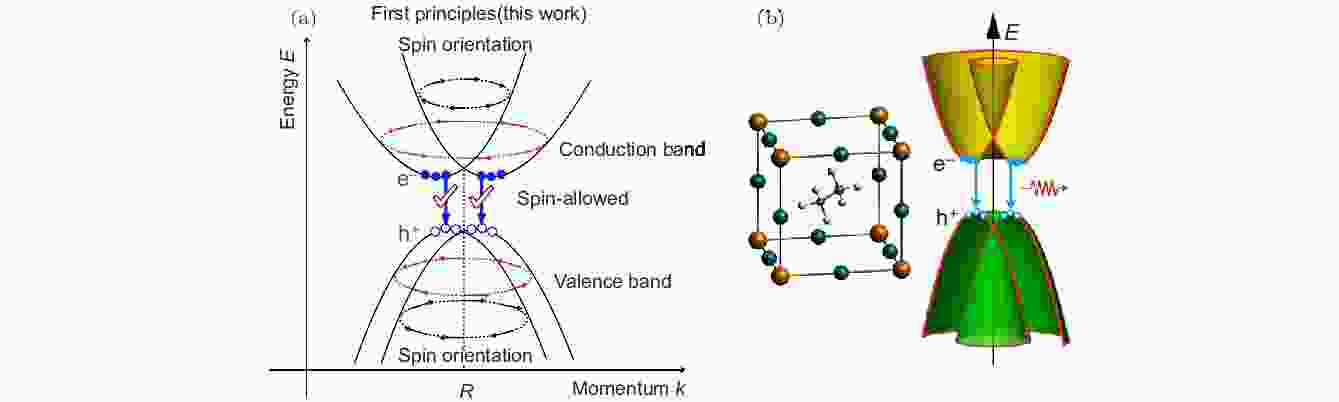图 19 (a)第一性原理计算结果表明虽然钙钛矿中存在Rashba效应, 但载流子复合并不是自旋禁阻的^[44]; (b) Rashba效应引起的动量不匹配对载流子复合速率的影响十分微弱^[43]
Figure19. Results of first-principles calculations show that the Rashba effect in perovskite does not lead to the spin forbidden of the carrier recombination ^[44]; (b) the influence of momentum mismatch caused by the Rashba effect on the carriers recombination is very weak ^[43].

一个非常值得注意的问题是, 即使导带与价带的自旋螺旋性是相反的, 仍然不存在自旋禁阻问题. 这是因为导带并非纯自旋态, 而是自旋轨道耦合态. 只不过其总角动量为J = 1/2, 所以表现出一些类似于自旋的性质而已(我们可以称之为赝自旋, pseudo-spin)^[31]. 正是由于这个原因, 导带与价带之间的跃迁并不需要满足自旋守恒规则(当自旋轨道耦合很弱时自旋守恒必须满足, 比如对于有机荧光分子), 仅需要满足总角动量守恒即可. 而由于光子具有量子数为1的角动量, 故导带到价带的跃迁是完全角动量守恒的, 符合电偶极跃迁的选择定则.
进一步, Zhang等^[43]还研究了动量不匹配对载流子复合的影响. 由于MA分子的结构是动态变化的, 所以他们将导带与价带之间的动量失配作为MA分子取向的函数来进行计算. 他们的计算结果表明, 由Rashba效应引起的动量失配对辐射复合速率的抑制作用十分有限, 计算出来的辐射复合系数与传统的直接带隙半导体相当(图19(b)).

毫无疑问, Rashba效应给金属卤化物钙钛矿领域带来了全新的研究课题. 首先, Rashba效应本身作为一种有趣的现象, 值得我们深入探讨它的物理本质; 其次, 对Rashba效应的深入分析, 必将对钙钛矿光电物理相关领域(如光电子学(optoelectronics)、自旋电子学(spintronics)、自旋轨道电子学(spin-orbitronics)等)产生深远影响; 再者, 如何利用Rashba效应开发多功能的钙钛矿光电磁器件, 也非常值得我们去尝试.
然而, 目前钙钛矿Rashba效应研究中存在一些亟待解决的问题, 而其中最重要的是确定材料中是否存在Rashba效应以及阐明其与材料成分/结构之间的关联性. 在第4节中, 我们回顾了目前的几个验证钙钛矿Rashba效应的实验工作. 他们大多采用的是间接推测法, 唯一的直接实验证据来自Niesner等^[38]的基于角分辨光电子能谱法的研究. 然而, 角分辨光电子能谱只能分析材料的价带, 且是一种表面分析方法, 对钙钛矿材料内部的Rashba特性以及导带的Rashba效应无能为力. 另外, 钙钛矿材料体系多样, 组分各异, 势必导致不同样品之间的Rashba效应千差万别, 而目前针对不同体系钙钛矿中Rashba效应的对比性研究尚未见报道. 因此, 我们呼吁领域内的研究者采用多种手段, 特别是一些角动量相关谱学法, 系统地讨论不同钙钛矿体系中的Rashba效应.
例如, 理论研究表明钙钛矿导带中的Rashba效应要远强于价带^[74], 因此采用角分辨反光电子能谱法对钙钛矿的导带进行分析, 将可能给出钙钛矿中Rashba效应更直接可靠的信息^[75]. 进一步, 为了更加精确地测量激发态的信息, 还可以采用圆偏振的泵浦脉冲来激发样品, 而利用时间分辨的角分辨光电子能谱进行分析^[76]. 此外, 精确测量不同钙钛矿样品的中心反演对称性也可以作为Rashba效应存在的间接证据. 因此, 测量样品的和频谱(sum-friquency generation)或者二次谐振谱(second harmonic generation)不失为良好的手段^[34], 因为它们都只在非中心反演对称的体系中才能被探测到.
另外, 测量材料中的自旋-电荷转化(Rashba-Edelstein效应)或电荷-自旋转化(反Rashba-Edelstein效应), 也可以用来验证钙钛矿中Rashba效应的存在与否以及研究其性质^[30]. 例如圆偏光生电流效应(circular photogalvanic effect)和自旋-动电效应(spin-galvanic effect)^[51]. 其中, 圆偏光生电流效应已经被用来研究了两种钙钛矿单晶中的Rashba效应, 我们不再赘述. 自旋-动电效应指的是系统中非平衡自旋极化引起的动生电流效应, 而产生自旋极化的方式可以是电注入自旋极化电荷或者圆偏光激发产生自旋极化电荷. 当然, 还有很多谱学手段都可以用来研究钙钛矿中的Rashba效应, 例如磁致旋光电流效应(magneto-gyrotropic photogalvanic effect)^[77]、共振非弹性光散射法(resonant inelastic light scattering)等^[78].
另一个值得期待的研究课题是Rashba效应在钙钛矿器件中的应用. 由于Rashba效应会减弱载流子的复合从而增大载流子的寿命和扩散长度, 因此调控钙钛矿中的Rashba效应将成为改善器件性能的一种手段. 在钙钛矿光伏器件中增大Rashba效应可以提升器件的性能, 当电子空穴的复合速率大幅度降低时, 我们可以预期光伏器件的开路电压将会得到有效提升. 此外, 利用相同的原理也可以提升钙钛矿光探测器的性能. 与之相反, 在发光器件中, 通过调控材料组分与构象或者优化设计器件结构来降低Rashba效应, 也将成为提升钙钛矿LED器件性能的一种思路.
钙钛矿Rashba效应在自旋电子学领域也展现出巨大的潜力. 基于Rashba效应, 我们可以设计器件, 用来产生、探测及控制自旋流. 例如自旋霍尔效应(spin Hall effect): 在没有外磁场的情况下, 利用材料固有的Rashba-Edelstein机制来产生自旋流^[79]. 如图20(a)所示, 当在x方向上给体系加一个偏压, 则费米面将会相应的产生一定的偏移, 使载流子感受到一个等效磁场, 从而在y方向上产生一个自旋流. 另外, 1990年提出的自旋场效应管(spin-FET)也有可能在钙钛矿中得到实现(图20(b))^[80]. 由于Rashba效应可以用来调控电子自旋, 而其本身又受外电场调控. 因此, 可以利用外电场调控电子自旋, 从而实现器件中电流大小的变化, 类似于FET中通过栅压调控源-漏极之间的电流大小.
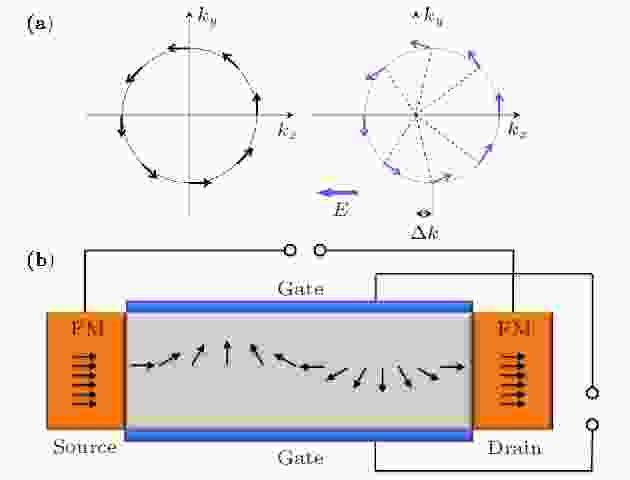图 20 (a)利用Rashba效应产生自旋流; (b)利用Rashba效应构造自旋FET^[30]
Figure20. (a) Generation of spin current by using the Rashba effect; (b) the spin-FET based on the Rashba effect ^[30].

至此, 我们回顾了钙钛矿Rashba效应的研究现状、面临的挑战以及未来的机遇. 目前对于钙钛矿中Rashba效应的研究还处于非常初级的阶段, 不管在理论还是实验上, 都充满着争论. 围绕钙钛矿中是否存在Rashba效应, 什么体系的钙钛矿中存在Rashba效应, Rashba效应的大小与材料结构的关系, 钙钛矿表面和内部的Rashba效应等方面存在激烈的争论. 我们期待该领域内的研究者采用更多样化的实验手段以及更加合理的计算方法去研究钙钛矿中的Rashba效应. 同时, 考虑到钙钛矿材料的组分与构象的多样性, 针对不同体系钙钛矿的系统性对比研究也已经迫在眉睫. 另一方面, 钙钛矿中Rashba效应在光电磁领域的应用也等待我们去探索. 很显然, 钙钛矿Rashba效应的发展与突破将不可避免地对钙钛矿光电子学及自旋电子学产生深远的影响.