摘要: 液滴撞击壁面是一种常见的现象, 减少撞击过程中液滴在壁面的驻留时间在很多应用中非常重要. 本文在对液滴撞击加热壁面的动力学过程的研究中, 发现了一种能够大幅减少液滴驻留时间的弹起模式, 即雾化弹起模式. 与液滴撞击壁面过程中的回缩弹起模式相比, 雾化弹起模式的液滴驻留时间能减少约40%. 与其他试图减少液滴驻留时间的手段相比, 本文中驻留时间的减少仅需加热壁面, 因此该方法容易实施而且非常可靠. 最后, 本文对雾化弹起模式下液滴驻留时间减少的机理进行了讨论, 提出了一个针对膜态沸腾区域雾化弹起模式发生条件的简化理论模型, 并得出了膜态沸腾区域液滴从雾化弹起模式到回缩弹起模式过渡边界的幂次关系, 该幂次关系与实验数据吻合良好. 此外, 该理论模型也能解释过渡沸腾区域两种弹起模式的过渡边界的变化规律.
关键词: 液滴撞击 /
Leidenfrost效应 /
驻留时间 /
反弹 English Abstract Bouncing-with-spray mode and residence time of droplet impact on heated surfaces Rong Song Shen Shi-Quan Wang Tian-You Che Zhi-Zhao State Key Laboratory of Engines, Tianjin University, Tianjin 300072, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51676137), the Natural Science Foundation of Tianjin City, China (Grant No. 16JCYBJC41100), and the National Science Fund for Distinguished Young Scholars, China (Grant No. 51525603).Received Date: 18 January 2019Accepted Date: 08 May 2019Available Online: 01 August 2019Published Online: 05 August 2019Abstract: The impact of droplets on surfaces is a ubiquitous phenomenon, and reducing the droplet residence time is the aim of many studies because of the potential applications in self-cleaning, anti-icing, corrosion resistance, etc. This study identifies a mode of droplet bouncing (bouncing-with-spray) that can reduce the residence time significantly. And compared with the way of using complex microstructures on the substrate employed in previous studies, simply heating the substrate to reduce the residence time is novel and simple. The dimensionless residence time decreases down to about 40% compared with that from the traditional retraction-bouncing mode. The reduction in the residence time is due to the burst of vapor bubbles in the liquid film, which results in holes forming in the liquid film and consequently the liquid film recoiling from the holes. The reduction in the recoiling distance leads to the reduction in the recoiling time. Then a simplified theoretical model with considering the energy balance and the critical condition of the bubble burst is proposed. According to this theoretical model, a scaling law is proposed for the transition boundary between the retraction-bouncing mode and the bouncing-with-spray mode in the film boiling regime, and it accords well with our experimental data. This model can also explain the transition boundary between these two modes in the transition boiling regime.Keywords: droplet impact /Leidenfrost effect /residence time /bouncing 全文HTML --> --> --> 1.引 言 液滴撞击壁面现象广泛见于自然界和工业应用中, 包括但不限于喷雾冷却、喷墨打印及内燃机缸内燃油喷雾撞壁[1 -3 ] . 液滴撞击不同温度的壁面的过程会极大地受到传热和相变的影响. 当壁面温度足够高时, 液滴和壁面之间会形成一层蒸汽膜, 即Leidenfrost效应[4 ] . 一般来说, 对于不同的壁面温度, 液滴沸腾会经历和池沸腾一致的沸腾形式, 即核态沸腾、过渡沸腾和膜态沸腾[5 -9 ] . Tran等[10 ] 以液滴底部是否与壁面接触(即是否存在子液滴喷射的现象)作为判别液滴处于膜态沸腾和其他沸腾区域的依据. 很多文献也依照这种方法判别液滴是否处于膜态沸腾区域, 并进一步研究了液滴的动态Leidenfrost温度会受到表面结构[11 ,12 ] 以及撞击韦伯数[7 ] 等因素的影响. Shirota等[13 ] 和van Limbeek等[14 ] 则通过全内反射技术, 对3个沸腾区域的液滴底部与壁面的接触情况进行了直接测量. 他们观察到在核态沸腾区域, 液滴底部一直完全与壁面接触; 在过渡沸腾区域, 由于液滴底部形成的蒸汽膜不稳定, 液滴底部中央区域会和壁面部分接触; 在膜态沸腾区域, 液滴底部不会接触壁面.[15 ] . 由于液滴接触时间会影响到液滴与壁面之间的物质、动量及能量的交换, 在很多应用中, 减少液滴接触时间是很重要的, 例如防结冰、自清洁、防腐蚀等. 因此, 大量研究者采用了多种方法去克服液滴接触时间的理论极限[15 ] , 例如, 使用带有微脊的表面[16 ] 、使用带有亚毫米级柱子的超疏水表面[17 ] 、弯曲表面上的不对称撞击[18 ] 及使用鸡蛋形状的液滴[19 ] 等.2.实验方法 实验装置示意图见图1 . 注射器中的液体在注射泵(Harvard Apparatus, Pump 11 elite Pico plus)的推力下以约4 μL·s–1 流速经过一根注射管后到达平口针头顶端, 当液滴所受重力大于表面张力时, 液滴从针头顶端脱离. 随后液滴撞击到一片被铜板加热的抛光硅表面上(表面粗糙度小于0.5 nm). 实验中将两根K型热电偶分别置于距撞击点1 cm的两侧, 并通过PID控制器实现对壁面温度的控制(精度$ \pm \;1\;{\rm ^\circ C}$ ). 实验通过高速相机(Photron Fastcam SA1.1)捕捉水平视角和倾斜视角下的液滴撞壁过程. 背景光源为一个发光二极管(LED)灯. 在进行多次重复实验的条件下, 通过一个Matlab程序进行图像处理, 获得液滴的尺寸(水和甘油的混合物液滴直径为${D_0} = $ 2.8 mm, 水滴为2.2—3.4 mm, 乙醇液滴为1.6 mm, 标准差变化范围为0.020—0.022 mm)、液滴的撞击速度(V = 0.9—2.1 m·s–1 , 标准差变化范围为0.006—0.009 m·s–1 )及撞击过程中的液滴轮廓变化情况. 其中液滴的撞击速度, 通过在图像处理中计算撞击前两帧图片中液滴质心位移和时间间隔的比值得到. 本文通过改变甘油和水的混合物中甘油的质量分数来实现液滴黏度的改变, 实验中采用液体的物性参数见表1 . 韦伯数用来定义液滴的动能和表面能的比值, 即图 1 液滴撞击加热壁面的实验装置示意图 (a)水平视角; (b)倾斜视角Figure1. Schematic diagram of the experimental setup for droplet impact on a heated surface: (a) Side-view; (b) aerial-view.液体种类 密度$\rho {\rm /kg} \cdot {{\rm m}^{{\rm - 3}}}$ 表面张力$\sigma /{\rm mN} \cdot {{\rm m}^{ - 1}}$ 动力黏度$\mu /{\rm mPa} \cdot {\rm s}$ 汽化潜热$\ell /{\rm kJ} \cdot {\rm k}{{\rm g}^{ - 1}}$ 水 998 72 1.00 2257 水 + 甘油(28 wt%) 1068 70 2.35 水 + 甘油(34 wt%) 1083 70 3.00 水 + 甘油(39 wt%) 1097 70 3.63 水 + 甘油(56 wt%) 1143 68 9.00 水 + 甘油(75 wt%) 1195 66 42.47 乙醇 790 22 1.07 853
表1 本实验中不同液体物性参数表Table1. Properties of the liquids used in this study.ρ 为液体密度, σ 为液体表面张力. 实验中不同种类液体的韦伯数变化范围为10—180.3.实验结果与讨论 23.1.液滴撞击形貌及驻留时间 3.1.液滴撞击形貌及驻留时间 本文首先讨论不同沸腾区域的液滴撞击形貌. 通过全内反射技术[13 ,14 ] 可以观察到在核态沸腾和过渡沸腾区域, 液滴底部和壁面的接触情况存在明显的区别: 在核态沸腾区域, 液滴底部会一直附着在壁面上; 在过渡沸腾区域, 液滴底部的中央区域会和壁面存在部分接触. 接触情况的不同会影响子液滴的喷射和液滴在铺展后的动力学行为: 对于核态沸腾区域, 在整个液膜上会产生大量的子液滴喷射, 并且液滴在铺展后, 底部仍然会附着在壁面上; 对于过渡沸腾区域, 子液滴喷射会集中在液膜中央部分, 并且液滴在铺展后, 会发生回缩并弹起离开壁面. 由于采用的表面为光学不透明的硅表面, 因此, 本文将子液滴喷射的不同现象及液滴铺展后是否弹起, 作为区分三种沸腾区域的依据.[8 ] , 随后蒸汽泡会在浮力的作用下上升至液滴的自由表面破碎, 并产生大量的子液滴喷射. 如图2(a) 所示, 可以看到在液滴铺展过程中存在大量子液滴喷射的现象, 这种现象可以解释为: 当上升到液滴自由表面的蒸汽泡破碎后, 破碎点处会在表面波的作用下产生射流喷射, 进一步喷射的射流会断裂形成子液滴. 在液滴铺展完成后(例如图2(a) 中5.1 ms时), 液滴的底部液体仍然附着在壁面上, 直到蒸发完毕.图 2 在3个沸腾区域水滴撞击加热壁面的形貌图, 子液滴的喷射如红色圆圈及箭头所示 (a)核态沸腾区域, $We = 37$ , $T = 260{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ; (b)过渡沸腾区域回缩弹起模式, $We = 37$ , $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ; (c)过渡沸腾区域雾化弹起模式, 其中(c1)为$We = 69$ , $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ , (c2)为$We = 105$ , $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ; (d)膜态沸腾区域回缩弹起模式, 其中(d1)为$We = 25$ , $T = 400{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ , (d2)为$We = 25$ , $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ; (e)膜态沸腾区域雾化弹起模式, 其中(e1)为$We = 60$ , $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ , (e2)为$We = 129$ , $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ Figure2. Morphologies of water droplet impacting on heated surfaces in three boiling regimes, the red circles and arrows highlight the spray-like ejection of tiny droplets: (a) Nucleate boiling, $We = 37$ and $T = 260{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ; (b) retraction-bouncing mode in transition boiling regime, $We = 37$ and $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ; (c) bouncing-with-spray mode in transition boiling regime, $We = 69$ and $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ for (c1), and $We = 105$ and $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ for (c2); (d) retraction-bouncing mode in film boiling regime, $We = 25$ and $T = 400{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ for (d1), and $We = 25$ and $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ for (d2); (e) bouncing-with-spray mode in film boiling regime, $We = 60$ and $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ for (e1), and $We = 129$ and $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ for (e2).$We = 37$ , $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}{\kern 1pt} $ 时, 如图2(b) 所示, 可以看到液滴在铺展后会发生回缩, 随后在撞击时刻12.0 ms时弹起离开壁面, 并且这个过程在液膜中央区域会伴随着子液滴喷射的现象(红色圆圈所示). 这种液滴在达到最大铺展后回缩弹起离开壁面的弹起模式被称为回缩弹起模式. 当撞击速度较大时, 例如在$We = 69$ , $T = 380{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}{\kern 1pt} $ 时, 如图2(c1) 所示, 可以看到液滴会在没有明显回缩的情况下, 在6.5 ms时弹起离开壁面, 并且同样在液膜中央区域伴随着子液滴喷射的现象(红色箭头所示). 我们称这种弹起模式为雾化弹起, 并且这种弹起模式下的液滴驻留时间要远远小于回缩弹起模式下的驻留时间(6.5 ms vs. 12.0 ms). 当撞击速度进一步增大时, 例如在$We = 105$ , $T = 380\; ^\circ {\rm C}$ 时, 如图2(c2) 所示, 可以看到液滴外围指迹结构的形成以及由指迹结构破碎而产生的小液滴, 这种现象可以解释为液滴在较大的惯性下发生溅射[20 ] , 但是液滴的中央部分仍然在没有明显回缩的情况下弹起离开壁面, 其驻留时间也比回缩弹起模式下的驻留时间小很多(6.3 ms vs. 12 ms). 因此该模式也被称为雾化弹起模式.[4 ] , 并且壁面传递给液滴的热流密度会随之减少. 一般来说, 没有子液滴喷射现象产生时的壁面温度定义为液滴的动态Leidenfrost温度[7 ,10 -12 ] . 在这个沸腾区域同样可以观察到上述的两种弹起模式. 对于回缩弹起模式, 相比图2(d2) , 图2(d1) 所呈现的现象发生于一个相对较低的壁面温度($400{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ vs. $440\; ^\circ {\rm C}$ ), 但有同样的撞击韦伯数($We = 25$ ). 可以看到在图2(d2) 中, 子液滴喷射的现象再次发生, 并且与过渡沸腾区域相比, 子液滴喷射的现象会在整个液膜上发生, 而与核态沸腾相比, 子液滴的粒径更小且分布更均匀. 这可以解释为: 在膜态沸腾区域虽然液滴底部存在一层完整的蒸汽膜, 但是随着壁面温度的升高, 液滴内部的蒸汽泡增长速率也随之增大, 从而使得蒸汽泡脱离蒸汽膜然后上升到自由表面破碎这一过程变得更容易[10 ] . 当撞击速度进一步增加时, 例如在$We = 60$ , $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}{\kern 1pt} $ 时, 如图2(e1) 所示, 可以看到雾化弹起模式. 当$We \!=\! 129$ , $T = 440{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}{\kern 1pt} $ 时, 则可以看到液滴溅射现象及雾化弹起的弹起模式.[10 ] 对水滴撞击加热壁面的沸腾区域的分类为: 当壁面温度较低时, 依据是否存在子液滴喷射的现象, 将其分为接触沸腾和膜态沸腾; 当壁面温度较高时, 在膜态沸腾区域由于水滴会再次发生子液滴喷射的现象, 故进一步将膜态沸腾区域分为了稳定膜态沸腾(gentle film boiling)和雾化膜态沸腾(spray film boiling). 本文为了更清楚地表征上述的两种弹起模式及驻留时间的变化, 通过考虑液滴底部与壁面的接触情形对子液滴喷射现象及液滴铺展后是否弹起的影响, 将文献[10 ]中的接触沸腾区域分类为核态沸腾区域和过渡沸腾区域, 但并没有对膜态沸腾区域进行文献[10 ]中的分类, 而是依据两种弹起模式对过渡沸腾区域和膜态沸腾区域进行了分类.${D_0}$ 和撞击速度$V$ , 本文发现该弹起模式下的液滴驻留时间不受液滴黏度的影响, 如图3 所示.图 3 液体黏度对雾化弹起模式下驻留时间的影响(液滴直径为2.8 mm, 撞击速度为$1.2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm m} \cdot {{\rm s}^{{\rm - 1}}}$ )Figure3. Effect of liquid viscosity on the residence time of the bouncing-with-spray mode. The droplet diameter is 2.8 mm, and the impact velocity is $1.2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm m} \cdot {{\rm s}^{{\rm - 1}}}$ .[21 ] , 即[12 ,22 ,23 ] . 在本实验中, 回缩弹起模式下的无量纲驻留时间为2.3, 为了更清楚地表示液滴驻留时间的减少程度, 将雾化弹起模式下的驻留时间进行相同的无量纲化处理, 得出其无量纲驻留时间为1.4, 如图4 所示. 因此, 相比于回缩弹起模式, 雾化弹起模式下液滴的驻留时间大约减少40%.图 4 回缩弹起模式(空心圆)和雾化弹起模式(实心圆)下的无量纲驻留时间比较Figure4. Comparison of the dimensionless residence time in the retraction-bouncing mode (hollow circles) and in the bouncing-with-spray mode (solid dots).3.2.液滴驻留时间减少机理及两种弹起模式的过渡 -->3.2.液滴驻留时间减少机理及两种弹起模式的过渡 图5 为倾斜视角下液滴雾化弹起模式的图片序列, 可以看到, 在液滴撞击过程中, 液膜上会产生一个接一个的孔洞, 并伴随着子液滴喷射的现象. 这些孔洞在表面张力的作用下迅速扩大, 整个液膜会从这些孔洞回缩成几个部分(如图5 中红色箭头所示), 随后弹起离开壁面. 由于液滴的回缩距离减少, 因此回缩时间也相应减少, 进而液滴在壁面上的驻留时间得到减少. 这种液滴驻留时间减少的机理与液滴撞击带有微脊的超疏水表面的驻留时间的减少机理[16 ] 相似, 即壁面上的微脊会造成液滴在回缩过程中破碎成几个部分, 从而减少了液滴的回缩距离, 最终导致了驻留时间的减少. 对于雾化弹起模式, 液膜的破碎是由于液膜中蒸汽泡破碎造成的, 所以这个过程会伴随着子液滴喷射的现象. 实验中在更大的放大倍率下, 能够看到在液膜出现孔洞时, 即在撞击时刻为4.07 ms时存在子液滴喷射现象, 如图6 箭头所示. 另外, 文献[16 ]中通过改变液滴撞击在壁面上微脊的位置, 可以实现对液膜上破碎地点的控制, 而本文由蒸汽泡破碎所产生的孔洞位置和数目具有随机性, 难以通过一个简化的理论模型对液滴驻留时间的减少程度进行直接预测. 下面主要针对膜态沸腾区域驻留时间减少的雾化弹起模式的发生条件进行分析.图 5 倾斜视角下雾化弹起模式的序列图片($We = 82$ , $T = 450{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ )Figure5. Image series of the bouncing-with-spray mode in aerial view ($We = 82$ and $T = 450{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ).图 6 更大的放大倍率下液膜孔洞形成的图片序列(We =122, $T = 480{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ )Figure6. Image series of hole formation in the liquid film using greater magnification ($We = 122$ and $T = 480{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ^\circ {\rm C}$ ).图7(a) 所示. 当蒸汽泡的半径小于液膜的最小厚度时, 液膜上不会产生孔洞; 而当蒸汽泡的半径大于液膜的厚度时, 蒸汽泡则会在液滴达到最大铺展前破碎, 并在液膜上留下孔洞.图 7 (a)蒸汽泡破碎理论模型的示意图; (b)采用液滴自由振荡周期无量纲化后的液滴最大铺展时间; (c)对数坐标下膜态沸腾区域水滴的无量纲最大铺展直径和撞击韦伯数的关系图, ${{{D_{\max }}} / {{D_0}}} \sim W{e^n}$ ; (d)对数坐标下水滴在膜态沸腾区域由回缩弹起到雾化弹起模式过渡的$\Delta T \sim {V^{ - 1}}$ 边界线, 液滴直径为2.2 mm; (e)水滴撞击加热硅片的相图及从回缩弹起到雾化弹起模式下的过渡, 图中红色虚线为示意, 液滴直径为2.2 mm, “过渡”为过渡腾区域, “膜态”指膜态沸腾区域Figure7. (a) Schematic diagram for the theoretical model for the burst of vapor bubbles; (b) the time of maximum spreading diameter of water droplets normalized by droplet free oscillation period; (c) log-log plot for the normalized maximal spreading diameter of water droplets versus We in the film boiling regime, showing ${{{D_{\max }}} / {{D_0}}} \sim W{e^n}$ ; (d) log-log plot for $\Delta T \sim {V^{ - 1}}$ boundary line between the retraction-bouncing mode and the bouncing-with-spray mode in the film boiling regime for water droplets, the droplet diameter is 2.2 mm; (e) regime map for a water droplet impacting on a heated silicon wafer and the transition between the retraction-bouncing mode and the bouncing-with-spray mode, the red dashed line is only for eye guidance, the droplet diameter is 2.2 mm.h 为平均传热系数, $\Delta T = T - {T_{\rm s}}$ 为壁面的过热度, T 和${T_{\rm s}}$ 分别为壁面的温度及液体的饱和温度, A 为蒸汽泡的热传递面积, $\ell $ 为液滴的汽化潜热, 下标v表示“蒸汽”. 热传递的时间间隔$\Delta \tau $ 可由液滴达到最大铺展时的时间${\tau _0}$ 给出, 如图7(b) 所示, 其并不随着撞击速度的改变而改变, 并且和液滴的自由振荡周期成比例[24 ] . 在临界条件下, 蒸汽泡的半径${r_{\rm{v}}}$ 和液膜的最小厚度${b_{\min }}$ 相当, 其中, 液膜的最小厚度可以表示为[25 ,26 ] 3 )式中的传热系数h , 考虑在膜态沸腾下, 蒸汽层内部的热传递主要以导热形式进行[27 ] , 假设液滴底部蒸汽层具有均匀厚度$ \delta $ , 则通过蒸汽层单位面积的热流密度可以表示为${{{\lambda_{\rm{v}}}\Delta T} / \delta }$ , 其中${\lambda_{\rm{v}}}$ 为蒸汽的热导率, 因此液滴流体的汽化质量速率可以表示为${{{\lambda_{\rm{v}}}\Delta T} / {\delta \ell }}$ . 考虑在蒸汽层半径r 的区域内, 向外流动的蒸汽和液滴产生的蒸汽体积平衡, 有6 )式代入到(7 )式中, 并对其进行积分, 可以获得蒸汽层内压力分布为${p_a}$ 为大气压力, R 为液膜的半径. 通过对压力梯度$\left( {p\left( r \right) - {p_a}} \right)$ 进行积分, 可以获得使液膜上升的力, 并且这个力与液滴的重力和浮力之差$\left[ {{\text{π}}{R^2}b\left( {{\rho _{\rm{l}}} - {\rho_{\rm{v}}}} \right)g} \right]$ 平衡, 如图7(a) 所示. 则蒸汽层的厚度可以表示为10 )式中的液膜半径R 可以近似为液滴的最大铺展半径, 即图7(c) 所示, 其中$n = 0.35$ . 事实上, 关于液滴撞击加热壁面情况下液滴铺展尺度的研究可以在大量的文献中找到[10 ,12 ,22 ,23 ,28 ] , 并且指数n 会因壁面的结构不同而不同, 本实验所求得的指数n 与Tran等[10 ] 的研究接近, 即$n = 0.39$ .10 )式代入(3 )式, 并分别代入(4 )和(11 )式所求得临界条件下的b 和R , 可以得到$G{r^*} =$ $ {{g{\rho_{\rm{v}}}\left( {{\rho _{\rm{l}}} - {\rho_{\rm{v}}}} \right)R_0^3} / {\mu_{\rm{v}}^2}}$ , 蒸汽的普朗特数$P{r_{\rm{v}}} =$ $ {{{c_{p{\rm{v}}}}{\mu_{\rm{v}}}} / {{\lambda_{\rm{v}}}}}$ , 雅各比数$Ja = {{{c_{p{\rm{l}}}}\Delta T} / \ell }$ , 以及一个修正的傅里叶数$F{o^*} = {{{\lambda_{\rm{v}}}{\tau _0}A} / {({\rho_{\rm{v}}}}}{c_{p{\rm{v}}}}R_0^4)$ , 可以得出如下无量纲关系式:A 为定值. 因此, $G{r^*}$ , $P{r_{\rm{v}}}$ 和$F{o^*}$ 主要受液体的物性及液滴初始尺寸的影响, 而对于相同液体及相同的初始液滴尺寸, 液滴的物性参数及液滴达到最大铺展尺寸的时间${\tau _0}$ 可视为常数. 代入图7(c) 中的$n = 0.35$ , 则可以得到图7(d) 所示, 可以看到该幂次关系与实验数据吻合良好. 另外, 该理论模型同样可以解释在过渡沸腾区域, 从回缩弹起到雾化弹起模式过渡的壁面温度随着撞击韦伯数的增加而增加, 如图7(e) 所示的相图. 在过渡沸腾区域, 壁面传递给液滴的热流密度会随着壁面温度的上升而下降, 故在一定时间间隔${\tau _0}$ 内, 蒸汽泡的最大尺寸会随着壁面温度的升高而减小, 因此液膜需要变得更薄, 即更大的韦伯数, 以满足临界条件下${r_{\rm v}} \sim {b_{\min }}$ . 所以在过渡沸腾区域, 从回缩弹起到雾化弹起模式过渡的撞击韦伯数会随着壁面温度的上升而增加.4.结 论 本文通过高速摄影技术对不同液体种类的液滴撞击加热壁面进行了研究, 主要结论如下:${r_{\rm v}} \sim {b_{\min }}$ 提出了一个简化理论模型, 依据该模型得出了膜态沸腾区域两种弹起模式的过渡边界的幂次关系, 即$\Delta T \sim {V^{ - 1}}$ , 并且与实验数据吻合良好; 

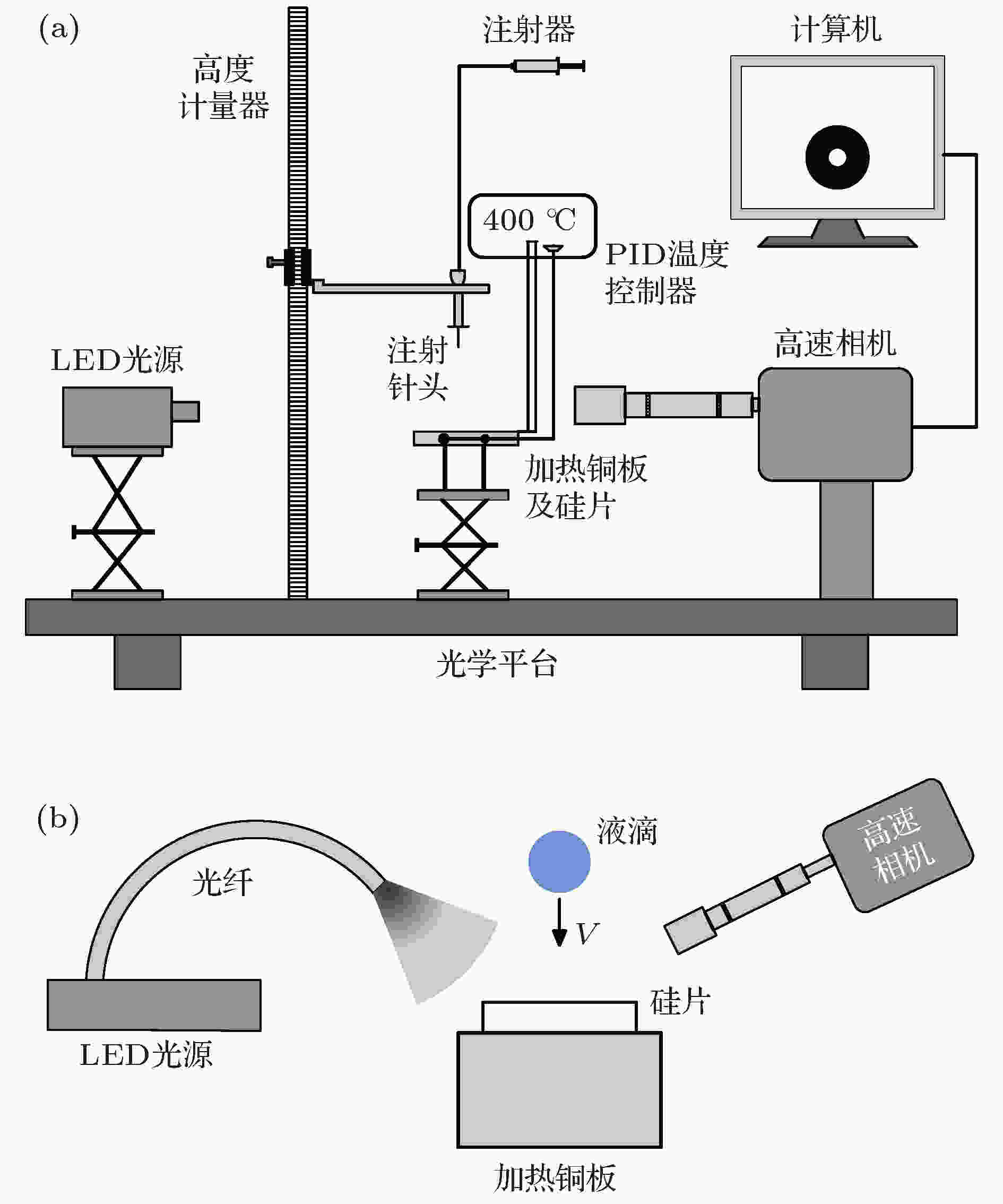 图 1 液滴撞击加热壁面的实验装置示意图 (a)水平视角; (b)倾斜视角
图 1 液滴撞击加热壁面的实验装置示意图 (a)水平视角; (b)倾斜视角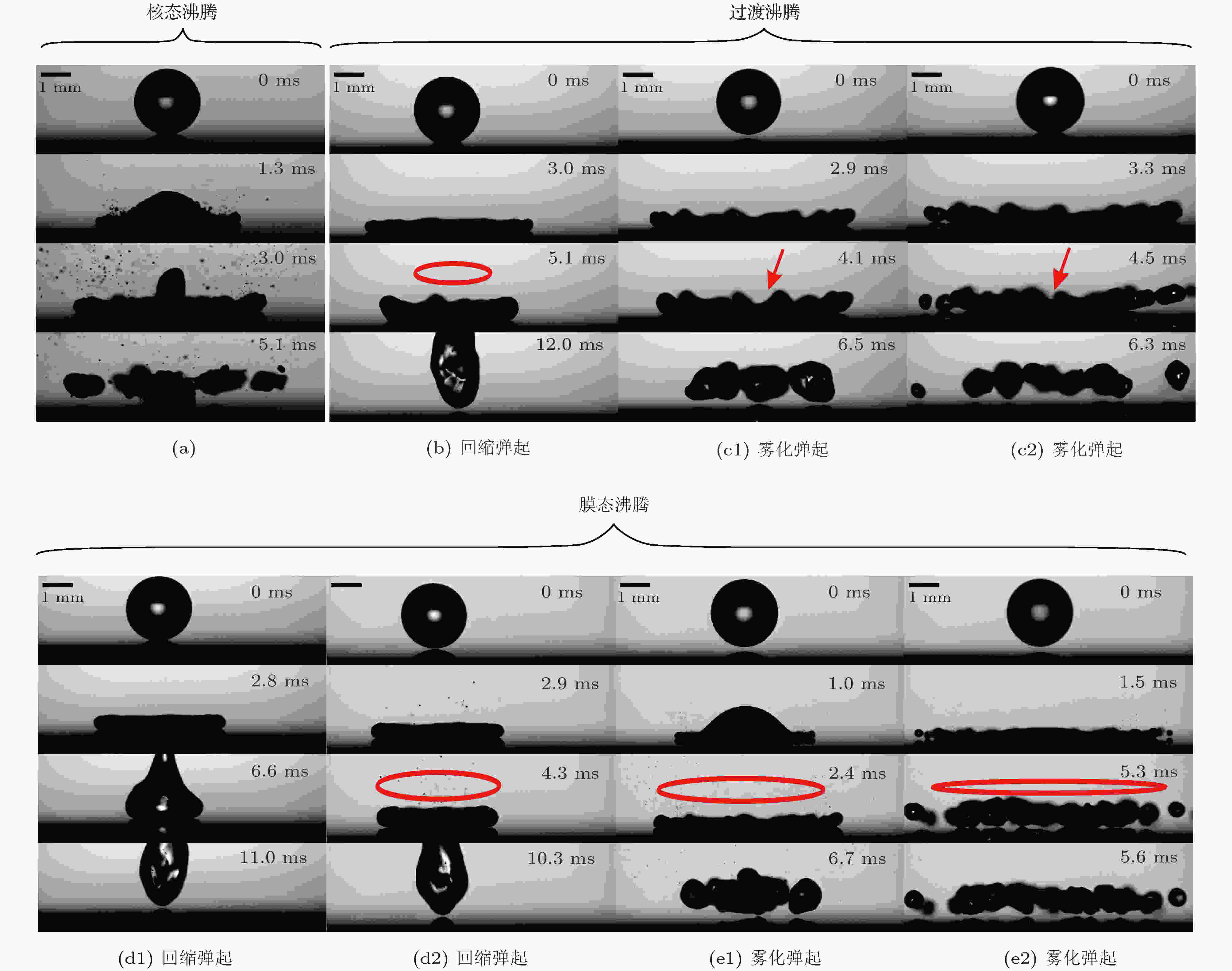 图 2 在3个沸腾区域水滴撞击加热壁面的形貌图, 子液滴的喷射如红色圆圈及箭头所示 (a)核态沸腾区域,
图 2 在3个沸腾区域水滴撞击加热壁面的形貌图, 子液滴的喷射如红色圆圈及箭头所示 (a)核态沸腾区域, 


















































































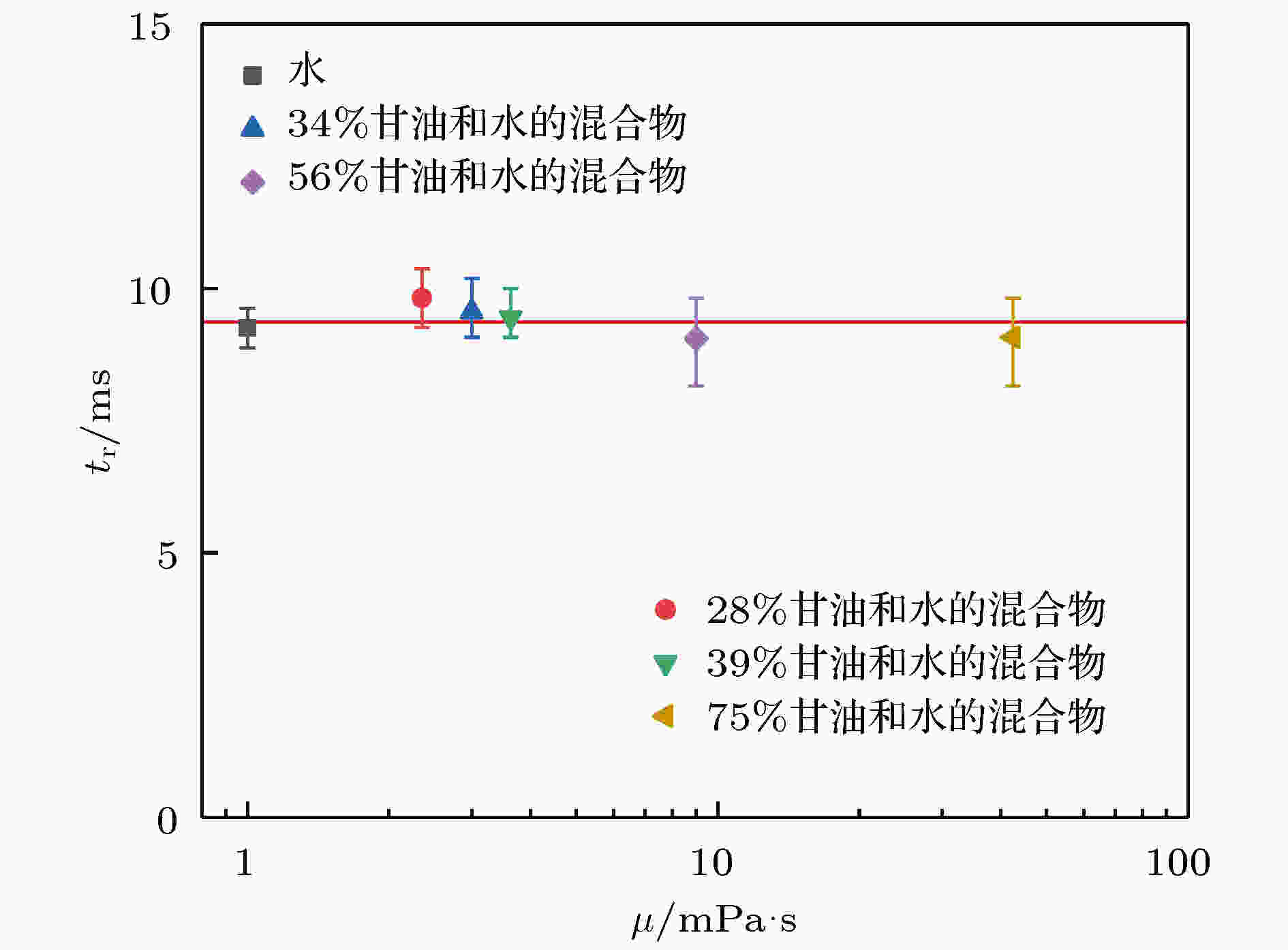 图 3 液体黏度对雾化弹起模式下驻留时间的影响(液滴直径为2.8 mm, 撞击速度为
图 3 液体黏度对雾化弹起模式下驻留时间的影响(液滴直径为2.8 mm, 撞击速度为

 图 4 回缩弹起模式(空心圆)和雾化弹起模式(实心圆)下的无量纲驻留时间比较
图 4 回缩弹起模式(空心圆)和雾化弹起模式(实心圆)下的无量纲驻留时间比较 图 5 倾斜视角下雾化弹起模式的序列图片(
图 5 倾斜视角下雾化弹起模式的序列图片(



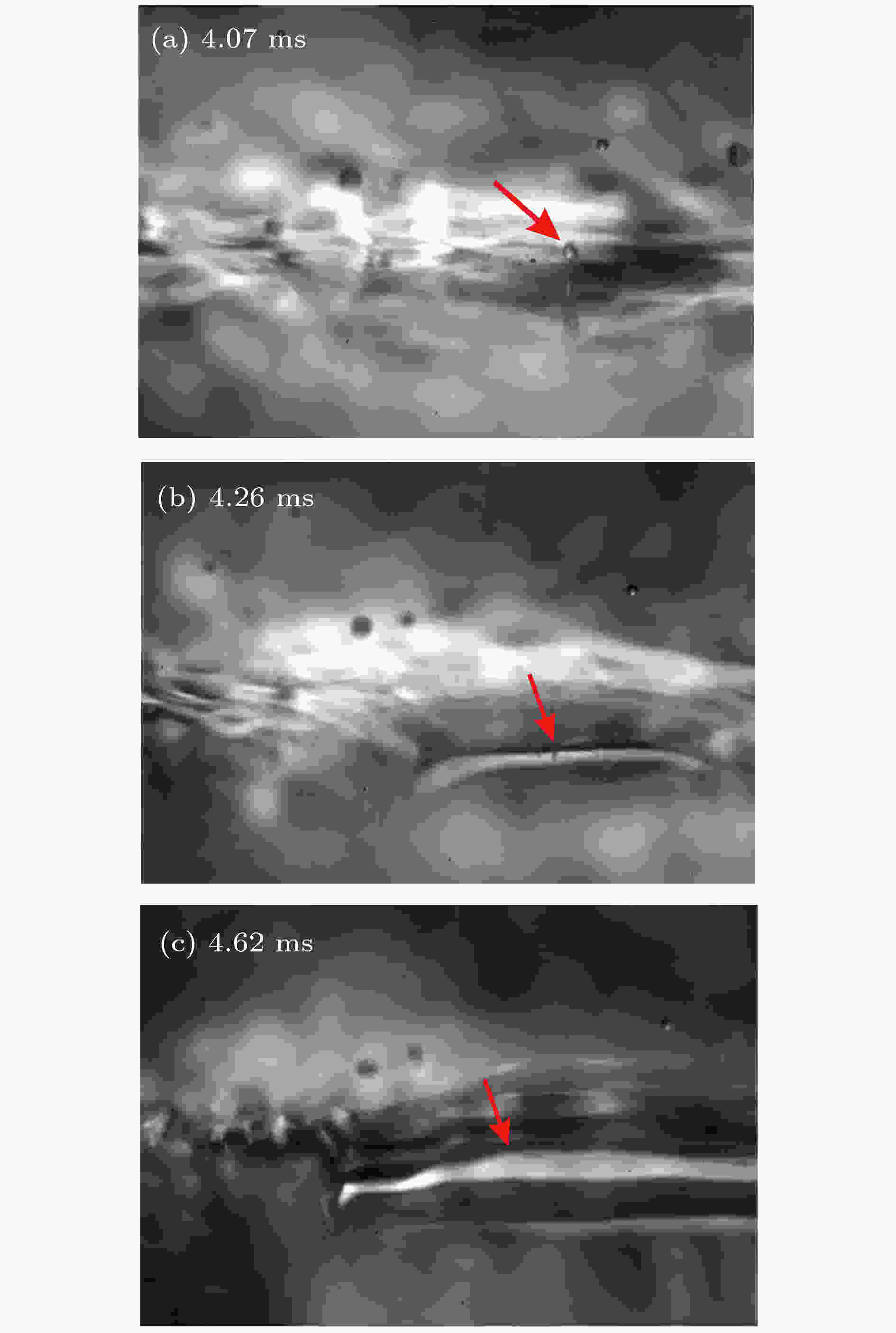 图 6 更大的放大倍率下液膜孔洞形成的图片序列(We =122,
图 6 更大的放大倍率下液膜孔洞形成的图片序列(We =122, 


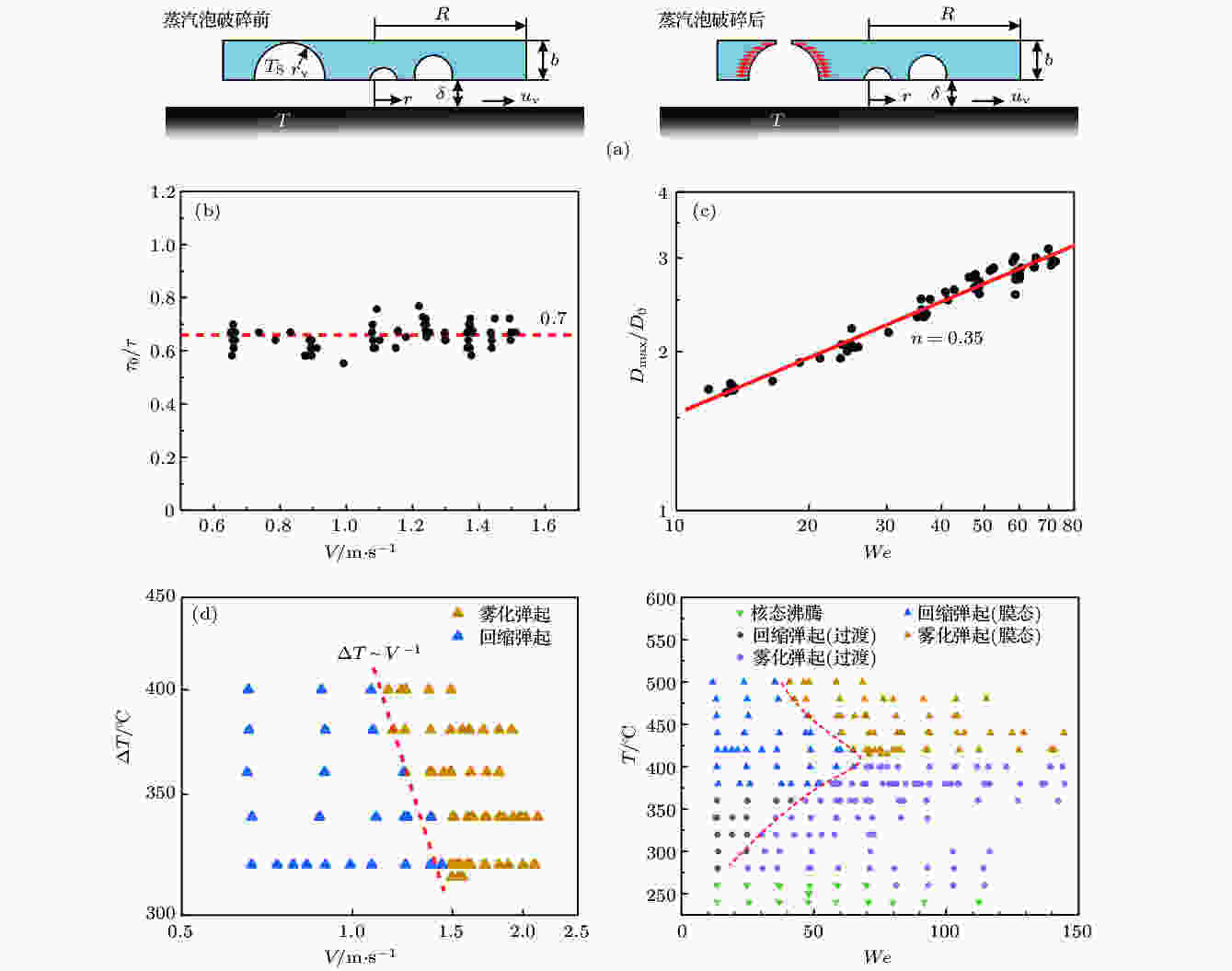 图 7 (a)蒸汽泡破碎理论模型的示意图; (b)采用液滴自由振荡周期无量纲化后的液滴最大铺展时间; (c)对数坐标下膜态沸腾区域水滴的无量纲最大铺展直径和撞击韦伯数的关系图,
图 7 (a)蒸汽泡破碎理论模型的示意图; (b)采用液滴自由振荡周期无量纲化后的液滴最大铺展时间; (c)对数坐标下膜态沸腾区域水滴的无量纲最大铺展直径和撞击韦伯数的关系图, 


































