摘要: 本文建立了考虑两种动力学起源的连续时间随机行走模型, 特别是在模型中明确区分了对流和扩散两种因素对粒子输运过程的影响. 通过改变各因素的相对权重, 描述了从正常输运到反常输运的过渡, 并建立了相应的输运方程. 该模型成功描述了复杂孔隙介质中溶质输运过程随着Péclet数的变化而经历的定性改变.
关键词: 动力学起源 /
连续时间随机行走 /
反常输运 /
宏观输运方程 English Abstract Continuous time random walk model with advection and diffusion as two distinct dynamical origins Yang Xiao-Rong 1 ,Wang Qiong 1 ,Ye Tang-Jin 2 ,Tudeng Ci-Ren 1 1.School of Science, Tibet University, Lhasa 850000, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11465017).Received Date: 17 January 2019Accepted Date: 09 April 2019Available Online: 01 July 2019Published Online: 05 July 2019Abstract: Modeling the solute transport in geological porous media is of both theoretical interest and practical importance. Of several approaches, the continuous time random walk method is a most successful one that can be used to quantitatively predict the statistical features of the process, which are ubiquitously anomalous in the case of high Péclet numbers and normal in the case of low Péclet numbers. It establishes a quantitative relation between the spatial moment of an ensemble of solute particles and the waiting time distribution in the model. However, despite its success, the classical version of this model is a " static” one in the sense that there is no tuning parameter in the waiting time distribution that can reflect the relative strength of advection and diffusion which are two mechanisms that underlie the transport process, hence it cannot be used to show the transition from anomalous to normal transport as the Péclet numbers decreases. In this work, a new continuous time random walk model is established by taking into account these two different origins of solute particle transport in a geological porous medium. In particular, solute transitions due to advection and diffusion are separately treated by using a mixture probability model for the particle’s waiting time distribution, which contains two terms representing the effects of advection and diffusion, respectively. By varying the weights of these two terms, two limiting cases can be obtained, i.e. the advection-dominated transport and the diffusion-dominated transport. The values of scaling exponent β of the mean square displacement versus time, ${\left( {\Delta {x} } \right)^2} \sim {t^{\rm{\beta }}}$ , are derived for both cases by using our model, which are consistent with previous results. In the advection dominant case with the Péclet number going to infinity, the scaling exponent β is found to be equal to $3 - {\rm{\alpha }}$ where ${\rm{\alpha }} \in \left( {1,2} \right)$ is the anomaly exponent in the advection-originated part of the waiting time distribution that ${{\rm{\omega }}_1}\left( {t} \right) \sim {{t}^{ - 1 - {\rm{\alpha }}}}$ . As the Péclet number decreases, the diffusion-originated part of the waiting time distribution begins to have a stronger influence on the transport process and in the limit of the Péclet number going to 0 we observe a gradual transition of β from $3 - {\rm{\alpha }}$ to 1, indicating that the underlying transport process changes from anomalous to normal transport. By incorporating advection and diffusion as two mechanisms giving rise to solute transport in the continuous time random walk model, we successfully capture the qualitative transition of the transport process as the Péclet number is varied, which is, however, elusive from the classical continuous time random walk model. Also established are the corresponding macroscopic transport equations for both anomalous and normal transport, which are consistent with previous findings as well. Our model hence fully describes the transition from normal to anomalous transport in a porous medium as the Péclet number increases in a qualitative and semi-quantitative way.Keywords: dynamical origins /continuous time random walk /anomalous transport /macroscopic transport equation 全文HTML --> --> --> 1.引 言 近年来, 反常输运的研究受到了极大的关注. 人们发现在很多地质和生物系统中广泛存在反常输运现象并提出了相应的研究模型[1 -9 ] . 与经典的正常输运过程不同, 反常输运通常表现出1)非高斯的传播子, 以及可能带来的2)粒子均方位移与时间的非线性标度关系. 比如, 一系列研究孔隙介质中示踪剂粒子输运过程的实验和数值模拟结果[10 -13 ] 表明: 当Péclet数(Pe)较大时, 即对流相比于扩散对粒子输运行为的影响重要得多时, 上述两种反常性质其实是“正常”的, 它们是一般孔隙介质输运过程的“典型”特征. 近期的研究表明这种反常输运的典型性是流体动力学与孔隙结构耦合的结果[14 -17 ] . 由于边界层的影响, 孔隙介质的壁面附近存在较大的速度梯度, 引起了非均匀的空间速度分布, 而孔隙空间的结构复杂性加剧了速度分布的异质性. 当流场对输运过程起主要影响, 并且流场的速度分布具有强烈的异质性时, 粒子的输运行为将严重偏离经典的对流扩散方程所做出的预测, 出现反常行为. 反之, 当Pe变小, 即扩散的作用变得大于对流的作用时, 上述的反常现象逐渐消失, 粒子的输运行为表现为正常的, 可以由达西尺度的对流扩散方程描述, 同时传播子为高斯型, 且粒子的均方位移与时间呈线性标度关系[18 -20 ] .[13 ,17 ] . 本文的目的即是对这种改变进行初步探索, 提出理论上的定性和半定量(如均方位移与时间的标度指数)理解. 本文的结果对于地下水污染物运移行为的认识、模拟以及预测具有一定的理论和现实意义.2.考虑对流和扩散两种动力学起源的连续时间随机行走模型 22.1.建模原则 2.1.建模原则 采取经典的连续时间随机行走模型对孔隙介质中的输运过程进行建模. 之前的工作表明该模型可以成功描述一系列反常输运过程, 包括有机大分子在细胞内的扩散过程, 以及溶质分子在孔隙介质中的输运等. 对于我们感兴趣的岩土介质中的输运过程, 近年来发展起一种新的技术, 即对岩土孔隙介质进行扫描, 并对扫描图像进行处理得到相应的孔隙空间. 在孔隙空间上, 人们可以进行流体动力学模拟, 直接求解Navier-Stokes方程和对流扩散方程来考察输运过程[13 ,17 ] ; 或者可以进一步对孔隙空间进行简化抽象, 将其看成一个网络, 这样可以利用复杂网络研究的一些结果考察网络结构对输运性质的影响[21 ] . 对于前者, 人们发现连续时间随机行走模型可以成功解释观察到的输运现象; 对于后者, 孔隙网络提供了一个天然的框架, 把经典的建立在规则晶格上的连续时间随机行走模型推广到网络上. 孔隙网络中的节点为较大的“孔”, 而连边为相对狭长的“喉道”. 孔隙空间的结构, 特别是孔和喉道的形成与具体的物理过程相关. 比如对于典型的沉积岩, 孔喉的形成是颗粒物质沉降后在长期的地质作用下形成的, 不同类型岩石的孔隙结构也有不同的特征. 图1 给出了取自拉萨周围地区的一块岩心样本的CT扫描图像, 以及相应的孔隙空间. 通过这些图像信息, 可以建立相应的孔隙网络. 我们发现连续时间随机行走理论仍然可以对网络上的输运性质进行解释. 关于这方面的具体数值模拟结果我们将在另外的工作中报道, 本文主要讨论与此相关的理论建模方面的问题.图 1 拉萨周边地区某岩心样本的CT扫描图像(左)及其对应的孔隙空间(右)Figure1. Left: Micro-CT image of a rock sample from Lhasa; Right: the corresponding pore space extracted from the left image.ω (t ). 本文不考虑前者可能带来的反常结果, 如Lévy飞行[6 ,7 ] , 因为当孔隙介质不存在宏观天然裂缝的时候, 不会出现长距离的输运. 因此只考虑后者可能带来的影响. 众所周知, 理论上当等待时间的一阶矩发散, 或者一阶矩有限而二阶矩发散时, 会出现反常输运现象[4 ,18 ] . 生物大分子在细胞内的反常扩散是第一种情况的典型代表; 而在存在对流的情况下孔隙介质中的溶质输运过程是后者的典型代表. 在此过程中, 粒子的输运过程明显受到对流和扩散的共同影响, 具有双重的动力学起源, 但是在传统的连续时间随机行走模型中, 等待时间分布并未区分这两者分别的影响, 从而物理意义不是特别明确, 无法用于考察对流和扩散两种机制对输运过程影响的区别.[3 ,4 ] , 在等待时间分布中明确引入了对流和扩散对粒子跃迁过程的影响. 为了引入等待时间分布, 我们先考虑复杂孔隙介质中的流速场分布. 假设孔隙介质的复杂结构可以使得流速场足够“随机”(通常是可以接受的), 并且我们主要关注的是宏观压力降方向的输运过程, 那么可以考虑速度绝对大小的分布f (v ). 对于一个局域特征长度l c , 粒子跃迁该长度所需要的时间是 $t = \dfrac{{{l_{\rm{c}}}}}{v} $ . 不失一般性, 令lc = 1, 以此定义粒子的等待时间, 则有 $\omega \left( t \right) = f\left( {\dfrac{1}{t}} \right)\left| {\dfrac{{{\rm{d}}v\left( t \right)}}{{{\rm{d}}t}}} \right| = f\left( {\dfrac{1}{t}} \right){t^{ - 2}}$ . 注意该公式实际上考虑的是Pe为无穷大的情况下等待时间的分布, 即只考虑对流, 并没有考虑扩散的影响. 然而数值计算的结果表明, 当Pe增加到一定程度时, 即对流相对于扩散的作用强到一定程度时, 该幂律分布即可以达到很好的近似[17 ] . 文献中一般以此时的ω (t )分布来分析反常输运的均方位移随时间变化的幂律指数. 但粒子实际上同时受到对流和扩散作用的影响, 一般来说, 速度大小的概率分布式是比较复杂的, 并且显式依赖于流场的边界条件、孔隙结构、温度、流体黏度等. 但在此并不关注其可能的精确表达式, 而是研究在一阶近似下这些可能的分布函数的共性特征. 为此, 作为对经典模型的一个直接推广, 本文把f(v) 写成一个混合模型的形式:a 1 ≥ 0, a 2 ≥ 0, 且a 1 +a 2 = 1, f 1 为对流引起的粒子跃迁速度大小的概率密度分布函数, 而f 2 为由扩散引起的粒子跃迁速度大小的概率密度分布函数. 该模型形式上区分了对流和扩散的不同影响, 在物理上, 不同的输运机制体现为f 1 和f 2 统计性质的定性区别. 对流和扩散对输运过程的相对影响力体现在权重因子a 1 和a 2 上. 当a 1 →1, 对流起主导作用; 当a 2 →1, 扩散起主导作用. 考虑到基于对流与基于扩散的输运过程呈现出定性上完全不同的特点, 本文在一阶近似下把总的速度分布写成这两种因素的线性叠加, 这就是本文分析的基本出发点. 基于该模型, 可以定性和半定量地研究输运过程统计特征的变化.$ \omega \left( t \right) = {a_1}{{\rm{\omega }}_1}\left( t \right) + {a_2}{{\rm{\omega }}_2}\left( t \right)$ , 其中${\omega _1}\left( {t} \right) = $ ${f_1}\left( {\dfrac{1}{t}} \right){t^{ - 2}}$ , ${\omega _2}\left( {t} \right) = {f_2}\left( {\dfrac{1}{t}} \right){t^{ - 2}}$ . 根据其物理意义, ω 1 和ω 2 也具有定性上完全不同的统计特征. 实验和数值模拟结果表明ω 1 一般会表现出幂律分布, 特别是在我们所关心的砂岩等典型的岩土介质模型中 ${\omega _1}\left( t \right)\sim{t^{ - 1 - \alpha }}{\rm{}}(1 < \alpha < 2)$ . 这即是说, 该分布的一阶矩有限而二阶矩发散. 而ω 2 对应着正常的扩散过程, 满足一、二阶矩均有限. 在此强调, 本文不关注这些分布函数的特定形式, 因为在定性和半定量上重要的是上述的统计特征, 而具体形式上的区别只会带来定量的区别. 对于0 < α < 1的情况, 虽然实验上尚不明确其在岩土介质中是否典型, 但也可以在本文的理论框架内研究, 本文第2.4 节将对其进行讨论. 图2 定性描绘了ω (t )的标度形式如何影响了输运行为的定性特征.图 2 等待时间分布ω (t )~t –1–α 示意图, 不同统计特征导致定性上不同的输运行为. 以α = 2为界, 当α > 2时输运行为是正常的, 当0 < α < 2时为反常.本文尤其关注1 < α < 2的情况Figure2. Schematic of the waiting time distribution ω (t )~t –1–α . The value of α qualitatively determines the transport dynamics. When α > 2, the transport behavior is normal; while when 0 < α < 2, anomalous transport appears. In this work, we focus on the case 1 < α < 2.2.2.理论分析 -->2.2.理论分析 仍然保留经典的连续时间随机行走模型的理论分析框架, 考虑在t = 0时刻粒子位于x = 0, 可以写出粒子的跃迁方程[3 ,10 ] :η (x ,t )是粒子“刚刚”在t 时刻到达x 点的概率密度, λ 是跃迁位移的概率密度. 那么粒子在t 时刻仍处于x 点的概率密度为$\psi \left( t \right) = 1 -\displaystyle\int_0^t \omega \left( {t'} \right){\rm{d}}t'$ 为粒子在t 这么长一段时间仍未离开x 的概率. 对空间变量x 进行Fourier变换, 对时间变量t 进行Laplace变换, 得到$\lambda \left( k \right) = \displaystyle\int_{ - \infty }^\infty {{\rm{e}}^{{\rm{i}}kx}}\lambda \left( x \right){\rm{d}}x$ , $\omega \left( u \right) = \displaystyle\int_0^\infty \omega \left( t \right)$ ${{\rm{e}}^{ - ut}}{\rm{d}}t$ , 则λ (k )具有良好的性质, 不会导致反常输运. 这在岩土类孔隙介质中是合理的假设, 因为溶质粒子的跃迁距离因为孔隙结构的限制而不会具有特别大的差异. 则可以在k = 0的邻域将λ (k )展开为$l = \displaystyle\int_{ - \infty }^\infty \lambda \left( x \right)x{\rm{d}}x$ , ${\sigma ^2} =\displaystyle\int_{ - \infty }^\infty \lambda \left( x \right){x^2}{\rm{d}}x$ .$\omega \left( u \right) = {a_1}{\omega _1}\left( u \right) + {a_2}{\omega _2}\left( u \right)$ . 如前所述, 研究 ${\omega _1}\left( t \right)\sim{t^{ - 1 - \alpha }}\left( {1 < \alpha < 2} \right)$ 的情况, 类似地, 在u = 0的邻域将其渐进展开得到:${\left\langle t \right\rangle _1}= \mathop \smallint \nolimits_0^\infty t{\omega _1}\left( t \right){\rm{d}}t$ , Cα 为某个常数. 对于ω 2 , 其具有有限的一、二阶矩, 同样将其展开得到 ${\omega _2}\left( u \right) \approx 1 - {\left\langle t \right\rangle _2}u + O\left( {{u^2}} \right)$ , 类似 ${\left\langle t \right\rangle _2} = \displaystyle\int_0^\infty t{\omega _2} $ $\left( t \right){\rm{d}}t$ . 综合这两个结果可以得到当u $\ll 1$ 时:$ A = \dfrac{1}{{{a_1}{\langle t\rangle_1} + {a_2}{\langle t\rangle_2}}} $ , $ B = - {a_1}{C_\alpha }{A^2}$ . 注意 A = $ A\left( {{a_1},{a_2}} \right) $ 是权重因子a 1 , a 2 的函数, 而B = B (a 1 )只是a 1 的函数. 这意味着当对流起主导时, A 和B 同时不为0; 当扩散起主导时, 只有A 不为0, 而B 为0, 即所有含有B 的表达式此时应该都趋近于0. 这点在下面的分析中会用到.$\langle x(t)\rangle$ , 其Laplace 变换 $ \left\langle {x\left( u \right)} \right\rangle = - {\rm{i}}\left.\dfrac{{\partial W}}{{\partial k}}\right |_{k=0} \approx \dfrac{l}{{u\left[ {1 - \omega \left( u \right)} \right]}} $ , 所以$ \left\langle {x\left( t \right)} \right\rangle \approx lAt + \dfrac{{lB}}{{\varGamma \left( {3 - \alpha } \right)}}{t^{2 - \alpha }}\sim t$ ($t→$ $ \infty $ ), 所以不论a 1 是否为零, 即不论是对流还是扩散主导输运行为, 粒子的平均位移与时间的标度关系总是线性的.$\left\langle {x^2(t)} \right\rangle $ , 它的Laplace变换为 $ \left\langle {{x^2}\left( u \right)} \right\rangle = - \left.\dfrac{{{\partial ^2}W}}{{\partial {k^2}}}\right |_{k=0} \approx $ $\dfrac{{2{l^2}}}{{u{{\left[ {1 - \omega \left( u \right)} \right]}^2}}} + \dfrac{{{\sigma ^2}}}{{u\left[ {1 - \omega \left( u \right)} \right]}} $ , 经过推导可得:$\left\langle {{x^2}\left( t \right)} \right\rangle \approx {l^2}{A^2}{t^2} + \dfrac{{4{l^2}AB}}{{\Gamma \left( {4 - \alpha } \right)}}{t^{3 - \alpha }} +$ $ \dfrac{{2{l^2}{B^2}}}{{\Gamma \left( {5 - 2\alpha } \right)}}{t^{4 - 2\alpha }} + {\sigma ^2}At + \dfrac{{{\sigma ^2}B}}{{\Gamma \left( {3 - \alpha } \right)}}{t^{2 - \alpha }}.$ 10 )式可见, 当a 1 → 0, 即B → 0, $\left\langle {\Delta {x^2}} \right\rangle$ ~ t , 否则$\left\langle {\Delta {x^2}} \right\rangle$ ~$t^{3-\alpha}$ . 物理上, a 1 → 0意味着对流的作用被极大削弱, 扩散为主导项, 所以表现出$\left\langle {\Delta {x^2}} \right\rangle$ ~t 的标度律, 即此时为正常扩散. 反之, 若a 2 →0, 则对流占据主导, 此时表现出反常输运的特征$\left\langle {\Delta {x^2}} \right\rangle$ ~$t^{3-\alpha} $ . 而在一般情况下, 两者都不可以被忽略时, $\left\langle {\Delta {x^2}} \right\rangle $ 随着时间的变化关系介于$ t^{3-\alpha}$ 和t 之间, 取决于(10 )式右边各项的相对大小关系.10 )式, 在定性和半定量上, 我们提出的考虑对流和扩散两种动力学起源的连续时间随机行走模型给出了输运过程的合理理论解释.2.3.宏观输运方程 -->2.3.宏观输运方程 基于上述结果, 还可以进一步发展具有工程意义的宏观输运方程, 用于描述地下水污染物的运移行为. 通过对感兴趣的地理区域的岩石进行扫描分析建模, 计算流体力学模拟[13 ,17 ] , 可以理论上得到反常幂指数α ; 通过岩心物理实验结果, 可以对下述方程中的各项系数进行拟合[3 ] , 最终可以得到符合该地区岩土介质特点的输运方程.$W\left( {k,u} \right) \!\approx\! \dfrac{1}{u}\dfrac{1}{{1 \!+\! \dfrac{{1 \!-\! \lambda \left( k \right)}}{{1 \!-\! \omega \left( u \right)}}}}$ . 将之前的$1-\lambda(k)$ 与 $1- \omega (u)$ 代入得:${v_1} = lA$ , ${D_1} = \dfrac{{{\sigma ^2}A}}{2}$ , ${v_\alpha } = lB$ , ${D_\alpha } = \dfrac{{{\sigma ^2}B}}{2}$ .$ {}_0 D_t^{\alpha - 1} $ 为Riemann-Liouville算子[4 ] .a 1 →0, 即B →0时, vα ,Dα →0, 得到了经典的对流扩散方程, 反之, 则得到了用于描述反常输运的分数阶对流方程. 注意(12 )式在形式上与以前得到过的方程一致[17 ,18 ] , 但本文是在区分对流和扩散的物理效果上重观此结果, 具有更清楚的物理意义. 这些系数(v 1 , D 1 , vα , Dα )一方面由对流和扩散的相对重要性决定, 另一方面也和孔隙空间的结构紧密相关. 特别是后两者, 它们实际上都依赖于α , 而如上所述, α 由流体动力学和孔隙结构给出[17 ] .2.4.讨 论 -->2.4.讨 论 以上主要研究的是在连续时间随机行走模型中, 由对流决定的那部分等待时间分布函数 ${{\rm{\omega }}_1}\left( t \right)\sim{t^{ - 1 - \alpha }}$ 中α 的取值范围是1 < α < 2. 这个取值范围是由之前工作的数值模拟结果决定的[17 ] , 具有明确的物理对应. 然而, 从理论完整性角度出发, 在这里接着讨论0 < α < 1的情况. 虽然在模拟中暂时并没有观察到这种情况出现的明确证据, 在理论上它仍是值得考虑的. 在这种情况下, ω 1 (t )的一阶矩发散, 而ω 2 (t )的一阶矩却仍然是有限的. 这与1 < α < 2的情况不同, 后者的ω 1 (t )和ω 2 (t )都是直到(1+α )阶矩为有限, 所以可以统一得到展开式(7 ), 而现在不能简单套用类似的展开. 将ω 1 (t )和ω 2 (t )分别进行Laplace变换, 可以得到 ${\omega _1}\left( u \right) \approx 1 - C{'_\alpha }{u^\alpha }$ , 其中$C{'_\alpha }$ 为一常数, 以及 ${\omega _2}\left( u \right) \approx 1 - {\left\langle t \right\rangle _2}u$ , 进而可知$1 - \omega \left( u \right) \approx $ $ {a_1}{{C'}_\alpha }{u^\alpha } + {a_2}{\left\langle t \right\rangle _2}u \equiv A'\left( {{a_1}} \right){u^\alpha } + B'\left( {{a_2}} \right)u$ , 其中A ′和B ′为两个分别依赖于权重a 1 和a 2 的常数, 并且 $\dfrac{1}{{1 - \omega \left( u \right)}} \approx \dfrac{1}{{A{\rm{'}}\left( {{a_1}} \right){u^\alpha } + B{\rm{'}}\left( {{a_2}} \right)u}}$ . 显然如果扩散效应主导时, 即a 1 = 0, 则A ′ (a 1 ) = 0; 而如果对流主导, 即a 2 = 0, 则B ′ (a 2 ) = 0. 重复上文的推导可得:a 1 = 0的极限下 $\left\langle {x\left( u \right)} \right\rangle \approx \dfrac{l}{{B'\left( {{a_2}} \right){u^2}}}$ , 即 $\left\langle {x\left( t \right)} \right\rangle \approx $ $\dfrac{l}{{B'\left( {{a_2}} \right)}}t$ , 而 $\left\langle {{x^2}\left( u \right)} \right\rangle \approx \dfrac{{2{l^2}}}{{u{{\left[ {B'\left( {{a_2}} \right)u} \right]}^2}}} + \dfrac{{{\sigma ^2}}}{{u\left[ {B'\left( {{a_2}} \right)u} \right]}}$ , 即 $\left\langle {{x^2}\left( t \right)} \right\rangle \approx \dfrac{{{l^2}}}{{{{\left[ {B'\left( {{a_2}} \right)} \right]}^2}}}{t^2} + \dfrac{{{\sigma ^2}}}{{B'\left( {{a_2}} \right)}}t$ , 所以$\left\langle {\Delta {x^2}} \right\rangle \approx$ $ \dfrac{{{\sigma ^2}}}{{B'\left( {{a_2}} \right)}}t \sim t$ , 这即是重现了正常输运的结果. 另一方面, 在对流主导, a 2 = 0的极限下$\left\langle {x\left( u \right)} \right\rangle \approx $ $\dfrac{l}{{A'\left( {{a_1}} \right){u^{1 + \alpha }}}}$ , 即 $\left\langle {x\left( t \right)} \right\rangle \approx \dfrac{l}{{A'\left( {{a_1}} \right)\varGamma \left( {1 + {\rm{\alpha }}} \right)}}{t^\alpha }$ , 而 $\left\langle {{x^2}\left( u \right)} \right\rangle \approx \dfrac{{2{l^2}}}{{u{{\left[ {A'\left( {{a_1}} \right){u^\alpha }} \right]}^2}}} + \dfrac{{{\sigma ^2}}}{{u\left[ {A'\left( {{a_1}} \right){u^\alpha }} \right]}}$ , 即$\left\langle {{x^2}\left( t \right)} \right\rangle \approx \dfrac{{2{l^2}}}{{{{\left[ {A'\left( {{a_1}} \right)} \right]}^2}\varGamma \left( {1 \!+\! 2{\rm{\alpha }}} \right)}}{t^{2\alpha }} \!+\! \dfrac{{{\sigma ^2}}}{{\left[ {A'\left( {{a_1}} \right)} \right]\varGamma \left( {1 \!+\! \alpha } \right)}}{t^\alpha },$ $ \begin{aligned}\left\langle {\Delta {x^2}} \right\rangle \approx & \left ( \dfrac{{2{l^2}}}{{{{\left[ {A'\left( {{a_1}} \right)} \right]}^2}\varGamma \left( {1 + 2\alpha } \right)}} - {\left[ {\dfrac{l}{{A'\left( {{a_1}} \right)\varGamma \left( {1 + \alpha } \right)}}} \right]^2}\right ) {t^{2\alpha }} +\\ &\dfrac{{{\sigma ^2}}}{{\left[ {A'\left( {{a_1}} \right)} \right]\varGamma \left( {1 + \alpha } \right)}}{t^\alpha } \sim {t^{2\alpha }},\end{aligned} $ $\dfrac{2}{{\varGamma \left( {1 + 2\alpha } \right)}} - \dfrac{1}{{\varGamma {{\left( {1 + \alpha } \right)}^2}}} > 0$ 在0 < α < 1的情况下总是成立的, 所以$\left\langle {\Delta {x^2}} \right\rangle $ 的主导项是t 2α . 这体现了另一种反常输运的特征, 这种类型的反常输运在岩土类孔隙介质中的普遍性还需要实验和数值模拟上的进一步探索. 当a 1 和a 2 都非零时, 输运行为介于这两者之间.a 1 = 0的极限下, 可以得到描述正常输运过程的经典对流扩散方程, 而在a 2 = 0的极限下, $W\left( {k,u} \right) \approx \dfrac{{{1/u}}}{{1 + \dfrac{{ - {\rm{i}}v{'_\alpha }k + D{'_\alpha }{k^2}}}{{{u^\alpha }}}}}$ , 其中$v{'_\alpha } = \dfrac{l}{{C{'_\alpha }}}$ , 而 $D{'_\alpha } = \dfrac{{{{\rm{\sigma }}^2}}}{{2C{'_\alpha }}}$ , 其逆变换得到相应的输运方程为α < 2的情况, 但是原则上可以把0 < α < 1的情况也包含进来. 因此推广的连续时间随机行走模型可以用来模拟一般的反常输运行为.3.总 结 本文通过考察复杂孔隙介质中输运过程的特征, 考虑了对流和扩散的不同效果, 提出具有不同动力学起源的等待时间分布函数, 补充了经典的连续时间随机行走模型, 得到了一般情况下溶质输运的长时间渐进行为, 讨论了对流和扩散效应的相对强弱对输运行为的定性和半定量影响, 并针对正常和反常输运分别得到了相应的宏观输运方程. 本文的结果有助于进一步认识和模拟复杂孔隙介质中的输运行为, 对于研究地下水污染物的运移行为具有一定的现实意义和工程价值.  图 1 拉萨周边地区某岩心样本的CT扫描图像(左)及其对应的孔隙空间(右)
图 1 拉萨周边地区某岩心样本的CT扫描图像(左)及其对应的孔隙空间(右)






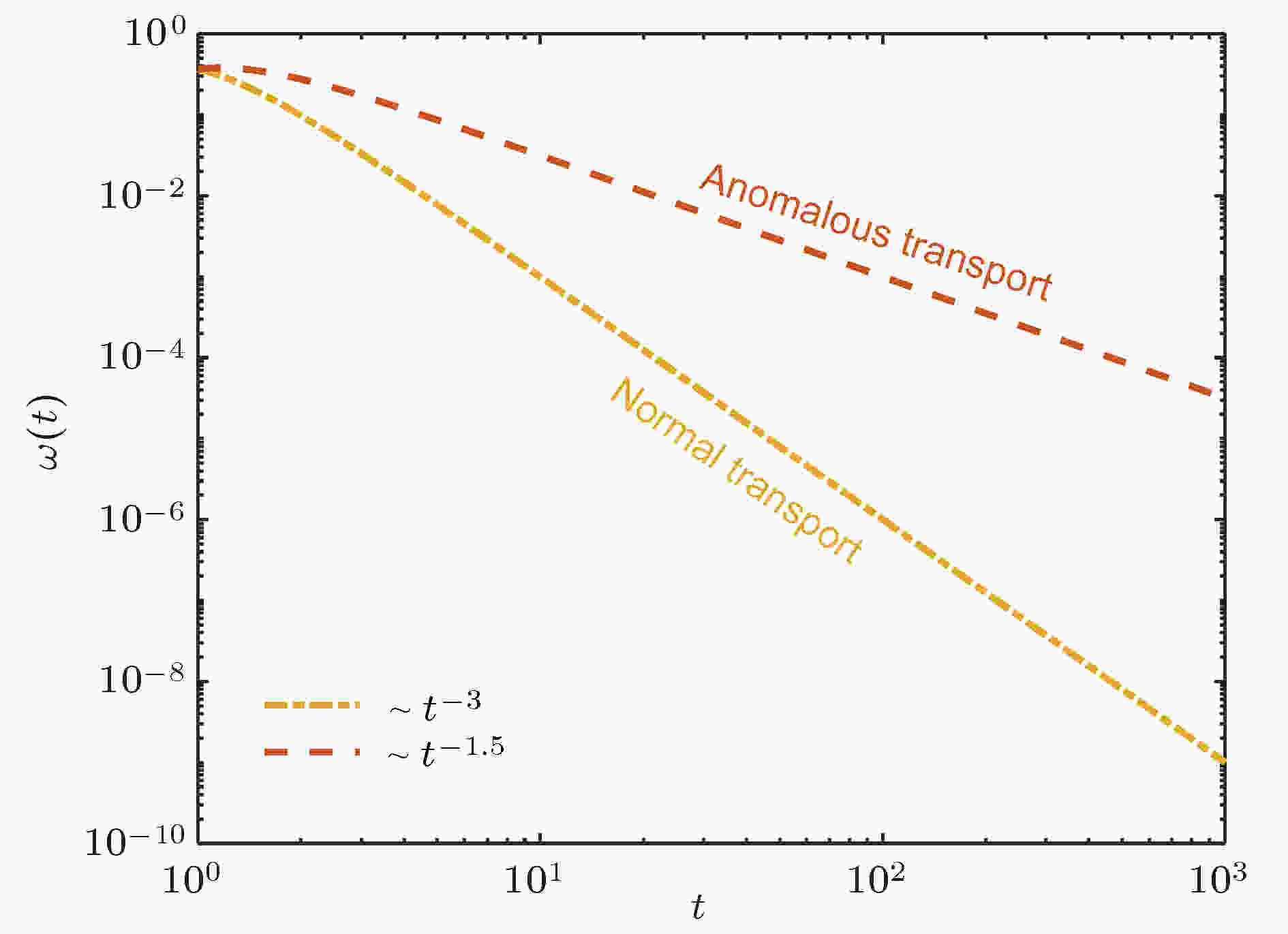 图 2 等待时间分布ω(t)~t–1–α示意图, 不同统计特征导致定性上不同的输运行为. 以α = 2为界, 当α > 2时输运行为是正常的, 当0 < α < 2时为反常.本文尤其关注1 < α < 2的情况
图 2 等待时间分布ω(t)~t–1–α示意图, 不同统计特征导致定性上不同的输运行为. 以α = 2为界, 当α > 2时输运行为是正常的, 当0 < α < 2时为反常.本文尤其关注1 < α < 2的情况


















































































