摘要:谐波平衡法是一种高效周期性非定常流动频域计算方法. 本文研究可变周期谐波平衡法, 通过求解Navier-Stokes方程模拟低速不可压条件下的二维钝体绕流周期性非定常涡脱落问题. 对于这类流动变化周期未知的非定常问题, 将涡脱落周期T作为变量, 采用基于残差导数的可变周期计算方法推进求解. 以圆柱绕流和方柱绕流为例, 研究考察了谐波平衡法的计算精度和效率, 并分析研究了不同参数对计算结果的影响. 针对圆柱绕流问题, 采用三种不同优化方法进行周期T的迭代计算, 对比研究了它们的计算精度和效率. 计算结果表明: 谐波平衡法采用3个谐波数就可以准确模拟周期性非定常涡脱落问题, 辨识的涡脱落频率和阻力系数与实验值及其他数值结果一致, 与时域方法相比该方法具有较高的计算效率. 不同优化方法的计算结果相同, 共轭梯度法和牛顿法的收敛速度与最速下降法采用较大搜索步长时的收敛速度一致. 由于牛顿法没有参数问题, 因此该方法在工程计算中更有优势.
关键词: 周期性非定常流动/
数值模拟/
谐波平衡法/
可变周期计算方法

English Abstract

全文HTML

--> --> -->

周期性非定常流动是流体力学领域科学研究与实际工程应用中常见的流动现象, 根据非定常性产生原因可以将其分为两类: 第一类是由物体周期性运动引起并强制驱动的, 这类流动都有一个明显的特征频率, 物理量的波动周期已知, 如涡轮机械内部转子和静子相对运动引起的非定常流动、直升机的旋翼绕流、翼形的俯仰振荡等; 第二类是由流动本身的不稳定性导致的, 这类流动的波动周期事先未知, 如圆柱绕流中的涡脱落现象及其他包括分离和自由剪切层的流动^[1].
通常采用时域方法(time domain method, TDM)数值求解周期性非定常流动问题, 即在时间方向上顺序求解流动控制方程, 直到流动达到周期性稳定状态. 时域计算方法思想简单, 可用于各种非定常流动问题. 但是, 时域计算方法没有利用流动的周期特性, 从初始条件迭代获得稳定周期解之前需要经历很长阶段的瞬态解的计算, 而这部分的计算时间通常比真实波动周期长很多^[2], 因此其计算效率较低. 同时, 时域计算通常使用较小的物理时间步长以满足稳定性条件, 从而导致非定常流动计算的时间较长.
对于周期性流动, 人们更关注的是流动达到周期性的稳定状态. 近二十年来, 许多****利用流动变化的周期性特点发展了各种不同的频域方法, 如线性频域方法、非线性谐波法、谐波平衡法、非线性频域法和时间谱方法等. 早期的线性频域方法^[3,4]把流动变量分解为时均值和周期性小扰动量的和, 将流动控制方程分解为不耦合的时均方程和扰动方程, 并基于小扰动线性化假设对扰动方程进行线性化处理, 通过求解线性化方程来模拟非定常扰动. 该方法求解速度较快, 但不适用于存在较强非线性的流动问题. 为了能够模拟非定常流场中的非线性效应, Ning和He^[5]提出了非线性谐波法, 该方法将时均方程和扰动方程耦合求解. 虽然这种方法能够模拟一些变换复杂的非线性非定常流动, 但仍然不能够求解非简谐周期性流动. 随后, Hall等^[6]提出了基于傅里叶展开的谐波平衡法(harmonic balance method, HBM), 该方法包含更多的非线性相互作用项. 由于非线性项在频域内的表示比较复杂, HBM不直接求解变量傅里叶级数中的谐波系数, 通过引入离散傅里叶变换, 将非定常流动求解过程转换为一个周期内几个等时间间隔的瞬时流动耦合求解. 计算采用的时刻点越多, HBM计算包含的谐波分量越多, 计算精度越高, 因此该方法可以获得较高的时间离散精度. Hall等^[6]采用HBM成功模拟了单级、多级涡轮机叶片绕流问题^[7], 计算表明即使是强非线性流动HBM也能在较少的谐波数下达到工程要求的精度. McMullen等^[8]发展了非线性频域方法, 该方法与HBM等价, 但在每一步迭代中都需要进行快速傅里叶变换. Gopinath和Jameson^[9]基于傅里叶变换进一步提出了完全在时域求解流动控制方程的时间谱方法, 该方法在本质上与HBM是相同的. 时间谱方法被成功应用到二维和三维非定常流动, 如翼形俯仰振荡和圆柱涡脱落问题.
与TDM相比, HBM能够在保证精度的同时大幅度地减少计算时间, 在周期性的内流和外流非定常问题中得到了广泛应用. 在内流计算中, HBM被广泛应用于计算叶轮机械内部的非定常流动^[10-17], 如振荡叶珊^[6]、压气机转静干涉^[13,14,17]、叶珊气动弹性颤振及极限环振动^[11,12]等问题, 与TDM相比, 计算效率可实现1—2个数量级的提升. 在外流计算中, Thomas等^[18,19]和Guillaume等^[20]对振荡翼形和机翼的非定常计算表明, HBM计算准确性高, 可以模拟流动中存在的激波等强非线性作用. Ekici等^[21]采用HBM数值模拟了直升机旋翼的非定常绕流问题. HBM在飞行器动导数快速预测方面的应用研究也取得了较好的效果^[22-27].
由于HBM是在傅里叶级数展开的基础上构建的, 需要事先知道流动稳定周期解变化的频率, 因此HBM特别适用于已知频率的第一类周期性非定常流动问题. 对于非定常周期事先不能确定的流动问题, 如钝体绕流中的涡脱落问题, HBM计算可以采用实验测得的频率或者TDM计算得到的频率作为基准频率^[28,29]. 由于钝体绕流的非定常流动是自发形成的, 达到稳定后的流动变化周期与几何布置和流动参数有关. 因此, 采用HBM计算时应将频率作为变量处理, 以适用于不同几何外形和来流条件.
为了求解这类周期不可预知的非定常问题, McMullen等^[30]提出了一种基于残差梯度的可变周期计算方法(gradient based variable time period method, GBVTP), 并与非线性频域方法相结合, 实现了流动变量和周期的同时迭代求解. McMullen等^[30]采用该方法成功模拟了低雷诺数定姿态圆柱绕流中的涡脱落周期. Gopinath 和 Jameson^[31]随后提出了基于残差梯度的可变周期时间谱方法, 成功模拟了低雷诺数定姿态圆柱绕流和 NACA0012 翼型大攻角绕流问题. Spiker等^[32]提出了一种基于相位差的方法确定圆柱绕流涡脱落频率, 并模拟了强迫振动圆柱绕流下的涡脱落问题. Mosahebi和Nadarajah^[2,33]将GBVTP应用到自适应HBM. Yao和Jaiman^[34]以及Yao和Marques^[35]采用可变周期HBM数值模拟了低雷诺数圆柱涡致振荡问题以及跨声速极限环振动问题, 成功模拟了极限环振动的振幅和频率. 国内关于可变周期频域方法的研究相对较少, 比较典型的是2009年张炜和席光^[36]采用基于残差梯度的可变周期时间谱方法求解了二维不可压方柱绕流问题. 总体来看, 可变周期HBM的研究还比较少, 需要开展深入研究.
本文基于上述文献, 进一步开展可变周期HBM在周期性非定常涡脱落问题中的应用研究. 以二维圆柱和方柱绕流为例, 详细考察了该方法的计算精度和效率, 并分析了不同参数对计算的影响. 在GBVTP中, 采用不同寻优方法搜索周期T, 对比研究了不同优化方法的计算性能.

2

-->

2.1.流动控制方程

以RANS方程为控制方程, 其有限体积离散形式可以写为

${J^{ - 1}}\frac{{\partial {{Q}}}}{{\partial t}} + {{R}}({{Q}}) = 0, $

其中J为雅克比行列式, 计算网格单元体积V = $J^{-1} $; Q = (ρ, ρu, ρv, ρw, ρe)^T为流动守恒变量; R(Q)为无黏通量E, F, G和黏性通量E_v, F_v, G_v空间离散产生的残差向量,

${{R}}({{Q}}) = {\delta _\xi }({{E}} - {{{E}}_v}) + {\delta _\eta }({{F}} - {{{F}}_v}) + {\delta _\zeta }({{G}} - {{{G}}_v}).$

本文无黏通量的空间离散采用AUSMPW+格式, 黏性通量空间离散采用格林公式.
2 -->

2.2.时域计算方法

非定常时域计算采用Jameson^[37]提出的含双时间步的LU-SGS隐式时间格式对控制方程进行时间离散, 推进求解如下方程:

$\begin{split} &\left(\frac{3}{{{{2\Delta t}/ {{J^{ - 1}}}}}} + \frac{1}{{{{\Delta \tau } / {{J^{ - 1}}}}}} + \frac{{\partial {{R}}}}{{\partial {{Q}}}}\right)\Delta {{Q}} \\ = & - \left( {{{R}}\left( {{Q}} \right) + \frac{{3{{{Q}}^{n + 1}} - 4{{{Q}}^n} + {{{Q}}^{n - 1}}}}{{{{2\Delta t} / {{J^{ - 1}}}}}}} \right),\end{split}$

其中?t为真实物理时间步长, ?τ为虚拟时间步长.
2 -->

2.3.谐波平衡法

对于周期性流动, 其流动守恒变量Q和残差R(Q)在时间上以频率ω周期变化, 可以表示为如下傅里叶级数的形式:

${{Q}}(t) \approx {{\hat {{Q}}}_0} + \sum\limits_{n = 1}^{{N_{\rm{H}}}} {({{\hat {{Q}}}_{{\rm{cn}}}}} \cos (\omega nt) + {{\hat {{Q}}}_{{\rm{sn}}}}\sin (\omega nt)),$

${{R}}(t) \approx {{\hat {{R}}}_0} + \sum\limits_{n = 1}^{{N_{\rm{H}}}} {({{\hat {{R}}}_{{\rm{cn}}}}} \cos (\omega nt) + {{\hat {{R}}}_{{\rm{sn}}}}\sin (\omega nt)),$

其中N_H为谐波数.
将方程(4)代入到方程(1)中, 整理可得频域形式谐波平衡方程. 由于直接求解频域方程十分困难, Hall等^[6]将一个周期分为N_T (N_T = 2N_H+1)等份, 利用离散傅里叶变换将频域方程转换回时域进行求解. 时域形式谐波平衡方程可以写为

${J^{ - 1}}\omega {{DQ}} + {{R}} = 0, $

详细推导过程可以参考文献[27]. 式中${J^{ - 1}}\omega {{DQ}}$为谐波源项, D是N_T × N_T系数矩阵, 且

${D_{ij}} = \frac{2}{{{N_T}}}\sum\limits_{k = 1}^{{N_{\rm{H}}}} k\sin \left( \frac{{2{\text{π}}k(j - i)}}{{{N_T}}}\right).$

Q和R表示这N_T个时刻的流动变量和残差向量, 则有

$\begin{split}& {{Q}} = {\left[{Q({t_0} + \Delta T)}\quad {Q({t_0} + 2\Delta T)}\quad \cdots \quad{Q({t_0} + T)}\right]^{\rm{T}}}, \\& {{R}} = {\left[{R({t_0} + \Delta T)}\quad {R({t_0} + 2\Delta T)}\quad \cdots \quad {R({t_0} + T)}\right]^{\rm{T}}},\end{split} $

式中?T = T/N_T.
引入虚拟时间导数项来推进求解方程(5):

${J^{ - 1}}\frac{{\partial {{Q}}}}{{\partial \tau }} + {J^{ - 1}}\omega {{DQ}} + {{R}} = 0.$

本文采用隐式LU-SGS方法求解方程(8), 其中谐波源项显式计算, 推进求解如下方程组:

$\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{\Delta \tau /{J^{ - 1}}}}{{I}} + \dfrac{{\partial {{R}}({{{Q}}_1})}}{{\partial {{{Q}}_1}}}}&0& \cdots &0 \\ 0&{\dfrac{1}{{\Delta \tau /{J^{ - 1}}}}{{I}} + \dfrac{{\partial {{R}}({{{Q}}_2})}}{{\partial {{{Q}}_1}}}}& \ddots & \vdots \\ \vdots & \ddots & \ddots &0 \\ 0& \cdots &0&{\dfrac{1}{{\Delta \tau /{J^{ - 1}}}}{{I}} + \dfrac{{\partial {{R}}({{{Q}}_{{N_T}}})}}{{\partial {{{Q}}_{{N_T}}}}}} \end{array}} \right]\left[ \begin{gathered} \Delta {{Q}}_1\\ \Delta {{Q}}_2\\ \vdots \\ \Delta {{Q}}_{{N_T}}\\\end{gathered} \right] = - \left[ \begin{gathered} {{R}}_{}^ * ({{Q}}_1) \\ {{R}}_{}^ * ({{Q}}_2) \\ \vdots \\ {{R}}_{}^ * ({{Q}}_{{N_T}})\end{gathered} \right], $

其中${{{Q}}_i}$表示第${t_i} = {t_0} + i\Delta t$时刻的守恒变量, ${{R}}_{}^ * ({{Q}}_i^{}) = {{R}}({{Q}}_i^{}) + {J^{ - 1}}\omega \sum\limits_{j = 1}^{{N_T}} {{D_{i, j}}} {{{Q}}_j}\;\;$.
2 -->

2.4.可变周期计算方法

时间频率$ \omega = 2{\text{π}} /T$, 谐波平衡方程(8)可写为

${J^{ - 1}}\frac{{\partial {{Q}}}}{{\partial \tau }} + {J^{ - 1}}\frac{{2{\text{π}}}}{T}{{DQ}} + {{R}} = 0.$

钝体绕流中的非定常性是自发形成的, 在不同参数下, 非定常流动的周期未知. 在非定常流动的每一时刻, 当且仅当T等于正确的周期T ^*时才能使控制方程组(10)相容, 同时正确地反映流动现象. 对于时间周期不可预知的这类周期性流动, 本文采用基于残差梯度的方法从初始猜测值开始迭代求解正确的时间周期.
定义残差

${{{R}}_{{\rm{HB}}}} = {J^{ - 1}}\frac{{2{\text{π}}}}{T}{{DQ}} + {{R}}.$

当T = T ^*时, 残差R_HB = 0, 否则R_HB≠0. 因此, 给定不同的周期T, HBM计算的残差将收敛到不同精度水平. T越接近真实值, 残差越接近于零. 可变周期HBM的目的是求解真实的周期T ^*使R_HB → 0, 这是无约束的最优化问题, 通常采用最速下降法(steepest descent method, SDM)进行求解.
定义变量

$\begin{split} L =\; & \frac{1}{2}{{{R}}^{\rm{T}}}_{{\rm{HB}}}{{{R}}_{{\rm{HB}}}} = R_{{\rm{HB}}}^2(\rho ) + R_{{\rm{HB}}}^2(\rho u) \\ &+ R_{{\rm{HB}}}^2(\rho v) + R_{{\rm{HB}}}^2(\rho w) + R_{{\rm{HB}}}^2(\rho e).\end{split}$

对于残差变量L, 不同研究采用的定义不同, 如文献[36]基于y方向动量方程的残差构造变量L. 数值计算表明, 不同的L定义对收敛速度影响较大, 当其量级较小时, 收敛较慢, 计算时间长. 计算表明, 本文采用所有残差分量平方之和的方式总体收敛速度较快. 后续研究可以围绕不同残差分量的归一化或者加权来构造残差变量L.
建立残差梯度

$\frac{{\partial L}}{{\partial T}} = {\left( {{J^{ - 1}}\frac{{ - 2{\text{π}}}}{{{T^2}}}{{DQ}}} \right)^{\rm{T}}}{{{R}}_{{\rm{HB}}}}, $

利用残差梯度更新时间周期:

${T^{p + 1}} = {T^p} - \lambda \frac{{\partial {L^p}}}{{\partial T}}.$

选择合适的初值T₀和步长λ, 通过求解方程(10)和方程(14)流动变量和周期T同时迭代更新并达到收敛.
周期搜索过程中, 采用残差的相对值判断收敛, 定义

$\varepsilon = {{{\rm{RHS}}} / {{\rm{RH}}{{\rm{S}}_0}}}, $

式中RHS为所有时刻所有网格点所有残差分量绝对值之和对总网格点的平均, RHS₀为初始迭代的残差. 对于本文算例, $\varepsilon \leqslant 10^{-3} $能够满足精度要求, 因此计算采用ε = 10^–3.

NACA0012翼型绕1/4弦点做俯仰振荡是一个典型的周期性非定常问题, 经常作为数值方法的验证算例. 翼型的正弦俯仰振荡运动采用如下攻角随时间的变换规律:

$\alpha = {\alpha _0} + {\alpha _{\rm{m}}}\sin (kt), $

式中α₀为平均攻角, α_m为振幅, $k = 2{\text{π}}\tilde f\dfrac{{\tilde L}}{{{{\tilde V}_\infty }}}$为减缩频率, $\tilde f$为俯仰振动的频率, ${\tilde V_\infty }$为来流速度, 无量纲化长度$\tilde L$取翼型的弦长. 本文计算选取AGARD实验中的CT5算例^[38], 主要的计算条件见表1.

Parameter	Value
Ma	0.755
α0	0.016°
αm	2.51°
k	0.1628

表1NACA0012翼型俯仰振荡AGARD CT5算例计算条件
Table1.Computational conditions of the AGARD CT5 test case for the NACA0012 airfoil.

2

-->

3.1.网格划分

图1是计算网格情况, 采用O型拓扑结构, 网格数量为84 × 287 (法向 × 周向). 为了保证远场边界对计算的影响较小, 远场边界设在20倍弦长以外.
图 1 NACA0012翼型计算网格
Figure1. Mesh for the NACA0012 airfoil.

2 -->

3.2.计算结果及分析

采用HBM计算时, 谐波数N_H = 1, 2, 3, 4, 即分别将一个周期3, 5, 7, 9等分, 计算得到各个时刻点的瞬时流场. 采用TDM计算时, 无量纲时间步长为0.01, 子迭代收敛的判据为残差下降两个量级. 一个周期内NACA0012翼型的升力系数和力矩系数随攻角的变化如图2所示. 将HBM与TDM的计算结果与AGARD的实验数据^[38]以及Batina^[39]的计算结果进行了比较. 对于线性特征明显的升力系数曲线, HBM在N_H = 1的计算结果与TDM计算结果符合良好, 且与Batina^[39]的计算结果一致, 但计算结果比实验结果偏小. 与升力系数相比, 俯仰力矩系数具有较强的非线性, HBM计算至少需要3个谐波数才能模拟力矩系数随攻角的变化规律. HBM重建的力矩系数曲线和时域计算结果及实验值能够较好地符合, 验证了HBM对周期性非定常运动的模拟能力.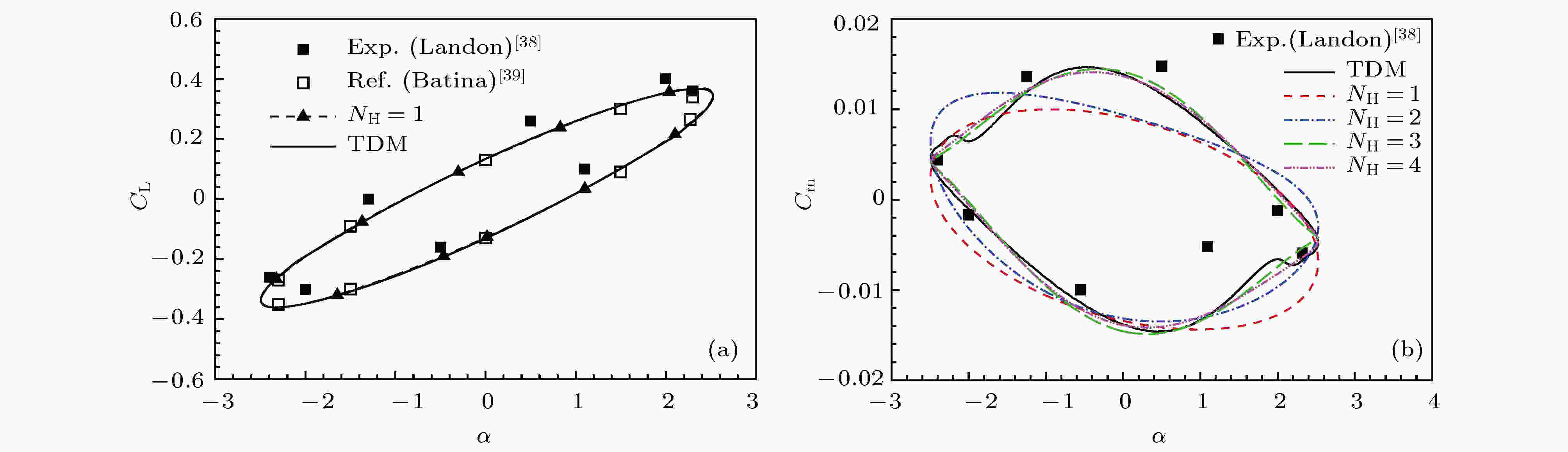
图 2 NACA0012翼型的(a)升力系数和(b)俯仰力矩系数迟滞曲线
Figure2. (a) Lift and (b) pitching moment coefficients dynamic dependence of NACA0012 airfoil.

图3展示了瞬时压力系数沿翼型表面的分布规律. 数值计算结果与实验数据^[38]基本符合. HBM计算保留前3阶谐波分量能够较为准确地模拟翼型表面压力系数的变化规律, 即使在激波出现的位置也具有较高的精度.
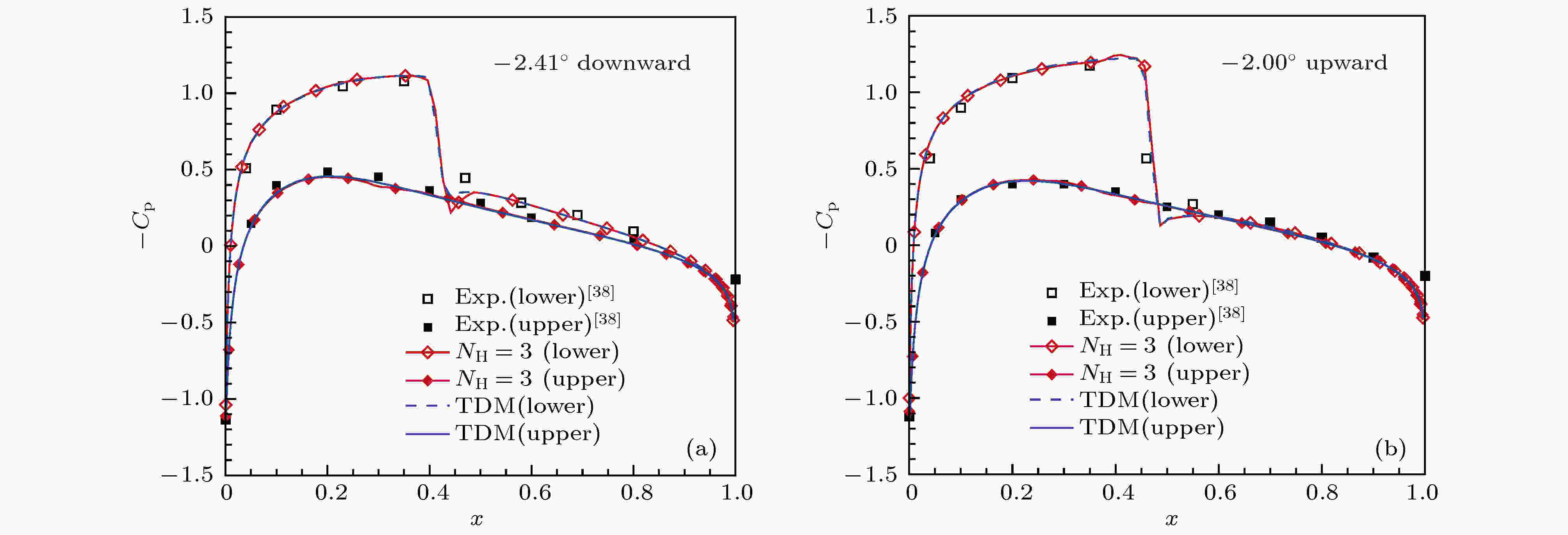图 3 NACA0012翼型俯仰振荡过程中的瞬时压力系数分布　(a) 攻角减小过程中α = –2.41°; (b) 攻角增大过程中α = –2.00°
Figure3. Instantaneous pressure coefficient distribution compared to experimental data of NACA0012 airfoil: (a) α = –2.41° for decreasing angle; (b) α = –2.00° for increasing angle.

采用HBM计算时, 俯仰力矩系数收敛速度几乎不受谐波数的影响, 如图4所示. HBM计算迭代3000步时, 动态气动力矩系数达到收敛状态. 为了定量分析HBM的计算效率, 定义加速比${\rm{speedup}} = \dfrac{{{\rm{CPU}}\;{\rm{tim}}{{\rm{e}}_{{\rm{TDM}}}}}}{{{\rm{CPU}}\;{\rm{tim}}{{\rm{e}}_{{\rm{HBM}}}}}}$. 图5给出了加速度比随谐波数的变化. 其中, 为了保证力矩系数的收敛性, TDM模拟两个周期的俯仰运动. HBM计算所需CPU时间按3000步计算. 由图5可知, 保留1阶谐波分量时, HBM的计算效率比TDM高一个量级, 随着谐波数的增加, HBM的计算效率下降. 谐波数等于3时, HBM计算比TDM大约快4倍.
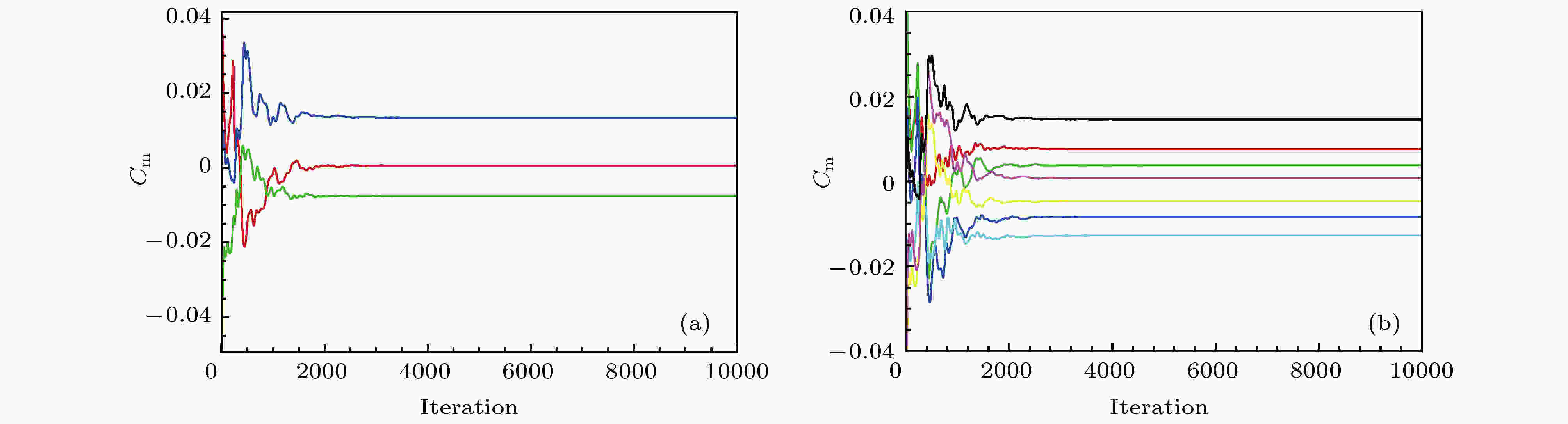图 4 HBM取不同谐波数时俯仰力矩系数收敛曲线　(a) N_H = 1; (b) N_H = 3
Figure4. Pitching moment coefficient convergence history for the HBM with respect to the number of harmonics: (a) N_H = 1; (b) N_H = 3.

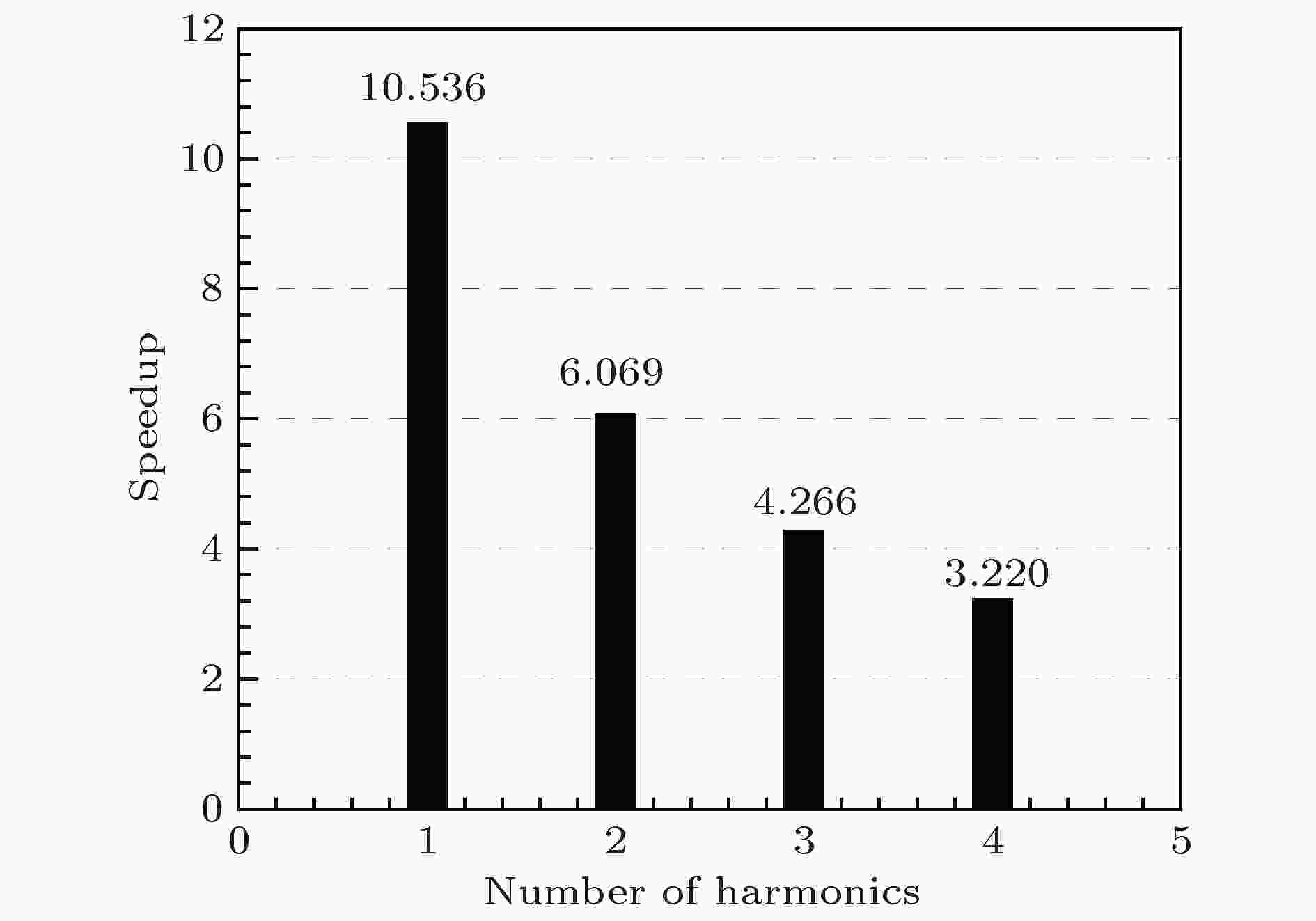图 5 CPU时间加速比随谐波数的变化
Figure5. CPU time speedup of the HBM with respect to the TDM.

非定常圆柱绕流的流态与雷诺数密切相关, 当雷诺数47 < Re < 194时, 圆柱底部会出现二维的周期性涡脱落, 称之为卡门涡街. 本文模拟低雷诺数下的二维非定常圆柱绕流, 来流马赫数为0.2, 将模拟结果与Williamson的实验数据^[43,44]及McMullen等^[30]和Spiker等^[32]的数值计算结果进行比较. 采用O型计算网格, 如图6所示, 计算网格大小为105 × 61 (流向 × 法向), 壁面第一层网格法向尺度为2.0 × 10^–4D, D为圆柱直径.
图 6 二维圆柱计算网格
Figure6. Computational grid for cylinder in cross flow.

2

-->

4.1.非定常时域计算

首先采用本课题组开发的非定常时域计算软件ADCRP, 对来流Re = 180条件下的圆柱绕流进行数值模拟, 计算得到升力系数C_L和阻力系数随时间的变化过程见图7. 计算得到的平均阻力系数C_D0 = 1.3457, 最大升力系数C_Lmax = 0.6347, 根据升力系数振动频率得到涡脱落频率St = 0.185, 对应无量纲周期T = 5.41. 计算结果与实验结果符合良好, 如表2所列.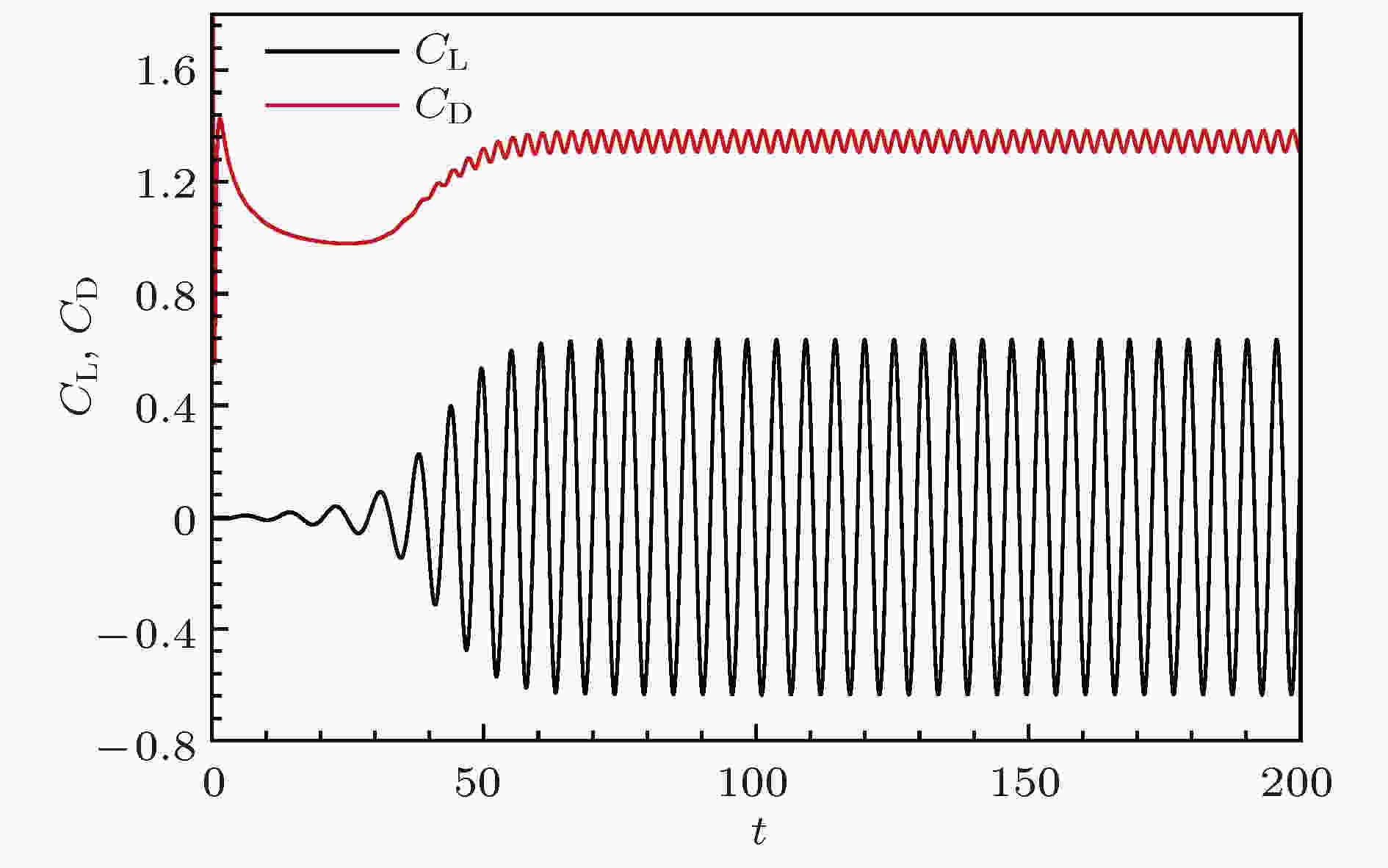
图 7 升、阻力系数收敛曲线
Figure7. Time history of lift coefficient C_L and drag C_D.

Experiment	CD0	St
Henderson[40]	1.336
Wieselsberge[41]	1.3
Roshko[42]		0.185
Williamson[43]		0.1919
Present	1.3457	0.185

表2时域计算结果与实验结果对比
Table2.Time-averaged coefficient and Strouhal number compared with experiment data.

2 -->

4.2.可变周期谐波平衡法计算

3 -->

4.2.1.谐波数收敛性分析

首先, 采用可变周期HBM对来流Re = 180条件下的圆柱绕流进行数值模拟, 考察计算所需谐波数. 初始周期T₀ = 4, 步长λ = 1.
图8为不同谐波数下计算得到的周期T收敛曲线, 图9为谐波数取3时不同时刻升力系数收敛曲线. 由图8和图9可知, 非定常涡脱落周期和气动力系数同时迭代更新并达到收敛. 图10和图11分别为不同谐波数下重建得到的升力系数和阻力系数在一个周期内的变化曲线. 表3列出了采用不同谐波数计算得到的涡脱落频率和平均阻力系数. 从计算结果可以看出, 随着谐波数的增加, 气动力及涡脱落周期逐渐收敛. 谐波数N_H = 3计算结果与实验数据及TDM计算结果相符合, 谐波数再增加时计算精度没有明显变化, 说明3个谐波数能够满足计算精度要求.
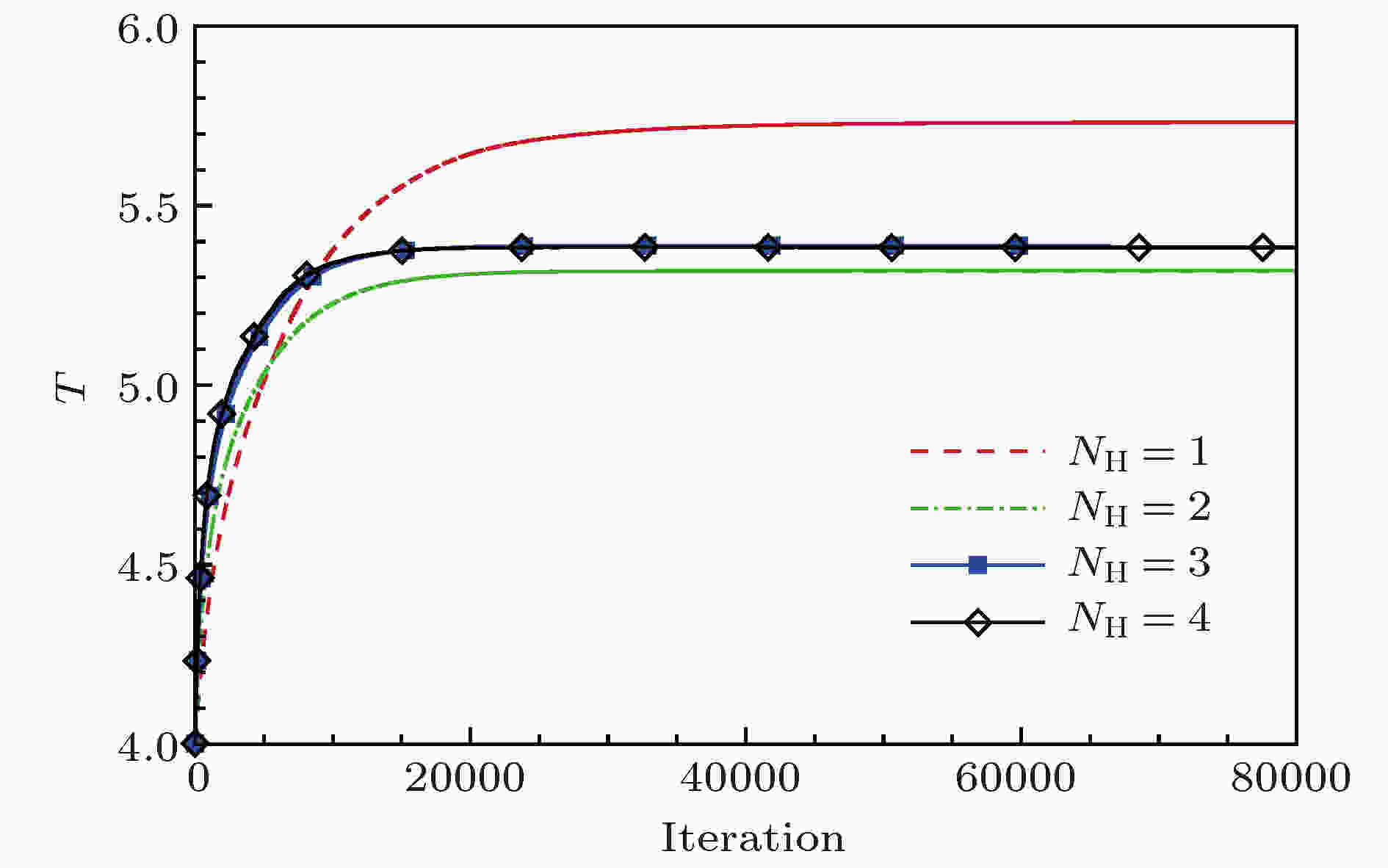图 8 不同谐波数下的周期T收敛曲线
Figure8. Convergence from initial guess to exact time period with varying number of harmonics.

图12为流动变化周期内3个等间隔时刻的流线图, 清晰地表现出圆柱后缘交替产生的涡脱落现象. 图13为HBM还原得到的升力系数最小时刻的非定常瞬态熵流场与时域计算结果的对比. 采用3阶谐波计算, 就可以很好地还原圆柱非定常涡脱落流场的多层次涡结构.
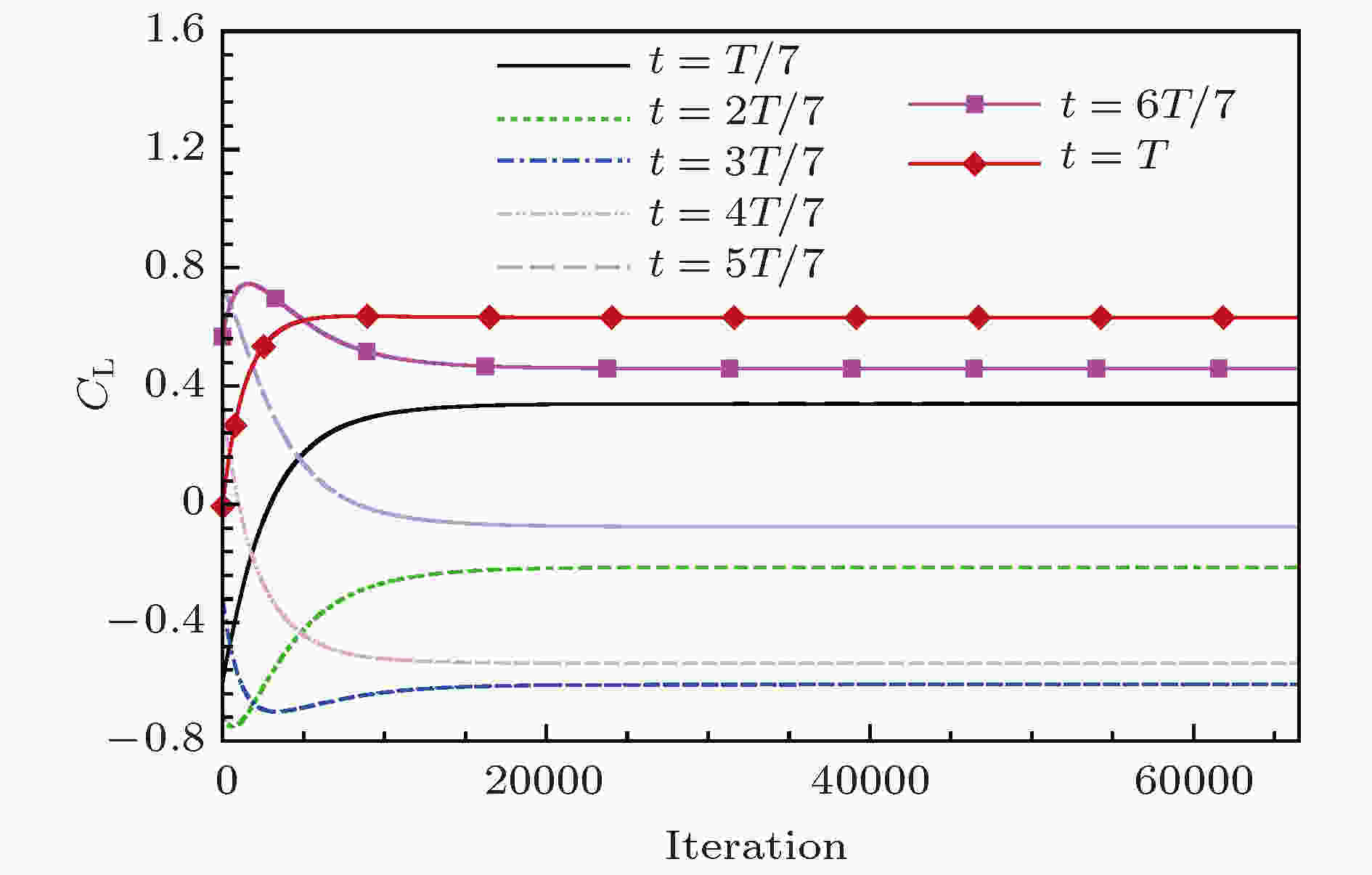图 9 升力系数收敛曲线(N_H = 3)
Figure9. Time history of lift coefficient C_L with N_H = 3.

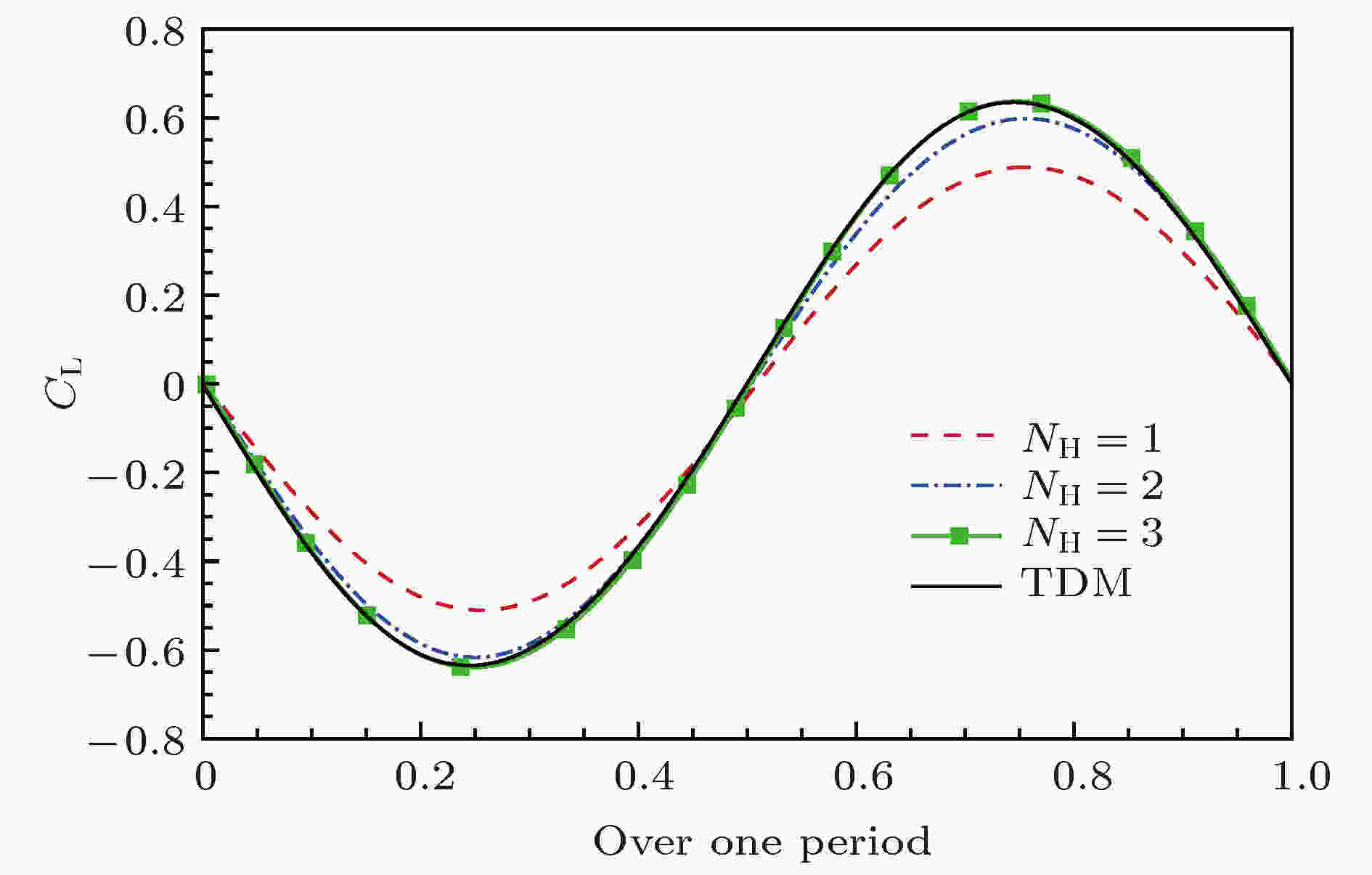图 10 升力系数随时间的变化
Figure10. Variation of C_L over one period.

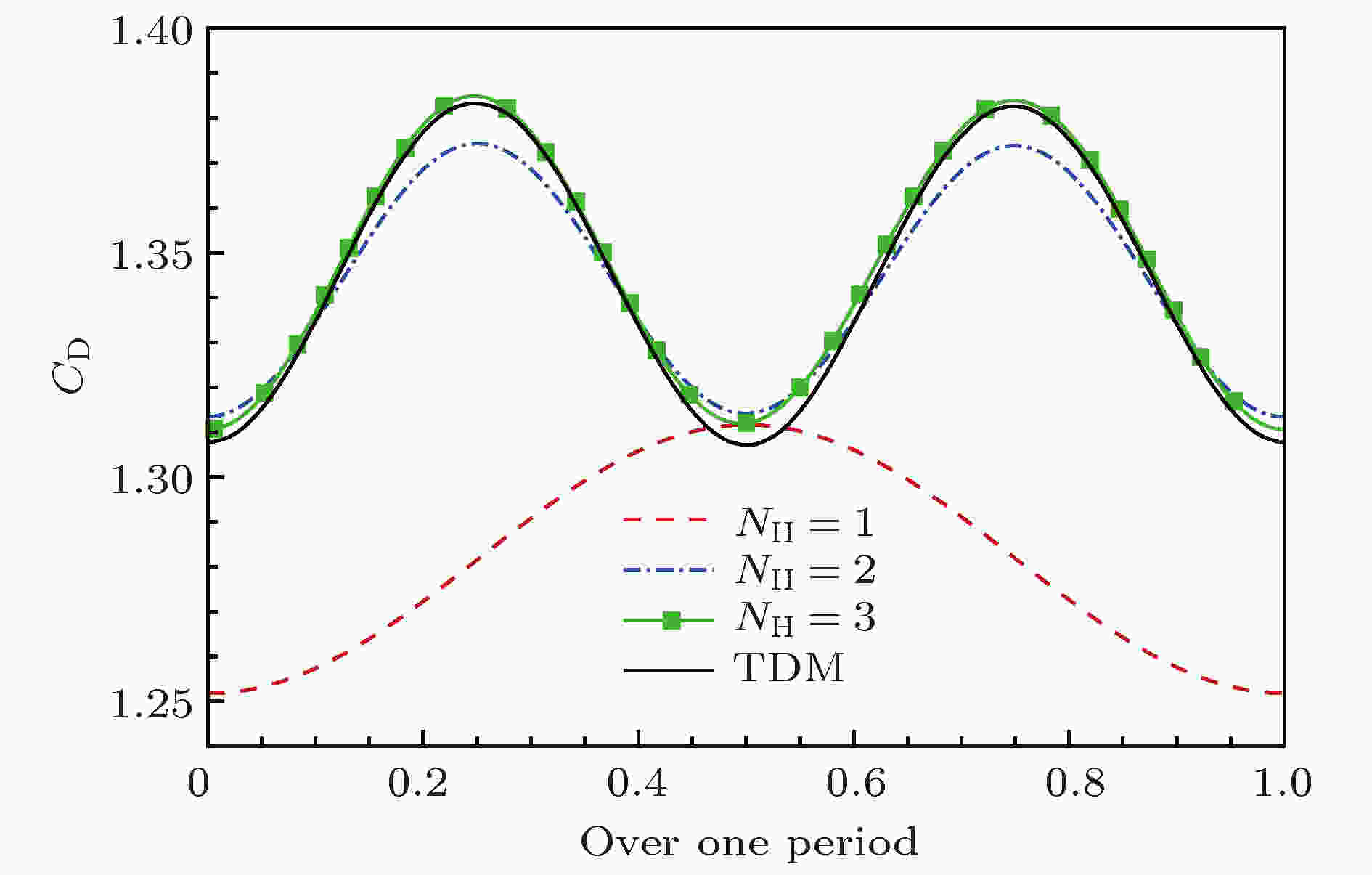图 11 阻力系数随时间的变化
Figure11. Variation of C_D over one period.

取3阶谐波对雷诺数$60 \leqslant Re \leqslant 180$的圆柱绕流进行数值模拟, 并将计算得到的斯特劳哈尔数St和C_D0与Williamson^[43,44]和Henderson^[40]的实验数据及McMullen等^[30]和Spiker等^[32]的数值计算结果相比较. 图14为表征非定常运动周期特征的St随雷诺数的变化, 图15为平均阻力系数C_D0随雷诺数的变化. 本文可变周期HBM在3阶谐波数下的计算结果与实验值符合良好, 误差在4%以内. 对于St, 数值计算结果都低于实验值, 本文计算结果与其他数值计算结果一致. 对于平均阻力系数, 可变周期HBM的计算结果比McMullen等^[30]采用可变周期非线性频域方法计算的结果更接近于实验值.

NH	St	CD0
1	0.1745	1.2817
2	0.188	1.3440
3	0.1856	1.3479
4	0.1857	1.3506
TDM	0.185	1.3457
Roshko[42]	0.185

表3不同谐波数下的计算结果
Table3.Strouhal number and time-averaged coefficient computed by different number of harmonics.

图 12 Re = 180, N_H = 3条件下不同时刻的流线图　(a) t = T/3; (b) t = 2T/3; (c) t = T
Figure12. Streamlines at various time instances over one period (Re = 180, N_H = 3): (a) t = T/3; (b) t = 2T/3; (c) t = T.

图 13 熵等值线图(C_L最小时刻)　(a) TDM计算结果; (b) HBM计算结果（N_H = 3）
Figure13. Comparison of instantaneous entropy contours: (a) TDM results; (b) HBM results (N_H = 3).

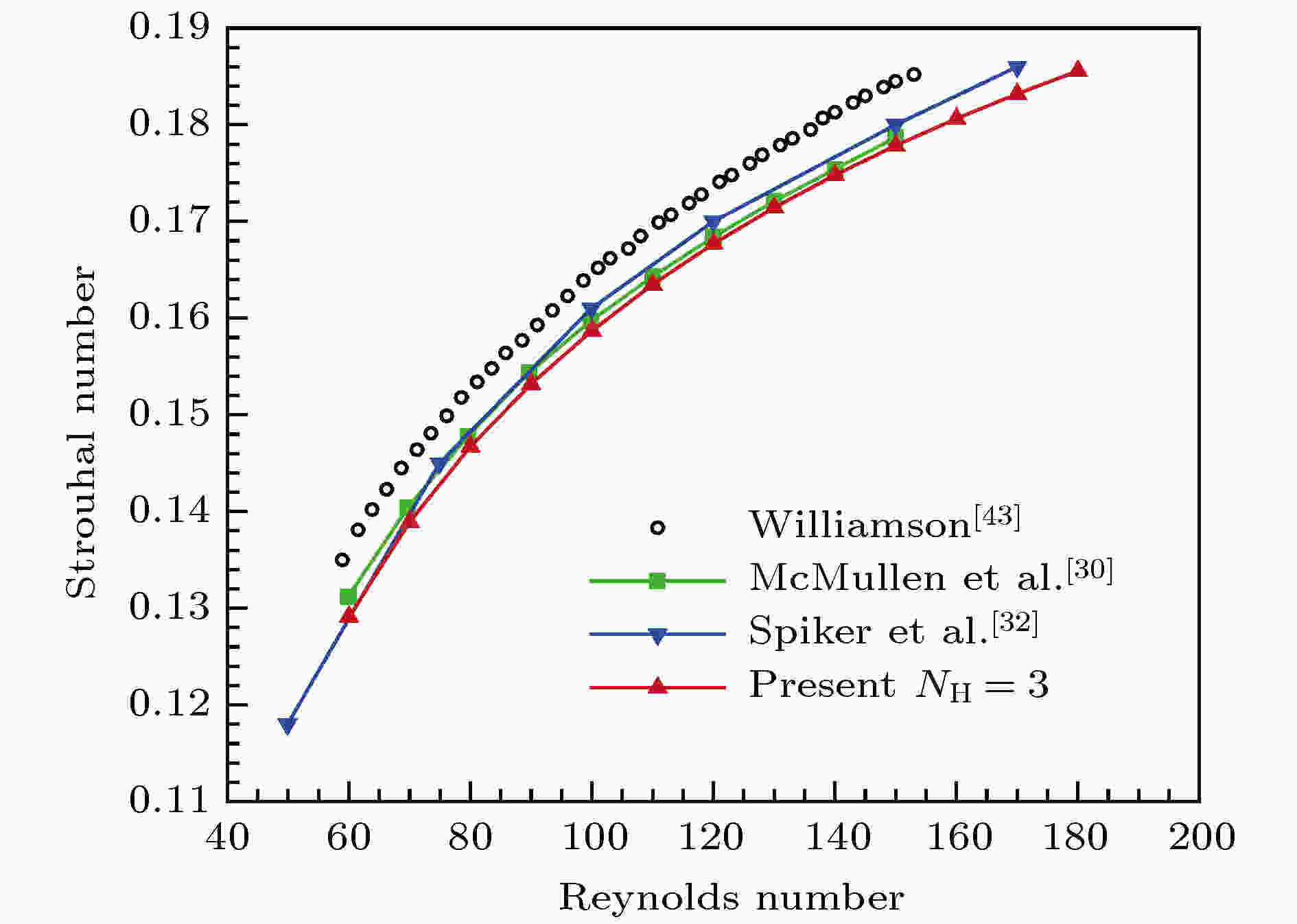图 14 Strouhal数随Re的变化
Figure14. Strouhal number as a function of Reynolds number.

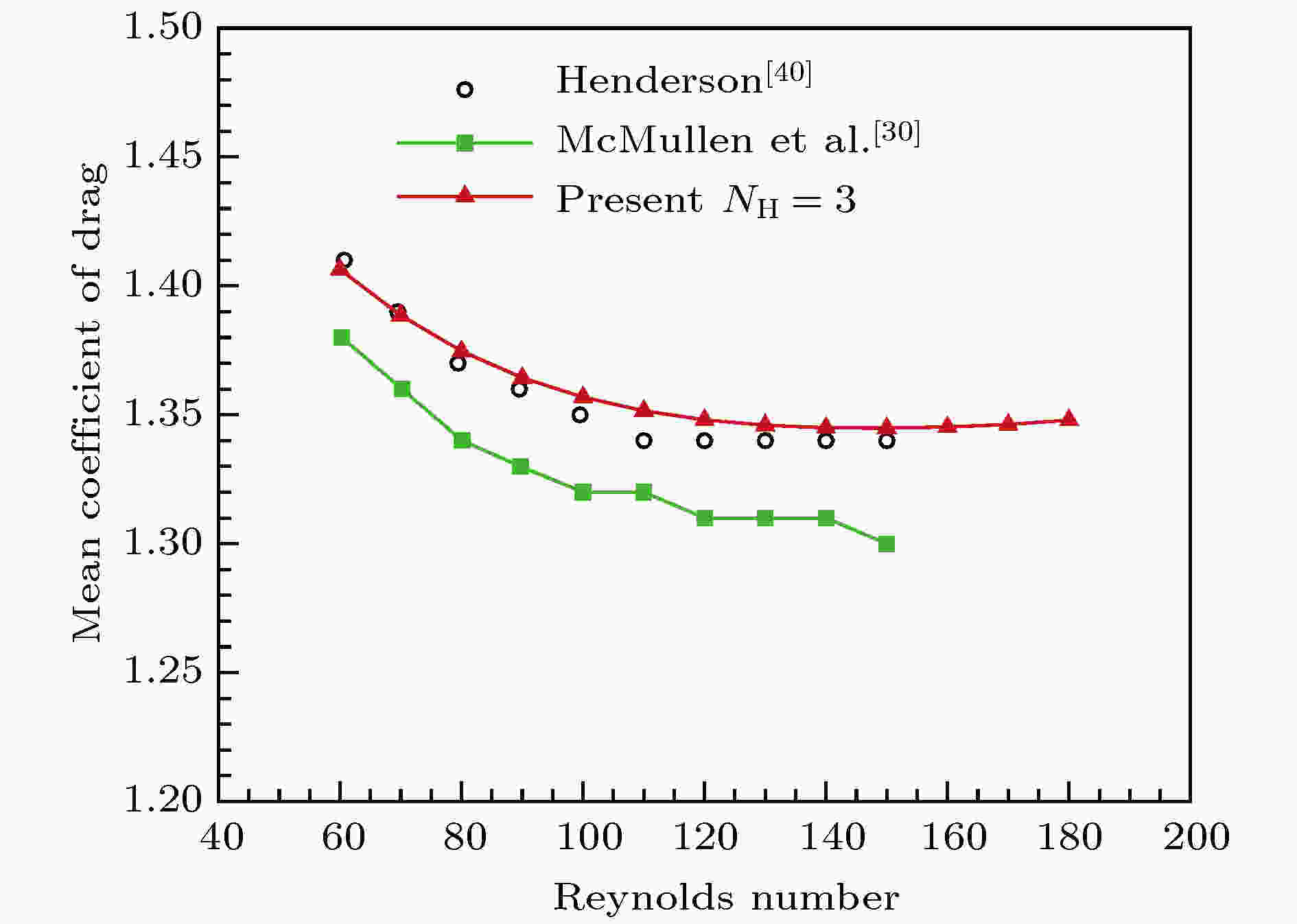图 15 平均阻力系数随Re的变化
Figure15. Mean coefficient of drag versus Reynolds number.

3 -->

4.2.2.迭代步长λ的影响分析

图16为Re = 180, N_H = 3情况下, 取不同步长λ计算得到的周期T. λ对最终结果影响较小, 非定常涡脱落周期都收敛到同一值. λ = 1时周期T收敛最慢, 步长增大收敛速度有所加快, 但λ > 10之后收敛曲线没有明显变化.
图 16 不同步长λ下的周期T收敛曲线
Figure16. Time period convergence computed with three different step sizes λ.

3 -->

4.2.3.初始周期T₀对计算的影响分析

图17为Re = 180, N_H = 3情况下, 取不同初始T₀计算得到的周期T. 当T₀ < 5.8时, 取不同初值T₀, 涡脱落周期最终都收敛到真实周期T ^* = 5.389; 当$ 5.8 \leqslant T_0 \leqslant 13$时, 取不同初值T₀, 最终结果都收敛到T = 11.43, 与T ^*近似成两倍的关系, 升力系数在$0 \leqslant t \leqslant 11.43 $内也确实变化两个周期, 如图18所示; 当T₀再增大到17和20的时候, 涡脱落周期最终都收敛到T = 16.834, 与T ^*近似成三倍的关系. 对于周期性非定常问题, 如果T ^*是流动变化周期, 那么2T ^*和3T ^*也是流动变化的周期. 对于可变周期HBM, 在周期T搜索过程中有可能收敛到nT ^* (n = 2, 3, ···). 值得注意的是, 实际计算结果并不是准确的倍数关系, 这可能与谐波数有关, 也可能是计算误差导致的, 此现象值得进一步深入研究. 同时, 有必要发展自动搜索最小周期的计算方法.
图 17 不同步长T₀下计算的周期T收敛曲线
Figure17. Time period convergence with various starting guesses T₀.

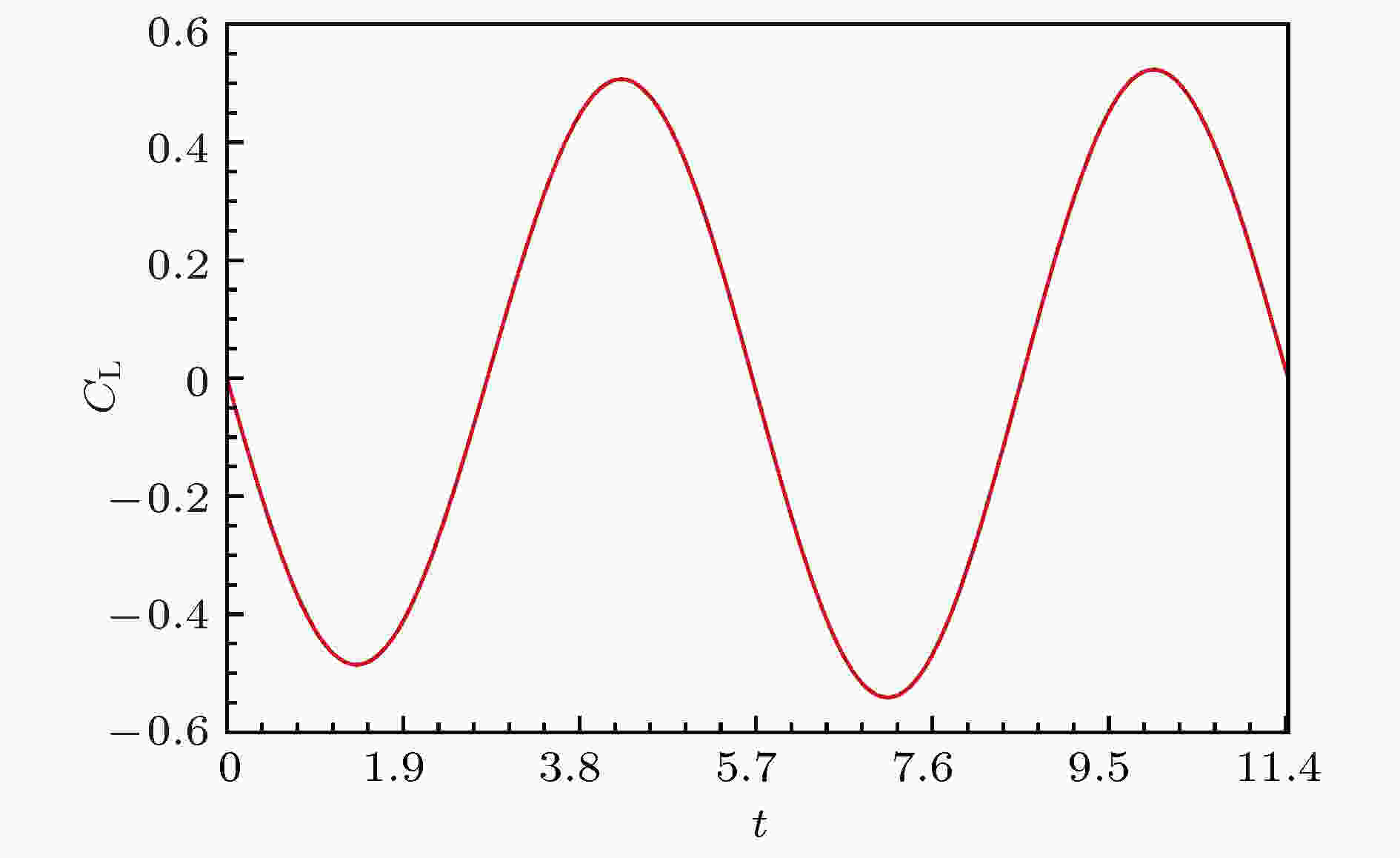图 18 T = 11.43 时重建的升力系数曲线
Figure18. Variation of C_L over one period with converged time period T = 11.43.

3 -->

4.2.4.计算效率分析

图19比较了采用HBM与TDM计算得到的St随雷诺数的变化曲线. 当时域计算选择时间步长为?t = 0.01时, 在雷诺数$ 80 \leqslant Re \leqslant 180$之间两种计算方法的结果符合良好, 雷诺数低于80时, HBM的计算结果比TDM结果更接近实验值. 但当TDM计算采用较小步长?t = 0.001时, 较低雷诺数下的TDM计算结果与HBM计算保留前3阶谐波分量的结果基本重合, 不同的是此时的TDM付出的计算代价更大. 图20为雷诺数Re = 180和Re = 60的加速比. 由图20可知, 来流雷诺数越低, HBM相对TDM的计算效率优势越明显.
图 19 HBM计算的St与TDM计算结果的对比
Figure19. Comparison of the HBM St data results with TDM results.

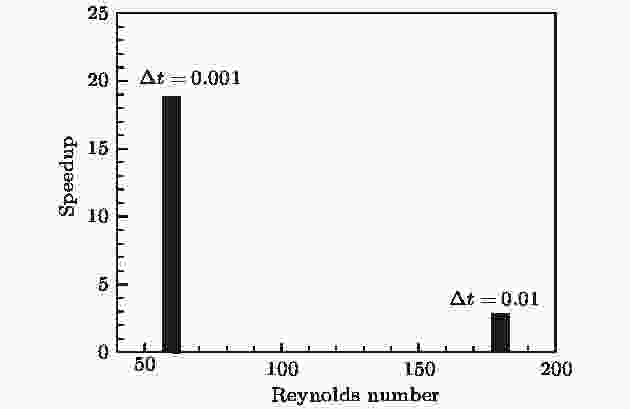图 20 不同雷诺下的加速比
Figure20. CPU time speedup of various Reynolds number.

2 -->

4.3.基于固定周期谐波平衡法的涡脱落周期辨识

对于固定周期HBM计算, 当给定的周期T不等于真实的物理周期T ^*时, 残差将下降到一定水平, 并且收敛后的残差和气动力会随着虚拟迭代步的增加呈现周期性变化, 如图21所示, 其中ρ为密度; u, v分别为x方向和y方向的速度; e为单位质量总能. 当Re = 180时, 采用可变周期HBM计算的圆柱绕流涡脱落周期为T ^* = 5.389. 固定周期HBM给定T = 4时, 计算得到的升力系数和残差都呈现周期性变化的趋势, 相邻迭代步重建的升力系数曲线之间存在相位差, 如图22所示. 对于给定的T, 当升力系数收敛后每一步虚拟迭代产生的相位差是常值. 而且这个相位差与给定的周期T呈近似线性的关系, 当且仅当给定的T为真实的周期T ^*时相位差为0, HBM计算得到各个时刻的升力系数曲线不再周期性振荡, 而是收敛到常值, 如图23所示. Spiker等^[32]提出的相位差方法正是基于这一点来辨识涡脱落的频率. 图24给出了固定周期HBM计算时, 相位差随周期的变化. 由图24可知, 在一定范围内, 相位差的确与T成线性关系, 采用固定周期HBM辨识涡脱落周期时, 只需计算两个不同周期对应的相位差就可以通过线性关系推算相位差等于0时对应的T ^*. 值得注意的是, 采用3阶谐波进行计算时, 当T = 11.43时相位差也等于0, 在该值附近也存在线性关系, 说明11.43也是旋涡脱落的周期, 这与之前可变周期HBM的计算结果一致.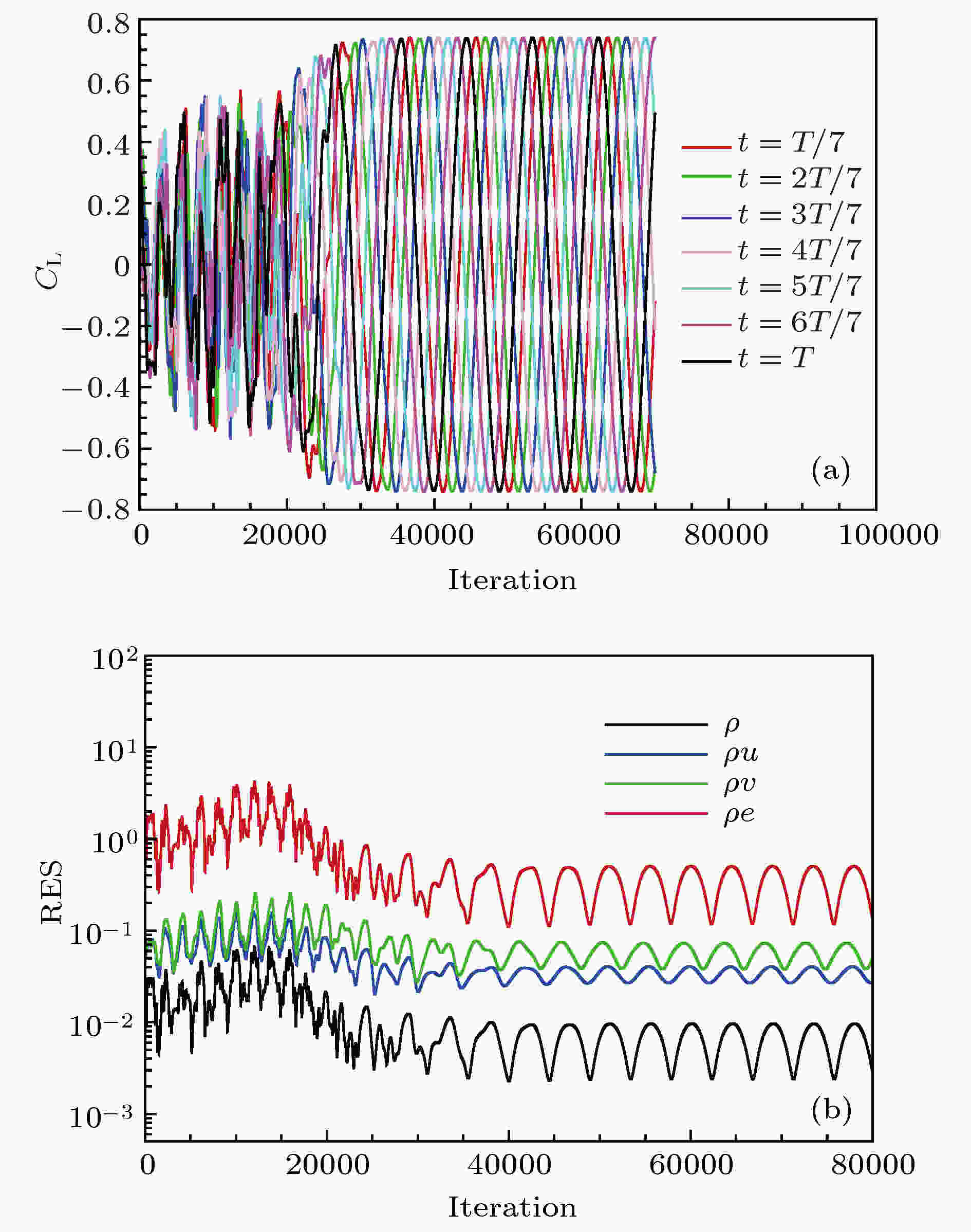
图 21 升力系数和t = T时刻的残差收敛曲线(Re = 180, T = 4, N_H = 3)　(a)升力系数; (b)残差
Figure21. Time history of lift coefficient C_L at various time instances over one period and residual at t = T (Re = 180, T = 4, N_H = 3): (a) Lift coefficient; (b) residual.

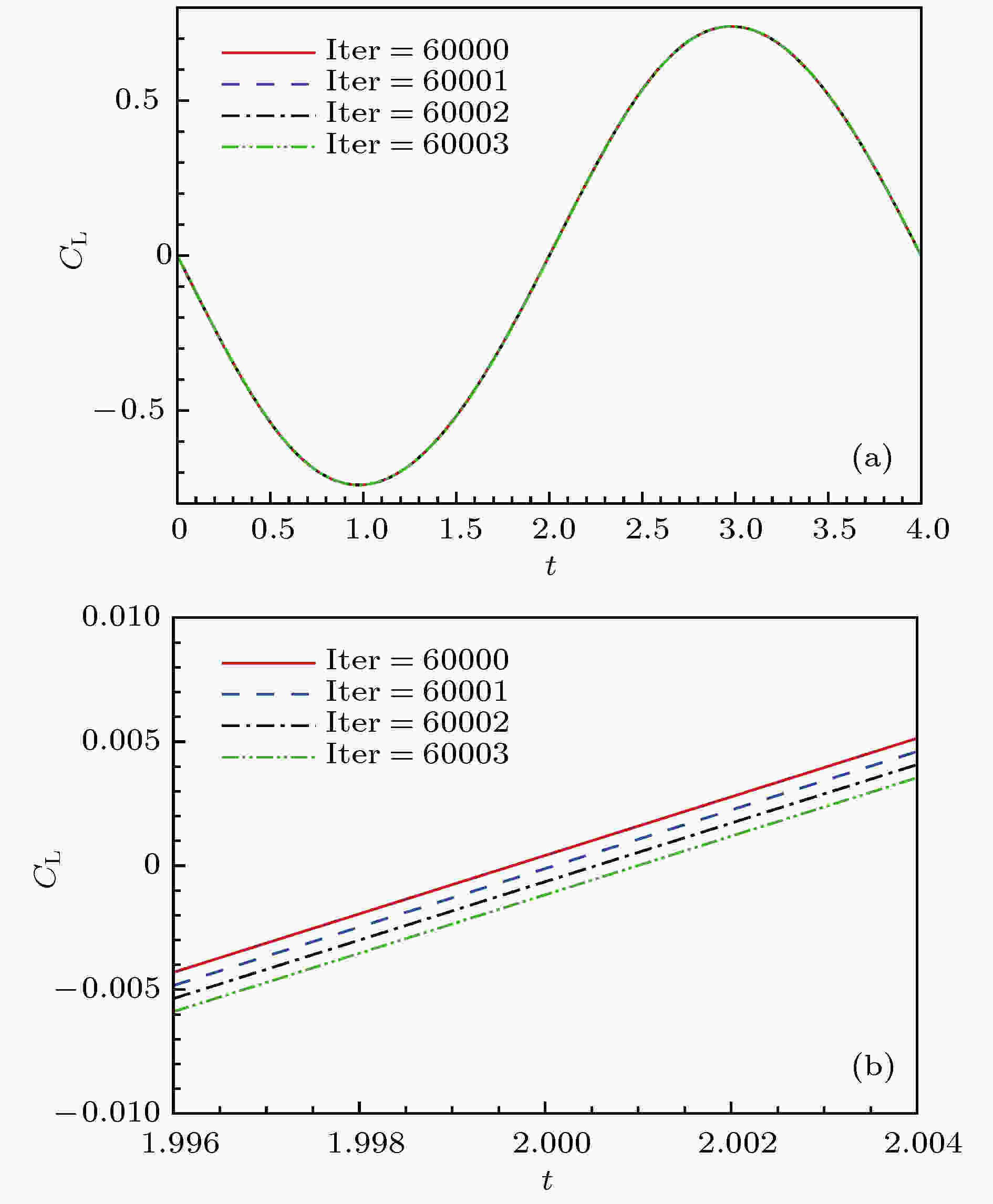图 22 不同迭代步重建的升力系数随时间的变化(Re = 180, T = 4, N_H = 3)　(a)整体; (b)局部
Figure22. Variation of C_L over one period at different iterations: (a) Overall; (b) local.

图 23 T = 5.389时各个时刻升力系数收敛曲线(N_H = 3)
Figure23. Time history of lift coefficient C_L at various time instances over one period with T = 5.389 (N_H = 3).

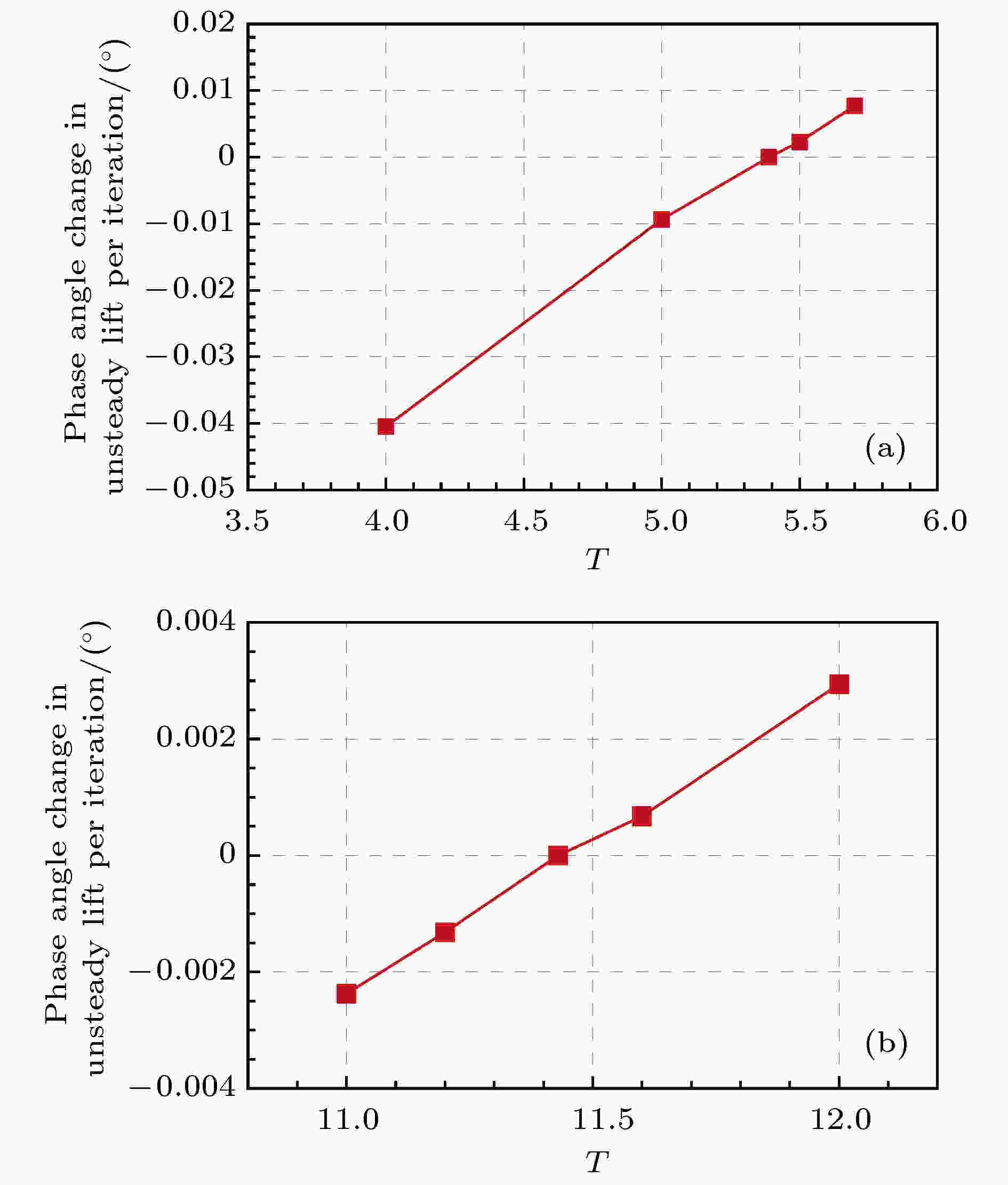图 24 相位差随周期T的变化(Re = 180, N_H = 3)
Figure24. Change in phase of unsteady lift versus time period for Re = 180 (N_H = 3).

GBVTP的实现是基于残差在T = T ^*时最小的物理事实, 采用SDM沿着残差下降的方向进行搜索. 图25为采用固定周期HBM计算的残差随周期T的变化. 由图25可知, T的精度决定了HBM计算的精度. 当给定的周期远离T ^*时, 残差下降越来越困难, 当T = T ^*时残差迅速下降. 因为, 当且仅当给定的T为真实的涡脱落周期才能满足非定常流动控制方程, 使得残差接近于0. 因此, 采用3个谐波数进行计算时, T = 5.389和11.43都是旋涡脱落的周期, 这与可变周期计算的结果也相一致.
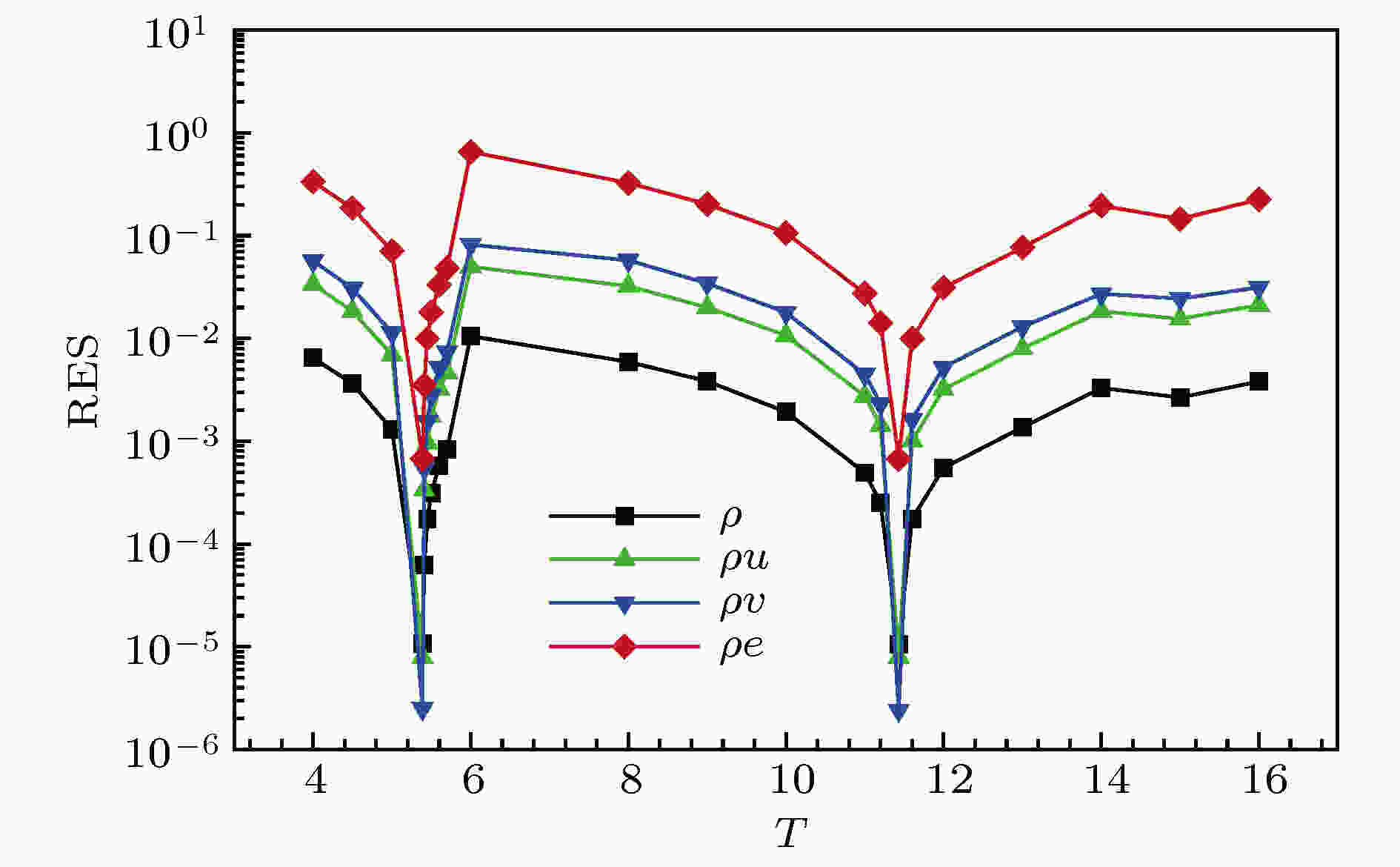图 25 残差随周期T的变化(Re = 180, N_H = 3)
Figure25. HBM solution residual versus time period for Re = 180 (N_H = 3).

GBVTP的核心思想是寻找T*使得残差趋于0, 这是单变量单目标函数的无约束最优化问题. 求解这类问题的最优化方法大致分为两类^[45]: 一类计算用到函数的导数; 一类只用目标函数不计算导数, 为直接方法. 这里考察了用到函数导数的另外两种方法: 牛顿法和Fletcher-Reeves共轭梯度法(简称FR法), 并和前面计算采用的SDM进行了比较.
2

-->

5.1.优化方法

考虑无约束问题:

$\begin{split} &\min L(T) = \frac{1}{2}{{{R}}^{\rm{T}}}_{{\rm{HB}}} \times {{{R}}_{{\rm{HB}}}}, \\ &{{{R}}_{{\rm{HB}}}} = {J^{ - 1}}\frac{{2{\text{π}}}}{T}{{DQ}} + {{R}}, \;\;T > 0, \end{split}$

其中R_HB表示谐波平衡方程的残差向量. 这个问题是求解T ^*使得L(T ^*) → 0.
采用SDM计算时, 沿着L下降最快的方向(负梯度方向)寻找T ^*, 迭代公式为

${T^{p + 1}} = {T^p} - \lambda \frac{{\partial {L^p}}}{{\partial T}}, $

其中λ表示搜索步长.
采用牛顿法计算时, 沿着牛顿方向计算T ^*, 迭代公式为

${T^{p + 1}} = {T^p} - \dfrac{{\dfrac{{\partial {L^p}}}{{\partial T}}}}{{\dfrac{{{\partial ^2}{L^p}}}{{\partial {T^2}}} + \varepsilon }}, $

其中${d^p} = - {{\dfrac{{\partial {L^p}}}{{\partial T}}} \bigg/ {\left( {\dfrac{{{\partial ^2}{L^p}}}{{\partial {T^2}}} + \varepsilon } \right)}}$为$ T^p$处的牛顿方向, ε是修正系数, 且ε > 0.
采用FR法计算时, 需要构造一组共轭方向, 然后沿着这组方向进行搜索, 求解T ^*:

$\begin{split}& {T^{p + 1}} = {T^p} + \lambda {d^p}, \\ & {d^p} = - \frac{{\partial {L^p}}}{{\partial T}} + {\beta _{p - 1}}{d^{p - 1}}\;, \\ &{\beta _{p - 1}} = {{{{\left( {\frac{{\partial {L^p}}}{{\partial T}}} \right)}^2}}\Bigg/ {{{\left( {\frac{{\partial {L^{p-1}}}}{{\partial T}}} \right)}^2}}}. \end{split} $

不可忽略的是, 在FR方法中, 初始的搜索方向必须选择最速下降方向, 即:

${d^1} = - \frac{{\partial {L^1}}}{{\partial T}}.$

2 -->

5.2.计算结果及分析

分别采用以上方法对Re = 180的圆柱绕流进行数值模拟, 对比他们的计算精度和效率. 图26给出了牛顿法及SDM的计算结果, 可以看出, 牛顿法模拟的涡脱落周期与SDM的结果一致. 采用SDM时, 需要设置搜索步长λ, 步长越大收敛越快. 而采用牛顿法计算时不需要设置此参数, 其收敛曲线介于SDM采用λ = 1和λ = 100的收敛曲线之间, 且接近于λ = 100的计算结果.
与SDM类似, 共轭梯度法也需要设置搜索步长λ. 在本文算例中, 取不同时间步长计算时, 共轭梯度法计算得到的周期T收敛曲线基本重合, 步长对共轭梯度法计算结果的影响不大, 如图27所示. 共轭梯度法的收敛速度与SDM采用λ = 100时的相同.
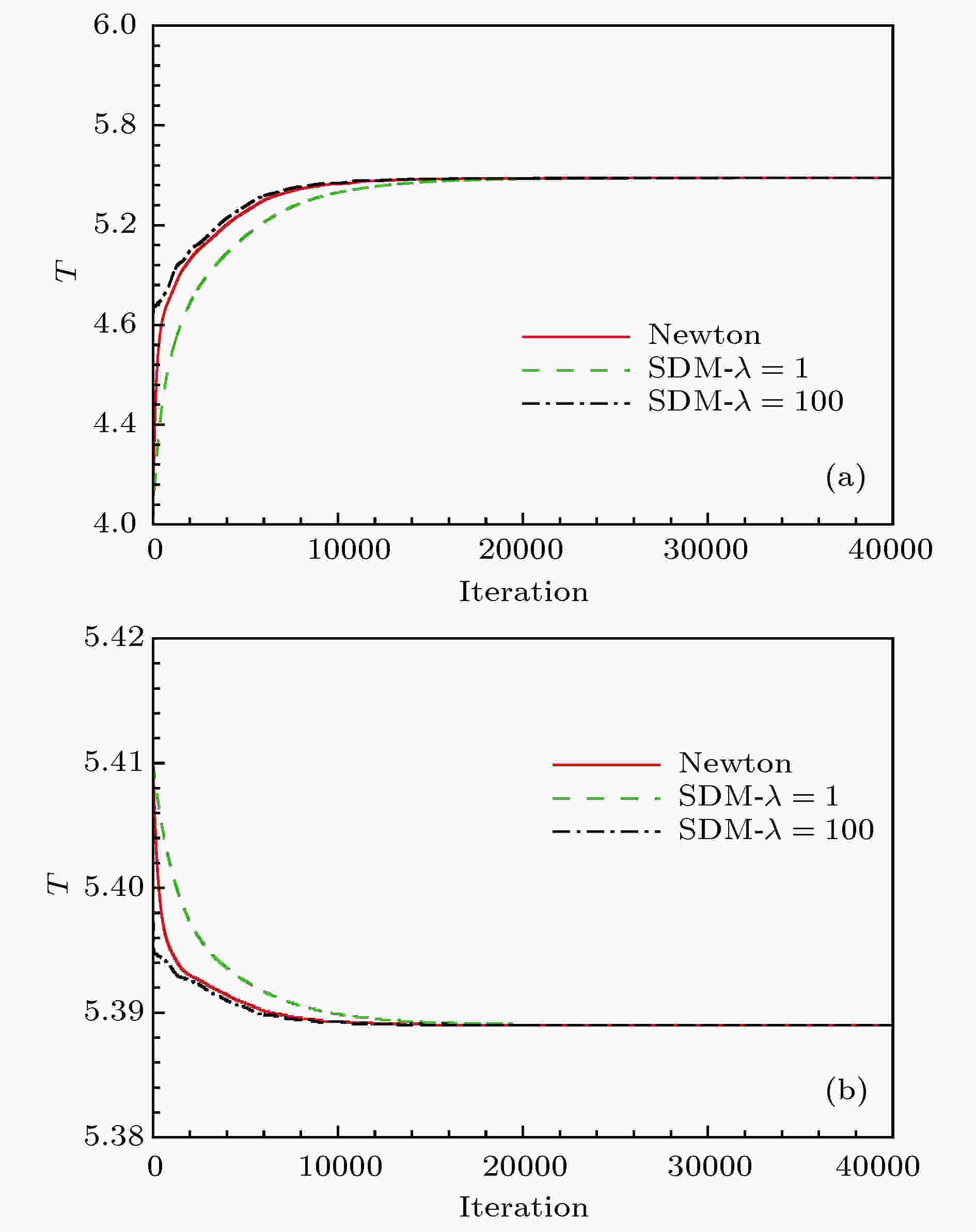图 26 采用牛顿法和SDM计算的周期T收敛曲线对比图　(a)初始T₀ = 4; (b)初始T₀ = 5.41
Figure26. Convergence of shedding time period computed by Newton method and SDM: (a) T₀ = 4; (b) T₀ = 5.41.

图 27 采用FR法计算的周期T收敛曲线(a)及其与SDM计算结果的比较(b)
Figure27. Convergence of shedding time period computed by FR conjugate gradient method (a) and compared with the SDM results (b).

可变周期HBM采用三种不同优化方法计算得到的周期T收敛曲线对比如图28所示. 由图28可知, 三种方法的计算精度相同, 最终计算得到的涡脱落周期T均为5.389. 共轭梯度法和牛顿法的收敛速度与SDM采用最大搜索步长时的收敛速度一致. 由于牛顿法不需要设置搜索步长等参数, 在实际工程计算中更有优势.
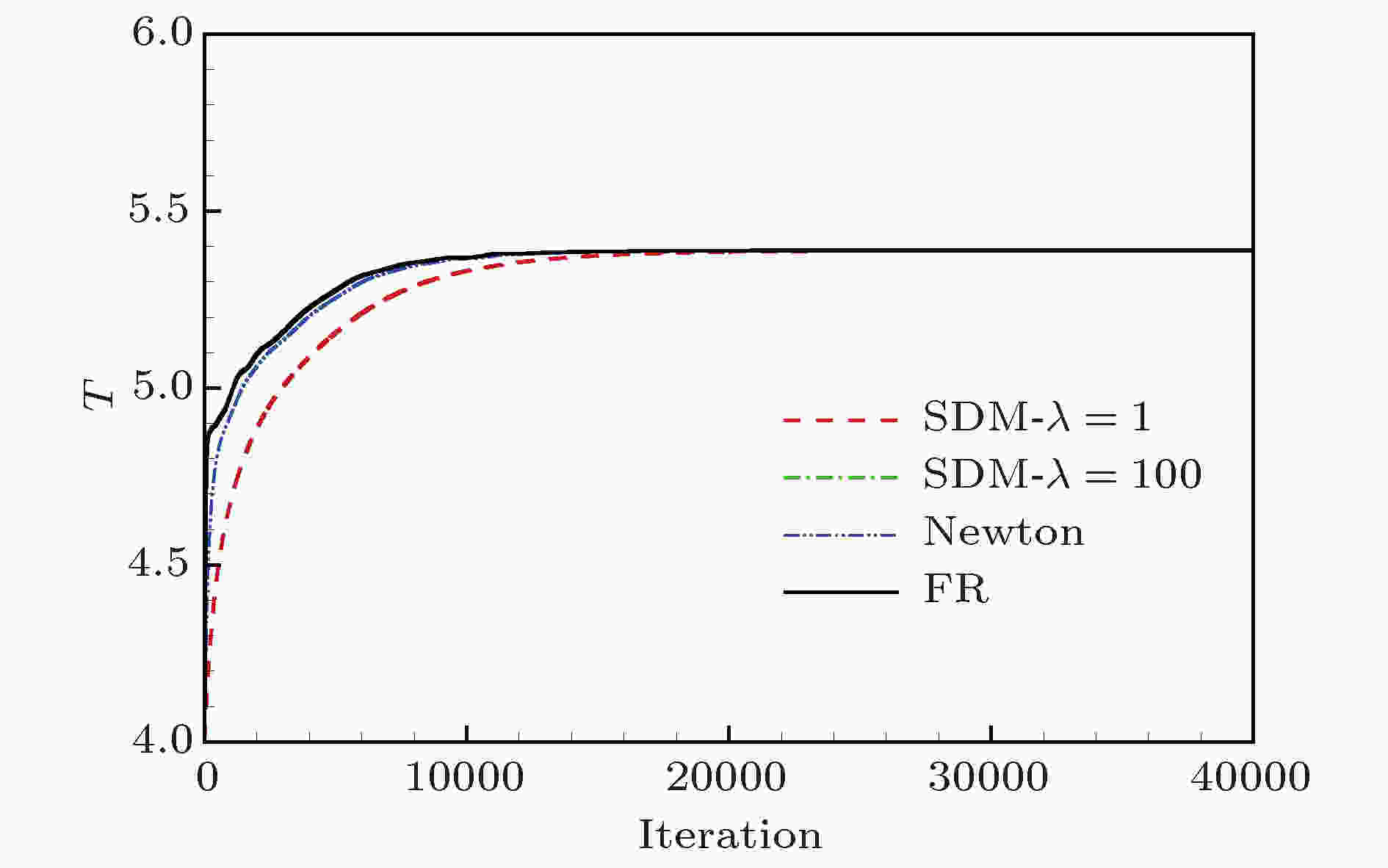图 28 采用三种不同优化方法计算得到的周期T收敛曲线图
Figure28. Convergence of shedding time period computed by three different methods of optimization.

采用可变周期HBM数值模拟二维不可压非定常方柱绕流. 来流雷诺数为Re = 100, 采用H型计算网格(如图29所示), 网格大小为147 × 106. 为了对比研究, 时域计算方法的结果列于表4. 计算结果表明, TDM计算采用时间步长0.01能够满足计算精度要求.
表5列出了涡脱落频率、平均阻力系数和加速比随谐波数的变化. 随着谐波数的增加, 计算结果逐渐收敛. 对于涡脱落频率, 采用3个谐波的计算结果与4个谐波的相同, 且与TDM计算及实验值相符合. 与TDM相比, HBM计算保留3个谐波数时计算效率提高了将近18倍. 谐波数越少, 计算速度越快, 但精度会有所损失. 当谐波数增加时, 需要减小虚拟时间步长以满足计算稳定性的要求, 因此收敛速度明显减慢. 一个周期内升力系数对比如图30所示. 图31为升力系数最小时刻对应的熵等值线图. 从图30和图31可以看出, HBM采用3个谐波数就能够重现时域结果, 达到时域计算的精度.
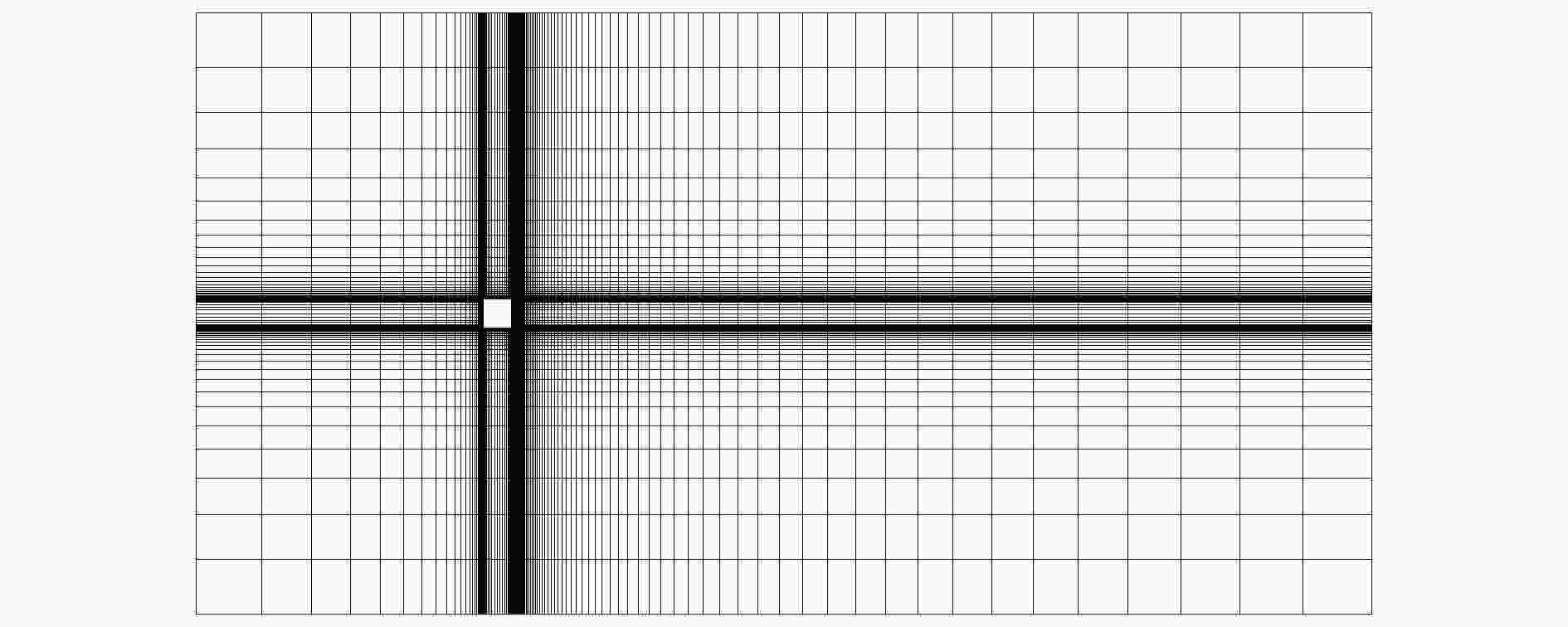图 29 二维方柱绕流计算网格
Figure29. Computational grid for rectangular in cross flow.

?t	St	Cd, avg
0.1	0.134	1.443
0.01	0.1415	1.487
Sohankar[46]	0.142	1.466

表4时域计算结果
Table4.Time-averaged coefficient and Strouhal number computed by time-domain solver using different physical time steps.

NH	St	Cd, avg	Speedup
2	0.1419	1.4846	23.27
3	0.1414	1.4863	17.88
4	0.1414	1.4865	1.944
TDM	0.1415	1.487	1

表5Re = 100时不同谐波数下的计算结果对比
Table5.Convergency of frequency and time-averaged coefficient with speedup estimates.

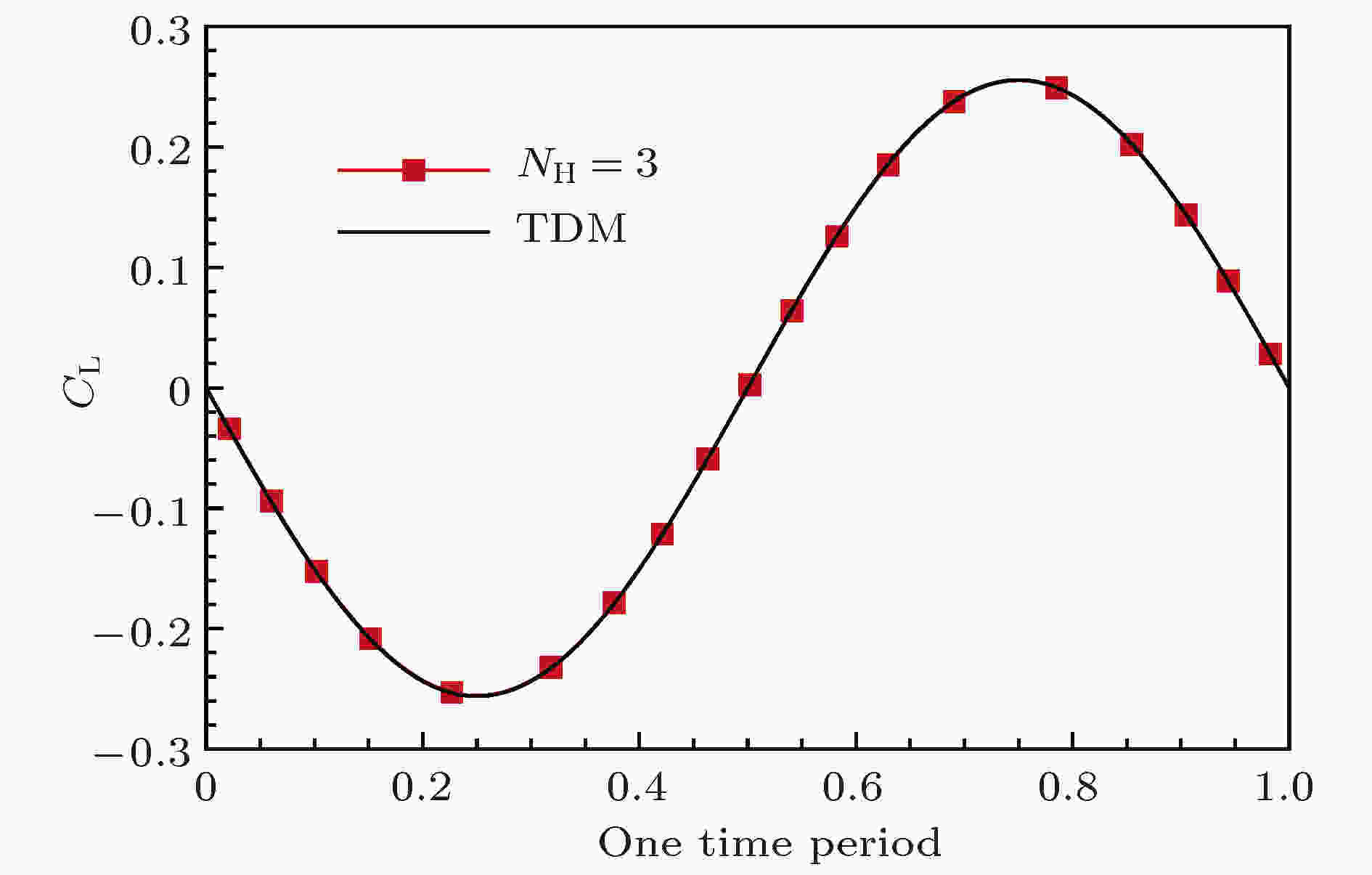图 30 升力系数随时间的变化
Figure30. Comparison of lift coefficients of HBM and TDM at Re = 100.

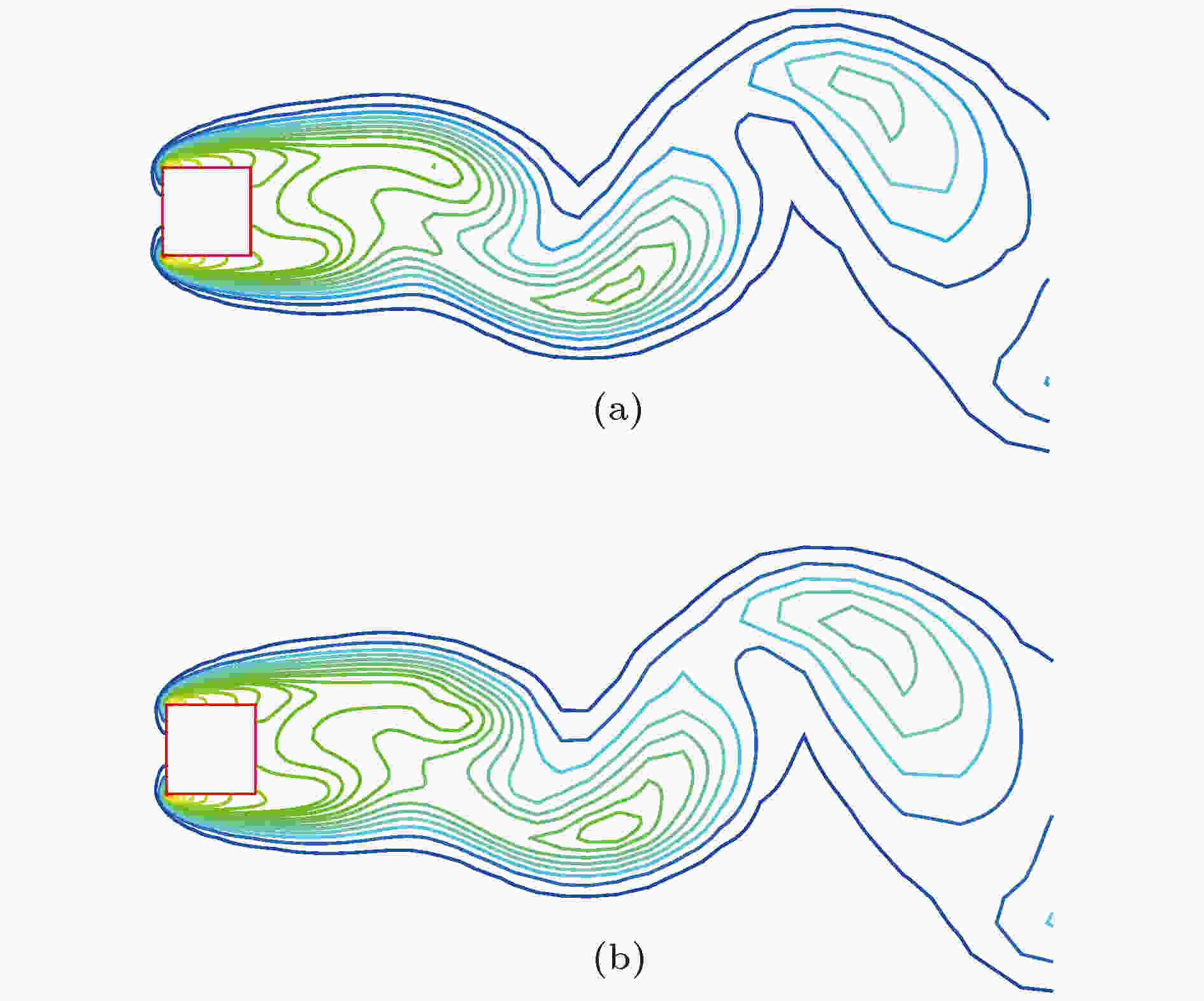图 31 熵等值线图(C_L最小时刻)　(a) TDM计算结果; (b) HBM计算结果(N_H = 3)
Figure31. Comparison of the instantaneous entropy contours: (a) TDM results; (b) HBM results (N_H = 3).

本文以RANS方程为控制方程, 采用HBM对低雷诺数二维不可压绕圆柱和方柱的周期性非定常流动进行了数值模拟. 对于这类流动周期未知的非定常流动问题, 采用基于残差导数的GBVTP求解涡脱落周期. 得到的以下主要结论.
1)可变周期HBM可以准确地模拟周期性非定常涡脱落问题, 计算得到的Strouhal数和平均阻力系数与实验值及其他数值计算数据符合良好, 与传统的TDM相比该方法具有较高的计算效率.
2)周期搜索步长λ对计算结果影响较小, 非定常涡脱落周期都收敛到同一值; 当初值T₀较大时, 最终计算得到的周期T可能会收敛到nT ^* (n = 2, 3, ···), 因此有必要发展自动搜索最小周期的计算方法.
3)基于不同优化策略的可变周期计算结果表明: 不同优化方法的计算精度相当; 牛顿法没有参数问题, 其收敛速度与共轭梯度法及SDM采用最大搜索步长时的收敛速度一致. 因此, 牛顿法在工程计算中更有优势.