摘要: 软泥底环境下沉积层参数的声学反演是国际水声领域的一个研究热点. 浅海中, 当高声速基底和海水之间存在一层低声速(小于海水声速)的沉积层时, 小掠射角情况下不同频率声传播损失会出现周期性增大现象. 基于此现象, 提出一种适用于低声速沉积层的海底参数声学反演方法. 首先, 推导给出小掠射角情况下传播损失周期增大的频率间隔与沉积层声速、厚度及近海底海水声速之间的解析表达式; 其次, 利用一次黄海实验中软泥底环境下的宽带声传播信号, 提取了小掠射角下传播损失增大的频率周期; 再次, 把该解析表达式作为约束条件, 结合Hamilton密度与声速的经验公式, 采用匹配场处理反演给出沉积层的声速、密度、厚度及基底的声速、密度; 然后, 利用声传播损失数据反演得到泥底环境下不同频率的声衰减系数, 通过拟合发现泥底声衰减系数随频率近似呈线性关系; 最后, 给出了双层海底模型和半无限大海底模型等效性的讨论. 反演结果为低声速沉积层海底声传播规律研究与应用提供了海底声学参数.
关键词: 低声速沉积层海底 /
声学参数反演 /
匹配场处理 /
传播损失 English Abstract Geoacoustic inversion for acoustic parameters of sediment layer with low sound speed Li Meng-Zhu 1,2 ,Li Zheng-Lin 1 ,Zhou Ji-Xun 1,3 ,Zhang Ren-He 1 1.State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11434012, 11874061).Received Date: 01 February 2019Accepted Date: 10 March 2019Available Online: 01 May 2019Published Online: 05 May 2019Abstract: Acoustic inversion of sediment parameters in muddy bottom environment has received much attention in the field of underwater acoustics. In shallow water, when there is a low-speed layer of unconsolidated sediment, such as mud in which the sound speed is lower than that of the sea water, on the top of a high-speed bottom, the transmission losses at different frequencies will increase periodically under the condition of small grazing angles. Based on this phenomenon, an acoustic inversion method of seabed parameters for low speed sediments is proposed. Firstly, the analytical expressions between the frequency interval of the transmission loss (TL) periodical increasing and geoacoustic parameters, including the sound speed and the thickness of sediment layer and the sound speed of seawater near the bottom, are derived under the condition of small grazing angles. Secondly, using the broadband sound propagation signals received under the thermocline in the 2002 summer acoustic experiment conducted in the Yellow Sea, the TL at small grazing angles increases periodically with the frequency, and it is determined that the sediment of this sea area is a low-speed sediment. Then, taking the analytical expression as the constraint condition and combining with Hamilton's empirical formula, the sound speed, density, thickness of sediment layer and the sound speed and density of the seabed are inverted by matched field processing. Finally, the bottom attenuation coefficients at different frequencies are inverted by using the long-range TL, and the linear relationship between the attenuation coefficients and the frequencies is obtained. The equivalence between the two different bottom models is discussed in the end. The inversion results can provide seabed parameters for the study and application of the sound propagation law in shallow water with a low-speed sediment.Keywords: low-speed sedimentary seabed /geoacoustic inversion /matched field processing /transmission loss 全文HTML --> --> --> 1.引 言 海底参数声学反演是快速低成本获取局部海域环境参数信息的有效方法. 浅海中, 由于声波与海底多次作用而携带了大量的海底信息, 可以很好地利用声信号进行地声反演. 基于高声速海底的地声反演方法有很多, 如: 匹配场反演[1 ,2 ] 、简正波频散特征反演[3 ] 、混响的垂直相关性反演[4 ,5 ] 、噪声场的相干性反演[6 ] 、海底反射系数反演[7 ] 、脉冲波形相关性反演[8 ] 及声传播损失(TL)反演[9 ] 等. 上述反演方法利用特定的实验数据验证了反演结果的可靠性, 但其适用条件都有一定限制. 例如, 采用低频群速度的地声反演能得到可信的海底声速, 但由于群速度对衰减系数不敏感, 所以该方法很难获取衰减系数; 利用传播损失反演海底声学参数时, 不同海底参数之间会存在较强的耦合关系, 偏大的海底声速引起的传播损失误差可以抵消偏大的衰减系数引起的传播损失误差进而得到与实验结果相符的传播损失. Li等在分析反演参数敏感性的基础上, 提出多物理量联合地声反演方法[10 -13 ] , 很好地解决了地声反演方案的多值问题, 并对黄海6种不同底质类型的声学参数进行了反演[7 ] . Zhou和Zhang[14 ] 通过总结全球20个浅海海域砂质海底的声学反演结果, 给出了砂质海底在50—600 Hz频段内海底声速与近海底海水声速比为1.061 ± 0.009, 在50—1000 Hz频段内海底等效衰减系数的经验关系满足α (dB/m) = (0.37 ± 0.01) × (f /1000)(1.80 ± 0.02) , 分析发现砂质海底的上述规律符合Biot-Stoll多孔弹性模型.[15 ] 给出了平面波假设下三层均匀液态低声速沉积层海洋环境模型下的本征方程及频散曲线图. 1979年, Rubano[16 ] 通过实测数据和理论仿真对比发现低声速沉积层对高频传播损失有显著影响. 1980年, Kuperman和Jensen[17 ] 阐述了声波在小掠射角入射低声速沉积层海底时海底反射损失会出现周期增大的现象. 2018年, Bonnel等[18 ] 使用warping变换分辨高阶模态, 提出了一种地声参数联合反演方法, 成功反演出低声速沉积层海底的地声参数. Wan等[19 ] 发现根据频散特性进行地声反演时, 考虑艾利相位频段可以降低反演的不确定性. 但Bonnel等[18 ] 和Wan等[19 ] 都利用了频散特性对同一低声速沉积层海底进行声学反演, 其地声参数敏感性分析及反演结果的不确定性分析都表明频散特性对基底声速敏感, 进而得到的反演结果可靠, 而频散特性对浅表层声速不敏感, 反演得到的浅表层声速虽小于海水声速, 但是反演结果的不确定性很大, 另外他们没有给出海底衰减系数. 总之, 针对低声速沉积层海底的声传播规律研究较少, 更缺乏有效的海底地声反演方案.2.低声速沉积层海底环境下的声传播特性理论分析 低声速沉积层指的是其声速比上面的海水声速及下面的无限大基底声速都小的中间层, 对应的海底模型见图1 , 各层对应的声学参数如图中标注. 声速满足${c_3} > {c_1} > {c_2}$ , 因此海水中声波都能折射进入沉积层, 而在沉积层-基底界面存在一个临界掠射角. 这里只考虑声波在沉积层-基底界面全反射的情况, 即海水中的掠射角$\theta <$ $ \arccos ({c_1}/{c_3})$ .图 1 低声速沉积层海底模型Figure1. Bottom model with a low speed sediment layer.图1 所示的低声速沉积层海底的反射系数可表示为掠射角θ 和频率f 的函数:$\phi = 2{k_2}d\sin \mu $ 是声波在沉积层内的垂直相移(k 2 为沉积层内波数); ${R_{12}} = \dfrac{{{k_{z1}}/{\rho _1} - {k_{z2}}/{\rho _2}}}{{{k_{z1}}/{\rho _1} + {k_{z2}}/{\rho _2}}}$ , ${R_{23}} = \dfrac{{{k_{z2}}/{\rho _2} - {k_{z3}}/{\rho _3}}}{{{k_{z2}}/{\rho _2} + {k_{z3}}/{\rho _3}}}$ 分别为声波在海水-沉积层、沉积层-基底界面的瑞利反射系数, kz 1 , kz 2 , kz 3 为各层对应的垂直波数. 对应的海底反射损失RL = $ - 10\log (|R(\theta ,f)|^2) $ . 由斯奈尔定律有$\dfrac{{\cos \theta }}{{\cos \mu }} = \dfrac{{{c_1}}}{{{c_2}}}$ 即$\mu =\arccos ({c_2}/{c_1}\cos \theta )$ , 从而可得$\theta $ 趋近于0时, $\dfrac{{{\rm{d}}\mu }}{{{\rm{d}}\theta }}$ 趋近于0, 于是有$\mu = {\mu _0} =$ $ \arccos ({c_2}/{c_1})$ . 小掠射角情况下R 12 , R 23 可以近似表示为指数形式:$Q = \dfrac{{2{\rho _2}/{\rho _1}}}{{\sqrt {{{({c_1}/{c_2})}^2} - 1} }}$ , $S = \dfrac{{2{\rho _3}/{\rho _2}}}{{\sqrt {1 - {{({c_2}/{c_3})}^2}} }}$ . 将(2 )和(3 )式代入(1 )式可得θ 趋近于0时, μ = μ 0 , 可得${{\rm{e}}^{{\rm{i}}(S{\mu _0} - {\rm{\text{π}}} + 2{k_2}d\sin {\mu _0})}} \ne 1$ 时$\mathop {R(\theta ,f)}\limits_{\theta \to 0} = - 1$ , 等价于有180 °相移的全反射; 当${{\rm{e}}^{{\rm{i}}(S{\mu _0} - {\rm{\text{π}}} + 2{k_2}d\sin {\mu _0})}} = 1$ 时, $\mathop {R(\theta ,f)}\limits_{\theta \to 0} $ 存在奇异点. 对应的奇异点满足图1 也可以从物理上进行阐述. 当θ 趋近于0时, 声波在沉积层-海水界面上的相移${\varphi _1} = 0$ , 在沉积层-基底层界面上的相移${\varphi _2} = S{\mu _0} - {\rm{\text{π}}}$ , 在沉积层内由点A 到点B 的相移为k 2 × AB , 由点B 到点C 的相移为k 2 × BC , 声波在沉积层内干涉满足条件 ${\varphi _1} + {\varphi _2} + (AB + BC) \cdot {k_2} = 2n{\rm{\text{π}}}\;(n = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }} \cdots )$ .AB +BC = 2d sinμ 0 , 因此小掠射情况下声波在沉积层内干涉满足的条件同(4 )式, 沉积层内很小的衰减也可以吸收大部分入射能量, 对应的海底反射损失增大.4 )式可以得到小掠射角条件下海底反射损失增大对应的起始频点及频率间隔满足图1 中各层声学参数如表1 所列, 根据(5 )和(6 )式求得海底反射损失周期性增大的起始频点和频率间隔分别为freq 0cal = 239 Hz和Δfreq cal = 756 Hz. 此理论计算结果同图2 中掠射角为1°时海底反射损失的仿真结果freq 0RL = 242 Hz和Δfreq RL = 750 Hz相差不大. 以表1 的声学参数为基准, 图3 给出了小掠射角条件下海底反射损失的敏感性分析. 从图3 可以看出, 沉积层厚度为零时对应半无限大高声速海底, 小掠射角条件下声波全反射, 海底反射损失为0 dB, 不存在海底反射损失周期增大的现象; 小掠射角情况下低声速沉积层海底反射损失周期性增大的频率周期只与沉积层厚度、声速有关, 且沉积层声速与厚度存在正耦合关系, 该规律同(6 )式一致; 当掠射角较小(< 2°)时, 不同小掠射角情况下海底反射损失周期增大的起始频率、频率间隔估计值与理论计算值相符, 满足(5 )和(6 )式; 基底声速、沉积层密度、基底密度、沉积层衰减系数、基底衰减系数与海底反射损失周期性增大的频率间隔无关, 对起始频点影响较小.c 1 /m·s–1 ρ 1 /g·cm–3 α 1 /dB·λ –1 c 2 /m·s–1 ρ 2 /g·cm–3 α 2 /dB·λ –1 d /mc 3 /m·s–1 ρ 3 /g·cm–3 α 3 /dB·λ –1 1488 1.0 0.0 1460 1.4 0.10 5 1620 1.8 0.10
表1 低声速沉积海底环境参数Table1. Seabed environmental parameters for low-speed sediment simulation.图 2 掠射角1°时对应的海底反射损失Figure2. Reflection loss for the grazing angle of 1°.图 3 小掠射角情况下参数敏感性分析Figure3. Sensitivity analyses of the bottom reflection loss to the geoacoustic parameters under the small grazing angle.extended – RLtop – RLbottom – Losswater , 其中, SL表示声源级; TLextended 表示声波的扩展损失; RLtop 表示海面反射损失(因空气声阻抗远小于海水声阻抗, 海面可视为理想边界其反射损失可忽略); Losswater 表示海水吸收损失; RLbottom 表示海底反射损失, 是掠射角和频率的函数. 为了定量估计海底有效掠射角与声源距离的关系, 这里定义一个有效海底掠射角$\overline \theta = \dfrac{{\sum\nolimits_i {{\theta _i}{I_i}} }}{{\sum\nolimits_i {{I_i}} }}$ , 式中θi 表示第i 条由声源到达接收点的声线入射海底的掠射角, Ii 表示第i 条由声源到达接收点的声线的能量. 表2 为由Bellhop理论[20 ] 计算得到的海深63.5 m, 声源频率300 Hz, 声源、接收深度50 m, 不同收发距离对应的有效海底掠射角及标准差, 其他声学参数同表1 . 近距离声场除小掠射角声波外还包括很多大掠射角声波, 所以海底有效掠射角及标准差都比较大. 随距离增大声波与海底的作用次数增多, 大掠射角声波的海底反射损失增大, 进而衰减加快, 所以远距离声场由小掠射角声波构成, 即表2 随距离增大海底有效掠射角及其标准差逐渐减小.收发距离/km 1 5 10 20 有效海底掠射角 10.41° 6.16° 2.15° 0.52° 标准差 7.84° 6.44° 3.75° 0.70°
表2 计算得到的不同距离下的有效海底掠射角Table2. Effective bottom grazing angles at different ranges.[21 ] 计算表1 所列低声速沉积层海底环境下不同中心频率时50 Hz带宽内平均的声传播损失, 其中声源深度z s 和接收深度z r 为50 m, 距离r 为20 km, 海深h 为63.5 m, 根据表2 可得此距离下的有效掠射角小于1°, 满足小掠射角条件. 图4 给出了计算得到的TL与掠射角1°时海底反射损失对比. 从图4 可以看出, 尽管TL随频率的变化规律会有小幅度起伏, 但受低声速沉积层影响, 小掠射角条件下TL在个别频率上的周期增大现象与海底反射损失的变化规律基本一致. TL周期性增大的初始频点freq 0TL = 285 Hz与理论公式计算结果freq 0cal = 239 Hz存在一定偏差, 但TL周期性增大的频率间隔Δfreq TL = 724 Hz与理论公式计算结果Δfreq cal = 756 Hz误差较小; 另外, 高频时声源激发的简正波号数较多, 接收信号包含的掠射角范围较大, 所以传播损失振荡比较明显, 因此用频率低于1000 Hz频段内的TL估计Δfreq TL 的结果误差会较小. 这种TL周期性增大的现象只在低声速沉积层海底小掠射角条件下成立, 在高声速海底不存在. 因此, 小掠射角条件下TL在特定频点存在周期性增大的现象可作为低声速沉积层存在的判别依据. 另外, 低声速沉积层海底小掠射角条件下TL周期性增大对应的初始频率及频率间隔与海底声学参数满足的关系式(5 )和(6 ), 可以进一步用于海底声学参数反演.图 4 声传播损失与海底反射损失随频率的变化Figure4. Comparison between the transmission?loss and reflection loss at different frequencies.3.低声速沉积层声学参数联合反演方法 针对低声速沉积层海底, 在理论分析小掠射角情况下TL周期性增大的基础上, 得到TL周期性增大特性的频率间隔与海底声学参数之间的解析表达式, 并参考高声速海底的声学反演方法[7 ] , 给出低声速沉积层海底的联合反演流程(图5 ).首先, 选择满足声波以小掠射角入射海底的声信号进行分析, 根据TL存在周期性增大现象判定海底为低声速沉积层海底, 并得到传播损失周期性增大的初始频点及频率间隔; 然后, 考虑到低频声场对海底衰减系数不太敏感, 可假定一个衰减系数用低频数据进行匹配场处理, 同时利用(6 )式作为约束条件间接反演沉积层厚度, 并由Hamilton经验公式c = 2330.4–1257.0ρ + 487.7ρ 2 间接反演基底密度[22 ] ; 最后, 在匹配场反演得到的沉积层声速、密度和厚度及基底声速、密度的基础上, 通过一维边缘概率密度分布对反演结果进行评价, 并根据不同距离下的传播损失反演不同频点对应的衰减系数.图 5 低声速沉积层声学参数联合反演流程Figure5. Flowchart of geoacoustic inversion for the sediment with lower sound speed.4.低声速沉积层声学反演实验及结果 声场声信息国家重点实验室于2002年夏季在青岛海域进行了浅海声学实验. 此次实验的主要目的是研究不同底质类型条件下的等效海底参数的声学反演方法及其与海底沉积物类型的映射关系, 同时研究水声信号在不同海底底质下的传播、混响及散射规律. Li等[7 ] 基于半无限大海底模型对该海域进行了系统的反演, 得到了不同海底底质类型下等效声学参数及衰减系数的非线性频率关系式. 其中第23站点的海底重力采样分析结果表明其底质类型为粉砂质粘土, 在该站位测得的声速剖面如图6(a) 所示, 为典型浅海夏季负跃层声速剖面, 温跃层深度位于10—42 m. 图6(b) 给出了实验设备布放示意图及声传播测线上的海深示意图, 在30 km范围内海深相对平坦, 在54—66 m变化. 混响实验时, 在第23站点发射2枚1 kg TNT宽带爆炸声源, 其标定深度50 m, 在距离第23站点9.2 km处的第24站点53.5 m深度的一个无前放水听器接收到了完整的声传播信号. SONY录影机记录的信号采样频率为6 kHz. 除了混响实验外, 在23—26站点之间还用标定深度25 m的38 g TNT宽带爆炸声源进行了声传播实验, 用 16阵元垂直接收阵进行接收, 水听器接收深度范围22—52 m, 采样频率为12 kHz.图 6 实验期间的水文环境和设备布设 (a) 声速剖面; (b) 设备布设及海深示意图Figure6. Water environment and experiment configuration during the experiment: (a) Measured sound speed profile; (b) experimental configuration and water depth.4.1.低声速沉积层声速联合反演 4.1.低声速沉积层声速联合反演 对实验环境的声场分析结果表明, 混响实验中获得的两枚声传播信号的声源和接收器都位于温跃层之下, 接收的声场满足小掠射角条件. 分析得到50 Hz带宽内平均的TL随频率变化结果如图7 所示, 从图7 可以看出, 在频率200 Hz附近传播损失增大6 dB, 在频率728 Hz附近传播损失增大8 dB, 在频率1215 Hz附近传播损失增大8 dB, 从而可以初步判断沉积层声速小于近海底的海水声速. 因为高频传播损失振荡比较大, 信号采样率只有6 kHz, 因此选用1000 Hz频段内的TL估计传播损失异常的初始频率freq 0 及频率间隔Δfreq , 得到freq 0exp = 200 Hz, Δfreq exp = 528 Hz.图 7 声传播损失随频率的变化 (r = 9.2 km, z s = 50.0 m, z r = 53.5 m)Figure7. Transmission losses at the different frequencies ( r = 9.2 km, z s = 50.0 m, z r = 53.5 m).6 )式可以得到沉积层厚度与频率间隔、沉积层声速、近海底海水声速的关系式:图8 中实线给出了实验条件下频率间隔为528 Hz时, 沉积层厚度d 与沉积层声速c 2 的关系. 另外, 假设实验数据提取的频率间隔存在 ± 50 Hz的误差, 对应的沉积层厚度与沉积层声速变化关系分别由虚线和点线给出. 从图8 可以看出, 频率间隔存在一定的误差时, 对应相同声速条件下沉积层厚度与真值的差别不大. 因此, 在图5 的反演流程中, 利用(7 )式由沉积层声速来间接地反演沉积层的厚度.图 8 给定频率间隔下沉积层厚度与声速的关系Figure8. Relationship between the thickness of sediment and its sound speed at the special frequency step.图5 中用匹配场进行反演时, 目标函数选用宽带非相干Bartlett处理器:$p_i^{\rm{e}}(f)$ 是第i 个垂直阵元测得的声压场, $p_i^{\rm{c}}(f,{m})$ 是基于绝热简正波理论计算得到的第i 个垂直阵元的拷贝场, ${m}$ 表示待反演参数向量, N 表示垂直阵元个数, M f 表示反演所用频点个数, j 表示频点序号, 上标“*”表示复数的共轭. 在实际反演中, 选取4个标定深度为25 m的宽带爆炸声信号进行处理, 选择信号频带为50—100 Hz, 共33个频点.13 ]假定基底为高声速海底, 利用Hamilton经验公式由基底声速间接反演基底密度, 同时参考文献[7 ]设基底衰减系数为0.169f 1.74 dB/m (f 的单位是kHz). 沉积层厚度根据(7 )式由待反演的沉积层声速间接求出. 另外, 匹配场对海深和声源距离较为敏感, 也加入到待反演参数向量中. 最后, 反演问题简化为以沉积层声速、沉积层密度、基底声速、海深、声源距离为待反演参数向量的五维最优化问题. 由于搜索空间大且维数高, 故采用改进的遗传算法进行寻优, 遗传算子的取值如下: 选择概率为0.5, 变异概率为0.05, 交叉概率为0.8, 种群数为64, 遗传代数为600代, 每个声信号采用10组并行计算确保收敛于相同的最小值[23 ] .表3 列出了待反演参数的搜索范围, 表中r 表示声源距离, GPS标称距离为9.2 km, 同时给出了计算结果的最优值、平均值, 采用参数的标准差来表示参数的估计值与其均值的离散程度. 从表3 可以看出, 反演得到的参数的最优值与平均值相差不大, 标准差较小, 反演结果具有一致性. 反演得到沉积层声速为1474 m/s, 其与近海底海水声速比为0.99, 符合粉砂质粘土底质的采样分析结果[24 ] ; 反演的沉积层厚度为10 m, 密度为1.35 g/cm3 , 稍小于海底采样结果1.47 g/cm3 , 海底采样测量是经海底采样后拿回实验室进行测量的, 在取样过程及保存样品过程中都会失去了部分海水, 会导致采样测量的海底密度结果略微偏大. 反演的基底声速为1580 m/s, 密度为1.64 g/cm3 , 将反演得到的声学参数代入(6 )式, 求得小掠射角情况下的传播损失周期性增大的初始频率freq 0inv = 188 Hz, 此结果与实验数据得到的初始频率freq 0exp = 200 Hz相差不大, 反演结果可以较好地解释实验中小掠射角声信号传播损失周期性增大的现象.c 2 /m·s–1 ρ 2 /g·cm–3 c 3 /m·s–1 ρ 3 /g·cm–3 d /mr /kmh /m搜索范围 1418—1487 1.1—1.6 1489—1800 — — 9.0—9.4 60—65 最优值 1474.01 1.35 1580.47 1.64 10.32 9.26 64.63 平均值 1474.12 1.39 1581.02 1.64 10.48 9.22 64.65 标准差 2.22 0.07 1.52 0.00 0.98 0.10 0.34
表3 待反演参数搜素范围及反演结果Table3. Search ranges of the unknown parameters and the inverted results.${m}$ 的后验概率密度$\sigma ({m})$ 、先验概率密度$\rho ({m})$ 以及似然概率密度$L({ m})$ 之间存在下述关系: $\sigma {\rm{(}}{m}{\rm{)}} \propto L{\rm{(}}{m}{\rm{)}}\rho {\rm{(}}{m}{\rm{)}}$ , 通常假设先验概率密度$\rho ({m})$ 为各个参数搜索区间上的均匀分布. 似然函数用来度量测量信号和拷贝信号的匹配程度, 可表示为代价函数$\phi ({m})$ 的经验指数关系式: $L{\rm{(}}{m}{\rm{)}} = {\rm{exp(}} - {\rm{[}}\phi {\rm{(}}{m}{\rm{)}} - \phi {\rm{(}}{{m}_0}){\rm{]/}}T{\rm{)}}$ , 其中, ${{m}_0}$ 表示反演过程中的最优参数向量; T 表示模拟退火算法中的“温度”, 取最优化过程中得到的前50个最小代价函数的均值[25 ] . 因此当观测为N obs 次时, 对第k 组待反演参数向量来说, 它的后验概率密度为i 个参数${{m}^i}$ 的一维边缘概率分布:9 )式由改进的遗传算法保存下来的样本获得待反演参数的后验概率密度, 代入(10 )式求得各参数的一维边缘概率分布, 结果如图9 所示, 图中箭头表示目标函数的最优值. 从图9 可以看出: 1)该反演方法对海底声学参数敏感, 目标函数的最优值与一维边缘概率密度分布的最优值重合, 海底声学参数以较高概率收敛到最优值, 反演的海底声学环境参数是可靠的; 2)沉积层厚度根据(7 )式间接反演得到, 所以沉积层厚度的概率密度分布同沉积层声速一致, 同理基底密度与基底声速的概率分布一致; 3)声源距离和海深的一维边缘概率密度分布较为分散, 反演结果不确定性较大. 分析其原因: 图10 给出了声源距离和海深的模糊度图, 可见声源距离和海深之间存在较强的正相关, 偏大的声源距离同偏大的海深也可以组合得到与实测声场匹配的测量场, 当海深在真值附近时, 目标函数对搜索范围内的声源距离不敏感, 因此一维边缘概率密度分布比较分散.图 9 参数的一维边缘概率密度分布Figure9. One-dimensional marginal posterior probability densities of the parameters.图 10 声源距离和海深的模糊度表面Figure10. Ambiguity surface of source range and water depth.4.2.海底衰减系数的声学反演 -->4.2.海底衰减系数的声学反演 在用匹配场方法反演得到沉积层声速、密度、厚度及基底声速、密度的基础上, 未知参数只有沉积层衰减系数和基底衰减系数. 远距离的TL对衰减系数比较敏感, 因此不同频率的衰减系数可用传播损失反演获得. 反演海底衰减系数时用到的代价函数为$T{L_{{\rm{exp}}}}\left( {{f_0},{r_i},{z_j}} \right)$ 为接收深度在${z_j}$ 、距离声源为${r_i}$ 、以${f_0}$ 为中心频率的 1/3倍频程带宽计算得到的传播损失; $T{L_{{\rm{cal}}}}\left( {{f_0},{r_i},{z_j},\alpha } \right)$ 为Kraken计算的拷贝场声传播损失; M 为阵元个数等于16; N 为声传播路径上宽带声源的个数, 25 km距离范围内N = 18. 图11 给出了频率为1000 Hz时, 采用遍历法(根据实际情况限定α 3 > α 2 )得到的代价函数的模糊度图, 图中黑色叉号表示沉积层和基底衰减系数的最优值. 从图11 可以看出, 存在低声速沉积层时, 高频的TL对基底的衰减系数并不敏感, 因为海水中的声波透射进入低声速沉积层后, 只有在沉积层-基底界面全反射的小掠射角声波才能远距离传播, 这部分声波受沉积层衰减影响较大, 受基底衰减影响较小. 低频的TL对基底衰减比较敏感, 因此这里把基底衰减限定为同一个位置用半无限大海底模型反演的海底衰减系数α 3 = 0.169f 1.74 dB/m (f 的单位是kHz)[7 ] , 然后来反演软沉积层内的衰减系数.图 11 代价函数随沉积层和基底衰减系数的模糊度表面Figure11. Ambiguity surface of sediment attenuation and basement attenuation.图12 给出了由实验TL反演得到的不同频率的沉积层衰减系数. 将反演结果进行拟合, 得到沉积层衰减系数随频率的变化关系为图 12 反演得到的不同频率的衰减系数Figure12. Inverted attenuation coefficients at different frequenciesf 的单位为kHz. 可见, 软泥底沉积层的衰减系数与频率近似呈一次方关系, 这与砂质海底的非线性关系不同.[24 ] 在理论建模及分析大量实验数据基础上提出泥海底的衰减系数在全频段内(几Hz至几兆Hz)与频率呈一次方关系, 本文的反演结果与上述结论一致. 利用反演得到的海底声速、密度和衰减系数, 计算声源深度25 m、接收深度为22 m (中心频率为100和600 Hz)、接收深度为50 m (中心频率300和1000 Hz)的传播损失, 并与实验数据对比, 结果如图13 所示. 从图13 可以看出, 数值计算结果与实验的传播损失符合较好, 反演得到的海底参数能很好地应用于不同频率、不同收发深度的TL预报.图 13 利用反演参数计算的不同频率传播损失与实验结果的对比 (a) z r = 22 m; (b) z r = 50 mFigure13. Comparison between the numerical TL and experimental TL at different frequencies: (a) z r = 22 m; (b) z r = 50 m.5.海底模型的讨论 文献[7 ]曾利用半无限大等效海底模型对本次实验中第23站点的海底声学参数进行反演. 本文使用了较复杂的双层海底模型进行反演. 本节将分析比较半无限大海底模型、双层海底模型的声场特性. 利用第4 节反演得到的双层海底模型参数计算得到不同频率和不同掠射角对应的海底反射损失, 并与文献[7 ]半无限大海底模型得到的海底反射损失进行对比, 结果如图14 所示. 大于海底临界掠射角的声波透射进入海底对声场贡献较小, 只有小于海底临界掠射角的声波才能远距离传播, 因此, 这里主要关注掠射角小于海底临界掠射角的海底反射损失. 图14(a) 为半无限大海底模型情况下, 掠射角小于15.3°的声波在海水-海底界面发生全反射, 对应的海底反射损失随频率和海底掠射角增大而增大. 当半无限大基底与海水之间存在低声速沉积层时, 海底反射损失如图14(b) 所示, 掠射角小于19.7°的声波会透射进入沉积层在沉积层-基底界面全反射, 其中频率满足(4 )式的声波在沉积层内发生干涉, 声能量陷入沉积层, 对应的海底反射损失周期性增大. 如图14(c) 所示, 掠射角为0.1°时低声速沉积层海底模型的海底反射损失在187和716 Hz附近增大, 这与图7 小掠射角情况下传播损失在200和728 Hz附近增大的现象基本一致, 而半无限大高声速海底不能解释小掠射角情况下传播损失周期增大的现象. 图14(d) 给出了掠射角为11.6° (即对应深度为25 m的声源以0°掠射角出射的声波穿越负跃层与海底作用时的海底掠射角)时的海底反射损失, 可见半无限大海底模型在此掠射角下随频率增大海底反射损失单调增大, 双层海底模型随频率增大海底反射损失小幅度振荡并增大, 但双层海底模型的平均变化趋势同半无限大海底模型基本一致, 因此两种海底模型反演得到的等效海底参数都能够较好地描述声源深度为25 m的声传播规律.图 14 不同海底模型的海底反射损失比较 (a) 半无限大海底模型; (b) 双层海底模型; (c) 掠射角0.1°; (d) 掠射角11.6°Figure14. Comparison of reflection?losses for different bottom models: (a) Uniform liquid half-space bottom model; (b) two layered bottom model; (c) at grazing angle 0.1°; (d) at grazing angle 11.6°.6.结 论 针对低声速沉积层海底反演问题, 理论分析了小掠射角条件下海底反射系数随频率的周期性增大现象, 该现象可用作软沉积层、硬沉积层海底的初步判定依据. 推导给出声传播损失的周期性增大的频率间隔与海底声学参数的解析表达式$d=\dfrac{C_{2}}{2 \Delta f r e q \sqrt{1-\left(C_{2} / C_{1}\right)^{2}}}$ , 可作为低声速沉积层海底反演的一个重要约束条件. 在此基础上, 提出了一种低声速沉积层海底的联合反演方案, 并利用2002年夏季黄海实验获得的宽带声传播信号对粉砂质粘土底质海域的海底声学参数进行了反演, 得出粉砂质粘土沉积层与海底附近海水声速之比约为0.99, 其衰减系数随频率近似呈一次方变化关系. 最后, 讨论了双层海底模型与半无限大海底模型的等效性, 低声速沉积层模型能更好地解释小掠射角条件下传播损失周期性增大的现象. 反演结果对低声速沉积层海底声场规律的研究和应用具有重要意义. 


 图 1 低声速沉积层海底模型
图 1 低声速沉积层海底模型


















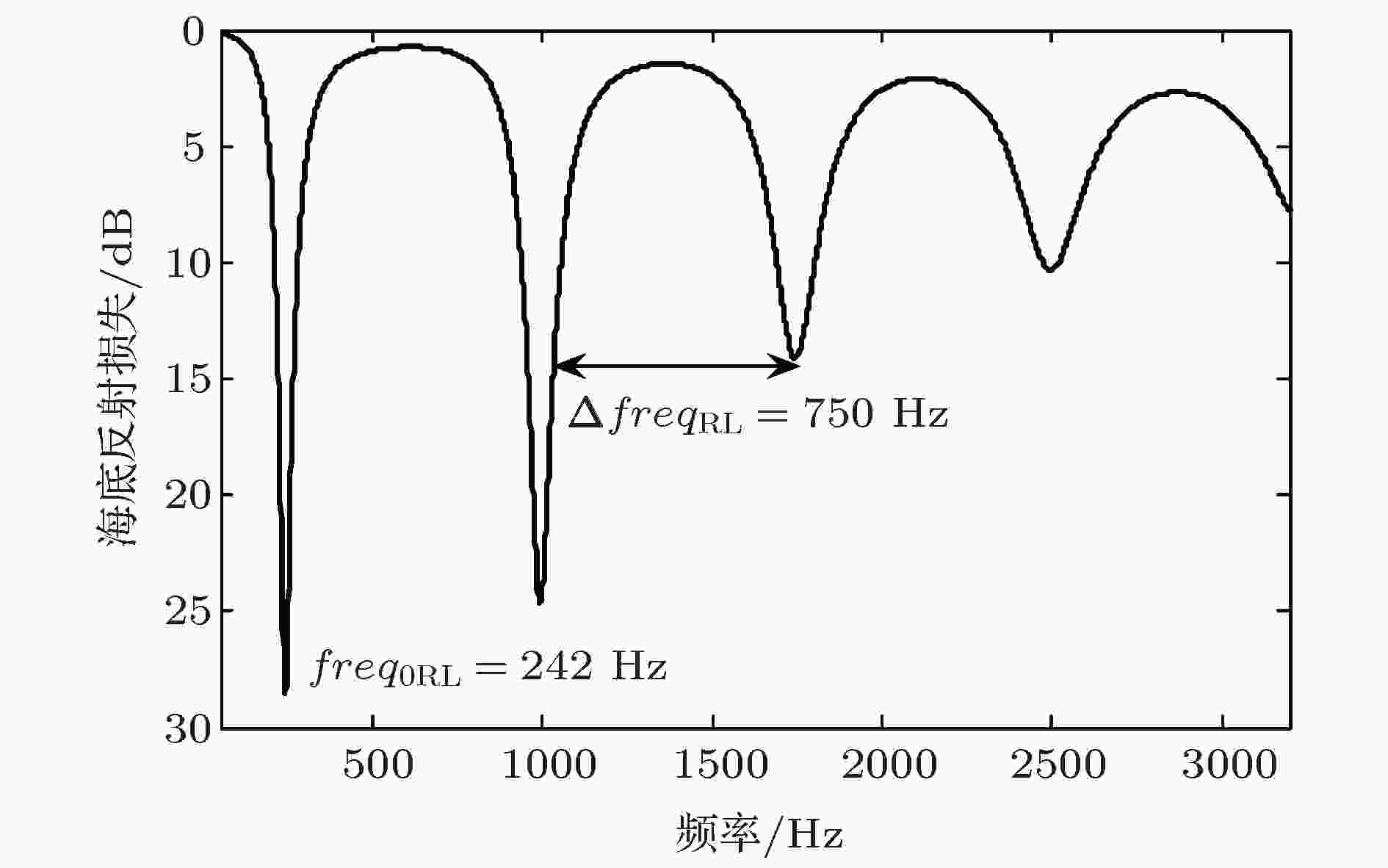 图 2 掠射角1°时对应的海底反射损失
图 2 掠射角1°时对应的海底反射损失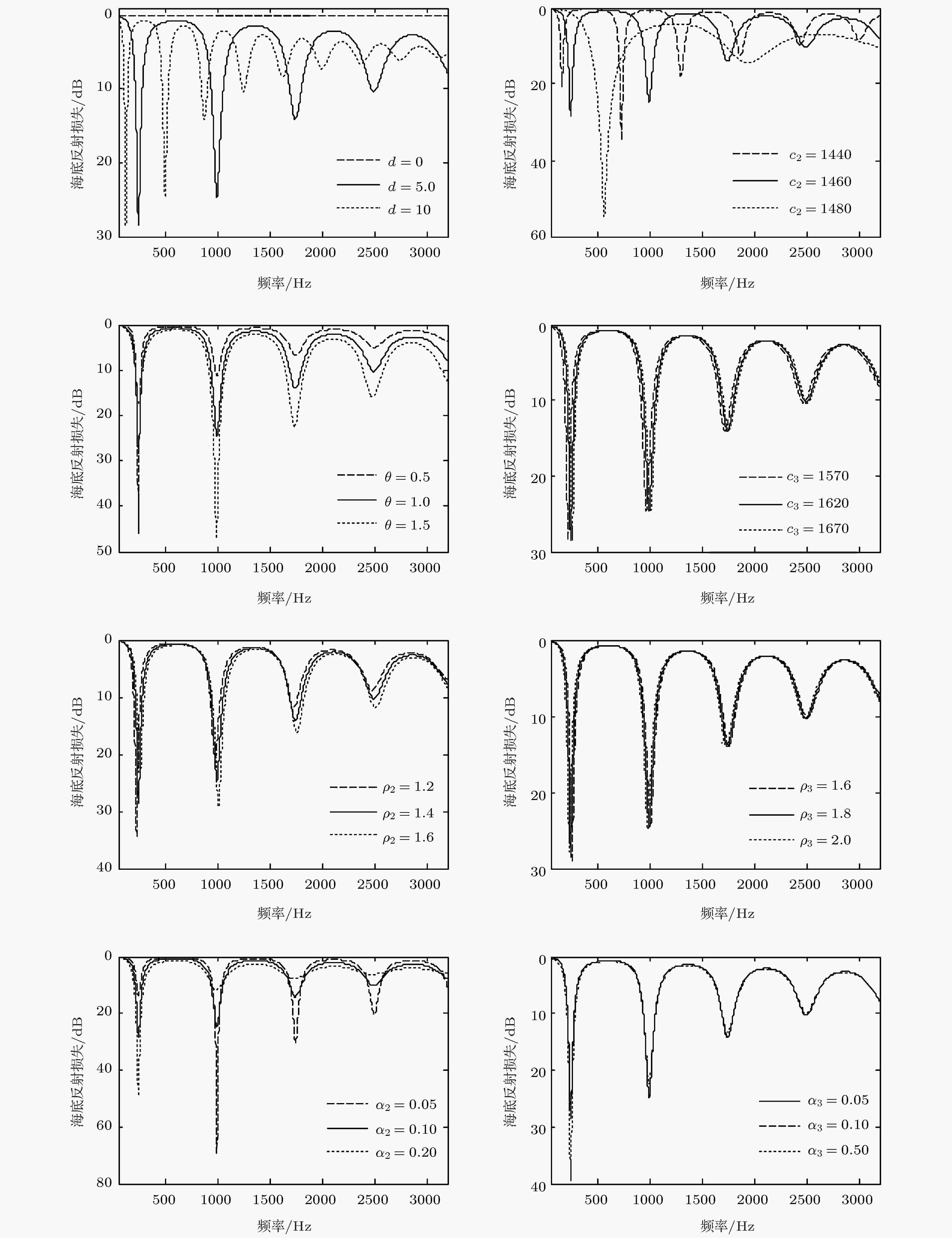 图 3 小掠射角情况下参数敏感性分析
图 3 小掠射角情况下参数敏感性分析
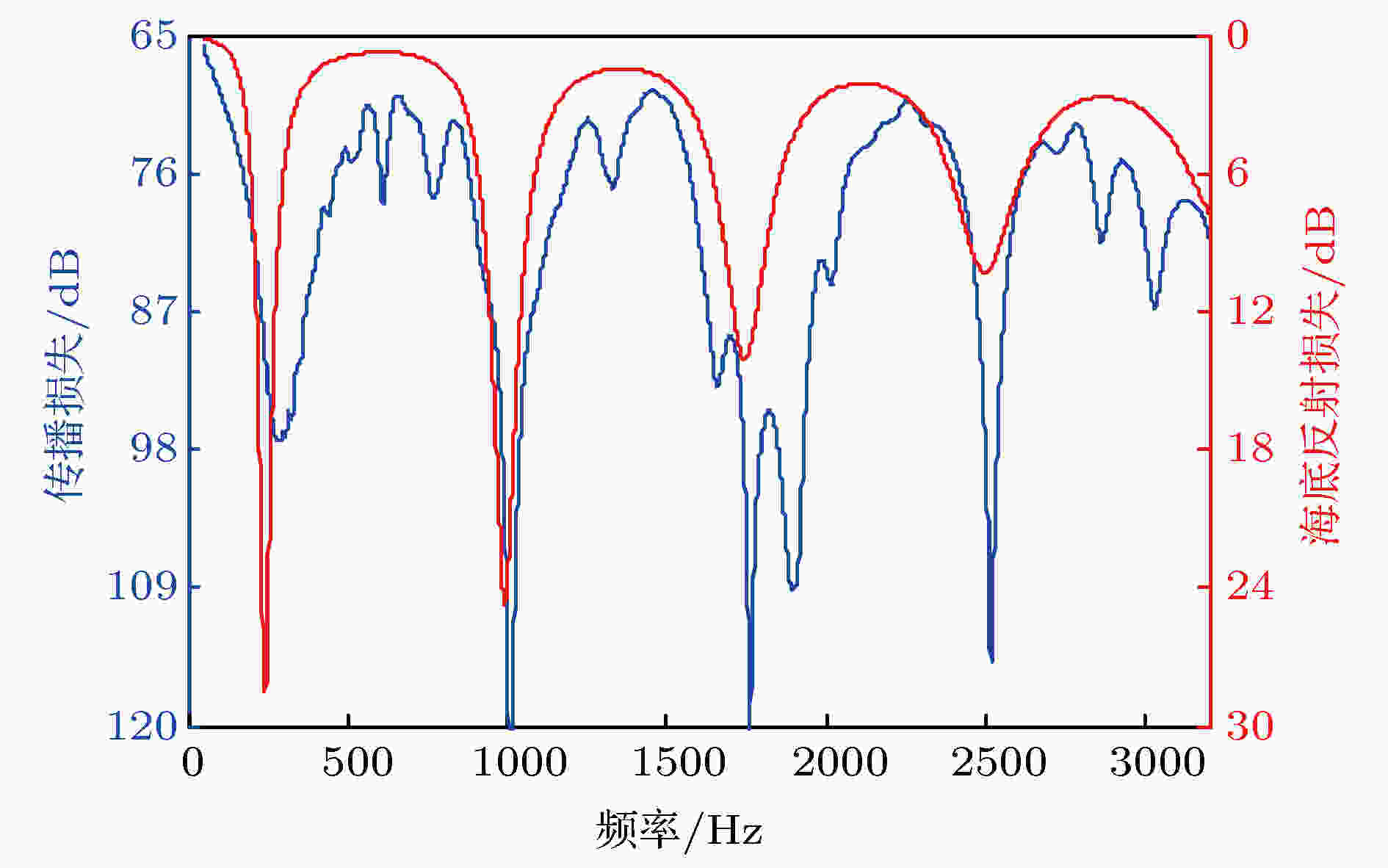 图 4 声传播损失与海底反射损失随频率的变化
图 4 声传播损失与海底反射损失随频率的变化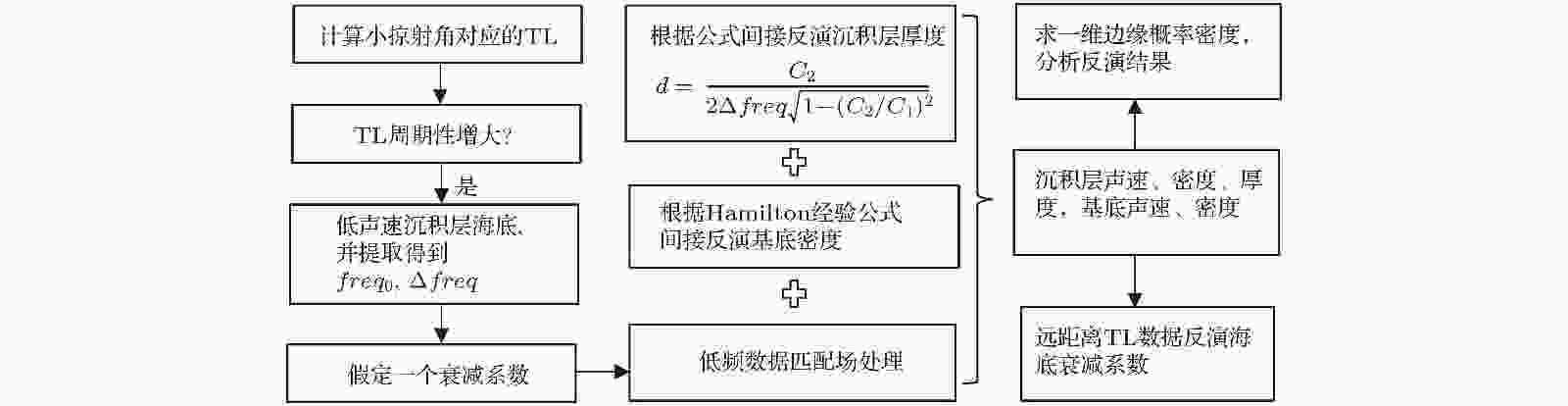 图 5 低声速沉积层声学参数联合反演流程
图 5 低声速沉积层声学参数联合反演流程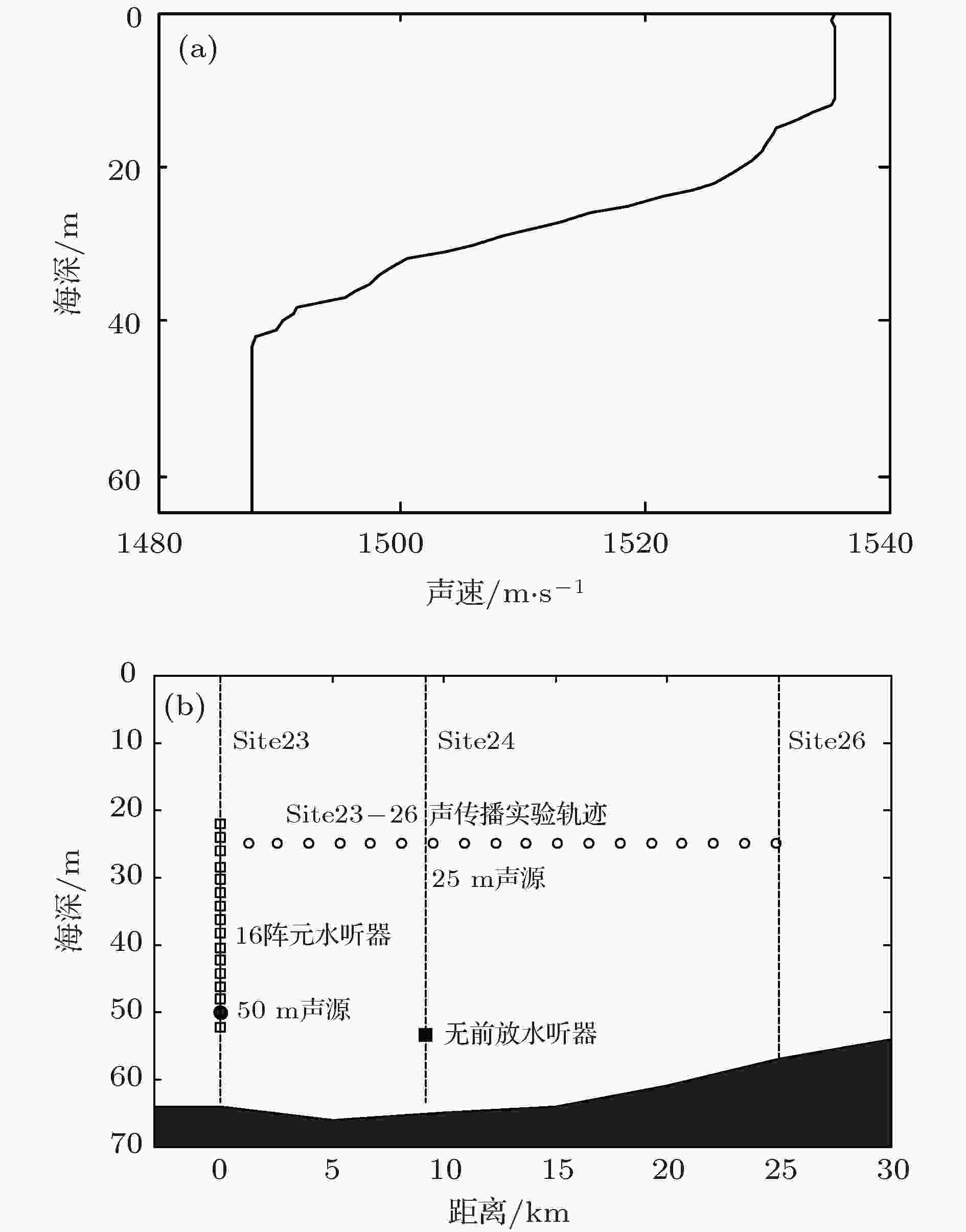 图 6 实验期间的水文环境和设备布设 (a) 声速剖面; (b) 设备布设及海深示意图
图 6 实验期间的水文环境和设备布设 (a) 声速剖面; (b) 设备布设及海深示意图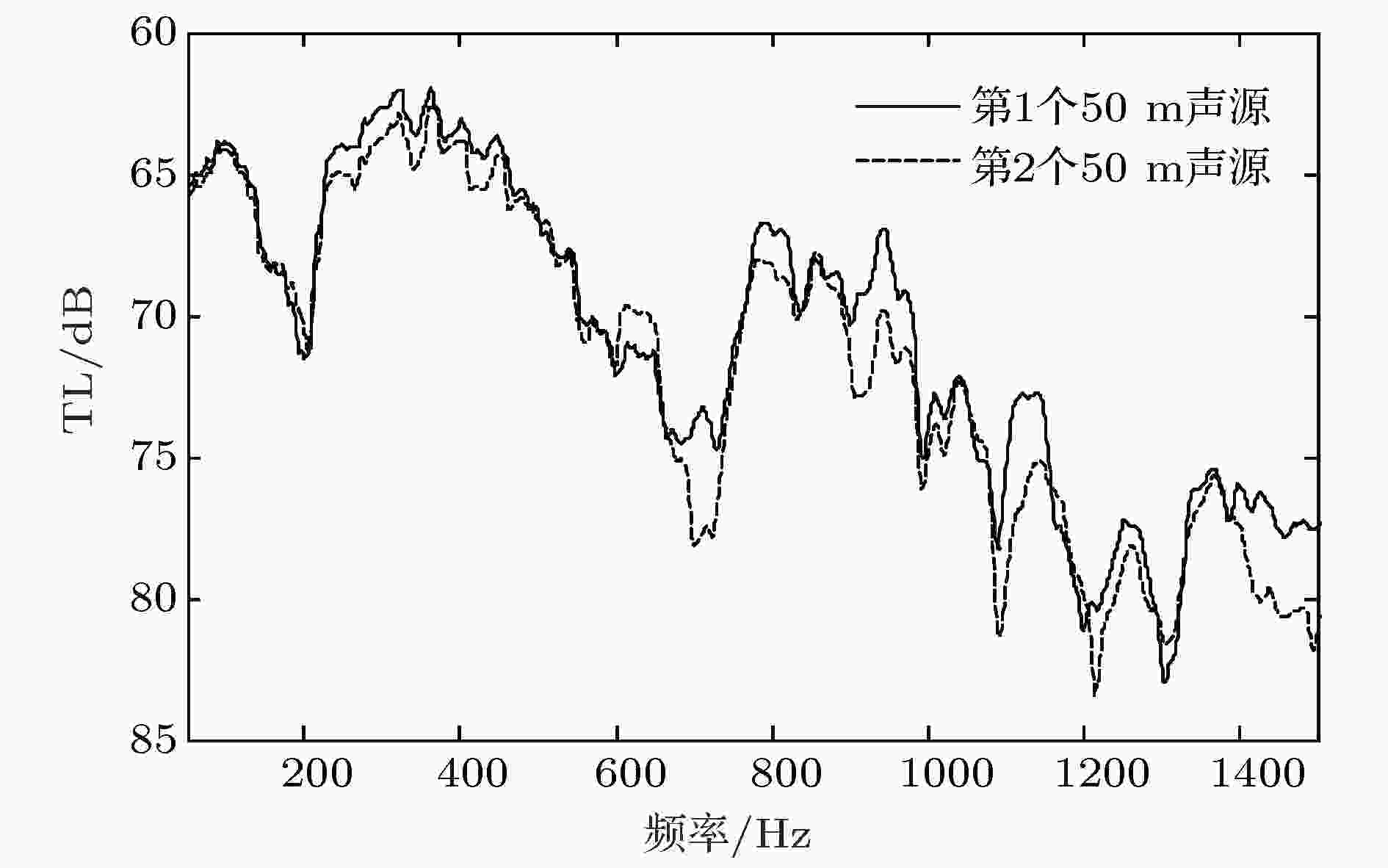 图 7 声传播损失随频率的变化 (r = 9.2 km, zs = 50.0 m, zr = 53.5 m)
图 7 声传播损失随频率的变化 (r = 9.2 km, zs = 50.0 m, zr = 53.5 m)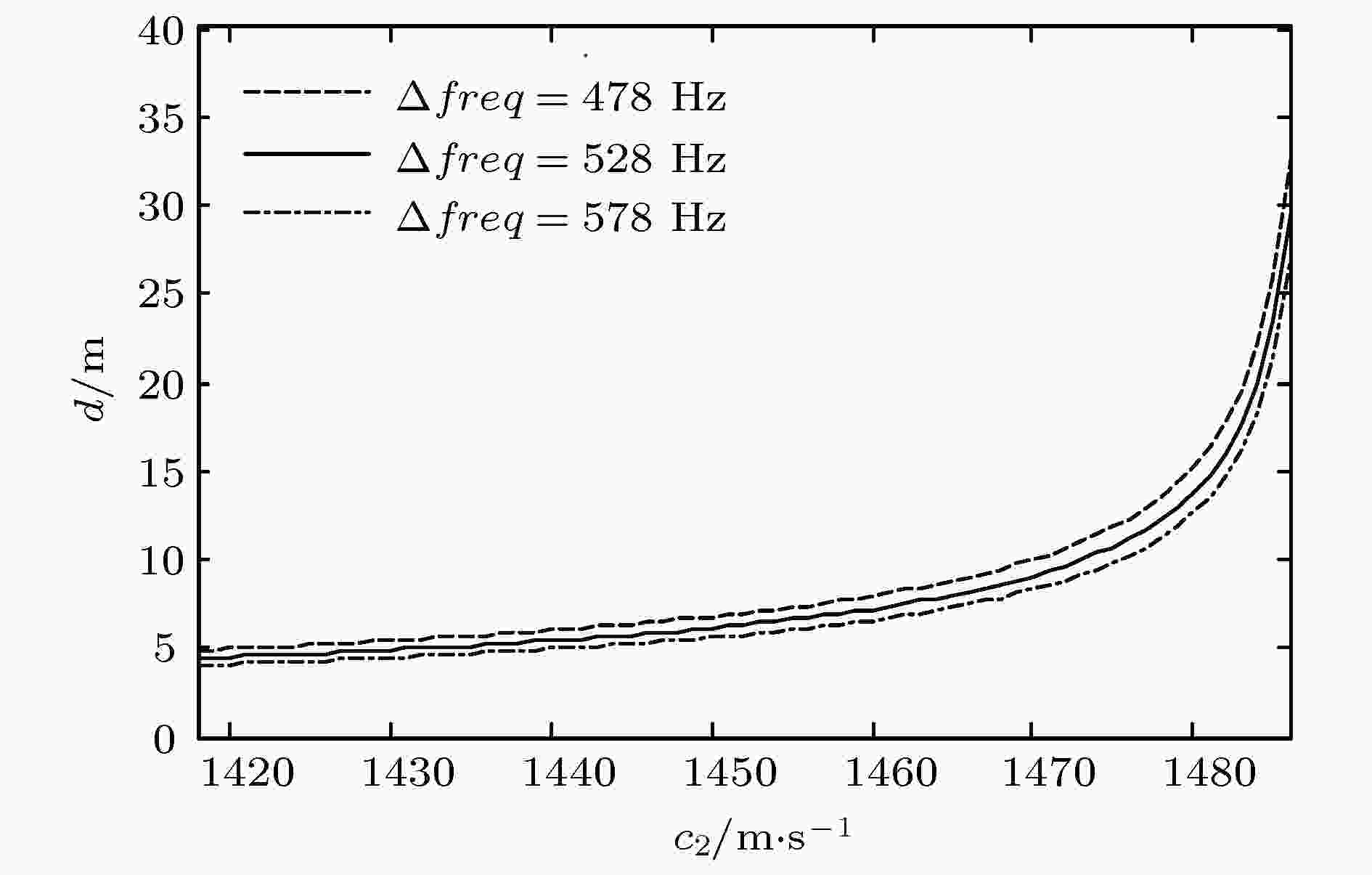 图 8 给定频率间隔下沉积层厚度与声速的关系
图 8 给定频率间隔下沉积层厚度与声速的关系














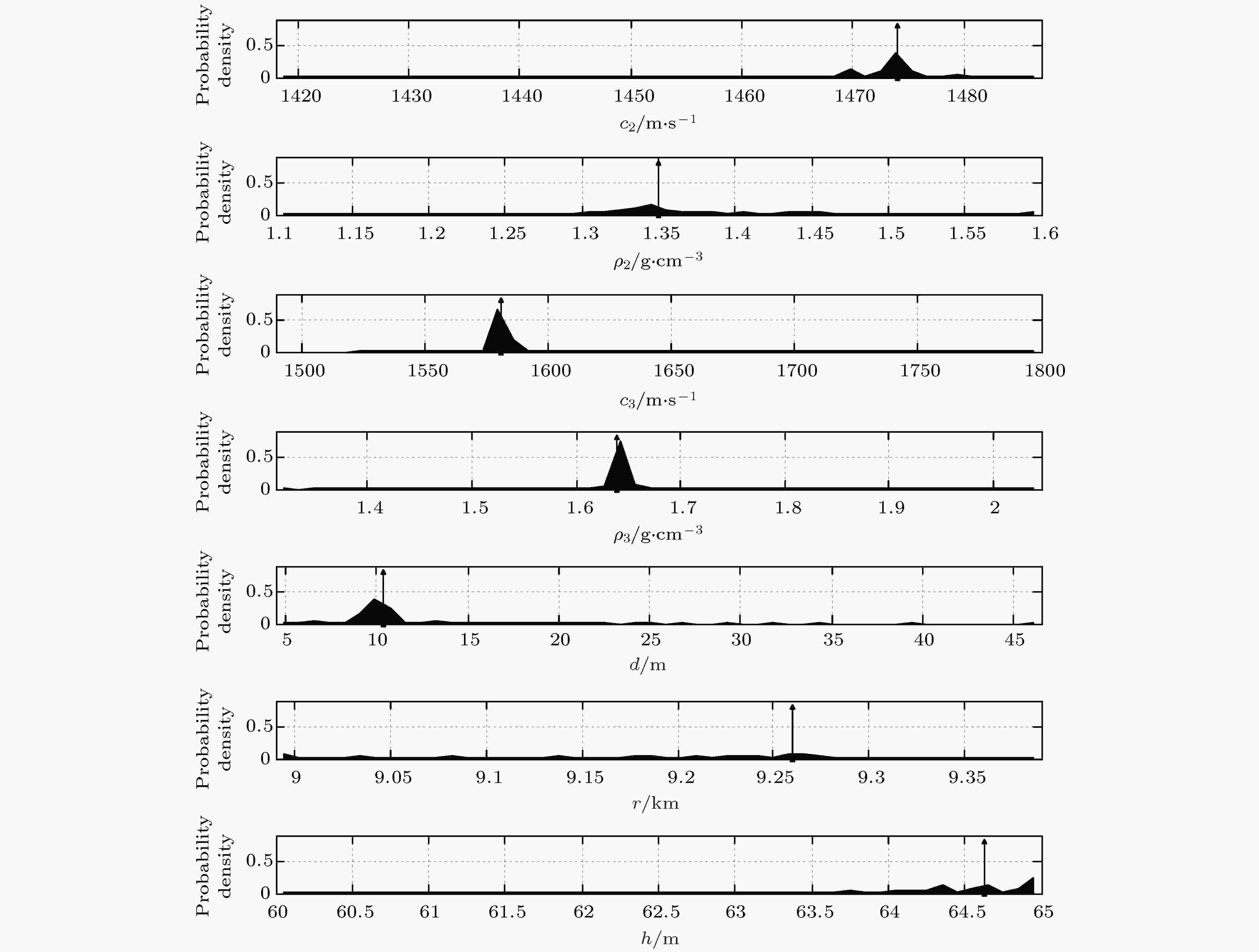 图 9 参数的一维边缘概率密度分布
图 9 参数的一维边缘概率密度分布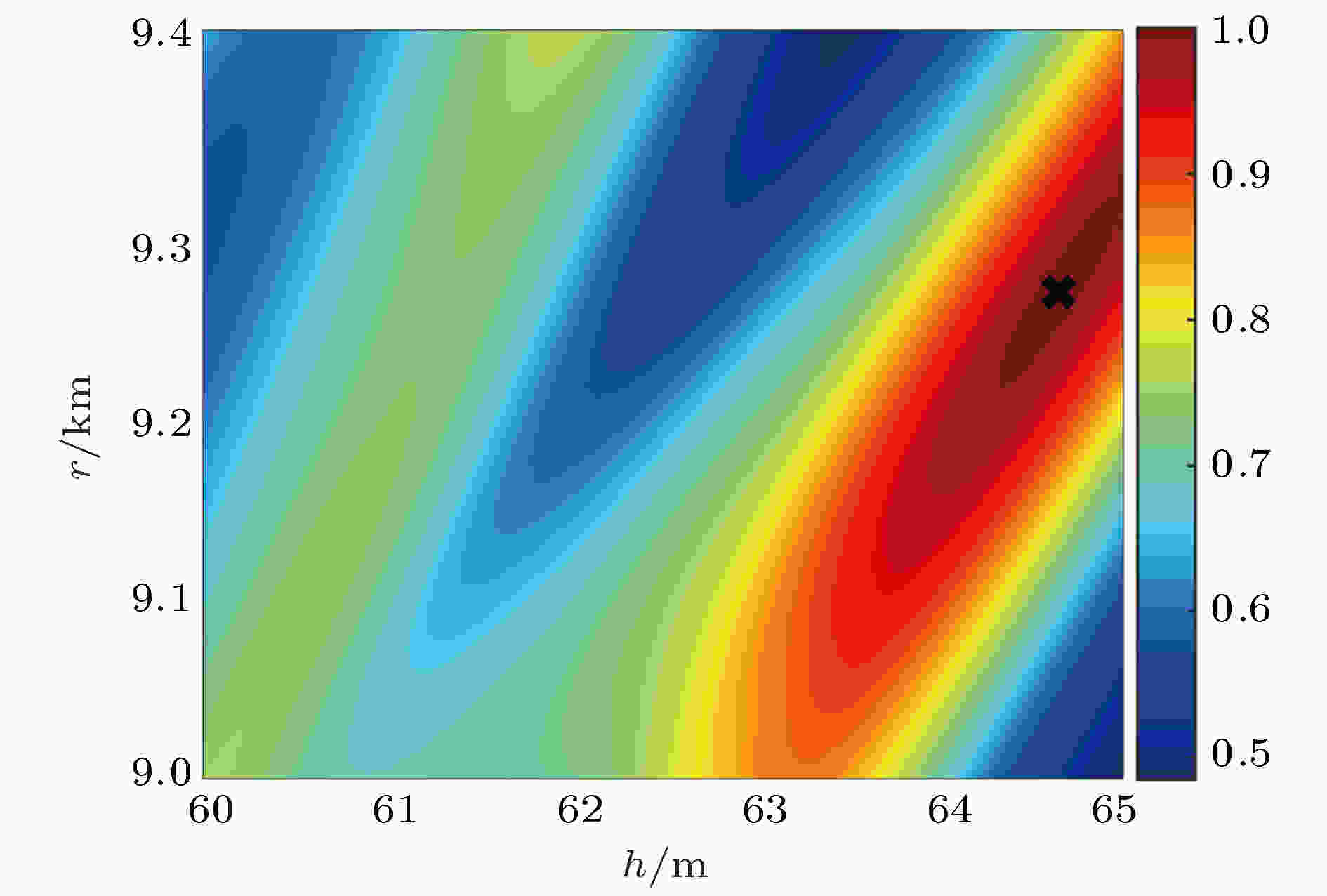 图 10 声源距离和海深的模糊度表面
图 10 声源距离和海深的模糊度表面




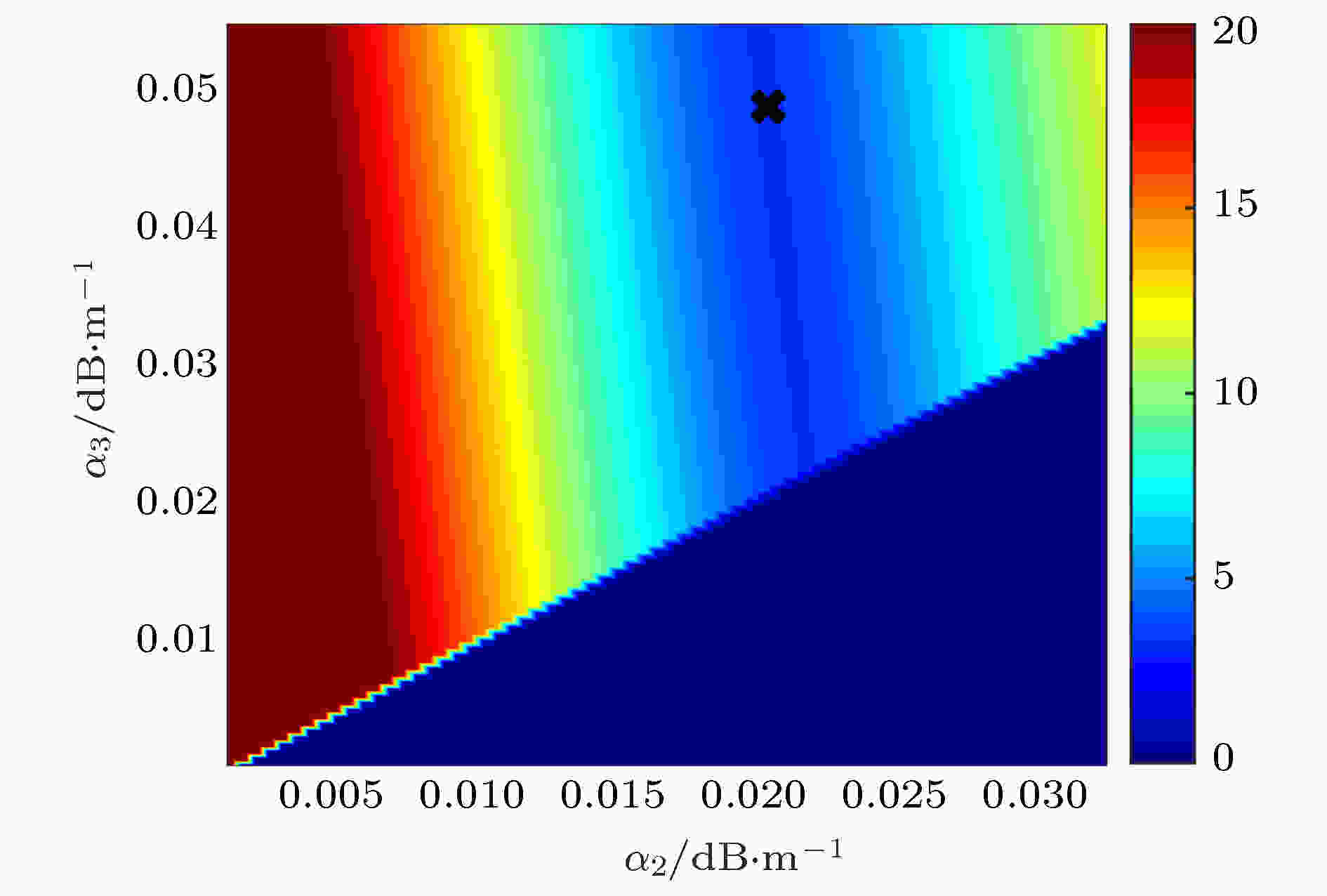 图 11 代价函数随沉积层和基底衰减系数的模糊度表面
图 11 代价函数随沉积层和基底衰减系数的模糊度表面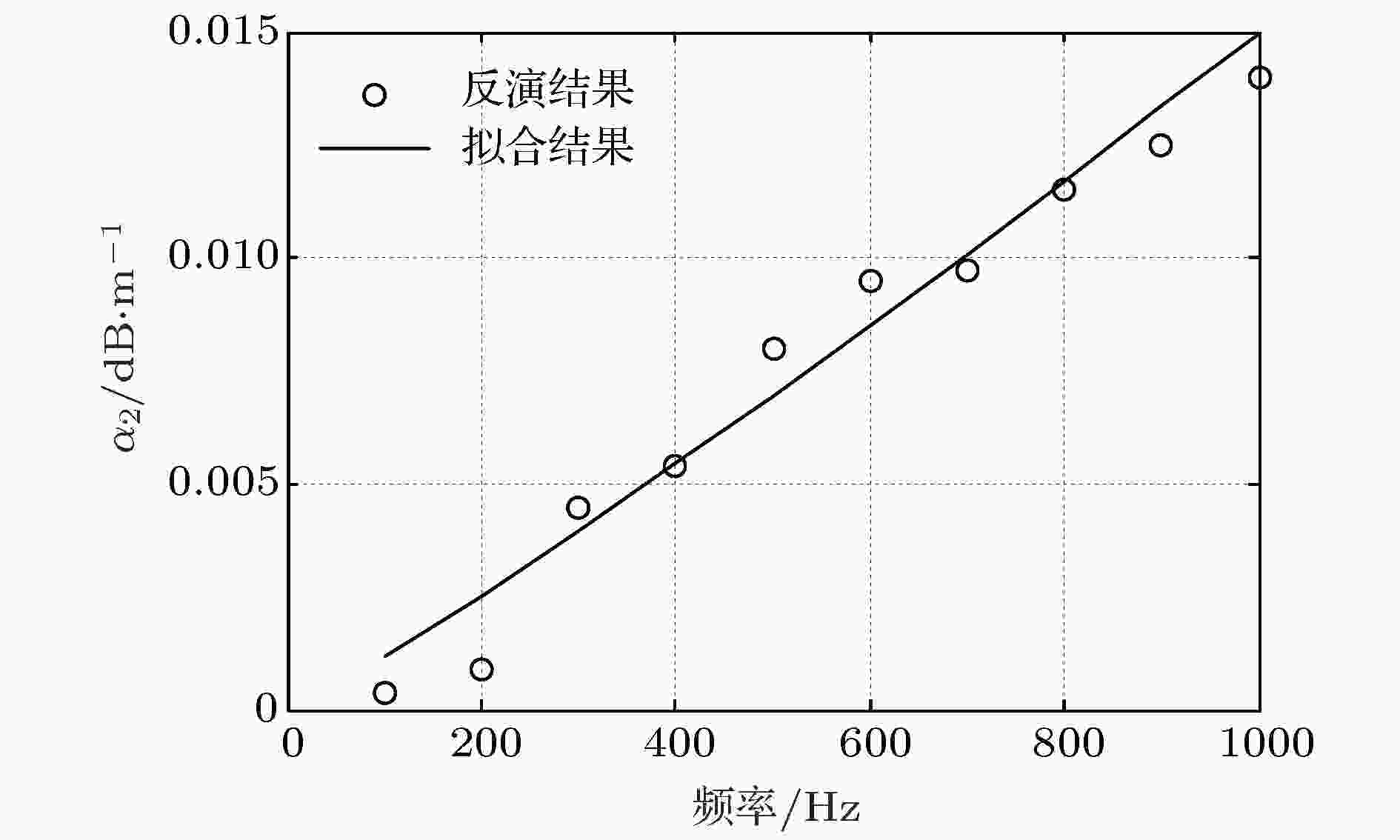 图 12 反演得到的不同频率的衰减系数
图 12 反演得到的不同频率的衰减系数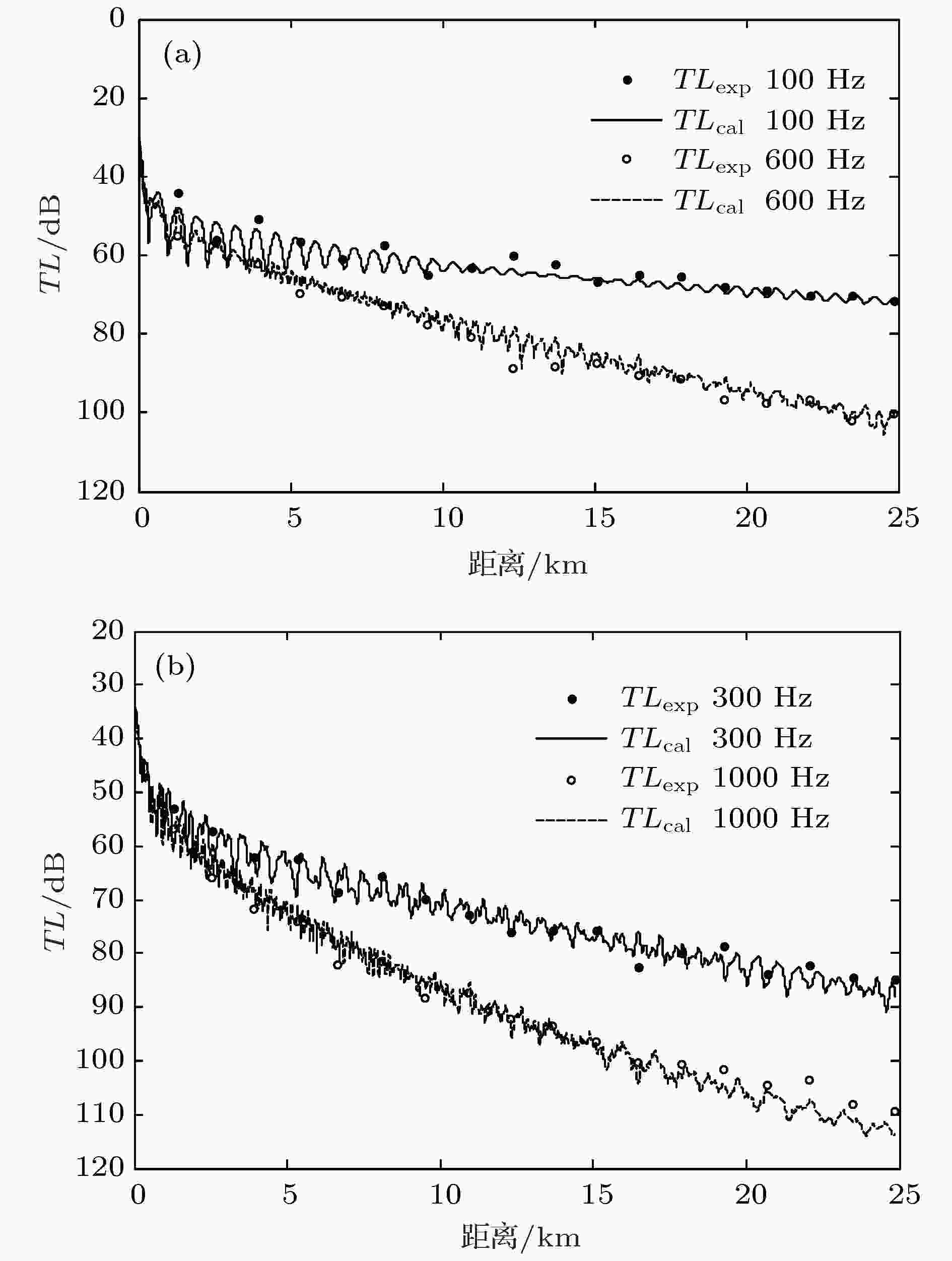 图 13 利用反演参数计算的不同频率传播损失与实验结果的对比 (a) zr = 22 m; (b) zr = 50 m
图 13 利用反演参数计算的不同频率传播损失与实验结果的对比 (a) zr = 22 m; (b) zr = 50 m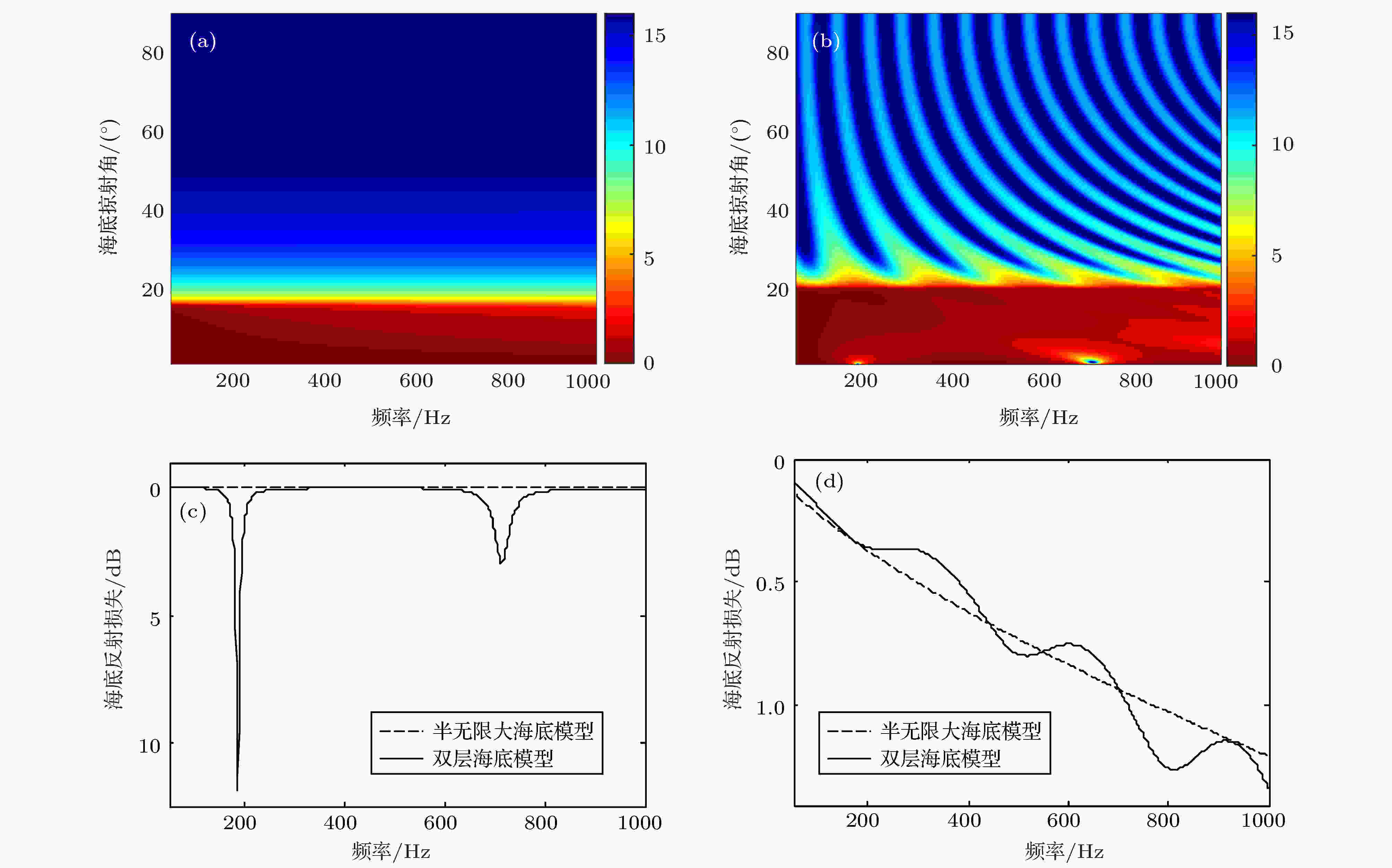 图 14 不同海底模型的海底反射损失比较 (a) 半无限大海底模型; (b) 双层海底模型; (c) 掠射角0.1°; (d) 掠射角11.6°
图 14 不同海底模型的海底反射损失比较 (a) 半无限大海底模型; (b) 双层海底模型; (c) 掠射角0.1°; (d) 掠射角11.6°
