摘要: 本文采用多组态相互作用及Davidson修正方法和全电子基组计算了SH
– 阴离子的
${{\rm{X}}^1}{\Sigma ^ + }$ ,
${{\rm{a}}^3}\Pi $ 和
${{\rm{A}}^1}\Pi $ 态的势能曲线、电偶极矩和跃迁偶极矩. 计算的光谱常数与实验值及已有的理论值符合得很好. 在计算中考虑了自旋-轨道耦合效应. 计算得到
${{\rm{a}}^3}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\nu '' = 0)$ 和
${{\rm{A}}^1}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\nu '' = 0)$ 跃迁具有高对角分布的弗兰克-康登因子, 分别为0.9990和0.9999; 计算得到
${{\rm{a}}^3}\Pi _1$ 和
${{\rm{A}}^1}\Pi _1$ 态的自发辐射寿命分别为1.472和0.188 ms.
${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁存在中间态
${{\rm{a}}^3}{\Pi _{{0^ + }}}$ 和
${{\rm{a}}^3}{\Pi _1}$ , 但中间态对激光冷却SH
– 阴离子的影响可以忽略. 分别利用
${{\rm{a}}^3}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\nu '' = 0)$ 和
${{\rm{A}}^1}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\nu '' = 0)$ 跃迁构建了准闭合的能级系统, 冷却所需的激光波长分别为492.27和478.57 nm. 最后预测了激光冷却SH
– 阴离子能达到的多普勒温度和反冲温度. 这些结果为进一步实验提供了理论参数.
关键词: 自旋-轨道耦合效应 /
弗兰克-康登因子 /
自发辐射寿命 /
激光冷却 English Abstract Theoretical study of laser-cooled SH– anion Wan Ming-Jie 1 ,Li Song 2 ,Jin Cheng-Guo 1 ,Luo Hua-Feng 3 1.Computational Physics Key Laboratory of Sichuan Province, Yibin University, Yibin 644007, China Fund Project: Project supported by the Special Foundation for Theoretical Physics Research Program of China (Grant Nos. 11647075, 11747071) and the Open Research Fund of Computational physics Key Laboratory of Sichuan Province, Yibin University, China (Grant No. JSWL2014KF05).Received Date: 16 November 2018Accepted Date: 02 January 2019Available Online: 01 March 2019Published Online: 20 March 2019Abstract: The potential energy curves, dipole moments, and transition dipole moments for the ${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ , and ${{\rm{A}}^1}\Pi $ electronic state of sulfur hydride anion (SH– ) are calculated by using the multi-reference configuration interaction method plus Davidson corrections (MRCI+Q ) with all-electron basis set. The scalar relativistic corrections and core-valence correlations are also considered. In the CASSCF calculations, H(1s) and S(3s3p4s) shells are chosen as active space, and the rest orbitals S(1s2s2p) as closed-shell. In the MRCI+Q calculations, the S(1s2s2p) shells are used for the core-valence correlation. Spectroscopic parameters, Einstein spontaneous emission coefficient, Franck-Condon factors, and spontaneous radiative lifetimes are obtained by using Le Roy’s LEVEL8.0 program. The calculated spectroscopic parameters are in good agreement with available experimental data and theoretical values. Spin-orbit coupling (SOC) effects are evaluated with Breit-Pauli operators at the MRCI+Q level. Transition dipole moments (TDMs) for the ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _{{0^ + }}}$ and ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ transitions are also calculated. The strength for the ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ is the strongest in these five transitions, the value of TDM at R e is –1.3636 D. We find that the value of TDM for the ${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition at R e is 0.5269 D. Therefore, this transition must be taken into account to build the scheme of laser-cooled SH– anion. Highly diagonally distributed Franck-Condon factor f 00 for the ${{\rm{a}}^3}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ $ (\nu '' = 0)$ transition is 0.9990 and the value for the ${{\rm{A}}^1}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\nu '' = 0)$ transition is 0.9999. Spontaneous radiative lifetimes of $\tau \left( {{{\rm{a}}^3}{\Pi _1}} \right)= 1.472 \;{\text{μ}}{\rm{s}}$ and $\tau \left( {{{\rm{A}}^1}{\Pi _1}} \right)=0.188 \;{\text{μ}}{\rm{s}}$ are obtained, which can ensure that laser cools SH– anion rapidly. To drive the ${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ and ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transitions, just one laser wavelength is required. The wavelengths are 492.27 nm and 478.57 nm for two transitions, respectively. Notably, the influences of the intervening states ${{\rm{a}}^3}{\Pi _1}$ and ${{\rm{a}}^3}{\Pi _{{0^{\rm{ + }}}}}$ on the ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {X^1}\Sigma _{{0^ + }}^ + $ transition are small enough to implement a laser cooling project. A spin-forbidden transition and a three-electronic-level transition optical scheme of laser-cooled SH– anion are constructed, respectively. In addition, the Doppler temperatures and recoil temperatures for the ${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ and ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transitions of laser-cooled SH– anion are also obtained, respectively.Keywords: spin-orbit coupling /Franck-Condon factors /spontaneous radiative lifetimes /laser cooling 全文HTML --> --> --> 1.引 言 由于双原子分子结构的复杂性, 其激光冷却的研究具有很大的挑战性, 近年来一直是原子分子物理和光学等领域的研究热点. 实验上[1 -3 ] 和理论上[4 -9 ] 针对激光冷却分子或分子阳离子都有大量研究.– [10 ] 和BH– [11 ] 阴离子的方案. 在设计激光冷却方案时, 两种阴离子都构建了${1^2}{\Sigma ^ + } \leftrightarrow {1^2}\Pi $ 准闭合能级系统. 计算得到了NH– 和BH– 阴离子的弗兰克-康登因子分别为0.999和0.942, 以及${1^2}{\Sigma ^ + }$ 态的自发辐射寿命分别50.4和91.8 ns. 最近本课题组[12 ] 在考虑自旋-轨道耦合 (SOC) 效应时对激光冷却OH– 阴离子的可能性进行了研究. 分别利用${{\rm{a}}^3}{\Pi _1}\! \leftrightarrow\! {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^1}{\Pi _1} \!\leftrightarrow\! {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁构建了准闭合能级, 并给出了冷却OH– 阴离子的方案. SH– 和OH– 具有类似的结构, 本文研究激光冷却SH– 阴离子的可能性.[13 ] 于1968年首次报道了SH– 阴离子基态${{\rm{X}}^1}{\Sigma ^ + }$ 的光谱常数. 1981年, Breyer等[14 ] 观测到了一系列阴离子的高分辨率光电子能谱. 得到了OH– , SH– 和SD– 阴离子的光谱常数, 其中转动常数为B 0 (OH– ) = (18.75 $\pm $ 0.15) cm–1 , B 0 (SH– ) = (9.39 $\pm $ 0.30) cm–1 , B 0 (SD– ) = (4.87 $ \pm$ 0.20) cm–1 . 同年, Janousek和Brauman[15 ] 在SH– 阴离子的光致分离频谱中观测到了转动结构, 并得到了SH分子的亲合能为(2.314 $ \pm$ 0.003) eV. 理论上, 1967年,Cade[16 ] 通过求解Hartree-Fock-Roothaan矩阵方程研究了SH– 阴离子的势能曲线. 1978年, Rosmus和Meyer[17 ] 采用赝势轨道组态相互作用和耦合电子对近似(CEPA)方法计算了第一行和第二行双原子氢化物阴离子基态的势能曲线, 并拟合得到了光谱常数. 1985年, Senekowitsch等[18 ] 采用CEPA方法计算了SH– 阴离子的势能曲线和偶极矩函数, 在平衡核间距R e 处的偶极矩为0.27 Debye (D). 2016年, Vamhindi和Nsangou[19 ] 采用包含Davidson修正的多参考组态相互作用(MRCI+Q )方法 [20 -22 ] 计算了SH– 阴离子${{\rm X}^1}{\Sigma ^ + }$ , ${{{\rm a}}^3}\Pi $ 和${{{\rm A}}^1}\Pi $ 态的势能函数. 拟合得到了其光谱常数R e (${{\rm{X}}^1}{\Sigma ^ + }$ ) = 1.344 ?, R e (${{\rm{a}}^3}\Pi $ ) = 1.3746 ?, R e (${{\rm{A}}^1}\Pi $ ) = 1.3432 ?, $\omega_{\rm{e}}\left({{\rm{X}}^1}{\Sigma ^ + }\right) = 2682.86$ cm–1 , $\omega_{\rm{e}}\left({{\rm{a}}^3}\Pi\right) = 1936.16 $ cm–1 , $\omega_{\rm{e}}\left({{\rm{A}}^1}\Pi \right) = 2554.97$ cm–1 . 但他们没有计算激发态到基态跃迁的弗兰克-康登因子和自发辐射速率以及激发态的自发辐射寿命.– 阴离子的光谱常数和跃迁性质, 构建准闭合的能级系统进行激光冷却SH– 阴离子, 给出冷却途径.2.计算方法 采用MRCI+Q 方法计算SH– 阴离子${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ , ${{\rm{A}}^1}\Pi $ , ${1^3}{\Sigma ^ + }$ 和${2^1}{\Sigma ^ + }$ 态的电子结构. 以完全活性空间自洽场方法(CASSCF)[23 ,24 ] 所产生的波函数为基础构造了CI波函数, 进行MRCI+Q 的计算. 同时在计算中通过三阶Douglas-Kroll哈密顿量(DKH3)[25 ,26 ] 考虑了标量相对论修正, 通过Breit-Pauli算符[27 ] 考虑了SOC效应. 所有计算都是由MOLPRO 2010程序[28 ] 得到.Q 计算中考虑了核-价电子(CV)关联效应, S的1s2s2p轨道参与CV关联计算. 在$\Lambda$ -S和$\Omega$ 的计算中, 对S原子选取了ACV5Z-DK全电子基组[29 ] , 对H原子选取了AV5Z-DK全电子基组[30 ] .[31 ] 来拟合SH– 阴离子$\Lambda$ -S和$\Omega$ 态的光谱常数. 同时使用均方根值 (RMS)来评估拟合效果. 弗兰克-康登因子(${f_{\nu ' \nu ''}}$ )、自发辐射速率(${A_{\nu ' \nu ''}}$ )和自发辐射寿命($\tau $ )均采用LEVEL8.0程序[32 ] 计算.3.结果与讨论 23.1.势能曲线与光谱常数 3.1.势能曲线与光谱常数 本文在MRCI+Q 水平下计算了SH– 阴离子的${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ , ${{\rm{A}}^1}\Pi $ , ${1^3}{\Sigma ^ + }$ 和${2^1}{\Sigma ^ + }$ 电子态的势能曲线, 结果如图1 所示. 从图1 可以看出, 在计算的5个态中${2^1}{\Sigma ^ + }$ 态为最高态, 说明${2^1}{\Sigma ^ + }$ 态在激光冷却SH– 阴离子过程中不是中间态. ${1^3}{\Sigma ^ + }$ 态为排斥态. ${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ , ${{\rm{A}}^1}\Pi $ 和${1^3}{\Sigma ^ + }$ 态对应于最低离解通道S– (2 Pu ) + H(2 Sg ), ${2^1}{\Sigma ^ + }$ 态则对应于第三离解通道S(1 Dg ) + H– (1 Sg ). 计算的两通道之间的能量差为19825.64 cm–1 . H和S原子的亲和能的实验值分别为6082.99 cm–1 [33 ] 和16752.83 cm–1 [34 ] , 而S原子基态3 Pg 与第一激发态1 Dg 的能量差为9239.0 cm–1 [35 ] , 可以计算出两通道之间的能量差的实验值为19908.84 cm–1 . 本文的计算值与实验值符合得很好, 仅有0.42%的误差.图 1 SH– 阴离子的${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ , ${{\rm{A}}^1}\Pi $ , ${1^3}{\Sigma ^ + }$ 和${2^1}{\Sigma ^ + }$ 态的势能曲线Figure1. Potential energy curves for the ${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ , ${{\rm{A}}^1}\Pi $ , and ${2^1}{\Sigma ^ + }$ states of SH– anion.${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ 和${{\rm{A}}^1}\Pi $ 态的光谱常数如表1 所列. SH– 基态${{\rm{X}}^1}{\Sigma ^ + }$ 的平衡核间距R e 为1.3435 ?, 与实验值[13 ] 相差0.0035 ?, 误差仅为0.26%; 谐振频率$\omega_{\rm{e}}$ 和转动常数B e 分别为2622.04和9.5590 cm–1 , 与最新实验值[14 ] 的误差分别为 0.98%和1.80%. 基态的非谐振频率$\omega_{\rm{e}}\chi_{\rm{e}}$ 和势阱深度D e 的结果与Rosmus和Meyer[17 ] 报道的理论结果更接近. 可以看出基态的计算结果与实验值及其他理论值符合得很好. 和以往的研究结果不同, ${{\rm{a}}^3}\Pi $ 和${{\rm{A}}^1}\Pi $ 态具有双势阱结构, 两个态分别在约1.89 和1.95 ?发生预解离. ${{\rm{a}}^3}\Pi $ 和${{\rm{A}}^1}\Pi $ 态第一势阱的平衡核间距R e 与Vamhindi和Nsangou [19 ] 报道的理论值符合很好, 误差分别为2.04%和0.07%. 本文得到了${{\rm{a}}^3}\Pi $ 和${{\rm{A}}^1}\Pi $ 态的两个势阱的谐振频率$\omega_{\rm{e}}$ 、非谐振频率$\omega_{\rm{e}}\chi_{\rm{e}}$ 和势阱深度D e , 结果列于表1 中.电子态 R e /?$\omega_{\rm{e}}$/cm–1 $\omega_{\rm{e}}\chi_{\rm{e}}$/cm–1 B e /cm–1 D e /eVT e /cm–1 RMS/cm–1 ${{\rm{X}}^1}{\Sigma ^ + }$ 本文工作 1.3435 2622.04 46.66 9.5590 3.8793 0 4.4107 实验值[13 ] 1.34—0.02 2700—300 9.46—0.32 实验值[14 ] 2648—110 9.39—0.3 理论值[17 ] 1.348 2642 52 9.49 3.902 0 理论值[18 ] 1.346 2637 52 9.52 理论值[19 ] 1.3440 2682.86 39.2 9.551 4.19 ${{\rm{a}}^3}\Pi $ 本文工作 第一势阱 1.3466 2583.61 73.22 9.5148 0.9598 20436.92 0.0604 理论值[19 ] 1.3746 1936.16 307.503 9.129 1.38 22082.7 本文工作 第二势阱 2.1021 778.72 133.34 3.9045 0.4356 27816.71 1.1556 ${{\rm{A}}^1}\Pi $ 本文工作 第一势阱 1.3441 2626.59 61.51 9.5511 1.1848 20852.70 0.0474 理论值[19 ] 1.3432 2554.97 44.186 9.561 1.33 22225.2 本文工作 第二势阱 2.2430 424.80 36.810 3.4296 0.1217 30299.28 0.3277
表1 SH- 阴离子的$\Lambda\text{-}\rm S$ 态的光谱常数Table1. Spectroscopic parameters for the $\Lambda\text{-}\rm S $ states of SH– anion.${{\rm{a}}^3}\Pi $ 态分裂成4个$\Omega$ 态(${{\rm{a}}^3}{\Pi _2}$ , ${{\rm{a}}^{3}}{\Pi _1}$ , ${{\rm{a}}^3}{\Pi _{{0^ - }}}$ , ${{\rm{a}}^3}{\Pi _{{0^{+}}}}$ ), S(2 P)原子态分裂为S(2 P3/2 )和S(2 P1/2 ). 其$\Omega$ 态的势能曲线如图2 所示. ${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _2}$ , ${{\rm{a}}^{3}}{\Pi _1}$ , ${{\rm{a}}^3}{\Pi _{{0^ - }}}$ 和${{\rm{A}}^{1}}{\Pi _1}$ 态具有相同的离解极限S– (2 P3/2 ) + H(2 S1/2 ); ${{\rm{a}}^3}{\Pi _{{0^{+}}}}$ , ${{\rm{b}}^3}\Sigma _{{0^ - }}^ + $ 和${{\rm{b}}^3}\Sigma _1^ + $ 态具有另一个离解极限S– (2 P1/2 ) + H(2 S1/2 ). 预测出S– 负离子2 P原子态的分裂值为505.79 cm–1 .图 2 SH– 阴离子的$\Omega$ 态的势能曲线Figure2. Potential energy curves for the $\Omega$ states of SH– anion.– 阴离子$\Omega$ 态的光谱常数, 如表2 所列. 可以看出SOC效应对不分裂的${{\rm{X}}^1}{\Sigma ^ + }$ 和${{\rm{A}}^1}\Pi $ 态的光谱常数影响很小. 此结果和OH– 阴离子[12 ] 类似. 也得到了${{\rm{a}}^3}\Pi $ 态的分裂常数A SO : A SO (${{\rm{a}}^3}{\Pi _1}$ – ${{\rm{a}}^3}{\Pi _2}$ ) = 116.06 cm–1 , A SO (${{\rm{a}}^3}{\Pi _{{0^ - }}}$ – ${{\rm{a}}^3}{\Pi _1}$ ) = 261.24 cm–1 以及A SO ($ {{\rm{a}}^{3}}{\Pi _{{0^{+}}}}$ – ${{\rm{a}}^3}{\Pi _{{0^ - }}}$ ) = 0.13 cm–1 . 而OH– 阴离子[12 ] : A SO (${{\rm{a}}^3}{\Pi _1}$ –${{\rm{a}}^{3}}{\Pi _2}$ ) = 58.41 cm–1 和A SO (${{\rm{a}}^{3}}{\Pi _0}$ –${{\rm{a}}^{3}}{\Pi _1}$ ) = 78.21 cm–1 . 对比两个离子${{\rm{a}}^3}\Pi $ 态的分裂值可以看出, SOC效应对SH– 阴离子的影响要更大.$\Omega$ state R e /?$\omega_{\rm{e}}$/cm–1 $\omega_{\rm{e}}\chi_{\rm{e}}$/cm–1 B e /cm–1 D e /eVT e /cm–1 RMS/cm–1 ${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 1.3435 2618.53 44.58 9.5589 3.8575 0 4.0232 ${{\rm{a}}^3}{\Pi _2}$ 第一势阱 1.3466 2584.13 72.08 9.5151 0.9607 20247.58 0.0257 第二势阱 2.1011 779.62 136.27 3.9082 0.4429 27639.82 1.1521 ${{\rm{a}}^{3}}{\Pi _1}$ 第一势阱 1.3463 2588.54 69.87 9.5196 0.9665 20363.64 0.0537 第二势阱 2.1005 773.93 135.45 3.9105 0.4173 27802.87 1.0389 ${{\rm{a}}^3}{\Pi _{{0^ - }}}$ 第一势阱 1.3466 2583.83 70.94 9.5149 0.9589 20624.88 0.0203 第二势阱 2.1036 776.84 132.77 3.8990 0.398 27989.31 1.1617 ${{\rm{a}}^3}{\Pi _{{0^ + }}}$ 第一势阱 1.3466 2583.89 70.92 9.5149 0.9594 20625.01 0.0195 第二势阱 2.1012 780.04 136.69 3.9079 0.4536 27999.08 1.3153 ${{\rm{A}}^1}{\Pi _1}$ 第一势阱 1.3444 2621.70 61.52 9.5464 1.2006 20924.71 0.0392 第二势阱 2.2449 422.69 37.82 3.4237 0.1026 30306.30 0.2834
表2 SH– 阴离子的$\Omega$ 态的光谱常数Table2. Spectroscopic parameters for the $\Omega$ states of SH– anion.$\Lambda$ -S和$\Omega$ 态的势能曲线的拟合质量, 本文给出RMS值, 列在表1 和表2 中. 最大RMS值仅为4.4107 cm–1 . 可以看出本文的计算结果是可靠的.3.2.跃迁偶极矩 -->3.2.跃迁偶极矩 当考虑SOC效应后, 根据跃迁选择定则可知, ${{\rm{a}}^3}{\Pi _2} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{a}}^3}{\Pi _{{0^ - }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁不被允许. 本文计算了${{\rm{A}}^{1}}{\Pi _1} \!\leftrightarrow \!{{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^{3}}{\Pi _{{0^ + }}} \!\leftrightarrow \!{{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _1}\! \leftrightarrow $ ${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _{{0^ + }}}$ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ 跃迁的跃迁偶极矩, 结果如图3 所示.图 3 SH– 阴离子的跃迁偶极矩 (a) ${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁; (b) ${{\rm{a}}^{3}}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^1}{\Pi _1} \!\leftrightarrow\!{{\rm{a}}^3}{\Pi _{{0^ + }}}$ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ 跃迁Figure3. Transition dipole moments of SH– anion: (a) The ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ and ${{\rm{a}}^{3}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transitions; (b) the ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _{{0^ + }}}$ and ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ transitions.${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的强度最大, 在平衡核间距处的跃迁偶极矩为–1.3636 D. 值得注意的是${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁在平衡核间距处的跃迁偶极矩为0.5269 D, 比之前得到的OH– 阴离子的值[12 ] 更大. 另一方面SH– 阴离子${{\rm{a}}^{3}}{\Pi _1}$ 的垂直跃迁能为20363.64 cm–1 , 比OH– 阴离子${{\rm{a}}^{3}}{\Pi _1}$ 的垂直跃迁能18664.98 cm–1 [12 ] 大. 由此说明SH– 阴离子${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的爱因斯坦辐射速率比OH– 阴离子大. 在构建激光冷却SH– 阴离子的方案时必须考虑${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^{1}}\Sigma _{{0^ + }}^ + $ 跃迁. 值得注意的是${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _{{0^ + }}}$ 和${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ 跃迁的跃迁偶极矩在平衡核间距处接近零, 说明这3种跃迁的强度很低.3.3.SH– 阴离子的激光冷却 -->3.3.SH– 阴离子的激光冷却 分子离子的辐射速率(${A_{\nu '\nu'' }}$ )、弗兰克-康登因子(${f_{\nu '\nu'' }}$ )和辐射寿命($\tau $ )决定了此体系是否适合激光冷却. 根据跃迁规则可知, 考虑SOC效应后只有${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁被允许. 本文采用LEVEL8.0程序计算${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^{3}}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^{1}}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^{3}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的${A_{\nu '\nu'' }}$ 和${f_{\nu '\nu'' }}$ , 并得到了${{\rm{a}}^{3}}{\Pi _1}$ , ${{\rm{A}}^{1}}{\Pi _1}$ 和${{\rm{a}}^{3}}{\Pi _{{0^ + }}}$ 态的辐射寿命, 所有数据如表3 所列.Transition A 00 A 01 A 02 A 03 A 0 f 00 f 01 f 02 f 03 $\tau $ = 1/A 0 A 10 A 11 A 12 A 13 f 10 f 11 f 12 f 13 ${\operatorname{a} ^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 677122 2184.69 25.3676 2.8984 679335 0.9990 0.0009 3.38 × 10–5 3.46 × 10–6 1.472 × 10–6 15577.8 561038 4025.17 35.1337 0.0010 0.9931 0.0054 0.0004 ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 5310820 33.9404 30.5746 0.1736 5310885 0.9999 0.0001 2.18 × 10–6 1.07 × 10–8 1.883 × 10–7 2970.05 5262790 1089.41 217.62 0.0006 0.9992 0.0002 4.13 × 10–5 ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{0^ + }^ + $ 2229.24 98.3384 0.2456 0.0126 2327.84 0.9989 0.0011 3.82 × 10–5 3.53 × 10–6 4.295 × 10–4 102.87 2852.21 284.48 3.3484 0.0317 0.8795 0.0877 0.0010
表3 SH– 阴离子的辐射速率(单位为s–1 )、弗兰克-康登因子和自发辐射寿命(单位为s)Table3. Emission rates ${A_{\nu ' \nu '' }}$ (unit of s–1 ), Franck-Condon factors ${f_{\nu ' \nu '' }}$ and spontaneous radiative lifetimes $\tau $ (unit of s) of SH– anion.3.3.1.自旋阻禁跃迁的激光冷却 -->3.3.1.自旋阻禁跃迁的激光冷却 首先讨论构建${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^{1}}\Sigma _{{0^ + }}^ + $ 准闭合能级进行激光冷却SH– 阴离子的可能性. 从表3 可以看出, ${{\rm{a}}^{3}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁具有高对角分布的${f_{\nu '\nu'' }}$ , 即f 00 = 0.9990. 且f 00 , f 01 , f 02 之和基本等于1, 可以保证此循环的准闭合. 除了具有高对角分布的${f_{\nu '\nu'' }}$ , 激光冷却离子还需要具备很强的循环速率(105 —108 s–1 )和短的自发辐射寿命, 从表3 可以看到${{\rm{a}}^{3}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的总自发辐射速率A 0 = 6.79 × 105 s–1 , 即自发辐射寿命为1.472 ${\text{μ}}{\rm{s}}$ . 此结果约为OH– 阴离子${{\rm{a}}^{3}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的总自发辐射速率的7倍[12 ] . 相比于OH– 阴离子, 激光冷却SH– 阴离子所需的时间更短. 和GaF分子类似[8 ] , 由于其f 00 足够大, 只需要一束主激光来驱动${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁, 所需的激光波长$ {\lambda _{00}} = 492.27$ nm. 由此构建了${{\rm{a}}^{3}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 自旋阻禁跃迁对SH– 阴离子进行激光冷却, 冷却方案如图4 所示.${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁, 虽然具有非常高的对角分布弗兰克-康登因子(f 00 = 0.9989), 能满足跃迁循环的准闭合, 但总自发辐射速率A 0 太小, 只有2229.24 s–1 , 不满足激光冷却分子离子对循环速率的要求.图 4 采用$\scriptstyle {{{\rm{a}}^3}{\Pi _1}}\leftrightarrow \scriptstyle {{{\rm{X}}^1}\Sigma _{{0^ + }}^ + }$ 跃迁进行激光冷却SH– 阴离子的方案, 实线为所需激光, 虚线为自发辐射的弗兰克-康登因子Figure4. Proposed laser cooling scheme for the $ \scriptstyle{{{\rm{a}}^3}{\Pi _1}}\leftrightarrow$ $\scriptstyle {{{\rm{X}}^1}\Sigma _{{0^ + }}^ + }$ transition (solid line) and spontaneous decay.3.3.2.三电子能级的激光冷却 -->3.3.2.三电子能级的激光冷却 从表3 中可以看出, 相比于${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁, ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁具有更高对角分布的弗兰克-康登因子(f 00 = 0.9999)和更大的自发辐射速率(A 0 = 5.31 × 106 s–1 ), ${{\rm{A}}^1}{\Pi _1}$ 态的自发辐射寿命$\tau (\nu ' = 0) = 0.188\; {\text{μ}}{\rm{s}}$ .${{\rm{a}}^3}{\Pi _1}$ 和${{\rm{a}}^3}{\Pi _{{0^ + }}}$ 的存在对${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 能级准闭合性的影响, 可以通过振动分支损失比来分析其影响. 振动分支损失比可以表示为: ${\eta _1} = {\gamma _1}/{\gamma _\Sigma }$ 或${\eta _2} = {\gamma _2}/{\gamma _\Sigma }$ , 其中${\gamma _1}$ , ${\gamma _2}$ 和${\gamma _\Sigma }$ 分别表示${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ , ${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{a}}^{3}}{\Pi _{{0^ + }}}$ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的总自发辐射速率. ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ 和${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _{{0^ + }}}$ 在弗兰克-康登区域的跃迁偶极矩接近零. 计算得到这两种跃迁的总自发辐射速率分别只有1.85 × 10–2 和7.24 × 10–3 s–1 . 而${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的总自发辐射速率为5.31 × 106 s–1 . 得到$ {\eta _1} < 5 \times {10^{ - 9}} $ 和$ {\eta _2} < 2\,\times $ ${10^{ - 9}}$ . $\eta$ 值远小于YO分子的实验值(4.0 × 10–3 )[3 ] , 说明中间态${{\rm{a}}^3}{\Pi _1}$ 和${{\rm{a}}^3}{\Pi _{{0^ + }}}$ 的存在对激光冷却的影响可以忽略不计.f 00 足够大, 只需要一束主激光来驱动${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^{1}}\Sigma _{{0^ + }}^ + $ 跃迁, 其波长$ {\lambda _{00}}$ = 478.57 nm. 由此构建了三电子能级跃迁对SH– 阴离子进行激光冷却, 冷却方案如图5 所示.图 5 采用${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁进行激光冷却SH– 阴离子的方案, 其中实线为所需激光, 虚线为自发辐射的弗兰克-康登因子Figure5. Proposed laser cooling scheme for the $ {{\rm{A}}^1}{\Pi _1} \leftrightarrow$ $ {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition (solid line) and spontaneous decay.3.3.3.多普勒温度和反冲温度 -->3.3.3.多普勒温度和反冲温度 多普勒温度的计算公式为${T_{{\rm{Doppler}}}} = h/4{k_{\rm{B}}}{\text{π}} \tau $ [36 ] , 其中h 为普朗克常数, k B 为玻尔兹曼常数, $\tau $ 为激发态的自发辐射寿命. 经计算, 采用${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ +$ 跃迁进行激光冷却SH– 阴离子的多普勒温度分别为2.6和20.28 $ {\text{μK}}$ .${T_{{\rm{recoil}}}} = {h^2}/m{k_{\rm{B}}}{\lambda ^2}$ [37 ] , 其中$ \lambda $ 为激光冷却离子的主激光波长. 采用${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^{1}}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁进行激光冷却SH– 阴离子的反冲温度分别为2.43和2.56 $ {\text{μK}}$ .– 阴离子所能达到的反冲温度都低于多普勒温度.4.结 论 采用MRCI+Q 计算了SH– 阴离子${{\rm{X}}^1}{\Sigma ^ + }$ , ${{\rm{a}}^3}\Pi $ 和${{\rm{A}}^1}\Pi $ 态的电子结构, 在计算过程中考虑了DKH3标量相对论修正和CV关联效应. 在MRCI+Q 水平下考虑SOC效应计算了$\Omega$ 态的势能曲线和跃迁偶极矩. 得到的光谱常数与已有实验值和理论值符合得很好. 本文第一次报道了$\Omega$ 态的光谱常数和跃迁性质. 计算发现${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的跃迁偶极矩很大, 在平衡核间距处为0.5269 D.– 阴离子${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^{1}}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的弗兰克-康登因子、辐射速率和辐射寿命. 计算结果表明, ${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁都具有非常高的对角分布弗兰克-康登因子, 分别为0.9990和0.9999, 同时具有大的自发辐射速率, 分别为6.79 × 105 和5.31 × 106 s–1 . 对于${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁存在中间态${{\rm{a}}^3}{\Pi _1}$ 和${{\rm{a}}^3}{\Pi _{{0^ + }}}$ , 但其振动分支损失比非常小, 可以忽略中间态的存在对循环跃迁的影响, 说明可以通过两种跃迁方式来对SH– 阴离子进行激光冷却. 本文分别制定了自旋阻禁跃迁和三电子能级跃迁进行激光冷却SH– 阴离子的方案, 最后预测了两种方案进行激光冷却SH– 阴离子的多普勒温度和反冲温度. 
图 1 SH–阴离子的
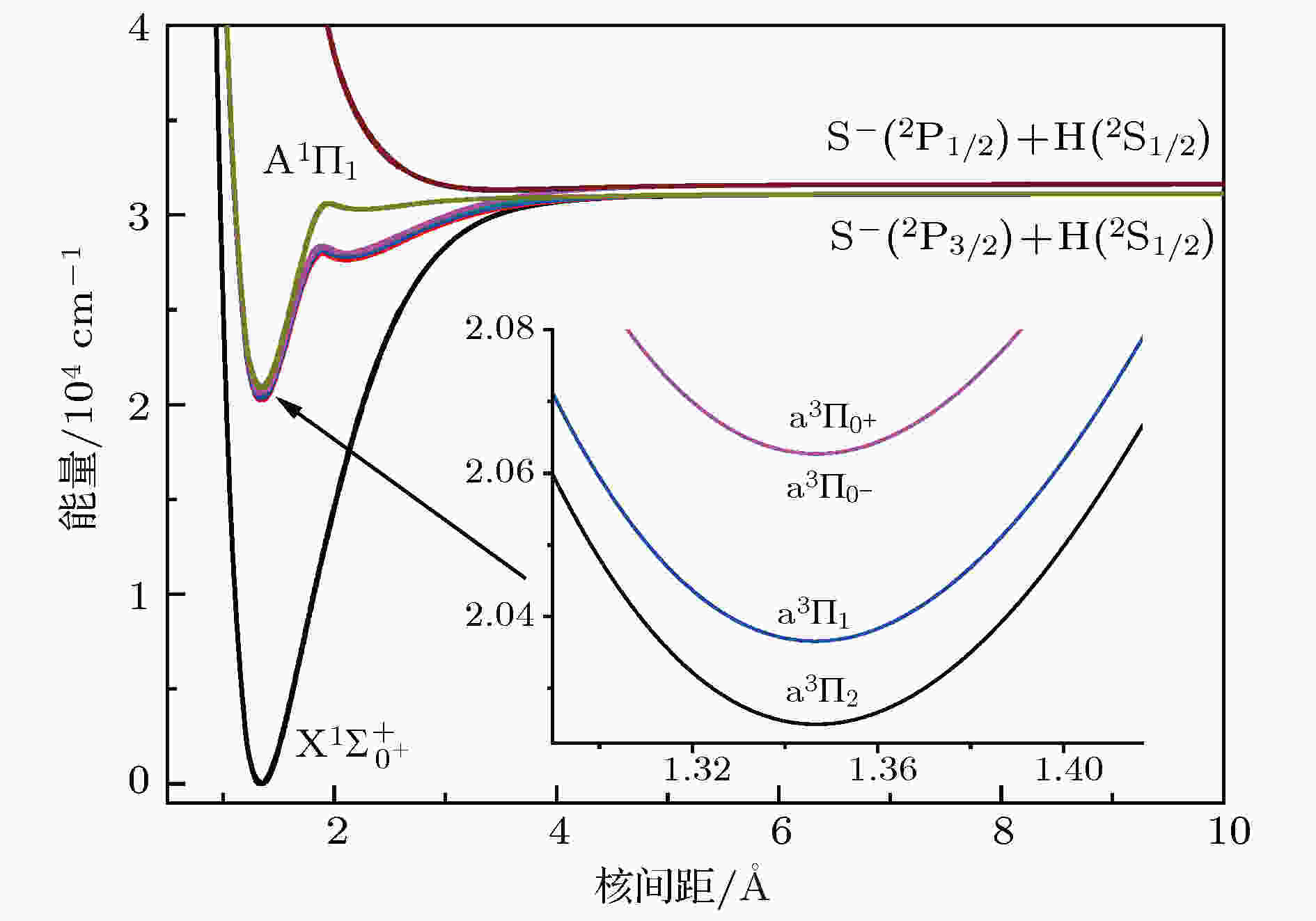图 2 SH–阴离子的
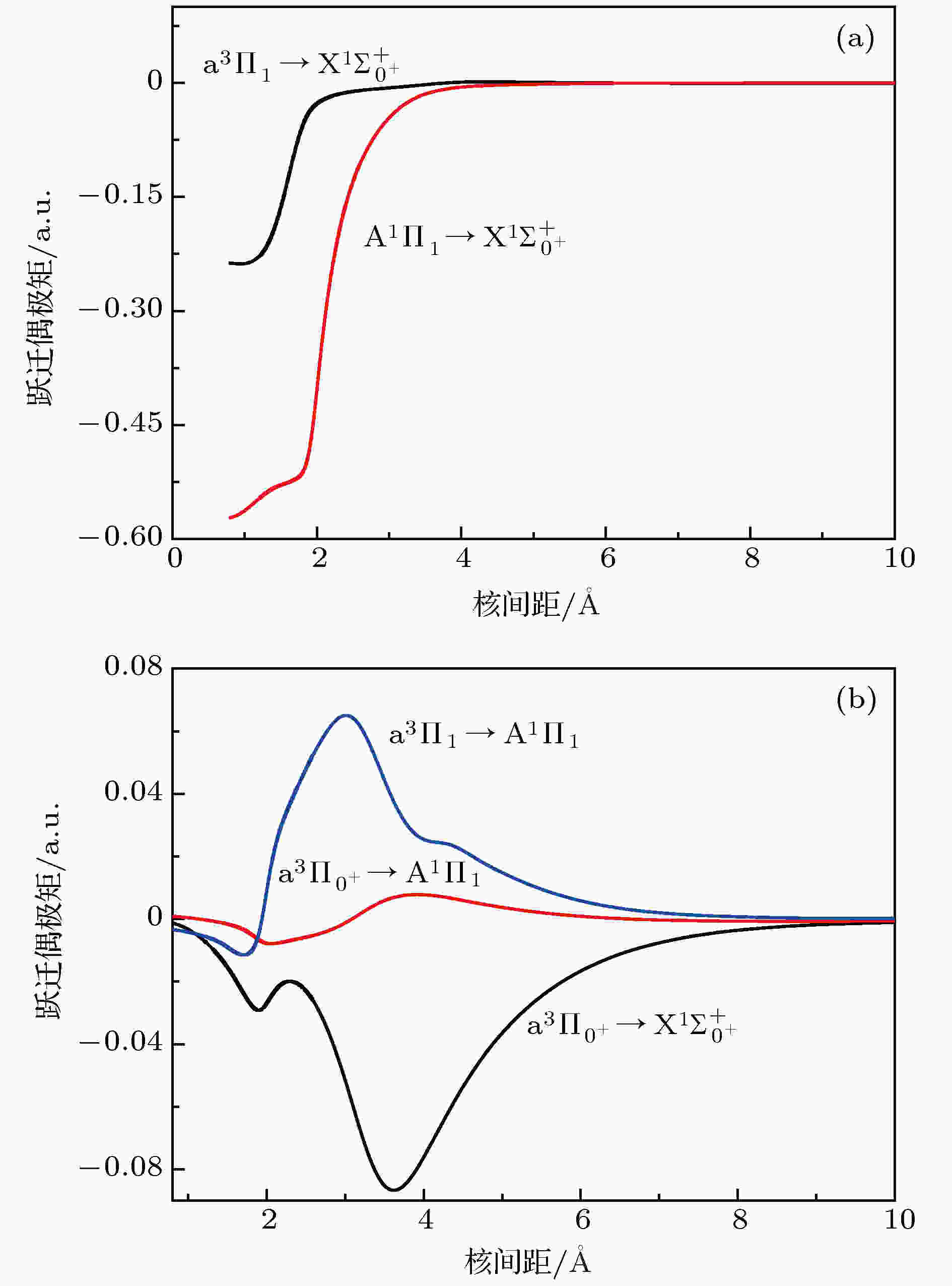图 3 SH–阴离子的跃迁偶极矩 (a) 
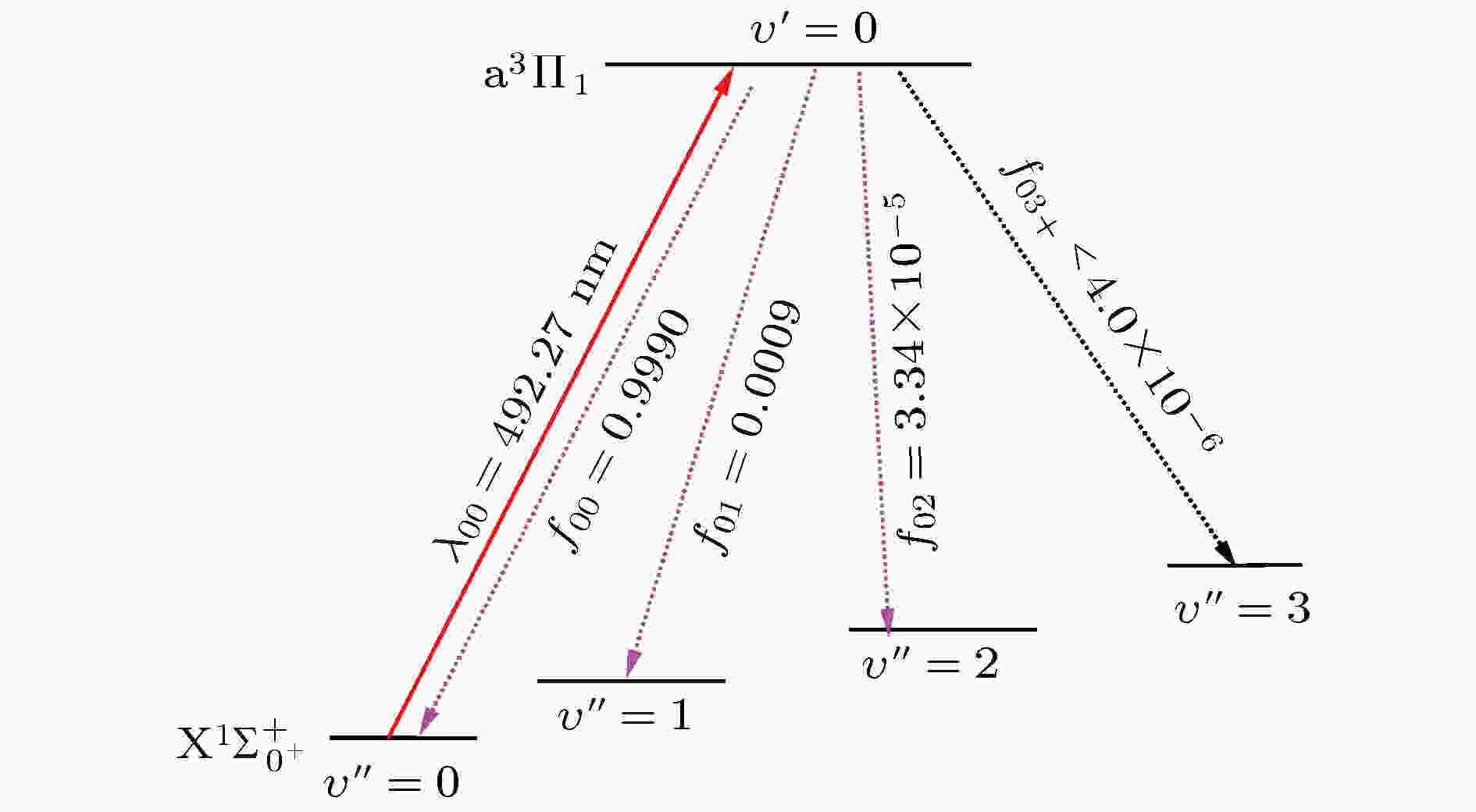图 4 采用
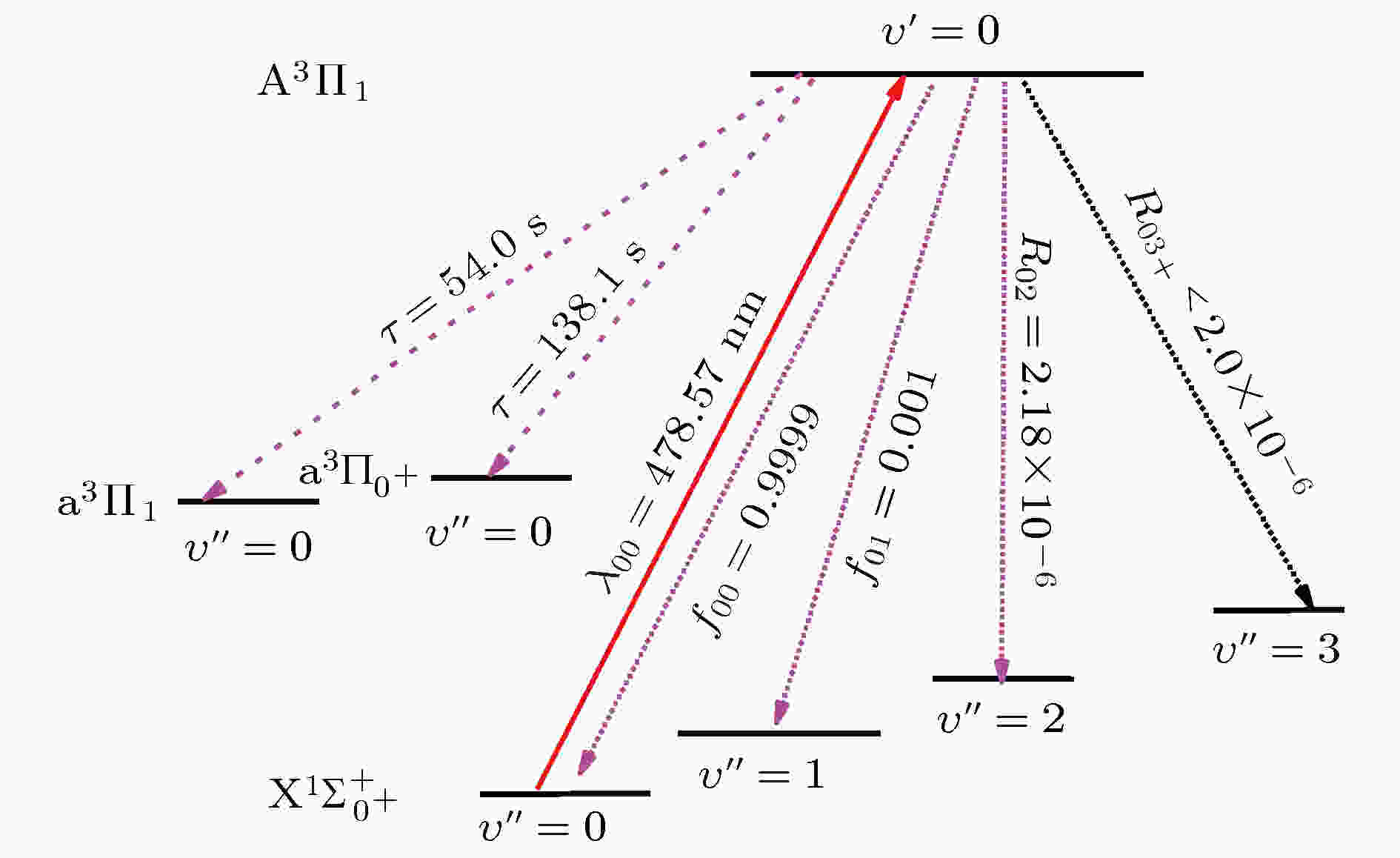图 5 采用
