摘要:目前对超冷原子的研究已经从最初的原子分子物理扩展到了物理的很多分支. 极性分子可以将电偶极相互作用引入到超冷体系, 同时分子又与原子类似, 可以灵活地被光和其他电磁场操控, 因而很多理论工作都预言了超冷极性分子在超冷化学、量子模拟和量子信息等领域会有重要的应用. 但由于超冷基态分子的制备非常困难, 如何把超冷物理从原子发展到分子还是一个方兴未艾的课题. 过去的10年间, 各种分子冷却技术都取得了很大突破, 本文回顾了这些进展, 并着重介绍了基于异核冷原子的磁缔合结合受激拉曼转移这一技术, 该技术在制备高密度的基态碱金属超冷极性分子上取得了较大的成功. 本文也总结了超冷极性碱金属分子基本碰撞特性研究的一些实验结果.
关键词: 超冷极性分子/
电偶极相互作用/
超冷化学反应/
量子模拟

English Abstract

全文HTML

--> --> -->

超冷(温度T < 1 ${\text{μK}}$)稀薄原子气体中的玻色爱因斯坦凝聚体(Bose-Einstein Condensation, BEC)在1995年第一次实现之后不久, 原子、分子和光物理领域的研究者们就认识到可以BEC为载体来构建与多体体系类似的哈密顿量, 从而模拟和理解这些体系的物理内容^[1]. 基于冷原子体系没有杂质和缺陷的特性及其非常灵活的调控能力, 过去十几年, 冷原子量子模拟、量子信息^[2]等方向已经取得了巨大的成功, 特别是冷原子和光晶格的完美结合, 开辟了利用原子分子体系研究凝聚态体系的道路, 实现了不同物理分支之间的交叉和融合, 大大地加深了我们对量子强相互作用体系的理解.
原子间的相互作用通常是很弱且短程的范德瓦耳斯作用, 即使Feshbach共振技术可以对相互作用强度进行任意调控^[3], 也并不能改变这一特性. 原子间相互作用的这些特性带来了一些限制, 很多凝聚态体系中非常重要的问题, 目前在超冷原子体系中还很难实现. 比如量子磁性问题, 由于原子间相互作用强度太小, 为了在光晶格中实现和观测磁性相变, 需要远远低于现有超冷技术能达到的温度. 目前, 很多研究组还在持续探索在超冷原子中获得更低温度的方法. 另一方面, 如果可以找到一种更强的、长程的相互作用, 也可以帮助解决这一问题. 超冷极性分子间的电偶极相互作用就可以满足这样的要求^[4-11](一些特殊的镧系和过渡金属元素, 包括铬^[12]、铒^[13]和镝^[14], 有很大的磁偶极矩, 因而可以有磁偶极相互作用; 磁性原子也是超冷物理研究的热点之一, 但不在本文讨论范围之内).
本文讨论的极性分子是指最简单的由两种不同原子结合形成的异核中性双原子分子, 比如钠(²³Na)原子和铷(⁸⁷Rb)原子. 由于两种原子对电子的亲和力不同, 对整个分子而言, 电荷的分布是不对称的, 导致分子中的正负电荷中心不重合, 因而产生了一个沿着分子轴向的永久电偶极矩. 需要注意的是, 由于电偶极算符是奇宇称的, 在没有外加电场的情况下, 极性分子在实验室坐标系中的电偶极矩的期望值为零, 因而分子间电偶极相互作用平均值为零. 外加电场可以将分子内部不同宇称的态混合, 或者说将分子极化, 从而诱导出沿着电场方向的有效电偶极矩$\mu $, 使得分子间可以有电偶极相互作用. 例如, 钠铷(²³Na⁸⁷Rb)分子的永久电偶极矩为3.2 Debye, 图1所示为处于最低振动能级v = 0的几个转动能级上(J = 0和J = 1)的²³Na⁸⁷Rb分子的有效电偶极矩随外加电场E的变化, 这里v和J分别是分子的振动和转动量子数, M_J为转动能级沿外电场方向的投影量子数. 可见$\mu $随着E的增强而增大, 逐渐趋近于饱和值, 也就是3.2 Debye. 需要说明的是, 图1所示的几条曲线, 包含了转动能级J从0到10的贡献. 由于电场可引起不同转动能级之间的耦合, 严格来讲J在非零电场时不再是一个好量子数.
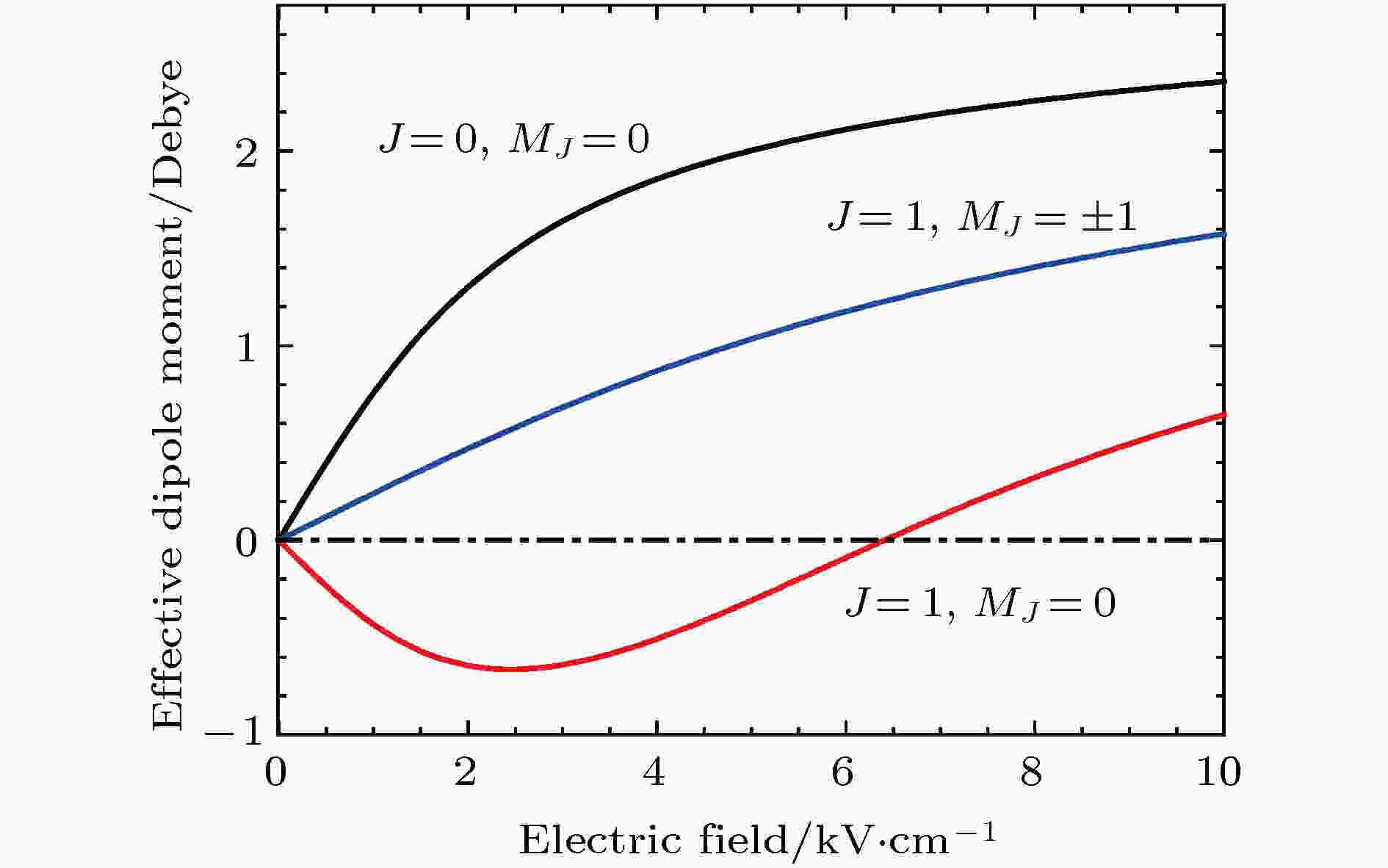图 1 电场诱导²³Na⁸⁷Rb分子产生的有效电偶极矩
Figure1. The induced effective dipole moments of the first two rotational states versus the electric field (²³Na⁸⁷Rb).

如图2所示, 两个在电场中被极化的极性分子间的相互作用可以表示为^[8]
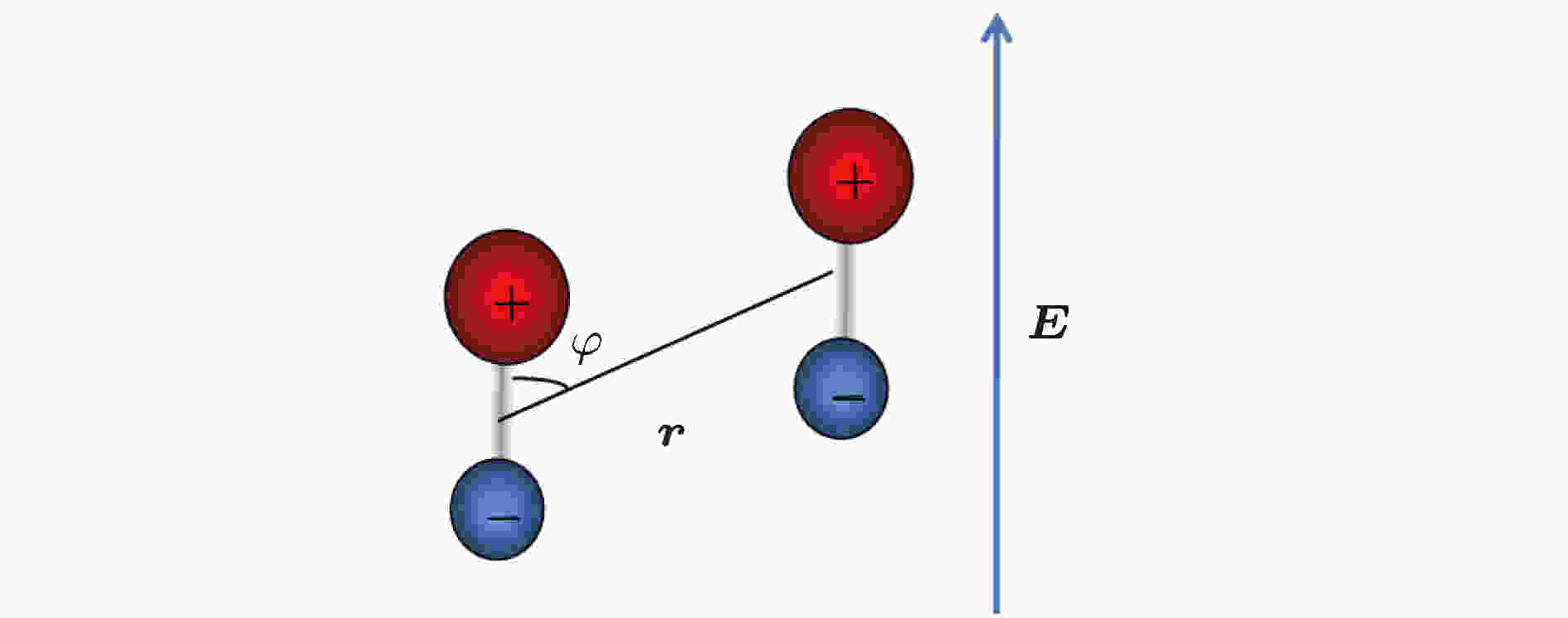图 2 极性分子在电场中可以产生电偶极相互作用
Figure2. Dipole-dipole interaction between polar molecules in an external electric field.

${U_{dd}}\left( {r,\varphi } \right) = \frac{{{\mu ^2}}}{{4{\text{π}}{\varepsilon _0}}}\frac{{1 - 3{{\cos }^2}\varphi }}{{{r^3}}},$

其中$\mu $为有效电偶极矩, $r = \left| {\vec r} \right|$是两个电偶极矩间的距离, $\varphi $为${\vec r}$与电场${\vec E}$之间的夹角. 和正比于1/r⁶的范德瓦耳斯作用相比, 正比于1/r³的电偶极相互作用随r的衰减更慢, 因而是长程力, 而且它是各向异性的, 随$\varphi $的不同, 电偶极相互作用可以是排斥势, 也可以是吸引势, 同时U_dd的强度也可以通过电场调节$\mu $来进行操控^[15](图1).
相比范德瓦耳斯作用, U_dd的强度要大很多. 例如, 把$\mu $ = 1 Debye的极性分子并排装载到晶格常数为532 nm的光晶格中, 处于相邻格点的分子间偶极排斥作用约为1 kHz, 而次近邻格点间的相互作用还有350 Hz. 因此, 这是一个真正的多体系统, 所有的格点间都有很强的关联. 同时, 和原子光晶格类似, 超冷分子光晶格系统哈密顿量的所有参数, 包括分子在格点间的隧穿能量和偶极相互作用的强度和方向也都是可操控的. 理论工作已经提出, 通过调节这些参数的相对关系, 可以实现很多有趣的多体量子相, 比如超固相^[16]. 而利用分子的转动能级作为赝自旋, 偶极相互作用也可以用来实现自旋交换, 在同时有微波和直流电场的情况下, 就可以实现XXZ自旋磁性模型^[17]. 而且, 由于这种自旋交换实际是通过角动量在格点间转移实现的, 所以会自然地带来自旋和轨道自由度的耦合^[18]. 最近, 在类似的体系中, 一些文献中也提出了利用多个微波操控来实现拓扑相的方法^[19].
总之, 对超冷极性分子体系的理论研究目前已经进行得非常深入, 但实验研究却大大滞后. 造成这种状况的原因主要有两个: 1)基态超冷极性分子非常难制备; 2)基态分子间的碰撞也比预期的复杂很多. 下面几个部分, 我们将围绕这两个问题, 对过去10年间的一些进展进行总结.
需要指出的是, 目前实验上已经有很多不同制备基态冷分子的方法. 近年, 分子的直接冷却, 特别是对一些特殊的自由基分子的直接激光冷却, 取得了长足的进步^[20-24], 但目前得到的分子样品温度还没有达到${\text{μ}}$K以下, 因而这一方向研究的焦点是如何得到温度更低、密度更高的分子样品. 而利用超冷原子的磁缔合技术^[3,25], 已经可以制备出量子简并的分子样品^[26]. 虽然由此制备的分子种类仅局限于异核碱金属双原子分子, 但目前已经可以用这些样品开展一些对超冷分子基本碰撞性质的研究. 结合作者的工作经验, 本文重点介绍后一种方法, 而对分子的直接冷却只做简单的归纳.

2

-->

2.1.研究现状

目前实验中用到的超冷原子, 都是首先通过激光冷却然后再进行蒸发冷却来获得的. 由于原子的能级结构简单, 比较容易找到接近闭合的两能级体系, 在它们之间进行连续的光子散射, 可以很快把原子从高温冷却到mK以下, 然后装载到磁阱或光阱中进行蒸发冷却. 由于磁阱和光阱的阱深都很浅, 必须经过激光冷却之后原子才能被囚禁住. 分子的情况就复杂得多, 由于分子有很多振动和转动能级, 一般来讲, 不存在闭合的两能级体系, 因此每一个基态分子吸收和散射几个光子之后, 就会转移到暗态, 导致其与冷却光的作用停止. 由于散射的光子数目太少, 不会使分子的温度显著降低, 以致磁阱和光阱无法囚禁.
为了克服这一问题, 过去的20年间, 很多研究组已经进行了不同的尝试, 也发展了几种技术. 大体上讲, 可以将这些技术分为两大类: 1)对已经存在的基态分子直接用各种方法冷却; 2)用间接的方法, 从超冷原子开始, 利用光或者磁缔合技术合成超冷分子^[27,28].
3 -->

2.1.1.基态分子直接冷却

在自然状态下, 绝大多数分子都处于基态, 因此只要把它们的温度降低就可以获得冷分子. 在各种冷却技术中, 由Harvard大学Doyle研究组^[29]发展的缓冲气体冷却(buffer gas cooling)是一种通用的技术, 可以对各种分子进行冷却, 但这种技术得到的温度由缓冲气体决定, 一般在4 K左右(液氦), 对这些分子直接进行保守势阱装载并进一步蒸发冷却仍很困难. 另一方面, 利用这种技术可以很快地冷却大量的处于最低振转能级的分子, 将它们引出缓冲气体冷却装置后, 可以获得亮度很高的分子束^[30], 为冷分子光谱提供了非常好的条件. 其他实验如直接激光冷却, 通常也需要先以此对分子进行预冷却. 目前, 国内华东师范大学和浙江大学的两个研究组已经掌握了这一技术, 并成功制备了基态MgF^[31]和BaF^[32]冷分子.
另一项研究得很广泛的技术是Stark(斯塔克)减速技术^[33]. 这种技术利用与分子束运动同步的交变高电场产生随时间变化的Stark效应来降低分子的运动速率, 因而只对极性分子有效. 由于这一方法涉及对高电场的快速操控, 技术上很有挑战性. 利用这一技术, 目前分子的温度可以达到几十mK量级, 而样品的密度还较低^[34]. 国内华东师范大学的研究组在这一方向做了多年的理论和实验工作, 取得了一系列成果^[35,36]. 南通大学的研究组近期也开始了这方面的探索^[37].
最近几年, 对一些特殊分子的直接激光冷却这一方向发展非常迅猛. 如SrF, YO, CaF等自由基分子, 可以找到与振动基态(v" = 0)闭合性很高的分子振动激发态(Franck-Condon因子在95%以上), 因而在光子散射后, 分子从激发态经自发辐射回到基态只占据少数几个振动态^[38]; 另一方面, 对处于振动基态的第一激发转动态(J′′ = 1)的分子, 由于角动量的选择定则, 冷却跃迁 J′′ = 1 ? J = 0对转动能级是完全闭合的, 即基态 J′′ = 1的分子被光子激发到J = 0后, 自发辐射只能回到基态J′′ = 1^[39]. 由于这两个原因, 对这些特殊分子, 只需利用少数几个回泵激光, 就可以获得准闭环系统, 使分子能够散射足够多的光子, 从而实现冷却.
分子的直接激光冷却最早是由Yale大学的DeMille研究组^[20]实现的. 目前已经有很多研究组在这个方向开展工作, 包括美国的JILA^[24], Harvard^[23], 以及英国的Imperial College London^[40]等的研究组最近都取得了很多突破. 例如在最新发表的文章中, Harvard大学的研究组已经可以将CaF分子的温度冷却到20 ${\text{μ}}$K并实现了光阱的装载^[41]. 虽然由于分子数目的限制, 样品的密度还比较低, 但距离实现超冷高密度分子已经没有基本原理上的限制^[23]. 国内的两个研究组最近也开始了在这一方向的探索, 其中华东师范大学的研究组选择的分子为MgF^[31], 浙江大学的研究组选择的分子为BaF^[32], 目前他们已经获得了一些初步的分子冷却信号.
3 -->

2.1.2.利用超冷原子缔合获得超冷分子

由于超冷原子的制备技术非常成熟, 结合光或者磁缔合技术, 就可以合成超冷分子^[27]. 其中光缔合技术非常适合用于进行超精细分子光谱的研究^[42], 国内山西大学的研究组多年来在此方向做了很多的工作^[43,44]. 光缔合之后的自发辐射可以形成电子基态的分子, 但这些分子一般分布在很多个振动态, 难以进行分子态的纯化. 而利用磁缔合技术形成的分子都处于同一能级, 因而更加适合进行后续的研究. 利用磁缔合技术获得的分子温度等于超冷原子的温度, 而且分子密度也较高, 但分子处于弱束缚态, 需要用受激拉曼过程才能转移到基态. 目前, 从相空间密度的角度(即最高密度和最低温度), 超冷原子磁缔合结合受激拉曼转移是最成功的制备基态超冷极性分子的方法^[45]. 利用这一方法, 最近JILA的研究组已经成功实现了钾铷(⁴⁰K⁸⁷Rb)分子的费米简并^[26,45], 而奥地利的Innsbruck (⁸⁷Rb¹³³Cs)^[46], 英国的Durham (⁸⁷Rb¹³³Cs)^[47], 美国麻省理工学院(MIT)(²³Na⁴⁰K)^[48], 德国马普研究所(MPQ)(²³Na⁴⁰K)^[49], 以及中国的香港中文大学(²³Na⁸⁷Rb)^[50]和中国科学技术大学(²³Na⁴⁰K)^[51]都已经成功地实现了基态超冷极性分子的制备. 下面我们将以²³Na⁸⁷Rb分子为例对这一方法进行更详细的讨论.
2 -->

2.2.Feshbach共振和磁缔合

两个碰撞原子间的Feshbach共振通常可按图3(a)所示的两通道模型来理解. 对碱金属, 这里的通道对应于两种原子的超精细能级的不同组合. 如果在不同通道中的两个原子以及它们形成的分子对磁场的响应不同, 在一定的磁场下, 在通道1中的两个原子的散射阈值就有可能和通道2的束缚态能级交叉, 从而引起共振散射, 即Feshbach共振. 在共振磁场B₀附近, 散射长度a随磁场B的变化为^[3]
图 3 (a)Feshbach共振的两通道模型; (b)利用Feshbach共振进行磁缔合产生弱束缚分子
Figure3. (a) Two-channel model for a Feshbach resonance; (b) formation of a weakly bound Feshbach molecule by magnetoassociation.

$a = {a_{{\rm{bg}}}}\left( {1 - \frac{{\Delta B}}{{B - {B_0}}}} \right),$

其中a_bg为远离共振时的背景散射长度, ${\Delta B}$为共振的宽度. 通过调节散射长度改变冷原子间的相互作用是Feshbach共振最重要的应用之一.
Feshbach共振的另一个重要应用是磁缔合. 如图3(b)所示, 磁缔合可以用Landau-Zener过程来理解. 在共振附近, 由于两个通道之间的耦合, 在能量交叉处产生了一个劈裂, 劈裂的大小由耦合强度决定, 一般和Feshbach共振的性质有关. 如果初始时磁场处于共振之上, 当把磁场绝热地扫描经过共振后, 两个原子就会缔合为一个Feshbach分子. 注意在共振的两端, 散射长度的符号相反, 分子处于散射长度为正的一端. 磁缔合是一种非常强大的技术, 它可以将各种相同或不同的玻色子、费米子及其混合物缔合为分子, 特别是在两分量的费米子中, a > 0和a < 0两端分别对应BEC(两个费米子合成的分子为玻色子)和BCS(Bardeen-Cooper-Schrieffer)区, 可以用来研究BEC和BCS crossover(跨接效应)的相关物理.
就超冷分子的研究而言, 磁缔合需要在两种原子的混合气体中进行, 这是一个很复杂的过程, 目前还很难达到很高的转换效率. 比如在²³Na⁸⁷Rb分子的实验中, 初始时²³Na和⁸⁷Rb原子的数目都约为2 × 10⁵, 而经过磁缔合后获得的Feshbach分子只有10⁴, 对应的转换效率只有5%. 其他类似实验上得到的转换效率也都在5%到10%^[45-49]. 如何提高转换效率, 从而得到更多的分子是一个有待解决的问题. 另外, 剩余的原子可以和分子发生碰撞, 从而引起分子的损耗, 因而必须尽快把它们从光阱中移除.
²³Na和⁸⁷Rb之间的Feshbach共振位于347.75 G附近^[52,53], 磁场从高到低扫描经过共振后, 一部分原子被缔合为分子, 如图4(a)所示. 利用分子和原子对磁场的相互作用不同, 可以加一个磁场梯度将剩余的原子从阱中移除, 而分子则不受影响. 探测是在磁场关断后, 对原子进行吸收成像. 在实验中, 为了确认磁场扫描共振后形成了Feshbach分子, 可以用如图4(a)所示的时序, 在把剩余的原子移除后直接关掉磁场, 利用吸收成像探测看不到信号, 这是由于探测光是与原子跃迁共振的, Feshbach分子对它的散射截面很小. 只有当再做一个反向的磁场扫描, 把不能直接探测到的分子离解成原子后, 才能重新看到信号, 如图4(b)所示, 这样就证明磁缔合形成了Feshbach分子.
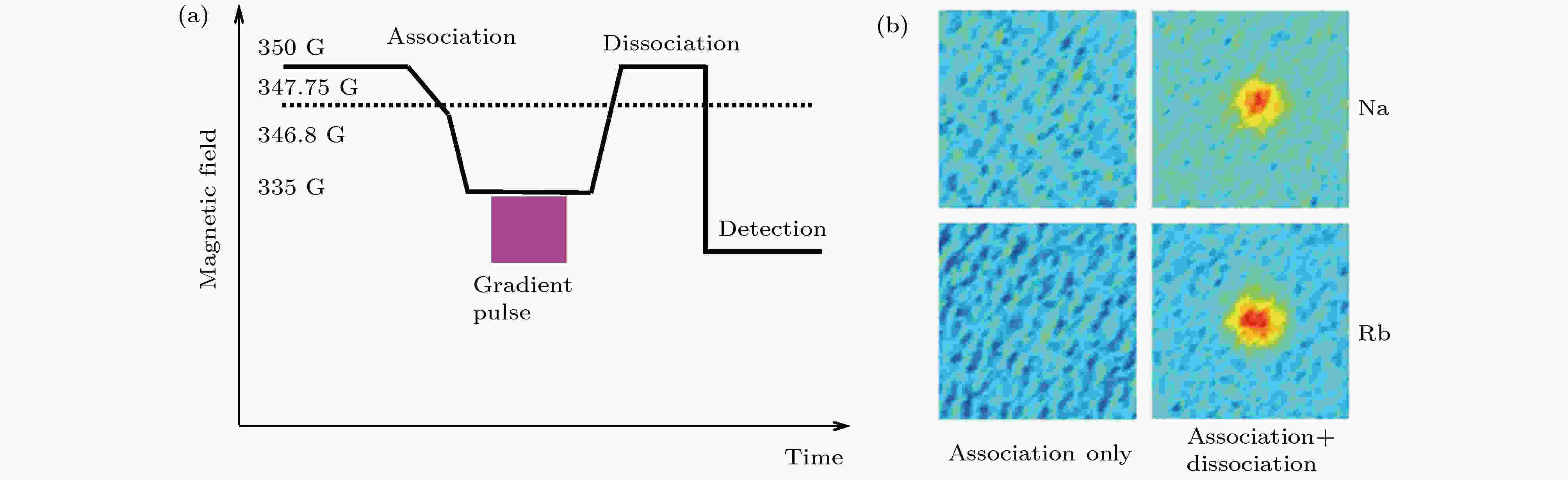图 4 利用磁缔合制备²³Na⁸⁷Rb Feshbach分子 (a)磁场改变的时序; (b)分别在离解和不离解的情况下探测钠和铷原子^[52]
Figure4. Creation of ²³Na⁸⁷Rb Feshbach molecule via magnetoassociation: (a) The magnetic field sequence; (b) absorption images of ²³Na and ⁸⁷Rb with and without dissociation procedure^[52].

在共振附近, Feshbach分子的结合能随磁场失谐的增大而增加. 一般而言, 对于两通道耦合较强的共振, 亦即所谓的宽共振, Feshbach分子的结合能E_b随散射长度的变化可以近似地表示为

${E_{\rm{b}}} = {\hbar ^2}/m{a^2},$

其中m = m₁m₂/(m₁ + m₂)为分子的约化质量, m₁和m₂为两个原子的质量. 这种情况下, 分子的波函数具有较多的原散射通道(open channel)成分. 对于通道间耦合较弱的共振, 如图5所示²³Na⁸⁷Rb Feshbach分子的情况, 只有在很接近共振时E_b才可以用(3)式来描述, 远离共振时, 结合能迅速增大, 而分子的波函数也具有较多的第二个通道(closed channel)的成分.
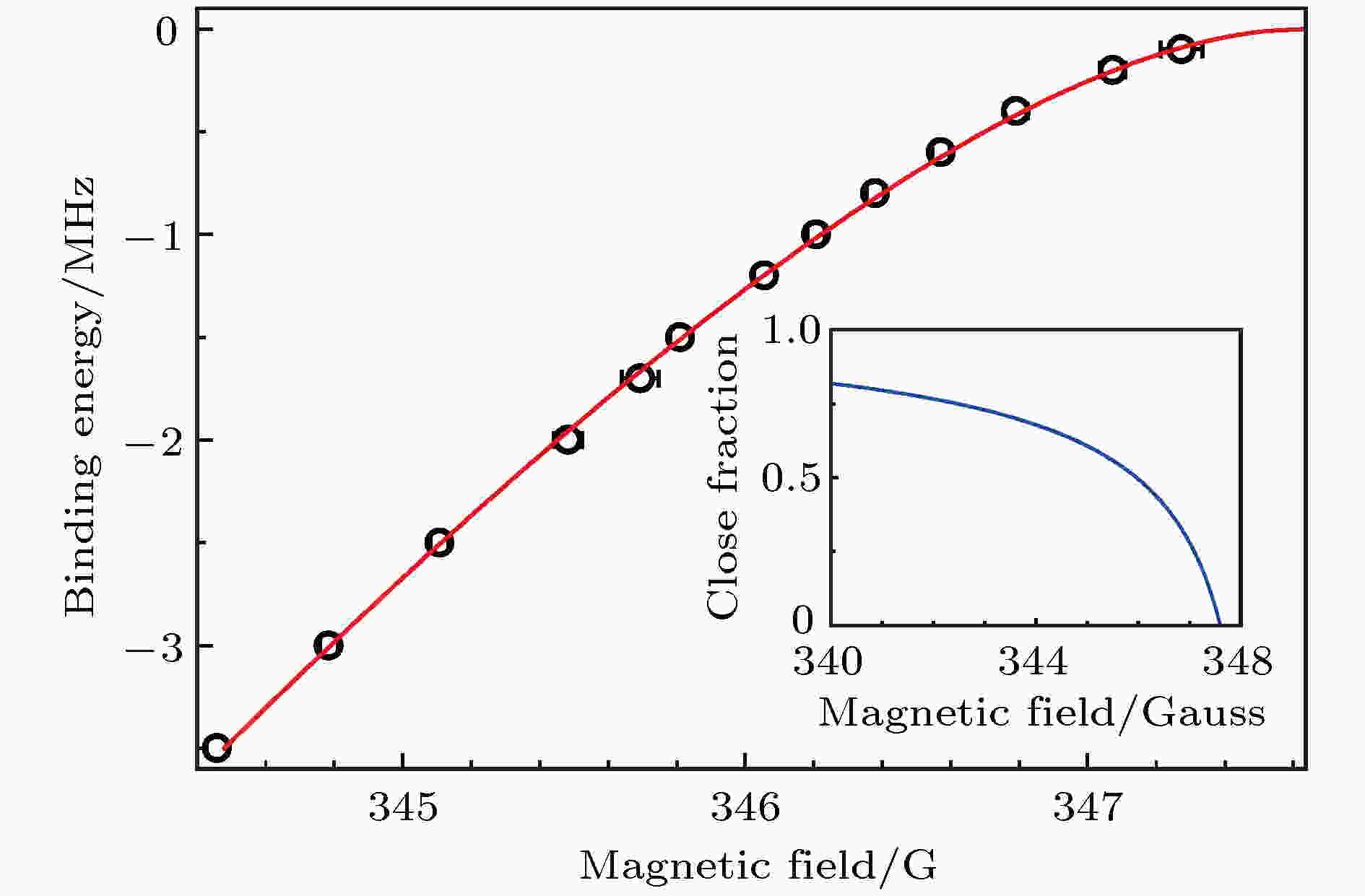图 5 ²³Na⁸⁷Rb Feshbach分子的结合能随磁场的变化, 插图表示离共振越远, 分子的closed channel成分越多^[52]
Figure5. Binding energy of ²³Na⁸⁷Rb Feshbach molecules versus magnetic field near 347.7 Gauss. The inset shows the closed-channel fraction of the Feshbach molecule versus magnetic field^[52].

通过磁缔合形成的Feshbach分子处于分子的最低电子能态, 但处于振转能级的高激发态. 比如²³Na⁸⁷Rb分子的电子基态, ${{\rm{X}}^1}{\Sigma ^ + }$态的势能曲线深度为5030 cm^–1 (1 cm^–1 ≈ 30 GHz), 而Feshbach分子的结合能很小仅为几个MHz(图5). 因此Feshbach分子的两个原子核的间距很大, 两个原子的电子云分布和单独的原子区别不大, 正负电荷的中心重合, 分子也就几乎没有永久电偶极矩, 因此异核Feshbach分子不是极性分子. 如图6所示, 只有在接近势能曲线底部, 两个原子核距离很近时, 分子才有大的永久电偶极矩. 而且一般认为非振转基态的分子会受振转弛豫影响而不稳定, 所以需要把Feshbach分子转移到振转基态(v = 0, J = 0).
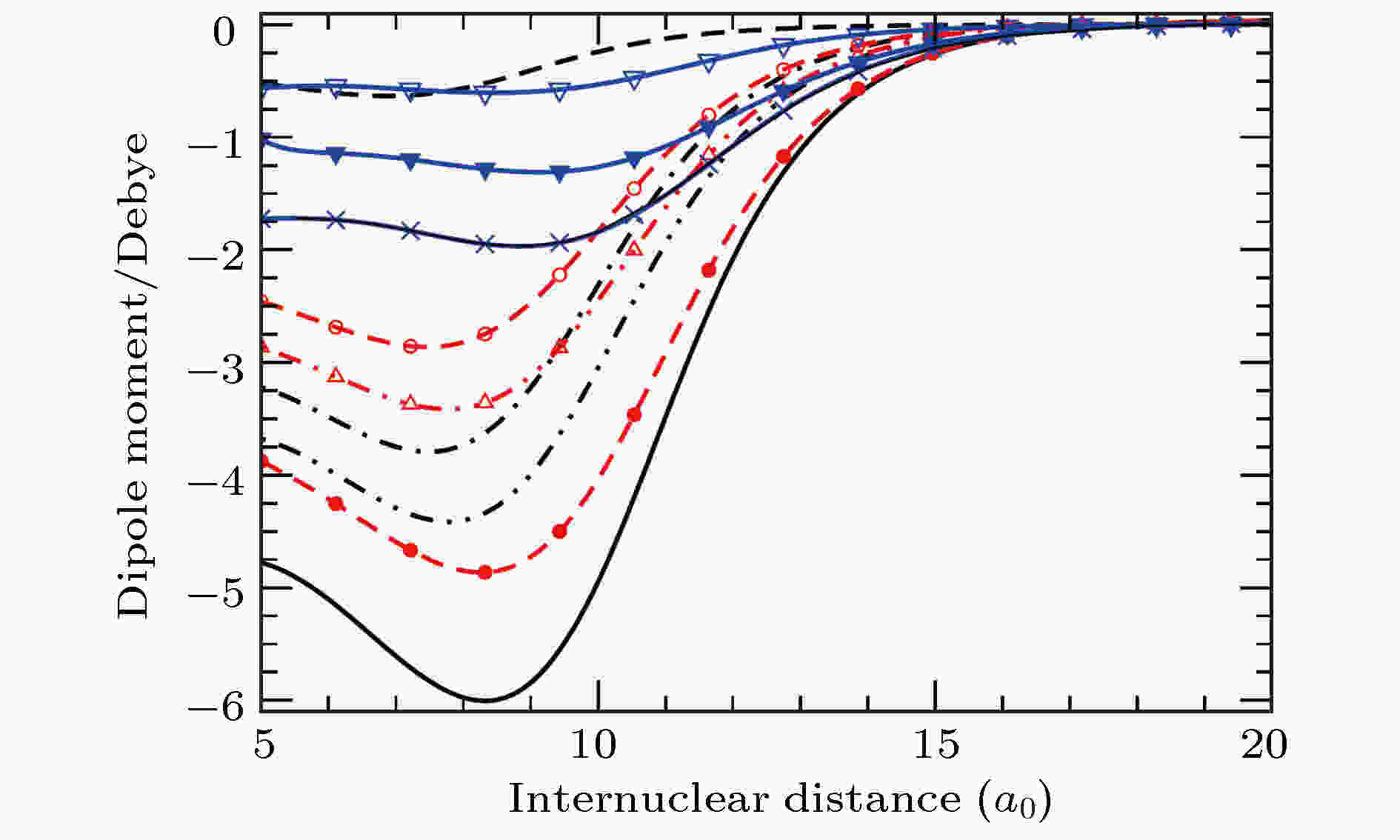图 6 异核碱金属双原子分子的电偶极矩和核间距(a₀为玻尔半径)的关系, 图中红色空心三角为²³Na⁸⁷Rb分子
Figure6. Electric-dipole moment of heteronuclear molecules as a function of internuclear distance (a₀ is the Bohr radius). The red up-pointing triangle is ²³Na⁸⁷Rb molecule.

2 -->

2.3.受激拉曼转移的方案选择及分子光谱研究

以²³Na⁸⁷Rb分子为例, 图7(a)为其相关能态的势能曲线, 其中Feshbach分子和振转基态分子的结合能差约为5000 cm^–1, 为了在完成转态的同时把这部分能量带走, 通用的方法是利用一个以Feshbach分子和基态分子为初态$\left| i \right\rangle $和末态$\left| g \right\rangle $的双光子受激拉曼过程, 而中间态$\left| e \right\rangle $为分子的电子激发态的特定振转能级.
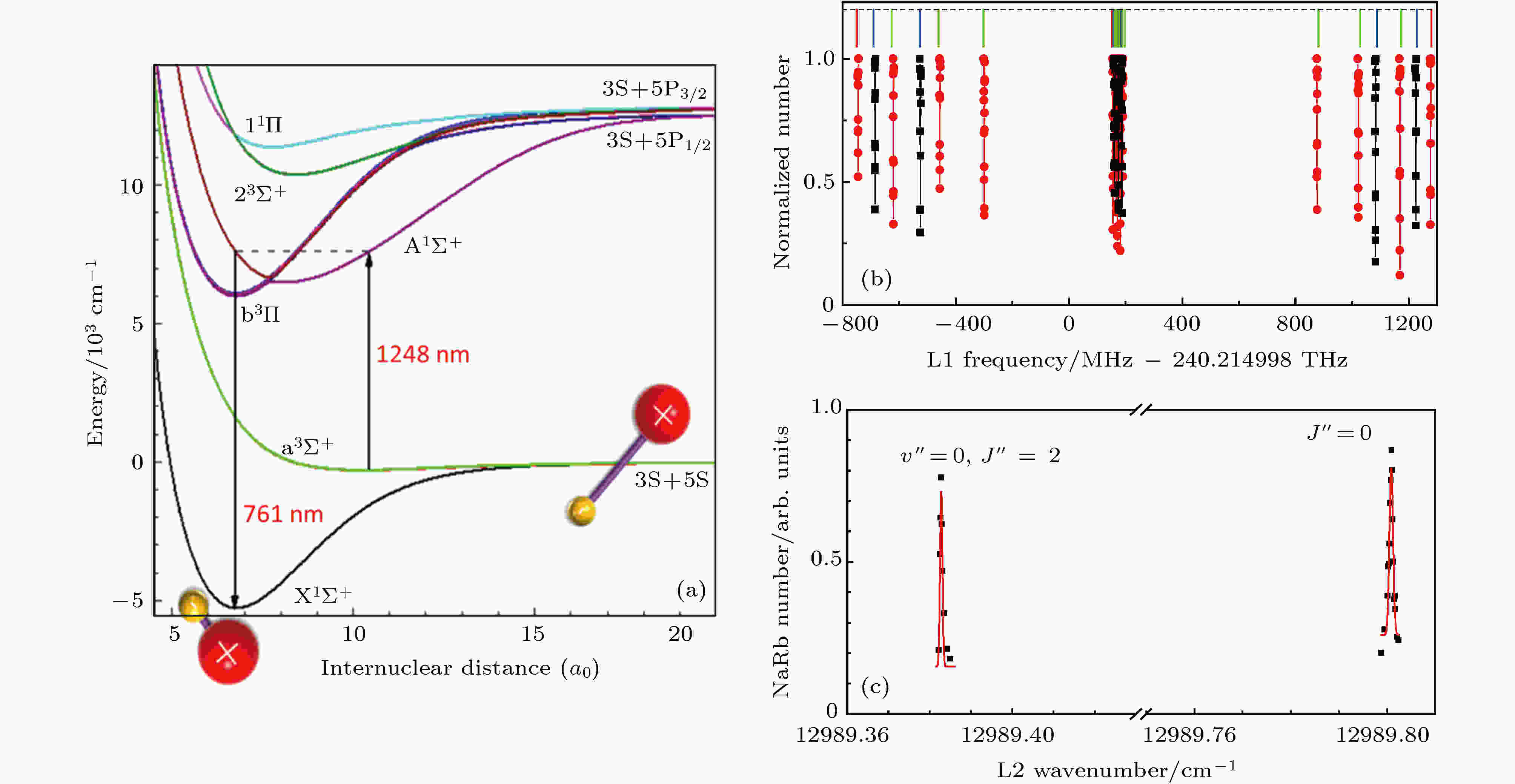图 7 (a) ²³Na⁸⁷Rb分子的相关势能曲线; (b)分子中间激发态的超高分辨谱; (c)基态转动能级; 其中${{{X}}^1}{\Sigma ^ + }$和${a^3}{\Sigma ^ + }$为电子的最低单重态和三重态, Feshbach分子处于这两个态的离解极限附近, 而振转基态则处于${{{X}}^1}{\Sigma ^ + }$态的底部; 作为受激拉曼转移中间态的能级为电子单重态${A^1}{\Sigma ^ + }$和三重态${b^3}\Pi$的混合态, 其超精细结构的劈裂可以被完全分辨
Figure7. (a) ²³Na⁸⁷Rb molecule potential energy curves and the two-photonRaman process forpopulation transfer, ${{{X}}^1}{\Sigma ^ + }$and ${a^3}{\Sigma ^ + }$are the lowest singlet and triplet state respectively; (b) high resolution one-photon spectrum of the transition from the Feshbach state to the intermediate level (singlet and triplet mixed vibrational levels of ${A^1}{\Sigma ^ + }$ and ${b^3}\Pi$), which hyperfine structure can be resolved; (c) two-photon spectroscopy of the ²³Na⁸⁷Rb vibrational ground state with two rotational states resolved.

考虑到分子初末态的一些性质, 中间态能级的选取需要满足以下条件: 1)基于Franck-Condon原理, 分子能级跃迁强度正比于上下能级振动波函数重叠的平方${\left| {\left\langle {\left| {v''{\rm{|}}v'} \right|} \right\rangle } \right|^2}$, 即Franck-Condon因子, 由于Feshbach分子的波函数$\left| v \right\rangle $分布范围很大, 而基态分子的波函数$\left| {v''} \right\rangle $只位于很窄的范围内, 中间态必须与它们都有足够的重叠才能在有限的激光功率下获得足够大的拉比频率; 2)由于实验中用的Feshbach分子具有较多的三重态${a^3}{\Sigma ^ + }$的成分, 而基态分子为纯的单重态${{\rm{X}}^1}{\Sigma ^ + }$, 中间态必须为单重态和三重态的混合态; 3)由于原子有核自旋, 每个振转能级还有更细小的超精细结构. 首先超精细结构间的跃迁有一定的选择定则, 其次超精细结构不可分辨时, 受激拉曼转移涉及多个能级, 对转移的效率会产生影响. 因此在选择中间态时, 最好是有一定的三重态成分, 使得超精细结构劈裂可以被充分分辨. 基于以上几个原则, 可以发现图7(a)中${A^1}{\Sigma ^ + }/{b^3}\Pi $势能曲线的底部, 或${2^3}{\Sigma ^ + }/{1^1}\Pi $势能曲线的顶端都可能找到符合条件的能级, 目前已有的实验也确实都是用这两种方案实现的^[54].
方案确定之后就需要进行分子光谱的研究以及找到具体的能级位置. 用超冷分子做光谱实验可以达到极高的分辨率, 包括所有跃迁定则允许的超精细结构(图7(b)), 这是之前的传统分子光谱学无法达到的. 但如果已经有一些其他方法获得的分子光谱数据和理论计算, 对加快这一十分耗时的步骤有很大帮助. 另外, 原则上可以从自由原子开始, 用光缔合技术研究激发态的光谱, 但Feshbach分子的束缚-束缚跃迁更强, 找到能级信号更快.
找到可能的中间态之后, 就可以利用Autler-Townes效应来确定振转基态的能级位置. 首先将耦合Feshbach分子和中间态的pump光(抽运光)保持共振, 这时应该看到Feshbach分子的损耗, 然后同时打开链接中间态和基态的dump光(倾泻光), 并扫描其频率. 当dump光与基态振动能级共振时, 如果其光强较大, 由于AC-Stark效应, 会导致激发态能级产生劈裂, 从而使pump光失谐. 在这种情况下, 基态能级的信号表现为Feshbach分子损耗的减少(图7(c)) .
2 -->

2.4.窄线宽激光器和受激拉曼转移

在超精细结构完全可分辨的情况下, 图7(a)所示的受激拉曼转移过程是一个标准的由$\left| i \right\rangle $, $\left| e \right\rangle $, $\left| g \right\rangle $构成的3能级体系. 假设激发态$\left| e \right\rangle $的自发辐射率为$\gamma $, 在两束光都为共振的情况下, 以$\left| i \right\rangle $, $\left| e \right\rangle $, $\left| g \right\rangle $为基矢, 系统的哈密顿量为

$H = \frac{\hbar }{2}\left[ {\begin{array}{*{20}{c}}0 & {{\Omega _{{\rm{pump}}}}\left( t \right)} & 0\\{{\Omega _{{\rm{pump}}}}\left( t \right)} & { - {\rm{i}}\gamma } & {{\Omega _{{\rm{dump}}}}\left( t \right)}\\0 & {{\Omega _{{\rm{dump}}}}\left( t \right)} & 0\end{array}} \right],$

其中${{\Omega _{{\rm{pump}}}}}$和${{\Omega _{{\rm{dump}}}}}$分别为pump跃迁和dump跃迁的拉比频率.
在超冷分子中实现态转移, 目前通用的技术为受激拉曼绝热通道(stimulated Raman adiabatic passage, STIRAP), 这种受激拉曼技术需要对${{\Omega _{{\rm{pump}}}}}$和${{\Omega _{{\rm{dump}}}}}$进行时间上的操控. 如图8(b)所示, 转移过程开始时, 先打开dump光, 之后在关断dump光的同时将pump光打开. 在此过程中, 分子总是处于系统的暗态,
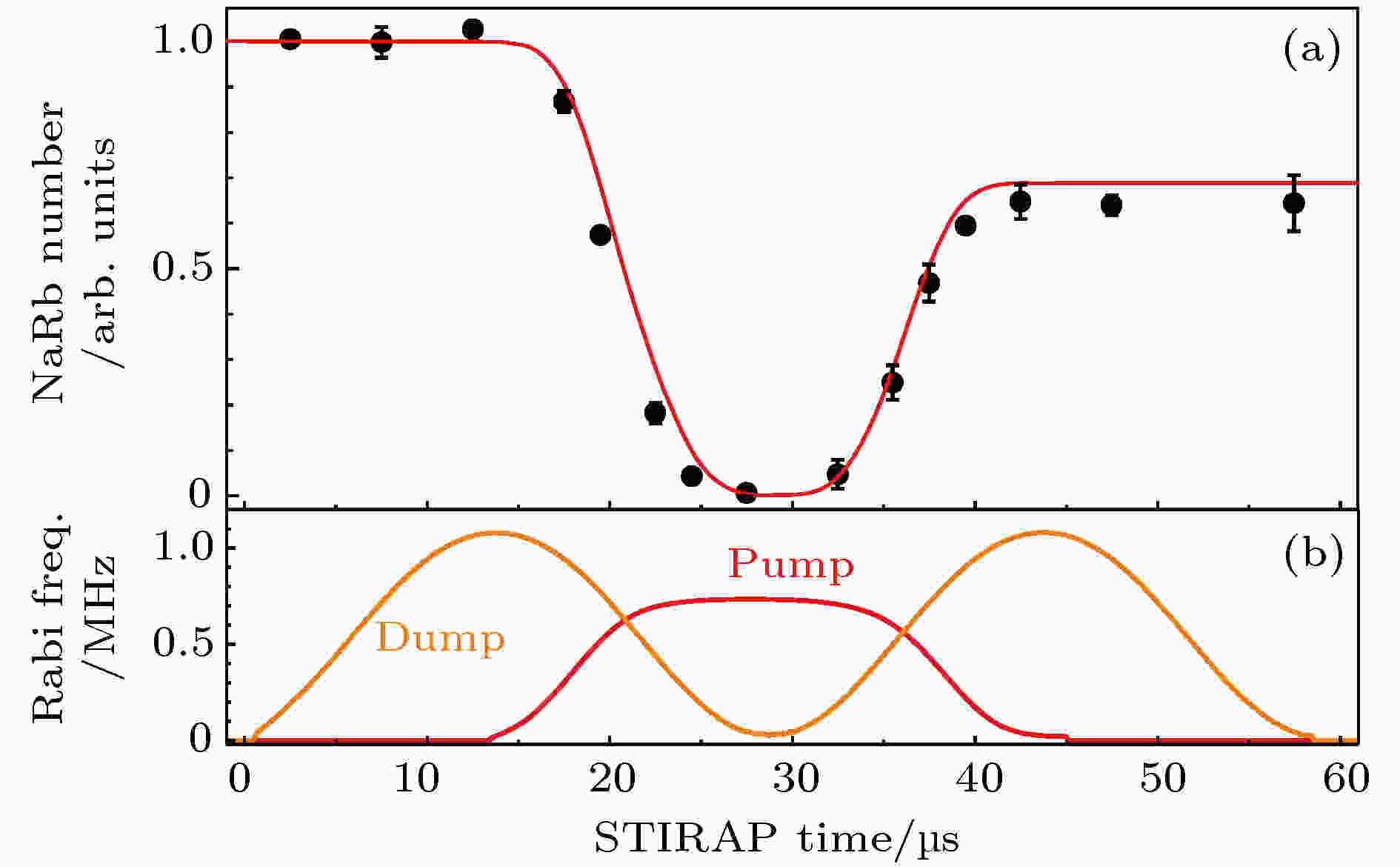图 8 利用STIRAP制备²³Na⁸⁷Rb基态分子 (a) STIRAP过程中Feshbach分子数目随时间的变化; (b)同一实验中pump和dump激光器的拉比频率随时间的变化; 为了探测基态分子, 需要一个逆过程将分子从基态转移回Feshbach 能级^[50]
Figure8. Creation of ²³Na⁸⁷Rb molecules in the rovibrational ground state via STIRAP: (a) Time evolution of the ²³Na⁸⁷Rb Feshbach molecule number during a round-trip STIRAP, the reversed STIRAP is necessary for detection; (b) the pump and dump beam Rabi frequency during the STIRAP pulse sequence^[50].

$\left| \phi \right\rangle = \cos \theta \left| i \right\rangle + \sin \theta \left| g \right\rangle ,$

其中$\theta = {\tan ^{ - 1}}\left( {\dfrac{{{\Omega _{{\rm{pump}}}}\left( t \right)}}{{{\Omega _{{\rm{dump}}}}\left( t \right)}}} \right)$. 可以看到, 在初始时分子处于Feshbach能级, 不与dump光直接作用, 在转移完成后, 分子处于基态, 不与pump光作用, 而且在整个过程中, 分子都不会处于中间态$\left| e \right\rangle $, 因而在理想情况下, 整个STIRAP过程都没有分子损耗, Feshbach分子可以被100%转移到振转基态.
为了实现高效率(接近100%)的分子转移, STIRAP过程必须满足绝热条件. 这需要双光子的有效拉比频率${\Omega _{{\rm{eff}}}} = \sqrt {\Omega _{{\rm{pump}}}^2 + \Omega _{{\rm{dump}}}^2} $和转移时间$\Delta \tau $的乘积满足${\Omega _{{\rm{eff}}}}\Delta \tau $ > 10的条件^[55]. 由于前面所讨论的Franck-Condon因子的关系, 在有限的激光功率下, $\Omega _{{\rm{pump}}}$和$\Omega _{{\rm{dump}}}$通常只能达到MHz量级, 因此要使用比较长的$\Delta \tau $才能满足绝热条件, 在目前的实验中用到的$\Delta \tau $一般为十到几十微秒.
由于$\Delta \tau $较长, 如果在转移过程中, 受激光噪声的影响, 两束激光的相对相位发生变化, 就会降低转移效率. 注意这里并不要求两束激光的相对相位完全锁定, 只要求在STIRAP过程中, 也就是在$\Delta \tau $这一时间内, 相对相位不发生抖动, 因此只要将两束激光的线宽都压窄到kHz左右就可以了. 利用Pound-Drever-Hall (PDH)技术将两束激光锁定到精细度为5000左右, 线宽为100 kHz左右的超稳光学腔上, 就可以满足这一要求^[56]. 在²³Na⁸⁷Rb实验中, 两束激光的波长分别为761 nm和1248 nm, 超稳光学腔为双色镀膜, 在每个波长附近的精细度都 > 20000, 最后获得的激光器线宽估计都在几百Hz^[57].
图8为利用STIRAP技术从Feshbach分子开始制备²³Na⁸⁷Rb基态分子的过程. 这里的实验探测手段为标准的吸收成像技术, 由于散射截面过小, 这一技术不能直接探测基态分子, 因此所有的信号都是通过探测Feshbach分子获得的. 如图8(a)所示, 初始时全部分子都处于Feshbach能级, 这时打开dump光对分子数没有影响, 但在dump光关断的同时打开pump光时, Feshbach分子数随之减少, 直到为零. 这是由于分子被转移到了基态, 不能被吸收成像探测到. 而之后再进行一个逆过程, 将分子从基态转移回Feshbach能级, 就可以看到分子数大部分恢复了. 一般可以假设两个过程的转换效率一样, 因此可以从初始的分子数N₀和恢复的分子数N估计出单次的转移效率和基态分子数分别为$\sqrt {N/{N_0}} $及$\sqrt {N \times {N_0}} $.
目前已知的几个实验中, STIRAP的单次转移效率都在90%以上^{[46-48, 50]}. 转换效率没有达到100%的原因可能是由于激光器的一些没有被压制的噪声, 例如在普遍采用的半导体激光器中, 增益介质的背景频谱很宽, 不能被反馈完全压制. 没有被转移到基态的10%左右的分子, 有可能是在转移过程中被激发到了中间态, 通过自发辐射, 这部分分子会分布到电子基态的很多振转能级. 实验上已经证实, 这一小部分分子对基态分子的动力学并不产生可观测的影响, 因此90%以上的转换效率, 已经完全可以接受.

当分子被转移到基态后, 就可以对其极化率、永久电偶极矩等基本参数进行测量, 也可以进行振动和超精细能级之间的操控.
2

-->

3.1.极化率

改变制备和探测这两个STIRAP过程中间的时间, 记录分子在光阱中的质心位置变化, 就可以测量基态分子在光阱中的振荡频率, 如图9所示. 再结合光阱的光强, 就可以计算出在光阱波长下基态分子的极化率^[58], 并与ab initio计算结果比较.
图 9 通过质心振荡运动测量基态²³Na⁸⁷Rb分子的囚禁频率
Figure9. Center-of-mass motion of the absolute ground-state molecules along the horizontal direction (X_c) and the vertical direction (Y_c) in the optical dipole trap.

2 -->

3.2.永久电偶极矩

另外一个非常重要的参数是基态分子的永久电偶极矩, 它可以通过测量基态分子在电场中的Stark效应来获得. 在²³Na⁸⁷Rb实验中, 电场是由一对加在真空玻璃腔外有ITO镀膜的导电玻璃平板电极提供的. 由于Feshbach分子的电偶极矩为零, 其能级不随电场变化, 基态分子的Stark频移就表现为pump和dump光频率差的变化. 图10所示为NaRb分子在电场中从0到1.5 kV/cm的Stark频移, 由拟合得到的永久电偶极矩为3.2(1) Debye. 另外也可以看到, 在1.5 kV/cm时, 有效电偶极矩已经达到了1.06 Debye .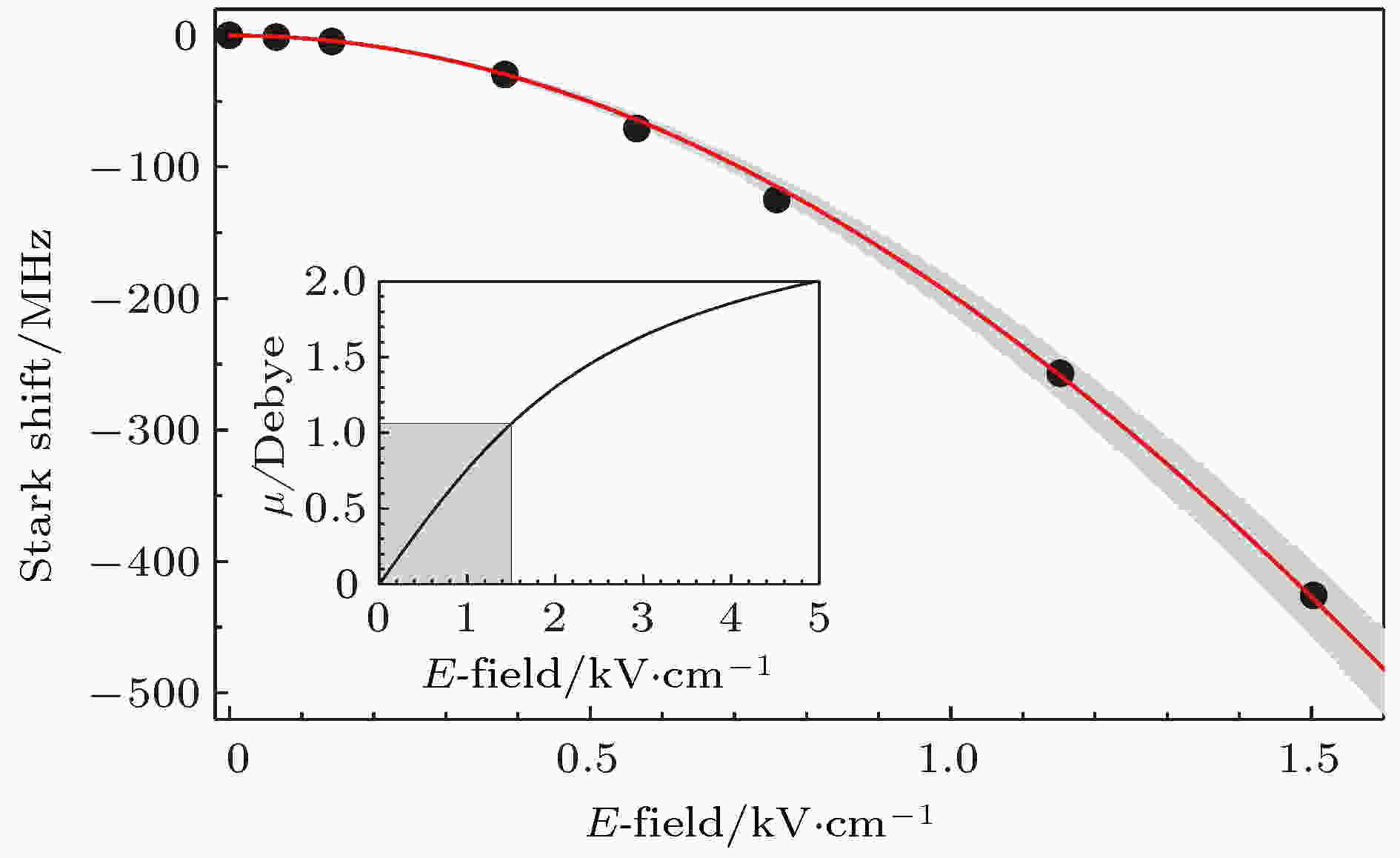
图 10 基态²³Na⁸⁷Rb分子在直流电场中的Stark频移. 红色曲线为对数据点的拟合. 插图为有效电偶极矩和电场的关系^[50]
Figure10. Stark shift of the rovibrational ground state ²³Na⁸⁷Rb molecule in electric field. The red curve is the fit to a model including contributions from several higher rotational levels. The inset shows the induced dipole moment vs the electric field with the currently accessible region marked by the shading area^[50].

2 -->

3.3.振动和超精细能级操控

由于${{{X}}^1}{\Sigma ^ + }$态的电子自旋和轨道角动量都为零, 基态分子的电子总角动量和磁偶极矩也为零, 但构成分子的两个原子都有核自旋, 在磁场中就会带来很小的核自旋的超精细能级劈裂. 例如在²³Na⁸⁷Rb分子中²³Na和⁸⁷Rb的核自旋分别为I_Na = 3/2及I_Rb = 3/2, 每个核自旋的磁量子数可以取从–3/2到3/2的值, 在磁场中的Zeeman能级共有(2I_Na + 1)(2I_Rb + 1) = 16个. 如图11(a)所示, 由于核自旋和磁场的作用很小, 在几百Gauss的磁场中, 所有能级的劈裂也只有几个MHz, 而相邻能级间的间距更小. 这种情况为制备单一量子态的基态分子带来了一定的困难, 虽然Feshbach分子是处于一个单量子态, 即全同的分子, 如果STIRAP过程的分辨率不够, 就有可能使制备的基态分子占据多个超精细能级, 即非全同的分子.
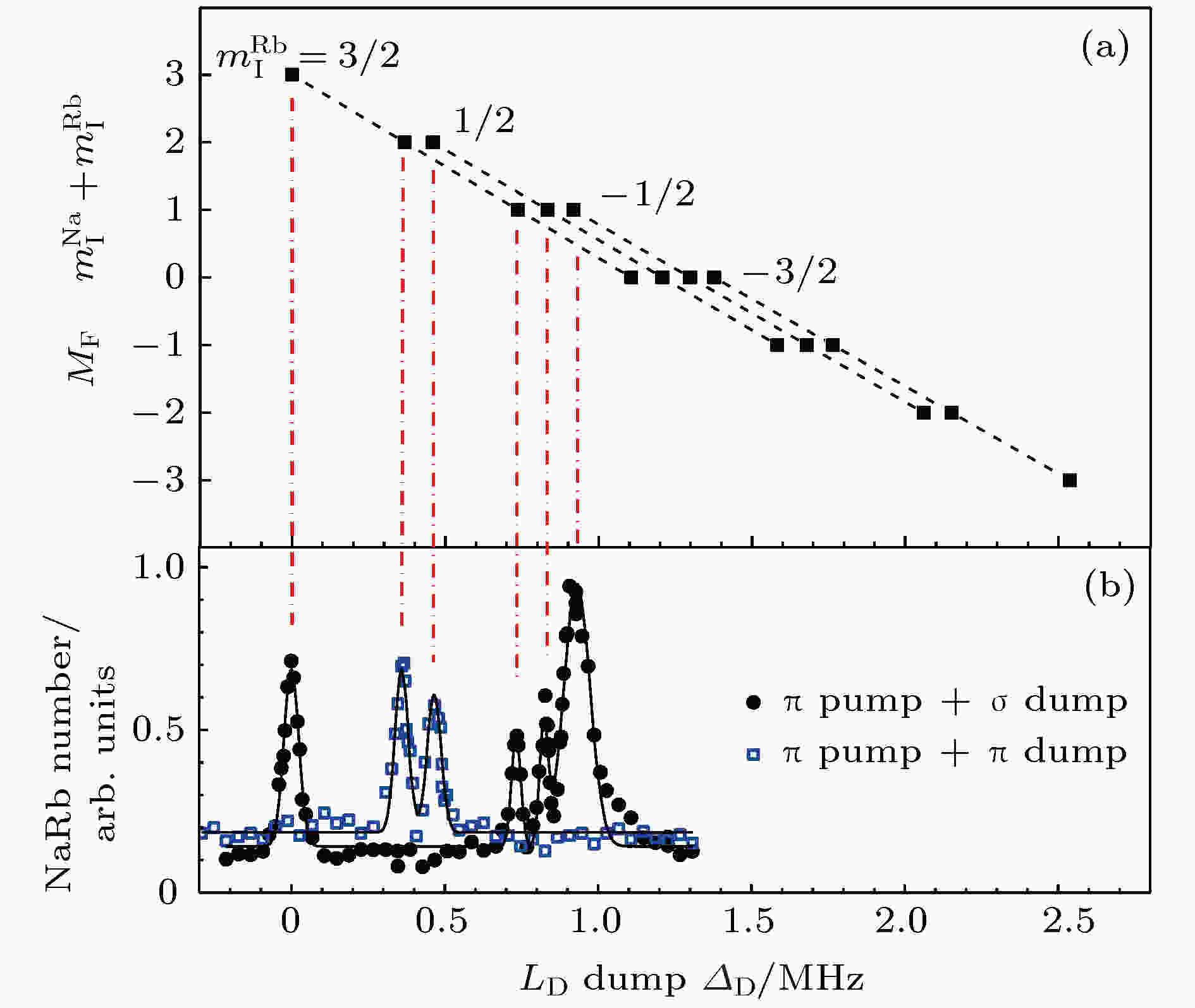图 11 (a) 基态²³Na⁸⁷Rb分子在340 Gauss磁场中的超精细结构, 其中$m_I^{{\rm{Na}}}$和$m_I^{{\rm{Rb}}}$分别为²³Na和⁸⁷Rb原子核自旋的磁量子数, 能量最低的超精细结构为$m_I^{{\rm{Na}}}$ = $m_I^{{\rm{Rb}}}$ = 3/2的态(最右端); (b) 利用仔细选择的STIRAP参数, 可以充分分辨跃迁允许的所有超精细结构, 从而实现处于单一超精细能级分子的制备^[50]
Figure11. (a) The calculated hyperfine Zeeman structures of the lowest rovibrational level of NaRb molecule at 340 Gauss, $m_I^{{\rm{Na}}}$ and $m_I^{{\rm{Rb}}}$ are nuclear spin projection of ²³Na and ⁸⁷Rb respectively; (b) two-photon spectrum obtained by dark resonance spectroscopy with six of the 16 hyperfine levels fully resolved^[50].

在²³Na⁸⁷Rb分子实验中, 由于使用的磁场较高, 再加上光偏振和跃迁选择定则的限制, 能量最低的超精细结构和相邻能级间的劈裂有几百kHz, 如图11(b)所示. 在两束拉曼激光的拉比频率都为1 MHz左右时, 实验中获得的双光子跃迁的半高宽为200 kHz, 足以分辨这些能级从而制备100%纯度的绝对基态分子(即处于最低电子、振动、转动、和超精细能级的分子).
在后续实验中, 经常需要制备处于转动激发态J = 1的分子或者J = 1和J = 0的叠加态. 在目前的几个实验中, 由于选择定则的限制, STIRAP过程不能直接制备J = 1的分子, 这一问题可以通过微波操控来解决. 对极性分子而言, 从J = 0到J = 1能级间的跃迁是由微波的电场和分子的永久电偶极矩直接作用来驱动的, 具有较高的跃迁强度, 因而用标准的微波器件就可以获得较大的拉比频率. 在²³Na⁸⁷Rb分子中, J = 0到J = 1的能量差为4.179 GHz, 对应的微波信号可以方便地用一个信号发生器和标准的微波天线获得.
微波的另外一个重要应用是操控分子的超精细结构. 一般而言, 由于核自旋与微波磁场的作用很微弱, 微波操控核自旋需要很大的微波功率. 但如图12所示, 由于电子四极矩作用以及核自旋和转动角动量的耦合, 使得不同的$\left| {J,{m_J},m_I^{{\rm{Na}}},m_I^{{\rm{Rb}}}} \right\rangle $态之间都有一定比例的混合, 因此通过操控转动能级, 也可以实现核自旋操控. 在实验中, 可以施加一个频率的微波信号将分子转移到J = 1态的不同m_J和${m_I^{{\rm{Na}}}}$, ${m_I^{{\rm{Rb}}}}$组合; 也可以增加另外一个频率, 利用微波的双光子跃迁实现J = 1的核自旋改变. 注意J = 1态的超精细结构比J = 0要复杂得多, 共有(2I_Na + 1)(2I_Rb + 1)(2J + 1) = 48个能级.
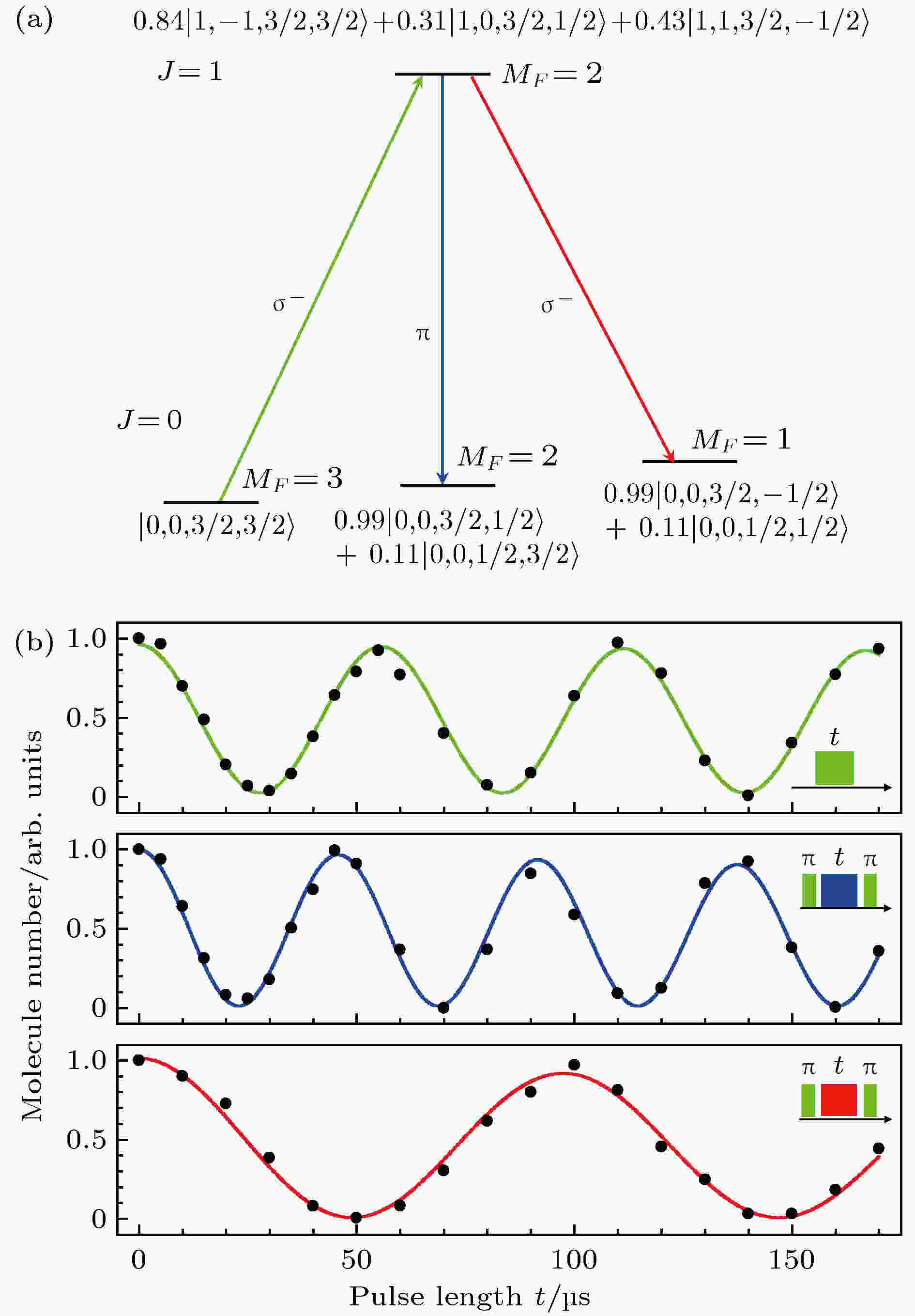图 12 (a) ²³Na⁸⁷Rb分子的J = 0和J = 1转动态具有不同核自旋态的成分; (b)利用单光子微波(上), 和双光子微波(中和下)操控, 可以实现对转动能级和核自旋的操控^[59]
Figure12. (a) ²³Na⁸⁷Rb molecule rotational states with J = 0, 1 consist of different nuclear spin components; (b) coherent manipulation with microwave pulses shows the observed Rabi oscillations for the three microwave transitions in (a)^[59].

2

-->

4.1.超冷基态分子的稳定性

如前所述, 超冷原子到Feshbach分子磁缔合的效率不高, 这就导致虽然初始原子混合物的相空间密度很高, 甚至是两团气体都为量子简并, 由此产生的Feshbach分子和基态分子的相空间密度还是远低于量子简并. 因此, 为了获得量子简并的超冷极性分子, 需要进一步降低温度和增加密度, 这些要求只能通过分子的蒸发冷却来实现.
蒸发冷却需要通过分子间的两体碰撞来进行. 与原子的情况类似, 分子的碰撞也可分为好的弹性碰撞和坏的非弹性碰撞, 只有弹性碰撞才可能在损耗粒子数目的同时增加相空间密度, 而非弹性碰撞在损耗粒子数目的同时有加热效应 (anti-evaporation effect), 因此并不能引起相空间密度的增加. 一般而言, 在超冷气体中, 弹性和非弹性碰撞总是同时存在, 但只要弹性碰撞对非弹性碰撞的比值足够大, 高效率的蒸发冷却就可以进行.
基于这样的认识, 在超冷分子实验的早期, 研究者们就已经认识到分子必须被制备到绝对基态才可能避免由于激发态弛豫引起的非弹性损耗, 可能的过程包括激发态振动、转动能级的弛豫以及超精细能级弛豫. 绝对基态的分子没有这些可能的损耗通道, 但2008年超冷基态极性分子第一次在JILA的⁴⁰K⁸⁷Rb实验中被成功制备后, 还是发现有很大的损耗. 随后的研究表明, 虽然对每一个分子来说, 绝对基态是其能量的最低点, 两个分子却可能发生化学反应.
两个相同的分子AB碰撞后, 从组合来说, 可能发生的过程有以下几种(图13):
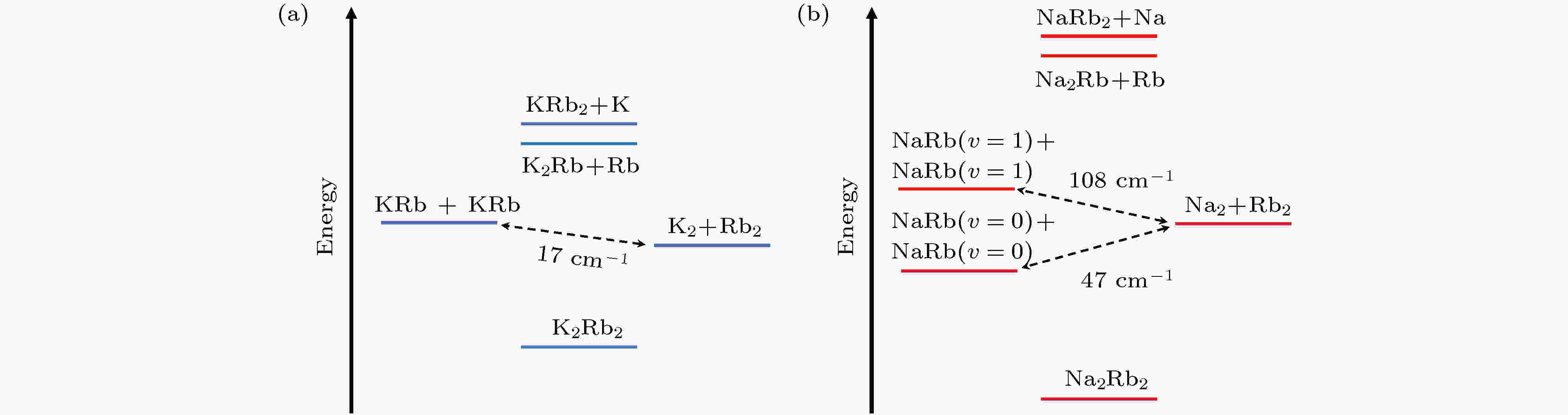图 13 (a) ⁴⁰K⁸⁷Rb分子和(b) ²³Na⁸⁷Rb分子体系两体反应的相关能级示意图, 两个基态⁴⁰K⁸⁷Rb分子间可以发生(6c)式中的化学反应, 两个基态²³Na⁸⁷Rb分子是化学稳定的, 将²³Na⁸⁷Rb分子制备到振动激发态, 可以允许化学反应发生
Figure13. Schematic energy-level diagram for chemical reactivity of (a) ⁴⁰K⁸⁷Rb molecules and (b) ²³Na⁸⁷Rb molecules. The schematic reaction coordinates for the ⁴⁰K⁸⁷Rb + ⁴⁰K⁸⁷Rb → ⁴⁰K₂ + ⁸⁷Rb₂ process is exothermic and thus allowed. But the same process is endothermic for ²³Na⁸⁷Rb and thus forbidden. For ²³Na⁸⁷Rb in the first excited rovibrational level (v = 1, J = 0), the same reaction is already exothermic and thus allowed.

$ \left\{ {\begin{aligned} & {AB + AB \to {A_2}{B_2}} & {\left( {6{\rm{a}}} \right)}\\ &{AB \!+\! AB \to {A_2}B \!+\! B{\rm {~or~} }AB \!+\! AB \to A{B_2} \!+\! A} & {\left( {6{\rm{b}}} \right)}\\ & {AB + AB \to {A_2} + {B_2}} & {\left( {6{\rm{c}}} \right)} \end{aligned}} \right. $

其中(6a)式的过程, 两个双原子分子AB碰撞直接形成一个四原子分子A₂B₂, 由于不能同时满足动量和能量守恒而不可能发生; 而(6b)式中的两个过程, 由于在碱金属体系两种三原子分子A₂B和AB₂的基态能量都远高于两个AB分子的碰撞阈值, 在超冷气体对应的超低碰撞能量下也不可能发生; 而两个AB分子碰撞形成两个同核分子A₂和B₂是否可以发生则取决于(6c)式两端的能量差, 即只有当两个AB分子的总结合能小于A₂和B₂两个分子的结合能之和时化学反应才可以发生.
超冷实验常用的5种碱金属原子⁶Li, ²³Na, ⁴⁰K, ⁸⁷Rb, ¹³³Cs, 可以两两组合出10种异核双原子体系. 经过比较它们和5种同核分子的基态结合能, 可以发现化学反应(6c)式可以在⁴⁰K⁸⁷Rb分子间发生^[60-62], 而不能在v = 0态的²³Na⁸⁷Rb分子间发生.
2 -->

4.2.费米⁴⁰K⁸⁷Rb分子间的化学反应

如图13(a)所示, ⁴⁰K⁸⁷Rb + ⁴⁰K⁸⁷Rb的结合能比⁴⁰K₂ + ⁸⁷Rb₂要小约17 cm^–1, 即两个基态⁴⁰K⁸⁷Rb分子碰撞的阈值比基态⁴⁰K₂ + ⁸⁷Rb₂的能量高约17 cm^–1, ⁴⁰K⁸⁷Rb (v = 0) + ⁴⁰K⁸⁷Rb (v = 0) → ⁴⁰K₂ (v = 0) + ⁸⁷Rb₂(v = 0)为放热反应, 可以发生.
在⁴⁰K⁸⁷Rb分子的碰撞实验中, 如图14(a)所示, 观察到基态分子在光阱中的密度n随囚禁时间损耗很快, 而且损耗曲线与两体碰撞速率方程
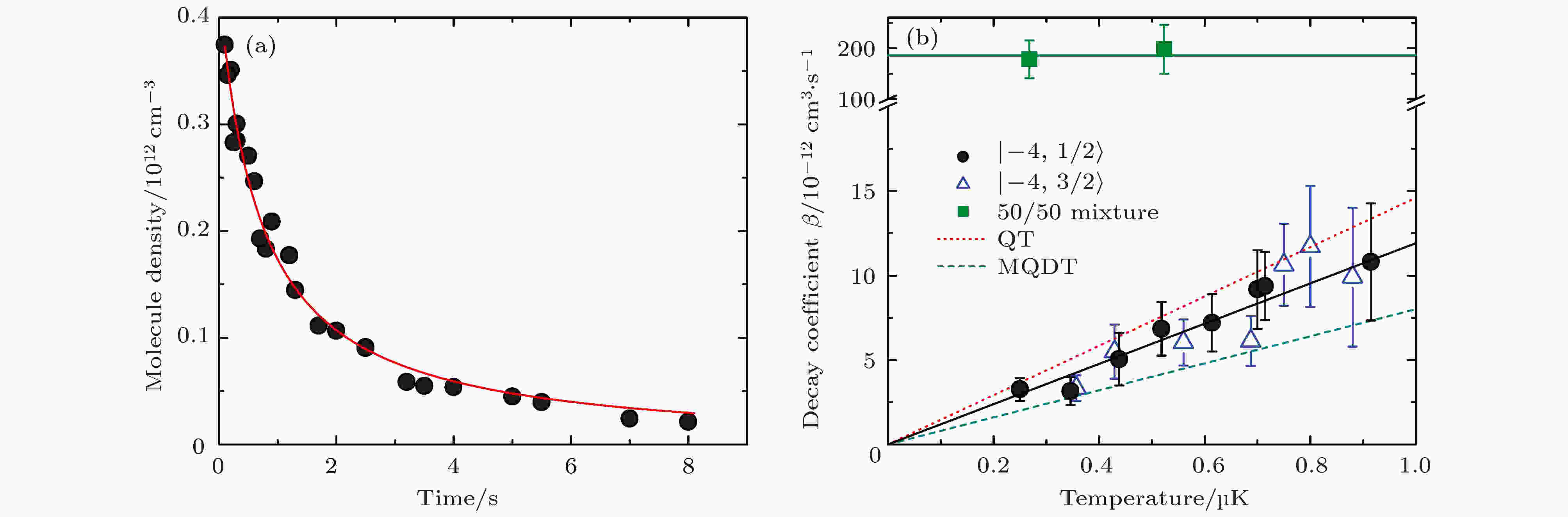图 14 基态费米⁴⁰K⁸⁷Rb分子的碰撞研究 (a) 分子密度随时间的变化, 红色曲线为用(7)式做的两体损耗拟合, 从中可以提取出损耗速率常数$\beta$; (b) 几种不同情况下样品温度对$\beta$的影响^[63]
Figure14. Inelastic collisions of fermionic ⁴⁰K⁸⁷Rb molecules in the rovibronic ground state: (a) Sample data shows the time dependence of the molecule number density, the solid line is the fit based on a two-body decay model; (b) loss rate coefficient versus temperature^[63].

$\dot n = - \beta {n^2}$

拟合得很好. (7)式中$\beta$为损耗速率常数, 其单位为cm³·s^–1. 图14(b)所示为从不同温度样品损耗曲线中得到的$\beta$值. 可以看到, 当样品中为全同分子时, 不管是在超精细能级的基态$\left|J = 0,{m_J} = 0,\right.$$\left. m_I^{\rm{K}} = - 4,m_I^{{\rm{Rb}}} = 1/2\right\rangle $还是在非基态$\left| {0,0, - 4,3/2} \right\rangle $, 在相同温度样品中测得的$\beta$值都基本相同, 而且随温度的增加呈线性上升. 而当分子样品为这两个态50/50的混合物时, $\beta$则大很多, 而且不随温度的变化而改变.
这些现象可以用超冷化学反应的普适模型(universal model)来解释. 由于化学反应涉及反应物分子键的断裂和生成物新分子键的形成, 只能在分子间的距离很短时才能发生, 而分子的碰撞是从长程开始的. 因此, 如图15所示, 一般可将分子的相互作用分为长程和短程区, 分界为两个分子的长程相互作用决定的特征长度, 即范德瓦耳斯长度. 在普适模型中, 当能量允许时, 分子在短程区发生化学反应的概率接近100%, 因此化学反应的速率是由分子从长程到达短程的速率决定的.
图 15 超冷化学反应的普适模型 (a) 全同费米分子通过p-波散射, 在长程有一个角动量引起的势垒; (b)非全同分子或全同玻色分子可以通过s-波散射, 没有长程势垒
Figure15. Universal model of the ultracold molecule reactivity: (a) Identical fermionic molecules react via p-wave scattering and the rate of chemical reactions is determined by the p-wave angular momentum barrier; (b) non-identical fermionic molecules and identical bosonic molecules react via s-wave scattering.

在没有外加电场的情况下, 分子还是通过范德瓦耳斯力作用, 因此在长程区, 两个距离为r的分子间的相互作用可以表示为

$V\left( r \right) = - \frac{{{C_6}}}{{{r^6}}} + \frac{{{\hbar ^2}l\left( {l + 1} \right)}}{{2m{r^2}}},$

其中第一项为范德瓦耳斯相互作用; 第二项为两个分子间的相对运动角动量, 即散射分波引起的离心势, 只有在l ≠ 0, 即非s-分波时才不为零; 式中C₆为分子间的长程色散常数, m为两个分子的约化质量.
由于JILA的研究组实验中所用的⁴⁰K⁸⁷Rb分子为费米子, 当分子全部在同一量子态时, 它们之间的超冷碰撞只能通过l = 1的p-分波进行, 因此如图15(a)所示, 在长程会产生一个势垒. 这种情况下, 反应速率由分子对从长程隧穿到短程的速率决定^[64]. 当分子不在同一量子态时, 分子也可以通过s-分波进行碰撞, 这种情况下, 没有长程的势垒, 这时反应速率由分子到达范德瓦耳斯长度的速率决定.
从图15(a)可以看到, 当分子为全同粒子时, p-分波势垒可以一定程度上压制化学反应的速率. 在非全同粒子中, 由于可以通过s-分波散射, 没有长程势垒, 因此化学反应要快得多. 其中$\beta$值随温度的变化也和Wigner阈值定量的结果$\beta \propto {T^l}$相符, 在有s-波通道时, l = 0, 因此$\beta$为常数; 在p-波散射时, l = 1, 因此$\beta \propto T$. 图14(b)中的几条直线展示的是基于这个普适模型^{[65, 66]} 计算的理论结果, 可以看到和实验的结果基本是符合的.
2 -->

4.3.玻色²³Na⁸⁷Rb分子的碰撞

如图13(b)所示, 处于v = 0态的²³Na⁸⁷Rb +²³Na⁸⁷Rb的结合能比²³Na₂+⁸⁷Rb₂要大47 cm^–1, ²³Na⁸⁷Rb (v = 0) + ²³Na⁸⁷Rb (v = 0) → ²³Na₂ (v = 0) + ⁸⁷Rb₂(v = 0)为吸热反应, 在超冷分子间由于碰撞能量太低而不可能发生^[67]. 但如图16(a)所示, 即便在这种情况下, ²³Na⁸⁷Rb分子在光阱中的损耗仍很快, 如果用两体碰撞来进行拟合, 得到的损耗速率常数$\beta$在10^–10 cm³·s^–1量级, 与s-波有化学反应时接近.
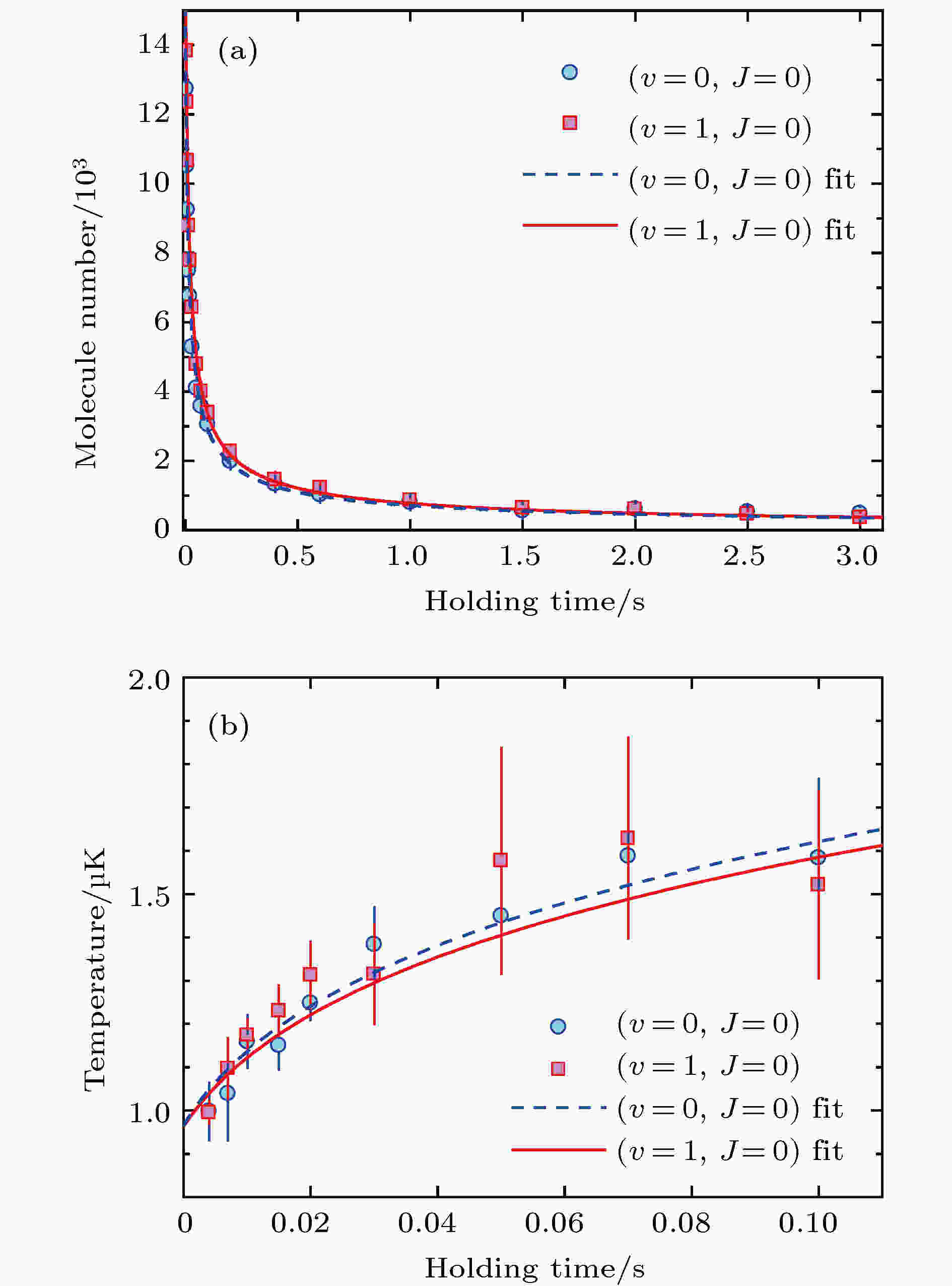图 16 化学稳定(v = 0, J = 0)和有化学反应(v = 1, J = 0)的²³Na⁸⁷Rb分子在光阱中的损耗(a)和加热(b), 图中的曲线由通过对分子数目和温度同时拟合获得^[68]
Figure16. Inelastic collisions with different chemical reactivities of ²³Na⁸⁷Rb molecules. Time evolutions of (a) molecule numbers and (b) temperatures for both nonreactive (v = 0, J = 0)(filled circles) and reactive (v = 1, J = 0) (filled squares) samples in optical dipole trap. The blue dashed and redsolid curves are fitting resultsofmolecule number and temperature using Eq. (9)^[68].

需要注意的是, 在分子损耗的测量中, 可以观察到比较明显的加热效应. 这是由于分子样品大致呈高斯分布, 中心的密度较高, 而碰撞损耗的速率和密度成正比, 因此损耗易于在分子样品的中心发生. 在样品中, 中心部分的分子的能量也是最低的, 当这一部分分子被从光阱中移除后, 剩余分子的平均能量就会上升, 导致加热现象. 这一过程和蒸发冷却正好相反, 因此也被称作反蒸发效应, 这种效应在所有的非弹性散射过程中都是存在的.
由于温度的增加会导致样品体积增大, 密度减小, 因此反蒸发效应对碰撞速率测量的影响不能忽略. 经过简单的推导, 可以得到以下两个耦合的速率方程来描述分子数目N和温度T随时间的演化^[69-71]:

$\begin{split}& \frac{{{\rm{d}}N\left( t \right)}}{{{\rm{d}}t}} = - \beta A\frac{{N{{\left( t \right)}^2}}}{{T{{\left( t \right)}^{\frac{3}{2}}}}}\\& \frac{{{\rm{d}}T\left( t \right)}}{{{\rm{d}}t}} = \frac{{\beta AN\left( t \right)}}{4}\frac{1}{{T{{\left( t \right)}^{1/2}}}},\end{split}$

其中$A = {\left( {m\bar \omega /4{\text{π}}{k_{\rm{B}}}} \right)^{3/2}}$为一个常数, 通过A和T可以确定样品的体积, $\bar \omega $为分子在光阱中沿三个方向振荡频率的几何平均. 图16中的曲线就是用(9)式同时对N和T随时间的演化拟合得到的.
为了验证有无化学反应情况下²³Na⁸⁷Rb分子的损耗是否有区别, 利用²³Na⁸⁷Rb分子的化学反应活性可以操控的特性, 来打开化学反应通道. 例如, 如图13(b)所示, 当²³Na⁸⁷Rb分子被制备到v = 1时, ²³Na⁸⁷Rb + ²³Na⁸⁷Rb的结合能比²³Na₂ + ⁸⁷Rb₂要小108 cm^–1, 因此²³Na⁸⁷Rb (v = 1) + ²³Na⁸⁷Rb (v = 1) → ²³Na₂ (v = 0) + ⁸⁷Rb₂(v = 0)为放热反应, 可以发生^[72-74]. 在实验中, 制备v = 1态的²³Na⁸⁷Rb分子可以比较容易地通过调节dump光的频率来实现.
图16中比较了两种化学反应活性不同的²³Na⁸⁷Rb分子样品的数目和温度随时间的演化. 让人惊讶的是, 这样两种非常不同的情况下, 分子的损耗和加热几乎看不到区别. 图17是由损耗测量得到的$\beta$和样品温度的关系, 从中可以看到两种情况下, $\beta$都随温度的增加而减小, 这和图14(b)中混合态⁴⁰K⁸⁷Rb分子间的s-波碰撞很不一样.
图 17 化学稳定(v = 0)和有化学反应(v = 1)的²³Na⁸⁷Rb分子在光阱中的损耗速率常数$\beta$与温度的关系, 图中的理论曲线为基于普适模型计算的结果. 在化学稳定的情况下, 可能的损耗通道为形成四体复合物(four-body complex)^[68]
Figure17. Temperature dependence of $\beta$ for chemical stable (v = 0) and chemical reactivity state (v = 1) of ²³Na⁸⁷Rb molecules. Theoretical curve based on the CC calculation are also shown. Four-atom collision complex formation is one of the possible mechanism of molecule loss for non-reactive molecules^[68].

在超冷温度下, 一般认为粒子的散射应该在Wigner区, 即$\beta \propto {T^l}$, 对s-波, l = 0, 因而$\beta$应该是常数. 在14(b)中, 随温度的变化, ⁴⁰K⁸⁷Rb分子的s-波损耗速率基本保持不变, 这是和Wigner区散射符合的, 而图17的结果表明²³Na⁸⁷Rb分子的碰撞不在Wigner区. 这种区别是由于基态极性分子间的长程作用常数C₆主要是由分子的转动能级跃迁决定的, 其关系为${C_6} \propto \dfrac{{\mu _0^4}}{{{B_v}}}$, 其中B_v为转动能级常数. 由于²³Na⁸⁷Rb分子的永久电偶极矩$\mu _0$比⁴⁰K⁸⁷Rb分子大很多, 导致²³Na⁸⁷Rb分子间的C₆比⁴⁰K⁸⁷Rb大一个数量级. 相应地, ²³Na⁸⁷Rb分子之间散射的特征长度(范德瓦耳斯长度)${r_6} =$$ {\left( {\dfrac{{m{C_6}}}{{{\hbar ^2}}}} \right)^{\frac{1}{4}}}$达到720a₀, 而特征能量${E_6} = \dfrac{{{\hbar ^2}}}{{mr_6^2}}$只有3 ${\text{μK}}$, 由于E₆和温度差不多, 不能满足Wigner区散射的条件, 因此才会看到图17中的结果.
图17的结果还表明, 没有化学反应的分子间的碰撞损耗与温度的关系和有化学反应的情况确实很接近. 在相关的另外一些实验中, 如奥地利Innsbruck和英国Durham研究组的⁸⁷Rb¹³³Cs实验中, 以及MIT的²³Na⁴⁰K实验中, 都观察到没有化学反应的超冷极性分子中有类似的损耗. 这就引出了一个问题, 即在没有化学反应的情况下, 处于绝对基态的分子的损耗通道是什么？目前, 由于对四原子分子势能曲面的精确计算还很困难, 因此对于这一问题还没有确定的答案.
对于这一问题, 现阶段最流行的解释是损耗是由形成四体复合物(four-body complex)引起的^[69,75]. 双原子分子的碰撞在短程涉及到四个原子, 由于系统的自由度较多, 描述它们之间的相互作用需要用到多维的势能曲面, 而且由于体系的质量较大, 势能曲面中的能态数目很大, 一般不能像双原子分子那样精确计算, 只能用态密度(density of states)描述. 在双原子分子的碰撞中, 两个分子由长程逐渐接近时, 可能会与很多个这些短程四体态共振, 在这种情况下, 两个分子会有很大的概率停留在一起, 形成一个不稳定的四体结构, 即四体复合物. 由于超冷分子实验的探测对四体复合物不敏感, 它们的形成就表现为分子的损耗. 图17中v = 0分子损耗的理论曲线, 就是基于这个模型, 可以看出, 理论上这个模型确实和化学反应是一样的.
目前的实验数据和这一模型是符合的, 但实验中并没有直接探测到四体复合物的任何信号, 这主要是由于一般超冷实验中探测手段的限制. 为了更好地回答化学稳定的超冷分子的损耗问题, 需要探测分子碰撞后的直接产物^[76-78], 目前还没有任何实验装置具备这种能力. 最近, Harvard大学Ni研究组^[79,80]利用光镊技术成功地形成了单个分子, 如果这一实验可以扩展到两个分子, 并能在单分子水平测量分子间的碰撞, 也可能为解决这一问题提供很好的答案.

超冷极性分子的制备是一项很有挑战性的工作, 经过将近20年的努力, 近几年终于取得了很多突破. 目前, 利用超冷原子缔合技术, 几种碱金属双原子分子, 包括费米分子⁴⁰K⁸⁷Rb^[26,45]和²³Na⁴⁰K^[48,49], 以及玻色分子⁸⁷Rb¹³³Cs^{[46, 47, 51]}和²³Na⁸⁷Rb^[50], 都已经被成功地制备和研究; 而其他如²³Na¹³³Cs^[79]和⁶Li⁴⁰K^[81]等的制备也都进展很快. 而基态分子的直接冷却, 特别是激光冷却, 最近两年取得的进展十分令人瞩目, 随着一些技术问题的解决, 相信由这种方法获得的分子很快可以进行蒸发冷却, 以达到 < 1 ${\text{μK}}$的超冷温度. 分子激光冷却这一技术可以应用于很多的分子, 如2017年, Harvard大学的研究组已经成功展示了对多原子分子的激光冷却^[82]. 可以预见, 分子直接激光冷却必将大大丰富超冷极性分子的研究内容.
本文对超冷分子的讨论主要着眼于研究超冷分子在长程作用下多体物理体系中的应用, 因而需要分子样品达到量子简并. 虽然JILA的研究组已经获得了KRb分子的简并样品^[26], 但分子间的化学反应依然存在, 类似的方法是否可以应用到其他分子体系还需要进一步的研究. 目前看来, 分子间相互作用的复杂程度远远超出了最初的想象, 特别是化学稳定分子样品的损耗问题, 使得进一步的分子的蒸发冷却变得很困难, 因此下一步的研究重点应该是揭示损耗的微观机理^[83]. 特别需要指出的是, 这些损耗机理的研究和化学反应的机理是有深刻联系的. 在超冷温度下, 由于分子的碰撞只能通过一个或少数几个分波进行, 化学反应的量子特性可以得到充分的体现, 因而这种极端条件下分子损耗机理的研究自身也是非常有价值的. 按照复合物形成模型, 超冷分子的损耗问题有可能是不可避免的, 为了获得长寿命的样品, 可以利用一些方法对损耗进行压制. 其中最直接的方法是把分子装载到三维光晶格中, 利用晶格势将分子隔绝开, 使得短程的碰撞不能发生. 这种方法已经在⁴⁰K⁸⁷Rb分子上得到了验证^[84-86].
不同温度的极性分子在其他方面的应用也同等重要, 一个最重要的例子就是利用极性冷分子进行电子电偶极矩(eEDM)的测量. 非零的eEDM必然违反时间反演对称性(T-violation), 从而导致违反电荷共轭和宇称对称性(CP-violation), 也就预示着标准模型之外还有新的物理内容. 由于eEDM非常小, 要利用光谱技术测量它就需要很大的电场以增强灵敏度, 而极化的极性分子的内部电场可以达到几十个GV/cm, 因而非常适合用来寻找eEDM. 在Harvard大学和Yale大学合作的ACME项目中, 利用缓冲气体冷却技术得到的ThO分子束, 已经可以界定eEDM小于1.1 × 10^–29 e·cm^[87]. 目前, 已经有理论工作指出^[88], 利用温度更低的分子, 例如激光冷却的分子, 可以进一步界定eEDM的值, 从而验证是否有超越标准模型的新物理内容.
总之, 超冷分子还是一个较新的研究方向, 随着分子冷却技术的成熟, 可用的、适合研究不同物理内容的超冷分子样品会越来越多. 虽然目前已经利用极性分子做了一些非常重要的工作, 但也只是超冷分子潜力的很小一部分, 因此这一方向未来还是大有可为的.