删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于XFEM-MBEM的嵌入式离散裂缝模型流固耦合数值模拟方法

本站小编 Free考研考试/2022-01-01


引 言


非常规裂缝性储层中, 岩石基质提供油气储存空间, 人工裂缝、诱导裂缝和天然裂缝提供其流动通道[1]. 目前油田实际历史数据已表明, 地质力学特性对裂缝性油藏的产量起重要作用, 会导致一些关键渗流参数发生改变, 如基岩的孔隙度和渗透率; 此外, 致密油藏以“缝控储量”为主[2], 岩石形变会引起裂缝开度变化, 这对于压裂水平井产能评价的影响极大. 传统的应力敏感模型无法揭示深层次的科学道理[3-4], 为了准确模拟此类裂缝性多孔介质中的裂缝动态行为和流体流动机理, 需要综合考虑流体和岩石两方面的力学性质.

岩石力学中有效应力的概念最早由Terzaghi[5]和Biot[6]提出, 并由Biot[7]发展为较完善的三维固结理论, 这是研究应力场与渗流场耦合的早期基础. 为了将上述的理论基础应用于传统的渗流模型, Barenblatt和Zheltov[8]首次提出了双重孔隙度/双重渗透率的概念, 基岩与裂缝为两种重叠的、不同的连续介质, 其中基岩完全被裂缝所围绕, 用于表征裂缝性多孔介质中的流体和岩石形变. 后续, Bai[9]提出了关于双重介质更为严格的物理解释即双孔有效应力理论, 用于分析不同尺度的裂缝和基质的形变. 针对多孔介质流固耦合数学模型的建立, Wilson和Aifantis[10]、Beskos和Aifantis[11]和Khaled等[12]建立了基于有限元法的双重介质流固耦合模型, 该模型的主要问题在于其忽视了基质与裂缝之间压差导致的耦合流动作用; Lewis和Schrefler[13]对于油藏中的流固耦合问题进行了研究, 分别考虑了单相流、多相流、线弹性变形以及弹塑性变形, 并给出了相应的有限元计算格式. 在上述早期的研究中, 采用连续介质力学理论表征裂缝性油藏, 将不连续的裂缝系统粗化为连续介质, 能在一定程度上刻画基岩和裂缝的流体流动及力学特征, 但对于裂缝的几何形状及传导率具有较强的约束, 更适用于描述小尺度裂缝, 对于大尺度裂缝处理精度较低, 无法满足以体积压裂为开发手段的非常规油气藏的矿场实际需求.

近年来, 基于离散裂缝的流固耦合理论受到了广泛关注, 此类模型将裂缝离散化显式表征, 能准确刻画大尺度裂缝对渗流场和应力场的影响, 根据前处理算法的不同, 可划分为离散裂缝模型[14] (DFM) 与嵌入式离散裂缝模型[15-16] (EDFM), 其中嵌入式裂缝模型最早由Li和Lee[17]开发, 旨在提高天然裂缝建模的精确程度. 与使用复杂非结构网格在空间上匹配裂缝几何结构的DFM方法相比, EDFM只需使用一组固定的结构化矩形网格, 裂缝在前处理中与网格分开并显式精确刻画, 这是EDFM相对于DFM的关键优势[18]. 流固耦合研究方面, 由于裂缝开度与油藏尺度存在极大差异, 需对裂缝进行降维处理避免裂缝周围局部加密以减小网格量, 而降维后裂缝两侧的位移场存在间断性[19]. 由于EDFM采用非匹配性网格, 使得其在表征裂缝力学间断效应方面极具挑战性. 目前主要处理方法有: 有限元法、位移不连续法和扩展有限元法[20] (XFEM). 其中, XFEM与EDFM具有相似的优点, 两者均基于结构化网格, 分别相较于传统的基于有限元法的应力场、渗流场计算, 避免了网格重构和非结构化网格剖分带来的困难. 基于此, Ren等[21-22]、Yan等[23]、Zeng等[24]先后实现了将EDFM与用于应力场计算的扩展有限元法的耦合研究; Ren等[25]进一步开发了pEDFM-XFEM流固耦合数值模拟器, 能更精确地模拟多相流情况下的岩石和流体的力学性质.

在上述前人的研究中, 仍亟待解决的主要问题有两点: 致密基质的渗透率极低, 大规模体积压裂之后储层中的大尺度水力压裂缝与大量被激活的、小尺度的天然裂缝共存, 对此类“人工裂缝性油藏”, 单一数学模型无法进行准确表征, 需要更一步发展综合数学模型; 目前现有数值模拟方法在计算包含裂缝单元的基质网格内的压力分布时, 采用了线性分布假设, 这导致了早期及非稳态流动计算精度的不足. 本文以上述突出的科学问题为导向, 建立了致密油藏基质-天然裂缝-水力压裂缝综合数学模型, 基于单孔模型表征基质渗流参数随着压力、应变场的改变, 基于双重介质模型表征天然裂缝渗流参数的变化, 基于嵌入式离散裂缝模型表征水力压裂缝的动态特征; 并提出了XFEM-MBEM的混合数值离散化方法, 用于计算基岩和裂缝间的非稳态窜流, 提高了模拟的早期精度, 可准确表征致密油藏开采过程中的裂缝变形及流体流动机理, 此研究为致密油气开发领域提供了理论基础.


1.
流固耦合数学模型



1.1
物理模型及基本假设


本文采用了黑油模型假设, 考虑基质和流体的压缩性, 油水两相流动均符合达西定律, 等温渗流, 岩石变形考虑为微小线弹性变形, 力学方程中采用常规弹性力学符号约定, 即拉伸为正, 压缩为负.


1.2
准静态力学平衡方程


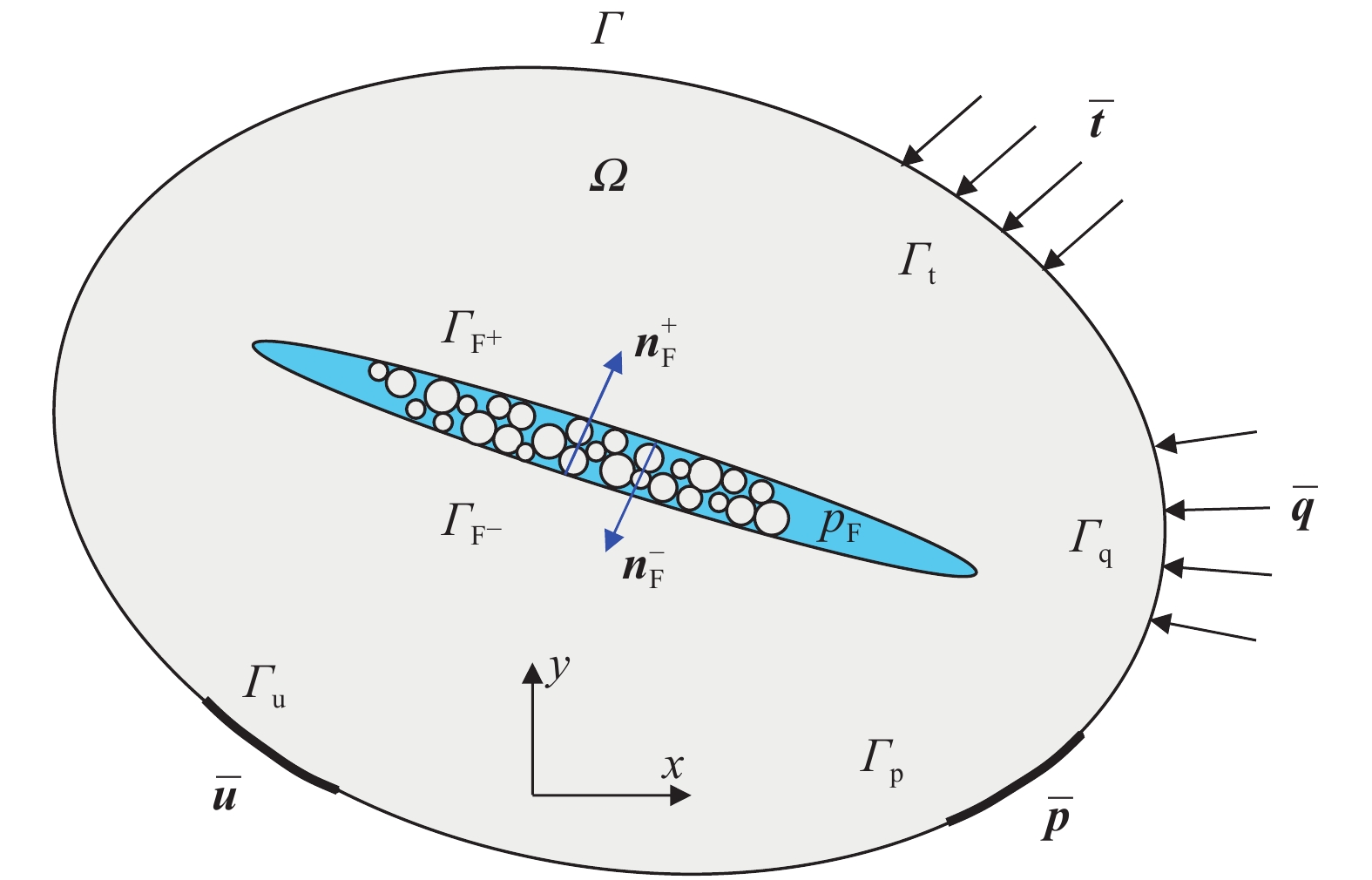
图1为弹性静力平衡状态下的多孔介质, 中间存在一条水力压裂缝, $ {p}_{mathrm{F}} $为作用裂缝内表面的缝内孔隙压力, $ {p}_{mathrm{p}} $为支撑剂颗粒的支撑力, $ {boldsymbol{n}}_{mathrm{F}}^{+} $和$ {boldsymbol{n}}_{mathrm{F}}^{-} $表示裂缝表面两侧$ {varGamma }_{mathrm{F}} $上的两个单位法向量, $ {boldsymbol{n}}_{mathrm{t}} $表示基岩应力外边界$ {{varGamma }}_{mathrm{t}} $上的单位外法向量, $ boldsymbol{t} $为应力外边界上的牵引力, $ {bar{boldsymbol{u}}} $为位移外边界$ {varGamma }_{mathrm{u}} $上的平均固体位移. 由此可建立准静态应力平衡方程式(1) ~ 式(4)







$$ nabla cdot {boldsymbol{sigma }}left( {{boldsymbol{u}},{p_{
m{m}}}}
ight) + {
ho _{
m{b}}}{boldsymbol{g}} = 0,;{text{ on }}{varOmega} $$
(1)







$$ {boldsymbol{sigma }} cdot {{boldsymbol{n}}_{
m{t}}} = {boldsymbol{t}},;{text{ on }}{{varGamma} _{
m{t}}} $$
(2)







$$ {boldsymbol{u}} = overline {boldsymbol{u}},; {text{ on }}{{varGamma} _{
m{u}}} $$
(3)







$$ {boldsymbol{sigma }} cdot {boldsymbol{n}}_{
m{F}}^ + = - {boldsymbol{sigma }} cdot {boldsymbol{n}}_{
m{F}}^ - {text{ = }}left( {{p_{
m{F}}} + {p_{
m{p}}}}
ight){boldsymbol{n}}_{
m{F}}^ - ,;{text{ on }}{{varGamma} _{
m{F}}} $$
(4)

式中, $ boldsymbol{sigma } $为总应力张量, Pa; $ boldsymbol{u} $为岩石固体位移, m; $ {P}_{mathrm{m}} $为基岩孔隙压力, Pa; $ {mathit{
ho }}_{mathrm{b}} $为多孔介质基岩密度, kg/m3; $ boldsymbol{g} $为重力加速度, N/kg.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
弹性静力平衡状态下的多孔介质



Figure
1.
Porous medium in elastostatic equilibrium state



下载:
全尺寸图片
幻灯片



1.3
油水渗流控制方程


基质体积单元中的油水两相质量平衡方程







$$ {left[ {frac{partial }{{partial t}}frac{{({
ho _{
m{o}}}phi _{
m{m}}^ * {s_{
m{o}}})}}{{{B_{
m{o}}}}} - nabla cdot left( {{
ho _{
m{o}}}frac{{k{k_{
m{ro}}}}}{{{mu _{
m{o}}}{B_{
m{o}}}}}nabla {p_{
m{o}}}}
ight)}
ight]^m} = {left[ {{
ho _{
m{o}}}{q_{
m{o}}}}
ight]^{mF}} + {left[ {{
ho _{
m{o}}}{q_{
m{o}}}}
ight]^{mw}} $$
(5)







$$ {left[ {frac{partial }{{partial t}}frac{{({
ho _{
m{w}}}phi _{
m{m}}^ * {s_{
m{w}}})}}{{{B_{
m{w}}}}} - nabla cdot left( {{
ho _{
m{w}}}frac{{k{k_{
m{rw}}}}}{{{mu _{
m{w}}}{B_{
m{w}}}}}nabla {p_{
m{w}}}}
ight)}
ight]^m} = {left[ {{
ho _{
m{w}}}{q_{
m{w}}}}
ight]^{mF}} + {left[ {{
ho _{
m{w}}}{q_{
m{w}}}}
ight]^{mw}} $$
(6)

离散裂缝单元中的油水两相质量平衡方程







$$ {left[ {frac{partial }{{partial t}}frac{{({
ho _{
m{o}}}phi _{
m{F}}^ * {s_{
m{o}}})}}{{{B_{
m{o}}}}} - nabla cdot left( {{
ho _{
m{o}}}frac{{k{k_{
m{ro}}}}}{{{mu _{
m{o}}}{B_{
m{o}}}}}nabla {p_{
m{o}}}}
ight)}
ight]^F} = {left[ {{
ho _{
m{o}}}{q_{
m{o}}}}
ight]^{mF}} + {left[ {{
ho _{
m{o}}}{q_{
m{o}}}}
ight]^{Fw}} $$
(7)







$$ {left[ {frac{partial }{{partial t}}frac{{({
ho _{
m{w}}}phi _{
m{F}}^ * {s_{
m{w}}})}}{{{B_{
m{w}}}}} - nabla cdot left( {{
ho _{
m{w}}}frac{{k{k_{
m{rw}}}}}{{{mu _{
m{w}}}{B_{
m{w}}}}}nabla {p_{
m{w}}}}
ight)}
ight]^F} = {left[ {{
ho _{
m{w}}}{q_{
m{w}}}}
ight]^{mF}} + {left[ {{
ho _{
m{w}}}{q_{
m{w}}}}
ight]^{Fw}} $$
(8)

附加方程







$$ qquadqquadqquad {s_{
m{o}}} + {s_{
m{w}}} = 1 $$
(9)







$$ qquadqquadqquad {p_{
m{w}}} = {p_{
m{o}}} - {p_{
m{c}}} $$
(10)

式中, $ k $为渗透率, m2; $ {k}_{mathrm{r}mathrm{o}} $为油相相对渗透率, 小数; $ {k}_{mathrm{r}mathrm{w}} $为水相相对渗透率, 小数; $ mu $为流体黏度, mPa·s; $ s $为流体饱和度, 小数; $ B $为流体体积系数, 小数; $ p $为流体压力, Pa; 要补充的是, 上述式中下标o和w分别表示油相和水相, 上标m和F分别表示基岩和水力压裂缝, 上标w表示井筒. $ {left[
ho q
ight]}^{mF} $表示基岩与裂缝之间的窜流量; $ {left[
ho q
ight]}^{mw} $表示基岩与井筒之间的流量; $ {phi }^{*} $表示为Lagrangen孔隙度, 后续进行详细阐述.


1.4
基质-裂缝传质方程


EDFM中存在4类非相邻连接关系 (NNRs): 相邻基质网格之间的连接; 位于不同基质网格中的相邻裂缝单元之间的连接; 位于同一基质网格中的相邻裂缝单元之间的连接; 基质网格与所包含裂缝单元之间的连接. 其中, 传导率可表示为流度与其几何因子的乘积, 以油相为例, 流度和几何因子可表示为







$$ {lambda _{ij}} = dfrac{{{k_{{
m{ro}}({
m{upstream}})}}}}{{left( {dfrac{{{mu _{{
m{o}},i}} + {mu _{{
m{o}},j}}}}{2}}
ight)left( {dfrac{{{B_{{
m{o}},i}} + {B_{{
m{o}},j}}}}{2}}
ight)}} $$
(11)







$$ {G_{ij}} = frac{{{G_i}{G_j}}}{{{G_i} + {G_j}}} $$
(12)







$$ T{I_{ij}} = {lambda _{ij}} cdot {G_{ij}} $$
(13)

式中, $ {lambda }_{ij} $表示单元$ i $和$ j $之间的油相流度; $ {k}_{mathrm{r}mathrm{o}left(mathrm{u}mathrm{p}mathrm{s}mathrm{t}mathrm{r}mathrm{e}mathrm{a}mathrm{m}
ight)} $表示利用上游权格式取值的油相相对渗透率; $ {G}_{ij} $为单元$ i $和$ j $之间的几何因子; $ {TI}_{ij} $表示单元$ i $和$ j $之间的传导系数.

基质与裂缝之间传质项的处理是基于EDFM中的第4类连接关系, 原始EDFM方法[26]在计算包含裂缝单元的基质网格内的压力分布时, 采用了Lee等[27]及Praditia等[28]提出的压力与到裂缝面的垂向距离成正比的线性分布假设如下







$$ qquadqquadqquad {G_i} = frac{{{k_i}A}}{{leftlangle d
ight
angle }} qquad$$
(14)







$$ qquadqquadqquad leftlangle d
ight
angle = dfrac{{displaystyleint {left| {{boldsymbol{n}} cdot x}
ight|{
m{d}}S} }}{S} $$
(15)

式中$ {k}_{i} $表示单元$ i $的渗透率, m2; $ A $代表接触面积, m2; $ leftlangle{d}
ight
angle $代表基质网格中心点与裂缝面之间的距离, m; $ S $为所在基质网格的面积, m2.

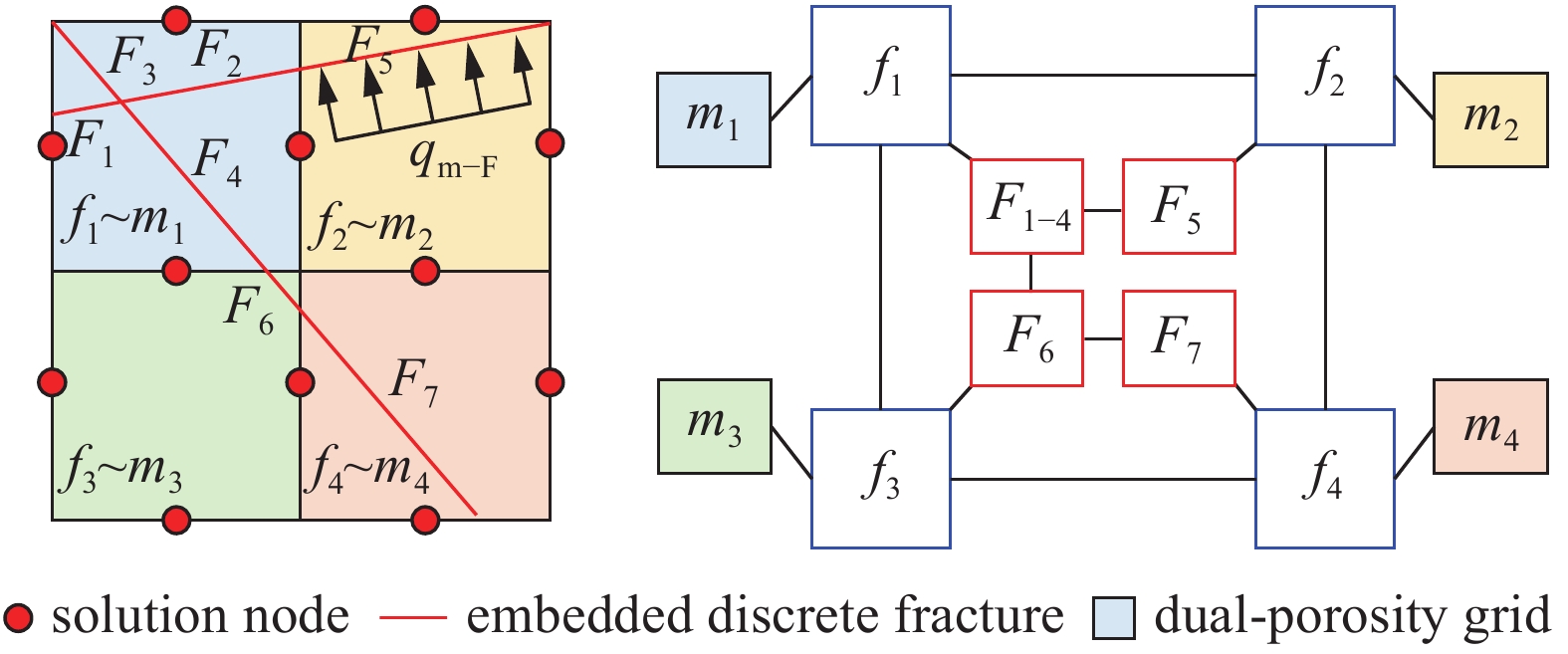
但在实际物理情景中由于裂缝与基质的渗透率级别相差极大, 这种求取“平均法向距离”的近似方法在处理非稳态传质时会导致一定的误差. 因此, 本文基于Fang等[29]与Cao等[30]所提出的混合边界元法, 利用稳态渗流控制方程的边界积分方程推导得到双孔基质网格向裂缝网格传质量的新近似格式, 以油相为例见式(16), EDFM中MBEM流量处理的连接关系示例见图2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
双孔系统EDFM中MBEM流量项处理的连接关系示例



Figure
2.
Example of connection list for MBEM handling flux in EDFM with dual-porosity system



下载:
全尺寸图片
幻灯片








$$ begin{split}&{left[ {{q_{{
m{omF}}}}}
ight]_{({n_{
m{F}}} times 1)}} = &quadfrac{{k{k_{{
m{ro}}}}h}}{{{mu _{
m{o}}}{B_{
m{o}}}}}{left( {{{{{boldsymbol{G}}_{
m{F}}}}_{({n_{
m{F}}} times 4)}}{boldsymbol{G}}_{(4 times 4)}^{ - 1}{{ {{{boldsymbol{G}}_{{
m{mF}}}}} }_{left. {(4 times {n_{
m{F}}}}
ight)}} - {{ {{{boldsymbol{G}}_{
m{FF}}}} }_{({n_{
m{F}}} times {n_{
m{F}}})}}}
ight)^{ - 1}} cdot &quad Bigg{ {left[ {{{left( {frac{{partial {{boldsymbol{G}}_{
m{F}}}}}{{partial {boldsymbol{n}}}}}
ight)}_{({n_{
m{F}}} times 4)}} - {{{{boldsymbol{G}}_{
m{F}}}}_{({n_{
m{F}}} times 4)}}{boldsymbol{G}}_{(4 times 4)}^{ - 1}{{left( {frac{{partial {boldsymbol{G}}}}{{partial {boldsymbol{n}}}}}
ight)}_{(4 times 4)}}}
ight]} cdot Bigg. &quadBigg. { {{{boldsymbol{G}}_{{
m{conv}}}}} _{(4 times 5)}}{ {{{boldsymbol{p}}_{
m{o}}}} _{(5 times 1)}} - { {{{boldsymbol{p}}_{
m{F}}}} _{({n_{
m{F}}} times 1)}}Bigg}end{split} $$
(16)

式中, $ {q}_{mathrm{o}mathrm{m}mathrm{F}} $为从裂缝单元流入基质网格的油相流量, m3; 下标$ {n}_{mathrm{F}} $代表裂缝单元个数; $ h $为基质网格厚度, m; $ boldsymbol{G} $, $ {boldsymbol{G}}_{mathrm{m}mathrm{F}} $, $ {boldsymbol{G}}_{mathrm{F}} $, $ {boldsymbol{G}}_{mathrm{F}mathrm{F}} $, $ dfrac{partial boldsymbol{G}}{partial {boldsymbol{n}}} $等矩阵形式见附录.


1.5
井方程


经典Peaceman公式[31]可用于计算井筒与基质或裂缝之间的流量. 以油相为例, 对于压裂水平井井筒与裂缝单元相连接







$$ left[ {{
ho _{
m{o}}}q_{
m{o}}}
ight]^{Fw} = {
ho _{
m{o}}}dfrac{{{{left( {k{k_{{
m{ro}}}}}
ight)}^F}}}{{{mu _{
m{o}}}{B_{
m{o}}}}} cdot dfrac{{ {dfrac{{2{text{π}} {w_{
m{F}}}}}{{cos theta }}} }}{{ln left( {dfrac{{{r_{
m{e}}}}}{{{r_{
m{w}}}}}}
ight)}}{left( {{p^F} - {p^w}}
ight)_{
m{o}}} $$
(17)







$$ {r_{
m{e}}} = 0.14{left( {{l_1}^2 + {l_2}^2}
ight)^{1/2}} $$
(18)

式中, $ {w}_{mathrm{F}} $为水力压裂缝的开度, m; $ {r}_{mathrm{e}} $为等效补给井径, m; $ {r}_{mathrm{w}} $为油井井径, m; $ {l}_{1} $和$ {l}_{2} $分别为裂缝矩形单元的两个边长, m.


2.
多孔介质本构关系



2.1
修正的Biot方程


为准确描述非常规储层中基质与小尺度裂缝间的流动和岩石形变, 可采用由Bai[32]提出的双孔有效应力原理, 对基质和裂缝分别建立具有严格物理意义的有效应力关系







$$ {{boldsymbol{sigma }}_{
m{m}}} = {{boldsymbol{sigma '}}_{
m{m}}} - {alpha _{
m{m}}}{p_{
m{m}}}{boldsymbol{I}} $$
(19)







$$ {{boldsymbol{sigma }}_{
m{f}}} = {{boldsymbol{sigma '}}_{
m{f}}} - {p_{
m{f}}}{boldsymbol{I}} $$
(20)







$$ {boldsymbol{sigma }} = {{boldsymbol{sigma }}_{
m{m}}} = {{boldsymbol{sigma }}_{
m{f}}} $$
(21)







$$ {boldsymbol{varepsilon }} = {{boldsymbol{varepsilon }}_{
m{m}}} + {{boldsymbol{varepsilon }}_{
m{f}}} $$
(22)

式中, $ {boldsymbol{sigma }}_{mathrm{m}} $表示基质总应力张量, Pa; $ {boldsymbol{sigma }}_{mathrm{f}} $为裂缝总应力张量, Pa; $ {boldsymbol{sigma }}_{mathrm{m}}' $为基质有效应力, Pa; $ {boldsymbol{sigma }}_{mathrm{f}}' $表示裂缝有效应力, Pa; $ {alpha }_{mathrm{m}} $表示毕渥系数, 小数; $ boldsymbol{varepsilon } $为总应变张量, m; $ {boldsymbol{varepsilon }}_{mathrm{m}} $为基质应变张量, m; $ {boldsymbol{varepsilon }}_{mathrm{f}} $为裂缝应变张量, m; 上述式中下标f表示小尺度裂缝.

Ren根据式(19) ~ 式(22)及胡克定律, 指出双重介质有效应力的表达式为[22]







$$ begin{split}& {boldsymbol{sigma '}} = {{boldsymbol{D}}_{{
m{mf}}}}:{boldsymbol{varepsilon }} - {{boldsymbol{D}}_{{
m{mf}}}}:{{boldsymbol{C}}_{
m{m}}}:{alpha _{
m{m}}}{p_{
m{m}}}{boldsymbol{I}} hfill &qquad - {{boldsymbol{D}}_{{
m{mf}}}}:{{boldsymbol{C}}_{
m{f}}}:{p_{
m{f}}}{boldsymbol{I}} hfill end{split} $$
(23)







$$ {boldsymbol{varepsilon}} = frac{1}{2}left( {{nabla ^{text{T}}}{boldsymbol{u}} + nabla {boldsymbol{u}}}
ight) $$
(24)

式中, $ {{boldsymbol{D}}}_{mathrm{m}mathrm{f}} $为弹性刚度张量, Pa; $ {{boldsymbol{C}}}_{mathrm{m}} $为基质柔度张量, Pa; $ {{boldsymbol{C}}}_{mathrm{f}} $为裂缝柔度张量, Pa.


2.2
孔渗参数表征方法


孔隙度是关于体积应变和流体压力的函数[25]. 考虑线弹性微小形变下的基岩Lagrangen孔隙度和大尺度裂缝Lagrangen孔隙度可分别由下式表征







$$ {phi }_{{
m{m}}}^{*}={phi }_{{
m{m}}}^{0}+{alpha }_{{
m{m}}}{epsilon}_{V}+frac{1}{M}left({p}_{{
m{m}}}-{p}_{{
m{m}}}^{0}
ight) $$
(25)







$$ {phi }_{{
m{F}}}^{*}={phi }_{{
m{F}}}^{0}left(1+{epsilon}_{{
m{V}}}
ight) $$
(26)

式中$ {phi }_{mathrm{m}}^{0} $为基岩原始孔隙度, 小数; $ {phi }_{mathrm{F}}^{0} $为大尺度裂缝原始孔隙度, 小数; $ {phi }_{mathrm{m}}^{0} $为基岩原始孔隙度, 小数; $ {p}_{mathrm{m}} $为基岩流体压力, Pa; $ {p}_{mathrm{m}}^{0} $为基岩原始流体压力, Pa; $ 1/M $物理意义同$ {alpha }_{mathrm{m}};{epsilon}_{mathrm{V}} $为体积应变, 即总应变张量的迹.

本文中将小尺度天然裂缝和基岩视为双重连续介质, 因此小尺度裂缝表征方法与基质相同. 对于大尺度水力压裂缝, 生产过程中由于缝内流体压力损失会导致裂缝面的闭合, 然而当存在支撑剂时, 支撑剂发生形变会对裂缝面施加支撑力阻止其闭合. 根据胡克定律, 由支撑剂引起的支撑力可表示为







$$ {p_{
m{p}}} = left{ {begin{array}{*{20}{c}} {{E_{
m{p}}}dfrac{{ - {boldsymbol{w}} cdot {{boldsymbol{n}}_{
m{F}}}}}{{w_{
m{F}}^0}},}&{{boldsymbol{w}} cdot {{boldsymbol{n}}_{
m{F}}} < 0} {0,}&{{text{else }}} end{array}}
ight. $$
(27)

式中, $ {E}_{mathrm{p}} $为支撑剂弹性模量, Pa; ${ boldsymbol{w} }$为裂缝开度的位移, m; $ {w}_{mathrm{F}}^{0} $为水力压裂缝的原始开度, m.

此过程中, 水力压裂缝的实际导流能力依赖于裂缝渗透率和开度的更新迭代[33]







$$ {k_{
m{F}}} = k_{
m{F}}^0{left( {frac{{{w_{
m{F}}}}}{{w_{
m{F}}^0}}}
ight)^2} $$
(28)

式中, $ {k}_{mathrm{F}}^{0} $为水力压裂缝的原始渗透率, m2.


3.
耦合模型的数值离散



3.1
有限体积法离散流动方程


XFEM与EDFM具有相似的优点, 两者均基于结构化网格, 网格划分容易且物理意义清晰. 因此本文采用正交矩形网格对基质进行几何离散, 针对EDFM前三类非相邻连接关系, 采用满足局部物质守恒且简单易行的块中心有限体积方法来获取渗流控制方程的离散格式, 仍以油相为例, 此时为公式简洁, 方程中去除可能存在的点源/汇项, 对式(5)的两侧对时间和控制体积进行积分







$$ int_t^{t + Delta t} {intlimits_{Delta V} {nabla cdot left( {{
ho _{
m{o}}}frac{{k{k_{{
m{ro}}}}}}{{{mu _{
m{o}}}{B_{
m{o}}}}}nabla {p_{
m{o}}}}
ight)} } {
m{d}}V{
m{d}}t = intlimits_{Delta V} {int_t^{t + Delta t} { {frac{partial }{{partial t}}left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)} } } {
m{d}}t{
m{d}}V $$
(29)

式中左侧利用散度定理将体积分转换为面积分, 并用符合物理意义的相邻网格之间的法向流量之和近似; 右侧对时间的积分精确求解, 对体积分采用矩形法估计, 由此式(29)可以写为







$$ int_t^{t + Delta t} {sumlimits_{j = 1}^n {left[ {{lambda _{ij}}{G_{ij}}left( {{p_{{
m{o}}i}} - {p_{{
m{o}}j}}}
ight)}
ight]} {
m{d}}t} = Delta {V_i}left[ {{{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^{t + Delta t}} - {{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^t}}
ight] $$
(30)

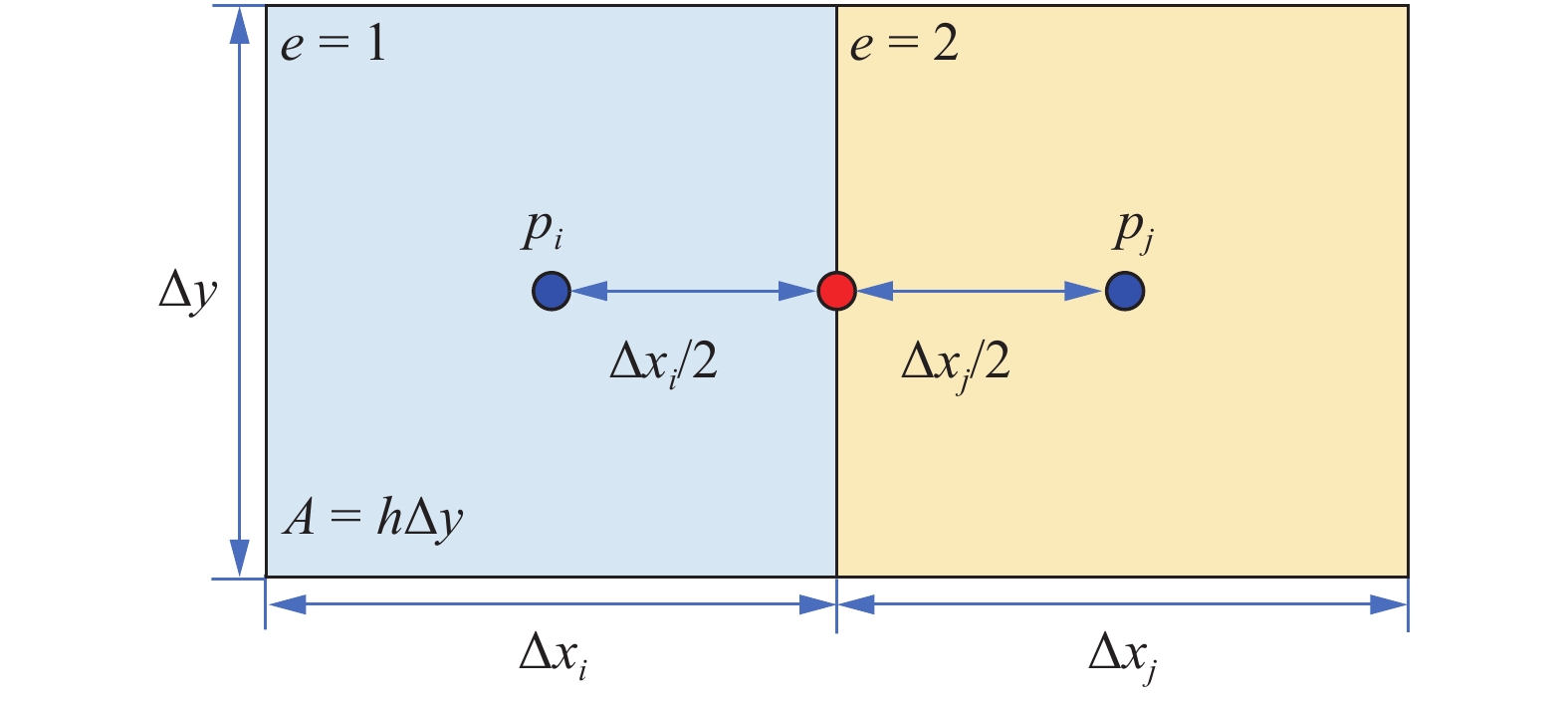
对于相邻基质网格如图3, 式(30)取隐式格式可改写为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
矩形网格离散示意图



Figure
3.
Sketch of discretization for rectangle grids



下载:
全尺寸图片
幻灯片








$$ sumlimits_{j = 1}^n {left[ {{lambda _{ij}}{G_{ij}}left( {p_{{
m{o}}i}^{t + Delta t} - p_{{
m{o}}j}^{t + Delta t}}
ight)}
ight]} = frac{{Delta {V_i}}}{{Delta t}}left[ {{{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^{t + Delta t}} - {{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^t}}
ight] $$
(31)

式中, $ n $表示与该基质网格相邻的网格数量, $ {Delta V}_{i} $为该基质网格的体积, $ Delta t $为相邻时间步.

根据式(29) ~ 式(31)的推导过程可以获得油水相的全隐式离散方程, 但对于裂缝与基质连接的第4类非相邻连接关系即含传质项, 需要进行单独考虑. 这里将已推导的多相流情况下EDFM第4类连接中基质网格与裂缝网格之间传质量的近似格式(16), 耦合到基质与裂缝之间多相流方程的有限体积离散格式中, 这也是混合边界元EDFM的核心思想. 仍以油相为例, 对于基质系统







$$ begin{split}& sumlimits_{j = 1}^n {left[ {{lambda _{o,ij}}{T_{ij}}left( {p_{oi}^{t + Delta t} - p_{oj}^{t + Delta t}}
ight)}
ight]} - sumlimits_{k = 1}^{{n_{
m{F}}}} {q_{{
m{omF}},k}^{t + Delta t}} hfill = &qquad frac{{Delta {V_i}}}{{Delta t}}left[ {{{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^{t + Delta t}} - {{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^t}}
ight] end{split} $$
(32)

同理, 对于裂缝系统







$$ begin{split}& sumlimits_{j = 1}^n {left[ {{lambda _{o,ij}}{T_{ij}}left( {p_{oi}^{t + Delta t} - p_{oj}^{t + Delta t}}
ight)}
ight]} + q_{{
m{omF}},i}^{t + Delta t} hfill = &qquad frac{{Delta {V_i}}}{{Delta t}}left[ {{{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^{t + Delta t}} - {{left( {frac{{phi _{
m{m}}^ * {s_{
m{o}}}}}{{{B_{
m{o}}}}}}
ight)}^t}}
ight] end{split} $$
(33)

式中, $ {q}_{mathrm{o}mathrm{m}mathrm{F},k}^{t+Delta t} $表示第$ i $个基质网格流入第$ k $个裂缝单元的油相流量, m3; 同理, $ {q}_{mathrm{o}mathrm{m}mathrm{F},i}^{t+Delta t} $表示基质网格向第$ i $个裂缝单元的油相流量, m3.


3.2
扩展有限元离散力学方程


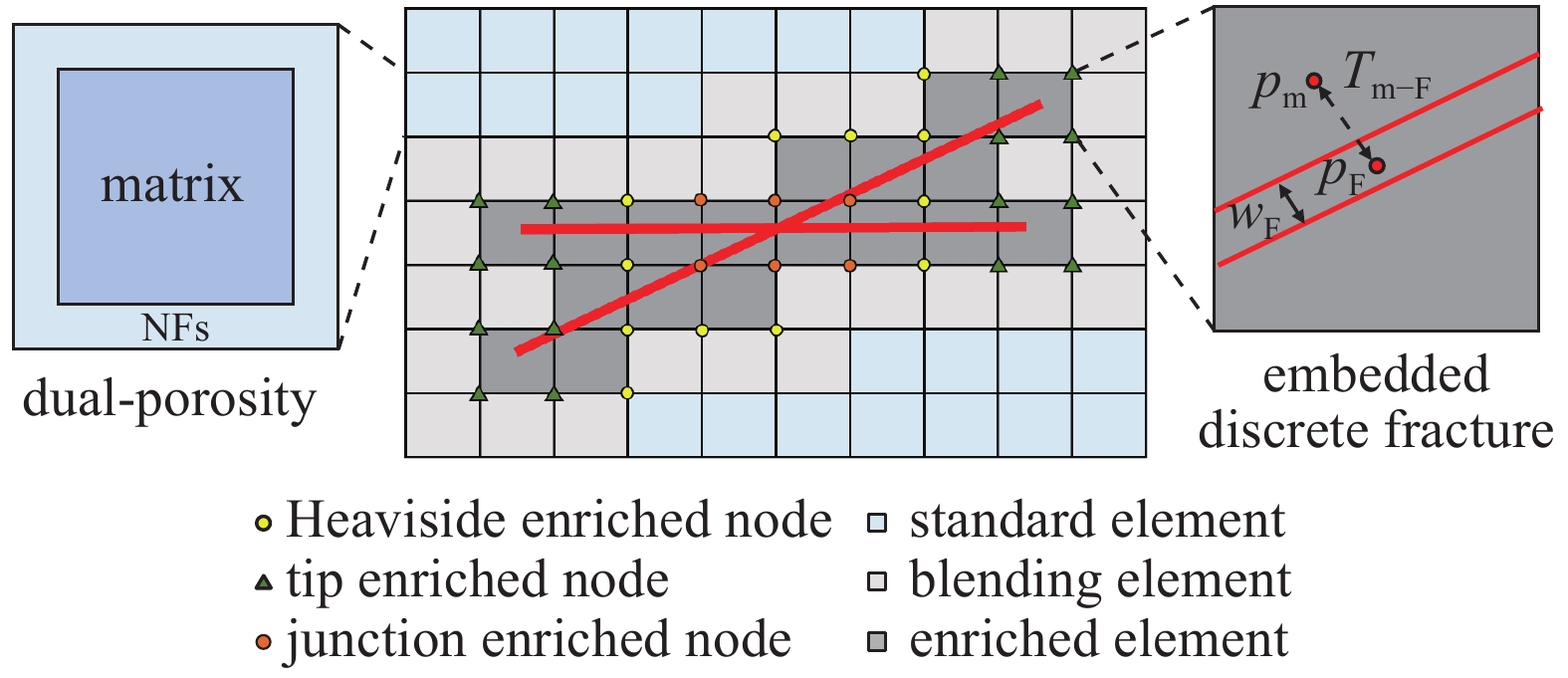
XFEM是在常规的有限元位移模式中根据单位分解的思想加引进一个跳跃函数和裂尖渐进位移场以反映位移不连续性的数值方法. XFEM中的不同节点和单元的类型见图4, 单元位移的近似解可以写成



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
混合模型离散化方法示意图



Figure
4.
Sketch of hybrid model discretization strategy



下载:
全尺寸图片
幻灯片








$$ begin{split}& {boldsymbol{u}} = sumlimits_{i in I} {{N_i}} {{boldsymbol{u}}_i} + sumlimits_{i in L} {sumlimits_{j in {mathcal{F}_L}(i)} {{N_i}} } left( {{H_j} - H_j^i}
ight){{boldsymbol{a}}_{i,j}} + &qquad sumlimits_{i in M} {sumlimits_{j in {mathcal{F}_M}(i)} {{N_i}} } left( {{J_j} - J_j^i}
ight){{boldsymbol{c}}_{i,j}} + &qquad sumlimits_{i in K} {sumlimits_{j in {mathcal{F}_K}(i)} {sumlimits_{l = 1}^4 {{N_i}} } } left( {{F_{jl}} - F_{jl}^i}
ight){boldsymbol{b}}_{i,j}^lend{split} $$
(34)

式中, $ I $表示网格中所有节点的集合, $ L $表示包含所有裂缝段所在单元的节点集合, $ M $为裂缝与裂缝相交的节点集合, $ K $表示裂缝尖端所在单元的节点集合; $ {N}_{i} $为节点位移形函数, $ {mathit{u}}_{i} $为节点位移矢量, $ {boldsymbol{a}}_{i,j} $, $ {boldsymbol{c}}_{i,j} $, $ {boldsymbol{b}}_{i,j}^{l} $为单元增强节点的额外自由度, $ H $表示Heaviside函数, $ J $表示裂间连接函数, $ F $表示裂尖渐进函数, 三者的表达式如下所示







$$ Hleft( {{xi _j}({boldsymbol{x}})}
ight) = left{ {begin{array}{*{20}{l}} {1,}&{forall {xi _j} > 0} { - 1,}&{forall {xi _j} < 0} end{array}}
ight. qquadqquadqquadqquad$$
(35)







$$ Jleft( {{xi _{j1}}({boldsymbol{x}}),{xi _{j2}}({boldsymbol{x}})}
ight) = left{ {begin{array}{*{20}{l}} {1,}&{forall {xi _{{j_1}}} cdot {xi _{{j_2}}} > 0} {0,}&{forall {xi _{{j_1}}} cdot {xi _{{j_2}}} = 0} { - 1,}&{forall {xi _{{j_1}}} cdot {xi _{{j_2}}} < 0} end{array}}
ight.qquadqquad $$
(36)







$$ {F_{jl}}(r,theta ) = left{ {sqrt r sin frac{theta }{2},sqrt r cos frac{theta }{2},sqrt r sin frac{theta }{2}sin theta ,sqrt r cos frac{theta }{2}sin theta }
ight} $$
(37)

将式(19)和式(20)代入式(1), 考虑边界条件式(2) ~ 式(4), 得到方程(1)的等效积分弱形式见式(38), 弱形式方程包含不同尺度裂缝以及基岩流体压力的相互作用







$$ begin{split} & int_varOmega delta {boldsymbol{varepsilon }}:{D_{{
m{mf}}}}:{boldsymbol{varepsilon }}{
m{d}}varOmega = int_varOmega delta {boldsymbol{varepsilon}} :left( {alpha _{
m{m}}^ * {p_{
m{m}}}{boldsymbol{I}}}
ight){
m{d}}varOmega +hfill & int_varOmega delta {boldsymbol{varepsilon}} :left( {{p_F}{boldsymbol{I}}}
ight){
m{d}}varOmega + int_{{varGamma _{
m{t}}}} delta {boldsymbol{u}} cdot {boldsymbol{t}}{
m{d}}{varGamma _{
m{t}}} +hfill & int_{{varGamma _{
m{F}}}} {left[kern-0.15emleft[ {delta {boldsymbol{u}}}
ight]kern-0.15em
ight] cdot left( {bar p + {p_{
m{p}}}}
ight) cdot {{boldsymbol{n}}_{
m{F}}}} {
m{d}}{varGamma _{
m{F}}} hfill end{split} $$
(38)

式中, $ delta {boldsymbol{varepsilon }} $表示试应变, $ delta boldsymbol{u} $表示试位移, $ ?delta {boldsymbol{u}}?={delta {boldsymbol{u}}}^{+}-delta {boldsymbol{u}}^{-} $.

裂缝开度位移可以表示为







$$ {boldsymbol{w}} = {{boldsymbol{n}}_{
m{F}}} cdot left[kern-0.15emleft[ {boldsymbol{u}}
ight]kern-0.15em
ight]{{boldsymbol{n}}_{
m{F}}} $$
(39)

采用标准伽辽金有限元法对系统整体进行离散, 可获得一个线性平衡方程组如下







$$ {boldsymbol{Ku}} = {boldsymbol{f}} $$
(40)

式中, K表示整体刚度矩阵, f表示整体力向量.


3.3
整体计算格式及求解策略


本文分别采用有限体积法和扩展有限元法求解渗流控制方程及力学平衡方程, 主要变量包括基岩及裂缝中的流体压力、含水饱和度以及分别设置在网格中心和角点的节点位移, 对时间项的离散采用一阶向后欧拉全隐式差分格式, 对完全耦合的全局方程组采用Newton-Raphson迭代求解, 并利用自动微分算法计算迭代过程中的雅可比矩阵







$$ left[ {begin{array}{*{20}{l}} {{{boldsymbol{A}}_{{
m{pp}}}}}&{{{boldsymbol{C}}_{{
m{ps}}}}}&{{{boldsymbol{C}}_{{
m{pu}}}}} {{{boldsymbol{C}}_{{
m{sp}}}}}&{{{boldsymbol{A}}_{{
m{ss}}}}}&{{{boldsymbol{C}}_{{
m{su}}}}} {{{boldsymbol{C}}_{{
m{up}}}}}&{{{boldsymbol{C}}_{{
m{us}}}}}&{{{boldsymbol{A}}_{{
m{uu}}}}} end{array}}
ight]left( {begin{array}{*{20}{c}} {delta {boldsymbol{p}}} {delta {boldsymbol{s}}} {delta {boldsymbol{u}}} end{array}}
ight) = - left( {begin{array}{*{20}{c}} {{{boldsymbol{R}}_{
m{p}}}} {{{boldsymbol{R}}_{
m{s}}}} {{{boldsymbol{R}}_{
m{u}}}} end{array}}
ight) $$
(41)

式中系数矩阵是非对称的, 其中反对角项是主变量之间的耦合项.


4.
模型验证分析



4.1
连续性介质流固耦合算例


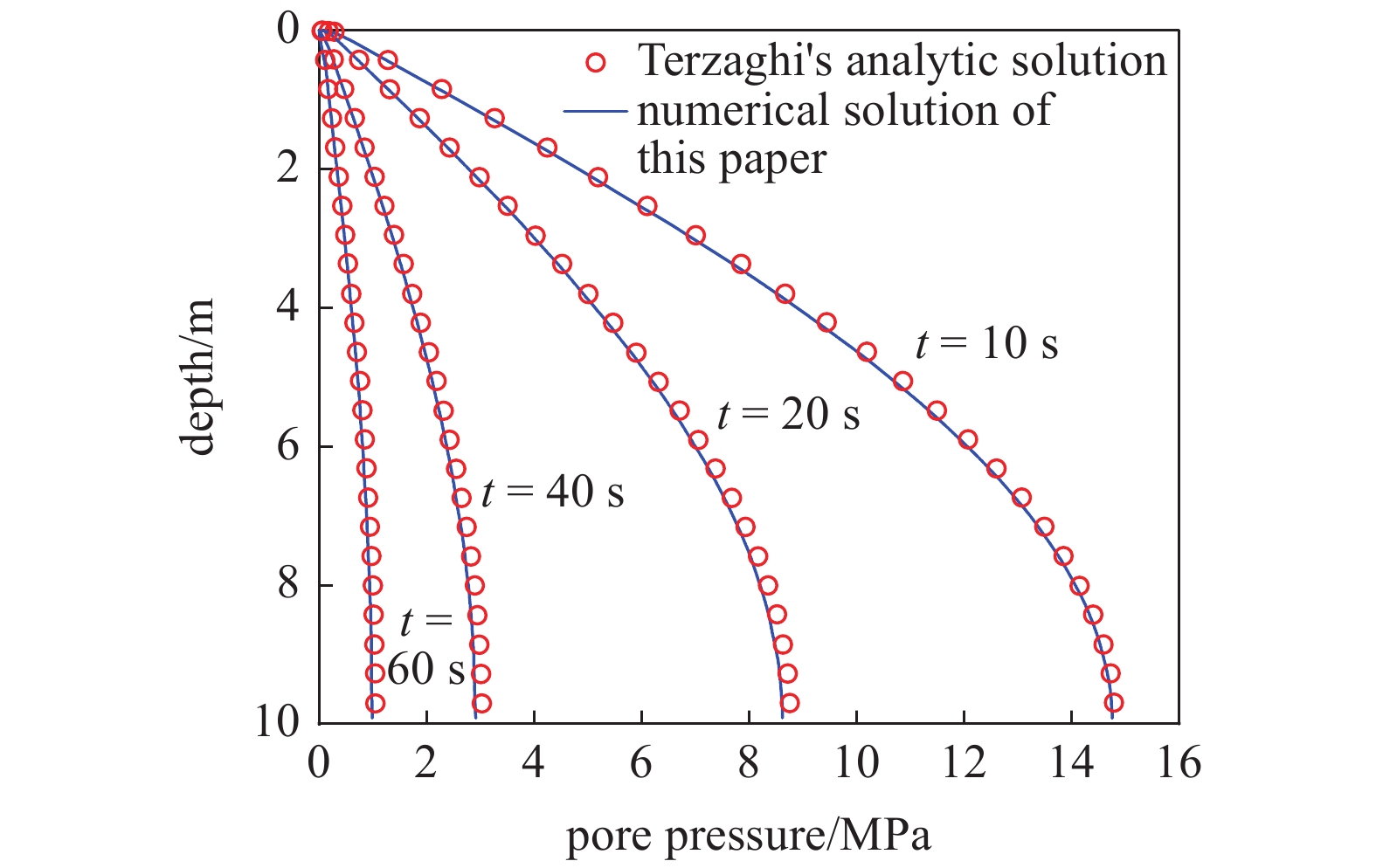
此算例选取了经典的一维弹性土固结的孔弹性问题, 将本文模型与Terzaghi[5]所提出的解析解进行对比. 假设等温多孔介质由单相流体和固体组成, 表现为线性孔弹性特征, 模型的宽度为5 m, 深度为10 m, 顶部为排水边界, 其余边界均不排水, 底部为零位移边界, 左右边界位移在水平方向上约束, 于顶部施加20 MPa的恒定载荷. 岩土的孔隙度为0.4, 渗透率为100 mD, 弹性模量为20 GPa, 泊松比为0.2, 孔隙比为0.4, 一维模型数值解与解析解对比结果如图5所示, 从图中可看出不同时间下本文提出的流固耦合数值解与Terzaghi解析解的结果较为吻合, 误差在合理范围之内, 能证明该模型的准确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
一维模型数值解与解析解的对比



Figure
5.
Comparison between numerical solution and analytical solution of one dimensional model



下载:
全尺寸图片
幻灯片



4.2
离散裂缝单相流算例


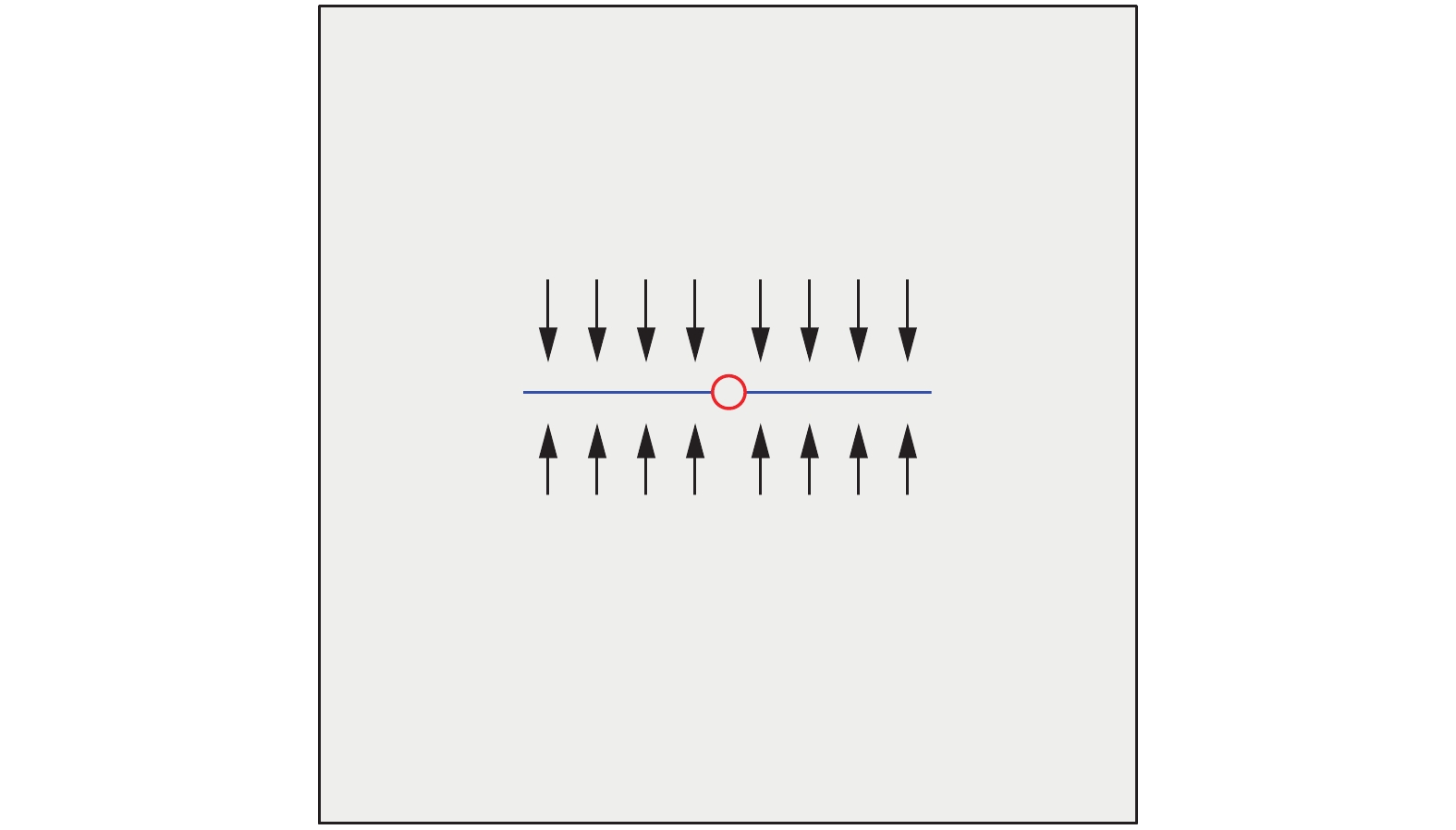
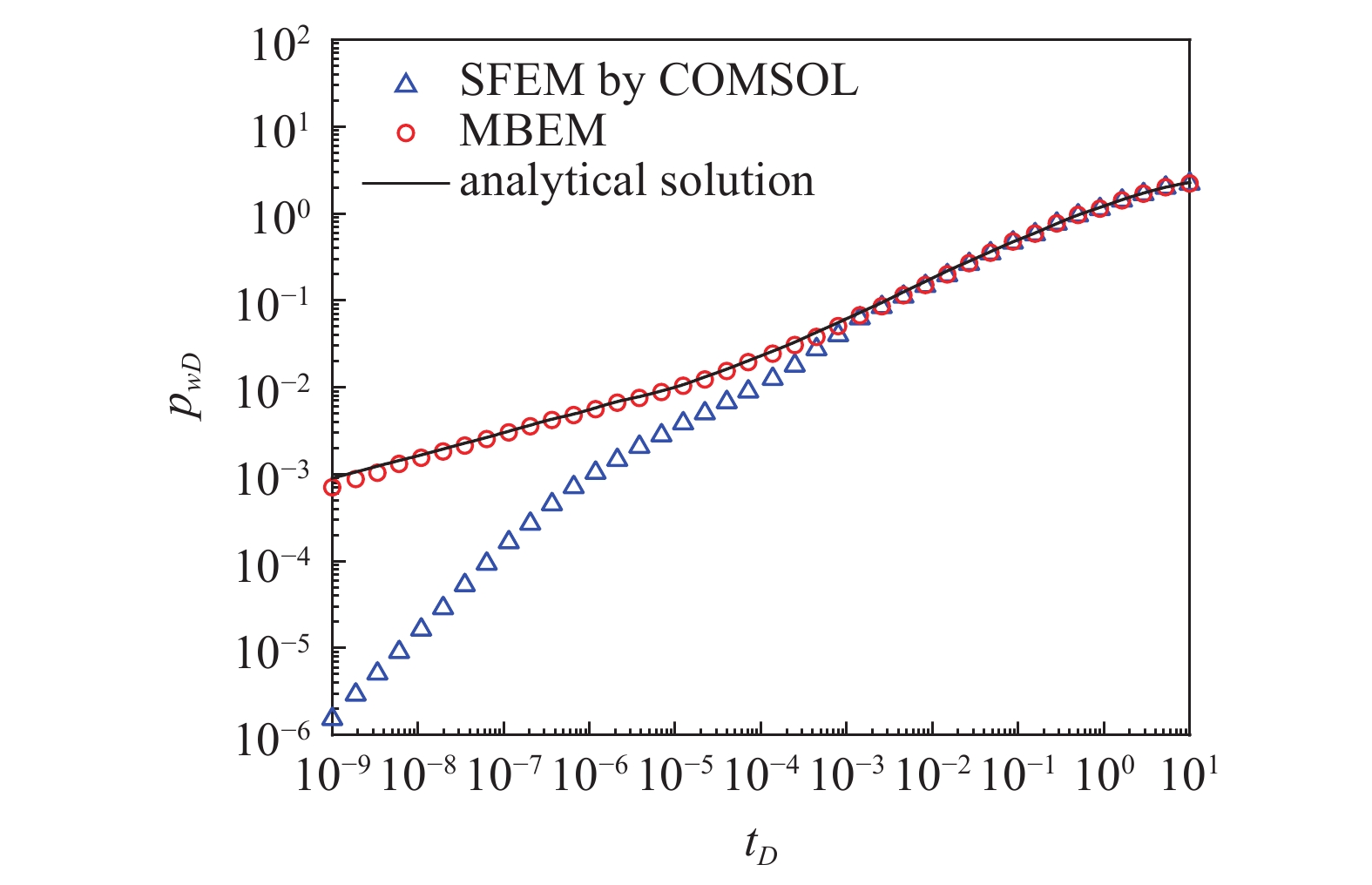
此算例是通过多物理场耦合模拟的商业模拟器COMSOL的标准有限元 (SFEM) 验证本文建立的流动模块. 物理模型为矩形油藏, 油藏中心有一条水力压裂缝, 设置裂缝半长为基础长度将整个区域无因次化, 裂缝无因次长度为4, 油藏在X方向的长度为10且Y方向长度为10, 见图6. 基于拉氏空间下无因次渗流方程, 将本文修正后的EDFM和有限元法与Blasingame精确解[34]进行对比, 其中裂缝无因次导流能力为200, 有限元网格裂缝采用局部加密如图7所示, 裂缝加密的个数为20, 如图8所示. 本文模型采用了非匹配性的矩形网格和混合边界元法, 不对裂缝进行局部加密, 分析离散裂缝压力动态曲线中不同数值算法的适应性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
单裂缝矩形油藏模型



Figure
6.
Single fracture in rectangular reservoir model



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
对裂缝网格加密示意图



Figure
7.
Sketch of fracture mesh refinement



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
不同数值解与解析解的对比



Figure
8.
Comparison of different numerical solutions and analytical solution



下载:
全尺寸图片
幻灯片


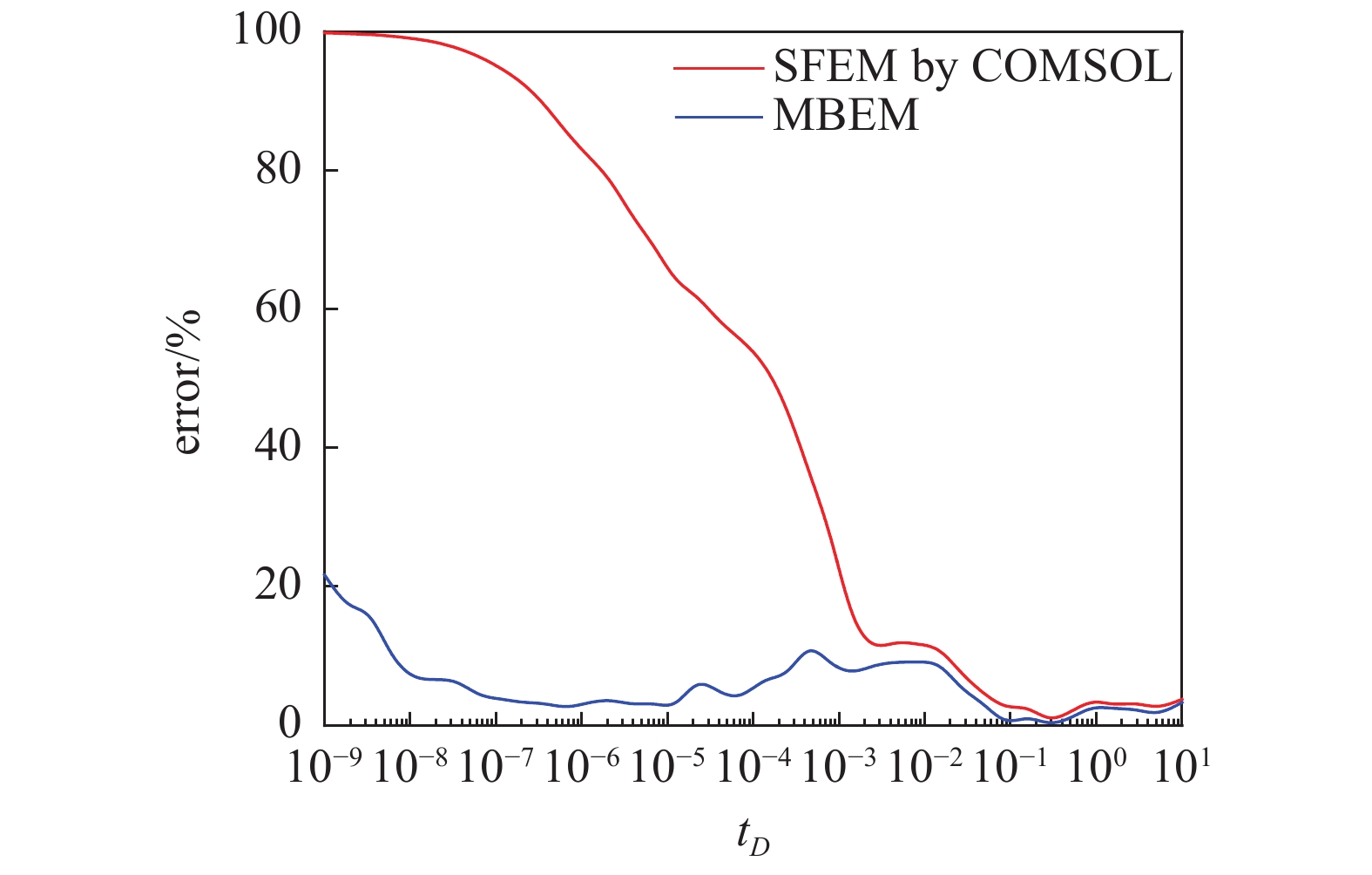
模拟结果如图7所示, 模拟无因次时间从10?9 ~ 10, 覆盖了有限导流能力的几个阶段, 可以看出修正后的EDFM方法与精确解无论从早期还是晚期都较为吻合, 而有限元模型在早期与解析解的差距很大, 中后期曲线重合, 这在图9的误差分析中也可以看出. 原因在于有限元法处理网格累积项时, 采用线性插值积分, 在一个时间步内是稳态过程, 而本文模型采用混合边界元法处理时采用了非稳态渗流的基本解, 能精确描述初期的流动特征, 根据对比结果可以说明本文模型的流动模块具有较高的早期精度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
误差分析



Figure
9.
Error analysis



下载:
全尺寸图片
幻灯片



4.3
裂缝性介质应力强度因子算例


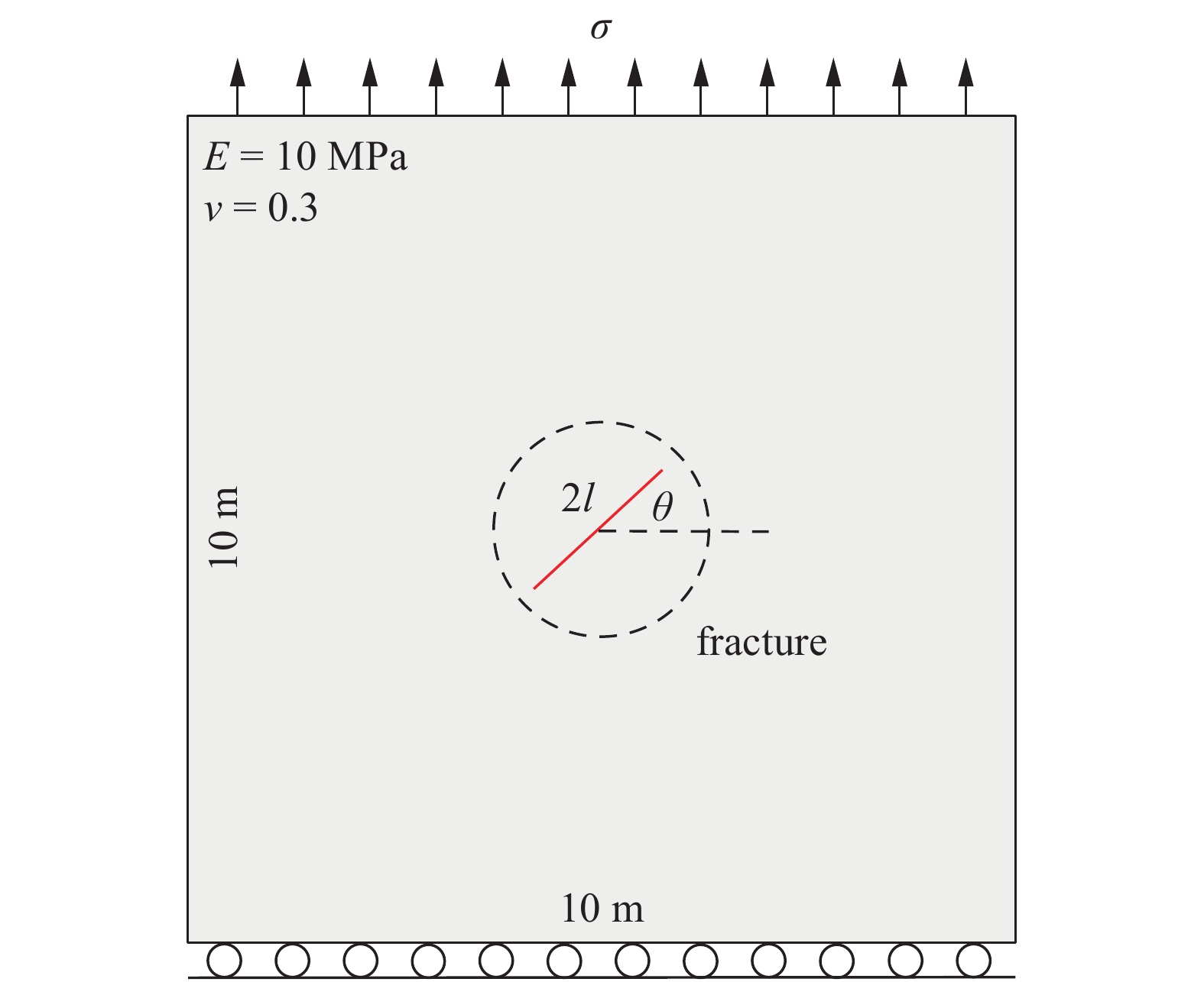
此算例是通过经典的Tada解析解[35]验证本文建立的力学模块计算裂缝尖端应力强度因子 (SIFs) 的准确性. 考虑一个平面应变模型 (10 m×10 m), 上边界为施加均匀的拉应力, 下边界为固定位移的滚轮边界, 模型内部中心存在一条倾斜裂缝, 裂缝半长l为1 m, 如图10所示. 解析解中应力强度因子是外部应力和裂缝几何尺寸和倾角的函数, 因此为方便对比, 定义无因次应力强度因子: $ {K}_{mathrm{I}}^{*}={K}_{mathrm{I}}∕left(sigma sqrt{{text{π}} l}
ight) $及$ {K}_{mathrm{I}mathrm{I}}^{*}={K}_{mathrm{I}mathrm{I}}∕left(sigma sqrt{{text{π}} l}
ight) $, 在裂缝尺寸保持不变的条件下, 计算不同裂缝倾角无因次应力强度因子数值解与解析解的结果见图11, 对比显示本文模型的数值解与经典解析解的结果几乎保持一致, 具有较高的可信度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
裂缝性介质示意图



Figure
10.
Schematic of fractured medium



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
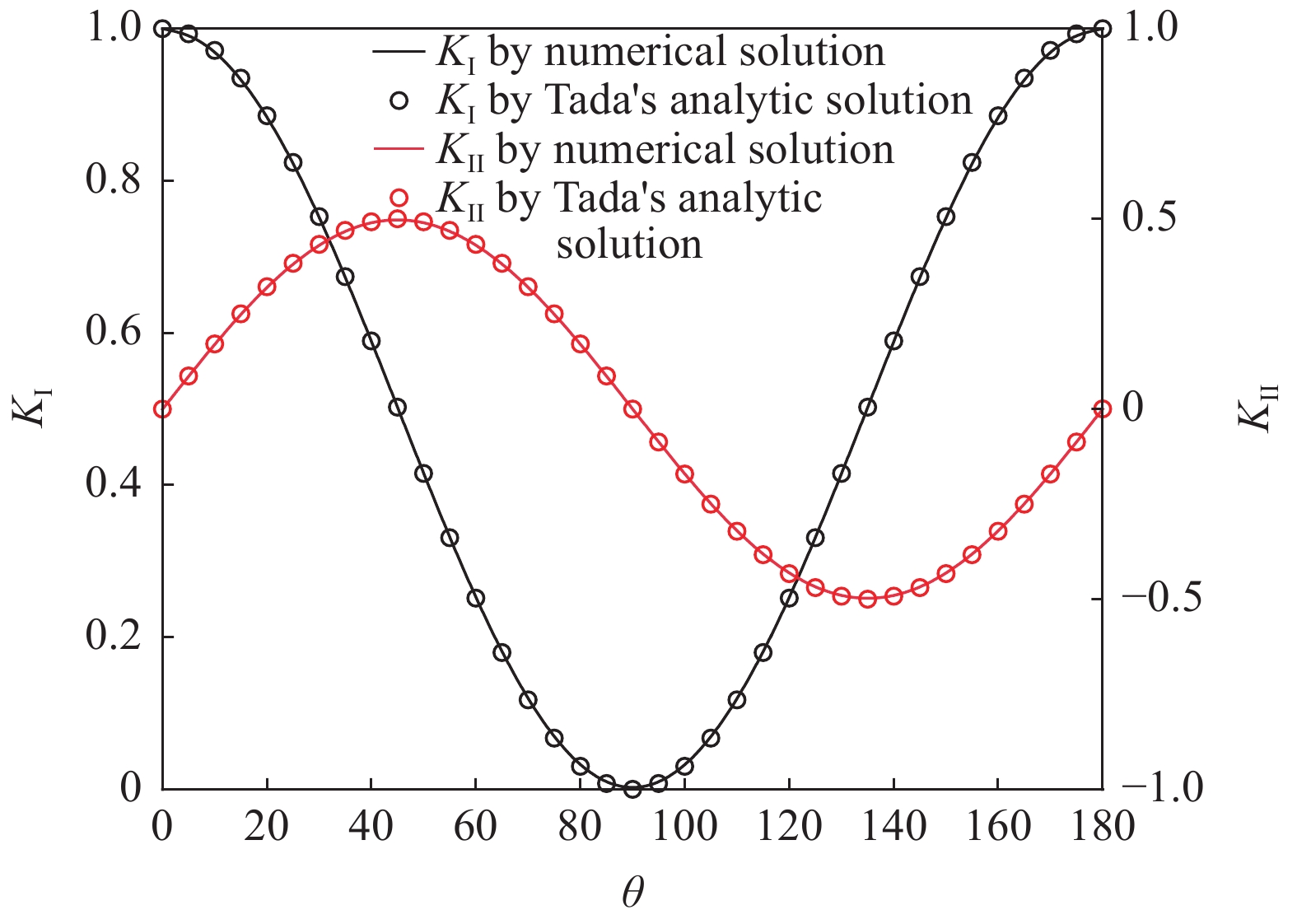
11
不同裂缝倾角无因次应力强度因子数值解与解析解的对比



Figure
11.
Comparison of numerical and analytical solutions for dimensionless SIFs with different fracture dip angles



下载:
全尺寸图片
幻灯片



5.
典型实例分析


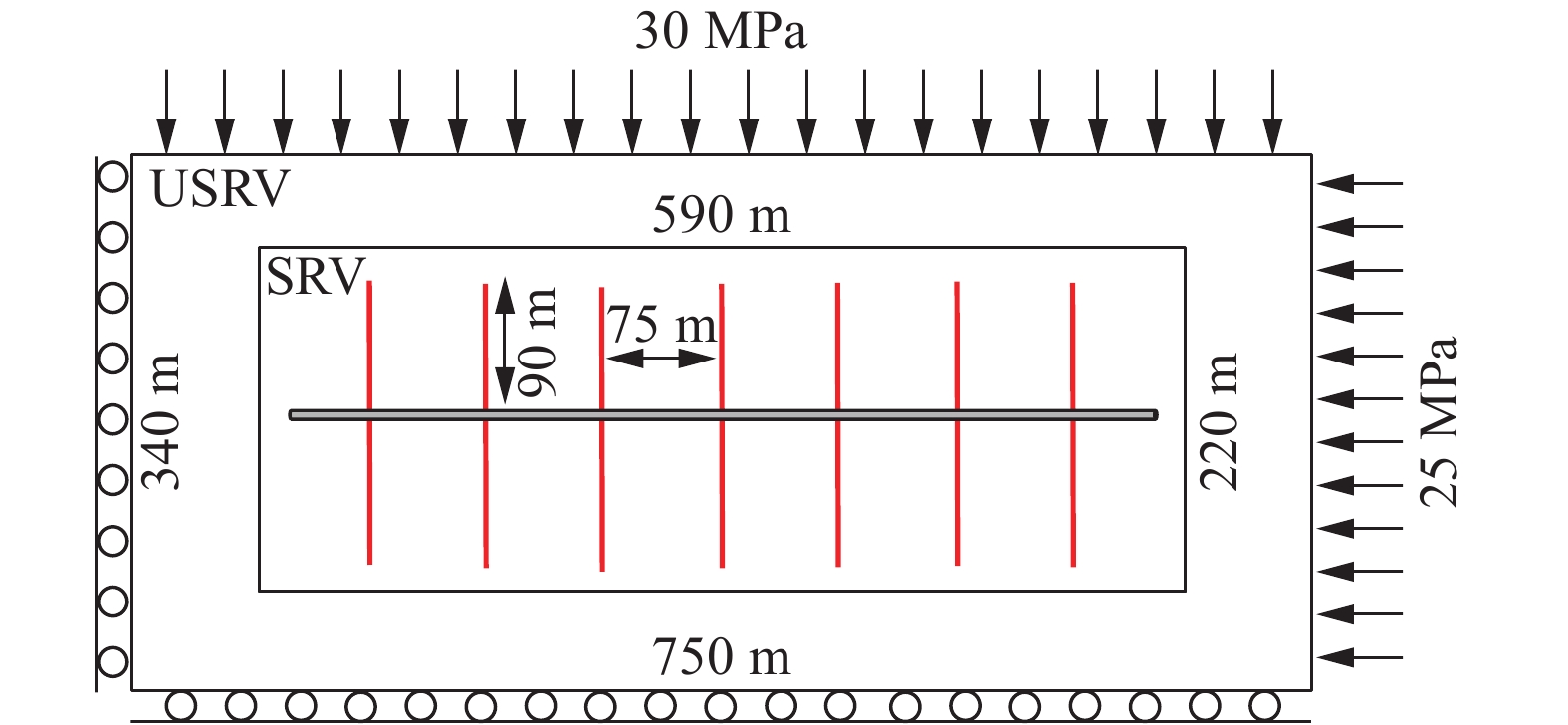
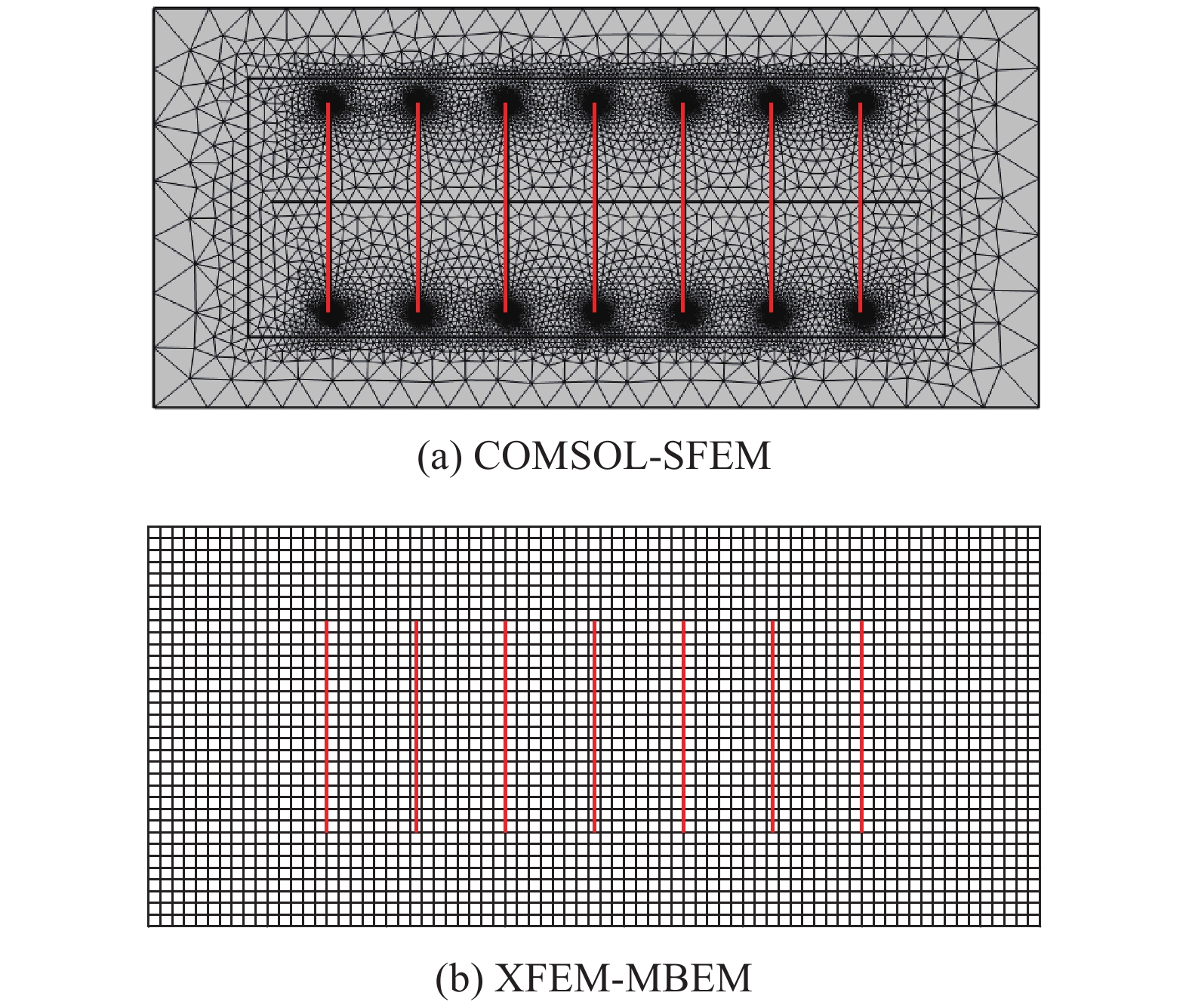
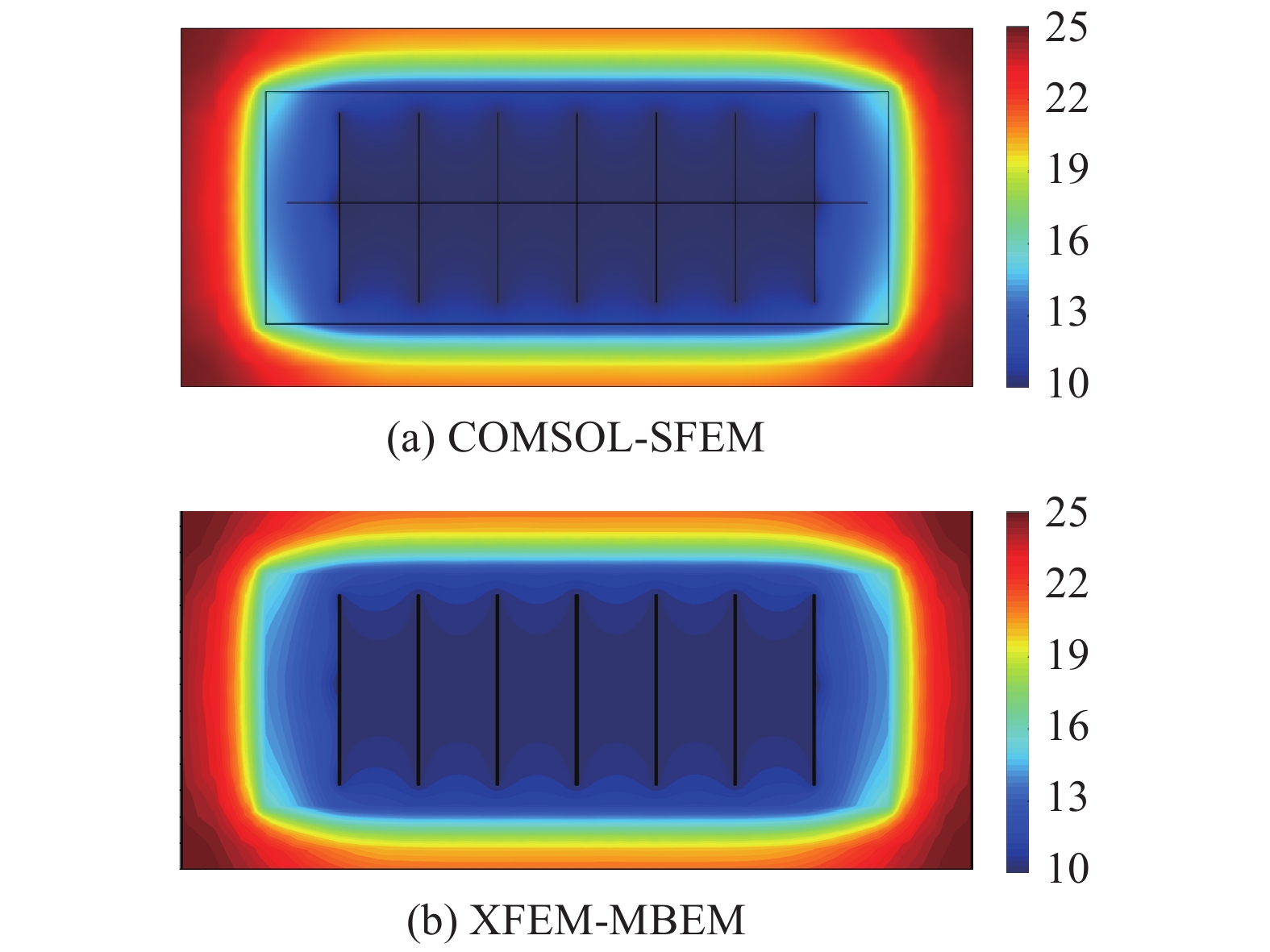
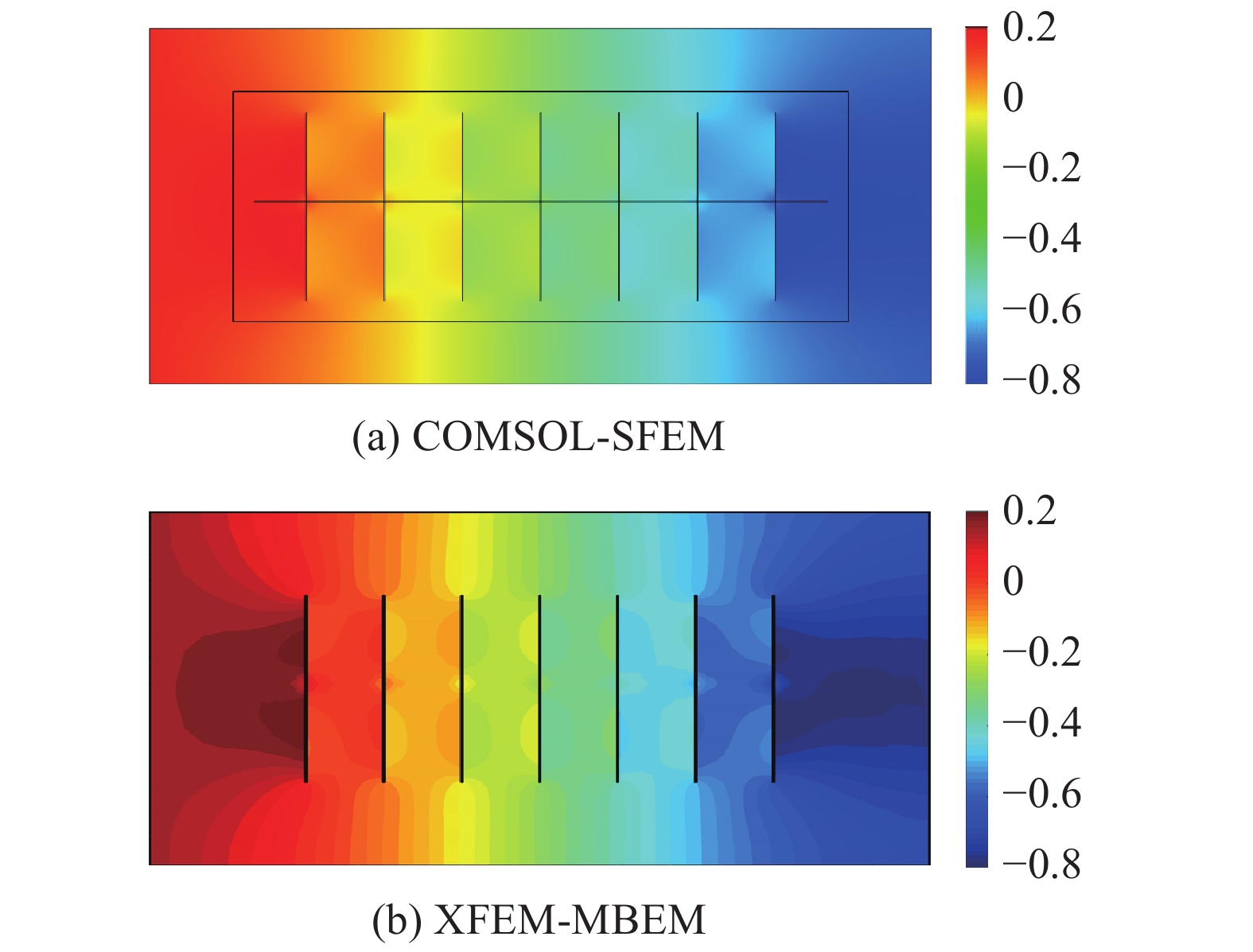
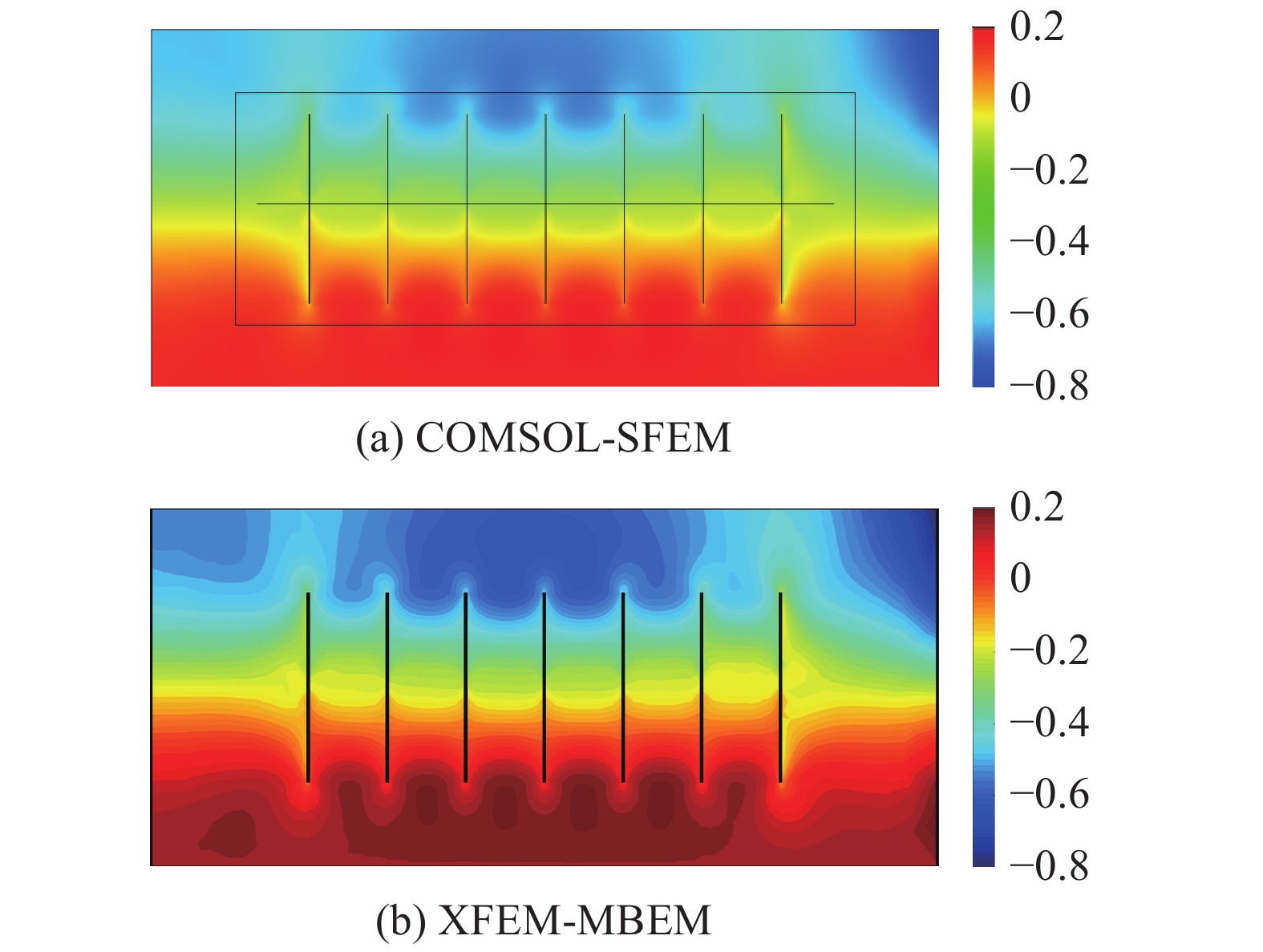
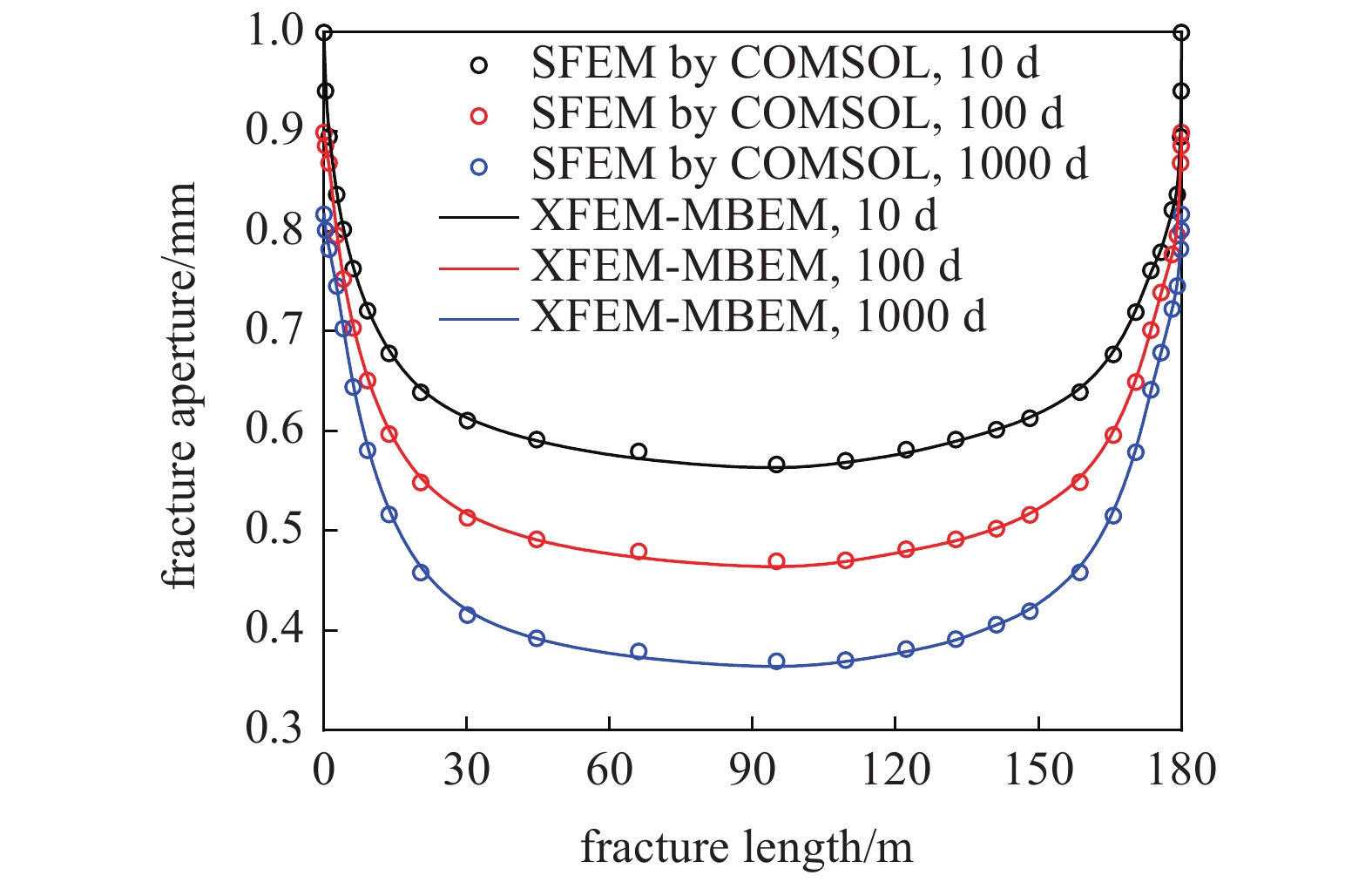
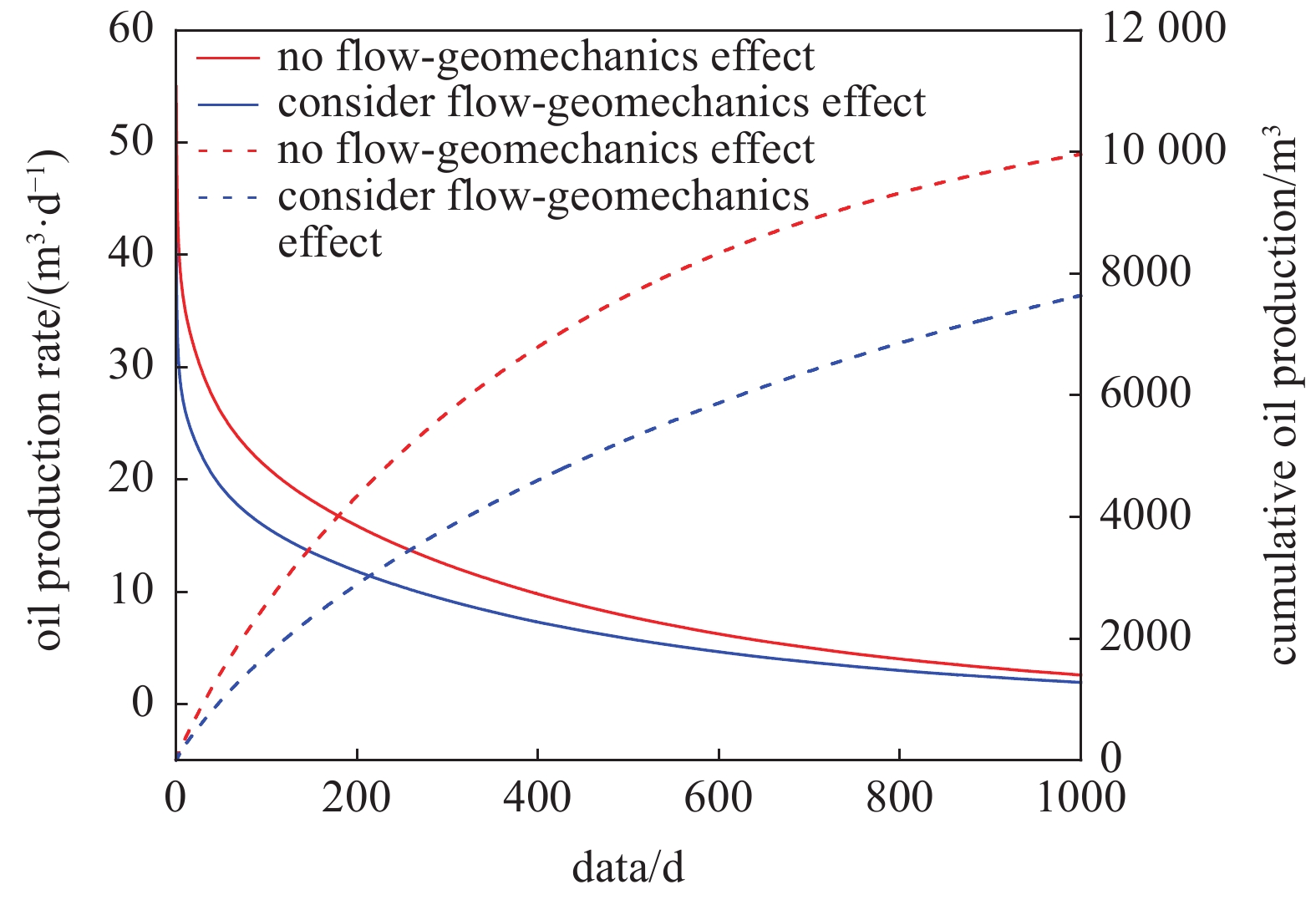
如图12所示的致密油藏, 考虑分为压裂改造区(SRV) 与非压裂改造区 (USRV), SRV内部存在一口水平井和7条水力压裂缝, 水力压裂缝中考虑支撑剂的作用. 采用平面应变模型, 油藏边界条件如图12所示. SRV内考虑微裂缝的影响, 采用双孔模型; USRV不考虑微裂缝的影响, 采用单孔模型. 致密油藏的基本参数见表1, 设置该水平井为定压生产1000 d, 井底流压为10 MPa, 并将模拟的结果与商业模拟器COMSOL的标准有限元 (SFEM) 作对比, 图13为两种数值模拟器的网格剖分, 其中COMSOL-SFEM中对SRV内部及裂缝尖端进行了局部加密处理, 本文模型XFEM-MBEM中采用非匹配性的矩形网格. 图14为两种数值模拟器在开发1000 d时刻的压力场对比, 图15和图16分别为X-位移场与Y-位移场的对比, 从上述场图可看出两种数值模拟器的结果基本一致. 以图12中SRV内部最中间的那条水力压裂缝为研究目标, 分析其不同时刻的开度分布见图17, 图中能看出XFEM-MBEM与COMSOL-SFEM不同时刻裂缝开度的计算结果较为吻合, 可以说明XFEM-MBEM流固耦合模拟的准确性. 此外, 从图中可以随着油藏的不断开发, 裂缝呈不断闭合的趋势, 定压生产下靠近井筒附近的裂缝段闭合更加剧烈. 图18为该模型在表1参数条件下考虑流固耦合作用与不考虑流固耦合作用的生产动态曲线对比, 可以看出应力场所引起的渗流参数改变及裂缝开度降低对产能的影响很大, 因此对致密油藏压裂水平井进行产能评价时, 地质力学效应的影响不可忽略.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
致密油藏示意图



Figure
12.
Sketch of tight oil reservoir



下载:
全尺寸图片
幻灯片





表
1
致密油藏基本参数



Table
1.
Basic parameters of tight oil reservoir



table_type1 ">
PropertiesValuePropertiesValue
reservoir scale/m750×340SRV scale/m590×220
initial reservoir pressure/MPa25reservoir thickness/m10
matrix porosity0.12matrix permeability/mD0.1
matrix Young’s modulus/GPa50matrix Poisson’s ratio0.3
matrix Biot’s coefficient0.8initial water saturation0.3
fracture porosity0.4fracture permeability/mD5000
initial fracture aperture/m0.001fracture proppant Young's modulus/MPa500





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
两种数值模拟器的网格剖分对比



Figure
13.
Comparison of mesh generation between two numerical simulators



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
两种数值模拟器开发1000 d的压力场对比(单位: MPa)



Figure
14.
Comparison of pressure distribution maps over 1000 days of two simulators (unit: MPa)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
两种数值模拟器开发1000 d的X-位移场对比(单位: mm)



Figure
15.
Comparison of X-displacement distribution maps over 1000 days of two simulators (unit: mm)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
两种数值模拟器开发1000 d的Y-位移场对比(单位: mm)



Figure
16.
Comparison of Y-displacement distribution maps over 1000 days of two simulators (unit: mm)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
不同时刻裂缝开度分布



Figure
17.
Fracture aperture distribution at different time



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-300-18.jpg'"
class="figure_img
figure_type1 bbb " id="Figure18" />



图
18
考虑与不考虑流固耦合作用的生产动态曲线对比



Figure
18.
Comparison of production dynamic curveswith and without flow-geomechanics coupled effect



下载:
全尺寸图片
幻灯片



6.
结 论


(1)本文提出了基于XFEM-MBEM的嵌入式离散裂缝模型流固耦合数值模拟方法, 采用正交的非匹配型网格进行几何离散, 其优势在于裂缝独立于计算网格, 与常规离散裂缝模型基于裂缝形状的匹配型网格相比, 网格划分难度大大降低, 能避免当裂缝间距或夹角非常小时, 网格划分质量不佳等问题. 本文通过几个实例分别验证了其力学模块、流动模块、耦合模块的准确性.

(2)传统EDFM方法对于第4类非相邻连接关系在计算包含裂缝单元的基质网格内的压力分布时采用了线性分布假设, 导致了开发早期及非稳态流动计算精度的不足. 局部网格加密技术可以减小包含裂缝网格的基质网格尺寸, 从而有效解决这个问题, 但会对前处理算法带来巨大的复杂性. 本文采用MBEM方法获取了双孔基质网格向裂缝网格传质量的新近似格式, 能在不加密情况下提高早期计算精度.

(3) SRV改造区内的微裂缝对提高储层流体的动用程度有重要影响. 然而, 用EDFM和XFEM进行显式表征是较为困难的, 且会增加计算耗时. 本文采用双孔有效应力原理耦合双重介质模型隐式表征SRV区内部的天然裂缝, 能有效模拟具有复合分区特征的此类裂缝性油藏问题.

(4)致密油藏开发过程中随着缝内流体被采出, 裂缝会出现不同程度的闭合, 从而导致了整体导流能力降低, 油藏采收率将降低. 考虑到非常规储层原油的产量对裂缝的依赖性如此之高. 因此, 考虑开发过程中流固耦合作用引起的参数变化对产量的评价具有重要意义.

附录






$$ {boldsymbol{G}} = left[ {begin{array}{*{20}{l}} {{c_{{
m{M}}1,1}}}&{{c_{{
m{M}}1,2}}}&{{c_{{
m{M}}1,3}}}&{{c_{{
m{M}}1,4}}} {{c_{{
m{M}}2,1}}}&{{c_{{
m{M}}2,2}}}&{{c_{{
m{M}}2,3}}}&{{c_{{
m{M}}2,4}}} {{c_{{
m{M}}3,1}}}&{{c_{{
m{M}}3,2}}}&{{c_{{
m{M}}3,3}}}&{{c_{{
m{M}}3,4}}} {{c_{{
m{M}}4,1}}}&{{c_{{
m{M}}4,2}}}&{{c_{{
m{M}}4,3}}}&{{c_{{
m{M}}4,4}}} end{array}}
ight]tag{A1} $$






$$ {c_{{
m{M}}i,j}} = int_{{S_{{
m{b}}j}}} {{G_{
m{H}}}} left( {{x_{{
m{m}}i}},{y_{{
m{m}}i}};x,y}
ight){
m{d}}s(x,y)tag{A2} $$






$$ partial {boldsymbol{G}}/partial{boldsymbol{ n }}= left[ {begin{array}{*{20}{l}} {{
m{d}}{c_{{
m{M}}1,1}}}&{{
m{d}}{c_{{
m{M}}1,2}}}&{{
m{d}}{c_{{
m{M}}1,3}}}&{{
m{d}}{c_{{
m{M}}1,4}}} {{
m{d}}{c_{{
m{M}}2,1}}}&{{
m{d}}{c_{{
m{M}}2,2}}}&{{
m{d}}{c_{{
m{M}}2,3}}}&{{
m{d}}{c_{{
m{M}}2,4}}} {{
m{d}}{c_{{
m{M}}3,1}}}&{{
m{d}}{c_{{
m{M}}3,2}}}&{{
m{d}}{c_{{
m{M}}3,3}}}&{{
m{d}}{c_{{
m{M}}3,4}}} {{
m{d}}{c_{{
m{M}}4,1}}}&{{
m{d}}{c_{{
m{M}}4,2}}}&{{
m{d}}{c_{{
m{M}}4,3}}}&{{
m{d}}{c_{{
m{M}}4,4}}} end{array}}
ight] tag{A3}$$






$$ {{{
m{d}}}}{c_{{
m{M}}i,j}} = left{ {begin{array}{*{20}{l}} {displaystyleint_{{S_{{
m{b}}j}}} {frac{{partial {G_{
m{H}}}left( {{x_{{
m{m}}i}},{y_{{
m{m}}i}};x,y}
ight)}}{{partial {boldsymbol{n}}}}} cdot {
m{d}}s(x,y) - lambda left( {{x_{{
m{m}}i}},{y_{{
m{m}}i}}}
ight),{text{ }}i = j} {displaystyleint_{{S_{{
m{b}}j}}} {frac{{partial {G_{
m{H}}}left( {{x_{{
m{m}}i}},{y_{{
m{m}}i}};x,y}
ight)}}{{partial {boldsymbol{n}}}}} cdot {
m{d}}s(x,y),{text{ }}i ne j} end{array}}
ight. tag{A4}$$






$$ {{boldsymbol{G}}_{{
m{mF}}}} = left[ {begin{array}{*{20}{c}} {{c_{{
m{FM}}1,1}}}&{{c_{{
m{FM}}1,2}}}& cdots &{{c_{{
m{FM}}1,{n_{
m{F}}}}}} {{c_{{
m{FM}}2,1}}}&{{c_{{
m{FM}}2,2}}}& cdots &{{c_{{
m{FM}}2,{n_{
m{F}}}}}} vdots & vdots & ddots & vdots {{c_{{
m{FM}}4,1}}}&{{c_{{
m{FM}}4,2}}}& cdots &{{c_{{
m{FM}}4,{n_{
m{F}}}}}} end{array}}
ight] tag{A5}$$






$$ {c_{{
m{FM}}i,j}} = int_{{S_{{
m{F}}j}}} {{G_{
m{H}}}} left( {{x_{{
m{m}}i}},{y_{{
m{m}}i}};x,y}
ight){
m{d}}s(x,y) tag{A6}$$






$$ {{boldsymbol{G}}_{
m{F}}} = left[ {begin{array}{*{20}{c}} {{c_{{
m{MF}}1,1}}}&{{c_{{
m{MF}}1,2}}}& ldots &{{c_{{
m{MF}}1,4}}} {{c_{{
m{MF}}2,1}}}&{{c_{{
m{MF}}2,2}}}& ldots &{{c_{{
m{MF}}2,4}}} vdots & vdots & ddots & vdots {{c_{{
m{MF}}{n_F},1}}}&{{c_{{
m{MF}}{n_F},2}}}& ldots &{{c_{{
m{MF}}{n_F},4}}} end{array}}
ight]tag{A7} $$






$$ {c_{{
m{MF}}i,j}} = int_{{S_{{
m{b}}j}}} {{G_{
m{H}}}} left( {{x_{{
m{F}}i}},{y_{{
m{F}}i}};x,y}
ight){
m{d}}s(x,y) tag{A8}$$






$$ partial {{boldsymbol{G}}_{
m{F}}}/partial {boldsymbol{n}} = left[ {begin{array}{*{20}{c}} {{
m{d}}{c_{{
m{MF}}1,1}}}&{{
m{d}}{c_{{
m{MF}}1,2}}}& cdots &{{
m{d}}{c_{{
m{MF}}1,4}}} {{
m{d}}{c_{{
m{MF}}2,1}}}&{{
m{d}}{c_{{
m{MF}}2,2}}}& cdots &{{
m{d}}{c_{{
m{MF}}2,4}}} vdots & vdots & ddots & vdots {{
m{d}}{c_{{
m{MF}}{n_{
m{F}}},1}}}&{{
m{d}}{c_{{
m{MF}}{n_{
m{F}}},2}}}& cdots &{{
m{d}}{c_{{
m{MF}}{n_{
m{F}}},4}}} end{array}}
ight] tag{A9}$$






$$ {{{
m{d}}}}{c_{{
m{MF}}i,j}} = int_{{S_{{
m{b}}j}}} {frac{{partial {G_{
m{H}}}left( {{x_{{
m{F}}i}},{y_{{
m{F}}i}};x,y}
ight)}}{{partial {boldsymbol{n}}}}} cdot {
m{d}}s(x,y) tag{A10}$$






$$ {{boldsymbol{G}}_{{
m{FF}}}} = left[ {begin{array}{*{20}{c}} {{c_{{
m{FF}}1,1}}}&{{c_{{
m{FF}}1,2}}}& ldots &{{c_{{
m{FF}}1,{n_F}}}} {{c_{{
m{FF}}2,1}}}&{{c_{{
m{FF}}2,2}}}& ldots &{{c_{{
m{FF}}2,{n_F}}}} vdots & vdots & ddots & vdots {{c_{{
m{FF}}{n_F},1}}}&{{c_{{
m{FF}}{n_F},2}}}& cdots &{{c_{{
m{FF}}{n_F},{n_F}}}} end{array}}
ight]tag{A11} $$






$$ {c_{{
m{FF}}i,j}} = int_{{S_{{
m{F}}j}}} {{G_{
m{H}}}} left( {{x_{{
m{F}}i}},{y_{{
m{F}}i}};x,y}
ight){
m{d}}s(x,y)tag{A12} $$

相关话题/计算 图片 力学 水力 裂缝
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 磁力耦合道路能量收集设计与动力学分析
    引言智慧城市[1-2]旨在利用互联网、物联网等通讯技术和传感技术构建万物互联的城市,使得城市管理更加有序和高效.智慧交通是智慧城市的重要组成之一.构建智慧交通需要布置大量传感器和网络通讯设备,传统的供能方式主要是电池和有线传输,但存在污染环境、寿命短、成本高、不易维护等问题.道路交通系统中蕴藏着丰富 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 压电与摩擦电复合型旋转能量采集动力学协同调控机制研究
    引言物联网技术的蓬勃发展开启了万物互联的时代,带领人类进入一个智能化的世界,如智能可穿戴设备、智慧家居、智能工业等[1-2].物联网的基础是数以亿万计的广泛分布的智能传感器,可以进行信息和数据的获取、分析、处理和传输[3-5].然而,如何为这些分布范围广、数量大的传感器提供长期有效的电能是物联网技术 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 线形?拱形组合梁式三稳态压电俘能器动力学特性研究
    引言无线监测技术在设备监测和安全监测等领域的应用越来越广泛[1-3],但无线监测系统的续航问题一直制约其发展,化学电池供电存在维护成本高、环境污染和寿命有限等问题[4].振动能量俘获技术可以将环境振动能收集并转换为电能,有望实现无线监测系统自供电[5-8].压电悬臂梁俘能器具有结构简单、尺寸紧凑等优 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 活性流体流变行为的布朗动力学模拟研究
    引言存在于自然界中(如大肠杆菌[1])或是人工合成的(如Janus粒子[2])活性粒子(activeparticles)能够将其周围环境中各种形式的能量转化为空间运动的动能,驱动自身运动并扰动周围流场.包含大量活性粒子的悬浮液被称为活性流体(activefluids).被动粒子(passivepar ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 正常和早期膝骨关节炎的软骨生物力学研究
    引言软骨是人体关节中非常重要的一种承重组织[1-2].它不仅可以减少关节的运动摩擦,而且能通过增大关节的接触面积来分散载荷、减少应力集中.软骨由纤维、蛋白聚糖、软骨细胞和大量的水分组成[1].根据内部纤维结构,软骨通常分为3层[1]:表层(占比10%~20%)、中层(占比40%~60%)和深层(占比 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 机器学习在力学模拟与控制中的应用专题序
    近几年来,随着高性能计算机和大数据科学的快速发展,机器学习方法在各个领域得到了越来越多的应用.力学学科在过去几十年积累了大量的数值模拟数据、实验测量数据和现场监测数据,这些大规模、高维度的数据蕴含了丰富的物理特征,但传统方法无法有效地处理这些庞大的数据群.机器学习方法可以从巨量的数据海洋中挖掘有用的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于离散单元法和人工神经网络的近壁颗粒动力学特征研究
    引言密集颗粒流及气粒两相流大量应用于食品和药物加工、石油化工和能源转化等行业.由于颗粒与颗粒之间及气体与颗粒之间存在强烈的非线性耗散作用,密集颗粒流及气粒流动中往往会出现复杂的非均匀多尺度流动现象[1-5].近年来,国内外诸多****致力于采用数值模拟方法来研究这种复杂流动,目前针对颗粒相的数值模拟 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 多相流动的光滑粒子流体动力学方法研究综述
    引言多相流广泛存在于自然界和工业应用中.对多相流进行高精度和高效率的建模和模拟非常重要.然而,其中流动形态和界面跟踪的复杂性限制了基于网格的传统方法模拟多相流能力,尤其对于存在界面大变形、不连续性和多物理过程的多相流动.而无网格方法可以很好地处理网格方法遇到的上述问题.在过去几十年发展起来的无网格方 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.