删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

正常和早期膝骨关节炎的软骨生物力学研究

本站小编 Free考研考试/2022-01-01


引言


软骨是人体关节中非常重要的一种承重组织[1-2]. 它不仅可以减少关节的运动摩擦, 而且能通过增大关节的接触面积来分散载荷、减少应力集中. 软骨由纤维、蛋白聚糖、软骨细胞和大量的水分组成[1]. 根据内部纤维结构, 软骨通常分为3层[1]: 表层(占比10% ~ 20%)、中层(占比40% ~ 60%)和深层(占比约30%). 在表层, 纤维方向平行于软骨表面; 在中层, 纤维分布没有特定方向; 在深层, 纤维方向垂直于软骨表面. 由于软骨复杂的组成成分和结构, 其具有特殊的力学性质[1]. 例如, 软骨是一种固?液双相材质, 其承受瞬间载荷时, 软骨中的液相会承担大部分载荷, 从而减少软骨固相基质的变形; 软骨内部纤维具有抗拉伸能力, 软骨表层中平行于软骨表面的纤维的抗拉伸能力可以有效地抵抗软骨的侧向扩张[3], 能有效减小软骨固相基质的变形, 避免软骨产生过大应变而导致软骨受损和退变.

膝骨关节炎是老年人中常见的慢性膝关节疾病[4], 其恶化伴随着软骨的退变、磨损和最终缺失[4-5]. 软骨的退变和磨损通常认为是从表层发展到深层, 该过程中软骨的组成成分、结构和力学性质会发生改变[5], 如蛋白聚糖降解、纤维退变、水含量和渗透率增大以及纤维方向变得无序等等. 由于这些改变, 软骨的液相承载能力和纤维的抗拉伸能力等等会大大下降, 从而进一步影响了关节的生物力学[4].

早期膝骨关节炎会对软骨生物力学造成影响[4], 有时也会造成关节疼痛[6]. 研究表明[4, 7], 早期内侧膝骨关节炎会引起内侧软骨流体压力下降以及外侧软骨接触应力增大等力学变化. 此外, 与内侧早期膝骨关节炎的患者相比, 内外侧膝骨关节炎的患者通常具有更严重滑膜炎[8]; 而且在日常活动中, 内外侧早期膝骨关节炎的患者感觉更加疼痛[6]. 但目前导致正常、内侧和内外侧早期膝骨关节炎3种情况下的临床差异的机理尚未明确. 因此, 研究正常、内侧与和内外侧早期膝骨关节炎的软骨生物力学差异, 能从生物力学角度为理解早期膝骨关节炎提供帮助, 以便更好地计划预防和治疗方案.

目前通过实验测定关节软骨生物力学参数十分困难, 因此人们通常应用有限元方法进行关节软骨生物力学的研究[9-10]. 由于建模简单且计算时间短, 单相各向同性的软骨有限元模型使用最广泛[11-14], 但其提供的计算精度和力学信息有限. 近期, 张吉超等[15]的综述报道, 国内近5年膝关节有限元研究中的软骨模型仍采用单相各向同性模型. 然而软骨的力学行为受其固相和液相的相互作用、纤维网络和深度相关属性的影响[10, 16-17]. 因此, 为了更精确地反映软骨内部复杂的纤维结构和组成成份, 需要构建更加先进的模型. 国外文献报道中, 固?液双相有限元模型[1]考虑了固?液双相成份; 双相纤维增强有限元模型[10, 18]考虑了软骨内部的纤维结构; 非均质双相纤维增强有限元模型[17, 19]考虑了软骨深度相关和应变相关的属性. 但截至目前, 国内尚未有膝关节有限元研究应用双相纤维增强的软骨模型进行力学分析. 因此, 构建基于双相纤维增强软骨模型的膝关节有限元模型对推动国内生物力学的发展有着重要的意义.

前期的膝骨关节炎有限元研究中, 国内张震等[12]通过轻度膝骨关节炎的MRI和CT数据构建了关节炎早期软组织的形貌特征, 分析了软骨和半月板的应力分布特征, 但是其模型没有考虑软骨和半月板的固液双相属性, 也没有考虑退变软骨的属性变化. 国外Dabiri和Li[4]构建了早期退变软骨模型来研究膝关节力学的变化, 虽然研究考虑了软骨和半月板的固液双相纤维增强属性, 但是该模型仅施加的0.1 mm的压缩载荷, 没有模拟体内膝关节真实的生理载荷. Mononen等[7]通过构建内侧股骨髁关节炎的固液双相纤维增强软骨模型, 在生理载荷下研究了纤维分布对软骨承载能力影响, 但其未考虑膝关节中真实的固液双相接触条件, 即接触区域的流体流动取决于接触区域界面的流体压力差, 而非接触区域允许流体自由流动[17, 20]. 综上所述, 目前尚未有研究应用固液双相纤维增强软骨模型及真实的双相接触条件分析早期膝骨关节炎的软骨生物力学.

本文构建了基于固液双相纤维增强软骨模型的膝关节有限元模型, 应用行走姿态下生理载荷和真实的固液双相接触条件, 对比研究了膝关节正常、内侧与内外侧早期膝骨关节炎3种情况下的软骨生物力学差异, 以期为临床上更好地理解、预防和治疗早期膝骨关节炎提供理论支撑.


1.
材料和方法


基于生物力学有限元软件FEBio(版本2.9, www.febio.org), 本文构建了正常膝关节模型、内侧早期膝骨关节炎模型和内外侧早期膝骨关节炎模型.


1.1
正常膝关节模型


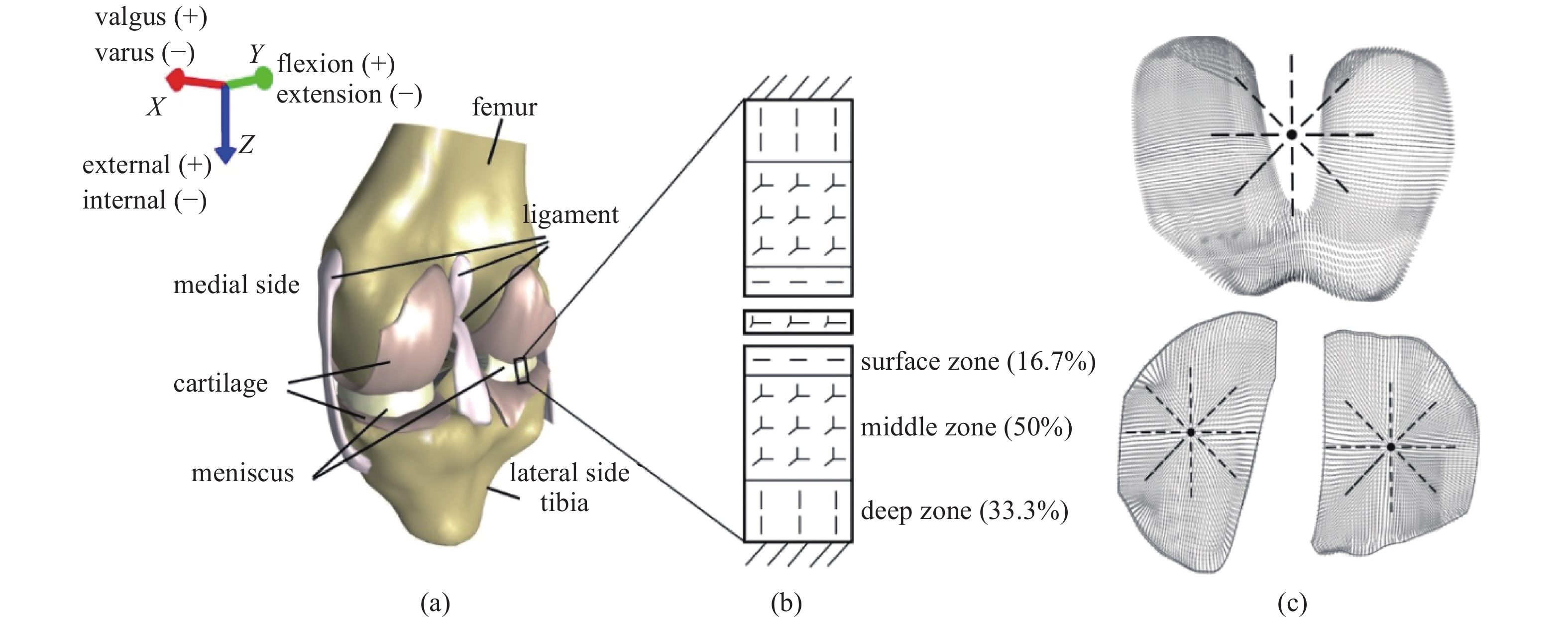
本文采用了来自“open knee project” 项目[21]中一名70岁女性捐献者(体重77.1 kg)的右膝关节模型, 该模型已在之前的研究中采用并验证[22]. 通过1.0 Tesla肢体扫描仪采集膝关节完全伸展位置的磁共振图像, 从图像中重建出包括股骨、胫骨、软骨、半月板和韧带在内的膝关节三维模型(如图1所示). 在Hypermesh (版本 14.0; Altair Engineering, Inc., Troy, MI, USA)对模型进行网格划分, 骨头使用四边形壳单元, 其他软组织使用六面体单元. 通过网格收敛性分析, 六面体单元数量为95000左右时, 相对于单元数量为190000左右时, 接触应力和流体压力变化小于5%[10, 22], 最终确定六面体单元的尺寸范围在0.5 ~ 1.0 mm之间.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//21-390-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />



图
1
(a)膝关节的几何模型; (b)软骨、半月板纤维分布模式; (c)软骨表层纤维的自然放射线分布模式



Figure
1.
(a) The geometry of the knee joint ; (b) fibrillar distributions pattern of cartilage and meniscus ; (c) the natural split-line patterns in surface zone



下载:
全尺寸图片
幻灯片


由于骨头的刚度远大于其他软组织, 因此将股骨和胫骨设为刚体[12, 23]. 软骨和半月板设为双相纤维增强材料[16-17], 由非纤维材料Neo-Hookean、纤维材料和液相组成. 参照先前开发的模型[17], 软骨设为深度相关的材料属性, 包括弹性模量、泊松比、固相比和渗透率[24-25](如表1所示). 软骨纤维方向在深度方向是变化的, 如图1所示, 纤维在表层平行于软骨表面, 而且呈放射线分布[7]; 纤维在中间层在3个方向上均匀分布; 纤维在深层垂直于软骨表面. 半月板内部纤维呈周向和径向分布[22].




表
1
本文中软骨、退变软骨和半月板的材料属性(E: 弹性模量; v: 泊松比; φs: 固相比; k: 渗透率)



Table
1.
Material properties of cartilage, degenerated cartilage and meniscus in this study (E: Young's modulus; ν: Poisson's ratio; φs: solid volume fraction; k: permeability)



table_type2 ">
TissueZoneE/MPavφsk/(mm4·N?1·s?1)Fibrillar modulus/MPa
cartilage[17, 24-25]surface zone0.620.140.110.001096 (parallel to surface)
middle zone1.190.250.180.001516 (randomly distributed)
deep zone1.940.40.270.000866 (perpendicular to surface)
degenerated cartilage[4, 7, 26]surface zone0.1860.140.060.001851.5 (randomly distributed)
middle zone0.3570.250.130.002571.5 (randomly distributed)
meniscus[22]?0.50.360.190.0010040 (circumferential),
10 (radial)





下载:
导出CSV
|显示表格



根据先前研究[17, 22], 材料Neo-Hookean的应变能函数定义为







$$ {{{W}}_1} = frac{mu }{2}({I_1} - 3) - mu {
m{ln}}J + frac{{
m{lambda}} }{2}{({
m{ln}}J)^2}$$
(1)

式中, J为相对体积(当前体积/初始体积); I1为右柯西-格林变形张量的第一不变量; μ和λ为拉梅常数, 通过泊松比v和弹性模量E可以计算获得







$$ left. begin{array}{l}lambda = dfrac{{vE}}{{(1 + v)(1 - 2v)}};mu = dfrac{E}{{2(1 + v)}}end{array}
ight} $$
(2)

纤维的应变能函数定义为[22, 27]







$$varPsi = frac{xi }{{alpha beta }}left[ {{
m{e}}^ {alpha {{left( {{I_{
m{n}}} - 1}
ight)}^beta }} - 1}
ight]$$
(3)

式中, ξ为纤维模量数值的1/4, α为指数参数的系数, β为指数参数的幂, In为纤维伸长量的平方.

当α→0时, 式(3)会产生一个幂法则







$$mathop {{
m{lim}}}limits_{alpha to 0} varPsi = frac{xi }{beta }{left( {{I_{
m{n}}} - 1}
ight)^beta }$$
(4)

纤维只能拉伸, 压缩时不起作用. 因此本文中选择α = 0和β = 2, 来实现应力从压缩到拉伸不连续性转变[17].

软骨应变相关的渗透率(k)呈指数递减[28]







$$k(J) = {k_0}{left( {frac{{J - {varphi _{
m{s}}}}}{{1 - {varphi _{
m{s}}}}}}
ight)^{{alpha _e}}}{{
m{e}}^{frac{1}{2}M({J^2}-1)}}$$
(5)

式中, k0为初始渗透率, φs为固相比, M为应变相关的指数常数, αe为幂法则指数. 根据先前实验[28], 本研究选择M = 4.638和αe = 0.0848来实现应变相关的渗透率.

韧带为纤维增强材料, 由非纤维材料Mooney-Rivlin和纤维材料组成, 包括前交叉韧带(anterior cruciate ligament, ACL)、后交叉韧带(posterior cruciate ligament, PCL)、内侧副韧带(medial collateral ligament, MCL)、外侧副韧带(lateral collateral ligament, LCL). 材料参数[21]如表2所示.




表
2
本文中韧带的材料属性[21]



Table
2.
Material properties of ligaments in this study[21]



table_type1 ">
LigamentC1C2KC3C4C5$ {{ {
m{lambda}} }}_{
m{m}} $
ACL1.95073.20.0139116.22535.0391.046
PCL3.2501220.119687.178431.0361.035
MCL1.4403970.5748467.11.063
LCL1.4403970.5748467.11.063





下载:
导出CSV
|显示表格



韧带材料的应变能函数定义为[21]







$$begin{split} {{{W}}_2} =& {C_1}left( {{{tilde I}_1} - 3}
ight) + {C_2}left( {{{tilde I}_2} - 3}
ight) + frac{K}{2}{left( {{
m{ln}}J}
ight)^2} + &left{ begin{aligned} &0 ,;;;;;;;qquadqquadqquadqquadqquadqquad{tilde {
m{lambda}} leqslant 1}&{{C_3}left{ {{{
m{e}}^{ - {C_4}}}left[ {{{Ei}}left( {{C_4}tilde {
m{lambda}} }
ight) - {{Ei}}left( {{C_4}}
ight)}
ight] - {
m{ln}}tilde {
m{lambda}} }
ight}},;;{1 < tilde {
m{lambda}} < {{
m{lambda}} _{
m{m}}}}&{{C_5}left( {tilde {
m{lambda}} - 1}
ight) + {C_6}{
m{ln}}tilde {
m{lambda}} },qquadqquadqquadquad;{tilde {
m{lambda}} geqslant {{
m{lambda}} _{
m{m}}}}end{aligned}
ight.end{split}$$
(6)

式中, C1和C2为Mooney-Rivlin常数, C3至C6为纤维函数常数; $ {tilde {I}}_{{1}} $和$ {tilde {I}}_{{2}} $分别为偏右柯西-格林变形张量的第一和第二不变量; K为体积弹性模量; Ei(?)为指数积分函数; $ tilde {{ {
m{lambda}} }} $为沿纤维方向拉伸的偏量; $ {{ {
m{lambda}} }}_{
m{m}} $为拉直纤维的伸展量.

软骨的底面和韧带的末端都固定在骨头上[12]. 半月板两端通过线性弹簧固定在胫骨上, 各端弹簧总刚度为2 kN/mm[18]. 软骨对软骨、软骨对半月板之间的接触设置为双相接触, 并且接触界面为无摩擦[22]. 在双相接触表面, 在接触区域流体的流动取决与接触界面的流体压力差, 在无接触区域流体可以自由流动[17, 20]. 该双相接触条件可以通过FEBio自带的“biphasic contact”接触条件来实现.


1.2
膝骨关节炎模型


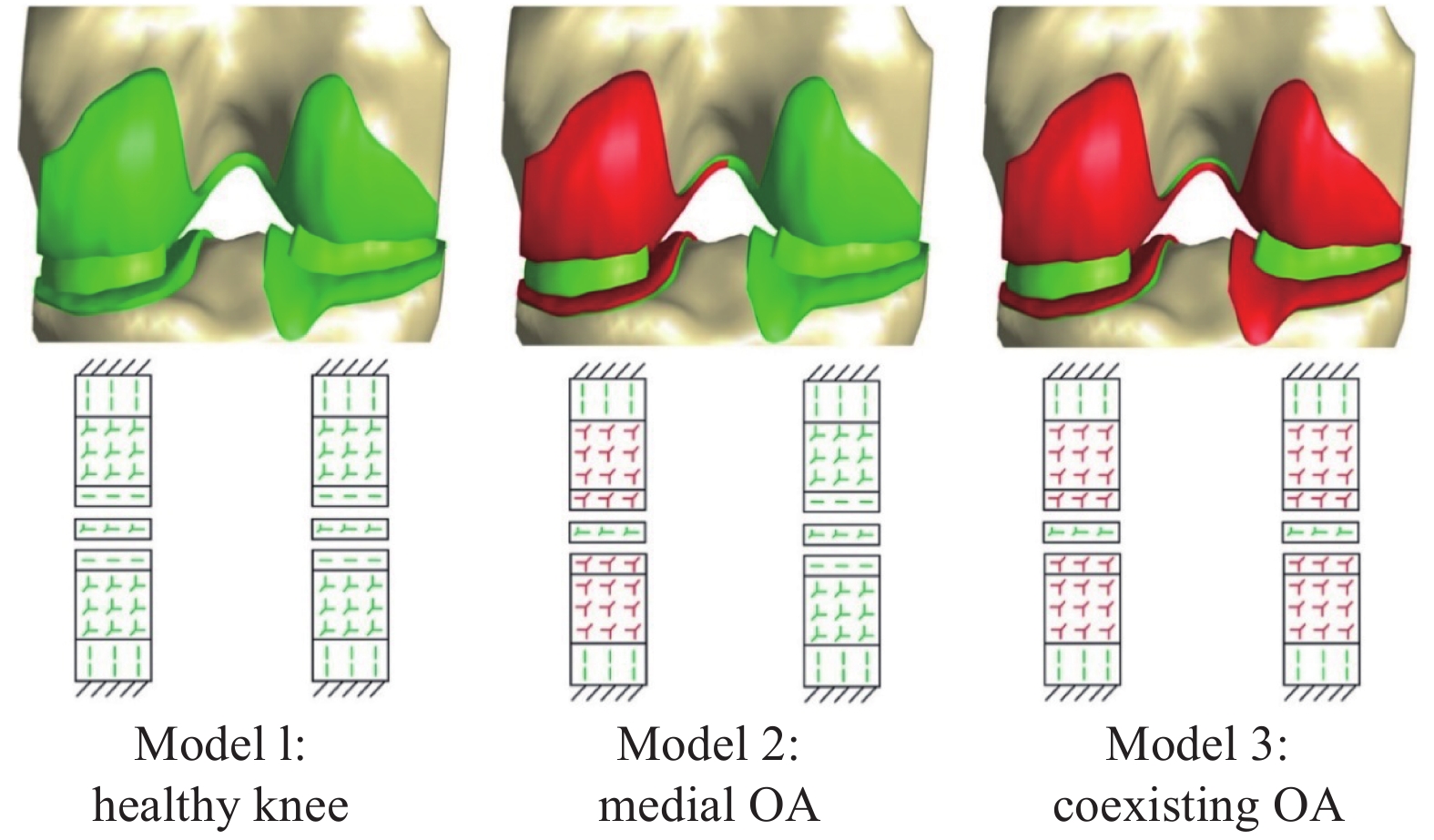
通过更改自然膝关节模型的软骨表层和中间层的材料属性和纤维分布来模拟早期关节炎. 根据研究报道[4, 7, 26], 相比自然膝关节模型, 早期膝骨关节炎模型中的退变软骨的表层和中间层的非纤维固相基质的弹性模量和纤维的弹性模量分别减少65%和75%; 渗透率增加70%; 固相比减少5%; 纤维方向随机分布(如表1和图2所示), 其他参数保持不变. 至此, 如图2所示, 在本研究中定义正常膝关节为模型1, 内侧早期膝骨关节炎为模型2, 内外侧早期膝骨关节炎为模型3.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//21-390-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
不同的膝骨关节炎模型以及它们的纤维分布模式, 绿色代表正常组织及正常的纤维方向, 红色代表退变组织及随机分布的纤维方向



Figure
2.
Different models of knee OA and their fibrillar distributions pattern. The green denoted the normal tissue and fibrillar direction, and the red denoted the degenerated tissue and randomly distributed fibrillar direction



下载:
全尺寸图片
幻灯片



1.3
载荷和边界条件


首先, 为了验证膝关节模型的合理性, 本研究对模型一的股骨施加1 kN的垂直载荷, 将求解的股骨垂直位移和软骨接触应力与文献结果[29-32]进行对比. 胫骨完全固定, 股骨屈曲运动被约束. 参考膝关节假体磨损试验的载荷施加ISO标准(ISO 14243—3:2014), 将1 kN压缩载荷施加在股骨的参考点上, 该参考点位于关节中心偏内侧5 mm处[22].

在模型验证之后, 在1 s内采用步态周期内最大载荷时刻(3倍体重[33], 13%步态周期)和最大屈曲角度时刻(屈曲58°, 72%步态周期)的力和运动作为边界条件, 分别对模型1 ~ 3进行求解计算, 输出了软骨的流体压力、应变和应力等力学信息.


2.
结果


如表3所示, 通过与先前实验测得的股骨垂直位移和关节接触应力对比, 对双相膝关节建模方法的合理性进行了验证. 在轴向载荷1 kN下, 本文中股骨垂直位移为1.11 mm, 文献[22, 29-30]报道范围在0.70 mm至1.25 mm之间; 本文中关节峰值接触应力为3.4 MPa, 文献[30-32]报道范围为2.68 ~ 5.85 MPa之间. 本文结果均在实验结果和仿真结果报道范围之内, 双相膝关节模型的合理性得到了验证. 在许多膝关节有限元研究中[7, 11, 22], 股骨垂直位移和关节接触应力分别经常被采用以验证模型的合理性, 它们分别体现了膝关节整体和局部信息. 股骨的垂直位移是膝关节软组织的整体刚度的体现[22, 29], 对应的是软组织在承受载荷时的总变形量, 是膝关节整体测得的数据; 接触应力是胫骨软骨和股骨软骨两个相对表面之间载荷传递和接触面积的体现[22, 30], 是膝关节局部测得的数据. 因此, 膝关节整体和局部信息结合可以有效地验证模型的合理性.




表
3
本文中模型1在1 kN载荷下的股骨垂直位移和软骨接触应力和先前实验/仿真结果的对比



Table
3.
Comparison of the femoral vertical displacement and the contact pressure under 1 kN load between the predicted results of Model 1 and published experimental/computational studies



table_type2 ">
StudiesFemoral displacement/mmContact pressure/MPa
mediallateral
experimentalRef. [29]0.87 ± 0.17??
Ref. [30]1.252.52.7
Ref. [31]?3.84 ± 1.245.08 ± 0.77
computationalRef. [22]1.02??
Ref. [32]?2.682.43
this study1.113.43.2





下载:
导出CSV
|显示表格



在最大载荷时刻, 模型1 ~ 3的软骨流体压力、固相等效应力和压缩应变如图3所示. 与模型1相比, 模型2的内侧软骨的流体压力和固相等效应力都明显减少, 分别减少18.1%和13.3%, 而外侧软骨的流体压力和固相等效应力变化小于2%; 模型3的内侧软骨的流体压力和固相等效应力都明显减少, 分别减少18.8%和13.3%, 外侧软骨的流体压力和固相等效应力也都有明显减少, 分别减少16.7%和14.5%. 模型2的内侧软骨的压缩应变增大5.0%; 模型3的内外侧软骨的压缩应变都有明显增大, 分别增大5.0%和13.2%. 与模型1相比, 模型2和模型3的退变软骨出现应力与应变相反的变化趋势是由于相同载荷下软骨的弹性模量下降所造成的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//21-390-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
模型1至模型3在最大载荷时刻下的预测结果: 流体压力、固相等效应力和压缩应变



Figure
3.
The predicted results of Model 1 to 3 under the maximum load situation: fluid pressure; effective solid stress; compressive strain.



下载:
全尺寸图片
幻灯片


在最大载荷时刻, 模型1 ~ 模型3的软骨第一主应变和最大剪应变如图4所示. 从图中可以得知, 与模型1相比, 模型2的内侧软骨的第一主应变和最大剪应变分别增大了19.8%和20.0%, 外侧软骨应变没有太大变化; 模型3的内外侧软骨的第一主应变和最大剪应变均明显增大了, 增大范围在19.0% ~ 46.0%之间.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//21-390-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
模型1 ~ 模型3在最大载荷时刻下的预测结果



Figure
4.
The predicted results of Model 1 to 3 under the maximum load situation



下载:
全尺寸图片
幻灯片


在最大屈曲角度时刻, 模型1 ~ 模型3的软骨流体压力、固相等效应力和压缩应变如图5所示, 结果与最大载荷时刻的结果趋势一致, 但数值相对较小. 从图中可以得知, 与模型1相比, 模型2的内侧软骨的流体压力和固相等效应力都明显减少, 分别减少25.9%和29.1%, 而外侧软骨的流体压力和固相等效应力变化小于5.5%; 模型3的内侧软骨的流体压力和固相等效应力都明显减少, 分别减少26.5%和32.1%, 外侧软骨的流体压力和固相等效应力也都有明显减少, 分别减少13.0%和28.3%%. 模型2的内侧软骨的压缩应变增大26.9%; 模型3的内侧和外侧软骨的压缩应变都有明显增大, 分别增大26.9%和20.8%.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//21-390-5.jpg'"
class="figure_img
figure_type2 ccc " id="Figure5" />



图
5
模型1 ~ 模型3在屈曲角度时刻下的预测结果: 流体压力、固相等效应力和压缩应变



Figure
5.
The predicted results of Model 1 to 3 under the maximum flexion angle situation: fluid pressure; effective solid stress; compressive strain



下载:
全尺寸图片
幻灯片


在最大屈曲角度时刻, 模型1至模型3的软骨第一主应变和最大剪应变如图6所示. 从图中可以得知, 与模型1相比, 模型2的内侧软骨的第一主应变和最大剪应变分别增大76.3%和59.6%, 外侧软骨应变没有太大变化; 当模型3的内侧软骨的第一主应变和最大剪应变分别增大73.2%和56.7%, 外侧软骨应变没有太大变化. 模型2和模型3的第一主应变和最大剪应变结果区别不大, 可能是因为最大屈曲角度时刻的载荷较小, 因此不同膝骨关节炎模型的第一主应变和最大主应变区别不明显.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//21-390-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
模型1 ~ 模型3在最大屈曲角度时刻下的预测结果



Figure
6.
The predicted results of Model 1 to 3 under the maximum flexion angle situation



下载:
全尺寸图片
幻灯片



3.
讨论


本文基于固液双相纤维增强的软骨有限元建模方法, 构建了正常膝关节双相有限元模型, 再根据正常模型建立了内侧和内外侧早期膝骨关节炎模型. 之后在步态周期内的瞬时承载情况下和真实的双相接触条件下, 对比研究了正常膝关节、内侧和内外侧早期膝骨关节炎的软骨生物力学差异.

早期膝骨关节炎中退变软骨属性变化对生物力学特征改变的映射关系是复杂的. 总的来说, 退变软骨的非纤维固相基质、纤维、渗透率等的变化导致了软骨流体压力下降、固相等效应力下降以及应变增大. 首先, 渗透率的增加导致退变软骨的流体压力下降. 渗透率的增加加快了流体流动的速度, 从而导致流体压力下降. 流体压力的下降对软骨的负载机制造成影响, 即导致软骨液相承载能力下降. 其次, 非纤维固相基质弹性模量的下降导致非纤维固相基质的强度下降, 从而导致退变软骨的固相等效应力下降, 与先前研究的结果一致[34]. 软骨非纤维固相基质变软会导致固相承载能力下降. 最后, 软骨表层和中间层纤维的纤维弹性模量下降以及纤维方向变得无序加剧了软骨侧向扩张变形, 进而削弱了软骨的抗拉伸能力. 此外, 液相承载能力下降、固相承载能力下降以及抗拉伸能力下降都会导致应变增大, 而应变增大又导致应变相关的渗透率继续增加, 从而又进一步削弱了软骨的液相承载能力. 因此, 膝骨关节炎的退变软骨属性变化对软骨生物力学产生的影响是复杂的、相互关联的, 最终导致软骨的承载能力和抗拉伸能力下降.

膝关节是一个复杂的系统, 退变软骨的承载能力下降和抗拉伸能力下降会加剧软骨进一步退变的风险[4], 进而可能加剧膝关节疼痛. 软骨的承载能力下降和抗拉伸能力下降可能导致软骨变形过大、软骨细胞死亡和纤维退变[19, 35], 甚至可能造成软骨细胞外基质受损从而释放出软骨细胞外基质的内部成分[36-37]. 这些成分通过与滑膜细胞上的受体结合, 从而导致滑膜炎进一步发展[36-37]. 有研究[38]表明滑膜炎反应与膝骨关节疼痛强烈相关. 因此, 内外侧膝骨退变软骨的内外侧承载能力和抗拉伸能力同时下降以及应变增大可能是疼痛感更明显的潜在因素.

将双相纤维增强软骨模型应用到膝关节双相有限元模型中是具有挑战性的. 首先, 软骨组织的组成成分和结构十分复杂[1], 因此其力学性能是高度非线性的, 例如深度相关性和应变相关性. 其成份、结构以及力学参数的测量常常面临着巨大的挑战, 需要进行多种实验才能测得[1, 27]. 其次, 构建一个层状双相纤维增强软骨有限元模型是具有难度的[17]. 由于真实软骨的几何形状十分不规则, 且厚度不均匀. 因此, 在有限元网格划分时, 将软骨划分成多层网格模型是比较困难的. 同时, 为了正确设置软骨内部纤维方向, 还需要调整网格分布方式和网格节点顺序. 再次, 膝关节双相有限元模型收敛难度大于单相模型. 双相有限元模型受载后容易导致网格变形过大, 常常造成收敛困难. 最后, 现有文献中的膝关节双相有限元模型[4, 12, 34]很少考虑和应用了真实的双相接触条件[17, 20]. 大部分膝关节双相有限元研究[4, 12, 34]都是使用Abaqus软件进行分析, 而在Abaqus中需要额外的子程序对接触面间的液体流动进行修正, 才能实现真实的双相接触条件; 而在FEBio软件中, 通过在软件界面设置双相接触就可实现真实的双相接触条件[20]. 总而言之, 目前膝关节双相有限元模型的应用仍存在一些挑战, 但其优势也是十分突出的, 例如能比单相模型提供更加深入的力学及摩擦学分析. 因此膝关节双相有限元模型的应用仍有巨大的潜力和很好的发展前景.

本文仍存在一些局限性. 首先, 当前模型没有考虑各向异性的渗透率[4, 17]. 据文献[4]报道, 平行于纤维方向的渗透率大于垂直于纤维方向的渗透率, 因此, 软骨的渗透率应该是各向异性的. 文献[39]研究表明, 各向异性的渗透率对软骨时间相关行为的影响可以忽略不计, 因为在短时间内, 软骨内部的流体还来不及流出. 本文主要研究和讨论瞬时承载状态, 因此是否采用各向异性的渗透率对本文结果影响不大. 此外, 目前能精确测得软骨各向异性的渗透率的装置设备还有待开发, 将各向异性的渗透率应用到膝盖双相模型中需要后续工作的不断补充与完善. 其次, 当前双相纤维增强软骨模型没有考虑内部的细胞分布[9]. 软骨细胞是软骨中唯一存在的细胞, 其生理状态受应力应变的调控[9, 40], 过大的应力应变会导致软骨细胞的死亡, 从而可能进一步导致软骨退变. 因此, 通过软骨的多尺度模型来研究软骨内部细胞级别的力学信息, 能为认识、预防和减缓软骨退化、关节炎进展提供更有力的帮助. 目前已有研究[9]采用非完全耦合的方法实现软骨的多尺度建模, 即将模型分为总模型(软骨模型)和局部模型(细胞模型). 总模型测得的局部应力和局部位移张量转移到局部模型上, 即可以预测软骨细胞的力学信息. 在未来, 完全耦合的双相多尺度软骨模型还可以耦合到骨肌系统模型中[41], 从而实现个性化边界条件以及精准生物力学的预测. 该方法还有待后续开发和应用. 尽管本文建立的模型仍存在局限性, 但是现有模型也能为研究内侧与内外侧膝骨关节炎的软骨生物力学差异提供一定帮助, 从而为临床上更好的理解、避免和减缓膝骨关节炎发展提供帮助.


4.
结论


本文在国内首次构建了基于固液双相纤维增强软骨模型的膝关节有限元模型, 并采用更真实的在体生理载荷和双相接触条件, 对比研究了膝关节正常、内侧与内外侧早期膝骨关节炎的软骨生物力学差异. 与正常膝关节相比, 早期的膝骨关节炎导致了关节软骨承载能力的降低. 相比内侧早期膝骨关节炎, 内外侧早期膝骨关节炎导致更大的内外侧软骨流体压力减少和应变增大. 基于固?液双相纤维增强软骨模型的膝关节有限元建模方法合理可行, 不仅可以用于体内膝骨关节炎模型的仿真, 还可以推广应用于髋、踝和脊柱等其他关节生物力学的研究. 本研究为更好的理解早期膝骨关节炎造成的关节疼痛, 提供了有力的生物力学依据.

相关话题/力学 生物 材料 软骨 细胞
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 机器学习在力学模拟与控制中的应用专题序
    近几年来,随着高性能计算机和大数据科学的快速发展,机器学习方法在各个领域得到了越来越多的应用.力学学科在过去几十年积累了大量的数值模拟数据、实验测量数据和现场监测数据,这些大规模、高维度的数据蕴含了丰富的物理特征,但传统方法无法有效地处理这些庞大的数据群.机器学习方法可以从巨量的数据海洋中挖掘有用的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于离散单元法和人工神经网络的近壁颗粒动力学特征研究
    引言密集颗粒流及气粒两相流大量应用于食品和药物加工、石油化工和能源转化等行业.由于颗粒与颗粒之间及气体与颗粒之间存在强烈的非线性耗散作用,密集颗粒流及气粒流动中往往会出现复杂的非均匀多尺度流动现象[1-5].近年来,国内外诸多****致力于采用数值模拟方法来研究这种复杂流动,目前针对颗粒相的数值模拟 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度强化学习算法的颗粒材料应力?应变关系数据驱动模拟研究
    引言在研究泥沙、岩土、粉体等颗粒材料宏观力学行为时,通常在连续介质力学框架下建立其唯象本构模型,通过引入内变量来描述颗粒材料的路径相关、历史相关等特性[1-5].虽然基于连续假设的唯象本构模型在描述颗粒材料宏观力学特性时具备很好的工程适用能力,但是颗粒材料由于其自身的离散特性,具有摩擦性,剪胀性,压 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 多相流动的光滑粒子流体动力学方法研究综述
    引言多相流广泛存在于自然界和工业应用中.对多相流进行高精度和高效率的建模和模拟非常重要.然而,其中流动形态和界面跟踪的复杂性限制了基于网格的传统方法模拟多相流能力,尤其对于存在界面大变形、不连续性和多物理过程的多相流动.而无网格方法可以很好地处理网格方法遇到的上述问题.在过去几十年发展起来的无网格方 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度学习和细观力学的颗粒材料本构关系研究
    引言颗粒材料广泛存在于各类自然环境和工程活动中,人类几乎所有的基础设施都建造于岩土材料这类典型的颗粒材料上,理解和预测此类材料在外载作用下的力学响应具有重要的意义.岩土材料通常由粒径不一,形状各异的矿物颗粒以及颗粒之间的空隙组成.颗粒间的互相滑动会引起不可恢复的塑性变形,因而,颗粒材料在剪切作用下极 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 冲击载荷下颗粒材料临边界区域的波动行为及变形特征分析
    引言作为离散颗粒材料的土壤(或岩体),是日常生活中最常见的随机多孔介质,冲击载荷作用下材料的动力学响应对于工程实践和地质灾害防控有着重要的指导意义.注意到应力波的传播行为与介质性质密切相关,基于应力波的行为特征分析可提供一种非侵入式研究颗粒材料性质的途径.因此有非常多的****致力于研究冲击载荷作用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 数据驱动印度洋海域全局动力学研究
    引言海洋系统天然受到多种环境因素(风速、温度、海水含盐量等)、人类活动和天体运动等不确定扰动的影响,导致其洋流运动复杂而多样[1-2].然而,一些观测和研究发现,其内部蕴含着能够对洋流的运动方向和趋势起限制和导向作用的复杂动力结构和特征,影响甚至主导了表面漂浮物的流动形式和演化路径.例如,经志友等[ ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 非常规油气资源渗流力学进展专题序
    石油和天然气在我国经济发展中起到了积极支撑作用.随着经济发展的后石油时代到来,我国油气资源对外依存度已超出了能源安全的警戒线.为保障国家能源安全,我国对非常规油气资源的开发力度大幅增加.自1996年以来,我国在页岩油气、煤层气、致密油气以及天然气水合物等非常规油气资源勘探开发领域取得了显著进展.作为 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 压电超构材料及其波动控制研究: 现状与展望
    引言超构材料或超材料(metamaterials)是将精心设计的基本单元通过一定的空间排列来实现普通材料所不具有的奇异或反常性能,如带隙、波导、负折射、负模量、负密度、超透镜、声学聚焦、声学隐身和拓扑态等[1-2],已成为一个多学科交叉的前沿研究领域.过去几十多年来陆续出现的左手材料[3]、光子晶体 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.