引言
新一轮的高超声速技术对飞行器在“极端”环境和“极端”动力条件下的飞行提出了新的挑战, 它也面临降热、减阻、控制等一系列的难题. 当飞行器以高超声速飞行时, 头部弓形会由于激波压缩和黏性阻滞减速而产生高温, 其温度高达几千度甚至上万度, 高温下气体化学反应产生的离子和电子在飞行器周围形成一个等离子体鞘层. 高超声速MHD流动控制是利用飞行器内部布置的磁场与电离气体的相互作用来达到流动控制的目的. 它作为一种非接触的主动流动控制方法, 在飞行器气动力操控、热环境管理、“电磁窗口”减弱“黑障”、“电磁舵面”飞行姿态控制、磁流体发电等领域均有广阔的应用前景, 受到国内外的广泛关注[1-3].
实验研究、数值模拟和理论分析是研究科学问题的常用手段, 三者相辅相成. 高超声速MHD流动控制的研究对实验条件要求较高, 需要高超声速设备能够模拟高速飞行状态下的来流以及产生高磁场强度的磁场发生装置; 同时, 电磁干扰以及脉冲设备较短的实验时间也会带来测量方面的困难[4]. 由于当前实验可进行测量的物理量较为有限, 所以研究主要是针对激波脱体距离[5-8]、模型气动力(阻力/磁阻力等)[8-12]以及模型表面热流[13]等方向来开展, 但总体来讲, 随着高超声速地面设备模拟能力及电磁技术的发展, 越来越多的****考虑通过地面实验来研究磁场流动控制的效果及规律.
数值模拟相较于实验研究而言, 所需要的研究成本大为降低, 通过数值模拟可以得到全流场信息, 有助于直观地了解流场规律. 经过近二三十年的发展, 尤其是对计算格式的不断修正[14-18], MHD数值模拟发挥着越来越重要的作用. 然而, MHD涉及多种复杂物理现象, 包括产生和维持带电粒子的过程、带电粒子与磁场的作用、非平衡能量输运机理以及电磁场中的霍尔效应等, 每一种效应都包含复杂的规律, 即使是全MHD的数值模拟也是基于一些简化假设(如电磁介质各向同性、无磁极化、忽略粒子滑移等). 因此, MHD数值模拟也亟待可靠的MHD流动控制实验数据来对计算方法及结果进行校验. 同时, 在相同的计算条件下, 它往往要比CFD模拟耗费更大的计算量; 除了CFD模拟存在的问题外, MHD模拟还存在一些如磁场散度、全MHD奇异性、导电壁面边界等特有的问题[19].
基于高超声速MHD的理论研究虽然起步非常早, 但相比于实验研究和数值模拟, 其研究工作仍然非常有限, 且成果主要集中于二十世纪五六十年代. 较为经典的是Bush[20]的研究工作, 他在激波层内常密度、常电导率、无黏、球形激波等假设下, 采用分离变量的方法求解流动方程和电磁方程, 将复杂的偏微分方程组化简为常微分方程组, 以转化为一个初值问题进行离散求解. Smith和Wu[21]、Porter和Cambel[22]沿用Bush的方法, 分别研究了黏性系数和Hall效应的影响. 该领域其他方面的理论研究工作也在同时期展开, Ludford和Murray[23]研究了不可压缩无黏导电流体流经磁化球的稳态流动问题. Meyer[24]采用Newton-Plus-Centrifugal近似方法, 发展了MHD回转体稳态流动理论. Lykoudis[25]引入Newton-Busemann压力定律, 通过对无黏动量方程进行积分得到激波脱体距离的表达式. Eriscon和Maciulaitis[26]研究了高度?速度图上的电离流与磁场相互作用的分布范围, 并进一步评估了较强相互作用流态下的磁流体控制作用力. Hooks和Lewis[27]基于激波坐标系和物体坐标系之间的关系, 得到了驻点处的无黏速度梯度、物体周围的静压分布和边界层外沿的速度分布等. 激波脱体距离作为高超声速飞行器飞行问题中的一个重要参数, 是气动领域研究的关注重点之一. 然而, 上述理论工作对于磁场影响下激波脱体距离的研究相对较少, 相关结果也较为有限. 有****采用的方法虽然可以得到驻点线附近的流场信息, 但其求解过程和结果不能直观快速的反映磁控效果, 有一定局限性[20-22]; 另一方面, Lykoudis[25]、Hooks和Lewis[27]对激波脱体距离解析形式的理论推导是基于激波层内磁场方向处处垂直于流速方向的条件下进行的, 该类型磁场可与电离流充分作用, 然而其分布形式较为理想, 且积分形式的激波脱体距离表达式需要进一步数值求解. 因此, 高超声速MHD激波脱体距离的快速求解方法仍有待进一步发展和完善, 以达到从理论上快速评估磁控效果以及能够反映MHD流动控制本质的目标.
本文通过理论分析的方法得到高超声速MHD无量纲激波脱体距离的解析表达式. 求解过程主要分为两部分, 首先对连续方程进行积分, 将无量纲激波脱体距离作为待求量包含在内; 进一步, 引入切向速度切向偏导数沿驻点线上的线性近似分布, 利用径向动量方程建立磁场与激波脱体距离的联系, 寻找球头驻点处切向速度沿切向的偏导数值. 最后, 通过求解关于激波脱体距离的一元二次方程, 获得包含磁场影响的解析表达式.
1.
无量纲激波脱体距离理论求解
磁场添加后对流动影响最直观的体现是脱体激波距离或激波结构的变化, ****在多种设备中均通过光学方法观测到了磁场对脱体激波距离的影响, 一般而言, 磁场越强, 脱体激波距离越大.
本文的理论研究是基于以下条件:
(1)低磁雷诺数假设, 对于高超声速飞行条件, 激波层内气体电离度一般较低, 磁雷诺数远小于1, 此时诱导磁场对于外加磁场的影响可以忽略不记[1, 28-29]. Porter和Cambel[29]详细研究了不同磁雷诺数条件下的磁场分布, 其结果也表明在低磁雷诺数条件下, 电流导致的诱导磁场对外加磁场的影响很小, 在激波层内只考虑外加磁场即可;
(2)激波层内流体不可压缩, 尽管自由来流速度是高超声速, 但强激波后激波层内驻点线附近马赫数较小, 该区域内的流体可当不可压缩流体近似处理, Bush[20]、Smith和Wu[21]在求解高超声速MHD问题时也采用了该假设;
(3)忽略黏性影响, 高超声速来流条件下, 流体雷诺数较大, 在关注脱体激波距离问题时可以忽略黏性项, 将问题简化为无黏流动问题[20, 25];
(4)激波层内电导率为常值, 电导率一般与温度相关, 在无黏假设条件下, 激波层内不考虑边界层, 沿驻点线温度变化较小, 可将其以常值近似处理[17, 20, 25].
1.1
对连续方程的处理
对连续方程的处理借鉴了Olivier[30]的方法, 他通过对连续方程积分的方式获得了包含激波脱体距离的方程, 本文在其基础上进一步考虑添加磁场对脱体激波距离的影响, 对该方法的具体应用过程如下.
球坐标系下的连续方程为
$$frac{partial }{{partial r}}({ ho u{r^2}sin theta } ) + frac{partial }{{partial theta }}left({ ho vrsin theta } ight) = 0$$  | (1) |
对连续方程中的变量进行无量纲化处理
$$begin{split}&bar r = dfrac{r}{{{r_b}}},;bar u = dfrac{u}{{{u_infty }}},;bar v = dfrac{v}{{{u_infty }}}&bar varDelta = dfrac{{{r_s} - {r_b}}}{{{r_b}}} = dfrac{varDelta }{{{r_b}}},;bar ho = dfrac{ ho }{{{ ho _s}}}end{split}$$  |
于是式(1)化为
$$frac{partial }{{partial bar r}}({bar ho bar u{{bar r}^2}sin theta } ) + frac{partial }{{partial theta }}left({bar ho bar vbar rsin theta } ight) = 0$$  | (2) |
其中
ho _infty }$
ho _s}$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-127-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
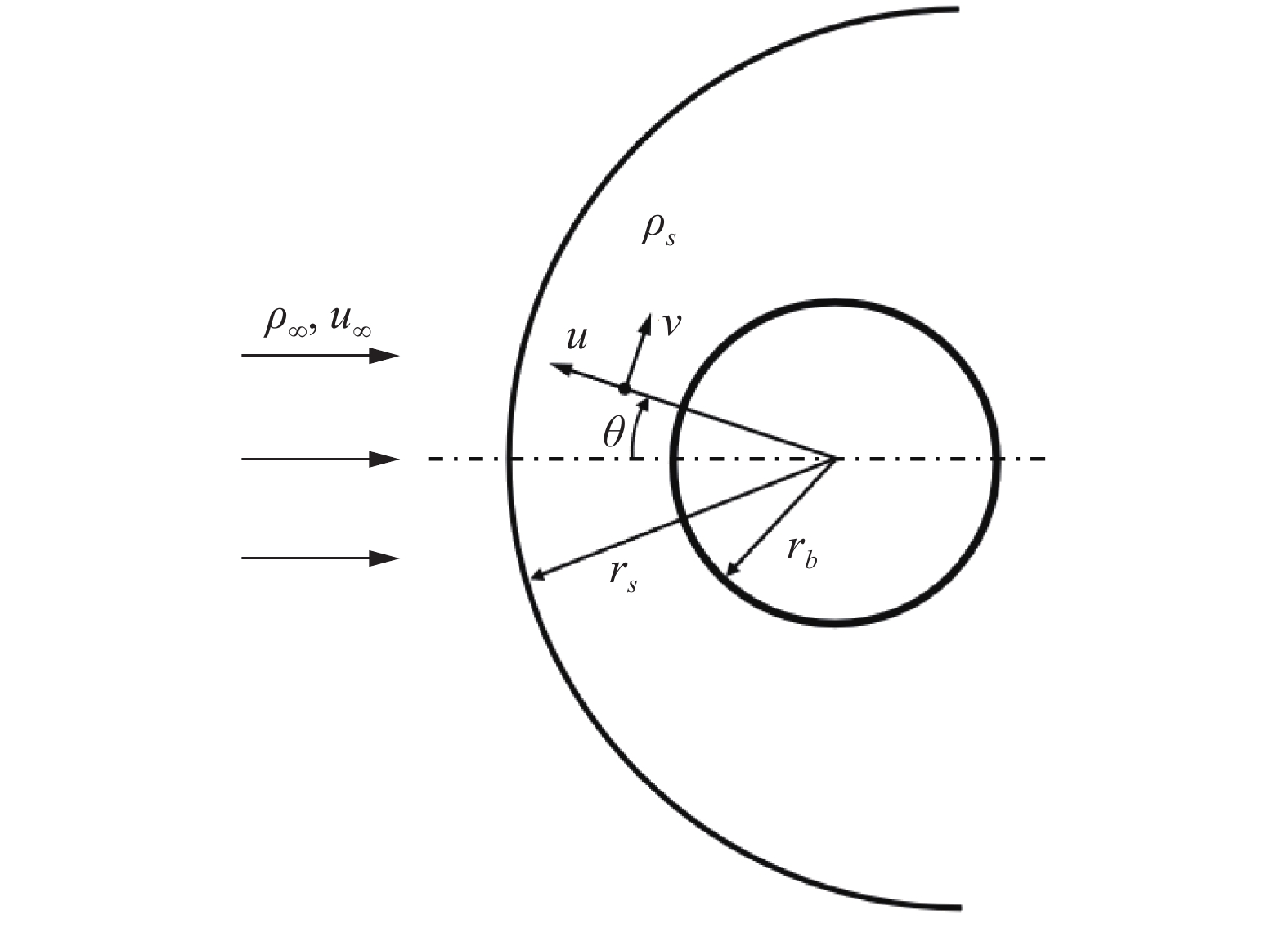
图
1
钝头体和激波结构示意图
Figure
1.
Schematic of the blunt body and the shock
下载: 全尺寸图片
幻灯片
将式(2)沿着驻点线由驻点向激波处进行积分, 积分的目的是将无量纲激波脱体距离加入到方程中, 将其作为待求量来进一步求解, 积分过程具体如下
$$begin{split}& intlimits_1^{{ m{1}} + bar varDelta } left[{{dfrac{partial }{{partial bar r}}({bar ho bar u{{bar r}^2}sin theta } ) + dfrac{partial }{{partial theta }}left({bar ho bar vbar rsin theta } ight)} ight] { m{d}}bar r} = 0 &qquad Rightarrow {{bar ho }_s}{{bar u}_s}{left({1 + bar varDelta } ight)^2}sin theta + intlimits_1^{1 + bar varDelta } {bar rdfrac{partial }{{partial theta }}left({bar ho bar vsin theta } ight){ m{d}}bar r} = { m{0}} [-15pt] end{split} $$  | (3) |
其中
由于求解过程在驻点线附近, 此时可以通过引入驻点线假设简化问题的求解过程, 此过程实质上是去除方程中的高阶小量, 同时保留低阶小量, 从而保证了低阶量的可求解性. 根据驻点线假设, 引入如下近似条件[30]
$${ m{sin}}theta = theta,;frac{{partial bar ho }}{{partial theta }} = { m{0}},;bar v = theta frac{{partial bar v}}{{partial theta }}$$  |
于是式(3)化为
$${bar ho _s}{bar u_s}{left({1 + bar varDelta } ight)^2} + intlimits_1^{1 + bar varDelta } {bar rbar ho left({{ m{2}}frac{{partial bar v}}{{partial theta }} + theta frac{{{partial ^{ m{2}}}bar v}}{{partial {theta ^{ m{2}}}}}} ight){ m{d}}bar r} = { m{0}}$$  | (4) |
忽略式(4)中含有小量
$${bar ho _s}{bar u_s}{left({1 + bar varDelta } ight)^2} + { m{2}}bar varDelta intlimits_0^1 {bar ho left({1 + bar varDelta {r^*}} ight)frac{{partial bar v}}{{partial theta }}{ m{d}}{r^{ m{*}}}} = { m{0}}$$  | (5) |
其中
ight){
m{/}}bar varDelta $
m{1}}$
Olivier[30]近似地给出了
m{/}}partial theta )_b}$
m{/}}partial theta )_b}$
$$frac{{partial bar v}}{{partial theta }} = {{{left({frac{{partial bar v}}{{partial theta }}} ight)}_b} + left[{1 - {{left({frac{{partial bar v}}{{partial theta }}} ight)}_b}} ight] {r^{ m{*}}}} $$  | (6) |
式(5)进一步整理为
$$begin{split}& {{bar u}_s}{left({1 + bar varDelta } ight)^2} + { m{2}}bar varDelta intlimits_{ m{0}}^1 left({bar varDelta {r^{ m{*}}} + { m{1}}} ight)cdot & qquadleft{ {{{left({frac{{partial bar v}}{{partial theta }}} ight)}_b} + left[{1 - {{left({frac{{partial bar v}}{{partial theta }}} ight)}_b}} ight] {r^{ m{*}}}} ight}{ m{d}}{r^{ m{*}}} = { m{0}} end{split} $$  | (7) |
1.2
对动量方程的处理
动量方程包含了待求问题的特征元素, 即电磁作用项, 同时需要通过对动量方程的处理, 寻找激波脱体距离与磁场影响的联系, 因此这一部分较为关键. 通过处理径向动量方程, 得到驻点处
m{/}}partial theta $
m{/}}partial theta )_b}$
$${ ho _s}ufrac{{partial u}}{{partial r}} - frac{{{ ho _s}{v^2}}}{r} + frac{{{ ho _s}v}}{r}frac{{partial u}}{{partial theta }} + frac{{partial p}}{{partial r}} = left({{j_theta }{B_phi } - {j_phi }{B_theta }} ight)$$  | (8) |
对于二维轴对称问题, 取B? = 0, 于是式(8)整理为
$${ ho _s}ufrac{{partial u}}{{partial r}} - frac{{{ ho _s}{v^2}}}{r} + frac{{{ ho _s}v}}{r}frac{{partial u}}{{partial theta }} + frac{{partial p}}{{partial r}} = - {j_phi }{B_theta }$$  | (9) |
根据广义Ohm定律(general Ohm’s law)
$${boldsymbol{J}} = sigma ;left({{boldsymbol{E}} + {boldsymbol{V}} times {boldsymbol{B}}} ight)$$  | (10) |
其中σ为电导率. 根据电磁感应定律, 变化的磁场会导致感生电场, 但由于本文涉及的是稳态磁场, 所以电场需要满足
$$ufrac{{partial u}}{{partial r}} - frac{{{v^2}}}{r} + frac{v}{r}frac{{partial u}}{{partial theta }} + frac{1}{{{ ho _s}}}frac{{partial p}}{{partial r}} = - frac{sigma }{{{ ho _s}}}left[ {left({u{B_theta } - v{B_r}} ight){B_theta }} ight]$$  | (11) |
将磁感强度和压力无量纲化
$${bar B_i} = frac{{{B_i}}}{{{B_0}}}, ; bar p = frac{{p - {p_infty }}}{{{ ho _infty }u_infty ^{ m{2}}}}$$  |
式(11)整理得到
$$bar ufrac{{partial bar u}}{{partial bar r}} - frac{{{{bar v}^2}}}{{bar r}} + frac{{bar v}}{{bar r}}frac{{partial bar u}}{{partial theta }} + varepsilon frac{{partial bar p}}{{partial bar r}} = - Qvarepsilon left[ {left({bar u{{bar B}_theta } - bar v{{bar B}_r}} ight){{bar B}_theta }} ight]$$  | (12) |
其中
m{/}}({
ho _infty }{u_infty })$
ho _infty }{
m{/}}{
ho _s}$
$$bar u = bar uleft({bar r} ight)cos theta, ; bar v = bar vleft({bar r} ight)sin theta, ; bar p = bar pleft({bar r} ight){cos ^2}theta $$  |
其中
ight) = partial bar v{
m{/}}partial theta $
$$begin{split}& bar uleft({bar r} ight)bar u'left({bar r} ight){cos ^{ m{2}}}theta - frac{{ m{1}}}{{bar r}}bar vleft({bar r} ight)bar vleft({bar r} ight){sin ^{ m{2}}}theta + & qquad frac{{bar vleft({bar r} ight)sin theta }}{{bar r}}left[{ - bar uleft({bar r} ight)sin theta } ight] + varepsilon bar p'left({bar r} ight){cos ^{ m{2}}}theta = & qquad - Qvarepsilon left{ {left[{bar uleft({bar r} ight)cos theta {{bar B}_theta } - bar vleft({bar r} ight)sin theta {{bar B}_r}} ight]{{bar B}_theta }} ight} end{split} $$  | (13) |
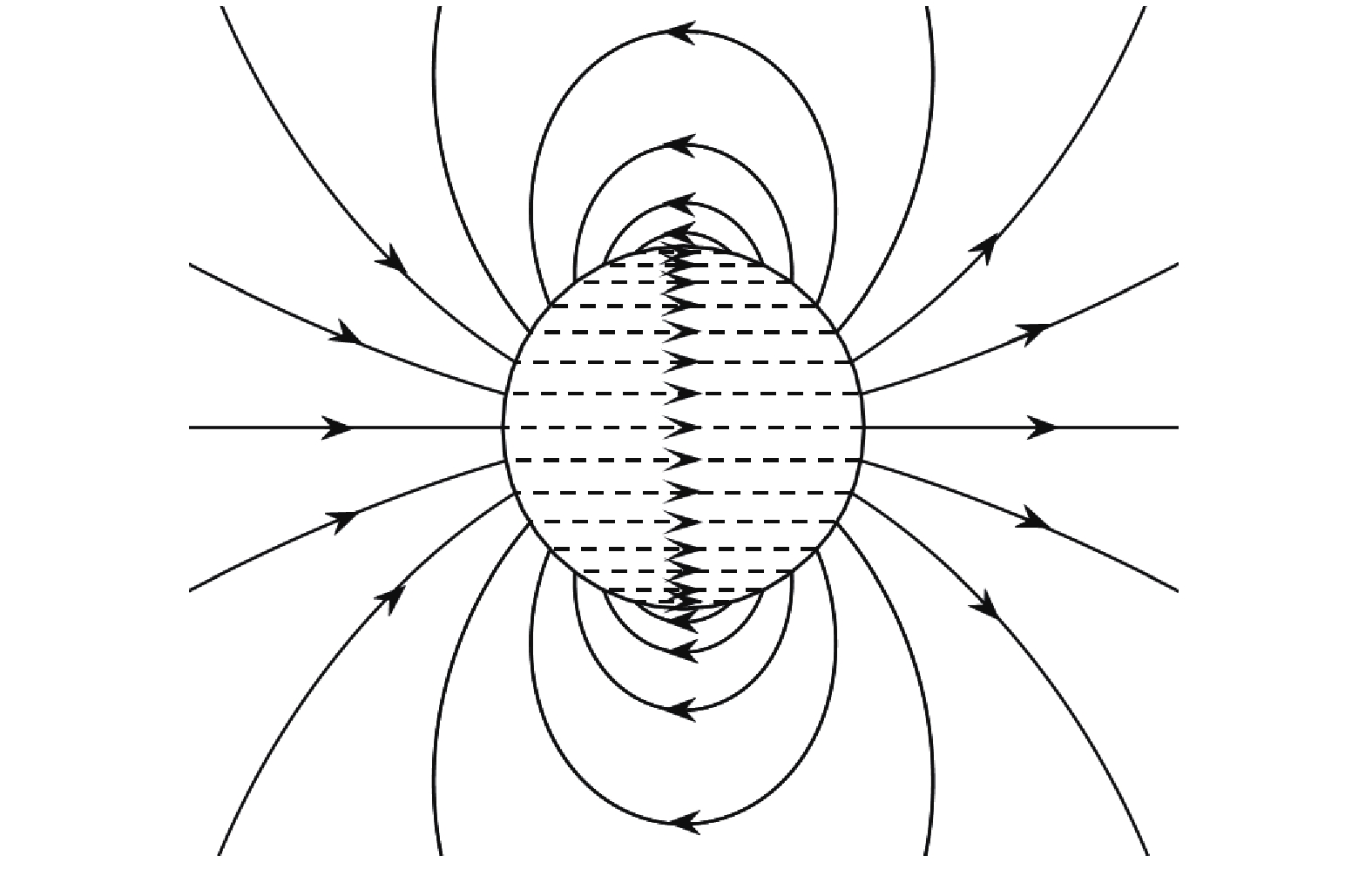
对于磁场分布, 选取较为常用的模型为均匀磁化球形磁体的磁场分布, 该模型的磁场分布简单, 存在解析形式的表达, 便于实验和理论的研究[12, 20, 22], 这种磁场的方向与激波层内电离流速度方向趋近于垂直, 可以较为充分地与电离流发生相互作用, 其分布形式见图2. 由式(10)知, 电流为环向, 垂直于磁场和速度矢量所在的面, 于是MHD动量方程中的电磁力项
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-127-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
均匀磁化球体磁感线分布示意图
Figure
2.
Distribution of magnetic induction lines of uniformly magnetized sphere
下载: 全尺寸图片
幻灯片
$$left{ {begin{array}{*{20}{l}} {{B_r} = {B_0}{{left({dfrac{{{R_b}}}{r}} ight)}^3}cos theta } {{B_theta } = dfrac{{{B_0}}}{2}{{left({dfrac{{{R_b}}}{r}} ight)}^3}sin theta } end{array}} ight. Rightarrow left{ {begin{array}{*{20}{l}} {{{bar B}_r} = {{left({dfrac{{ m{1}}}{{bar r}}} ight)}^3}cos theta } {{{bar B}_theta } = dfrac{{ m{1}}}{2}{{left({dfrac{{ m{1}}}{{bar r}}} ight)}^3}sin theta } end{array}} ight.$$  |
该磁场分布满足散度和旋度为0的条件
$$nabla cdot {boldsymbol{B}} = 0,;nabla times {boldsymbol{B}} = {bf{0}}$$  |
其中旋度为0意味着低磁雷诺数, 即忽略电流对磁场产生的影响. 将上述磁场分布代入式(13)
$$begin{split}& bar uleft({bar r} ight)bar u'left({bar r} ight){cos ^{ m{2}}}theta - dfrac{{ m{1}}}{{bar r}}bar vleft({bar r} ight)bar vleft({bar r} ight){sin ^{ m{2}}}theta + & qquaddfrac{{bar vleft({bar r} ight)sin theta }}{{bar r}}left[{ - bar uleft({bar r} ight)sin theta } ight] + varepsilon dfrac{{partial bar pleft({bar r} ight)}}{{partial bar r}}{cos ^{ m{2}}}theta = & qquad - Qvarepsilon cdot dfrac{{ m{1}}}{2}{left({dfrac{{ m{1}}}{{bar r}}} ight)^3}sin theta cdot left[ { {bar uleft( {bar r} ight)cos theta frac{{ m{1}}}{2}{{left( {frac{{ m{1}}}{{bar r}}} ight)}^3}sin theta - } } ight. & qquadleft. { {bar vleft( {bar r} ight)sin theta {{left( {frac{{ m{1}}}{{bar r}}} ight)}^3}cos theta } } ight] end{split} $$  | (14) |
驻点线附近取
m{sin}}theta = theta $
m{cos}}theta = {
m{1}}$
$$begin{split}& bar uleft({bar r} ight)bar u'left({bar r} ight) - dfrac{{ m{1}}}{{bar r}}bar vleft({bar r} ight)bar vleft({bar r} ight){theta ^2} + dfrac{{bar vleft({bar r} ight)}}{{bar r}}left[{ - bar uleft({bar r} ight)} ight]{theta ^2} + varepsilon dfrac{{partial bar pleft({bar r} ight)}}{{partial bar r}} = &qquad - dfrac{{Qvarepsilon }}{{ m{2}}}left{ {left[{bar uleft({bar r} ight) dfrac{{ m{1}}}{2} - bar vleft({bar r} ight)} ight]{{left({dfrac{{ m{1}}}{{bar r}}} ight)}^{ m{6}}}} ight}{theta ^{ m{2}}} [-15pt] end{split} $$  | (15) |
对于壁面处
m{1}}$
ight) = {
m{0}}$
$$ - bar vleft({ m{1}} ight)bar vleft({ m{1}} ight){theta ^2} + varepsilon {left[{frac{{partial bar pleft({bar r} ight)}}{{partial bar r}}} ight]_{bar r = 1}} = frac{{ m{1}}}{2}Qvarepsilon bar vleft({ m{1}} ight){theta ^{ m{2}}}$$  | (16) |
根据量级分析, 式(16)的压力项不包含小量
$$ - bar vleft({ m{1}} ight)bar vleft({ m{1}} ight){theta ^2} = frac{{ m{1}}}{2}Qvarepsilon bar vleft({ m{1}} ight){theta ^{ m{2}}}$$  | (17) |
由式(17)的二次方程可以解得
$$bar vleft({ m{1}} ight) = { m{0}} ;;{text{或}} ;;bar vleft({ m{1}} ight) = - frac{{Qvarepsilon }}{2}$$  | (18) |
由于磁场会明显影响流场, 切向速度需要包含磁场以及来流所带来的影响, 所以这里选取第二个解. 额外地, 由式(16)还会得到
m{/}}partial bar r]_{bar r = 1}} = {
m{0}}$
$$bar vleft({bar r} ight) = - bar uleft({bar r} ight) - frac{{bar r}}{2}bar u'left({bar r} ight)$$  | (19) |
同样取
m{1}} $
$$bar u'left({ m{1}} ight) = Qvarepsilon $$  | (20) |
此结果说明, 驻点附近径向速度方向有与来流相反的趋势.
根据激波前后质量守恒关系, 激波处驻点线上的速度有[19]
$${bar u_s} = - varepsilon {u_infty }$$  | (21) |
将式(21)及式(18)代入式(7), 整理如下
$$a {bar varDelta ^{ m{2}}} + b bar varDelta - varepsilon = 0$$  | (22) |
其中
$$a = frac{{ m{2}}}{{ m{3}}} + frac{{ m{1}}}{{ m{3}}}{left({frac{{partial bar v}}{{partial theta }}} ight)_b} - varepsilon $$  |
$$b = 1 + {left({frac{{partial bar v}}{{partial theta }}} ight)_b} - { m{2}}varepsilon $$  |
可以看到, 这是一个关于
$$bar varDelta = frac{{ m{1}}}{{{ m{2}}a}}left( { - b + sqrt {{b^2} + 4avarepsilon } } ight)$$  | (23) |
2.
结果与分析
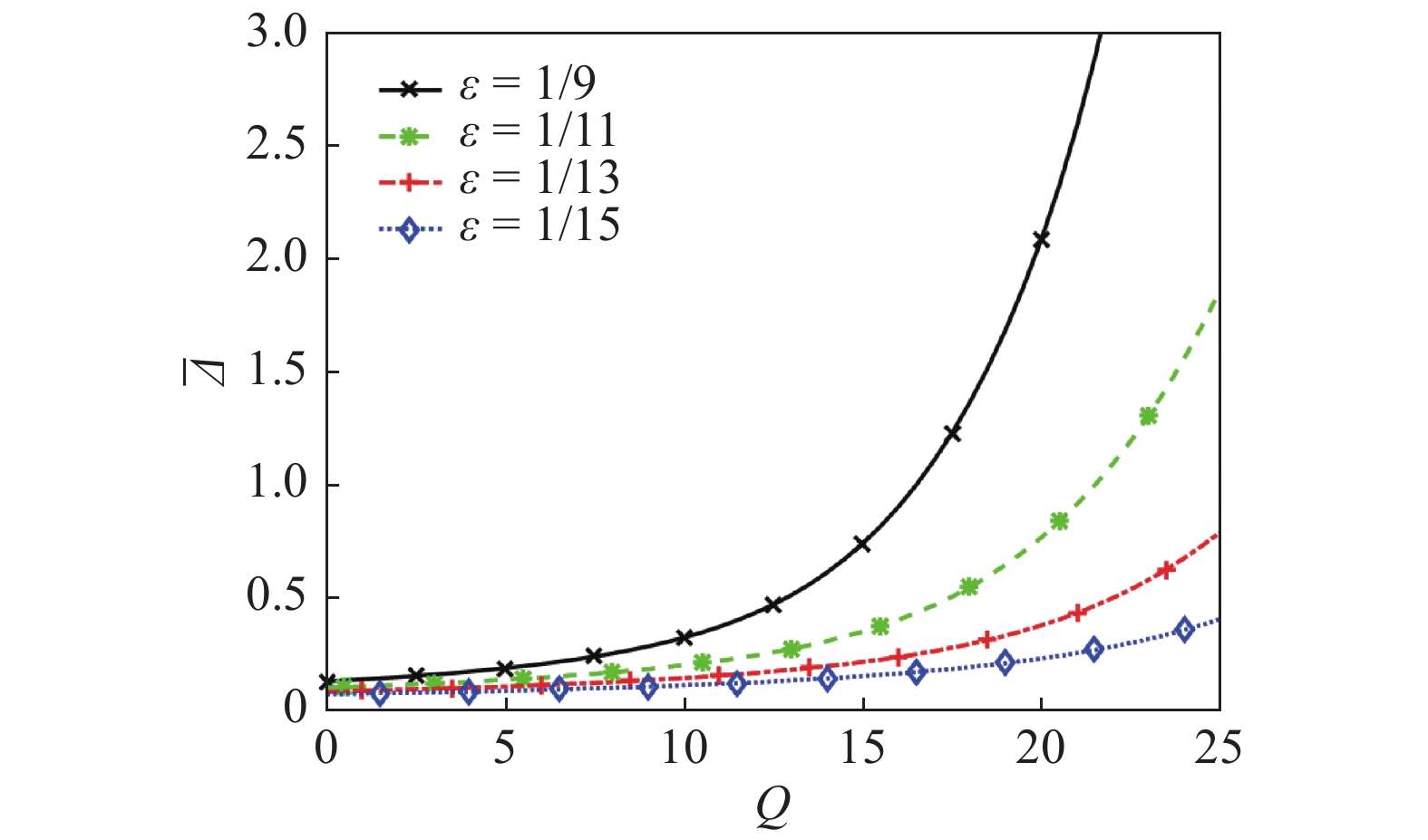
根据图3, 对于相同的相互作用系数Q, 随着ε的增加(来流速度降低)无量纲激波脱体距离变大. 对于相同的ε, 随着Q增加激波无量纲脱体距离增加. 从图3中也可以观察到随着ε的减小, 无量纲激波脱体距离关于ε的灵敏度降低, 在高超声速MHD实验或数值模拟开始之前, 可以通过合理估计的ε值以及由初始条件构成的Q来预测结果, 这有助于快速评估磁控效果.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-127-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
无量纲激波脱体距离
Figure
3.
The curve of dimensionless shock stand-off distance
下载: 全尺寸图片
幻灯片
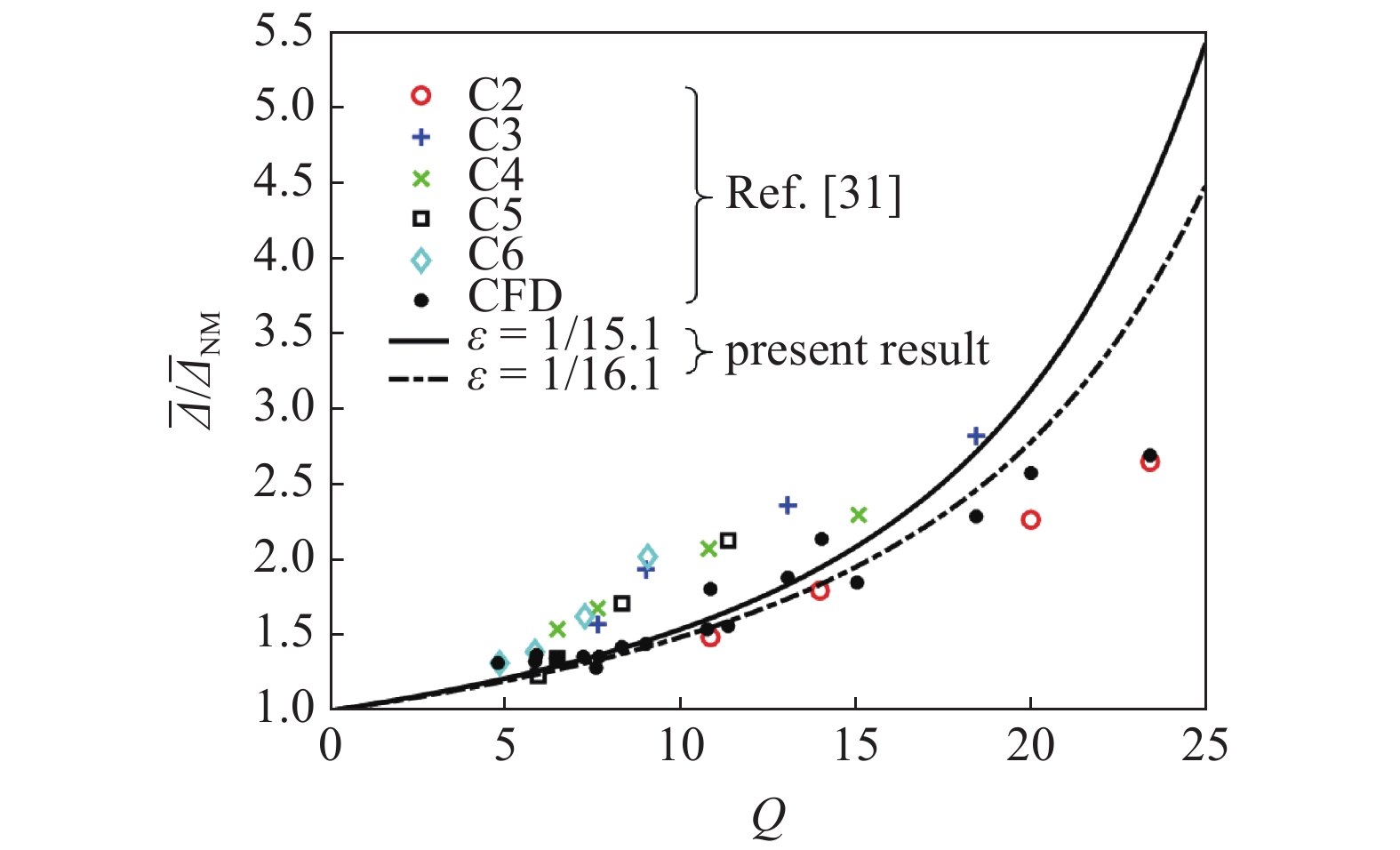
图4对比了本文结果与Lefevre等[31]在膨胀管中的实验结果. C2 ~ C6代表Lefevre选取的不同实验条件, 每一个实验条件对应着不同的相互作用系数Q以及激波前后气流密度比ε, 但由于实验时间很短, 不足以形成稳定流场, 文章以20 μs为间隔进行数据取点, Lefevre同时对比了MHD的CFD模拟结果. 从图4中可以看到, 理论结果、实验和数值结果符合得较好.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-127-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
无量纲激波脱体距离比
m{NM}}}}$
Figure
4.
The curve of ratio of shock stand-off distance
m{NM}}}}$
下载: 全尺寸图片
幻灯片
Lykoudis[25]同样在低磁雷诺数以及激波层内常值密度、常值电导率、无黏的假设条件下推导了球头激波脱体距离表达式, 他采用了较为理想的磁场分布模型:
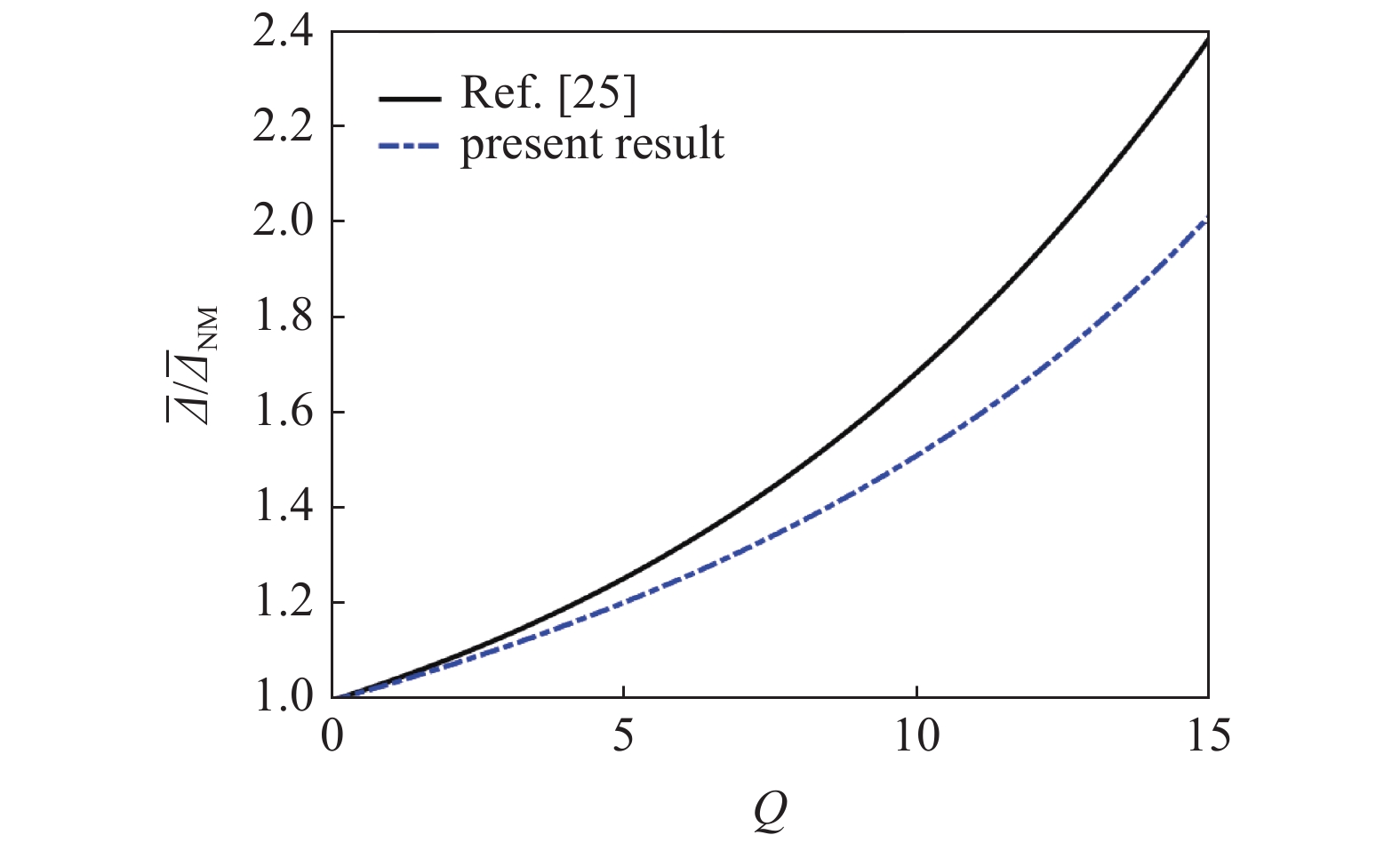
图5给出了本文与Lykoudis理论结果的对比, 两者结果趋势一致, 都体现了磁场与导电流体相互作用产生的阻滞效应, 但两者也存在一定偏差, 主要原因如下: Lykoudis采用的磁场分布模型与本文存在一定的差别, 他的推导是基于激波层内磁场处处垂直于流速的条件, 相较于偶极子磁场而言, Lykoudis使用的磁场可与流场进行更加充分的相互作用, 这也会产生更强的阻滞作用, 使激波层厚度增益效果更加明显, 从而导致其结果在一定Q值范围内高于本文所得的结果. 当然, 由于Lykoudis采用的磁场过于理想, 在现实中难以用磁场装置产生该类磁场, 在实验研究中难以采用. 另外, 需要注意的是, 包括Lykoudis文章在内的一些文献中的相互作用系数表达式为
m{/}}({
ho _infty }{u_infty })$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-127-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
本文结果与Lykoudis结果对比图[25]
Figure
5.
Comparison between results of this paper and the Lykoudis’s
下载: 全尺寸图片
幻灯片
通常情况下, 理论分析引入的假设条件会导致模型存在一定的局限性. 根据线性近似分布假设,
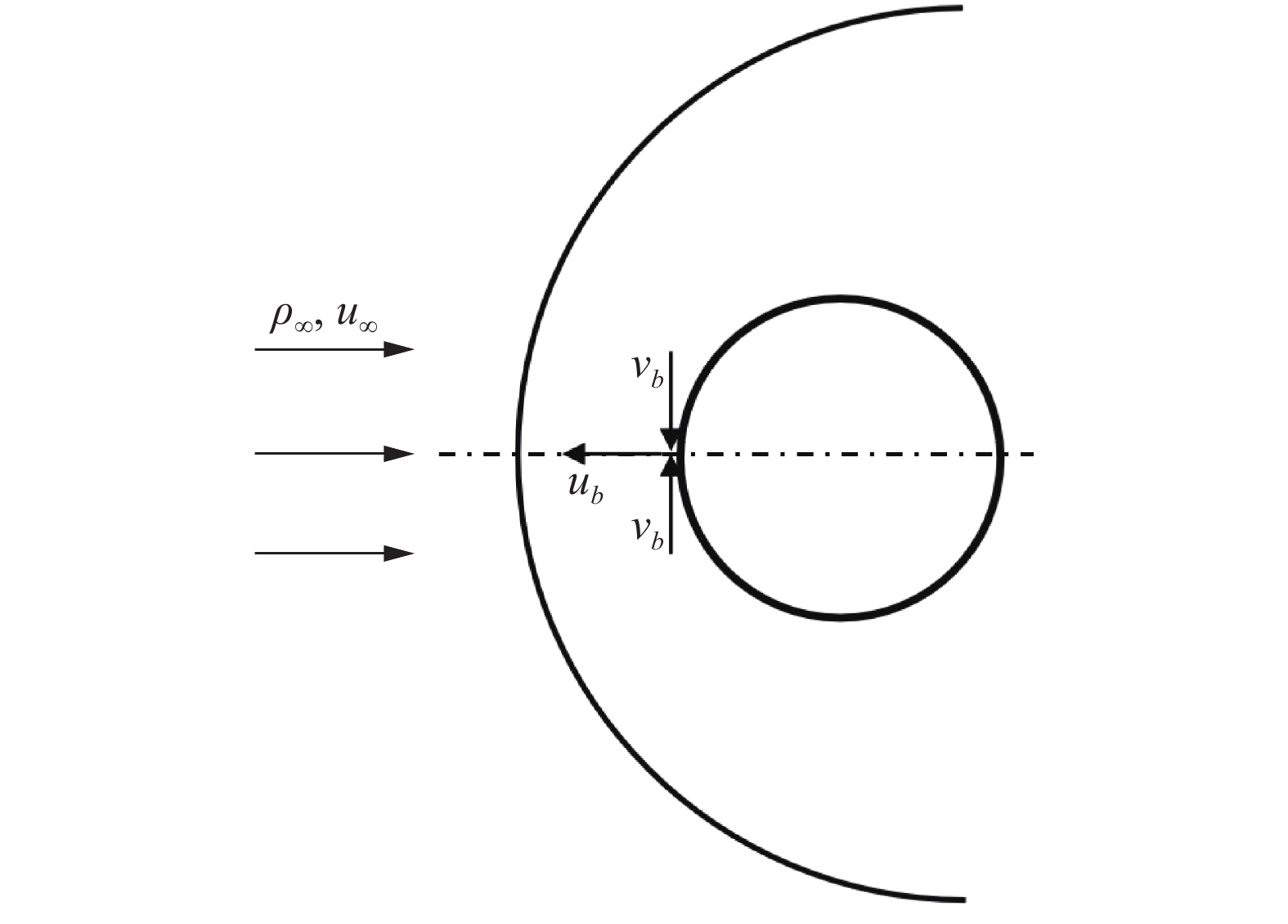
本文的结果中有一个值得关注的地方, 当磁场存在时, 驻点附近的切向速度有指向驻点的趋势, 通过连续方程得到与来流相反的径向速度, 如图6. 这里认为该结果是低磁条件假设造成的, 原因是磁场的旋度方程中, 如果考虑电流对磁场的影响, 该影响将会是一个小量, 这个小量会影响径向动量方程的量级分析过程, 从而改变求解结果. 然而这种流动趋势是实际存在的, 由于电离流与磁场相互作用的影响, 流体会受到与流动相反方向的洛伦兹力, 从而使激波层内的流速降低, 从而导致了激波脱体距离的增加.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-127-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
驻点处流动示意图
Figure
6.
Schematic of flow near stagnation point
下载: 全尺寸图片
幻灯片
3.
结论
本文利用连续方程建立了关于激波脱体距离的待求方程, 通过径向动量方程寻找
(1)理论分析结果表明, 当磁相互作用系数增加时, 激波脱体距离增加, 即磁控效果增强. 将本文结果与Lefevre的实验数据、Lykoudis的结果进行了对比, 三者吻合较好. 本文理论模型对高超声速MHD实验设计和结果分析具有较好的指导意义;
(2)本文模型的建立是基于特定的假设条件, 存在一定的适用范围, 在Q较大时,
