致密油藏动态裂缝扩展机理及应用

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

引言

致密油藏水平井体积压裂投产后, 随着地层能量不断释放, 采油能力衰减, 产量递减快. 在注水吞吐、水驱、CO₂驱等能量补充方式中, 长庆、吐哈等油田采用注水吞吐, 初期增油效果好. 注水吞吐成为接替衰竭开采、补充地层能量的有效方式^[1-2]. Hagoort等^[3]、Fan等^[4]和Wang等^[5]提出注水易诱导部分天然裂缝扩展. 田虓丰等^[6]和蒲春生等^[7]根据储层应力阴影效应, 从数值模拟角度分析了水力裂缝同步扩展到多裂缝的动态延伸特征. Rountree等^[8]、王勃等^[9]和唐巨鹏等^[10]认为周期注水应力改造可以减小水平地应力差对裂缝扩展的约束能力, 促进微裂缝大量发育、沟通天然裂缝形成缝网. 王友净等^[11]、汪洋等^[12]、严谨等^[13]、Wang等^[14]注意到天然裂缝扩展形成的不规则复杂缝网极大的增加了焖井期间裂缝与基质的接触面积, 注入水通过缝网与基质发生静态渗吸. 杨正明等^[15-16]、Gao等^[17]和汪勇等^[18]发现裂缝性致密储层与普通油藏不同的渗流机理使得逆向渗吸、正向渗吸共同作用置换原油. 蔡建超和郁伯铭^[19]、许建红和马丽丽^[20]明确了注水吞吐初期主要是逆向渗吸作用置换采油. 程志林等^[21]和Ghasemi等^[22]研究了致密砂岩油水系统自发渗吸特征及规律, 通过T₂谱反映不同边界条件对渗吸采收率的影响. 随着吞吐轮次的增加, 地层能量不断释放, 导致每一轮次的采油能力都在衰减, 又因为致密油藏注水波及范围小, 逆向渗吸减弱, 注水吞吐效果变差, 产量递减快. 王家禄等^[23]认为在一定的驱替速度范围内, 油水黏度比越小, 动态渗吸效果越好. 徐中一等^[24-25]从油藏尺度及实例分析致密储层中注水吞吐效果, 以期利用逆向渗吸作用提高开发效果, 但效果不明显. 王向阳等^[26]、Liu等^[27]、马剑等^[28]和李帅等^[29]建立了不同尺度岩心渗吸物理模拟实验方法, 研究了致密储集层渗吸过程的影响因素, 并构建了水驱油时渗吸作用的定量评价方法, 提出了渗吸及驱替采油的新思想. 计秉玉等^[30]为更有效地增大驱替作用, 针对高含水油井提出改变液流方向的开发方式, 提高整体水驱油效率. 吴忠宝等^[31]和李伟才^[32]采用缩小井距及油水井互换的思想提高水驱动用储量, 应用于低渗油藏大港油田某区块, 初步实施效果显著.

目前裂缝性致密油藏动态裂缝延伸规律、逆向渗吸及驱替机理不清楚, 注水吞吐转变开发方式尚未成熟. 笔者根据艾尔文理论、弹性力学及渗流力学分析裂缝尖端附近的应力场分布, 结合注水诱导裂缝扩展机理及致密油藏发生逆向渗吸原理, 提出将注水吞吐转为不稳定脉冲注水开发方式. 利用逆向渗吸及线性驱替开发方式, 模拟实例井生产10年, 预测累计采油、压力及剩余油分布情况, 探讨了此方法的可行性.

1.
注水诱导裂缝扩展机理

致密油藏大规模压裂水平井注水吞吐后, 注水期间井底压力高于裂缝扩展压力, 天然微细缝被激发、扩展及延伸, 或者天然微细裂缝的充填物被冲刷. 相互沟通的天然微细缝形成了新的渗流空间, 储层渗透率增加, 导流能力增加.

1.1
天然裂缝扩展机理

注水诱导裂缝扩展之前天然裂缝已经存在, 第i次裂缝扩展压力计算不同于第一次. 艾尔文理论能够用裂缝尖端附近的应力场强度分析第i次裂缝扩展问题, 该理论是艾尔文等在格里菲斯脆性断裂理论基础上经过不断丰富和发展而形成的, 主要适用于小范围裂缝尖端应力与应变场分析^[33-34]. 在注水后原本闭合的天然裂缝发生扩展, 扩展的天然微细裂缝可以视为小范围裂缝, 分为3种类型: I型裂缝张开、II型裂缝划开、III型裂缝撕开(图1). 注水诱发裂缝扩展的形式可视为I型、II型及交叉裂缝扩展. 由于II型模拟难度系数比较大, 本文只对I型及交叉扩展型开展研究.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />

图
1
裂缝3种类型

Figure
1.
Three types of fractures

下载:
全尺寸图片
幻灯片

1.1.1
I型裂缝扩展规律

假设闭合的天然裂缝只发生I型破坏, 采用Westergaard应力函数求解, 根据拉氏变换和广义胡克定律得到解析函数, 进而求裂缝尖端附近的应变分量及应力场强度因子K_I.

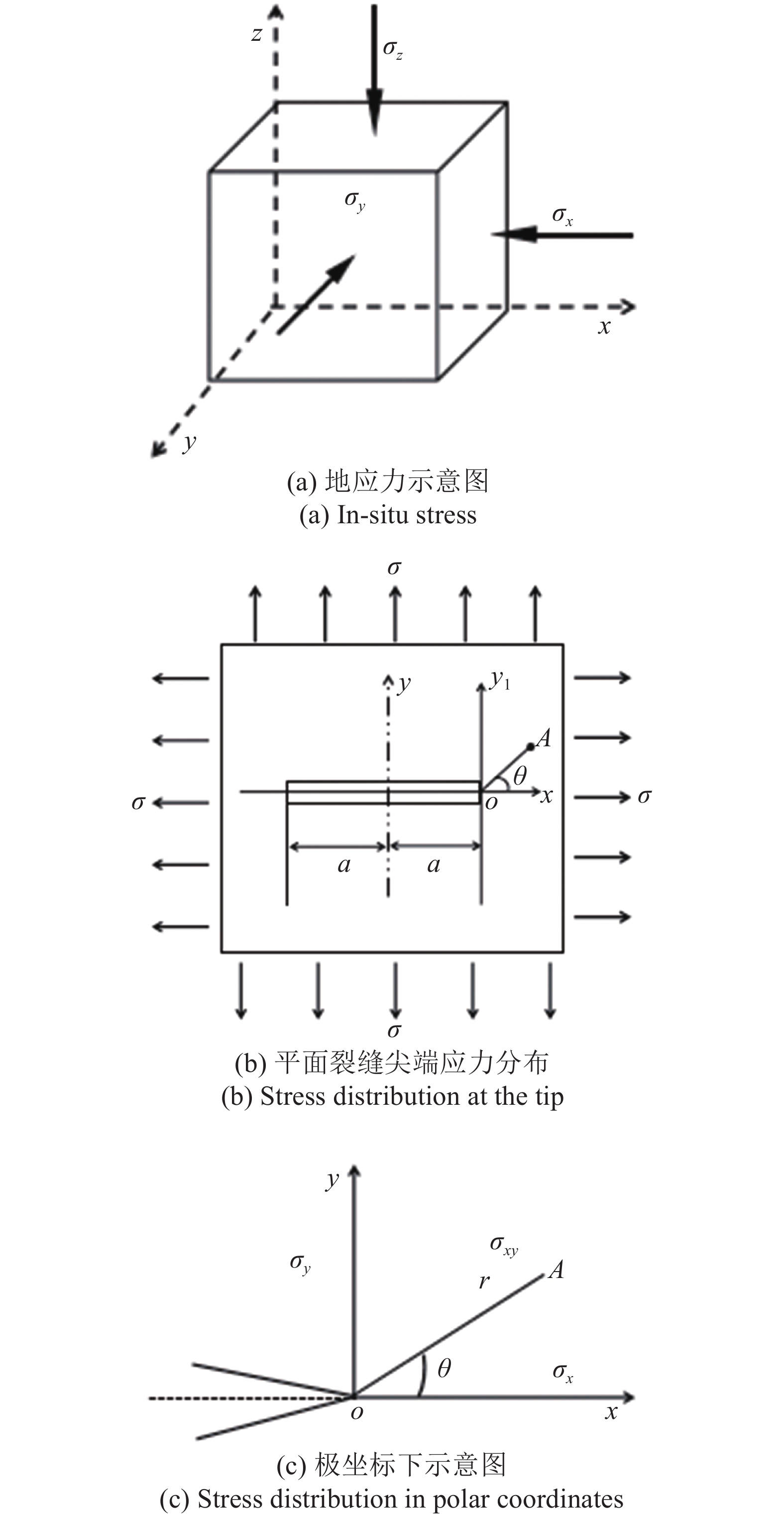
致密油藏在开发扰动之前就已经承受应力的作用, 这个应力一般称为原地应力(或地应力). 原地应力状态由上覆岩层压力和两个水平方向的主应力组成, x方向为最大水平主应力方向, y方向为最小水平主应力方向, z方向为铅垂方向(图2(a)).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />

图
2
应力分布示意图

Figure
2.
Schematic diagram of stress distribution

下载:
全尺寸图片
幻灯片

对于二维平面裂缝, 假设“无限大”板, 板上有一个长为2a的矩形中心贯穿裂纹(图2(b)), 这个板在无限远处受双向等值拉伸应力的作用, 忽略流动过程中流体剪切强度的影响、注液系统内各种摩擦力影响、流体与岩石表面间的摩擦阻力，假设在任一时刻, 缝内各点的压力均相等. 针对平面裂缝体, 为研究方便取极坐标系, 坐标原点取在裂缝尖端(图2(c)). 其中, σ为板两端承受的均匀拉应力, MPa; a为贯穿的矩形切口的半长轴, m; r为裂缝尖端控制区极半径, m; θ为以裂缝尖端为圆心区域上的方位角, (°).

基于裂缝尖端应力场强度的观点, 运用线弹性理论和复变函数理论可以求得裂缝尖端附近任意一点A(r, θ)处的应力分布如式(1). 裂缝尖端附近的应力场分布^[35-36]形式为

$${sigma _{ij}} = frac{K}{{sqrt {2{text{π}} r} }}{f_{ij}}left( theta
ight)$$

(1)

其中, f_ij(θ)为角分布函数; K为裂缝尖端应力场强度因子, 其国际单位为MPa?m^1/2. 应力场强度因子的临界值即断裂韧度, 它反映了裂缝扩展即抵抗脆断的能力^[37]. 针对不同的地层, K值可以通过实验测得.

根据艾尔文理论及裂缝尖端的扩展准则^[38], K表达式为

$$K = {P_{{
m{net}}}}left( t
ight)sqrt {{text{π}} L} $$

(2)

其中, P_net(t)裂缝张开的净内压, MPa; L为裂缝半长, m. 将式(2)代入式(1)得到裂缝尖端附近的应力场与净内压的关系表达式为

$${sigma _{ij}} = frac{{{P_{{
m{net}}}}left( t
ight)sqrt L }}{{sqrt {2r} }}{f_{ij}}left( theta
ight)$$

(3)

由于储层应力场计算过程较繁琐, 本节仅利用式(3)定性地分析裂缝尖端的应力与裂缝面受内压的关系. 注水初期, 裂缝净内压随着注水量的增加而升高, 由式(2)可知, 应力场强度因子也随之升高. 当应力场强度因子K达到断裂韧度K_IC, 在裂缝尖端会发生扩展. 断裂韧度可以实验获得或者查询已有成果^[39].

该简化模型有一定的局限性, 适用于单一裂缝的判据, 且对Ⅰ型裂缝问题比较适用. K_I是表征裂缝尖端区域应力场强弱程度的参量, 而且是唯一的参量, 局限于裂缝尖端附近区域的应力场分析.

1.1.2
多裂缝交叉裂缝扩展渗流模型

致密油藏注水吞吐后, 地层中因存在天然裂缝及非均质等因素, 还会发生裂缝交叉扩展(图3(a)和图3(b)). 交叉扩展的天然裂缝沟通压裂裂缝形成了动态缝网(图3(c)). 但由于交叉裂缝扩展从断裂力学分析难度系数较大, 因此, 从渗流力学的角开展研究.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />

图
3
多裂缝交叉扩展形成动态缝网

Figure
3.
Multi-fractures cross and expand to form a dynamic fracture network

下载:
全尺寸图片
幻灯片

裂缝发生交叉扩展, 假设油、水两相流动且等温, 考虑地层岩石及流体的可压缩性, 建立注水吞吐油水两相连续性方程、渗流模型以及传导率计算方程.

(1) 注水吞吐油水两相连续性方程

对于注水吞吐油水两相渗流, 注入水和原油产出导致储层含水及含油饱和度是动态变化的, 则油相及水相的连续方程表示为

$$frac{{partial left[ {phi left( {{p_{
m{o}}}}
ight){
ho _{
m{o}}}left( {p{}_{
m{o}}}
ight){s_{
m{o}}}}
ight]}}{{partial t}} + left[ {{
ho _{
m{o}}}left( {p{}_{
m{o}}}
ight) cdot left( {frac{{k{k_{{
m{ro}}}}left( {{s_{
m{o}}}}
ight)}}{{{mu _{
m{o}}}}}nabla p{}_{
m{o}}}
ight)}
ight] = {q_{
m{o}}};;;;;;;;$$

(4)

$$begin{split} &frac{{partial left[ {phi left( {{p_{
m{w}}}}
ight){
ho _{
m{w}}}left( {p{}_{
m{w}}}
ight){s_{
m{w}}}}
ight]}}{{partial t}} + &qquadnabla cdot left[ {{
ho _{{{
m{w}}}}}left( {{p_{
m{w}}}}
ight) cdot left( { - frac{{k{k_{{
m{rw}}}}left( {{s_{
m{w}}}}
ight)}}{{{mu _{
m{w}}}}}nabla {p_{
m{w}}}}
ight)}
ight] = {q_{
m{w}}}end{split}$$

(5)

$${s_{
m{o}}} + {s_{
m{w}}} = 1$$

(6)

其中, p_o及p_w分别为油相和水相压力, MPa; ρ_o及ρ_w分别为油层条件下原油密度和地层水的密度, 10³t/m³; k_ro和k_rw分别为油相和水相对渗透率, 10^?3μm²; k是基质绝对渗透率, 10^?3μm²; μ_o及μ_w分别为油和水的黏度, cp; q_o及q_w分别为产液量和注入量, m³; s_o及s_w分别为含油饱和度和含水饱和度, %.

随着注水吞吐开发, 油层流体的采出, 地层压力不断下降, 导致岩石发生变形、流体被压缩. 基质及流体的状态方程为

$${
ho _{
m{o}}} = {
ho _{{
m{o}},0}}exp left[ { - {c_{
m{o}}}left( {{p_{
m{o}}} - {p_{{
m{o}},0}}}
ight)}
ight];;$$

(7)

$$
ho_ {
m{w}} = {p_{{
m{w}},{
m{0}}}}exp left[ { - c_{
m{w}}left( {{p_{
m{w}}} - {p_{{
m{w}},0}}}
ight)}
ight]$$

(8)

$$phi = {phi _0}exp left[ { - {c_{
m{r}}}left( {p - {p_0}}
ight)}
ight];;;;;;;;;;;;$$

(9)

其中, p_o,0为油相初始压力, MPa; p_w,0为水相初始压力, MPa; ρ_o,0为油层条件下原油初始密度, 10³ kg/m³; ρ_w,0为油层条件下地层水初始密度, t/m³; $phi $

为油层条件下孔隙度, 无量纲; $phi_{
m{o}} $

为原始油层孔隙度, 无量纲; c_o为原油压缩系数, MPa^?1; c_r为岩石压缩系数, MPa^?1; c_w为地层水压缩系数, MPa^?1; p₀为原始地层压力, MPa; p为地层压力, MPa.

(2)渗流模型

致密油藏基质与裂缝的接触面主要发生逆向渗吸, 毛管力占主导作用. 则毛管力辅助方程为

$${p_{
m{w}}} - {p_{
m{o}}} = {p_{
m{c}}}left( {{s_{
m{w}}}}
ight)$$

(10)

由于致密油藏基质渗透率极低, 原油从基质和天然裂缝以及压裂裂缝流动到水平井筒中, 其产量方程为

$${q_{
m{o}}} = -
ho left( {p_{
m{o}}^{}}
ight) cdot W{I_{
m{o}}} cdot left( {{p_{
m{o}}} - {p_{{
m{wf}}}}}
ight);;;$$

(11)

$${q_{
m{w}}} = -
ho left( {{p_{
m{w}}}}
ight) cdot W{I_{
m{w}}} cdot left( {{p_{
m{w}}} - {p_{{
m{wf}}}}}
ight)$$

(12)

其中, p_c为毛管力, MPa^?1; p_wf为井底流压, MPa; WI_o及WI_w为井指数公式. 采用Peaceman模型^[40-41]概念并予以修正, 其井指数计算公式如下

$$W{I_{
m{o}}} = frac{{2{text{π}} k{k_{
m{o}}}left( {{s_{
m{w}}}}
ight)h}}{{{mu _{
m{o}}}{B_{
m{o}}}left( {ln dfrac{{{r_{
m{e}}}}}{{{r_{
m{w}}}}} - 0.75 + s}
ight)}}$$

(13)

$$W{I_{
m{w}}} = dfrac{{2{text{π}} k{k_{
m{o}}}left( {{s_{
m{w}}}}
ight)h}}{{{mu _{
m{w}}}{B_{
m{w}}}left( {ln dfrac{{{r_{
m{e}}}}}{{{r_{
m{w}}}}} - 0.75 + s}
ight)}}$$

(14)

其中, r_e为供给半径, m; r_w为井半径, m; h为基质中裂缝高度, m; B_o及B_w分别为原油及水的体积系数, 无因次; s为表皮系数, 无因次.

由于致密油藏储层及流体的复杂性, 考虑启动压力, 渗流速度方程为

$$v = frac{k}{mu }nabla pleft( {1 - frac{G}{{nabla P}}}
ight)$$

(15)

其中v表示渗流速度, m/s; $nabla $

p为地层压力变化量, 无因次; k为储层渗透率, 10^?3μm², μ为流体黏度, cp; G为启动压力梯度, MPa/m.

基于储层存在的应力敏感效应, 根据基质和裂缝的敏感程度设置模型

$$frac{k}{{{k_{
m{o}}}}} = exp left[ { - {alpha _{
m{k}}}left( {{p_0} - p}
ight)}
ight]$$

(16)

其中, k是有效渗透率, 10^?3μm²; k_o为初始压力下基质的渗透率, 10^?3μm²; α_k为应力敏感系数, 无因次.

考虑裂缝导流系数的动态变化, 得到计算公式

$${F_{
m{c}}} = {F_{
m{c}}}left( t
ight) = {k_{
m{f}}}left( t
ight) cdot {w_{
m{f}}}left( t
ight)$$

(17)

其中, k_f(t)是动态裂缝渗透率, 10^?3μm²; w_f(t)表示动态裂缝宽度, m.

(3)传导率计算方程

针对交叉裂缝的情况, 将交叉裂缝单元之间的传导率近似处理, 将裂缝网格可看作普通网格, 此时裂缝网格与基质网格传导率表示为

$${T_i} = frac{{{k_{
m{f}}}_i cdot {A_{
m{f}}}_i}}{{{d_{
m{f}}}_i}}$$

(18)

式中T_i为裂缝网格与基质网格传导率, k_f_i是裂缝和基质渗透率的调和平均值, 10^?3μm²; A_f_i是裂缝与基质接触面积, m²; d_f_i是两条裂缝中心距离, m.

当两条裂缝相交时, 裂缝网格与裂缝网格传导率^[42-43]为

$${T_{
m{j}}} = frac{{{T_1} cdot {T_2}}}{{{T_1} + {T_2}}},{T_1} = frac{{{k_{{
m{f1}}}} cdot {A_{
m{f1}}}}}{{{d_{
m{f1}}}}},{T_2} = frac{{{k_{
m{f2}}} cdot {A_{
m{f2}}}}}{{{d_{
m{f2}}}}}$$

(19)

其中, k_f1和k_f2是裂缝段的渗透率, 10^?3μm ²; d_f1和d_f2是裂缝段到相交线的平均距离, A_f1及A_f2是裂缝段接触面积, m².

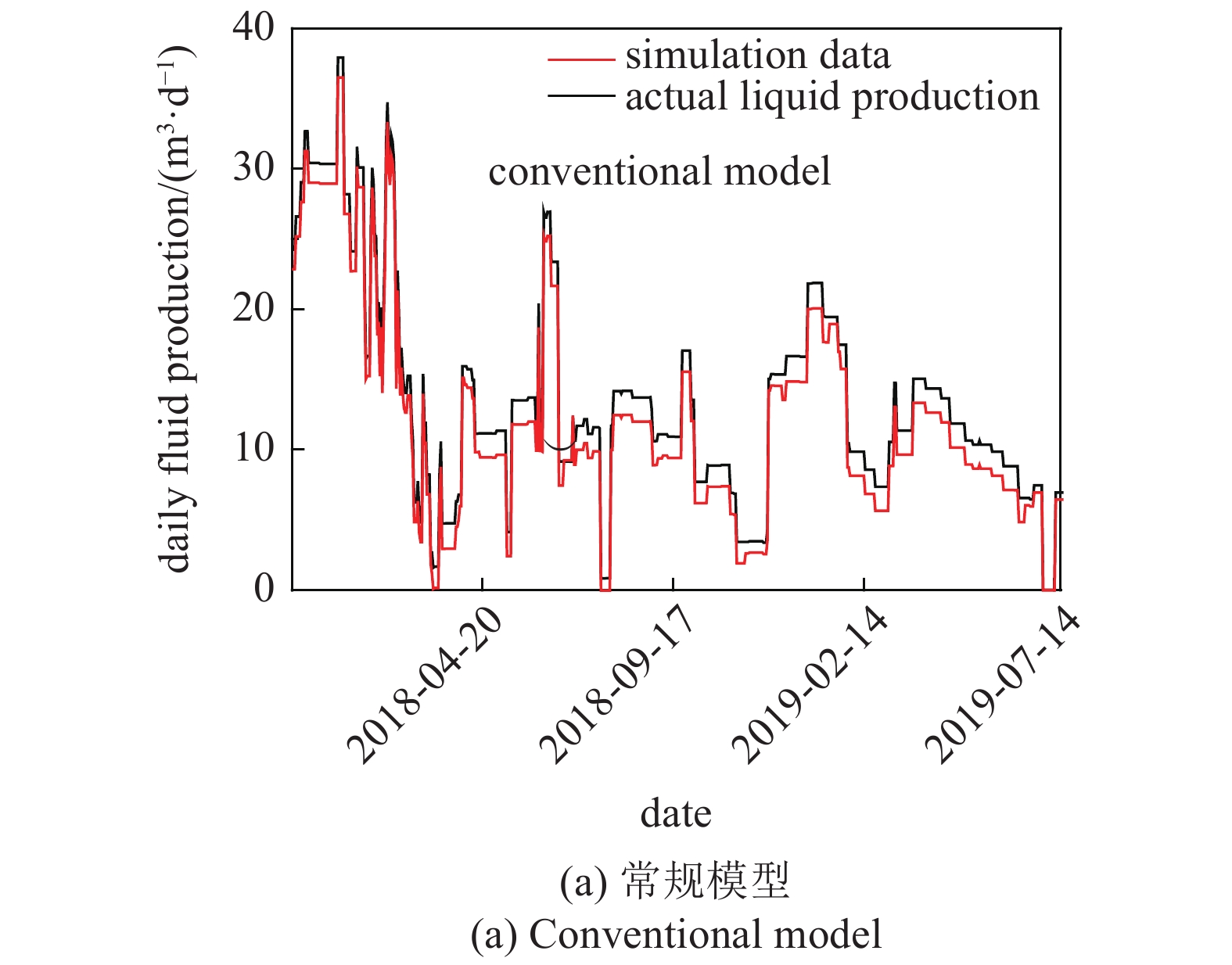
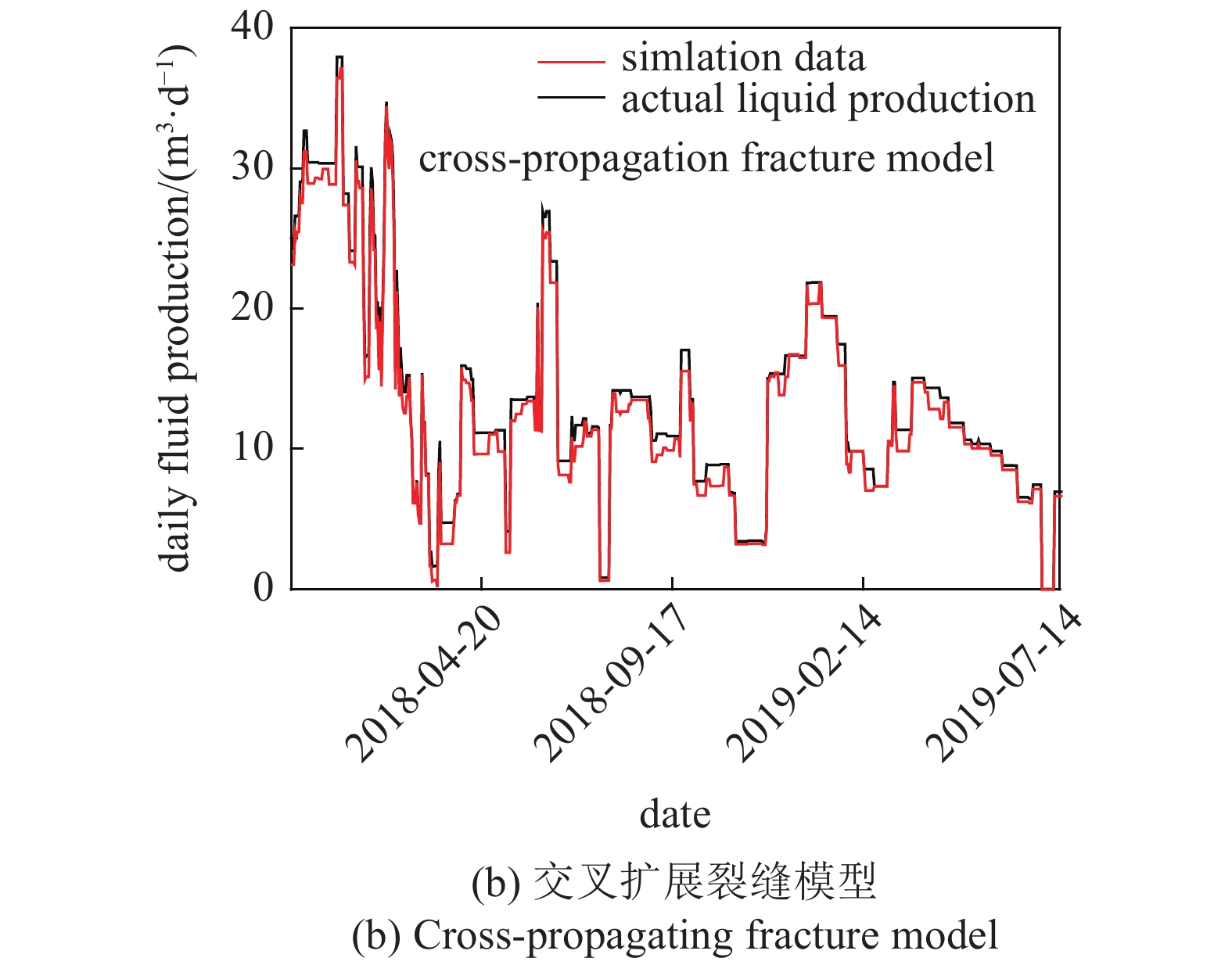
建立压裂水平井M56-152H常规数值模型及交叉裂缝数值模型, 常规模型模拟日产液与实际数据有差异(图4(a)), 交叉裂缝扩展形成的动态缝网模型模拟日产液, 历史拟合较好(图4(b)).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-4-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4-1" />

4
M56-152H产液量历史拟合结果

4.
M56-152H Production history matching results

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />

图
4
M56-152H产液量历史拟合结果 (续)

Figure
4.
M56-152H Production history matching results (continued)

下载:
全尺寸图片
幻灯片

致密油藏在不同区域均能使用相同形式的运动方程构建统一的控制方程. 因此, 可以对模型进行离散化求解, 降低耦合问题的复杂性, 使模型求解变得简单统一.

下面研究主要以I型扩展为主, 推导裂缝扩展长度、刻画动态缝网渗流规律.

1.2
裂缝扩展长度

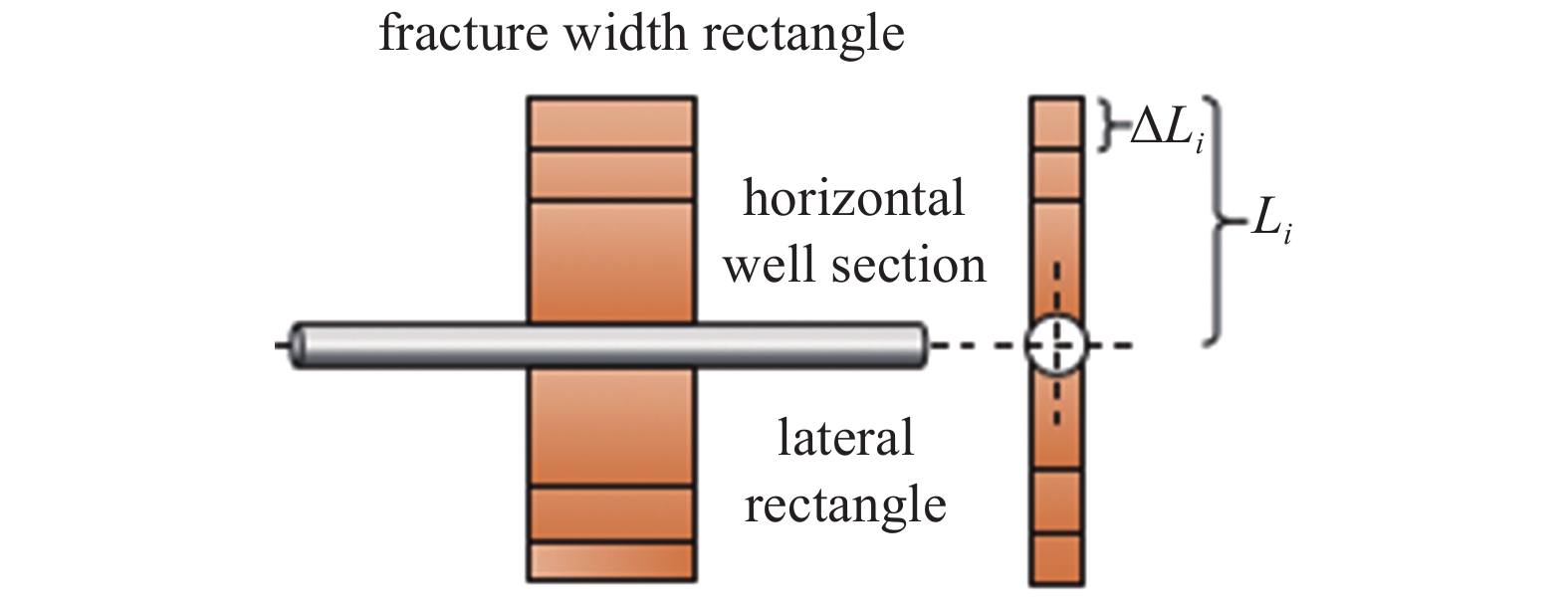
注水诱发裂缝扩展后, 裂缝扩展长度及裂缝半长是主要的关键参数. 根据艾尔文裂缝扩展原理, 当K > K_IC, 裂缝尖端压力达到地层破裂压力, 天然裂缝发生扩展. 由图2(b)模型假设裂缝扩展缝宽为矩形, 第i次扩展长度L_i, 长度增量为ΔL_i (图5).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />

图
5
裂缝扩展长度示意图

Figure
5.
Schematic diagram of crack propagation length

下载:
全尺寸图片
幻灯片

假设10级压裂水平井存在60条天然裂缝, 天然裂缝扩展瞬间, 根据格里菲斯准则采用断裂力学的能量平衡原理^[44-46], 从旧裂缝生成且还未充填流体的瞬间开始, 到新裂缝产生且还未充填流体的瞬间结束为单元, 对整个系统进行线弹性求解为

$$Delta {E_i} = Delta {E_{
m{l}}}_i + Delta {E_{
m{f}}}_i + Delta {E_{
m{rs}}}_{_{i + 1}} + Delta {E_{{i{
m{c}}}}}_{_{i + 1}}$$

(20)

其中, ΔE_i表示地面流入的能量, ΔE_l表示滤失的能量, ΔE_f表示缝内弹性能量, ΔE_rs表示基质内弹性能, ΔE_ic表示新的裂缝的能量

$$Delta {E_i} = intlimits_{{T_{i0}}}^{{T_i}} {Pleft( t
ight)} Q{
m{d}}t$$

(21)

$$Delta {E_{
m{l}}}_i = 120 sumlimits_{j = 1}^i {intlimits_{{T_{i0}}}^{{T_i}} {left[ {Pleft( t
ight) + {P_{
m{H}}} - {P_{
m{P}}}}
ight] cdot frac{{Cleft( t
ight)}}{{sqrt t }}} {A_j}{{{
m{d}}}}t}!!!!!!!! $$

(22)

$$Delta {E_{
m{f}}}_i = 120 left( {P - {P_{
m{H}}} - {P_{i0}}}
ight) omega H {L_i}qquadqquad$$

(23)

可根据格里菲斯准则, 克服基质内储存的弹性能

$$Delta {E_{{{
m{rs}}}_{i + 1}}} = frac{{{text{π}} sigma _{
m{h}}^2left( {60{A_{i + 1}}}
ight)}}{{16EH}}$$

(24)

产生新裂缝表面所吸收的能量E_{rc_i+1}为

$$Delta {E_{i{{{
m{c}}}_{i{
m{ + 1}}}}}} = 120 {A_{i + 1}} gamma $$

(25)

裂缝扩展的整个系统中能量平衡方程为

$$begin{split}& intlimits_{{T_{i0}}}^{{T_i}} {Pleft( t
ight)} Q{
m{d}}t = 120 sumlimits_{j = 1}^i {intlimits_{{T_{i0}}}^{{T_i}} {left[ {Pleft( t
ight) + {P_{
m{H}}} - {P_{
m{P}}}}
ight] frac{{Cleft( t
ight)}}{{sqrt t }}} {A_j}{
m{d}}t} !+! &quad 120 left( {P - {P_{
m{H}}} - {P_{i0}}}
ight) omega H {L_i} + frac{{{text{π}} sigma _{
m{h}}^2left( {60{A_{i + 1}}}
ight)}}{{16EH}} + 120 {A_{i + 1}} gamma end{split} $$

(26)

整理式(26)得到裂缝扩展长度的计算公式

$$begin{split}{L_i} =& Biggr{intlimits_{{T_{i0}}}^{{T_i}} {Pleft( t
ight)} Q{
m{d}}t - 120sumlimits_{j = 1}^i {intlimits_{{T_{i0}}}^{{T_i}} {left[ {Pleft( t
ight) + {P_{
m{H}}} - {P_{
m{P}}}}
ight]frac{{Cleft( t
ight)}}{{sqrt t }}} {A_j}{
m{d}}t} - &dfrac{{{text{π}} sigma _{
m{h}}^2left( {60{A_{i + 1}}}
ight)}}{{16EH}} - 120{A_{i + 1}}gamma Biggr}Biggr/Biggr[120left( {P - {P_{
m{H}}} - {P_{i0}}}
ight)omega HBiggr]end{split}$$

(27)

其中, Q为注入量, m³; P(t)注入压力, MPa; L_i为第i次裂缝扩展的裂缝半长, m; P_P地层孔隙压力, MPa; ρ注入流体的密度, kg/m³; P_H井筒液柱产生的压力, MPa; P为裂缝扩展压力, MPa; T_i为扩展周期, d; A_i+1第i+1次扩展中半裂缝的侧面积, m²; σ_h地层最小水平主应力, MPa; E地层岩石弹性模量, MPa; ω为裂缝宽度, m; H油层厚度, m; $gamma $

表面能密度, MPa/m²; C_L扩展后的滤失系数, m/d^1/2; P_i_o第i次裂缝产生时, 地面压力, MPa; T_i为扩展周期, d; T_i0扩展周期初始时间, d; C(t)滤失系数, 无因次.

根据某致密油藏M56块注水吞吐期间的5几口井的注入量数据, 计算得到滤失系数C(t)为

$$Cleft( t
ight) = - 9.27x + 10.905$$

(28)

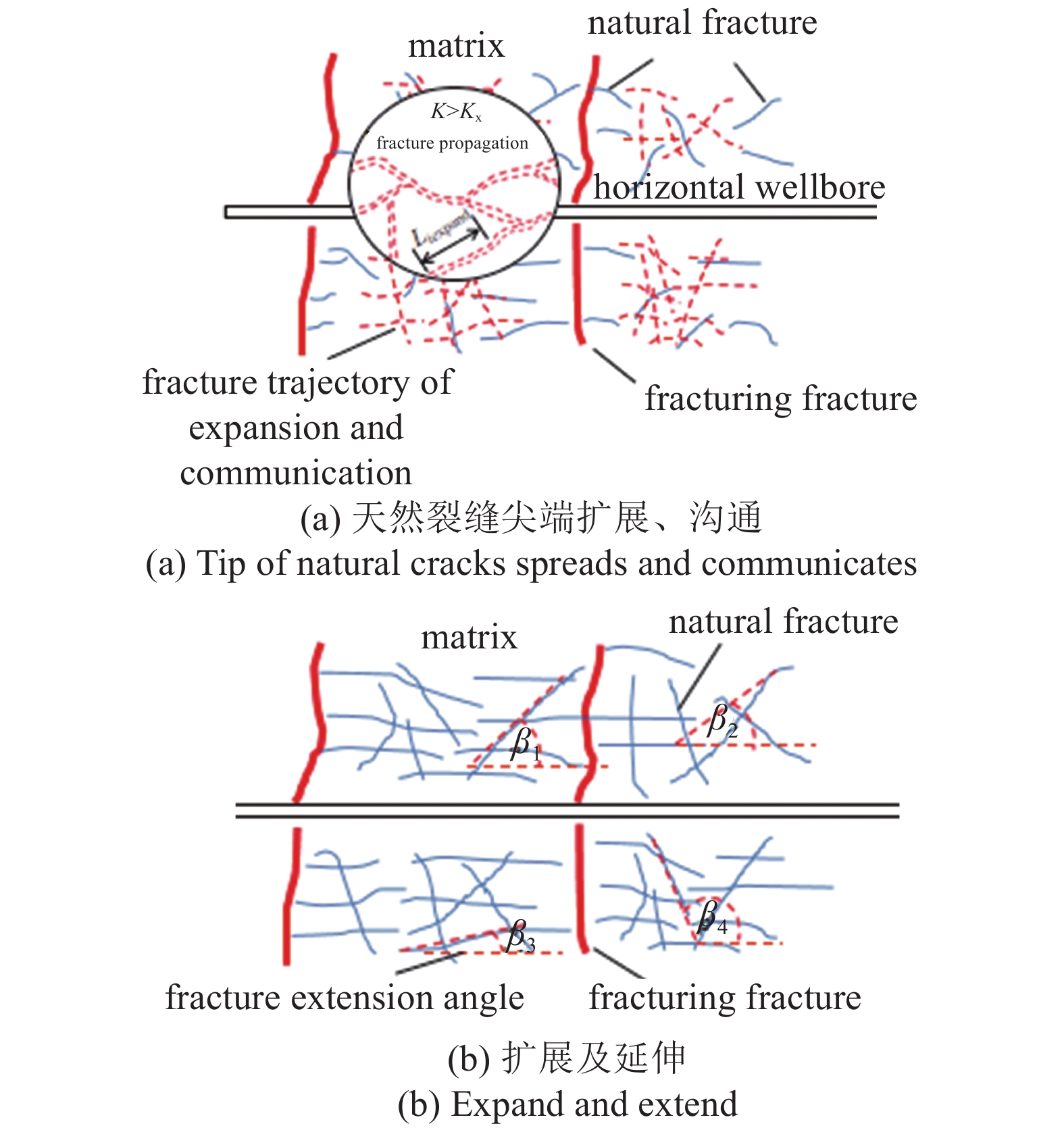
随着注水时间延长, 扩展的天然裂缝延伸, 开发过程中需将缝长控制在合理的范围, 防止井间裂缝水窜. 由式(2)可知储层中裂缝尖端方位角θ是随机分布的, 天然裂缝会扩展、延伸并相互沟通, 呈现不规则复杂缝网(图6(b)), 此时储层中流体的渗流机理比较复杂. 因此, 揭示致密油藏动态裂缝的渗流规律是转变开发方式的关键.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />

图
6
注水诱发天然裂缝扩展

Figure
6.
Water-induced the expansion of natural fractures

下载:
全尺寸图片
幻灯片

1.3
裂缝扩展过程中的逆向渗吸判别

自发渗吸是低渗透裂缝水驱油藏的重要开采机理^[47]. 衰竭开采及注水吞吐都会有大量注入水通过不规则复杂缝网进入地层, 与基质大面积接触, 发生正向及逆向渗吸作用. 为了确定两种渗吸主控作用, 根据渗吸物理机理的判别标准^[48], 计算N_B^?1 (重力与毛管力的比值Bond数的倒数)的数值. 利用N_B^?1数值的范围判定基质渗吸过程中毛细管力和重力的贡献. 当N_B^?1>5时, 毛管力支配渗吸过程, 与基质的接触面主要发生逆向渗吸; 当N_B^?1<0.2时, 重力支配渗吸过程, 主要发生正向渗吸; 当0.2<N_B^?1<5时, 则是毛细管力和重力共同作用的渗吸过程. N_B^?1的表达式为

$${N_{
m{B}}}^{ - 1} = Bfrac{delta }{{Delta
ho {{gH}}}}sqrt {frac{phi }{K}} $$

(29)

式中, B为结构常数, 无因次; Δρ为油水密度差, kg/m³; g为重力加速度, 取9.8 m/s²; H为多孔介质高度, m; K为渗透率, 10^?3μm²; Φ为孔隙度, 无因次; δ为表面张力, mN/m. 式(29)没有考虑基质的润湿性, 而润湿性对基质渗吸有重要的影响. Iffly等^[49]对上述渗吸机理判别方程进行修正, 刘卫东等^[50]和姚同玉等^[51]也做过类似研究, 并做了大量实验. 改进后的N_B^?1的表达式为

$${N_{
m{B}}}^{ - 1} = Bfrac{{delta cos alpha }}{{Delta
ho {gH}}}sqrt {frac{phi }{K}} $$

(30)

式中, α为润湿接触角, (°). Standnes等^[52]进一步实验研究了润湿性对渗吸机理的影响. 润湿性越弱, 润湿接触角越大, 界面张力越大. 当接触角大于90°时, 界面张力成为渗流阻力. 其中B的数值是由孔隙结构常数的表达式^[53]计算得出, 该公式为

$$B = sqrt {frac{{1left( {4 - {D_{
m{f}}}}
ight)left( {2 - {D_{
m{f}}}}
ight)}}{{2tau {{left( {3 - {D_{
m{f}}}}
ight)}^2}left( {1 - phi }
ight)}}} $$

(31)

式中, τ是流体流线的迂曲度, 无因次; D_f为孔隙分形维数, 且0 < D_f < 2. 迂曲度公式为

$$tau = 1 + beta ln left( {1/phi }
ight)$$

(32)

式中, β为拟合常数. 裂缝性致密油藏具有低孔、低渗的特征, 致密储层渗吸过程毛管力比常规油藏大. 某致密油藏M56块, 孔隙度?为0.165, β取值0.51. 在天然裂缝扩展后形成的动态缝网中, 裂缝视为海岸线科赫曲线类型, 根据文献[54], D_f取值为1.2618, 由式(31)计算得到B₁ = 0.45. 动态缝网中的基质视为Sierpinski垫片和Sierpinski地毯型, D_f分别取值1.585及1.892, 计算得到B₂=0.394及B₃ = 0.22. 本文的结构系数近似取三类型的平均值, 即B ≈ 0.4.

某致密油藏M56块, Δρ=1.9 × 10² kg/m³, 重力加速度g取9.8 m/s²; H=20 m, K=1×10^?5 μm²,Φ = 16.5%, δ = 30 mN/m, α = 33.6°. 由式(30)计算得到致密油藏M56块N_B^?1 = 35.7.

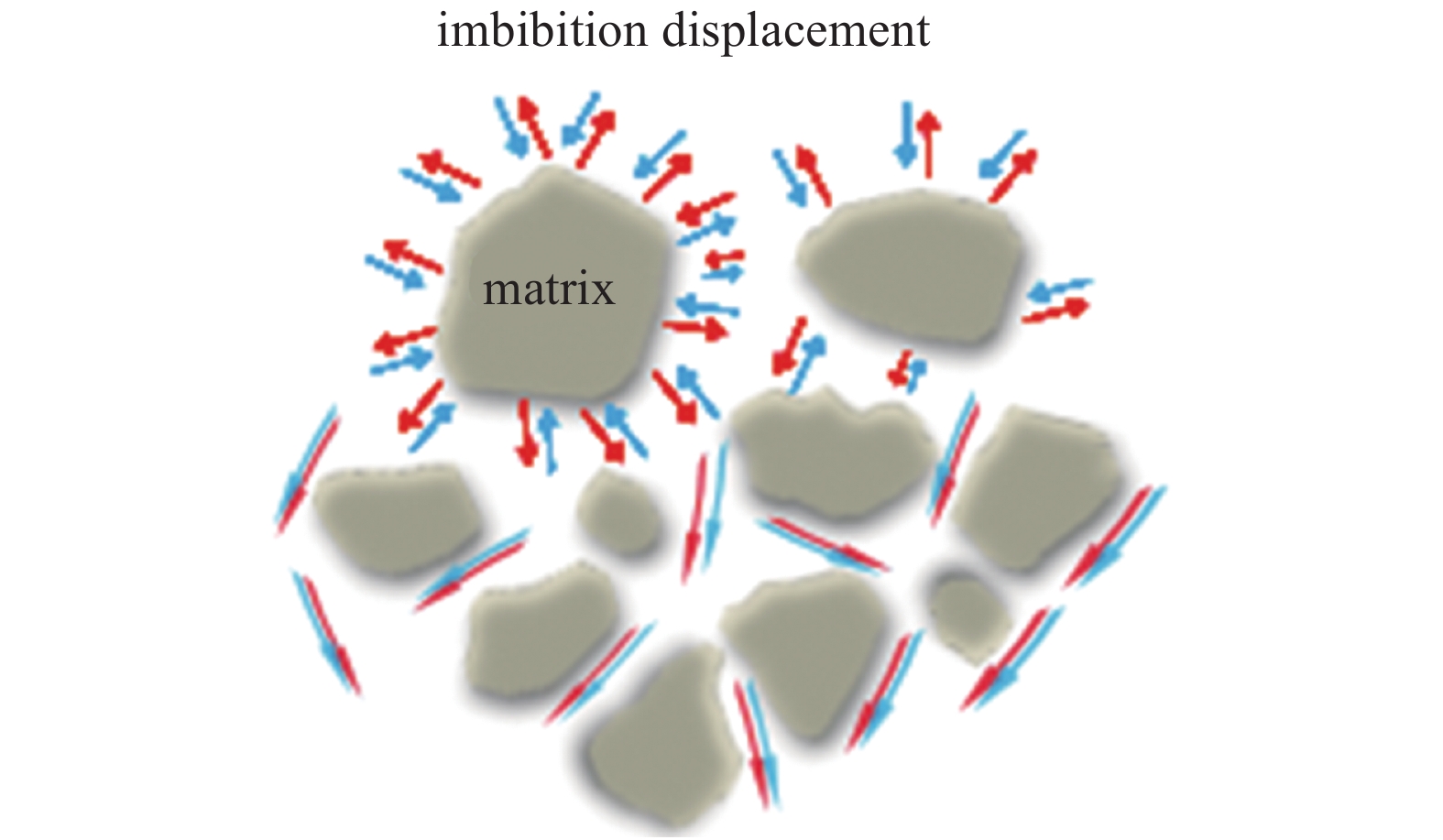
根据Schechter提出的判别标准, 当N_B^?1>5时, 毛管力支配渗吸过程, 与基质的接触面主要发生逆向渗吸. 在毛管力作用下, 致密油藏M56块发生大规模的逆向渗吸, 将原油置换到复杂缝网中, 这为注水吞吐转变为脉冲注水开发方式提供了大量可驱替的原油(图7).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />

图
7
逆向渗吸作用

Figure
7.
Reverse imbibition

下载:
全尺寸图片
幻灯片

注水初期, 毛管力是逆向渗吸的动力. 随着注水吞吐轮次的增加, 地层能量不断释放, 注水波及面积范围降低, 导致岩石润湿性减弱. 润湿接触角α变大, 毛管力变成了逆向渗吸阻力. 逆向渗吸作用减弱, 由逆向渗吸作用置换原油数量将减少, 注水吞吐效果变差.

2.
致密油藏线性驱替方式

裂缝性致密油藏注水吞吐主要发生径向驱替及逆向渗吸作用, 多轮次注水吞吐后, 渗吸置换作用减弱, 产量降低明显. 合理利用天然裂缝扩展形成的高导流通道, 尽可能地发挥逆向渗吸加驱替作用, 是目前裂缝性致密油藏亟待解决的难题.

下面研究将注水吞吐转为脉冲注水的可行性.

2.1
脉冲注水原理

脉冲注水充分发挥注入水在动态裂缝中的线性驱替作用, 增加流体的流动, 促使注水波及面积迅速增加, 逆向渗吸范围增加. 脉冲注水与注水吞吐主要不同点在于, 注水吞吐只发生在本井附近, 多轮次吞吐后, 致密油藏注入水推进速度较为缓慢, 两井之间部分区域的原油未能被波及. 脉冲注水是通过注水井周期性地改变注水量, 造成地层压力周期性升高和降低, 从而在裂缝和基质之间产生压差. 压力升高到高于裂缝开启压力时, 天然裂缝扩展、延伸并沟通压裂裂缝而形成的复杂缝网. 注入水驱替原油, 向前推进, 在生产井被采出.

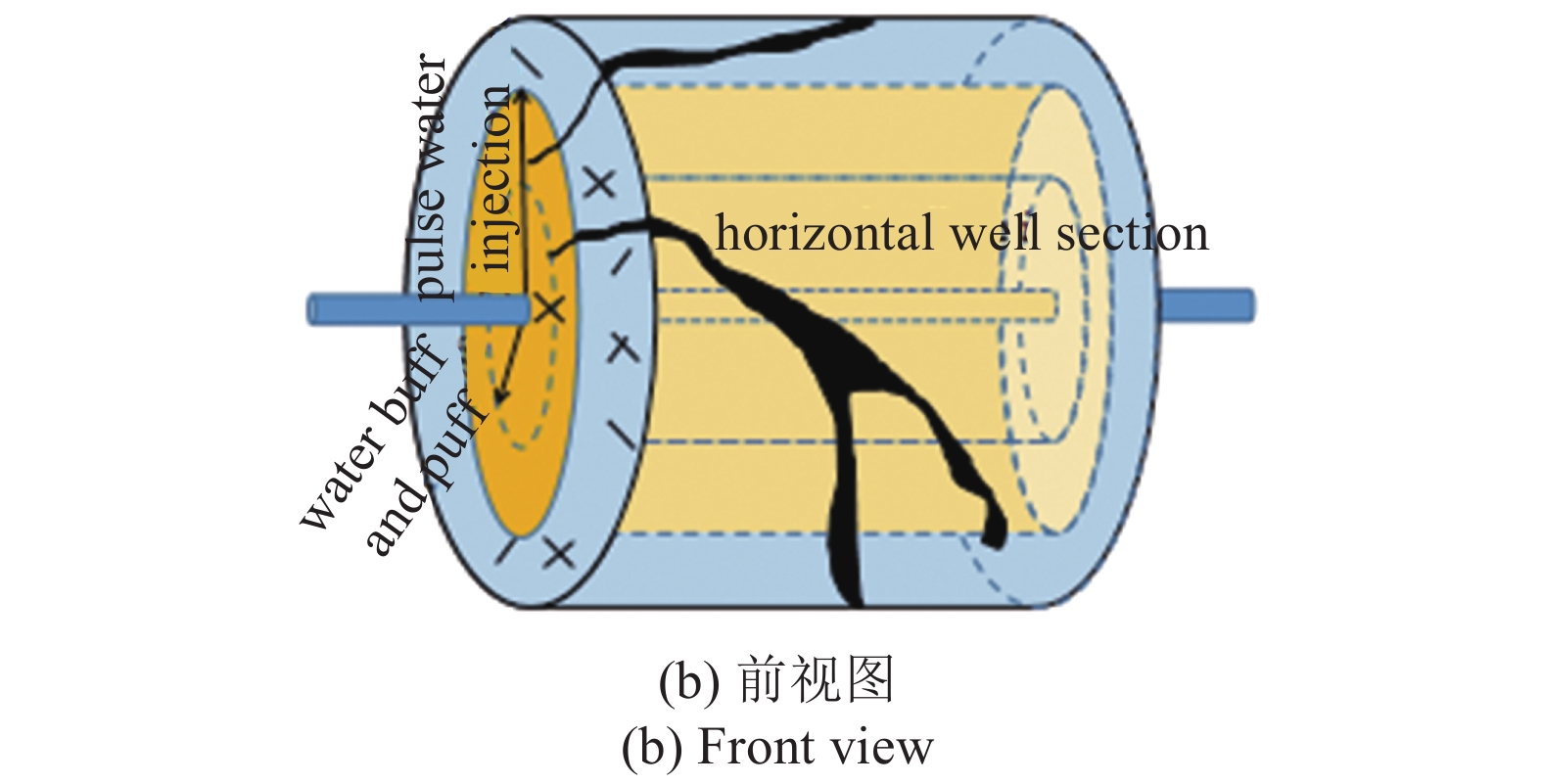
从宏观上分析, 注水吞吐在注水阶段驱替作用方向是径向的(图8(a)), 脉冲注水主要是线性驱替作用占主导地位, 主要沿着井间裂缝线性向前驱替(图8(b)).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />

图
8
径向和线性驱替作用示意图

Figure
8.
Diagram of radial and linear displacement

下载:
全尺寸图片
幻灯片

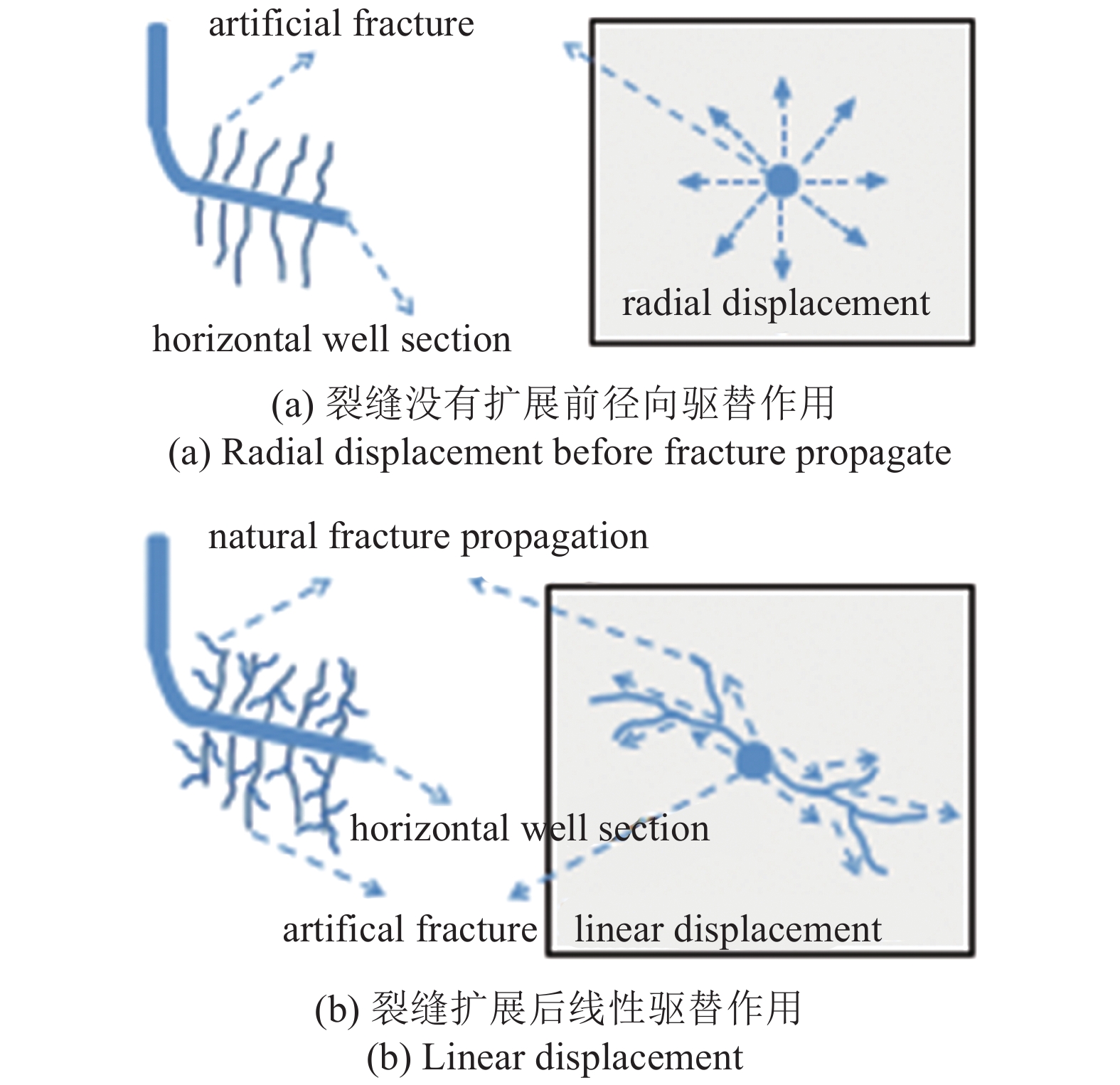
从油藏尺度分析, 注水吞吐方式在基质中的注水波及主要是拟径向的(图9(a)), 脉冲注水波及主要是沿着注水诱导裂缝扩展方向发生线性驱替作用(图9(b)).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />

图
9
裂缝扩展前后径向和线性驱替作用示意图

Figure
9.
Diagram of radial and linear displacement

下载:
全尺寸图片
幻灯片

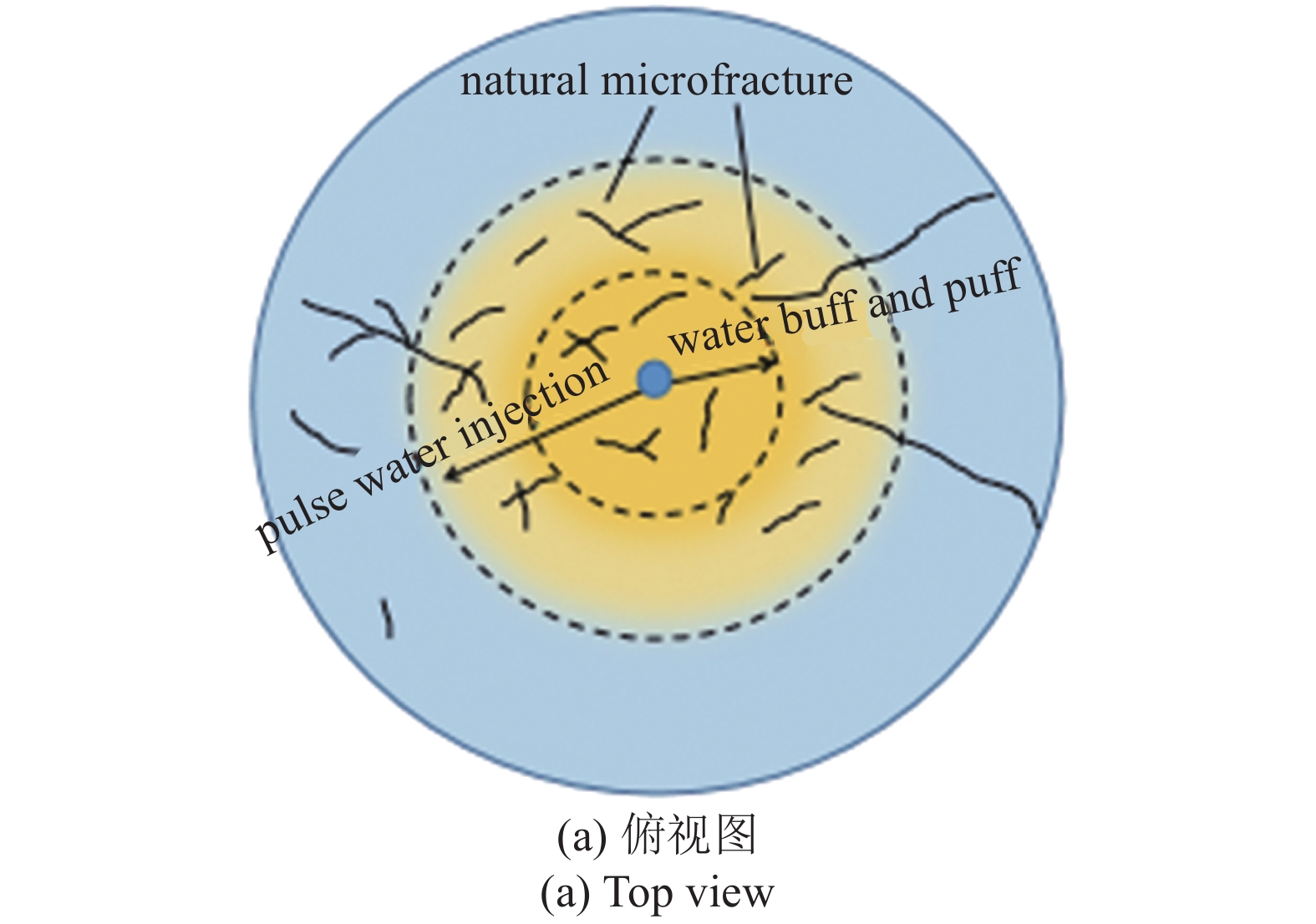
动态缝网中注入水受毛细管力作用和水动力效应, 加之天然裂缝扩展形成的高导流通道, 注水波及面积迅速增加, 逆向渗吸范围扩大(图10(a)和图10(b)). 逆向渗吸作用加强, 缝网与基质之间的流体交换速度和质量发生质变, 置换出更多的原油.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-10-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10-1" />

10
注水吞吐和脉冲注水逆向渗吸作用范围对比

10.
Comparison of water-injection huff and puff and pulse water injection imbibition range

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />

图
10
注水吞吐和脉冲注水逆向渗吸作用范围对比(续)

Figure
10.
Comparison of water-injection huff and puff and pulse water injection imbibition range (continued)

下载:
全尺寸图片
幻灯片

在下一个脉冲注水期间, 裂缝中被置换的原油及无渗吸作用波及区域的原油, 在线性驱替作用下流动到井筒. 水平井脉冲注水利用了逆向渗吸及线性驱替的采油原理(图11), 与注水吞吐开发方式相比极大地提高了驱油效率. 下面以某实际区块为例, 讨论该开发方式合理的油井工作制度.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />

图
11
脉冲注水逆向渗吸及线性驱替作用

Figure
11.
Reverse imbibition and linear displacement

下载:
全尺寸图片
幻灯片

2.2
脉冲注水可行性探讨

某致密油藏属于凝灰岩裂缝性致密油藏, 是国内外规模较大的致密油藏水平井注水吞吐试验区. 该区块天然微细裂缝比较发育, 地层压力系数为1.013, 井距为100 m ~ 200 m, 断裂韧度K_IC为0.908 MPa·m^1/2. 2015年开始注水吞吐, 截止2020年9月注水吞吐120井次, 其中56口井吞吐3 ~ 6轮次. 该油藏M56块为例, 模拟实际井注水吞吐转化为脉冲注水的累计采油及平均地层压力.

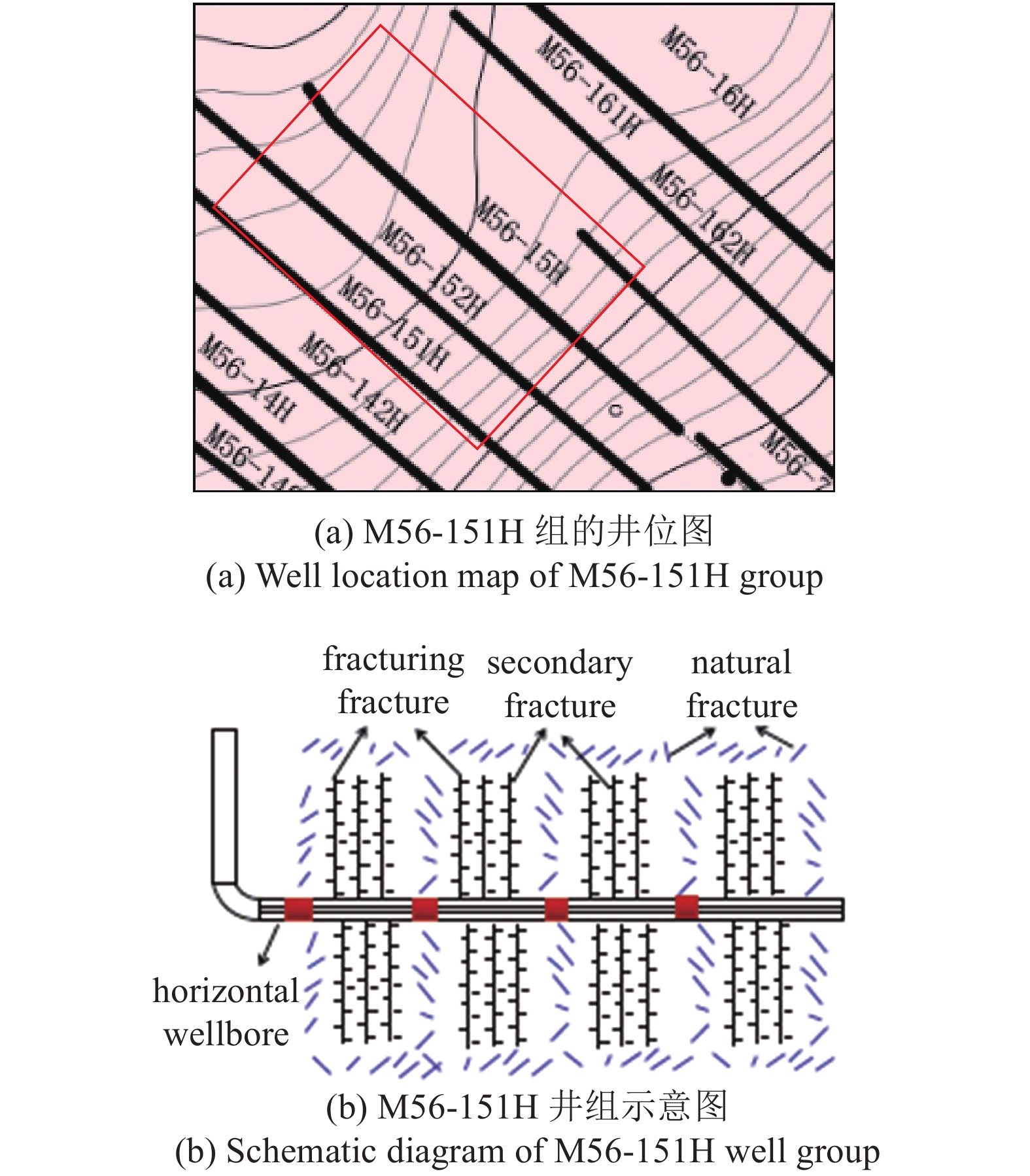
M56-151H井(图12(a)) 于2017年5月开始注水吞吐, 建立该井数值模型, 有关地层参数、初始地层条件等参数等见表1.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />

图
12
M56-151H井组井位图及裂缝发育情况

Figure
12.
Well location and fracture development

下载:
全尺寸图片
幻灯片

表
1
数值模拟参数表

Table
1.
Numerical simulation parameter table

table_type1 ">

	Parameter	Value
size	model size/m	1000 × 800
size	grid size/m	10 × 10 × 1
reservoir parameters	depth in the middle of the oil layer/m	2285
	oil layer thickness/m	25 ~ 40
	matrix permeability/μm²	1.8 × 10^?5
	porosity/%	0.145
	reservoir temperature/°C	65.3
	original formation pressure/MPa	21.7
	formation fracture pressure/MPa	60 ± 5
	formation pore pressure/MPa	26.5
	minimum horizontal principal stress of formation/MPa	45 ± 10
	pressure gradient/(MPa·hm^?1)	8.59
	rock compressibility/MPa^?1	1.4254 × 10^?3
	comprehensive compression factor/MPa^?1	4 × 10^?4
fluid parameter	viscosity of water/(MPa·s)	0.6
	oil viscosity/(MPa·s)	158
	crude oil density/(g·cm^?3)	0.89
	oil saturation/%	0.624
	compression system of liquid/MPa^?1	1.425 × 10^?3
	water saturation/%	23.90%
	volume factor/%	1.18
	crude oil compression factor/MPa^?1	9 × 10^?4
well parameters	horizontal well length/m	1000
	fracture half-length/m	30
	fracture width/m	0.003
	number of fracture	11
	well spacing/m	100?200
	distance between segments/m	25?60
	well radius/m	0.1
	initial surface injection pressure/MPa	31

下载:
导出CSV
|显示表格

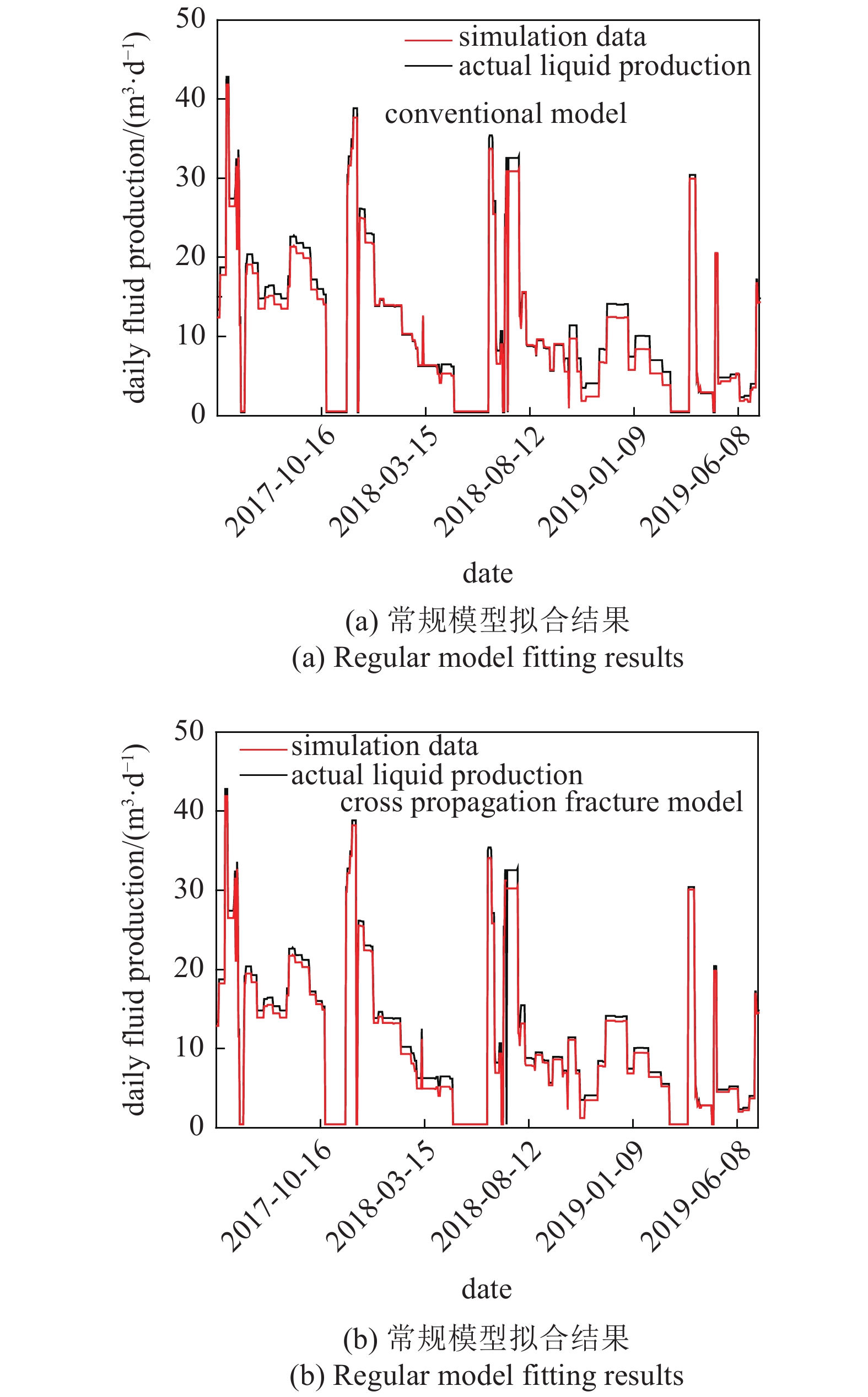
模拟结果显示, 注水初期裂缝净内压随着注水量的增加而升高, 应力场强度因子也随之升高. 当应力场强度因子K达到0.908 MPa·m^1/2, 天然微细缝发生开启及扩展现象. 模拟结果还表明, 采用定产液方法拟合的实际产液, 历史拟合效果较好(图13).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />

图
13
M56-151H产液量历史拟合结果

Figure
13.
M56-151H Production history matching results

下载:
全尺寸图片
幻灯片

2.3
注水吞吐转脉冲注水

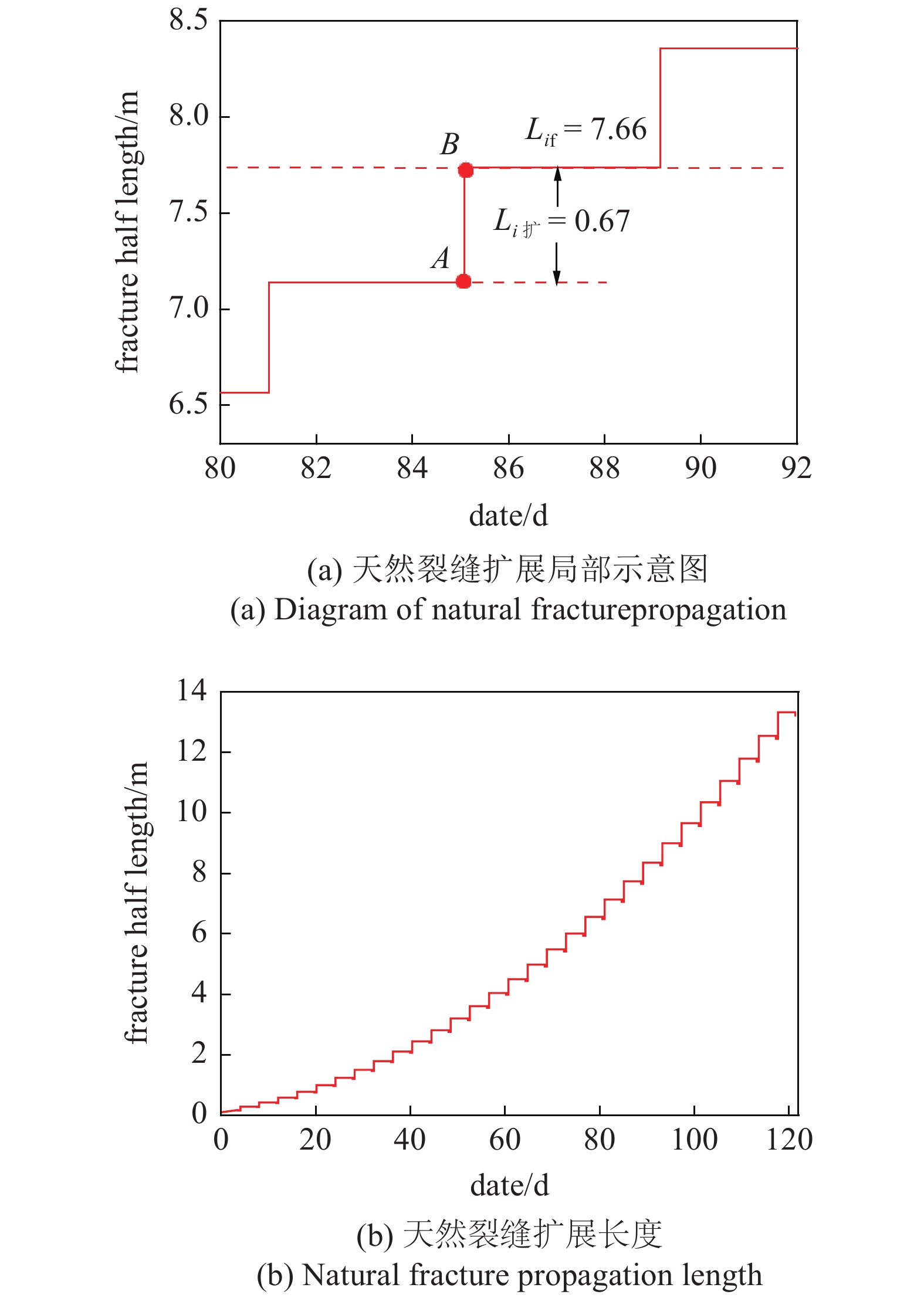
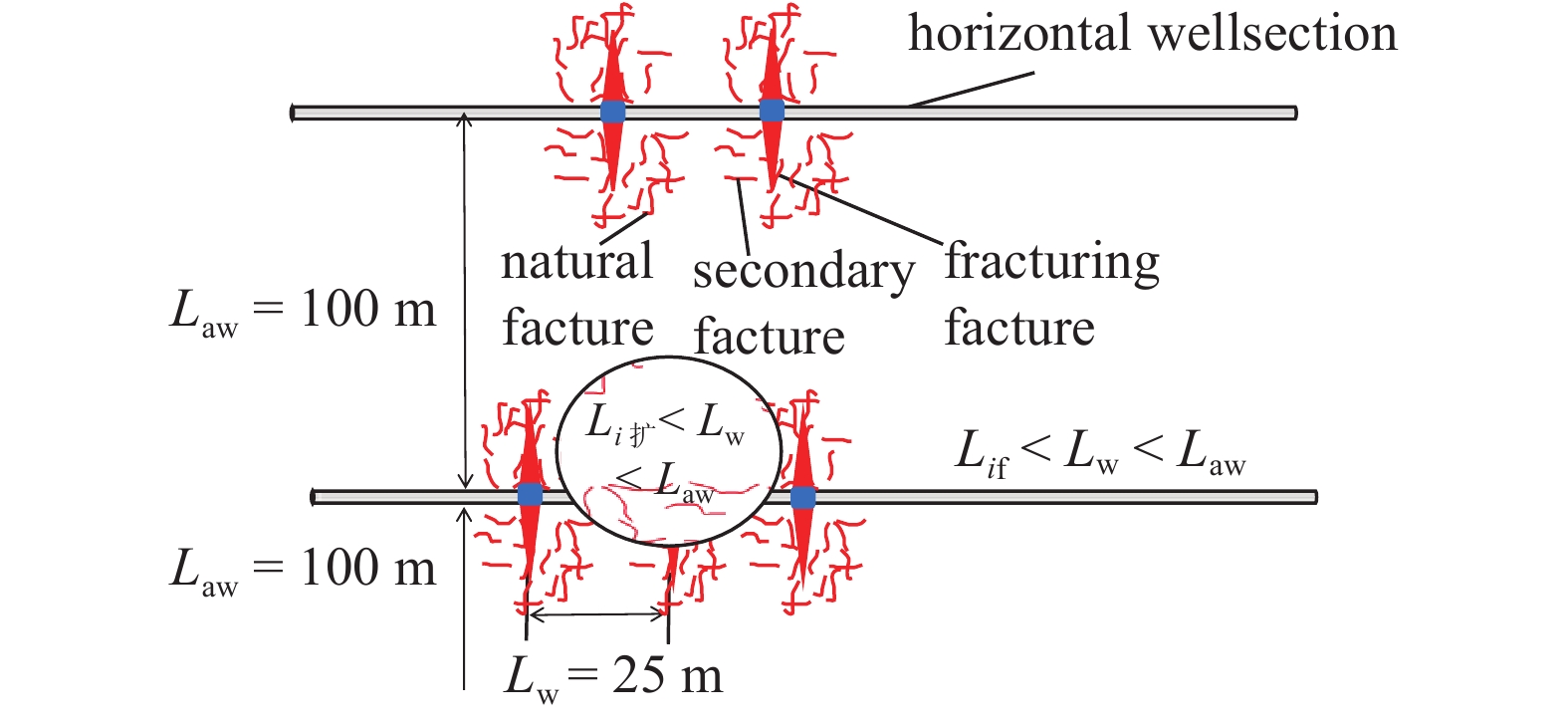
注水吞吐转为脉冲注水前, 在设计井距及段间距离时, 要着重考虑裂缝扩展长度, 以期确保不会发生水窜. 图14(a)中A点至B点为第i次裂缝扩展长度, 根据式(20)及式(27)计算得到${L_{i{text{扩}} }} $

= 0.67 m, L_i_f = 7.66. 注水120天, 天然裂缝扩展长度为13.33 m(图14(b)). 每次天然裂缝扩展, ${L_{i{text{扩}} }} $

及L_i_f均小于区块的井距和段距, 水平井段和邻井之间没有发生水窜现象(图15).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />

图
14
模拟裂缝扩展长度结果

Figure
14.
Simulated fracture propagation length

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />

图
15
裂缝扩展长度与井距段距对比

Figure
15.
Result of simulated fracture propagation length

下载:
全尺寸图片
幻灯片

随着脉冲注水周期的增加, 被置换的原油大幅度增多. 分析原因, 裂缝扩展形成的动态缝网加强了脉冲注水的驱替作用, 提高了注入水与基质接触的面积. 逆向渗吸范围扩大, 逆向渗吸作用加强, 置换原油的速度及数量发生了质变.

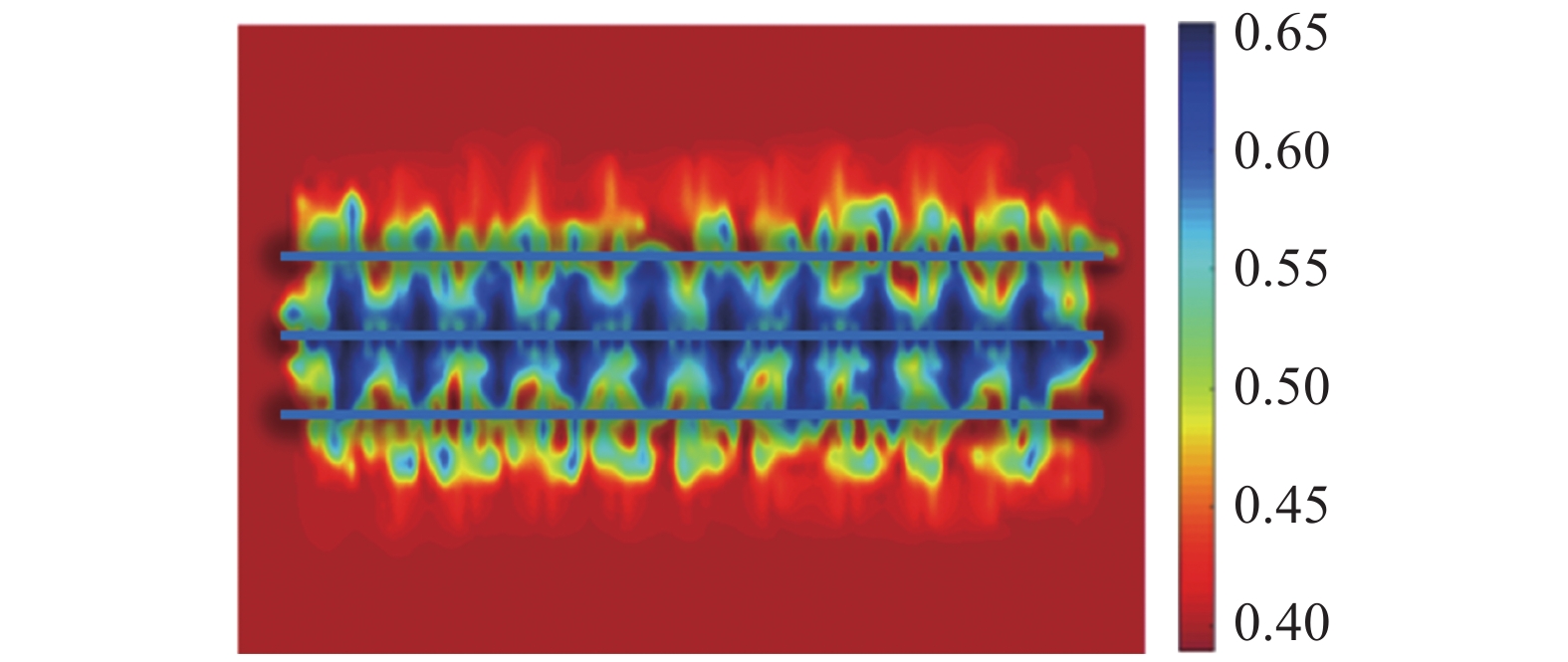
以M56-152H井组为例, 分别设计3种方案, 注入时间设置为1 d, 2 d, 3 d. 设计注入量设置为300 m³/d, 但在模拟含水饱和度场图时发现, 水平井间发生明显水窜现象(图16).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />

图
16
注水量300 m³/d时发生水窜

Figure
16.
Water breakthrough occurs when the water injection volume is 300 m³/d

下载:
全尺寸图片
幻灯片

经过反复调整参数, 当注入量设置为100 m³/d时, 井底压力达到裂缝开启压力41.7 MPa, 低于地层破裂压力60 MPa. 停注时间设置为1 d, 2 d, 3 d, 两口采油井一直以50 m³/d的采油量生产10年(表2).

表
2
脉冲注水3种方案

Table
2.
Three schemes of pulse water injection

table_type1 ">

plan	injection time/ d	shut-in time/ d	water injection/ (m³·d^?1)	oil production/ (m³·d^?1)
1	1	1	100	50
2	2	2	100	50
3	3	3	100	50

下载:
导出CSV
|显示表格

M56-151H井3种设计方案生产10年的累计采油在1.02 × 10⁵ ~ 1.05 × 10⁵ m³, 方案3累计采油最高, 预测10年累计采油量为1.05 × 10⁵ m³ (图17(a)). 该方案的工作制度是注3天停3天, 注入量100 m³/d, 产油量50 m³/d. 预测10年后地层压力降至20 MPa, 但仍然保持较高的水平(图17(b)).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />

图
17
模拟脉冲注水3种方案生产10年预测产量

Figure
17.
Predicted output of the three schemes of simulated pulse water injection in 10 years

下载:
全尺寸图片
幻灯片

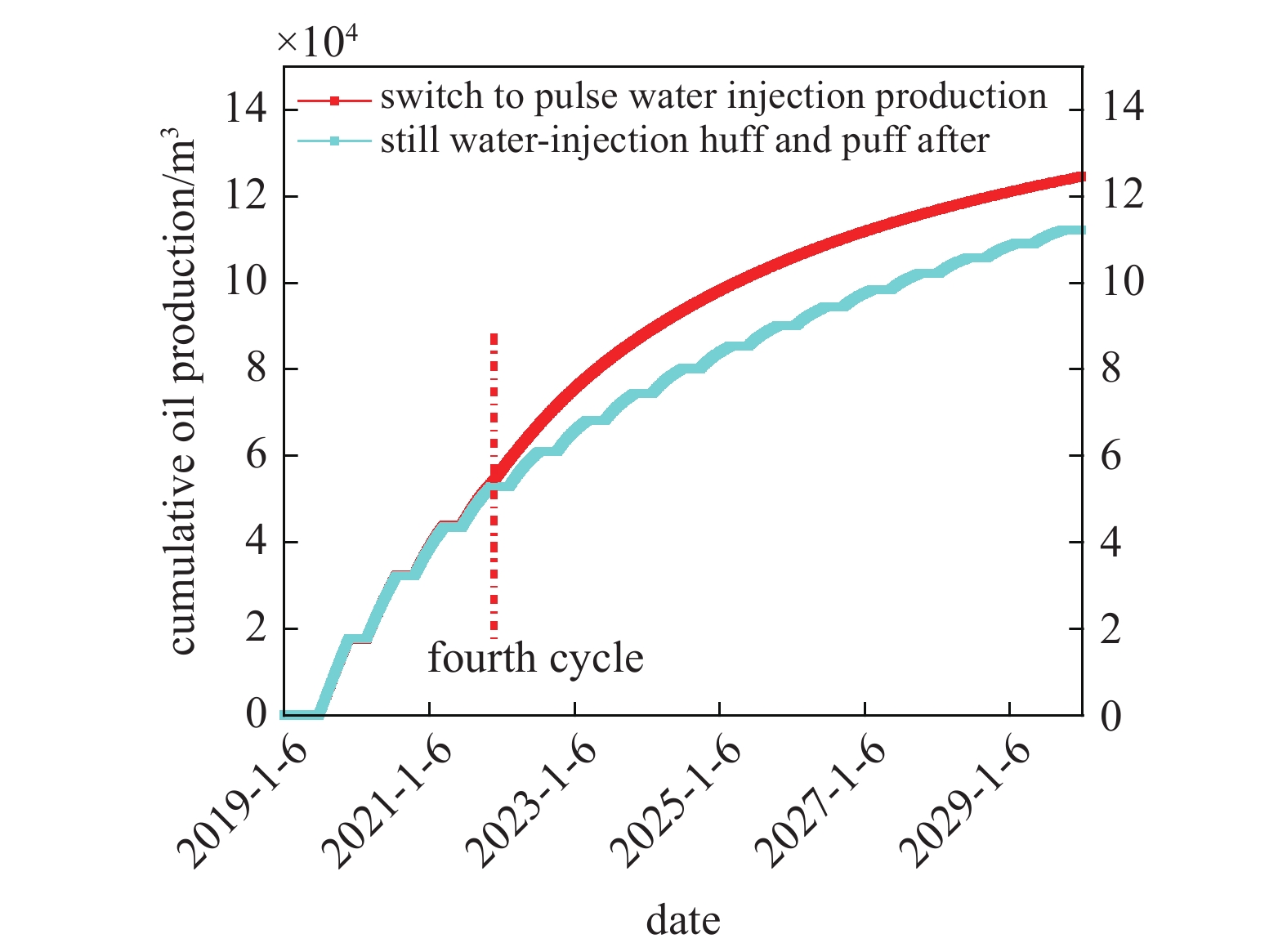
模拟M56-152H井注水吞吐4轮次后转变为脉冲注水, 并按照方案3开采制度, 模拟马56-152H井4轮次后仍以注水吞吐方式生产至2029年. 对比两者的累计采油量, 转为脉冲注水预测10年累计采油量高于注水吞吐(图18).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-18.jpg'"
class="figure_img
figure_type1 bbb " id="Figure18" />

图
18
注水吞吐与脉冲注水生产10年预测产量

Figure
18.
Predicted output of water-injection huff and puff and pulsed water injection production for 10 years

下载:
全尺寸图片
幻灯片

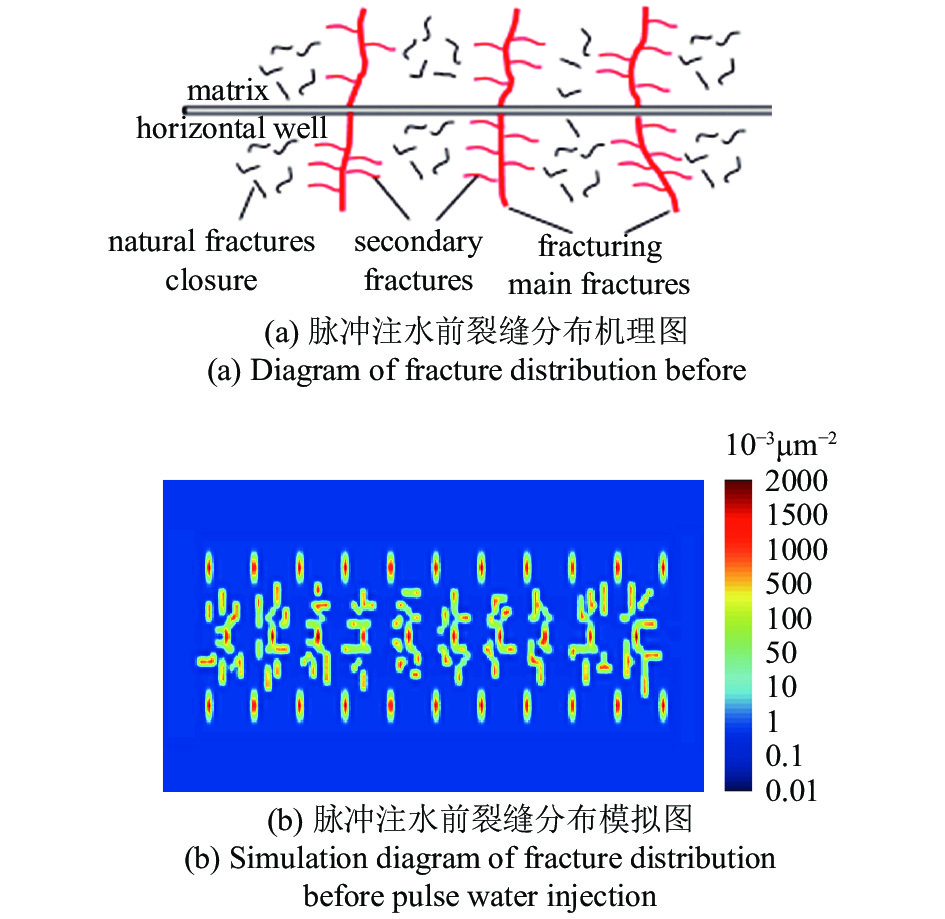
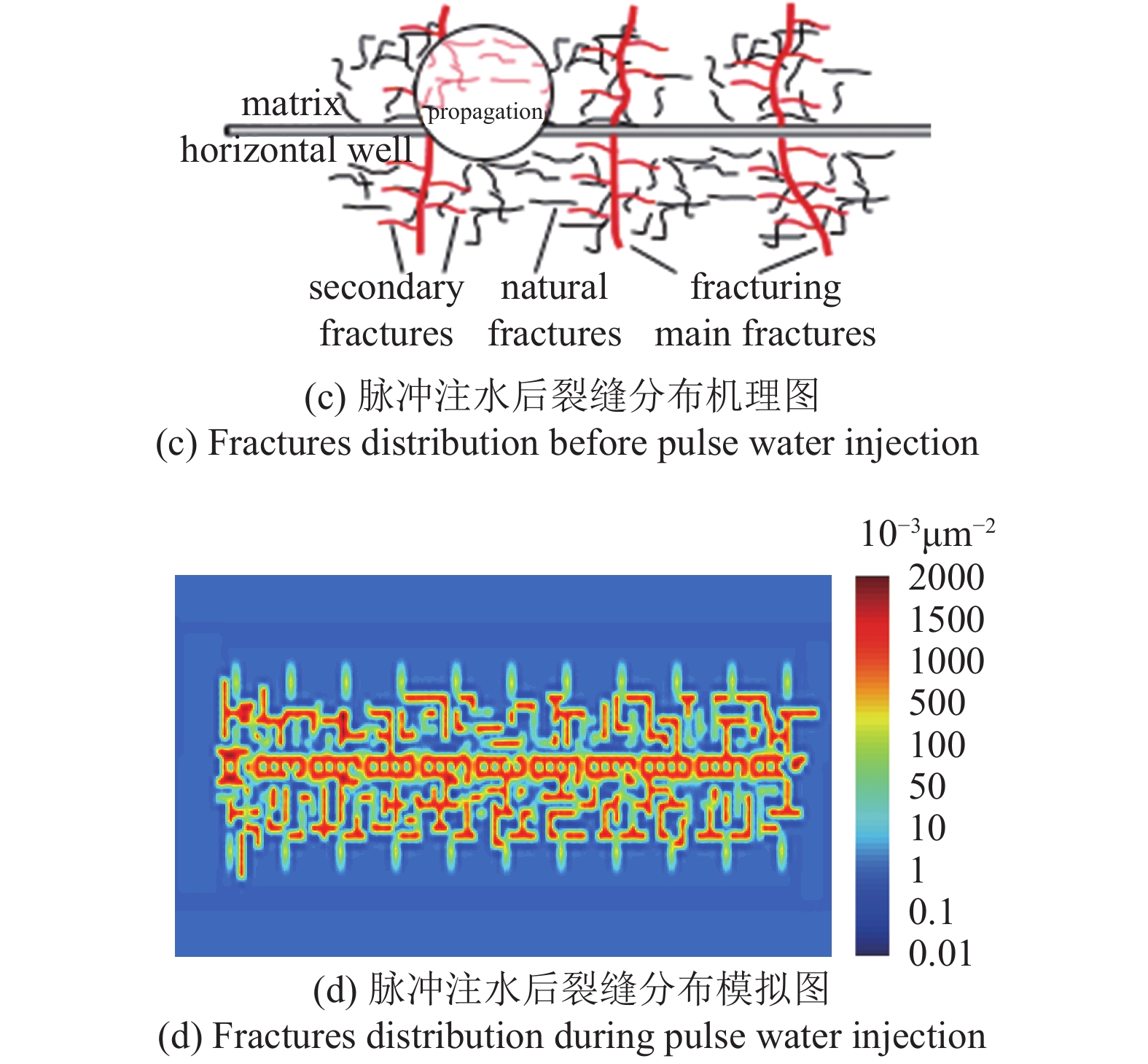
M56-152H在脉冲注水前, 储层中部分天然裂缝处于闭合状态(图19(a), 图19(b)). 脉冲注水后天然裂缝形态发生了扩展延伸、并沟通了压裂裂缝形成了动态缝网(图19(c), 图19(d)).

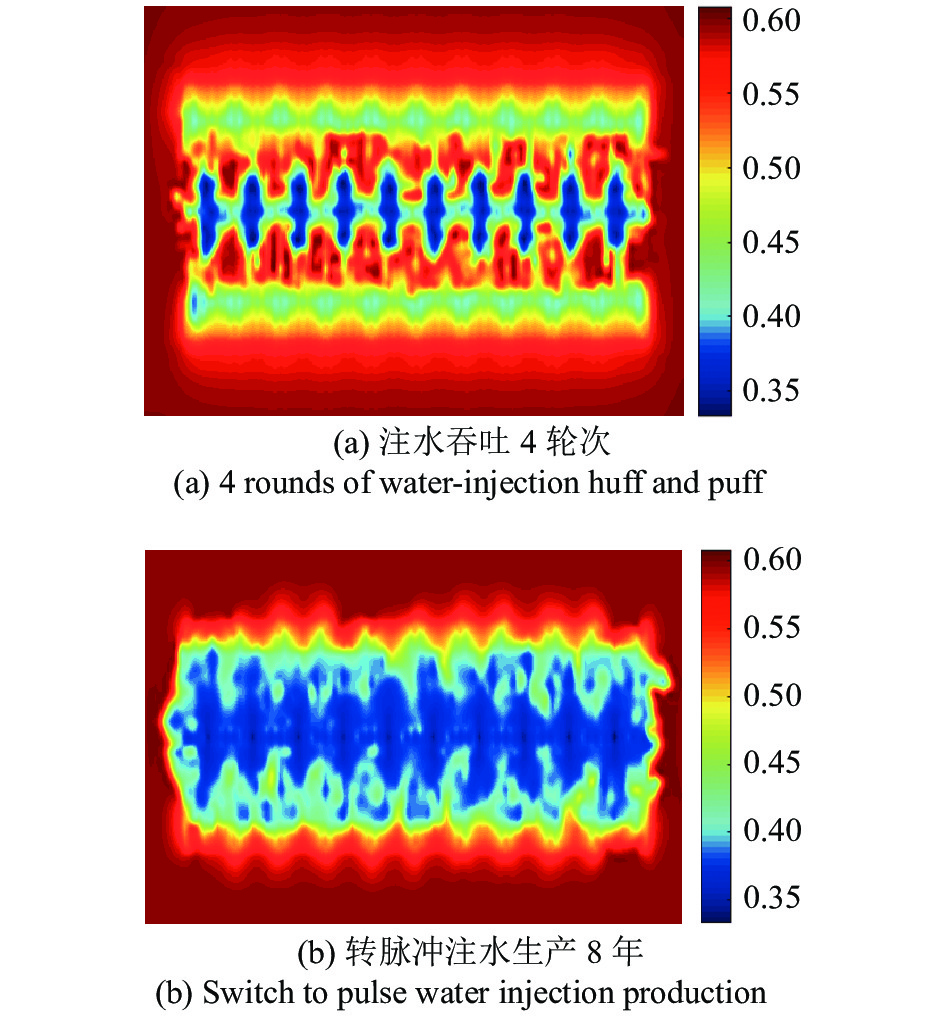
模拟M56-151H井底剩余油分布, 脉冲注水方式的剩余油饱和度较低. 说明注水吞吐4轮次后转为脉冲注水方式生产8年, 剩余油充分动用(图20).

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-19-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure19-1" />

19
脉冲注水前后裂缝分布形态

19.
Fracture distribution

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-19.jpg'"
class="figure_img
figure_type1 bbb " id="Figure19" />

图
19
脉冲注水前后裂缝分布形态 (续)

Figure
19.
Fracture distribution (continued)

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-154-20.jpg'"
class="figure_img
figure_type1 bbb " id="Figure20" />

图
20
注水吞吐与脉冲注水剩余油分布对比

Figure
20.
Comparison of remaining oil distribution

下载:
全尺寸图片
幻灯片

3.
结论

(1)裂缝性致密油藏注水诱导裂缝扩展可视为张开裂缝及交叉扩展型. 注水期间, 裂缝净内压随着注水量的增加而升高时, 应力场强度因子也随之升高. 当应力场强度因子K达到断裂韧度K_IC, 在裂缝尖端会发生扩展、延伸并相互沟通, 呈现不规则复杂缝网. 提出的裂缝扩展长度计算方法可用于确定裂缝延伸位置, 预防裂缝水窜. 改进的逆向渗吸的判别公式确定M56区块动态裂缝发生了大规模的逆向渗吸.

(2)周期性地改变注水量, 从而产生裂缝和基质压差, 造成地层中压力场的不稳定分布. 在压力上升过程中, 注入水通过天然裂缝扩展形成的高导流通道进入到基质, 极大地增加了注水波及面积. 促使逆向渗吸范围扩大, 逆向渗吸作用加强, 缝网与基质之间的流体交换速度和数量均发生质变. 更多的原油被置换到缝网中, 在下一个脉冲注水周期的线性驱替作用下流向采油井.

(3)讨论了裂缝性致密油藏水平井注水吞吐转变为脉冲注水方式, 即由逆向渗吸与径向驱替作用转变为逆向渗吸及线性驱替作用. 脉冲注水累计产油高、逆向渗吸作用强, 充分发挥逆向渗吸及线性驱替作用, 能够实现有效驱油的目的.

(4)实际注水时, 应当控制注水量, 使得注入期间井底压力接近天然裂缝开启压力, 但要低于地层破裂压力, 其目的是增加地层有效渗流能力, 同时防止注入水沿裂缝水窜.