引言
随着常规油气资源储量不断降低, 全球非常规油气资源勘探开发进入活跃期, 致密油、页岩油等非常规油气资源探明储量不断上升[1-3]. 特别是近5年, 中国非常规油气进入了规模发现与开发上产阶段, 致密、页岩油气展现出了巨大的资源潜力[4-7]. 与常规储层不同, 致密储层多为源储一体, 储集层致密, 未经压裂储层难以形成工业油流. 开发中需采用体积压裂技术将储层“打碎”, 形成“人工油气藏”[8,9]. 通常认为压裂缝沿最大主应力方向延伸[10-12], 但受原始地应力及压裂工艺影响, 压裂阶段储层应力状态非常复杂, 现场微地震数据及耦合应力场压裂模拟结果表明, 体积压裂后储层缝网展布复杂, 存在不同的倾角、形态及穿透比[13-16].
对于上述储层, 其渗流规律较为复杂, 单一线性流难以表征其流动状态[17-19], 樊冬艳等[20]、Al Rbeawi等[21-22]基于点源函数叠加原理研究了相同倾斜方向下多段压裂无限导流倾斜缝典型试井曲线特征. 贾品等[23-25]、Teng和Li[26]、万义钊等[27]通过将裂缝离散为微元的方法实现不同裂缝形态的表征, 同时Teng和Li[28-29]、王苏冉[30]通过引入空间倾斜面源实现单条倾斜缝压力、产量瞬态分析. 但上述研究所考虑的裂缝只能沿单一方向倾斜, 在此条件下, 可通过调整坐标系的方法降低模型复杂度实现模型有效求解. 但唐慧莹等[14]研究表明, 即使在常规多段压裂过程中, 压裂缝也会因缝间应力干扰发生裂缝面弯曲, 出现裂缝倾斜方向不同的现象. 因此为更准确表征水力压裂缝空间展布, 建立可表征任意方向倾斜、任意形态展布的多段压裂井压力瞬态分析模型[31-34]是非常必要的.
本文通过离散裂缝网络表征不同裂缝形态, 结合点源函数面积分与裂缝微元局部坐标系, 构建了不受空间坐标系约束的封闭盒式储层任意平面缝源函数, 并验证了其准确性. 针对三重积分面源积分函数存在的计算效率较低的问题, 提出了应用点源或特殊线源代替面源的方法实现了倾斜裂缝快速求解, 探讨了此类求解方法的准确性及可行性, 基于此模型划分了单段、多段倾斜压裂缝流态, 分析了裂缝导流能力、裂缝倾角、裂缝高度以及裂缝段间距等因素的影响.
1.
多段压裂井三维缝不稳定渗流模型
1.1
物理模型及模型假设
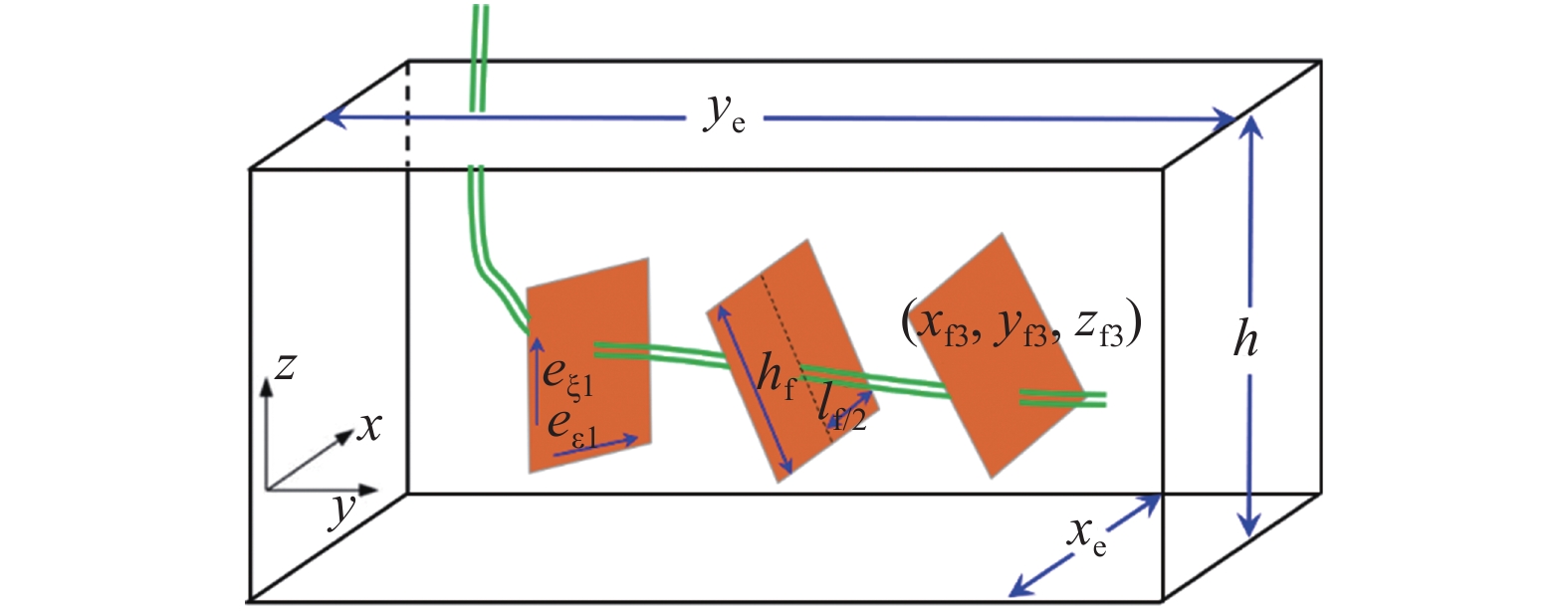
如图1所示, 均质封闭储层 (xe, ye, h) 中存在一口体积压裂大斜度井, 沿井筒延伸方向存在M条倾斜缝, 裂缝半缝长为
m{varepsilon I}}}},{e_{{
m{xi I}}}})$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
多段压裂井三维缝物理模型
Figure
1.
Physical model of multi-fractured well with 3D fractures
下载: 全尺寸图片
幻灯片
储层及裂缝孔隙度为
模型基本假设如下:
(1) 将渗流阶段划分为基质向裂缝渗流及裂缝向井筒流动两部分, 不考虑基质向井筒的直接渗流;
(2) 不考虑井筒沿程压力降, 忽略渗流过程中的重力影响;
(3) 裂缝有限导流, 单条裂缝内孔渗数据保持一致;
(4) 储层内流体为油单相, 无毛管力影响.
1.2
裂缝内部流动模型
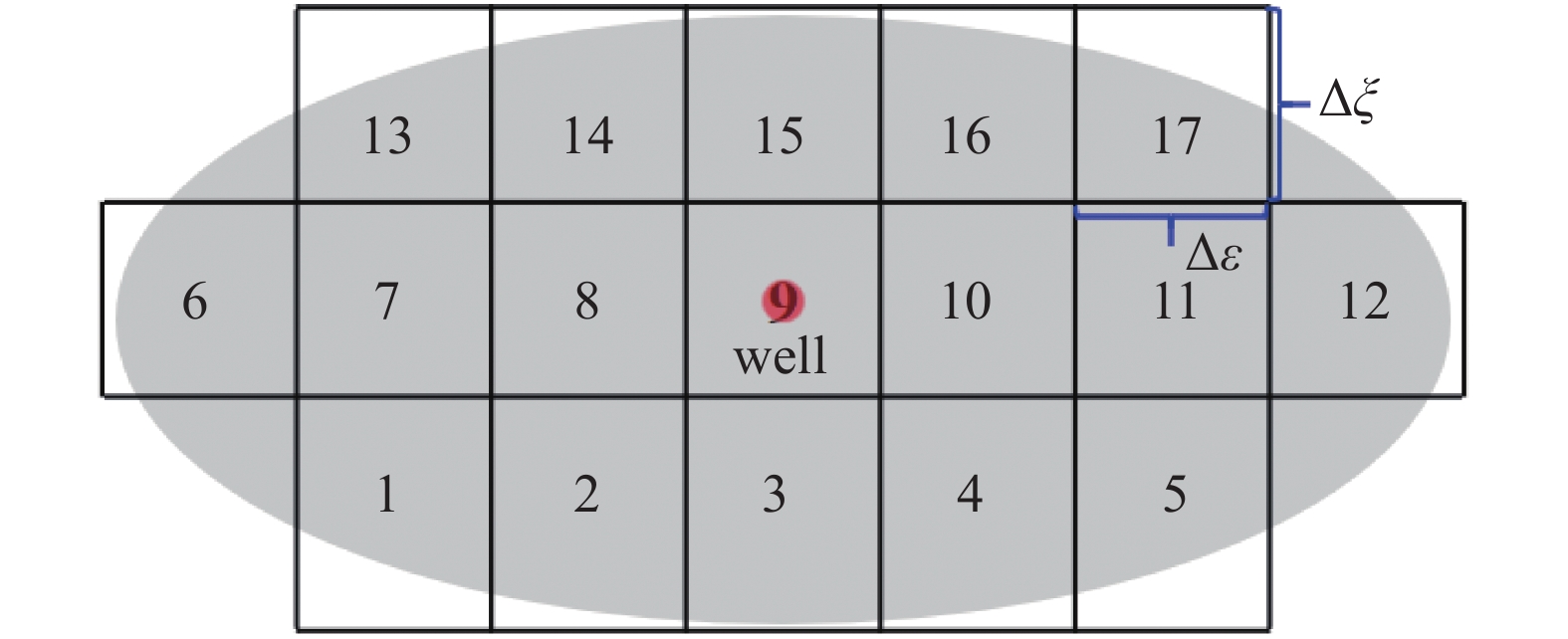
水力裂缝形态受储层物性及压裂工艺影响[35], 常见裂缝形态有矩形缝、椭圆缝、菱形缝等. 本文将裂缝离散为矩形微元, 实现不同形态裂缝有效表征. 如图2所示, 井筒穿过椭圆缝中心, 结合椭圆裂缝形态将其离散为17个矩形微元, 其中中心点微元(编号9)为井筒所在微元.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
椭圆缝离散表征
Figure
2.
Discrete characterization of elliptical fracture
下载: 全尺寸图片
幻灯片
模型推导与计算过程中, 裂缝微元相关参数定义如下: 第I条裂缝微元总量为NfI, 其中井筒所在微元编号NfwI; 裂缝系统微元总量为Nf; 第i个微元的长、宽为
基于裂缝内二维不稳定渗流,建立裂缝内流动综合控制方程.
$$begin{split}&frac{partial }{{partial varepsilon }}left( {beta frac{{Delta {xi _{{i}}}w{k_{ m{f}}}}}{{mu B}}frac{{partial p}}{{partial varepsilon }}} ight)Delta {varepsilon _{{i}}} +frac{partial }{{partial xi }}left( {beta frac{{Delta {varepsilon_{{i}}}w{k_{ m{f}}}}}{{mu B}}frac{{partial p}}{{partial xi }}} ight)Delta {xi _{{i}}} + &qquad{q_{{ m{s}}{{ m{c}}_{{i}}}}} = left( {frac{{Delta {varepsilon _{{i}}}Delta {xi _{{i}}}w{phi _{ m{f}}}{C_{{ m{tf}}}}}}{B}} ight)frac{{partial p}}{{partial t}} end{split} $$  | (1) |
考虑井筒与椭圆缝相交于微元9, 以该微元为研究对象, 采用有限差分方法将公式(1)离散处理
$$begin{split}&frac{{beta Delta {xi _9}w{k_{ m{f}}}}}{{mu B{d_{(8,9)}}}}left( {p_{{ m{f9}}}^n - p_{{ m{f8}}}^n} ight) + frac{{beta Delta {xi _9}w{k_{ m{f}}}}}{{mu B{d_{(9,10)}}}}left( {p_{{ m{f9}}}^n - p_{{ m{f10}}}^n} ight) +&qquadfrac{{beta Delta {varepsilon _9}w{k_{ m{f}}}}}{{mu BDelta {d_{(3,9)}}}}left( {p_{{ m{f9}}}^n - p_{{ m{f3}}}^n} ight) + frac{{beta Delta {varepsilon _9}w{k_{ m{f}}}}}{{mu B{d_{(9,15)}}}}left( {p_{{ m{f9}}}^n - p_{{ m{f15}}}^n} ight) + &qquad(q_{{ m{f9}}}^n - q_{{ m{fw1}}}^n) = frac{{Delta {varepsilon _9}Delta {xi _9}w{phi _{ m{f}}}{C_{{ m{tf}}}}}}{{BDelta t}}left( {p_{{ m{f9}}}^{n - 1} - p_{{ m{f9}}}^n} ight)end{split} $$  | (2) |
式中,
为简化模型推导过程, 引入无量纲参数
m{D}}} = dfrac{x}{{{l_{{
m{f/2}}}}}}$
m{D}}} = dfrac{y}{{{l_{{
m{f/2}}}}}}$
m{D}}} = dfrac{{textit{z}}}{{{l_{{
m{f/2}}}}}}$
m{D}}} = dfrac{w}{{{l_{{
m{f/2}}}}}}$
m{D}}} = dfrac{h}{{{l_{{
m{f/2}}}}}}$
m{eD}}}} = dfrac{{{x_e}}}{{{l_{{
m{f/2}}}}}}$
m{eD}}}} = dfrac{{{y_e}}}{{{l_{{
m{f/2}}}}}}$
m{D}}} = dfrac{{Delta varepsilon }}{{{l_{{
m{f/2}}}}}}$
m{D}}(i,j)}}}} = dfrac{{Delta {d_{{{(i,j)}}}}}}{{{l_{{
m{f/2}}}}}}$
m{D}}} = dfrac{{Delta xi }}{{{l_{{
m{f/2}}}}}}$
m{D}}} = dfrac{q}{{{q_{
m{w}}}}}$
m{fD}}}} = dfrac{{{k_{
m{f}}}w}}{{{k_m}{l_{{
m{f/2}}}}}}$
m{s}}} = dfrac{{{phi _{
m{f}}}{C_{{
m{tf}}}}}}{{{phi _{
m{m}}}{C_{{
m{tm}}}}}}$
m{D}}} = $
m{w}}}Bmu }}$
m{fD}}}} = dfrac{{2{text{π}} beta {k_m}hDelta {p_{
m{f}}}}}{{{q_{
m{w}}}Bmu }}$
m{D}}} = dfrac{{beta {k_m}t}}{{{phi _{
m{m}}}mu {C_{{
m{tm}}}}l_{{
m{f/2}}}^2}}$
m{D}}} = $
m{m}}}{C_{{
m{tm}}}}r_w^2}}$
m{f/2}}}^2}}$
m{fD}}}} = dfrac{{{h_{
m{f}}}}}{{l_{{
m{f/2}}}^{}}}$
将无量纲参数代入式(2)
$$begin{split}&frac{{{C_{{ m{fD}}}}Delta {xi _{{ m{D9}}}}}}{{2{text{π}} {h_{ m{D}}}{d_{{ m{D(8,9)}}}}}}left( {p_{{ m{fD}}9}^n - p_{{ m{fD}}8}^n} ight) + frac{{{C_{{ m{fD}}}}Delta {xi _{{ m{D9}}}}}}{{2{text{π}} {h_{ m{D}}}{d_{{ m{D(9,10)}}}}}}left( {p_{{ m{fD}}9}^n - p_{{ m{fD}}10}^n} ight) + &qquadfrac{{{C_{{ m{fD}}}}Delta {varepsilon _{{ m{D9}}}}}}{{2{text{π}} {h_{ m{D}}}{d_{{ m{D(3,9)}}}}}}left( {p_{{ m{fD}}9}^n !-! p_{{ m{fD}}3}^n} ight) !+! frac{{{C_{{ m{fD}}}}Delta {varepsilon _{{ m{D9}}}}}}{{2{text{π}} {h_{ m{D}}}{d_{{ m{D(9,15)}}}}}}(p_{{ m{fD}}9}^n !-! p_{{ m{fD}}15}^n) +&qquad (q_{{ m{fD9}}}^n -q_{{ m{fwD1}}}^n) = frac{{Delta {varepsilon _{{ m{D9}}}}Delta {xi _{{ m{D9}}}}{w_{ m{D}}}{C_{ m{s}}}}}{{2{text{π}} Delta{t_{ m{D}}}{h_{ m{D}}}}}(p_{{ m{fD9}}}^{n - 1} - p_{{ m{fD9}}}^n) end{split} $$  | (3) |
化简可得
$$begin{split}& sumlimits_{{{j = 1}}}^{{N_{ m{f}}}} {{T_{{{{ m{D}}(i,j)}}}}} p_{{{{ m{fD}}i}}}^{{n}} - left( {sumlimits_{{{j}} = { m{1}}}^{{N_{ m{f}}}} {{T_{{{{ m{D}}(i,j)}}}}} + {alpha _{{ m{D9}}}}} ight)p_{{ m{fD9}}}^{{n}} - &qquad (q_{{ m{fD9}}}^n - q_{{ m{fwD1}}}^n) = - {alpha _{{ m{D9}}}}p_{{ m{fD9}}}^{{{n - 1}}} end{split} $$  | (4) |
式中, TD(i,j)为i, j两裂缝微元间的无因次传导率,
m{D}}i}} $
$${T_{{{{ m{D}}(i,j)}}}} = frac{{{C_{{ m{fD}}}}Delta {n_{{{{ m{D}}(i,j)}}}}}}{{2{text{π}} {h_{ m{D}}}{d_{{ m{D}}({{i,j}})}}}}qquad$$  | (5) |
$${alpha _{{{{ m{D}}i}}}} = frac{{Delta {varepsilon _{{{{ m{D}}i}}}}Delta {xi _{{{{ m{D}}i}}}}{w_{ m{D}}}{C_{ m{s}}}}}{{2{text{π}} Delta {t_{ m{D}}}{h_{ m{D}}}}};;$$  | (6) |
$$Delta {n_{{{{ m{D}}(i,j)}}}} = left{ {begin{array}{*{20}{l}}{Delta {xi _{{{{ m{D}}i}}}}},&{i ,j;;{text{在}} varepsilon{text{方向上相邻}} }{Delta {varepsilon _{{{{ m{D}}i}}}}},&{i ,j;;{text{在}} varepsilon{text{方向上相邻}}}0,&{i ,j;;{text{不相邻}}}end{array}} ight.$$  | (7) |
将式(4)应用到离散裂缝系统所有微元上, 可得包含Nf个裂缝微元的流动方程有限差分方程组
$$left[ {{boldsymbol{T}}, - {{boldsymbol{I}}_{{N_{ m{f}}}}},{boldsymbol{0}},{boldsymbol{a}}} ight] cdot left[ {begin{array}{*{20}{c}} {{{boldsymbol{p}}_{{ m{fD}}}}} {{{boldsymbol{q}}_{{ m{fD}}}}} {{{boldsymbol{p}}_{{ m{fwD}}}}} {{{boldsymbol{q}}_{{ m{fwD}}}}} end{array}} ight] = {{boldsymbol{R}}_1}$$  | (8) |
式中, 矩阵
m{f}}}$
$${boldsymbol{a}} != !{left[ {begin{array}{*{20}{l}} {left. {begin{array}{*{20}{c}} 0 vdots 0 1 end{array}} ight}{{{N}}_{{ m{FW1}}}}}&!!!{}&!!!{left. {begin{array}{*{20}{c}} 0 vdots 0 1 end{array}} ight}{{{N}}_{{{{ m{FW}}i}}}}}&!!!{}&!!!{left. {begin{array}{*{20}{c}} 0 vdots 0 1 end{array}} ight}{N_{{{{ m{FW}}M}}}}} 0&!!! cdots &!!!0&!!! cdots &!!!0 vdots &!!!{}&!!! vdots &!!!{}&!!! vdots 0&!!!{}&!!!0&!!!{}&!!!0 !!!!!end{array}} ight]_{{N_{ m{f}}} times {{M}}}}$$  | (9) |
$${{boldsymbol{p}}_{{ m{fD}}}} !=! {left[ {begin{array}{*{20}{c}} {{boldsymbol{p}}_{{ m{fD1}}}^n} {{boldsymbol{p}}_{{ m{fD2}}}^n} vdots {{boldsymbol{p}}_{{ m{fD}}{{ m{N}}_{ m{f}}}}^n} !!!!end{array}} ight]_{{N_{ m{f}}} times 1}},{{boldsymbol{q}}_{{ m{fD}}}} !=! {left[ {begin{array}{*{20}{c}} {{boldsymbol{q}}_{{ m{fD1}}}^n} {{boldsymbol{q}}_{{ m{fD2}}}^n} vdots {{boldsymbol{q}}_{{ m{fD}}{{ m{N}}_{ m{f}}}}^n} !!!!end{array}} ight]_{{N_{ m{f}}} times 1}},{{boldsymbol{p}}_{{ m{fw}}}} !=! {left[ {begin{array}{*{20}{c}} {{boldsymbol{p}}_{{ m{fwD1}}}^n} {{boldsymbol{p}}_{{ m{fwD2}}}^n} vdots {{boldsymbol{p}}_{{ m{fwDM}}}^n} !!!!end{array}} ight]_{{{M}} times 1}}$$  | (10) |
$${{boldsymbol{q}}_{{ m{fw}}}} = {left[ {begin{array}{*{20}{c}} {{boldsymbol{q}}_{{ m{fwD1}}}^n} {{boldsymbol{q}}_{{ m{fwD2}}}^n} vdots {{boldsymbol{q}}_{{ m{fwDM}}}^n} end{array}} ight]_{{boldsymbol{M }}times 1}},{{boldsymbol{R}}_1} = {left[ {begin{array}{*{20}{c}} { - {{boldsymbol{alpha }}_{{ m{D}}1}}{boldsymbol{p}}_{{ m{fD1}}}^{n - 1}} { - {{boldsymbol{alpha }}_{{ m{D}}2}}{boldsymbol{p}}_{{ m{fD2}}}^{n - 1}} vdots { - {{boldsymbol{alpha}} _{{ m{D}}{N_{ m{f}}}}}{boldsymbol{p}}_{{ m{fD}}{{ m{N}}_{ m{f}}}}^{n - 1}} end{array}} ight]_{{{{N}}_{ m{f}}} times 1}}$$  | (11) |
1.3
油藏流动模型
考虑上述离散方法所得第I个微元中心点坐标为
m{varepsilon I}}}},{{boldsymbol{e}}_{{
m{xi I}}}})$
$$left. {begin{array}{*{20}{c}} {{{boldsymbol{e}}_{{ m{varepsilon I}}}} = ({x_{{ m{varepsilon I}}}},{y_{{ m{varepsilon I}}}},{{textit{z}}_{{ m{varepsilon I}}}})} {{{boldsymbol{e}}_{xi { m{I}}}} = ({x_{xi { m{I}}}},{y_{xi { m{I}}}},{{textit{z}}_{xi { m{I}}}})} end{array}} ight}$$  | (12) |
$$left. {begin{array}{*{20}{c}} {{x_{ m{D}}}(varepsilon,xi ) = {x_{{ m{DI}}}} + varepsilon cdot {x_{varepsilon { m{I}}}} + xi cdot {x_{xi { m{I}}}}} {{y_{ m{D}}}(varepsilon,xi ) = {y_{{ m{DI}}}} + varepsilon cdot {y_{varepsilon { m{I}}}} + xi cdot {y_{xi { m{I}}}}} {{{textit{z}}_{ m{D}}}(varepsilon,xi ) = {{textit{z}}_{{ m{DI}}}} + varepsilon cdot {{textit{z}}_{varepsilon { m{I}}}} + xi cdot {{textit{z}}_{xi { m{I}}}}} end{array}} ight}$$  | (13) |
结合Newman乘积与封闭边界无限大平面源经典解[36]可得封闭储层(x, y, z)处单一点源以定产q生产时在点(x0, y0, z0)处产生压力降
$$begin{split} {p_{ m{e}}} - &{p_{ m{0}}} = frac{{Bq}}{{{phi _{ m{m}}}{c_{{ m{tm}}}}}} cdot & frac{1}{{{x_e}}}left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - frac{{{m^2}{{text{π}} ^2}beta eta t}}{{x_e^2}}} ight)cosleft( frac{{m{text{π}} {x_0}}}{{{x_e}}} ight)cos left( frac{{m{text{π}} x}}{{{x_e}}} ight)} ight] cdot & frac{1}{{{y_e}}}left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - frac{{{m^2}{{text{π}} ^2}beta eta t}}{{y_e^2}}} ight)cosleft( frac{{m{text{π}} {y_0}}}{{{y_e}}} ight)cos left(frac{{m{text{π}} y}}{{{y_e}}} ight)} ight] cdot & frac{1}{h}left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - frac{{{m^2}{{text{π}} ^2}beta eta t}}{{{h^2}}}} ight)cos left(frac{{m{text{π}} {{textit{z}}_0}}}{h} ight)cosleft( frac{{m{text{π}} {textit{z}}}}{h} ight)} ight] end{split} $$  | (14) |
将无量纲参数代入式(14)
$$begin{split} {p_{{ m{D0}}}} = &frac{{2{text{π}} {q_{ m{D}}}}}{{{x_{{ m{eD}}}}{y_{{ m{eD}}}}}} cdot & left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - frac{{{m^2}{{text{π}} ^2}{t_{ m{D}}}}}{{x_{{ m{eD}}}^2}}} ight)cos left(frac{{m{text{π}} {x_{{ m{D0}}}}}}{{{x_{{ m{eD}}}}}} ight)cos left( frac{{m{text{π}} {x_{ m{D}}}}}{{{x_{{ m{eD}}}}}} ight)} ight] cdot & left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - frac{{{m^2}{{text{π}} ^2}{t_{ m{D}}}}}{{y_{{ m{eD}}}^2}}} ight)cos left(frac{{m{text{π}} {y_{{ m{D0}}}}}}{{{y_{{ m{eD}}}}}} ight)cos left( frac{{m{text{π}} {y_{ m{D}}}}}{{{y_{{ m{eD}}}}}} ight)} ight] cdot & left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - frac{{{m^2}{{text{π}} ^2}{t_{ m{D}}}}}{{h_{ m{D}}^2}}} ight)cos left(frac{{m{text{π}} {{textit{z}}_{{ m{D0}}}}}}{{{h_{ m{D}}}}} ight)cos left( frac{{m{text{π}} {{textit{z}}_{ m{D}}}}}{{{h_{ m{D}}}}} ight)} ight] end{split} $$  | (15) |
由叠加原理可知, 空间面源可由空间点源沿微元面积分获得, 因此空间面源函数表达式
$$begin{split} &{p_{{ m{D0}}}} = dfrac{{2{text{π}} {q_{ m{D}}}}}{{{x_{{ m{eD}}}}{y_{{ m{eD}}}}Delta {varepsilon _{ m{D}}}Delta {xi _{ m{D}}}}} cdot displaystyleint_{varepsilon = - frac{{Delta {varepsilon _{ m{D}}}}}{2}}^{varepsilon = frac{{Delta {varepsilon _{ m{D}}}}}{2}} {displaystyleint_{xi = - frac{{Delta {xi _{ m{D}}}}}{2}}^{xi = frac{{Delta {xi _{ m{D}}}}}{2}} {} } & left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - dfrac{{{m^2}{{text{π}} ^2}{t_{ m{D}}}}}{{x_{{ m{eD}}}^2}}} ight)cos left(dfrac{{m{text{π}} {x_{{ m{D0}}}}}}{{{x_{{ m{eD}}}}}} ight)cos left(dfrac{{m{text{π}} {x_{ m{D}}}(varepsilon,xi )}}{{{x_{{ m{eD}}}}}} ight)} ight] cdot & left[ {1 + 2sumlimits_{m = 1}^infty {exp } left( { - dfrac{{{m^2}{{text{π}} ^2}{t_{ m{D}}}}}{{y_{{ m{eD}}}^2}}} ight)cos left(dfrac{{m{text{π}} {y_{{ m{D0}}}}}}{{{y_{{ m{eD}}}}}} ight)cos left(dfrac{{m{text{π}} {y_{ m{D}}}(varepsilon,xi )}}{{{y_{{ m{eD}}}}}} ight)} ight] cdot & left[ {1 !!+!! 2sumlimits_{m = 1}^infty {exp } left( { - dfrac{{{m^2}{{text{π}} ^2}{t_{ m{D}}}}}{{h_{ m{D}}^2}}} ight)cos left(dfrac{{m{text{π}} {{textit{z}}_{{ m{D0}}}}}}{{{h_{ m{D}}}}} ight)cos left(dfrac{{m{text{π}} {{textit{z}}_{ m{D}}}(varepsilon,xi )}}{{{h_{ m{D}}}}} ight)} ight]{ m{d}}varepsilon { m{d}}xi end{split} $$  | (16) |
基于空间面源压力分布, 结合压力叠加原理及杜哈美原理得第i个微元第n时间步在第j个微元处产生的压力降
$$begin{split}& p_{{{{ m{D}}j}}}^n = frac{{2{text{π}} }}{{Delta {varepsilon _{ m{D}}}Delta {xi _{ m{D}}}{x_{{ m{eD}}}}{y_{{ m{eD}}}}}}sumlimits_{i = 1}^{{N_{ m{f}}}} {sumlimits_{k = 1}^n {q_{{{{ m{D}}i}}}^kint_{t_{ m{D}}^{{{k - 1}}}}^{t_{ m{D}}^{{k}}} {int_{varepsilon = - frac{{Delta {varepsilon _{ m{D}}}}}{2}}^{varepsilon = frac{{Delta {varepsilon _{ m{D}}}}}{2}} {int_{xi = - frac{{Delta {xi _{ m{D}}}}}{2}}^{xi = frac{{Delta {xi _{ m{D}}}}}{2}} {} } } } } cdot & left{ !!{1 !!+!! 2sumlimits_{m = 1}^infty {!!exp !!} left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{x_{{ m{eD}}}^2}}} ight]!cos!left( frac{{m{text{π}} {x_{{ m{Dj}}}}}}{{{x_{{ m{eD}}}}}} ight)!cos! left( frac{{m{text{π}} {x_{{ m{Di}}}}(varepsilon,xi )}}{{{x_{{ m{eD}}}}}} ight)} ight} cdot & left{ !!{1 !!+!! 2sumlimits_{m = 1}^infty {!!exp !!} left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{y_{{ m{eD}}}^2}}} ight]!cos! left(frac{{m{text{π}} {y_{{ m{Dj}}}}}}{{{y_{{ m{eD}}}}}} ight)!cos! left(frac{{m{text{π}} {y_{{ m{Di}}}}(varepsilon,xi )}}{{{y_{{ m{eD}}}}}} ight)} ight} cdot & left{ !!{1 !!+!! 2sumlimits_{m = 1}^infty {!!exp !!} left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{h_{ m{D}}^2}}} ight]!cos! left(frac{{m{text{π}} {z_{{ m{Dj}}}}}}{{{h_{ m{D}}}}} ight)!cos! left(frac{{m{text{π}} {z_{{ m{Di}}}}(varepsilon,xi )}}{{{h_{ m{D}}}}} ight)} ight} & { m{d}}varepsilon { m{d}}xi { m{d}}tau end{split} $$  | (17) |
为简化方程形式, 定义式(16)中的积分项为参数
$$begin{split}& G_{i,j}^{n,k} = frac{{2{text{π}} }}{{Delta {varepsilon _{ m{D}}}Delta {xi _{ m{D}}}{x_{{ m{eD}}}}{y_{{ m{eD}}}}}}int_{t_{ m{D}}^{{{k - 1}}}}^{t_{ m{D}}^{{k}}} {int_{varepsilon = - frac{{Delta {varepsilon _{ m{D}}}}}{2}}^{varepsilon = frac{{Delta {varepsilon _{ m{D}}}}}{2}} {int_{xi = - frac{{Delta {xi _{ m{D}}}}}{2}}^{xi = frac{{Delta {xi _{ m{D}}}}}{2}} {} } } & left{!!{1 !!+!! 2sumlimits_{m = 1}^infty {!!exp !!} left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{x_{{ m{eD}}}^2}}} ight]!cos! left( frac{{m{text{π}} {x_{{ m{Dj}}}}}}{{{x_{{ m{eD}}}}}} ight)!cos! left( frac{{m{text{π}} {x_{{ m{Di}}}}(varepsilon,xi )}}{{{x_{{ m{eD}}}}}} ight)} ight} cdot & left{ !!{1 !!+!! 2sumlimits_{m = 1}^infty {!!exp !!} left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{y_{{ m{eD}}}^2}}} ight]!cos! left( frac{{m{text{π}} {y_{{ m{Dj}}}}}}{{{y_{{ m{eD}}}}}} ight)!cos! left( frac{{m{text{π}} {y_{{ m{Di}}}}(varepsilon,xi )}}{{{y_{{ m{eD}}}}}} ight)} ight} cdot & left{ !!{1 !!+!! 2sumlimits_{m = 1}^infty {!!exp !!} left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{h_{ m{D}}^2}}} ight]!cos! left( frac{{m{text{π}} {z_{{ m{Dj}}}}}}{{{h_{ m{D}}}}} ight)!cos! left( frac{{m{text{π}} {z_{{ m{Di}}}}(varepsilon,xi )}}{{{h_{ m{D}}}}} ight)} ight} &{ m{d}}varepsilon { m{d}}xi { m{d}}tau end{split} $$  | (18) |
从而
$$p_{{{{ m{D}}j}}}^n = sumlimits_{i = 1}^{{N_{ m{f}}}} {sumlimits_{k = 1}^n {q_{{{{ m{D}}i}}}^kG_{i,j}^{n,k}} } = q_{{{{ m{D}}i}}}^ksumlimits_{i = 1}^{{N_{ m{f}}}} {G_{i,j}^{n,k}} + sumlimits_{i = 1}^{{N_{ m{f}}}} {sumlimits_{k = 1}^{n - 1} {q_{{{{ m{D}}i}}}^kG_{i,j}^{n,k}} } $$  | (19) |
基于式(19)建立基质向裂缝流动矩阵
$${boldsymbol{B}} cdot left[ {begin{array}{*{20}{c}} {{{boldsymbol{p}}_{{ m{fD}}}}} {{{boldsymbol{q}}_{{ m{fD}}}}} {{{boldsymbol{p}}_{{ m{fwD}}}}} {{{boldsymbol{q}}_{{ m{fwD}}}}} end{array}} ight] = {{boldsymbol{R}}_2}$$  | (20) |
式中, 矩阵B大小为Nf × 2(Nf + M), 表征基质向各微元流动的影响; 矩阵R2大小为Nf × 1, 由n ? 1时间步中压力及流量参数构成
$${boldsymbol{B}} !!=!! {left[ {begin{array}{*{20}{c}} {underbrace {1{ m{ }}0 cdots 0}_{{N_{ m{f}}}}}&{underbrace { - {boldsymbol{G}}_{1,1}^{n,n} cdots - {boldsymbol{G}}_{{N_{ m{f}}},1}^{n,n}}_{{N_{ m{f}}}}}&{underbrace {0 cdots 0}_{2M}} {}& vdots &{} {underbrace {overbrace {0 cdots 0}^{g - 1}{ m{ }}1{ m{ }}0 cdots 0}_{{N_{ m{f}}}}}&{underbrace { - {boldsymbol{G}}_{1,g}^{n,n} cdots - {boldsymbol{G}}_{{N_{ m{f}}},g}^{n,n}}_{{N_{ m{f}}}}}&{underbrace {0 cdots 0}_{2M}} {}& vdots &{} {underbrace {0 cdots 0{ m{ }}1}_{{N_{ m{f}}}}}&{underbrace { - {boldsymbol{G}}_{1,{N_{ m{f}}}}^{n,n} cdots - {boldsymbol{G}}_{{N_{ m{f}}},{N_{ m{f}}}}^{n,n}}_{{N_{ m{f}}}}}&{underbrace {0 cdots 0}_{2M}} end{array}} ight]_{{N_{ m{f}}} !times! 2({N_{ m{f}}} !!+!! M)}}$$  | (21) |
$${{boldsymbol{R}}_2} = {left[ {begin{array}{*{20}{c}} {displaystylesumlimits_{k = 1}^{n - 1} {displaystylesumlimits_{i = 1}^{{N_{ m{f}}}} {{boldsymbol{q}}_{{ m{fi}}}^k{boldsymbol{G}}_{i,1}^{n,k}} } } {displaystylesumlimits_{k = 1}^{n - 1} {displaystylesumlimits_{i = 1}^{{N_{ m{f}}}} {{boldsymbol{q}}_{{ m{fi}}}^k{boldsymbol{G}}_{i,2}^{n,k}} } } vdots {displaystylesumlimits_{k = 1}^{n - 1} {displaystylesumlimits_{i = 1}^{{N_{ m{f}}}} {{boldsymbol{q}}_{{ m{fi}}}^k{boldsymbol{G}}_{i,{N_{ m{f}}}}^{n,k}} } } end{array}} ight]_{{N_{ m{f}}} times 1}}$$  | (22) |
由式(19)可知, 随着Nf及n的增大, 式(18)的调用次数迅速升高, 而式(18)中的三重积分会导致参数
(1) 线源代替面源
当多条裂缝法向量共面时, 可建立坐标轴(x, y, z)使其中一条坐标轴与裂缝微元局部坐标系
m{varepsilon I}}}},{{boldsymbol{e}}_{{
m{xi I}}}}}
ight) $
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
裂缝微元局部坐标系示意图
Figure
3.
Schematic diagram of local coordinate system of fracture elements
下载: 全尺寸图片
幻灯片
以局部坐标轴eε与坐标轴x平行为例, 此时xξ,
m{D}}}(varepsilon,xi ) $
m{D}}}(varepsilon,xi ) $
$$left. {begin{array}{*{20}{c}} {{x_{ m{D}}}(varepsilon ) = {x_{{ m{DI}}}} + varepsilon {e_x}} {{y_{ m{D}}}(xi ) = {y_{{ m{DI}}}} + xi {y_{xi { m{I}}}}} {{{textit{z}}_{ m{D}}}(xi ) = {{textit{z}}_{{ m{DI}}}} + xi {{textit{z}}_{xi { m{I}}}}} end{array}} ight}$$  | (23) |
相应的参数
$$begin{split}&{ m{G}}_{i,j}^{n,k} = frac{{2{text{π}} }}{{Delta {xi _{ m{D}}}{x_{{ m{eD}}}}{y_{{ m{eD}}}}}}int_{t_{ m{D}}^{{{k - 1}}}}^{t_{ m{D}}^{{k}}} {int_{xi = - frac{{Delta {xi _{ m{D}}}}}{2}}^{xi = frac{{Delta {xi _{ m{D}}}}}{2}} {left{ {1 + frac{{4{x_{{ m{eD}}}}}}{{{text{π}} Delta {x_{ m{D}}}}}} ight.} } cdot sumlimits_{m = 1}^infty {frac{1}{m}} cdot&left. {!!exp !! left[ { !!-! frac{{{m^2}{{text{π}} ^2}(t_{ m{D}}^n - {tau _{ m{D}}})}}{{x_{{ m{eD}}}^2}}} ight]sin left(frac{{m{text{π}} Delta {x_{ m{D}}}}}{{2{x_{{ m{eD}}}}}} ight)!cos! left( frac{{m{text{π}} {x_{{ m{D}}i}}}}{{{x_{{ m{eD}}}}}} ight)!cos! left(frac{{m{text{π}} {x_{{ m{DI}}}}}}{{{x_{ m{e}}}}} ight)} ight} cdot & left{ {1 + 2sumlimits_{m = 1}^infty {!!exp !! } left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{y_{{ m{eD}}}^2}}} ight]!cos! left(frac{{m{text{π}} {y_{{ m{Dj}}}}}}{{{y_{{ m{eD}}}}}} ight)!cos! left(frac{{m{text{π}} {y_{{ m{Di}}}}(xi )}}{{{y_{{ m{eD}}}}}} ight)} ight} cdot & left{ {1 !!+!! 2sumlimits_{m = 1}^infty {!!exp !! } left[{ - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{h_{ m{D}}^2}}} ight]!!cos!left( frac{{m{text{π}} {{textit{z}}_{{ m{Dj}}}}}}{{{h_{ m{D}}}}} ight)!!cos! left(frac{{m{text{π}} {{textit{z}}_{{ m{Di}}}}(xi )}}{{{h_{ m{D}}}}} ight)} ight} &{ m{d}}xi { m{d}}tau end{split} $$  | (24) |
考虑参数
$$begin{split}& {{G}}_{i,j}^{n,k} = frac{{2{text{π}} }}{{{x_{{ m{eD}}}}{y_{{ m{eD}}}}}}int_{t_{ m{D}}^{{{k - 1}}}}^{t_{ m{D}}^{{k}}} {left{ {1 + frac{{4{x_{{ m{eD}}}}}}{{{text{π}} Delta {x_{ m{D}}}}}} ight.} cdot sumlimits_{m = 1}^infty {frac{1}{m} cdot } & exp!! left[ { !!- frac{{{m^2}{{text{π}} ^2}(t_{ m{D}}^n !-! {tau _{ m{D}}})}}{{x_{{ m{eD}}}^2}}} ight]left. {!!!sin! left( frac{{m{text{π}} Delta {x_{ m{D}}}}}{{2{x_{{ m{eD}}}}}}!! ight)!cos! left( frac{{m{text{π}} {x_{Di}}}}{{{x_{{ m{eD}}}}}} ight)!cos! left( frac{{m{text{π}} {x_{{ m{DI}}}}}}{{{x_e}}} ight)} ight} cdot & left{ {1 !!+!! 2sumlimits_{m = 1}^infty {exp } left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{y_{{ m{eD}}}^2}}} ight]!cos! left( frac{{m{text{π}} {y_{{ m{Dj}}}}}}{{{y_{{ m{eD}}}}}} ight)!cos!left( frac{{m{text{π}} {y_{{ m{Di}}}}}}{{{y_{{ m{eD}}}}}} ight)} ight} cdot & left{ {1 !!+!! 2sumlimits_{m = 1}^infty {exp } left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{h_{ m{D}}^2}}} ight]!cos!left( frac{{m{text{π}} {{textit{z}}_{{ m{Dj}}}}}}{{{h_{ m{D}}}}} ight)!cos!left( frac{{m{text{π}} {{textit{z}}_{{ m{Di}}}}}}{{{h_{ m{D}}}}} ight)} ight}{ m{d}}tau end{split} $$  | (25) |
(2) 点源代替面源
参照方案一的思路, 直接对三重积分形式下参数
$$begin{split}& G_{i,j}^{n,k} = frac{{2{text{π}} }}{{{x_{{ m{eD}}}}{y_{{ m{eD}}}}}}int_{t_{ m{D}}^{{{k - 1}}}}^{t_{ m{D}}^{{k}}} {} & left{ {1 + 2sumlimits_{m = 1}^infty {exp } left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{x_{{ m{eD}}}^2}}} ight]cos left(frac{{m{text{π}} {x_{{ m{Dj}}}}}}{{{x_{{ m{eD}}}}}} ight)cos left( frac{{m{text{π}} {x_{{ m{Di}}}}}}{{{x_{{ m{eD}}}}}} ight)} ight} cdot & left{ {1 + 2sumlimits_{m = 1}^infty {exp } left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{y_{{ m{eD}}}^2}}} ight]cos left(frac{{m{text{π}} {y_{{ m{Dj}}}}}}{{{y_{{ m{eD}}}}}} ight)cos left(frac{{m{text{π}} {y_{{ m{Di}}}}}}{{{y_{{ m{eD}}}}}} ight)} ight} cdot & left{ {1 !+! 2sumlimits_{m = 1}^infty {exp } left[ { - frac{{{m^2}{{text{π}} ^2}({t_{ m{D}}} - tau )}}{{h_{ m{D}}^2}}} ight]cosleft( frac{{m{text{π}} {{textit{z}}_{{ m{Dj}}}}}}{{{h_{ m{D}}}}} ight)cosleft( frac{{m{text{π}} {{textit{z}}_{{ m{Di}}}}}}{{{h_{ m{D}}}}} ight)} ight}{ m{d}}tau end{split} $$  | (26) |
将上述方案中的
1.4
模型耦合及求解
由Peaceman公式[37]可知井筒所在微元内边界条件可由稳态径向流公式处理
$$p_{{ m{fwD}}}^n - p_{{ m{fD}}}^n = frac{{{w_{ m{D}}}q_{{ m{fwD}}}^nln ({r_{{ m{eqD}}}}{ m{/}}{r_{{ m{wD}}}})}}{{{C_{{ m{fD}}}}}}$$  | (27) |
式中
m{D}}}
ight)}^{2}+{left(Delta {m}_{{
m{D}}}
ight)}^{2}}$
基于Hurst等人[38]的研究, 在模型中考虑井储系数CwD的影响.
$$1 - frac{{gamma {C_{{ m{wD}}}}}}{{Delta t_{ m{D}}^n}}left( {p_{{ m{wD}}}^n - p_{{ m{wD}}}^{n - 1}} ight) = sumlimits_{i = 1}^M {q_{{{{ m{fwD}}i}}}^n} $$  | (28) |
式中
m{f/2}}}^2}}$
同时, 井筒无限导流条件下, 各裂缝处井筒压力相等, 即
$$p_{{{{ m{fwD}}i}}}^n = p_{{{{ m{fwD}}(i + 1)}}}^n,;;i in (2,3, cdots, M)$$  | (29) |
结合式(27)?(29)建立与井筒内流动相关渗流方程组
$${boldsymbol{C}}left[ {begin{array}{*{20}{c}} {{{boldsymbol{p}}_{{ m{fD}}}}} {{{boldsymbol{q}}_{{ m{fD}}}}} {{{boldsymbol{p}}_{{ m{fwD}}}}} {{{boldsymbol{q}}_{{ m{fwD}}}}} end{array}} ight] = {{boldsymbol{R}}_3}$$  | (30) |
式中, 矩阵C大小为2M × 2(Nf + M), 表征了式(27)?(29)中第n时间步压力及产量的系数项, 矩阵R3大小为Nf × 1, 由n?1时间步相关参数构成.
令
ight] $
$$left[ {begin{array}{*{20}{c}} {boldsymbol{A}} {boldsymbol{B}} {boldsymbol{C}} end{array}} ight] cdot left[ {begin{array}{*{20}{c}} {{{boldsymbol{p}}_{{ m{fD}}}}} {{{boldsymbol{q}}_{{ m{fD}}}}} {{{boldsymbol{p}}_{{ m{fwD}}}}} {{{boldsymbol{q}}_{{ m{fwD}}}}} end{array}} ight] = left[ {begin{array}{*{20}{c}} {{{boldsymbol{R}}_1}} {{{boldsymbol{R}}_2}} {{{boldsymbol{R}}_3}} end{array}} ight]$$  | (31) |
该方程组中存在2(Nf + M)个方程, 其中未知量包含Nf个裂缝微元的压力
2.
模型验证分析
2.1
三重积分模型验证
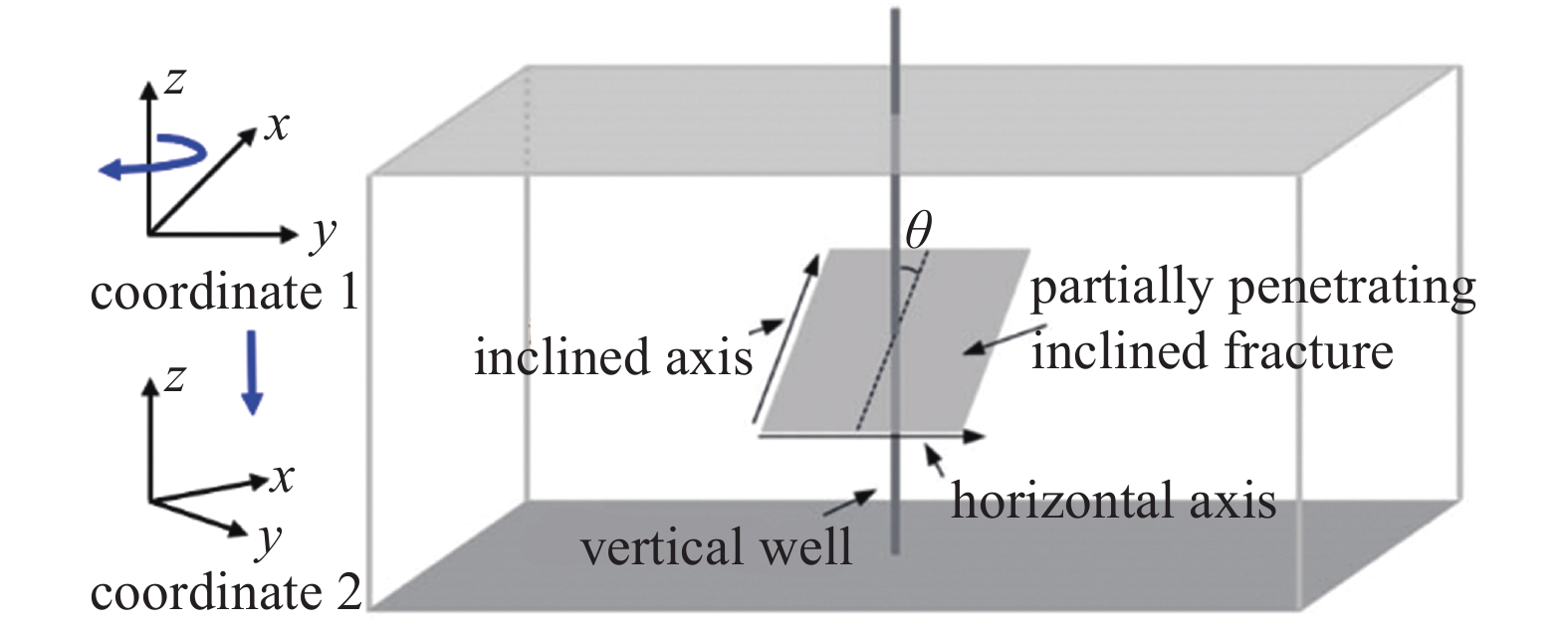
本模型中, 考虑多段压裂大斜度井压裂缝为有限导流, 且裂缝面沿任意方向展布, 现有文献相关研究较少. 为验证模型准确性, 分别验证有限导流单一倾斜缝与无限导流多段压裂缝求解的准确性. 针对图4所示部分贯穿倾斜缝(partially penetrating inclined fracture, PPIF), Teng和Li[28]通过建立坐标轴1 (Coordinate 1)实现模型点源函数求解简化. 为验证本文模型三重积分求解的准确性, 将坐标轴1沿z轴旋转45°建立新坐标轴2, 增加模型复杂度.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
坐标轴转换示意图
Figure
4.
Schematic diagram of coordinate axis transformation
下载: 全尺寸图片
幻灯片
模型数据与Teng图4数据相同, 具体无因次参数如下: xeD = yeD = 20, hD = 0.5, θ = 45°, hfD =
坐标轴2条件下微元内局部坐标系如下
$$left. {begin{array}{*{20}{c}} {{{boldsymbol{e}}_{{ m{varepsilon I}}}} = left( {dfrac{{sqrt 2 }}{2}, - dfrac{{sqrt 2 }}{2},0} ight)} {{{boldsymbol{e}}_{xi { m{I}}}} = left( {dfrac{{sqrt 6 }}{6},dfrac{{sqrt 6 }}{6}, - dfrac{{sqrt 6 }}{3}} ight)} end{array}} ight}$$  | (32) |
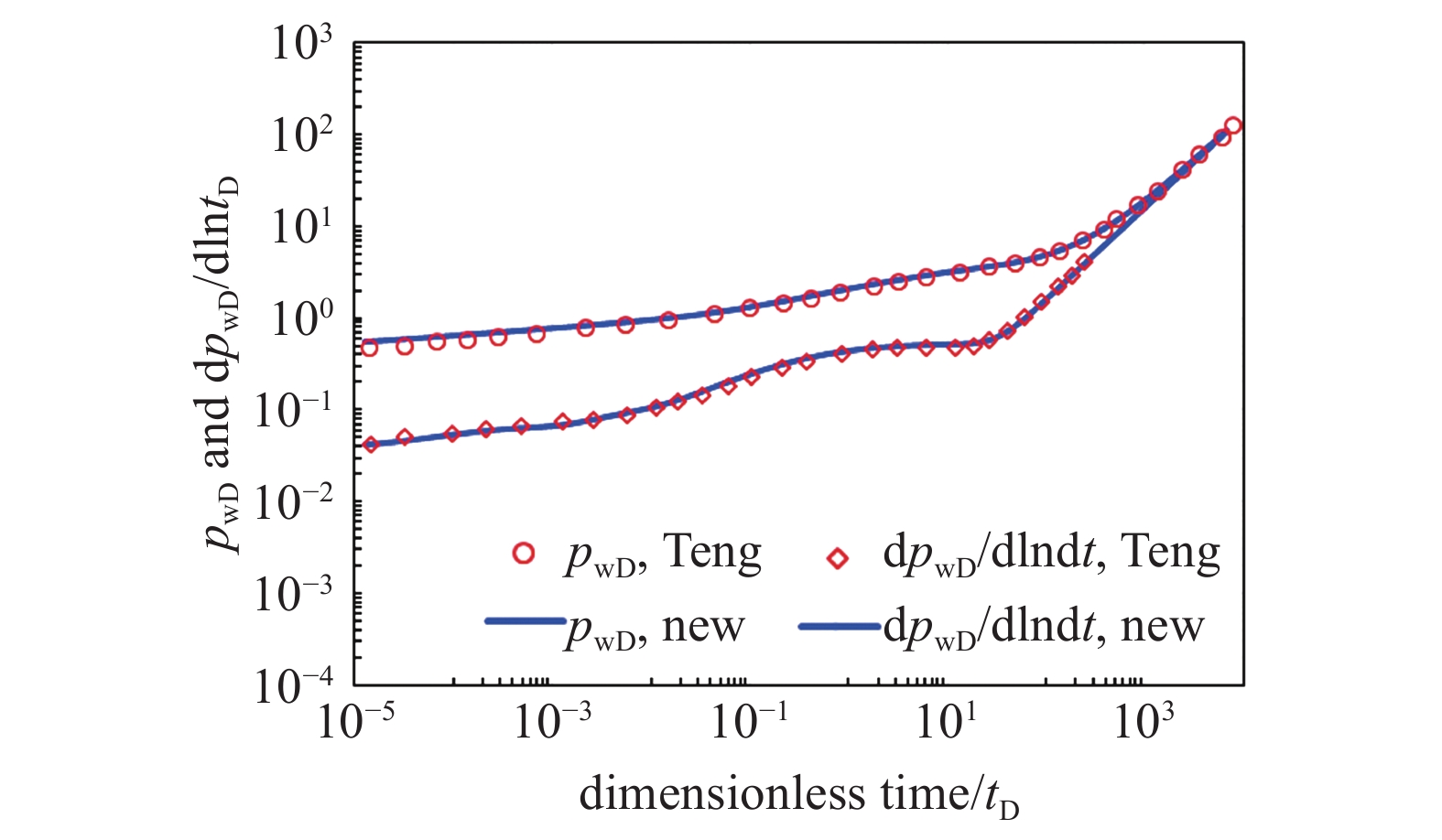
如图5所示, 本模型所得不同时间下无因次压力及压力导数曲线与Teng模型结果基本吻合.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
本文模型与Teng模型[28]结果对比
Figure
5.
Comparison of the result of our model with Teng model[28]
下载: 全尺寸图片
幻灯片
为研究多缝条件下模型求解准确性, 选取Al Rbeawi和Tiab[22]2013年提出的无限大地层多段压裂倾斜缝图版(A-1)进行对比验证, 选取裂缝倾角为15°, hD = 1, 无因次段间距DD = 1. 如图6所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
本文模型与Al Rbeawi模型结果对比
Figure
6.
Comparison of the result of our model with Al Rbeawi model
下载: 全尺寸图片
幻灯片
可以看出, 不同时间下两模型计算结果基本吻合, 由于本模型采用封闭边界, 当tD > 10压力响应到达封闭边界后的压力及压力导数变化与Al Rbeawi模型不同由于该模型采用三重积分进行源函数计算, 求解时间较长(数小时), 适用性较差, 考虑对点源函数求解进行进一步调整.
2.2
源函数调整准确性验证
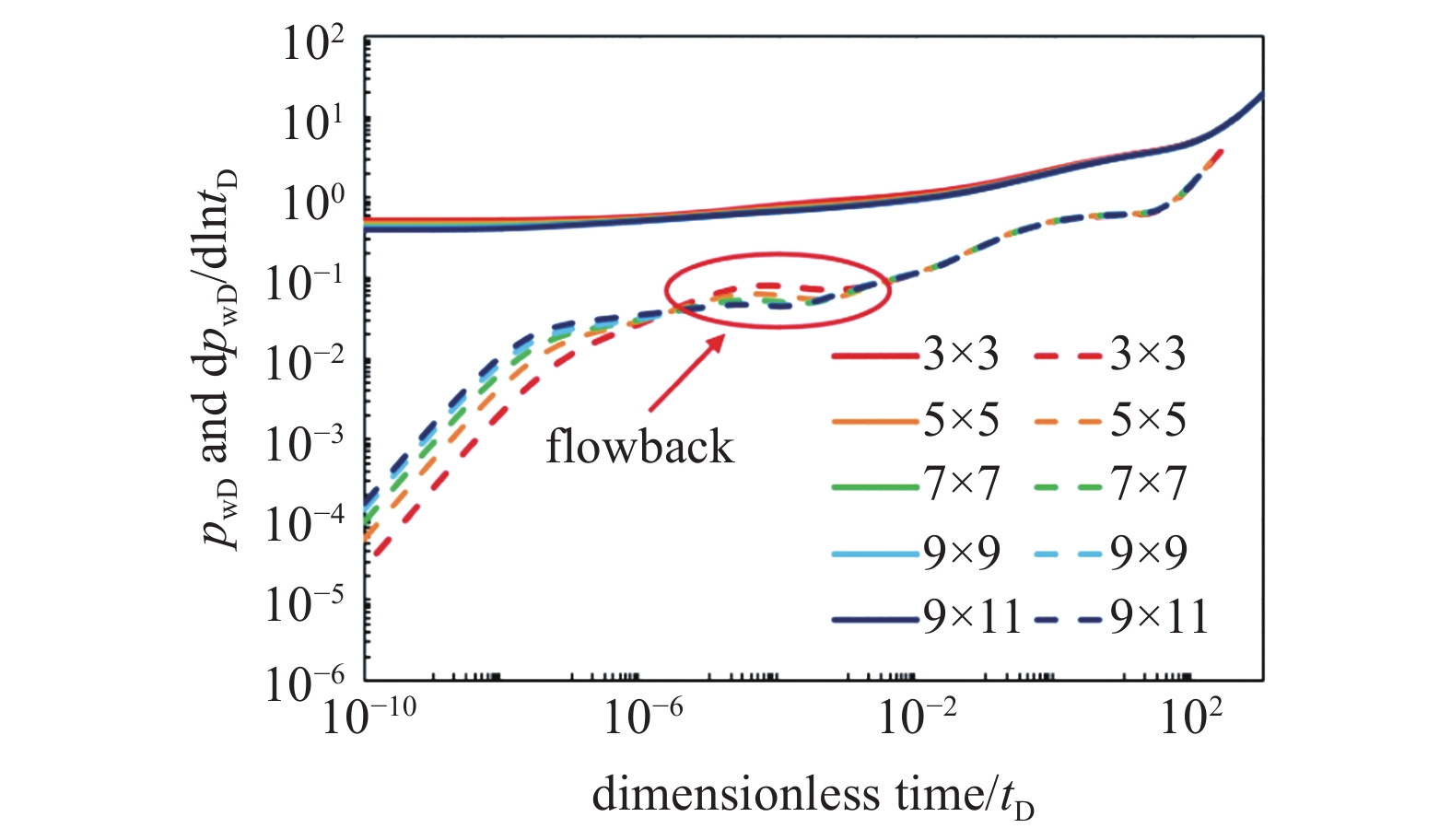
线源、点源简化模型求解主要误差来自于积分中值的选取, 当裂缝微元沿积分方向的长度足够小时, 点源函数沿积分方向上单调变化, 此时选取积分中点作为积分中值可取得较好的积分效果. 图7为不同网格划分下线源求解所得曲线变化对比.可以看出, 当网格划分较为粗糙时, 线源法所得初期压力及压力导数曲线误差较大. 特别的压力导数曲线存在较为明显的回流特征, 考虑是由于中心线所在线源与积分中值相差较大, 各线源之间存在流向各微元中心线源的径向流动所致(图8).
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
网格划分对线源求解效果影响
Figure
7.
Effect of meshing on line source solution
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
回流段流动示意图
Figure
8.
Diagram of flow in flowback period
下载: 全尺寸图片
幻灯片
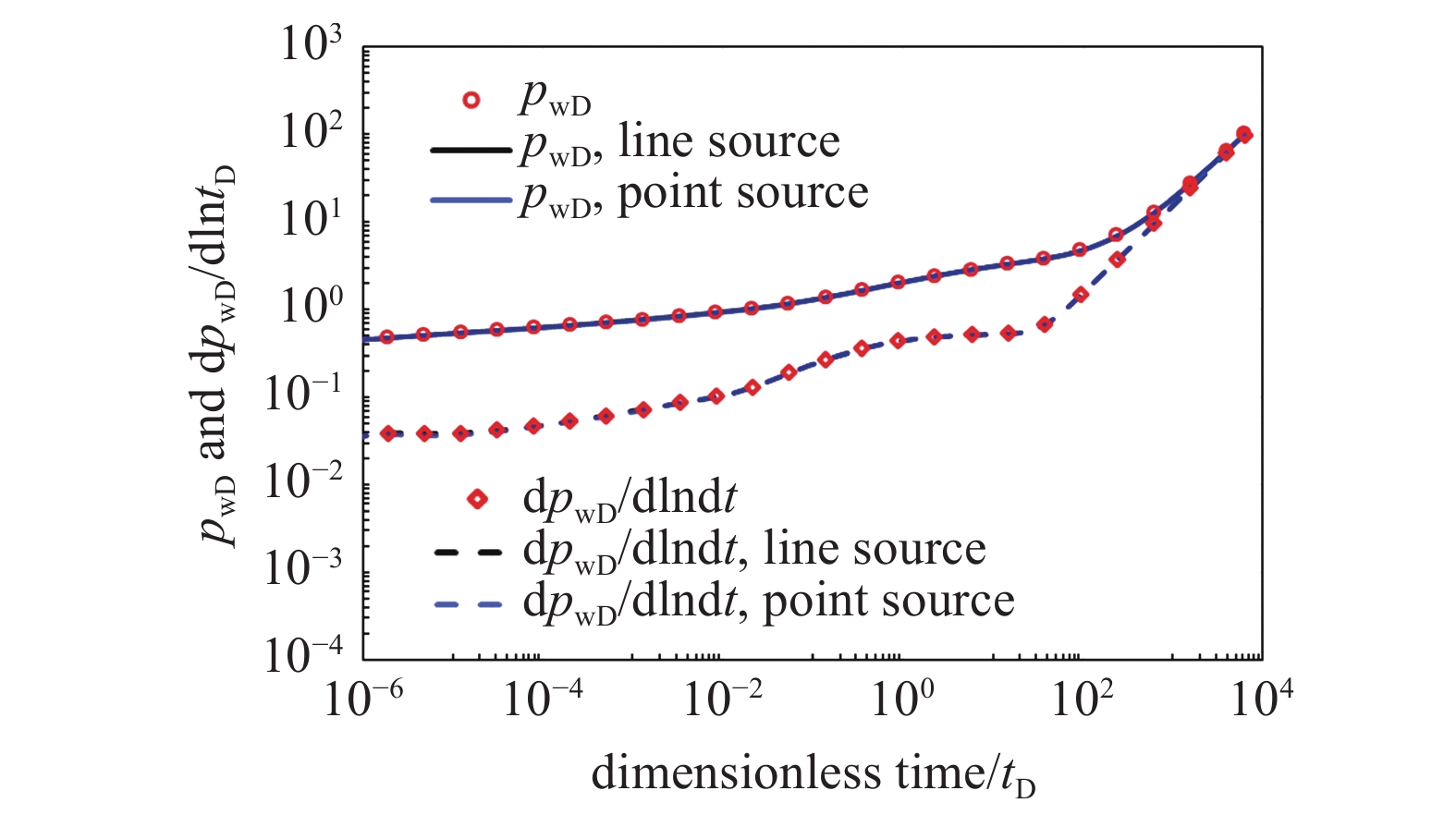
随着划分微元数目增多, 简化模型所得压力及压力导数曲线与面源积分所得压力及压力导数曲线趋于一致. 大量模拟表明当所划分微元无因次边长在0.15左右时, 采用点源或线源代替面源的方法可获得较高的精度. 选取hfD =
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
简化模型求解效果示意图
Figure
9.
Diagram of simplified model
下载: 全尺寸图片
幻灯片
3.
典型曲线分析
3.1
流动阶段划分
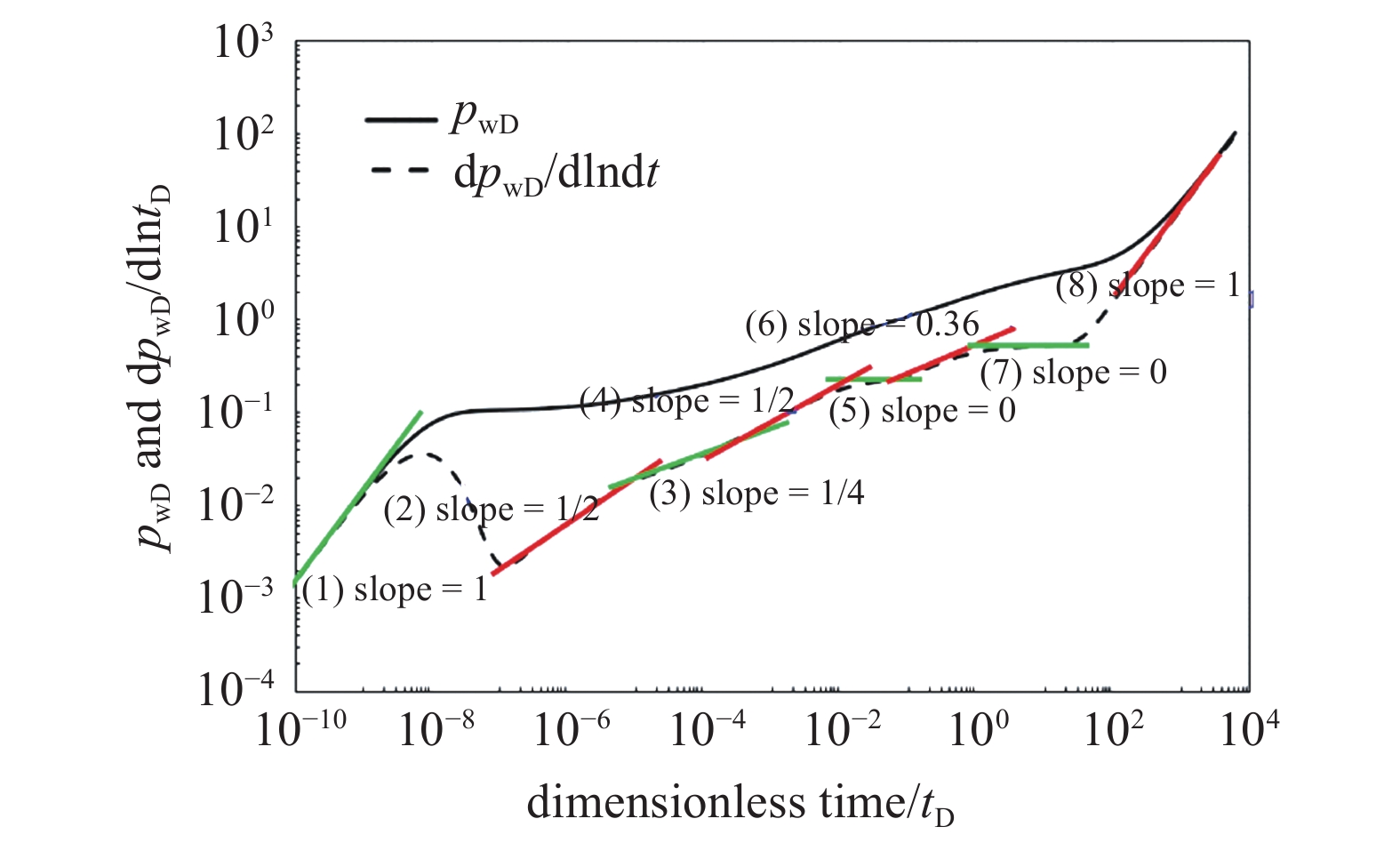
通过分析典型试井曲线中的压力及压力导数曲线特征, 可实现不同流动阶段识别. 选取无因次参数xeD = yeD = 20, hD = 0.5, θ = 45°, hfD =
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
单一倾斜缝流动阶段划分
Figure
10.
Identification of the flow regimes of incline fracture
下载: 全尺寸图片
幻灯片
(1)井筒储集及过渡阶段: 井储阶段压力及压力导数曲线重合, 均为斜率等于1的直线, 该阶段主要流体供给来自井筒;
(2)裂缝线性流阶段: 压力导数曲线斜率为1/2, 该阶段基质暂未动用, 与井相连的裂缝内部流体近线性流入井筒;
(3)双线性流阶段: 压力导数曲线斜率为1/4, 该阶段除裂缝内部流动外, 近缝基质向裂缝的线性流动开始出现;
(4)基质线性流阶段: 压力导数曲线斜率为1/2, 该阶段裂缝内压力趋于稳定, 近缝基质向裂缝的流动仍以线性流为主;
(5)早期径向流阶段: 压力导数曲线斜率为0, 此时波及范围扩大, 基质向裂缝的供给由线性流转变为径向流;
(6)椭圆流阶段: 压力导数曲线斜率近似为0.36, 通常认为该阶段为缝周基质径向流向裂缝系统径向流过渡的阶段;
(7)晚期径向流阶段: 压力导数为斜率等于0的直线, 流体围绕裂缝整体成径向流;
(8)边界控制流阶段: 流体流动到封闭边界, 压力及压力导数响应主要受边界影响, 压力及压力导数均为斜率等于1的直线.
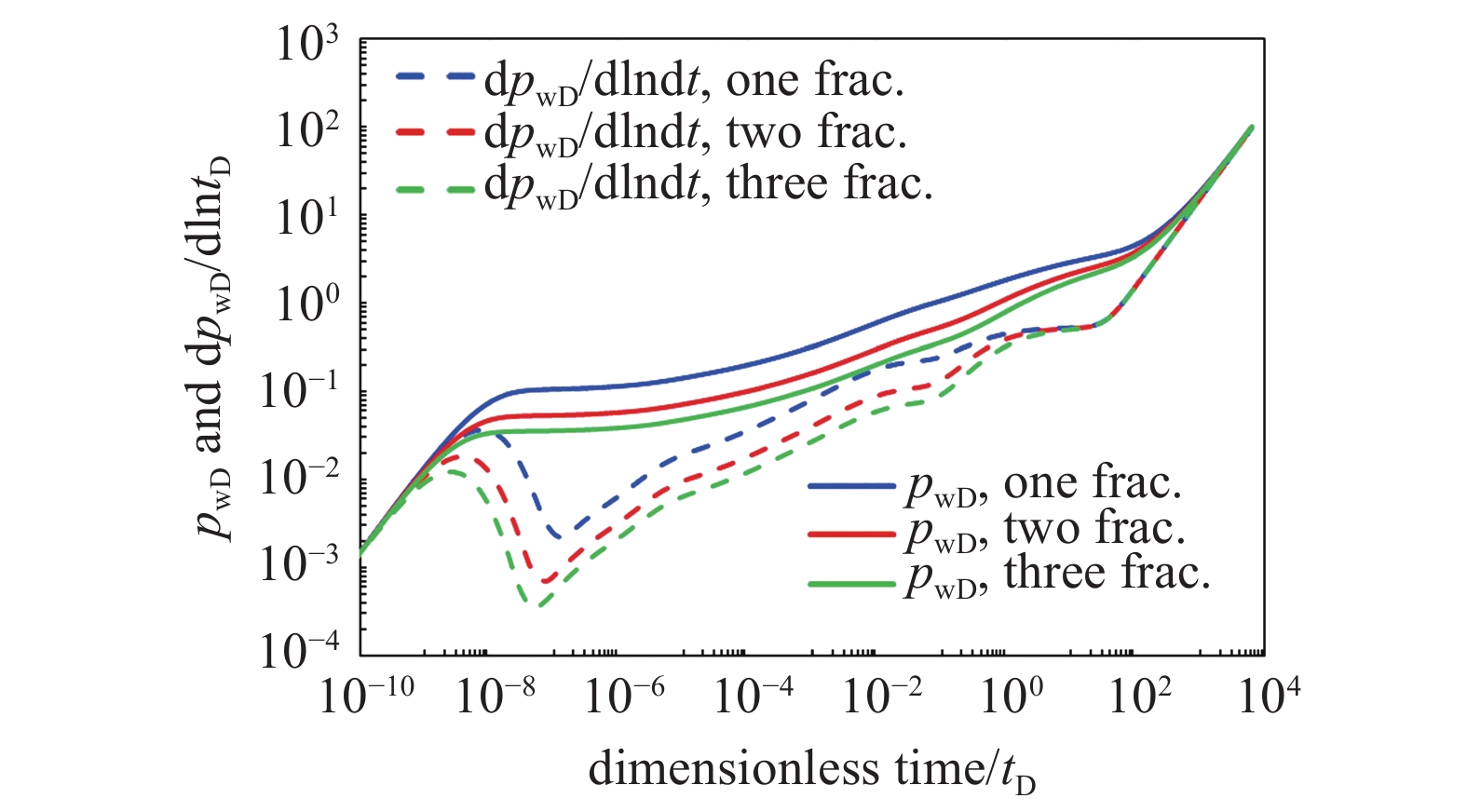
为研究裂缝条数对流动阶段影响, 取缝间距DD = 1, 对比裂缝条数分别为1, 2, 3条件下压力及压力导数曲线(图11)可以看出, 随着裂缝条数增加, 主要流动阶段仍为8个, 但与单条缝相比存在一定的差别. 随着裂缝段数增多, 裂缝及近缝区域流动影响增强, 井储阶段提前进入过渡阶段, 相应的双线性流阶段出现时间略有提前; 由于缝间干扰的存在, 裂缝条数越多, 早期径向流阶段越不太明显, 过渡阶段斜率更大, 晚期径向流及边界控制流阶段, 流体相对于裂缝系统进行流动, 不同裂缝条数下压力及压力导数曲线基本重合.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
多段压裂倾斜缝流动阶段
Figure
11.
Flow regimes of multi-stage incline fractures
下载: 全尺寸图片
幻灯片
3.2
影响因素分析
本文所建模型在处理裂缝过程中主要进行了以下几点考虑: 多段压裂缝、裂缝有限导流、裂缝以任意形态展布以及裂缝向任意方向倾斜, 因此针对上述几点考虑分别进行裂缝导流能力、裂缝倾角、井筒倾角、裂缝纵向高度以及裂缝段间距等参数敏感性分析.
(1)裂缝导流能力敏感性分析
图12给出了无因次裂缝导流系数分别为0.5, 5, 50及500时压力及压力导数曲线响应, 可以看出随着裂缝导流能力的升高, 井储阶段及过渡阶段更早结束, 早期及晚期径向流阶段时间变短, 特别是早期径向流阶段基本消失.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
裂缝导流能力敏感性分析
Figure
12.
Sensitivity analysis of well storage coefficient
下载: 全尺寸图片
幻灯片
(2)裂缝倾角敏感性分析
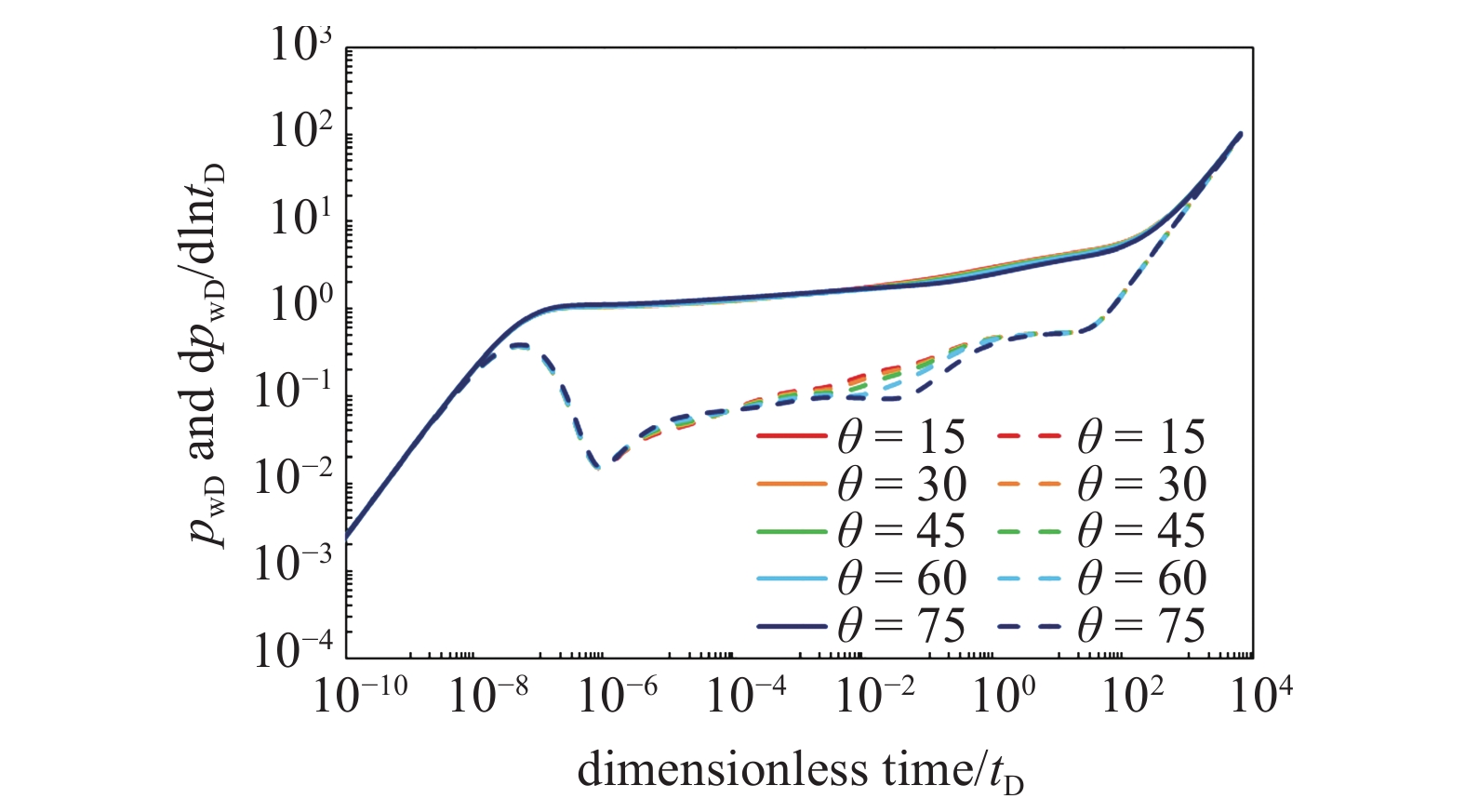
考虑裂缝纵向高度保持一致, 对比裂缝面倾角分别为15, 30, 45, 60以及75时压力及压力导数曲线变化, 由图13可以看出, 裂缝面倾角主要影响双线性流阶段至椭圆流阶段的压力导数曲线, 当裂缝倾角小于45°时, 倾角影响较小, 随着倾角进一步增大, 双线性流作用时间增长, 早期径向流更为明显, 相应的椭圆流阶段倾角增大.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-13.jpg'" class="figure_img
figure_type1 bbb " id="Figure13" />
图
13
裂缝倾角敏感性分析
Figure
13.
Sensitivity analysis of well storage coefficient
下载: 全尺寸图片
幻灯片
(3)裂缝高度敏感性分析
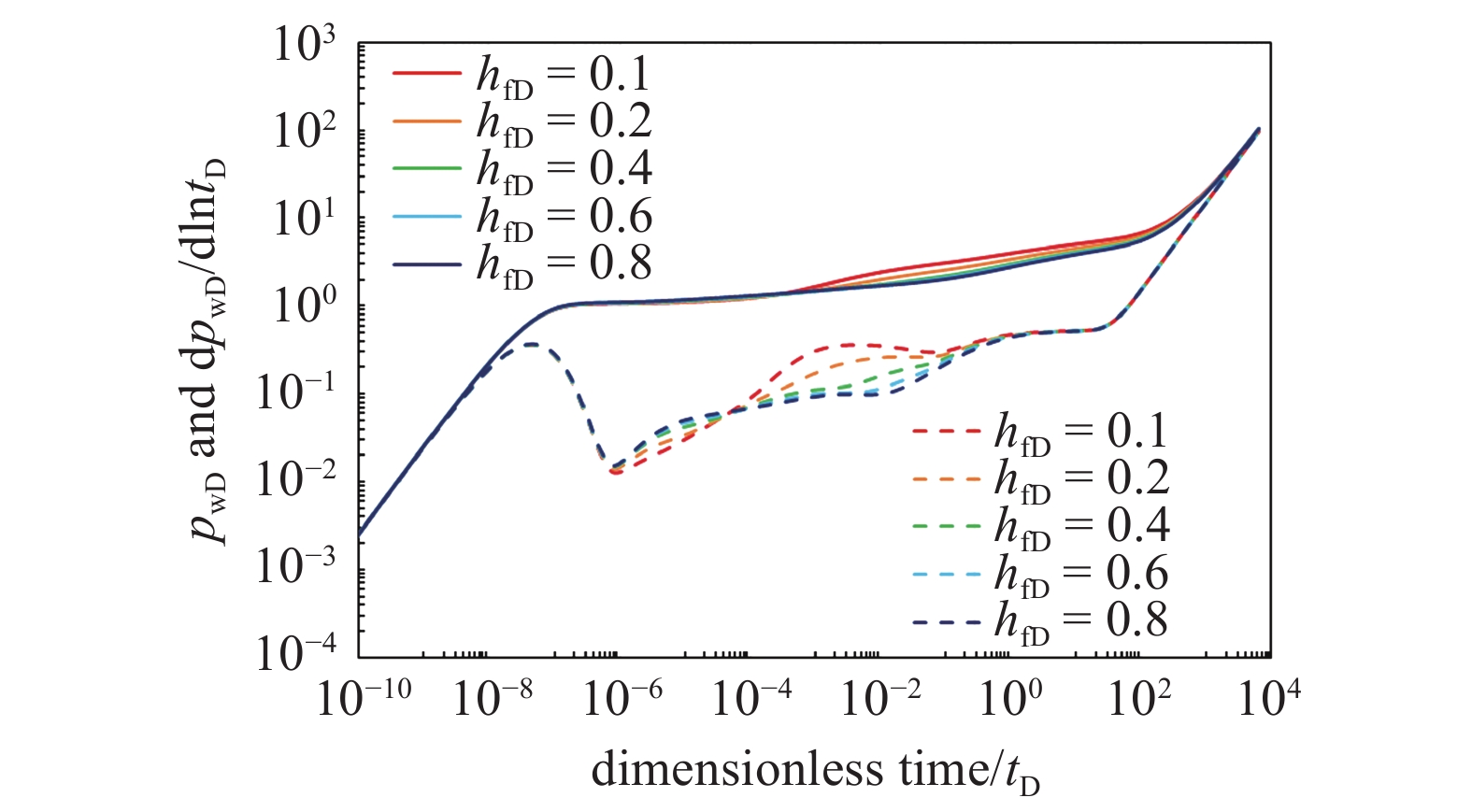
取裂缝倾角为45°, 考虑裂缝无因次纵向高度在0.2–1.0范围内变化. 由图14可以看出, 当裂缝高度较小时, 裂缝内线性流即双线性流阶段较不明显, 且基质线性流后期存在一定的回流现象, 随着裂缝高度的升高, 随着裂缝高度的增大, 各阶段流态逐渐出现.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-14.jpg'" class="figure_img
figure_type1 bbb " id="Figure14" />
图
14
裂缝高度敏感性分析
Figure
14.
Sensitivity analysis of fracture height
下载: 全尺寸图片
幻灯片
(4)裂缝段间距敏感性分析
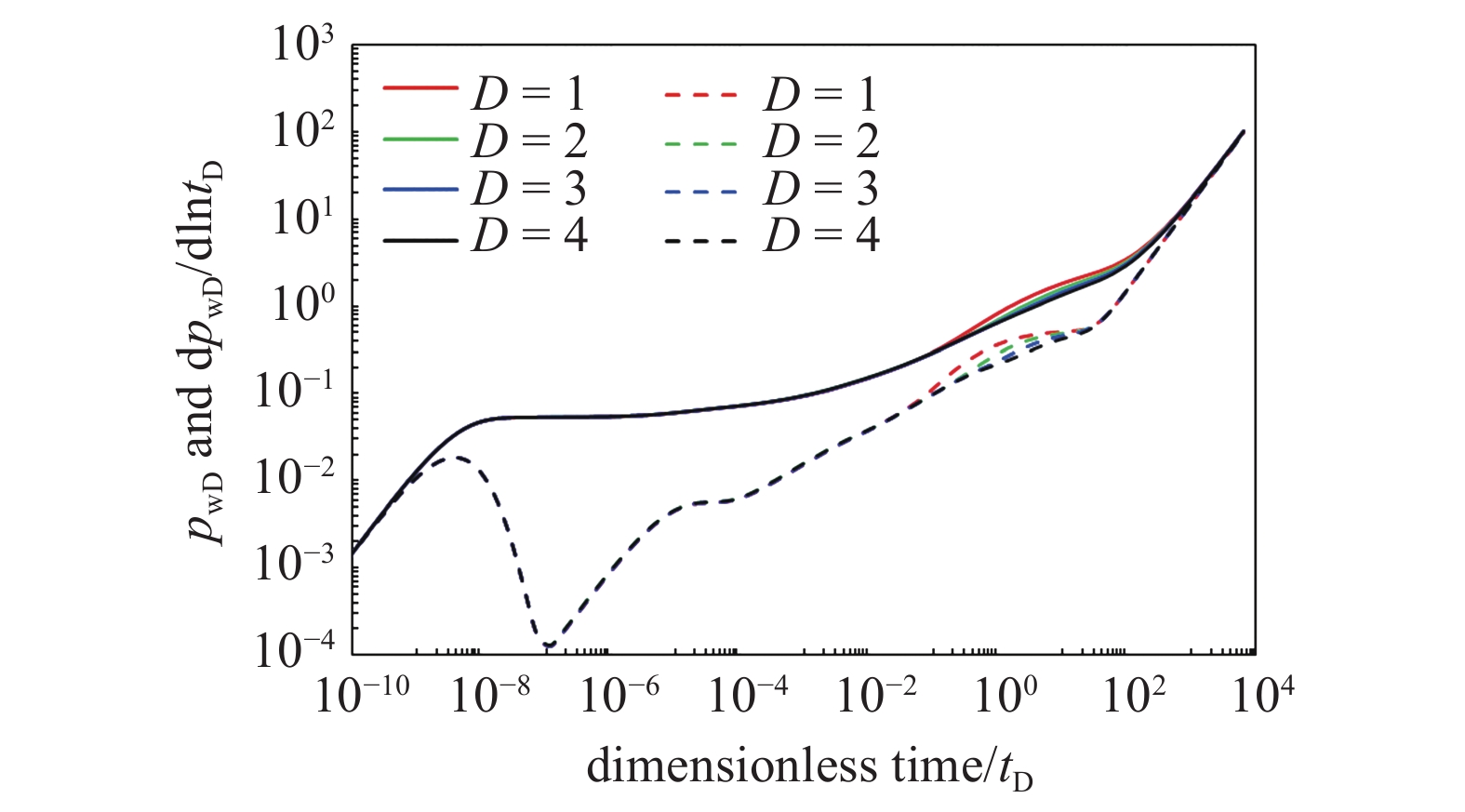
取裂缝倾角为15°, 考虑无因次裂缝段间距在1–4范围内变化, 由图15可以看出, 随着裂缝段间距增大, 早期径向流至晚期径向流阶段的特征更为不明显, 表明随着裂缝段间距的增大, 缝间干扰越晚出现且系统径向流出现时间越晚.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-183-15.jpg'" class="figure_img
figure_type1 bbb " id="Figure15" />
图
15
段间距敏感性分析
Figure
15.
Sensitivity analysis of fracturing interval
下载: 全尺寸图片
幻灯片
4.
结论
(1)对于任意方向展布裂缝可通过裂缝离散表征, 耦合裂缝内数值解与基质内面源函数解析解的方法进行求解, 但存在计算效率低的问题. 借助点源、特殊线源替代面源的方法可大大提升计算效率, 且在裂缝微元划分较为精细(微元无因次边长小于0.15)时精度较高.
(2)倾斜缝典型试井曲线可划分为井筒储集及过渡流、裂缝线性流、双线性流、基质线性流、早期径向流、椭圆流、晚期径向流及边界控制流八个流动阶段. 随着裂缝段数增多, 缝间影响增强, 井储、过渡阶段及径向流阶段特征减弱.
(3)裂缝倾角及裂缝段间距主要影响裂缝线性流到早期径向流阶段压力及压力导数曲线, 特别的当裂缝高度较小时压力导数存在回流现象.
