陈凌峰^*, 于佳佳^,*,2), 李友荣^*, 黄映洲^†, 李谷元^**重庆大学能源与动力工程学院低品位能源利用技术及系统教育部重点实验室, 重庆 400044
^†重庆大学软凝聚态物理及智能材料研究重庆市重点实验室, 重庆 400044

STUDY ON ROTATIONAL VISCOSITY OF NEMATIC LYOTROPIC LIQUID CRYSTAL¹⁾

Chen Lingfeng^*, Yu Jiajia^,*,2), Li Yourong^*, Huang Yingzhou^†, Li Guyuan^{* *}Key Laboratory of Low-grade Energy Utilization Technologies and Systems of Ministry of Education, School of Energy and Power Engineering, Chongqing University, Chongqing 400044, China
^†Chongqing Key Laboratory of Soft Condensed Matter Physics and Smart Materials, College of Physics, Chongqing University, Chongqing 400044, China

通讯作者: 2)于佳佳, 副教授, 主要研究方向: 复杂流体流动传热及控制. E-mail:yujiajia@cqu.edu.cn

收稿日期:2020-08-4接受日期:2021-01-5网络出版日期:2021-04-08

基金资助:

1)国家自然科学基金青年科学基金 .51806025 重庆市留学人员创业创新支持计划 .cx2019053 油气藏地质及开发工程国家重点实验室(西南石油大学)开放基金.PLN2020-8 中央高校基本科研业务费.2018CDXYDL0001

Received:2020-08-4Accepted:2021-01-5Online:2021-04-08
作者简介 About authors


摘要
溶致液晶具有良好的生物相容性、无毒性、生物降解性以及光学、电磁学各向异性等, 在细胞相互作用、神经刺激传递、脂肪吸收、药物智能输运等生命活动研究、医药工程和液晶显示等领域有广泛应用. 本文采用旋转磁场法测得溶致液晶日落黄在不同温度和溶液浓度下向列相时旋转黏度, 并结合溶致液晶分子自组装过程, 理论分析了溶致液晶向列相旋转黏度随温度和溶液浓度的变化规律. 研究结果表明: 溶致液晶旋转黏度与液晶分子自组装柱状体平均长度的平方呈正比增大关系, 随溶液浓度的增大而增大, 随温度的升高表现出指数减小的规律. 构建了与向列相溶致液晶温度和浓度相关的旋转黏度经验表达式, 经验表达式计算结果与实验值吻合较好, 最大误差仅为18.56${\%}$. 提出采用旋转流变仪间接获得溶致液晶剪切能的新方法, 溶致液晶剪切能随溶液浓度的增大而增大, 但在实验温度范围内, 溶致液晶剪切能几乎不随温度而改变. 利用旋转流变仪间接获得的溶致液晶剪切能与报道的利用X-Ray检测所得的结果之间最大误差仅为3${\%}$. 成功地利用了液晶分子自组装能力随温度的变化规律来研究柱状体长径比对旋转黏度的影响规律, 创新地提出了"一步法"测量研究, 大大减少相关实验研究的成本和复杂性.
关键词： 溶致液晶;向列相;旋转黏度;剪切能;经验表达式

Abstract
Lyotropic liquid crystal exhibits excellent biocompatibility, non-toxicity, biodegradability, optical anisotropy, and electromagnetic anisotropy. It has been widely used in the areas of biology, medical engineering and liquid crystal displaying, such as cell interaction, nerve stimulation transmission, fat absorption and intelligent drug transport. In this paper, the rotational viscosity of the lyotropic liquid crystal Sunset Yellow in the nematic phase at different temperature and solution concentration is measured by the rotating magnetic field method. Combined with the self-assembly process of lyotropic liquid crystal molecules, the variation of rotational viscosity of lyotropic liquid crystal in the nematic phase with temperature and solution concentration is analyzed theoretically. The results show that the rotational viscosity of the lyotropic liquid crystal is positively correlated with the square of the average length of the self-assembled columns, increasing with the increase of concentration, but decreasing exponentially with the increase of temperature. The empirical expression of rotational viscosity related to temperature and concentration of nematic lyotropic liquid crystal is constructed. The calculated results of the empirical expression are in good agreement with the experimental values, with the maximum error of 18.56${\%}$. A new indirect method of obtaining the shear energy of lyotropic liquid crystal by using rotating rheometer is proposed. The shear energy of lyotropic liquid crystal increases with the increase of solution concentration, but it is hardly related with the change of temperature in the experimental range. The shear energy obtained in this paper is in good agreement with the results of Joshi et al. who used the X-ray detection method, with the maximum error of 3${\%}$. The influence of length-diameter ratio of the columns on the rotational viscosity is investigated by using the variation of self-assembly capacity of liquid crystal molecules with temperature. The "one-step method" measurement is proposed, which greatly reduces the expenses and complexity of related experimental researches.
Keywords：lyotropic liquid crystal;nematic phase;rotational viscosity;shear energy;empirical expression


PDF (1705KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
陈凌峰, 于佳佳, 李友荣, 黄映洲, 李谷元. 向列相溶致液晶旋转黏度研究¹⁾. 力学学报[J], 2021, 53(4): 998-1007 DOI:10.6052/0459-1879-20-272
Chen Lingfeng, Yu Jiajia, Li Yourong, Huang Yingzhou, Li Guyuan. STUDY ON ROTATIONAL VISCOSITY OF NEMATIC LYOTROPIC LIQUID CRYSTAL¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(4): 998-1007 DOI:10.6052/0459-1879-20-272

引言

1888年, 奥地利植物学家Friendrich Reinitzer首次发现液晶态物质^[1]. 随后, ****们将液晶分为两大类: 热致液晶和溶致液晶. 液晶是晶体的另一种相态, 既有液体的流动性和连续性, 也会像晶体一样, 呈现出光学各向异性和双折射现象. 20世纪60年代末, 随着动态光散射技术的迅猛发展, ****们研制出了动态散射型液晶显示器(DS-LCD), 液晶在显示方面拥有了前所未有的前景^[1-2]. 液晶分子在电(磁)场作用下会产生旋光效应, 因此, 通过改善液晶旋转黏度来缩减液晶分子取向变化的弛豫时间, 对提升液晶显示器响应速度有着重大意义^[3-4].

溶致液晶(lyotropic liquid crystal, LLC)一般是由双亲分子化合物和极性溶剂等二元或多元组分在一定温度和浓度下形成的长程有序聚集结构, 兼具晶体的各向异性和液体的流动性, 表现出丰富的相态^[5]. 与热致液晶相比, 溶致液晶具有良好的生物相容性、无毒性和生物降解性, 在细胞相互作用、神经刺激传递、脂肪吸收、药物智能输运等生命活动研究及医药工程领域也有广泛应用^[6-9]. 然而, 现有关于溶致液晶的报道相对较少, 与其动力学特性相关的旋转黏度及其相关理论未见报道, 因此, 开展关于溶致液晶分子结构及其对旋转黏度影响规律的研究具有较强的学术和工程价值^[10-11].

目前, 国内外****使用差示扫描量热法、电容衰减技术和光学相位衰减时间测量法等, 测得了热致液晶5CB, 8CB, MBBA和BP(联苯)等纯工质、混合物及掺杂混合物在不同温度下的向列相旋转黏度. 利用Freederiks转变理论进行分析, 初步建立了向列相热致液晶旋转黏度数据库和相关理论体系^[12-16]. Gerber^[12]研究了向列相热致液晶MBBA的旋转黏度, 发现其旋转黏度随温度的升高而减小, 但其旋转黏度远大于剪切黏度. Pashkovski和Litvina^[13]研究了热致液晶相对分子质量对旋转黏度的影响, 结果表明, 随着热致液晶相对分子质量的增大, 向列相旋转黏度会随之增大. Denolf等^[14-15] 研究了热致液晶8CB和BP混合物向列相旋转黏度, 研究发现, 热致液晶混合物旋转黏度随温度升高呈指数下降趋势, 与纯工质热致液晶旋转黏度随温度变化的规律相同. Yadav等^[16]研究了是否掺杂Fe$_{2}$O$_{3}$纳米颗粒的热致液晶D5AOB 的旋转黏度, 发现掺杂Fe$_{2}$O$_{3}$纳米颗粒的热致液晶D5AOB旋转黏度比纯热致液晶要小. 他们认为, 掺杂纳米颗粒可以有效缩短液晶弛豫时间, 是提高液晶显示器响应速度的有效途径.

近年, 国内外****利用X射线散射技术、动态光散射技术和双光子激光写入制造表面形貌方法对不同温度和浓度下溶致液晶日落黄(sunset yellow, SSY)和色苷酸二钠(disodium cromoglycate, DSCG)的有序聚集体形成和聚集体结构进行了一系列实验研究^[17-20]. Horowitz等^[17]研究了溶致液晶相变随浓度的变化, 研究发现随着溶液浓度的增大, SSY溶致液晶将从各向同相转变为向列相, 液晶分子自组装成柱状体, 柱状体的轴线基本保持平行. 当溶液浓度继续增大, 溶致液晶将从向列相转变为片状相, 柱状体消失. Park等^[18]研究了离子对溶致液晶自组装能力的影响, 发现NaOH, MgSO$_{4}$和NaCl均能显著地改变液晶分子自组装能力. MgSO$_{4}$和NaCl溶液中的离子基团能有效地提升SSY溶致液晶分子自组装能力, 柱状体长度相应增长. 而NaOH溶液中OH与SSY分子的侧链基团发生化学反应, 削弱了SSY溶致液晶分子自组装能力, 从而减少了柱状体的长度. Zhang和Kitzerow^[19]研究了离子浓度对溶致液晶溶液的影响, 在DSCG溶致液晶中, 当Mg$^{2+}$浓度超过其临界浓度(0.6 $\sim$ 0.7 mmol/L)时, DSCG溶质将会析出. 由于溶致液晶自组装过程与温度、溶液浓度以及游离离子性质等密切相关, 与热致液晶相比, 溶致液晶旋转黏度的变化规律相对较为复杂, 但现有关于溶致液晶旋转黏度的报道却相对较少. Zhou等^[21-22]研究了溶致液晶的自组装过程, 发现向列相DSCG溶致液晶旋转黏度与液晶分子自组装过程密切相关. 但仅有的较少研究结果未能系统地反映向列相溶致液晶旋转黏度特性, 尚无对向列相溶致液晶旋转黏度相关理论的系统研究和报道.

本文基于流变学理论^[23], 采用旋转磁场法测得SSY溶致液晶在不同温度和浓度下的旋转黏度. 基于溶致液晶分子自组装过程与温度和溶液浓度的相关性, 分析向列相溶致液晶旋转黏度随温度和浓度的变化规律, 构建溶致液晶旋转黏度随温度和浓度变化的经验表达式, 明确溶致液晶分子剪切能在不同温度和浓度下的理论关系.

1 实验原理

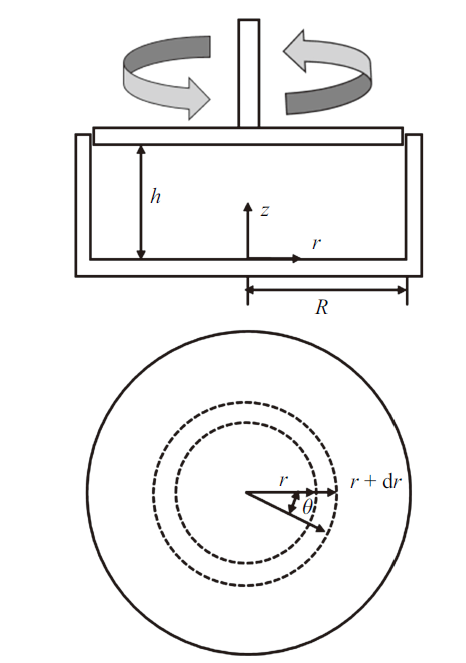
液晶在一定锚定边界条件下, 液晶分子呈定向排列(指向矢). 根据Frank弹性形变理论^[24], 当液晶指向矢发生变化时, 在弹性力的作用下, 液晶分子将恢复原有指向. 而在电(磁)场作用下, 液晶分子会感生电偶极矩, 并且电偶极矩的大小受电(磁)场强度影响. 当外加电 (磁)场强度超过某一临界值时, 电偶极矩克服弹性力矩, 液晶分子将随电(磁)场发生转动. 对于正性液晶($\Delta \varepsilon =\varepsilon_{//}-\varepsilon_{\bot }>0$, $\varepsilon $为介电常数, $//$为与电(磁)场方向平行, $\bot $为与电(磁)场方向垂直), 液晶指向矢与电(磁)场方向平行; 反之, 负性液晶($\Delta \varepsilon =\varepsilon_{\parallel}-\varepsilon_{\bot}<0$)指向矢将与电(磁)场方向垂直^[4].

本文采用旋转磁场法来测量溶致液晶旋转黏度^[25], 测量设备为安东帕旋转流变仪(Anton Paar MCR302)^[26]. 根据溶致液晶流变特性^[27], 选用应力控制型, 即恒定切应力模式. 安东帕旋转流变仪马达产生电磁转矩, 转矩作用于平行板转子上, 使平行板转子以恒定转速转动, 如图1所示. 安东帕旋转流变仪的角位移精度和扭矩精度分别为$\pm$10 nrad和0.1 nN$\cdot$m. 平行板转子下方设有半径$R=10$ mm和深度$h=3$ mm的圆柱形试剂池.

图1

新窗口打开|下载原图ZIP|生成PPT
图1液晶试剂池与平行板转子及坐标系

Fig.1Liquid crystal reagent pool, parallel plate rotor and coordinate system



当平行板转子以恒定转速进行旋转时, 试剂池内局部径向速度为

(1)$\begin{eqnarray} \label{eq1} v=\varOmega r\frac{z}{h} \end{eqnarray} $
式中, $\varOmega $为平行板转子旋转角速度. 在任意$z\in [0, h]$处, 局部径向速度梯度为$\dot{v}={\partial v}/{\partial z}$

(2)$\begin{eqnarray} \label{eq2} \dot{v}=\varOmega \frac{r}{h} \end{eqnarray} $
对于非牛顿流体而言, 其黏度$\gamma $与施加的扭矩不成正比关系, 因此, 需要将扭矩进行Robinowitsh型推导^[28].

在微元区间[$r, r+{d}r]$圆环上, 如图1所示, 旋转剪切产生的扭矩$T_{s}$为

(3)$\begin{eqnarray} \label{eq3} {d}T_{s} =\tau (r)\cdot r\cdot {d}S=\gamma (r)\cdot \frac{\varOmega r}{h}\cdot2\pi r^{2}{d}r \end{eqnarray} $
式中, $\tau (r)$, $\gamma (r)$ 和d$S$分别为局部切应力、局部旋转黏度和微元面积. 在$[0, R]$区间内, 平行板转子旋转剪切而产生的扭矩$T_{s}$为

(4)$\begin{eqnarray} \label{eq4} T_{s} =\int_0^{R} {{d}T_{s} } =2\pi \frac{\varOmega }{h}\int_0^{R} {\gamma (r)r^3} {d}r \end{eqnarray} $
式(2)可转换为

(5)$\begin{eqnarray} \label{eq5} {d}r=\frac{\varOmega }{h}{d}\dot{v} \end{eqnarray} $
因此, 式(4)可转换为

(6)$\begin{eqnarray} \label{eq6} T_{s} =2\pi \left(\frac{h}{\varOmega }\right)^3\int_{0}^{\dot{v}_{R} } {\gamma (\dot{v})\dot{v}^3} {d}\dot{v} \end{eqnarray} $
式(6)可以转化为

(7)$\begin{eqnarray} \label{eq7} T_{s} =2\pi \left(\frac{R}{\dot{v}_{R}}\right)^3\int_{0}^{\dot{v}_{R} } {\gamma (\dot{v})\dot{v}^3} {d}\dot{v} \end{eqnarray} $
由式(7)得

(8)$\begin{eqnarray} \label{eq8} \frac{T_{s} }{2 \pi R^{3}}=\left(\frac{1}{\dot{v}_{R} }\right)^{3}\int_0^{\dot{v}_{R} } {\gamma (\dot{v})\dot{v}^{3}} {d}\dot{v} \end{eqnarray} $
自由边界上的界面压力和应力对扭矩和轴向应力测量的影响可忽略, 黏度在数值上等于自由边界上的数值. 运用Leibniz法则, 可得

(9)$\begin{eqnarray} \label{eq9} \frac{{d}\left(\dfrac{T_{s} }{2\pi R^{3}}\right)}{{d}\dot{v}_{R}}=\gamma (\dot{v}_{R} )-3\frac{1}{(\dot{v}_{R})^{4}}\int_0^{\dot{v}_{R} } {\gamma (\dot{v})} \dot{v}^{3}{d}\dot{v} \end{eqnarray} $
式(9)可以转换为

(10)$\begin{eqnarray} \label{eq10} \gamma (\dot{v}_{R} )=\frac{{d}\left(\dfrac{T_{s} }{2\pi R^{3}}\right)}{{d}\dot{v}_{R}}+3\frac{1}{(\dot{v}_{R} )^{4}}\int_0^{\dot{v}_{R} } {\gamma (\dot{v})}\dot{v}^{3}{d}\dot{v} \end{eqnarray} $
由式(8)可得

(11)$\begin{eqnarray} \label{eq11} \int_0^{\dot{v}_{R} } {\gamma (\dot{v})\dot{v}^{3}} {d}\dot{v}=\frac{T_{s} }{2{\pi R}^{3}}\dot{v}_{R}^{3} \end{eqnarray} $
将式(11)代入式(10)中, 并进行转换可得

(12)$\begin{eqnarray} \label{eq12} && \gamma (\dot{v}_{R} )=\frac{{d}\left(\dfrac{T_{s} }{2{\pi R}^{3}}\right)}{{d}\dot{v}_{R} }+3\frac{1}{\dot{v}_{R} }\cdot \frac{T_{s} }{2{\pi R}^{3}} = \\ && \frac{T_{s} }{2{\pi R}^{3}}\frac{1}{\dot{v}_{R}} \left\{\left[\dfrac{2\pi R^{3}}{T_{s}}\cdot {d}\left(\dfrac{T_{s} }{2{\pi R}^{3}}\right)\right] \dot{v}_{R}{d}\dot{v}_{R}+3\right\} \end{eqnarray} $
将式(12)转换可得

(13)$\begin{eqnarray} \gamma (\dot{v}_{R} )=\frac{T_{s} }{2{\pi R}^{3}\dot{v}_{R} }\left[\frac{{d}\ln \left(\dfrac{T_{s} }{2{\pi R}^{3}}\right)}{{d}\ln \dot{v}_{R} }+3\right] \end{eqnarray} $
通过平行板转子旋转剪切而产生的扭矩$T_{s}$和剪切速率$\dot{v}_{R} $得到${{d}(T_{s} /2{\pi R}^{3})}/{{d}\ln \dot{v}_{R} }$ , 结合式(13), 从而获得向列相溶致液晶的旋转黏度.

2 实验结果与讨论

2.1 材料制备与实验过程

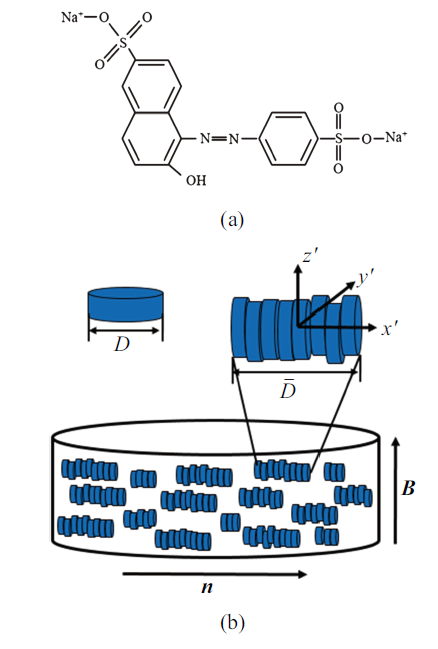
溶致液晶选用SSY, 购置于SigmaAldrich公司, 纯度为98${\%}$. SSY分子式为C$_{10}$H$_{10}$N$_{2}$Na$_{2}$O$_{7}$S$_{2 }$, 相对分子质量452.38 g/mol, 分子结构如图2(a)所示. SSY分子中含有大量的苯环结构, 呈现长链形式. 苯环之间主要通过弱电子云的相互作用, 即$\pi $ - $\pi $堆积, 形成分子自组装柱状体^[29-31], 如图2 (b)所示.

图2

新窗口打开|下载原图ZIP|生成PPT
图2SSY的分子结构式(a)和液晶分子自组装示意图 (b)

Fig.2Schematic diagram of molecular structure of SSY (a) and liquid crystal molecule self-assembly (b)



采用超纯水(DI water, 电阻率为18.2 M$\Omega $ $\cdot$ cm)和SSY粉末混合配制成不同浓度的SSY水溶液. 本文研究的质量百分比浓度范围为30${\%}$ $\sim$ 41${\%}$, 温度范围为299 $\sim$ 315 K的向列相溶致液晶SSY水溶液. 夹具为平行板转子, 其旋转平面方向和磁场方向垂直. 旋转流变仪可施加的电流强度范围为1 $\sim$ 5 A, 对应磁感应强度的范围为1 $\sim$ 5 T. 由于SSY液晶为负性液晶^[29], 液晶指向矢垂直于磁场方向, 如图2(b)所示. 采用温度精度为$\pm$0.1 K的恒温水浴来维持试剂池内样品的恒定温度.

安东帕旋转流变仪放置于防震平台, 平行板至液池底部的距离仅为$h=1.8$ mm, 因此, 在实验过程液池内SSY溶致液晶可视为无湍流和回流产生^[26]. 实验过程中, 设置平行板转子旋转速度为定值, 磁感应强度为1 T^[22], 可获得施加于平行板转子上的扭矩以及旋转速度梯度. 最后, 利用式(13), 即可计算获得SSY溶致液晶旋转黏度$\gamma_{1}$.

2.2 浓度对旋转黏度的影响

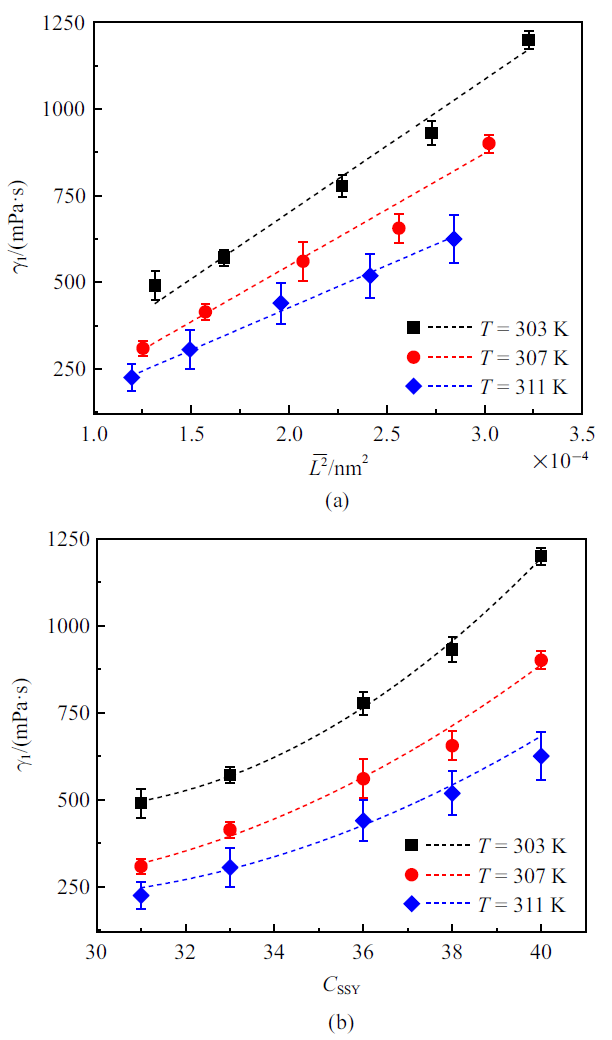
溶致液晶相态会随液晶溶液温度和浓度发生改变^[4]. 溶致液晶相态的形成是分子$\pi $ - $\pi $堆积、静电作用以及分子亲疏水性协同作用的结果^[29]. 溶致液晶分子与水在静电作用下形成饼状分子基元, 饼状分子基元在$\pi $ - $\pi $堆积和静电作用以及亲疏水性三者共同驱动下, 形成柱状体^[30], 如图2 (b)所示. 溶致液晶分子自组装过程会随温度和浓度的变化而发生可逆转变.

图3给出了温度为303 K, 307 K和311 K时SSY向列相溶致液晶旋转黏度$\gamma _{1}$随液晶分子自组装柱状体平均长度的平方$\bar{{L}}^{2}$和溶液浓度$C_{SSY}$的变化. 从图3(a)中可知, SSY向列相溶致液晶旋转黏度$\gamma_{1}$随液晶分子自组装柱状体平均长度的平方$\bar{{L}}^{2}$呈正比增大. 研究表明, 在温度恒定时, SSY溶致液晶分子自组装柱状体平均长度随溶液浓度单调递增^[31-32]. 旋转黏度$\gamma_{1}$随着SSY溶致液晶溶液浓度$C_{SSY}$的增大, 呈现出二次抛物线型增长的趋势, 如图3(b)所示.

图3

新窗口打开|下载原图ZIP|生成PPT
图3SSY向列相溶致液晶旋转黏度$\gamma_{1}$随液晶分子自组装柱状体平均长度平方$\bar{{L}}^{2}$ (a)和溶液浓度$C_{SSY}$的变化关系(b) (符号:实验值; 虚线: 拟合线)

Fig.3Variations of the rotational viscosity $\gamma_{1}$ of lyotropic liquid crystal SSY with the square of the average length of the self-assembled column $\bar{{L}}^{2}$(a) and solution concentration $C_{SSY}$ (b) (symbol: experimental data; dotted line: fitting line)



Meyer等^[31,33]研究表明, 在恒定旋转速度剪切下, 单个自组装柱状体引起的能量消耗$\delta P$可以表达为

(14)$\begin{eqnarray} \delta P=\mu (x'\dot{v}_{R} )^{2}{d}x' \end{eqnarray}$
式中, $\mu $为摩擦系数, $x'$为液晶分子自组装柱状体轴向方向位置, 如图2(b)所示. 由于液晶分子自组装柱状体平均长度$\bar{{L}}$远远小于试剂池深度$h$, 因此, 在试剂池内任意$z$处, $\dot{v}_{R} $可视为定值. 在旋转剪切下, 自组装柱状体引起的平均能量消耗$\bar{{P}}$为

(15)$\begin{eqnarray} \label{eq15} \bar{{P}}=\frac{1}{\bar{{L}}}\int_{-\bar{L}/2}^{-\bar{L}/2}{\mu } (x'\dot{v}_{R} )^{2}{d}x'=\mu \frac{\bar{{L}}^{2}}{12}\dot{v}_{R}^{2} \end{eqnarray} $
在实验中, 由于能量消耗是由旋转黏度引起, 因此结合式(15)可知, 溶致液晶旋转黏度$\gamma_{1}$与液晶分子自组装柱状体平均长度的平方$\bar{{L}}^{2}$成正比关系, 如图3(a)所示. 溶致液晶旋转黏度$\gamma_{1}$与液晶分子自组装柱状体平均长度的平方$\bar{{L}}^{2}$可以表达为

(16)$\begin{eqnarray} \label{eq16} \gamma_{1} =k_{1} \bar{{L}}^{2} \end{eqnarray} $
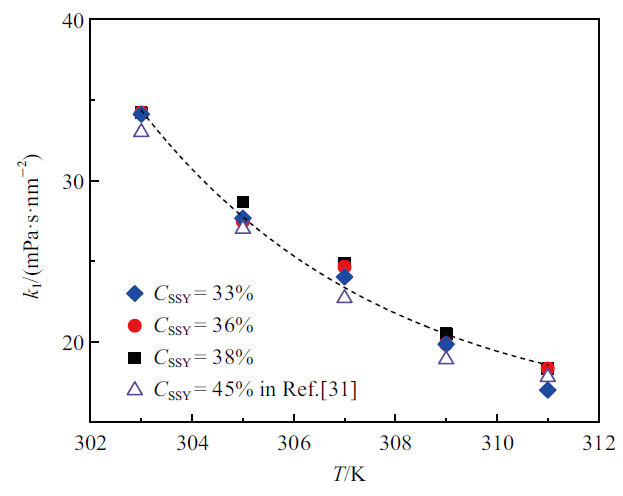
式中, $k_{1}$为比例系数. 图4给出了比例系数$k_{1}$随温度$T$的变化. 当温度$T$从303 K升高到311 K时, 比例系数$k_{1}$从0.34减小到0.19, 但与浓度无关. 本文研究结果与文献[31]中溶液浓度为45${\%}$的SSY溶致液晶比例系数$k_{1}$吻合较好, 最大误差仅为9${\%}$, 如图4所示. 由于自组装柱状体平均长度随溶液浓度增大而单调递增, 结合式(16)和图3可知, 旋转黏度$\gamma_{1}$随液晶分子自组装柱状体平均长度的平方$\bar{{L}}^{2}$和溶液浓度$C_{SSY}$分别呈线性和 二次抛物线型的变化规律与理论表达式(16)吻合较好.

图4

新窗口打开|下载原图ZIP|生成PPT
图4比例系数$k_{1}$与温度$T$的变化(符号: 实验值; 虚线: 拟合线)

Fig.4Variation of the scaling factor $k_{1}$ with temperature $T$ (symbol:experimental data; dotted line: fitting line)

2.3 温度对旋转黏度的影响

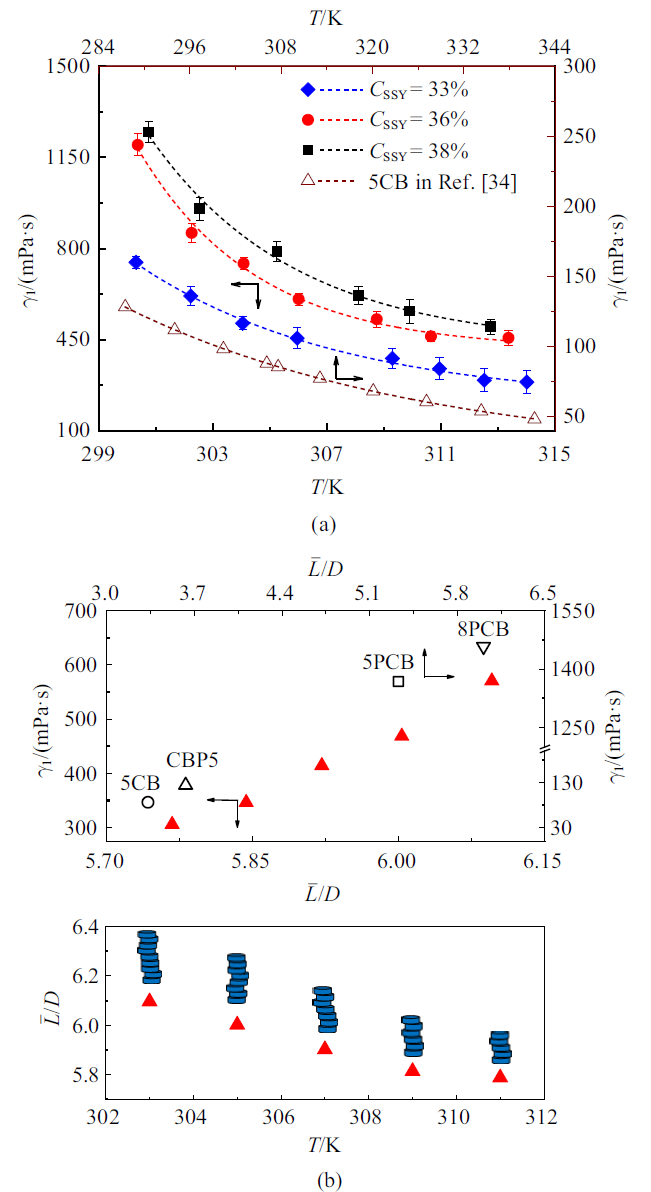
图5给出了SSY溶致液晶溶液质量百分比浓度为33${\%}$, 36${\%}$和38${\%}$时, 向列相旋转黏度$\gamma_{1}$随温度$T$和液晶分子自组装柱状体长径比$\bar{{L}}/D$的变化. SSY溶致液晶旋转黏度$\gamma_{1}$随温度$T$的升高呈指数减小. 溶致液晶SSY旋转黏度$\gamma _{1}$随温度$T$的变化规律与热致液晶5CB相同^[34], 但向列相热致液晶5CB旋转黏度$\gamma_{1}$远小于SSY溶致液晶, 如图5(a)所示. 在相同温升情况下, 溶致液晶溶液浓度越高, 其旋转黏度减小的趋势越明显.

图5

新窗口打开|下载原图ZIP|生成PPT
图5SSY向列相溶致液晶旋转黏度$\gamma_{1}(C_{SSY}=33${\%}$$)随温度$T$(a)和分子长径比$\bar{{L}}/D$的变化(b) (图5(b)中, 实心: 实验值; 空心:文献[36])

Fig.5Variations of the rotational viscosity $\gamma_{1}$ of lyotropic liquid crystal SSY with the temperature $T$ (a) and molecular aspect ratio $\bar{{L}}/D$ (b) (solid symbol: experimental data; hollow symbol: Fig.5(b) in Ref.[36])



向列相溶致液晶分子自组装柱状体中相邻液晶分子受$\pi $ - $\pi $堆积和静电力的共同作用而相互吸引. 当液晶分子的活化能足以克服分子自组装的吸引作用时, 液晶分子将脱离自组装柱状体, 进入游离态^[35].

Zhou等^[31]研究表明, 溶致液晶分子自组装柱状体平均长度$\bar{{L}}$与温度$T$有如下关系

(17)$\begin{eqnarray} \bar{{L}}\propto \mbox{e}^{\frac{E}{2{K}_{B} T}} \end{eqnarray} $
式(17)中$E$为剪切能, $K_{B}$为玻尔兹曼常数, $T$为热力学温度.

由于溶致液晶旋转黏度$\gamma _{1}$与液晶分子自组装柱状体平均长度的平方$\bar{{L}}^{2}$成正比关系, 式(16)可以转化为下式

(18)$\begin{eqnarray} \label{eq17} \gamma_{1} =k_{2} \mbox{e}^{\frac{E}{ K_{B} T}} \end{eqnarray} $
式(18)中$k_{2}$为比例系数. 向列相旋转黏度与温度变化的实验结果(图5(a))与理论式(18)吻合较好. 随着温度的升高, 液晶分子的活化能增大, 分子拥有的富余能量足以挣脱自组装柱状体中相邻液晶分子的束缚作用. 自组装柱状体中部分液晶分子实现游离, 从而使得溶致液晶无序度增大, 宏观上表现出旋转黏度降低.

从图5(b)中可知, 当SSY溶致液晶溶液浓度为33${\%}$时, 随着温度从302 K升高至312 K, 溶致液晶分子自组装柱状体长径比$\bar{{L}}/D$将从6.09减小到5.76, 其旋转黏度从570 mPa $\cdot$ s减小至305 mPa $\cdot$ s. Dark等^[36] 研究了4种热致型液晶的旋转黏度$\gamma_{1}$, 结果表明, 热致型液晶旋转黏度$\gamma_{1}$会随着液晶分子长径比的增大而增大. 该实验结果与溶致液晶旋转黏度$\gamma_{1}$随分子自组装柱状体长径比$\bar{{L}}/D$的变化规律相同, 如图5(b)所示. 利用SSY溶致液晶分子自组装能力随温度变化的规律, 通过改变溶致液晶样品的温度来实现自组装柱状体长径比变化, 从而研究溶致液晶分子自组装柱状体长径比对其旋转黏度的影响. 创新地提出并成功利用了"一步法"来探索分子长径比对研究对象的影响规律, 大大降低实验研究的成本和复杂性.

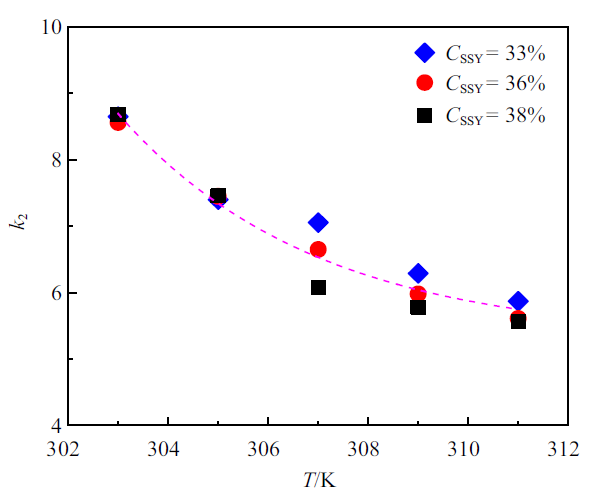
式(18)则为SSY向列相溶致液晶旋转黏度$\gamma_{1}$的经验表达式. 在式(18)中, 溶致液晶剪切能$E$与溶液浓度$C_{SSY}$相关, 而比例系数$k_{2}$随温度$T$变化. 当温度$T$从303 K升高到311 K时, 比例系数$k_{2}$从8.68减小到5.57, 但与浓度无关. 从图4和图6中可以发现, 随着温度的升高, 溶液浓度对比例系数$k_{1}$和$k_{2}$逐渐产生微弱影响, 比例系数$k_{1}$和$k_{2}$分别与溶液浓度无关性相对减弱. Park等^[18]研究了温度对SSY溶致液晶分子自组装柱状体长度的影响, 发现SSY溶致液晶分子自组装柱状体长度的不均匀性随着温度的升高和溶液浓度的减小而逐渐增大. 在本文理论研究中(式(15)), 假设分子自组装柱状体长度均相同, 即为$\bar{{L}}$, 实验获得的比例系数$k_{1}$和$k_{2}$与理论结果存有一定误差, 并且该误差会随着温度的升高和溶液浓度的减小而逐渐增大, 如图4和图6.

图6

新窗口打开|下载原图ZIP|生成PPT
图6比例系数$k_{2}$随温度$T$的变化 (符号: 实验值; 虚线: 拟合线)

Fig.6Variation of the scaling factor$ k_{2}$ with temperature $T$ (symbol: experimental data; dotted line: fitting line)



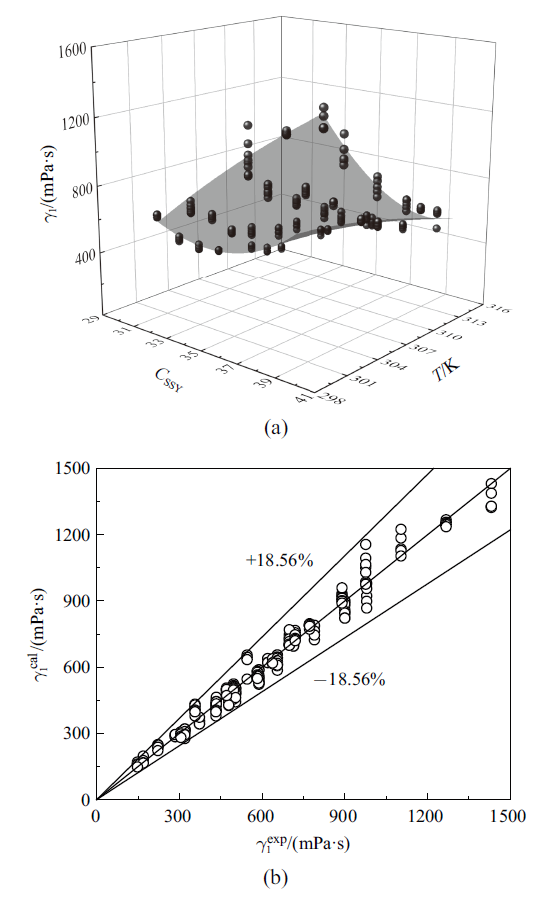
图7(a)给出了利用式(18)计算和实验所获得的不同温度$T$和溶液浓度$C_{SSY}$下SSY向列相溶致液晶的旋转黏度$\gamma_{1}$. SSY向列相溶致液晶旋转黏度$\gamma_{1}$随温度$T$和溶液浓度$C_{SSY}$的减小而逐渐增大. 实验结果相对均匀分布于理论计算值附近, 理论计算值与实验结果吻合较好, 最大误差仅为18.56${\%}$, 平均误差为11.21${\%}$, 如图7(b)所示.

图7

新窗口打开|下载原图ZIP|生成PPT
图7SSY向列相溶致液晶旋转黏度$\gamma_{1}$随温度$T$、溶液浓度$C_{SSY}$的变化(a)和旋转黏度$\gamma_{1}$理论计算值与实验值的比较(灰面: 理论计算值; 符号: 实验值)

Fig.7Variation of the rotational viscosity $\gamma_{1}$ of lyotropic liquid crystal SSY with temperature $T$, solution concentration $C_{SSY}$ (a) and the comparison of the theoretical calculatong and experimental results (grey surface: theoretical calculating data; symbol: experimental data)

2.4 剪切能

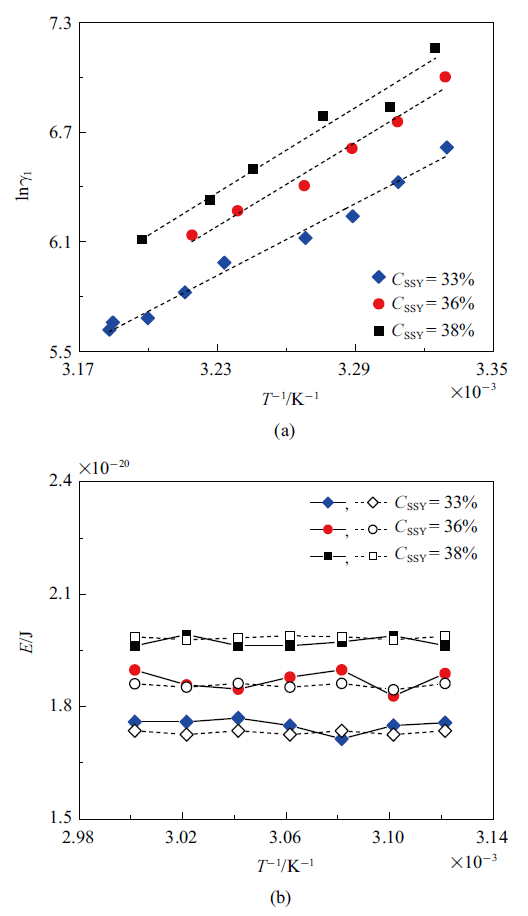
剪切能是将液晶分子自组装柱状体中相邻分子进行分解所需要的能量^[30]. 由向列相溶致液晶旋转黏度经验表达式(18)可获得剪切能$E$与旋转黏度$\gamma _{1}$之间的关系

(19)$\begin{eqnarray} \label{eq18} \mbox{ln}\gamma_{1} =\frac{1}{T}\frac{E}{ K_{B} }+\ln k_{2} \end{eqnarray} $
从图8(a)可知, 实验获得的不同浓度下ln$\gamma_{1}$随1/$T$呈线性增大, 实验结果与式(19)吻合较好. 图8(b)给出了不同溶液浓度SSY溶致液晶剪切能$E$随温度$T$的变化. SSY溶致液晶剪切能$E$随溶液浓度$C_{SSY}$的增大而增大^[37-38], 在实验温度范围内, 剪切能$E$几乎不随温度$T$而改变. 当$C_{SSY}=33${\%}$$, 36${\%}$和38${\%}$时, SSY溶致液晶剪切能值$E$分别为$1.74\times 10^{-20}$ J, $1.87\times 10^{-20}$ J 和$1.96\times 10^{-20}$ J. 随着溶致液晶溶液浓度的增大, 液晶分子之间的$\pi $ - $\pi $效应逐渐增强, SSY液晶分子自组装柱状体中分子挣脱其相邻分子所需的能量也会相应增大, 因此, 溶致液晶剪切能会随溶液浓度增大而增大. 结合式(19)并利用旋转流变仪所获得的SSY溶致液晶剪切能与Joshi等^[32]利用X-Ray检测所获得的结果吻合较好, 最大误差仅为3${\%}$. 本文提出的基于溶致液晶旋转黏度$\gamma_{1}$获取剪切能$E$的新方法, 其具备设备成本低、操作简单和精度高等优势, 具有较强的推广价值.

图8

新窗口打开|下载原图ZIP|生成PPT
图8SSY向列相溶致液晶旋转黏度ln$\gamma_{1}$与$T^{-1}$的关系(a)和剪切能$E$随$T^{-1}$的变化(b)(实心: 实验值; 空心: 文献[32])

Fig.8The relationship between the rotational viscosity ln$\gamma_{1}$ of lyotropic liquid crystal SSY and $T^{-1}$ (a) and the variation of shear energy $E$ with $T^{-1}$ (b) (solid symbol: experimental data; hollow symbol: Ref.[32])

3 结论

本文采用旋转磁场法测得溶致液晶Sunset Yellow在不同温度和溶液浓度下向列相时的旋转黏度, 并结合溶致液晶分子自组装过程, 理论分析向列相溶致液晶旋转黏度随温度和溶液浓度的变化规律, 获得以下结论:

(1) 溶致液晶旋转黏度与液晶分子自组装柱状体平均长度的平方呈正比增大关系, 其随着浓度的增大而增大, 但随着温度的升高表现出指数减小的规律. 构建了与温度和浓度相关的旋转黏度经验表达式, 经验表达式计算结果与实验值吻合较好, 最大误差仅为18.56${\%}$, 平均误差为11.21${\%}$.

(2)利用旋转流变仪间接获取了溶致液晶剪切能. 溶致液晶剪切能随溶液浓度的增大而增大, 与Joshi等^[32]利用X-Ray检测所获得的剪切能结果最大误差仅为3${\%}$. 但在实验温度范围内, 溶致液晶剪切能几乎不随温度而改变.

(3) 成功地利用了液晶分子自组装能力随温度变化的规律来研究柱状体长径比对旋转黏度的影响. 创新地提出了"一步法"研究方法, 大大减少相关实验研究的成本和复杂性.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 谢毓章. 液晶物理学. 北京: 科学出版社, 1988
[本文引用: 2]

(Xie Yuzhang. The Physics of Liquid Crystals. Beijing: Science Press, 1988 (in Chinese))
[本文引用: 2]

[2] Goldburg WI. Dynamic light scattering
American Journal of Physics, 1999,67(12):1152-1160
[本文引用: 1]

[3] Lee H, Yang S, Lee JH, et al. Improvement of the relaxation time and the order parameter of nematic liquid crystal using a hybrid alignment mixture of carbon nanotube and polyimide
Applied Physics Letters, 2014,104(19):191601
[本文引用: 1]

[4] Nazarenko VG, Boiko OP, Anisimov MI, et al. Lyotropic chromonic liquid crystal semiconductors for water-solution processable organic electronics
Applied Physics Letters, 2010,97(26):263305
[本文引用: 3]

[5] Tang MJ, Ding S, Zhou CR, et al. Liquid crystal biomaterials
Chemical World, 2010,51(12):756-760
[本文引用: 1]

[6] 罗丙红, 周长忍, 鲁路 等. 液晶种类对聚氨酯液晶复合膜血液相容性的影
功能高分子学报, 2009,22(2):119-123
[本文引用: 1]

(Luo Binghong, Zhou Changren, Lu Lu, et al. Effect of different kinds of liquid crystals on the blood compatibility of PCU-liquid crystal composite membranes
Journal of Functional Polymers, 2009,22(2):119-123(in Chinese))
[本文引用: 1]

[7] 贵丽红, 丰景义, 史子谦 等. 向列相液晶旋转黏度测试方法的研究
液晶与显示, 2013,28(4):527-533


(Gui Lihong, Feng Jingyi, Shi Ziqian, et al. Method of measuring nematic LC rotational viscosity
Chinese Journal of Liquid Crystals and Displays, 2013,28(4):527-533 (in Chinese))


[8] 刘赵淼, 杨刚, 逄燕 等. 不同心排出量下主动脉瓣血流动力学的PIV实验研究
力学学报, 2019,51(6):1918-1926


(Liu Zhaomiao, Yang Gang, Pang Yan, et al. Experimental study on hemodynamics of aortic valve under varied cardiac output using PIV
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(6):1918-1926 (in Chinese))


[9] 魏进家, 刘飞, 刘冬洁. 减阻用表面活性剂溶液分子动力学模拟研究进展
力学学报, 2019,51(4):971-990
[本文引用: 1]

(Wei Jinjia, Liu Fei, Liu Dongjie. Progress in molecular dynamics simulations of surfactant solution for turbulent drag reduction
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(4):971-990 (in Chinese))
[本文引用: 1]

[10] 万征, 孟达. 基于t准则的各向异性强度准则及变换应力法
力学学报, 2020,52(5):1519-1537
[本文引用: 1]

(Wan Zheng, Meng Da. Anisotropic strength criterion based on t criterion and the transformation stress method
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(5):1519-1537 (in Chinese))
[本文引用: 1]

[11] 彭向峰, 李录贤. 超弹性材料本构关系的最新研究进展
力学学报, 2020,52(5):1221-1234
[本文引用: 1]

(Peng Xiangfeng, Li Luxian. State of the art of constitutive relations of hyperelastic materials
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(5):1221-1234 (in Chinese))
[本文引用: 1]

[12] Gerber PR. Measurement of the rotational viscosity of nematic liquid crystals
Applied Physics A-Materials Science & Processing, 1981,26(3):139-142
[本文引用: 2]

[13] Pashkovsky EE, Litvina TG. Influence of polymer molecules on the rotational viscosity and backflow effect at the bend Freedericksz transition in nematic liquid crystals
Macromolecules, 1995,28(6):1818-1824
[本文引用: 1]

[14] Denolf K, Cordoyiannis G, Glorieux C, et al. Effect of nonmesogenic impurities on the liquid crystalline phase transitions of octylcyanobiphenyl
Physical Review E, 2007,76(5):051702
[本文引用: 1]

[15] Oswald P, Scalliet C. Measurements of the dielectric and viscoelastic constants in mixtures of 4,4'-n-octyl-cyanobiphenyl and biphenyl
Physical Review E, Statistical Nonlinear & Soft Matter Physics, 2014,89(3):032504
[本文引用: 1]

[16] Yadav G, Pathak G, Agrahari K, et al. Improved dielectric and electro-optical parameters of nematic liquid crystal doped with magnetic nanoparticles
Chinese Physics B, 2019,28(3):34209
[本文引用: 2]

[17] Horowitz VR, Janowitz LA, Modic AL, et al. Aggregation behavior and chromonic liquid crystal properties of an anionic monoazo dye
Physical Review E, 2005,72(4):041710
[本文引用: 2]

[18] Park HS, Kang SW, Tortora L, et al. Self-assembly of lyotropic chromonic liquid crystal sunset yellow and effects of ionic additives
The Journal of Physical Chemistry B, 2008,112(51):16307-16319
DOIURLPMID [本文引用: 2]
Lyotropic chromonic liquid crystals (LCLCs) are formed by molecules with ionic groups at the periphery that associate into stacks through noncovalent self-assembly while in water. The very existence of the nematic (N) phase in the typical LCLC, the dye Sunset Yellow (SSY) is a puzzle, as the correlation length associated with the stacking, as measured in the X-ray experiments, is too short to explain the orientational order by the Onsager model. We propose that the aggregates can be more complex than simple rods and contain

[19] Zhang B, Kitzerow HS. Influence of proton and salt concentration on the chromonic liquid crystal phase diagram of disodium cromoglycate solutions: Prospects and limitations of a host for DNA nanostructures
Journal of Physical Chemistry B, 2016,120(12):3250-3256
[本文引用: 1]

[20] Osipov M, Terentjev EM. The Molecular theory for the viscosity of nematic and smectic C liquid crystals
Molecular Crystals and Liquid Crystals, 1991,198:429-435
[本文引用: 1]

[21] Zhou S, Neupane K, Nastishin YA, et al. Elasticity, viscosity and orientational fluctuations of a lyotropic chromonic nematic liquid crystal disodium cromoglycate
Soft Matter, 2014,10(34):6571-6581
DOIURLPMID [本文引用: 1]
Using dynamic light scattering, we study orientational fluctuation modes in the nematic phase of a self-assembled lyotropic chromonic liquid crystal (LCLC) disodium cromoglycate and measure the Frank elastic moduli and viscosity coefficients. The elastic moduli of splay (K1) and bend (K3) are in the order of 10 pN while the twist modulus (K2) is an order of magnitude smaller. The splay constant K1 and the ratio K1/K3 both increase substantially as the temperature T decreases, which we attribute to the elongation of the chromonic aggregates at lower temperatures. The bend viscosity is comparable to that of thermotropic liquid crystals, while the splay and twist viscosities are several orders of magnitude larger. The temperature dependence of bend viscosity is weak. The splay and twist viscosities change exponentially with the temperature. In addition to the director modes, the fluctuation spectrum reveals an additional mode that is attributed to diffusion of structural defects in the column-like aggregates.

[22] Zhou S, Nastishin YA, Omelchenko MM, et al. Elasticity of lyotropic chromonic liquid crystals probed by director reorientation in a magnetic field,
Physical Review Letters, 2012,109(3):037801
[本文引用: 2]

[23] 韩式方 . 液晶高分子各向异性黏弹流体本构方程理论
力学学报, 2001,33(5):588-600
[本文引用: 1]

( Han Shifang. Constitutive equation for liquid crystalline polymer anisotropic visc-elastic fluid
Chinese Journal of Theoretical and Applied Mechanics, 2001,33(5):588-600 (in Chinese))
[本文引用: 1]

[24] 刘春波, 关炎芳, 辻知宏, 等. 电场作用下向列相液晶指向矢与流动的耦合机理
应用力学学报, 2012,29(3):262-268
[本文引用: 1]

(Liu Chunbo, Guan Yanfang, Tsuji Tomohiro, et al, Coupling mechanism of electric field induced nematic liquid crystal director and backflow
Chinese Journal of Applied Mechanics, 2012,29(3):262-268 (in Chinese))
[本文引用: 1]

[25] Belyaev VV. Physical methods for measuring the viscosity coefficients of nematic liquid crystals
Physics-Uspekhi, 2001,44(3):255
[本文引用: 1]

[26] 徐继润, 徐俊杰, 丁仕强. 旋转流变仪测量空间的探讨
中国过滤与分离, 2010,20(1):1-3
[本文引用: 2]

(Xu Jirun, Xu Junjie, Ding Shiqiang, Discussion of spatial-measurement with rotation rheometers
China Filtration & Separation, 2010,20(1):1-3 (in Chinese))
[本文引用: 2]

[27] 范天佑. Poisson括号方法及其在准晶、液晶和一类软物质中的应用
力学学报, 2013,45(4):548-559
[本文引用: 1]

(Fan Tianyou, Poisson bracket method and its applications to quasicrystals, liquid crystals and a class of soft matter
Chinese Journal of Theoretical and Applied Mechanics, 2013,45(4):548-559 (in Chinese))
[本文引用: 1]

[28] 史铁钧, 吴德峰. 高分子流变学基础. 北京: 化学工业出版社, 2009
[本文引用: 1]

(Shi Tiejun, Wu Defeng. Fundamentals of Polymer Rheology. Beijing: Chemical Industry Press, 2009 (in Chinese))
[本文引用: 1]

[29] Tschierske C. Development of structural complexity by liquid crystal selfassembly
Angewandte Chemie-International Edition, 2013,52(34):8828-8878
URLPMID [本文引用: 3]

[30] Hassanfiroozi A, Huang YP. Effect of noncovalent interaction of a polymer dispersed liquid crystal for interferometric applications over a range of low frequencies
ACS Applied Polymer Materials, 2019,1(11):2840-2845
[本文引用: 2]

[31] Zhou S, Cervenka AJ, Lavrentovich OD. Ionic-content dependence of viscoelasticity of the lyotropic chromonic liquid crystal sunset yellow
Physical Review E, 2014,90(4):042505
[本文引用: 5]

[32] Joshi L, Kang SW, Agra-Kooijman DM, et al. Concentration, temperature, and pH dependence of sunset-yellow aggregates in aqueous solutions: An X-ray investigation
Physical Review E, 2009,80(4):041703
[本文引用: 5]

[33] Meyer BR. Macroscopic phenomena in nematic polymers
Molecular Crystals And Liquid Crystals, 1984,106(3-4):414-414
[本文引用: 1]

[34] Orr R, Pethrick RA. Viscosity coefficients of nematic liquid crystals: I. Oscillating plate viscometer measurements and rotational viscosity measurements: K15$^{+}$
Liquid Crystals, 2011,38(9):1169-1181
[本文引用: 1]

[35] Wang L, Augustine MU, Quan L. Nature-inspired emerging chiral liquid crystal nanostructures: From molecular self-assembly to DNA mesophase and nanocolloids
Advanced Materials, 2020,32(41):2586536
[本文引用: 1]

[36] Dark ML, Moore MH, Shenoy DK, et al. Rotational viscosity and molecular structure of nematic liquid crystals
Liquid Crystals, 2006,33(1):67-73
[本文引用: 3]

[37] Patnaik AS, Goldfarb JL. Continuous activation energy representation of the arrhenius equation for the pyrolysis of cellulosic materials: Feed corn stover and cocoa shell biomass
Cellulose Chemistry And Technology, 2016,50(2):311-320
[本文引用: 1]

[38] Sierra CA. Temperature sensitivity of organic matter decomposition in the Arrhenius equation: Some theoretical considerations
Biogeochemistry, 2018,108(1-3):1-15
[本文引用: 1]