,*,†,2), 申永军**, 陈许敏††STUDY ON THE BANDGAPS OF DEFECT STATES AND APPLICATION OF ENERGY HARVESTING OF LOCAL RESONANT PHONONIC CRYSTAL PLATE1)
Lu Yiming*,†, Cao Dongxing,*,†,2), Shen Yongjun**, Chen Xumin††通讯作者: 2)曹东兴, 教授, 主要研究方向: 振动能量采集. E-mail:caostar@bjut.edu.cn
收稿日期:2020-04-25接受日期:2020-01-24网络出版日期:2021-04-08
| 基金资助: |
Received:2020-04-25Accepted:2020-01-24Online:2021-04-08
作者简介 About authors
摘要
设计了一种由圆柱形散射体嵌入环氧树脂基体而组成的周期阵列局域共振型声子晶体板结构, 分析了其平直带区域以及缺陷态的能量集中特性, 并研究了其振动能量采集特性. 首先基于超元胞法结合有限元方法分析了5 $\times$ 5完美声子晶体结构和缺陷态声子晶体结构的能带曲线和能量传输特性; 考虑点缺陷局域共振声子晶体结构的能量集中特性, 利用压电材料代替超元胞中某点的散射体材料引入点缺陷, 分析其振动能量采集特性, 结果表明单个5 $\times$ 5点缺陷超胞结构共振频带较窄; 为提升俘能效率, 提出两种由3个具有不同缺陷态数量和构型的5 $\times$ 5超元胞结构并联而成的5 $\times$ 15声子晶体板结构, 机电耦合特性分析结果表明: 所提出的局域共振型声子晶体板结构克服了单个点缺陷超胞结构缺陷模过少、共振频带过窄的局限性, 拓宽了俘能器的工作频带, 提高了输出电压; 此外, 引入不同的缺陷态数量和构型, 可以进一步拓宽俘能带宽, 实现更好的俘能效果.
关键词：
Abstract
A local resonant phononic crystal plate, which is composed by quadrangular epoxy resin matrix embedded with cylindrical scatterers, is proposed to study the vibration energy harvesting performance. The bandgaps and energy concentration characteristics for the defect state structure are analyzed in detail. Firstly, the bandgap curve and energy transmission characteristics are analyzed for perfect and point defect phononic plate with 5 $\times$ 5 array structure based on supercell theory and finite element method. Considering the energy concentration characteristics of the point defect local resonance phononic crystal structure, piezoelectric material is used to replace the scatterer material of defect point, and the vibration energy characteristics are then analyzed. The results show that it has narrow resonance frequency band for the 5 $\times$ 5 point defect supercell structure. In order to improve the energy capture efficiency, two kind of new phononic crystal plate composed of three 5 $\times$ 5 supercells with different defect numbers and layout are proposed as the vibration energy harvester. According to the results of the electromechanical coupling analysis, it shows that the proposed local resonant phononic crystal plate overcomes the disadvantages of the single point defect supercell structure, such as too few defect modes and too narrow resonance frequency band. The working frequency band of the energy harvester is widened and the output voltage is increased. Additionally, it can further broaden the energy harvesting bandwidth and achieve better efficiency by introducing different number and configuration of defect states.
Keywords：
PDF (9151KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
卢一铭, 曹东兴, 申永军, 陈许敏. 局域共振型声子晶体板缺陷态带隙及其俘能特性研究1). 力学学报[J], 2021, 53(4): 1114-1123 DOI:10.6052/0459-1879-20-436
Lu Yiming, Cao Dongxing, Shen Yongjun, Chen Xumin.
引言
类似于光子晶体的概念, 声子晶体是具有弹性波带隙的周期性结构功能材料, 在声子晶体带隙频率范围内的弹性波不能够在其内部传播, 并且随着材料成分以及周期性排列方式的不同, 声子晶体的弹性波带隙特征(如带隙范围、带宽等)也会发生改变[1-2]. Liu等[3-4]提出局域共振型声子晶体的概念, 从而开拓了声子晶体研究的新领域. 其显著特征是由小尺寸控制大波长, 带结构中存在平直带, 内部波场具有局域化共振现象[5-7]. Ei-Borgi等[8]分析了局域共振线性超材料梁的多重带隙形成. 王刚等[9]推导了一维黏弹性声子晶体的色散与耗散关系. 当声子晶体的完美周期性被破坏时, 就会在原本的带隙内产生缺陷带, 研究表明带隙内的弹性波只能被局限在缺陷处或者沿着缺陷传播[10].基于声子晶体结构的波调控特性以及局域共振声子晶体的能量集中特性, 本文提出设计一种局域共振型声子晶体板结构并用于振动能量采集. 近年来, 随着微电子技术的发展, 低功耗元器件在无线传感、植入式医疗、柔性器件等领域被广泛应用, 其无源供电技术也引起科学家的研究兴趣, 环境振动能量采集则是研究热点之一[11-13].
目前, 将周围环境中的振动能转换为电能主要包括静电式、 电磁式和压电式三种机电转换方式, 其中压电式振动能量采集技术具有能量密度高、响应快、寿命长、无污染、结构简单且易于集成到微电子系统等优点, 成为近年来该领域的研究热点. 压电式振动能量采集器的动力学设计重点在于如何实现低频、宽频带的特性, 许多****设计了多种多样的采集器结构进行了深入研究[14-19], 这些结构主要还是传统的梁、板结构. 另外, 也有一些****利用声子晶体结构的带隙特性设计振动能量采集器, Chen等[20]阐述了利用超材料进行振动能、声能和电磁能收集的研究进展. Shin等[21]研究了用于增强压电能量收集的四分之一波电堆的声子带隙. Soo等[22]设计了一种具有缺陷态的声子晶体进行能量的定位及采集. Wang等[23]对具有狭缝管缺陷二维声子晶体的声波定位特性进行了理论和实验研究. Lv等[24]通过在一个完美的声子晶体移除一个棒, 利用点缺陷声子晶体和压电材料构成振动能量采集装置. 孙伟彬等[25]通过改变声子晶体某处压电散射体的电边界条件引入缺陷态进行压电能量采集. Chen等[26]创新指出一维声子晶体压电悬臂梁(PPCB)的振动带隙可以看作是振动能量采集器的带宽, 即带隙内的波能量完全集中于结构的前几个单元并在此处进行能量采集. Wang等[27]介绍了一种由声子晶体和压电屈曲梁组合而成的声能采集发生器, 利用声子晶体的谐振腔来定义声波并将压电梁置于缺陷点处进行能量采集. Assouar等[28]研究了一个超材料缺陷薄板的声能采集特性. Wu等[29]介绍了一种利用声波晶体和压电材料研制而成的声波能量采集器. Ma等[30]研究了一种二维局域共振型超材料能量采集器, 利用局域共振超材料的缺陷模增强电压输出. 上述文献声子晶体俘能器多用于声能采集, 而针对环境振动能的采集相对较少. 因此, 本文提出设计一种针对环境振动能量采集的局域共振型声子晶体板结构并对其能带特性和俘能特性进行分析.
本文首先设计一种由四棱柱环氧树脂基体内部嵌入圆柱形散射体的新型局域共振声子晶体板结构, 并分析其元胞结构平直带区域及缺陷态的能量集中特性; 然后利用有限元方法分析5 $\times$ 5声子晶体结构的能带结构以及能量传输特性; 进一步将3个引入不同点缺陷的5 $\times$ 5超胞结构组合形成一种新型局域共振型声子晶体板结构并用于环境振动能量采集, 使其具有宽频带响应特性.
1 模型及仿真分析
1.1 有限元模型
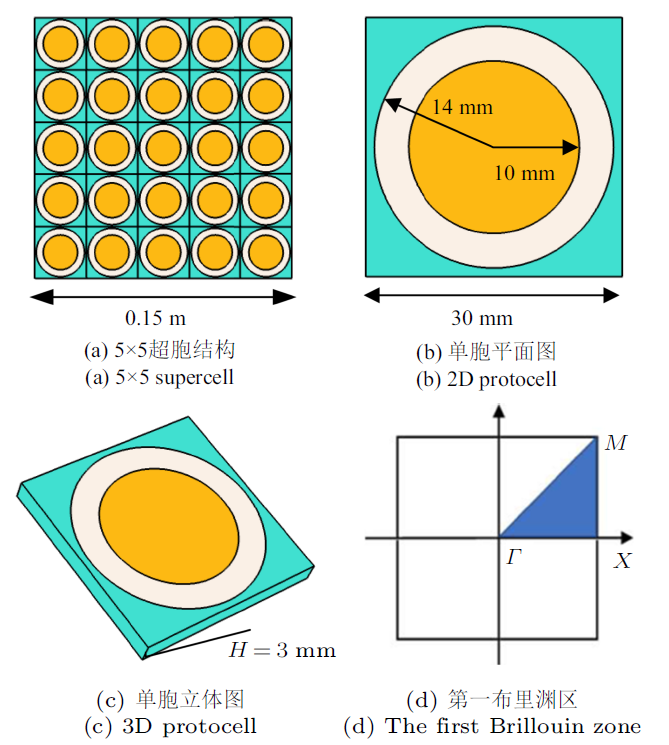
局域共振结构通常有两种构成方式: 一种是三组元结构, 即用软橡胶包覆重金属球(柱)后周期性埋没在基体材料中, 另一种是二组元结构, 即软橡胶柱周期性埋没在硬基体材料中. 这两种局域共振结构的构成方式均可以产生低频的局域共振带隙. 本文选用二维三组元结构形式, 图1所示为5 $\times$ 5超原胞声子晶体板以及其单胞示意图, 其中图1(a) $\sim\!$图1(d)分别为超原胞平面结构、单胞立体结构、单胞平面示意图和单胞第一布里渊区以及不可约布里渊区. 该单胞结构由包裹着软硅胶的金属芯体按照正方形晶格排列在基体材料中, 晶格常数为0.03 m, 中间的芯柱体半径为0.01 m, 橡胶层的外半径为0.014 m, 芯体材料为重金属材料金(材料参数见表1).图1
新窗口打开|下载原图ZIP|生成PPT图15 $\times$ 5超胞声子晶体板及单胞示意图
Fig.15 $\times$ 5 2D phononic crystal plate and its protocell structure
Table 1
表1
表1材料参数[29]
Table 1
 |
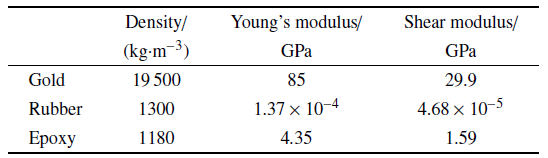新窗口打开|下载CSV
1.2 能带结构
对于给定的波矢, 通过有限元软件求解特征值得到相应的一系列特征频率, 从而最终得到该二维声子晶体的能带结构如图2所示.图2
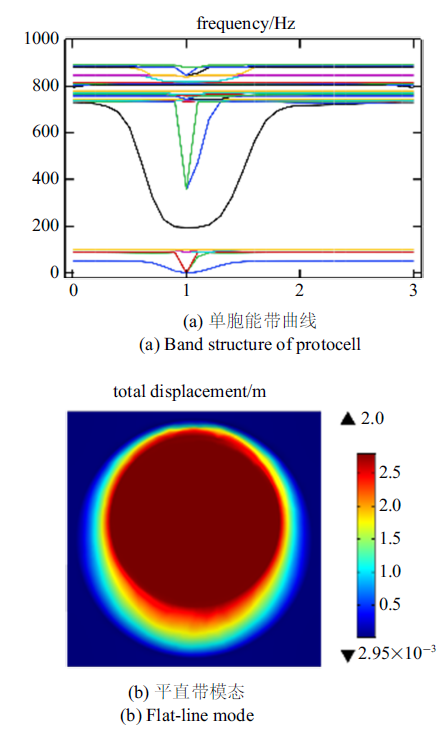
新窗口打开|下载原图ZIP|生成PPT图2单胞能带曲线及平直带振动模式
Fig.2Band structure of the unit and the vibration mode of flat strip
图中0-1-2-3分别对应简约布里渊区的$M-\varGamma -X-M$的方向, 通过图示能带曲线可知: (1) 局域共振型声子晶体其带隙频率远远低于相同晶格尺寸的Bragg带隙, 实现了"小尺寸控制大波长". (2) 局域共振型声子晶体带隙的边沿, 都存在一个平直带, 其意味着在绝大多数波矢方向上, 不同的波矢对应着相同的特征频率. 也就是说不同方向、不同大小的波场对应着相同的振动模式.
1.3 应力云图
从二维三组元局域共振型声子晶体带隙边缘平直带对应的振动模式可看出, 芯体的振动幅度远大于橡胶包覆层以及基体层, 此时振动主要集中在金属球, 即该平直带对应着金属球的局域化共振模式. 沿$\varGamma -X$和$X-M$方向分别给单胞局域共振型声子晶体施加$z$向和$y$向的单位加速度激励, 可得激励情况下的应力云图如图3所示. 图示可知, 局域共振型声子晶体带结构中存在平直带, 其对应振动模式为重金属芯体的局域共振, 此时内部波场存在局域共振现象. 且从任何方向输入的弹性波在平直带对应频率处均可以引起散射体的局域共振. 这一现象在超元胞结构中也同样存在, 可以应用于声子晶体能量采集相关研究.图3
新窗口打开|下载原图ZIP|生成PPT图3共振频率激励应力云图
Fig.3Stress cloud map with resonant frequency
2 缺陷态结构
声子晶体内部结构的周期性直接导致了带隙的产生, 如果在某一个局部破坏原有晶格结构的平移周期性以及对称性, 既引入一个缺陷, 则会改变原晶格结构的能带结构. 按照空间结构的不同, 通常将孤立的缺陷称为点缺陷; 一维连续分布的缺陷称为线缺陷; 二维连续分布的缺陷称为面缺陷. 研究表明[2,9], 引入缺陷后, 在完美声子晶体色散曲线图上会产生反映缺陷结构的新能带曲线, 部分缺陷结构的能带曲线进入无缺陷声子晶体带隙的频率范围, 这些带隙内的新能带通常被称为缺陷态, 相应的本征模被称为缺陷模. 当弹性波以缺陷带频率入射到声子晶体时, 会在声子晶体缺陷处周围出现安德森局域化效应, 使能量局域到缺陷处.2.1 超胞结构有限元模型
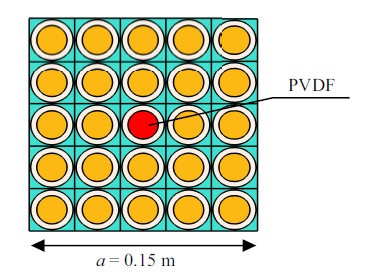
完美声子晶体一般可以通过移除局域共振型声子晶体中的散射体单元、改变散射体形状、材料等方式来形成点缺陷. 如图4所示, 本文选择5 $\times$ 5完美声子晶体板作为引入缺陷的超原胞结构, 利用超晶胞法结合有限元的方法来模拟声子晶体弹性波波导并计算能带结构. 通过在超晶胞的$x$, $y$方向施加Bloch周期边界条件, 在5 $\times$ 5完美声子晶体中心位置改变散射体材料(散射体材料选用聚偏氟乙烯-PVDF)来形成点缺陷.图4
新窗口打开|下载原图ZIP|生成PPT图4中心点缺陷超胞结构
Fig.4Supercell structure of central point defect
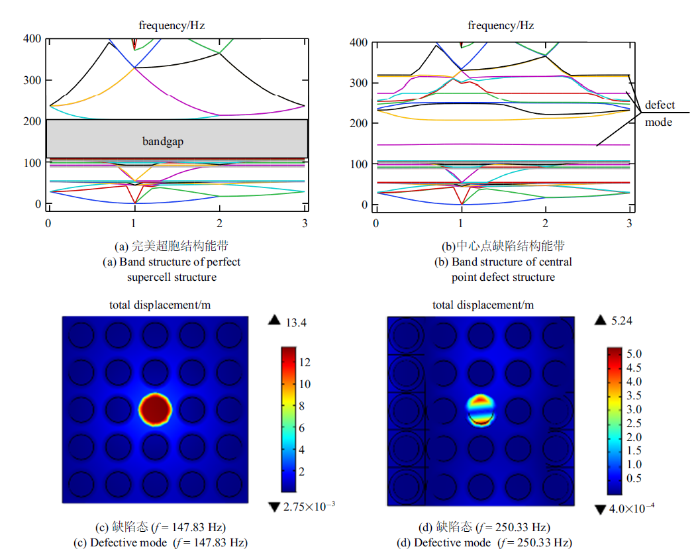
图5(a)和图5(b)分别展示了完美声子晶体超胞结构和点缺陷超胞结构的能带曲线, 对比可知, 在完全带隙中出现了147.83 Hz的缺陷带, 方向带隙内出现了250.33 Hz的缺陷带. 图5(c)和图5(d)则展示了缺陷点周围的弹性波聚焦现象.
图5
新窗口打开|下载原图ZIP|生成PPT图5完美及中心点缺陷结构能带曲线及缺陷态模式
Fig.5Band structures of perfect and central point defect structure and the defect patterns
2.2 缺陷态传输特性
通过对比完美板结构以及缺陷态结构的能带结构图可以发现, 在107 $\sim$ 202 Hz的完全带隙内, 因为缺陷态的引入而出现一条新的能带曲线其频率为147.83 Hz, 对应缺陷模中弹性波聚焦在缺陷点处. 同样的, 缺陷态能带结构中频率250.33 Hz处亦出现新的能带曲线且其对应缺陷模亦表现出缺陷态特性. 为了更为完整的说明缺陷态特性, 本文选择在板结构左侧引入$z$向激励, 即弹性波沿着$\varGamma -X$方向传播, 通过稳态激励下的真实位移变形图来反映声子晶体板结构的传输特性.图6分别展示了2个缺陷态频率处以及带隙内和通带传输曲线共振频率所对应的稳态位移振型图.
图6
新窗口打开|下载原图ZIP|生成PPT图6稳态位移振型
Fig.6Steady displacement results
从图6的位移振型图可以看出, 带隙内激励处的位移最大, 沿着弹性波的传播方向逐步衰减, 另外一边的接收端基本上衰减至零即弹性波没有沿着点缺陷超胞结构传播. 而通带内频率激励下的位移振型图中显示, 在接收端的共振位移远远大于结构其他部位的振幅, 说明通带频率下的波可以在声子晶体中传播, 且传播效率较高. 从缺陷态频率激励位移云图可发现, 点缺陷超胞结构中缺陷点处的振动幅度最大, 相比而言其他部位振幅基本趋近于零, 这正反映出弹性波在缺陷态超胞结构中传播的能量局域化现象, 为声子晶体周期性结构的能量采集研究奠定了理论基础.
3 振动俘能特性分析
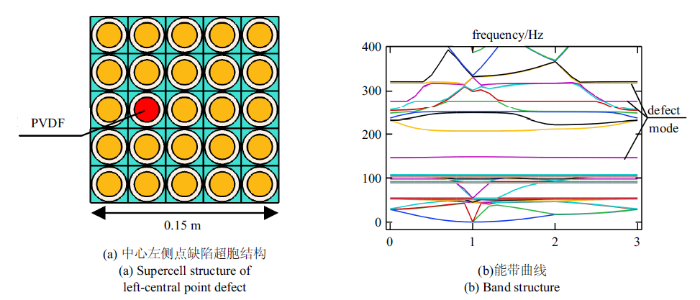
压电材料的压电性能集中体现为材料具有的弹性应变以及电极化之间的耦合效应, 声子晶体缺陷态在点缺陷频率处的能量局限特性会使得点 输出电压, 因此利用压电材料的压电效应来采集声子晶体缺陷处的这部分能量可以作为声子晶体应用于俘能领域的指导.考虑将完美声子晶体板的某一处散射体材料改为PVDF压电材料, 从而形成缺陷以达到能量集中的目的. 通过将二维声子晶体板中心左侧散射体材料替换为PVDF材料来引入缺陷态, 并利用超原胞以及有限元方法计算其能带结构如图7所示.
图7
新窗口打开|下载原图ZIP|生成PPT图7点缺陷超胞结构及能带曲线
Fig.7Point defective supercell and its band structure
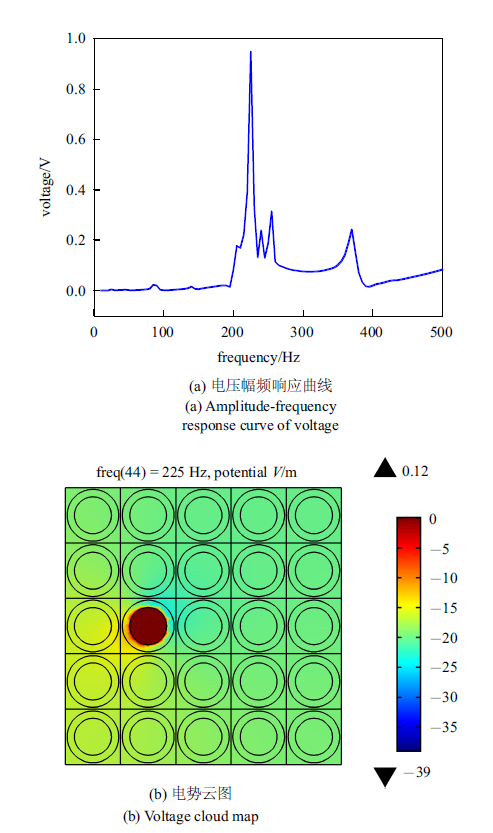
相比于原超胞结构的能带曲线, 很容易发现在频率148 Hz/225 Hz/260 hz/330 Hz等出现新的色散曲线. 在声子晶体板下边缘施加幅值为1 mm的$z$向位移激励, 设置瑞利阻尼为$\alpha =7$, $\beta =10^{-5}$, 外接负载电阻为$1.0\times 10^{9} \Omega $, 同时使弹性波沿着$X-M$方向传播, 则可得到电压的幅频响应输出如图8所示, 图示可知电压在缺陷态共振频率处达到峰值, 缺陷态225 Hz频率对应电势云图表明在缺陷模对应频率处存在能量集中现象.
图8
新窗口打开|下载原图ZIP|生成PPT图8电压幅频响应曲线及225Hz电势云图
Fig.8Voltage amplitude-frequency response curve and the voltage cloud map of 225 Hz
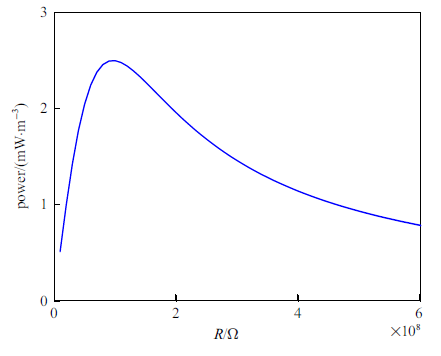
根据电压幅频曲线可知, 电压在上述几个缺陷态频率处取得峰值, 体现了缺陷态能量集中的特性, 说明缺陷态频率对应的输出电压优于一般的通带共振频率从而适合作为该声子晶体板结构的能量采集频率. 对缺陷态225 Hz对应的输出电压与外接负载电阻之间的关系进行有限元仿真分析, 结果如图9所示, 可得最优外接负载电阻为$0.9\times 10^{8} \Omega $.
图9
新窗口打开|下载原图ZIP|生成PPT图9电压随负载电阻的变化曲线
Fig.9Variation curve of voltage with load resistance
上述结果证明通过引入缺陷态以及压电材料可将压电声子晶体振动的机械能集中到点缺陷处, 并且当外激励与点缺陷处的共振频率相一致时候可以得到较高电压输出, 然而其缺点在于峰值电压对应频带较窄, 而环境振动的频率是分散的, 因此如何扩展点缺陷声子晶体板的响应频带需要进一步优化. 考虑引入双点缺陷来构造出更多的缺陷模, 以更好地匹配环境中的频率范围. 如图10所示, 构建两种点缺陷声子晶体超胞结构, 分别对应模式A和模式B.
图10
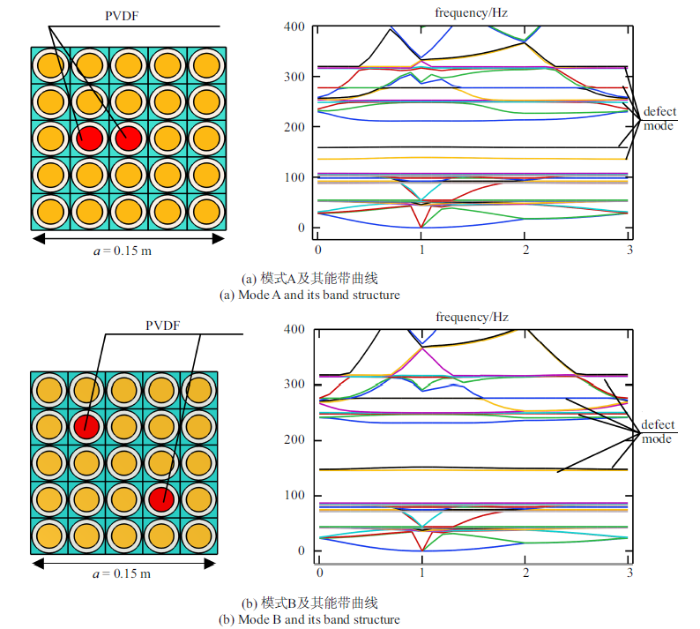
新窗口打开|下载原图ZIP|生成PPT图10两种点缺陷声子晶体超胞结构及其带隙特性
Fig.10Two kinds of supercell structure and its bandgaps
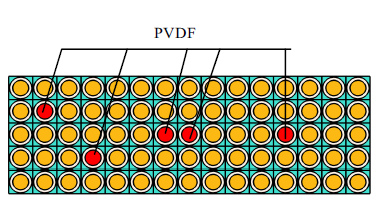
通过对比模式A的能带曲线与完美声子晶体能带曲线可以发现, 完全带隙内缺陷模对应频率为140 Hz, 153 Hz, 2-3 ($X-M)$方向带隙内出现新的色散曲线频率为: 213 Hz, 260 Hz, 270 Hz, 318 Hz等; 模式B所对应完全带隙内缺陷模对应频率为147 Hz, 151 Hz, 2-3 ($X-M)$方向带隙内新的色散曲线对应频率为: 235 Hz, 275 Hz, 330 Hz. 综合考虑, 本文构造一种新型声子晶体板结构如图11所示, 其结构由3块具有不同点缺陷形式的5 $\times$ 5超胞元结构通过横向排列组合而成一块5 $\times$ 15的薄板结构.
图11
新窗口打开|下载原图ZIP|生成PPT图11新型声子晶体板缺陷态结构
Fig.11New defective phononic crystal plate
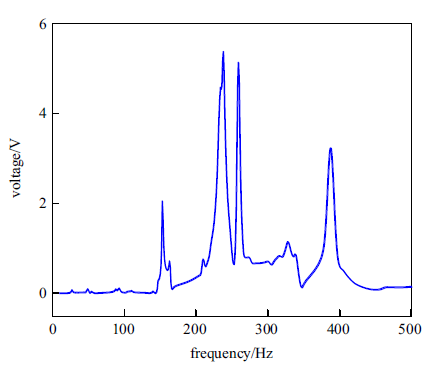
对缺陷态声子晶体板进行激励, 其谐响应分析结果如图12所示. 由图示可知, 电压峰值对应频率与各个声子晶体缺陷态结构的缺陷态频率可以较好的对应, 且该结构得到的电压峰值频响区间较宽. 基于频响曲线, 分别在频率为153 Hz, 235 Hz, 260 Hz以及387 Hz处对板结构施加幅值为1mm的位移激励, 阻尼同上, 外接负载电阻为$0.9\times 10^{8} \Omega $, 分析其俘能特性, 结果如图13所示. 结果表明, 通过在不同区域引入不同缺陷态得到不同的共振频率以及缺陷模, 可以克服单个超胞结构的峰值电压对应频带过窄的问题, 能够实现多缺陷态缺陷模对应的频率响应, 即拓宽了俘能器的工作频带, 从而适应振动环境中较宽的频率范围.
图12
新窗口打开|下载原图ZIP|生成PPT图12新型板结构电压幅频响应曲线
Fig.12Voltage response curve of new plate structure
图13
新窗口打开|下载原图ZIP|生成PPT图13新型板结构时域分析
Fig.13Transient analysis of new plate structure
前面证明了所设计的新型板结构可以实现不同缺陷态频率之间的耦合, 拓宽共振频带. 为了对比在同样外激励下新型板结构相较于单个声子晶体超胞结构的优势, 图14所示为在225 Hz情况下施加幅值为1 mm的位移激励时两种板结构的对比. 结果表明, 在同样位移激励下, 新型板结构幅值稳定在1.6 V左右, 而声子晶体缺陷态超胞结构(中心左侧型缺陷态结构)输出电压为0.5 V, 输出电压提高了3.2倍. 因此上述所提出的新型板结构具有低频、宽频带、高效率的俘能特性.
图14
新窗口打开|下载原图ZIP|生成PPT图14新型板结构和单点缺陷态结构电压输出对比
Fig.14Comparison of voltage output of new plate structure and single point defective structure
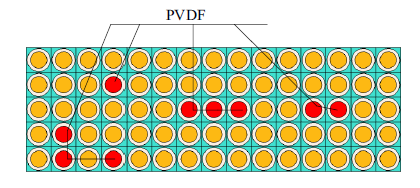
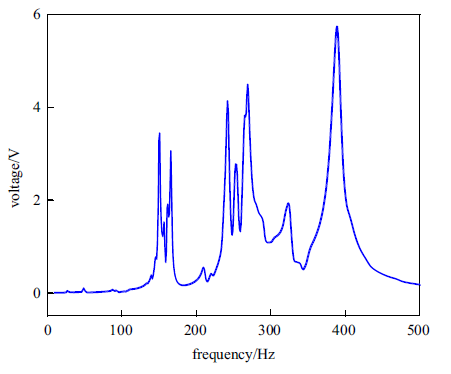
为了阐明点缺陷构型对前述所提出的并联板结构俘能器能量采集的影响, 进一步将具有更多缺陷态的超胞结构进行耦合并联, 构造出如图15所示的II型板结构. 对其施加同样位移激励得到电压幅频响应曲线如图16所示, 对比图12可以看出, 引入不同的缺陷态数量和构型, 可以进一步拓宽俘能带宽, 实现更好的俘能效果.
图15
新窗口打开|下载原图ZIP|生成PPT图15II型缺陷态声子晶体板结构
Fig.15Defective phononic crystal plate of type II
图16
新窗口打开|下载原图ZIP|生成PPT图16II型板结构电压幅频响应曲线
Fig.16Voltage response curve of type II plate structure
4 结论
本文设计了一种由圆柱形散射体嵌入环氧树脂基体而组成的5 $\times$ 5声子晶体超胞结构, 利用有限元方法计算了完美声子晶体结构和缺陷态声子晶体结构的能带曲线、传输特性以及电压响应. 最终提出两种二维三组元局域共振型声子晶体板结构, 将不同缺陷态下的电压峰值区域并联在一起以达到拓宽共振频率的效果, 使得环境中所存在的低频宽带能量得以充分的利用. 主要得到以下几点结论:(1) 通过对比不同频率(带隙内频率、通带内频率、缺陷态频率)下中心点缺陷超胞结构的稳态位移振型, 结果表明: 缺陷态频率激励作用下结构存在能量局域化现象, 且集中在点缺陷处, 为能量采集研究奠定了理论基础.
(2) 由不同点缺陷构型的5 $\times$ 5超胞结构组合而成的并联板结构, 能够克服单个超胞结构频带过窄的缺点, 实现拓宽频带的目的, 从而更加适应较宽频带的振动环境.
(3) 基于两种不同点缺陷构型的声子晶体超胞并联板结构的分析结果, 引入不同的缺陷态数量和构型, 可以进一步拓宽俘能带宽, 实现更好的俘能效果.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
URLPMID [本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
