环形槽对通气空泡融合的促进作用分析1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

孙龙泉^,²⁾, 颜皓, 马贵辉^,³⁾, 赵纪鹏哈尔滨工程大学船舶工程学院, 哈尔滨 150001

ANALYSIS OF THE PROMOTING EFFECT OF ANNULAR GROOVE ON THE COALESCENCE OF VENTILATED CAVITY¹⁾

Sun Longquan^,²⁾, Yan Hao, Ma Guihui^,³⁾, Zhao JipengCollege of Shipbuilding Engineering, Harbin Engineering of University, Harbin 150001, China

通讯作者: 2) 孙龙泉, 副教授, 主要研究方向: 水下发射, 空泡动力学, 流固耦合分析. E-mail:sunlongquan@hrbeu.edu.cn;3) 马贵辉, 讲师, 主要研究方向: 流动控制, 多相流, 水下发射. E-mail：maguihui@hrbeu.edu.cn

收稿日期:2020-08-4接受日期:2020-11-9网络出版日期:2021-02-07

基金资助:

1) 基础加强计划技术领域基金项目.2019-JCJQ-JJ-293
国家自然科学基金企业创新发展联合基金重点支持项目.U20B2005
黑龙江省博士后面上资助项目资助.002010830607

Received:2020-08-4Accepted:2020-11-9Online:2021-02-07
作者简介 About authors

摘要
航行体出水过程中肩部的自然空化将影响航行体的载荷分布及出水姿态,工程上常采用肩部开孔通气的方式改善航行体表面的力学环境, 进而解决此类问题.本文针对水下航行体通气空泡周向融合效果不理想问题, 基于有限体积法,采用VOF (volume of fluid)多相流模型和动态铺层的动网格技术,数值研究了排气孔下游增加小尺度环形凹槽促进空泡融合的作用机制,以及不同发展阶段、不同工况下环形凹槽对空泡融合的促进作用. 结果表明,凹槽可以有效改善通气空泡的融合效果.运动坐标系下来流经过环形凹槽时因为流动膨胀发生了边界层的流动分离,其诱导产生的卷吸作用一方面迟滞了空泡的轴向发展,促进空泡产生周向尺寸更大的剪切涡并沿周向膨胀发展,另一方面将部分通气气体吸入环形凹槽,吸入槽内的气体通过挤压破碎实现了周向融合,且槽内融合气泡溢出下泄促进融合边界上移. 此外,凹槽可以通过改善空泡内部的流动状态,使空泡的形态和内部压力在不同工况下都更加稳定.
关键词： 水下航行体;均压通气;空泡融合;环形槽;剪切涡

Abstract
The load distribution and the water-existing attitude of the vehicle will be affected by the natural cavitation on the shoulder of vehicles during the water-exit process. In engineering, active ventilation by opening vent at shoulder is often employed to improve the mechanical environment of vehicle surface so as to solve such problems. This article is aimed at solving the problem that the ventilated cavity circumferential coalescence of underwater vehicles is unsatisfactory. Using the VOF (volume of fluid) multi-phase flow model and dynamic grid technique of dynamic layering based on finite volume method, the mechanism of adding a small-scale annular groove at the downstream of the vent to promote the cavity coalescence was numerically investigated. And the promotion effect of the annular groove on cavity coalescence at different development stages and different working conditions was also studied. The results show that the cavity coalescence is greatly improved by the annular groove. Flow separation in boundary layer occurs when the incoming flow passes through the annular groove in the moving coordinate system because of flow expansion. The induced entrainment of annular groove, on the one hand, retards the axial development of cavity, and promotes the generation of a larger circumferential shear vortex along with expanding in the circumferential direction. On the other hand, part of the ventilation gas is sucked into the annular groove. The gas sucked into the groove is squeezed and broken contributing to the circumferential coalescence. The coalescence cavity in the groove overflows and leaks to promote the upward movement of the cavity coalescence boundary. In addition, under different working conditions, the shape and internal pressure of the cavity become more stable for the groove improving the internal flow state of the cavity.
Keywords：underwater vehicle;steady-pressure ventilation;cavity coalescence;annular groove;shear vortex

PDF (12694KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
孙龙泉, 颜皓, 马贵辉, 赵纪鹏. 环形槽对通气空泡融合的促进作用分析¹⁾. 力学学报[J], 2021, 53(2): 386-394 DOI:10.6052/0459-1879-20-271
Sun Longquan, Yan Hao, Ma Guihui, Zhao Jipeng. ANALYSIS OF THE PROMOTING EFFECT OF ANNULAR GROOVE ON THE COALESCENCE OF VENTILATED CAVITY¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(2): 386-394 DOI:10.6052/0459-1879-20-271

引言

航行体水下高速航行时, 流体流经航行体曲率变化较大的肩部时流速发生变化, 此位置出现低压区并引起自然空化, 形成覆盖航行体表面的自然空泡^[1]. 自然空泡由流体内低压形成, 其初生, 发展, 脱落和溃灭等现象改变了航行体表面的载荷分布^[2-5], 不仅影响航行体的水中航行轨迹, 还可能损毁出水航行体内精密元件, 并对航行体自身结构造成破坏^[6-10]. Reichardt^[11]最早提出主动通气技术, 通过空泡内注入不可凝气体提升泡内压力及其空间尺寸, 该方法被广泛证实可行^[12-13]. 人工通气的目标是产生稳定的空泡包裹航行体, 以改善其表面的载荷分布, 从而实现航行体的姿态调节^[1,14-15].

自然空泡和通气空泡涉及到复杂的多相流理论, 相关****对空泡的发展与融合进行了较丰富的研究. 王国玉等^[16]将气孔附近的旋涡结构分类, 通过孔板通气实验研究了空泡的发展机制. 王悦柔等^[17]采用数值仿真研究了电场作用下气泡上升过程中的演化规律以及载荷特性. 陈玮琪等^[18]建立了垂直空泡泡长变化数学方程, 导出了非定常空泡的泡长计算公式. 张忠宇等^[19]采用数值方法系统地研究了攻角, 头型和空化数等参数对空泡发展形态的影响. 秦勇^[20]采用流场插值的方法研究了波浪条件下均压通气空泡的演化规律. 张耐民等^[21-22]建立了基于空泡独立膨胀原理的多孔等压通气空泡形态计算模型, 研究了开孔数量和流场的无量纲参数对空泡融合的影响. 张孝石等^[23]通过高速摄像研究了通气航行体的云状空泡, 分析了不同空化数下空泡的脉动压力特性. 王聪等^[24]实验研究了受水流影响的喷射气流的发展形态, 得出不同水流流速下喷射气流的剪切涡的流动变化规律以及空泡压力脉动特征. 胡少峰^[25]和龚瑞岩^[26]采用缩尺实验和数值计算相结合的方法, 研究了不同弗劳德数和不同通气率下双层孔排气和孔缝联合排气的通气空泡形态特征及其发展过程. 马贵辉等^[27-28]利用Fluent研究了空腔等压排气的空泡发展机制, 并研究了不同结构参数下等压空泡的融合机理.

当前工程上的均压排气主要采用多孔排气技术, 传统的单层多孔排气技术存在通气空泡融合效果不明显, 融合速度缓慢, 空泡形态不稳定易脱落, 对通气参数要求苛刻等缺点^[25-26], 因此, 改善非定常空泡的周向融合效果, 维持通气空泡稳定的形态变得十分重要. 常用的改善通气效果的方式有双层孔通气和孔缝联合排气, 龚瑞岩^[26]与胡少峰^[25]的缩尺实验研究表明, 双层孔通气实现了空泡的周向融合, 但空泡表面呈现不光滑的绺状形态; 孔缝联合排气改善了融合效果, 但是通气装置的内部结构更为复杂, 对通气参数要求比较苛刻, 并且受下方出气孔的气流冲击影响, 通气空泡发展过程容易断裂脱落. 崔震宇^[29]研究了环形槽内部开孔的通气空泡, 结果表明环槽结构有利于消除孔前滞止高压和孔间分流而导致的通气空泡初生辫状结构形态, 促进通气空泡融合,但是槽内开孔通气又会造成航行体结构强度的减弱, 槽内融合气体的能量耗散又会导致流出环槽的空泡被来流冲击割断. 考虑到贴壁发展的非定常空泡内部存在受来流影响较大的旋涡, 本文尝试在通气孔下游设置一个小尺度周向凹槽, 在不增加结构复杂性、不破坏结构强度的前提下, 达到改善空泡周向融合的效果, 并探究其针对不同工况的适应性. 研究方法基于有限体积法, 利用VOF (volume of fluid)模型和动态铺层的动网格技术对航行体出水排气过程进行数值仿真, 通过对比有槽和无槽航行体在不同工况下的空泡发展形态, 探究凹槽对空泡周向融合的影响, 利用非定常空泡的形态发展和力学特性揭示环形凹槽促进空泡融合的作用机制.

1 计算域设置以及网格划分

如图1(a)所示, 数值仿真模型采用半圆球头回转体. 航行体沿其长度, 即全局坐标系的$z$轴正方向行进. 航行体直径$D=40$ mm, 总长$L=4.5D$, 孔槽联合方案中航行体周向均匀设置三十个通气孔, 孔直径为0.01$D$, 槽宽$d_{1}=0.125D$, 孔槽距$d_{2}=0.075D$, 运动坐标系的零点设置为航行体底部中心位置, $X$为航行体上点到航行体尾部垂向距离. 如图1(b)所示, 计算域沿径向划分为动域和静止域两部分, 两者分界面设置成"interface"滑移界面进行数据交换, 根据气泡非定常发展最大尺寸在航行体周围划出一个包裹域进行网格加密处理以捕捉精细化流场. 计算域外边界所有表面设置成压力出口边界条件, 通过UDF确定边界位置压力分布及相体积分数分布规律. 静域、动域以及包裹域的直径分别为8$D$, 3$D$和2$D$, 计算初始时刻航行体运动前头距水面3$L$, 气孔设置成质量入口边界条件, 航行体表面设置成壁面边界条件.

图1

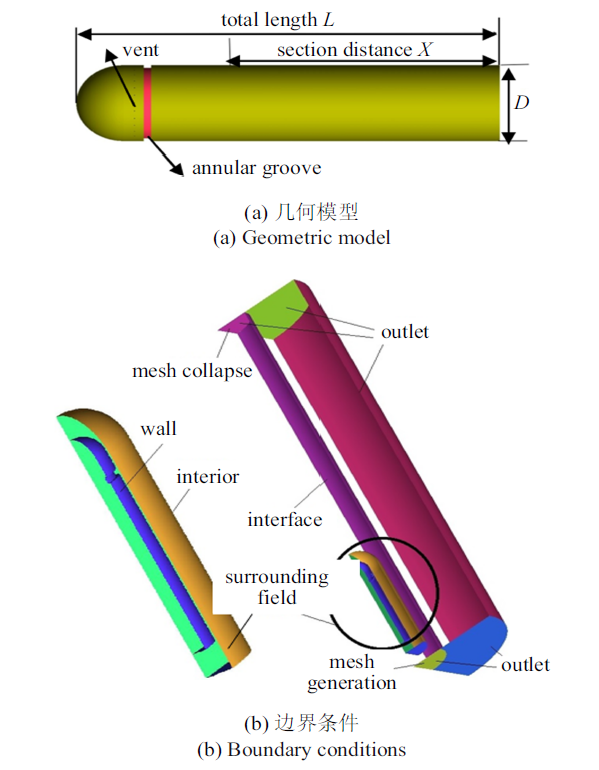新窗口打开|下载原图ZIP|生成PPT
图1几何及边界条件设置

Fig.1Geometry and boundary condition settings

流场选用结构化网格进行划分, 边界层设置10层, 增长率为1.2. 动域的上下边界设置为动网格层变区域, 通过UDF (user-defined function)控制航行体运动. 图2给出了不同网格数量下航行体头部压力的变化情况, 对比发现当网格总量达到200万时头部压力系数趋于恒定, 故本文的仿真网格选取200万的划分策略.

图2

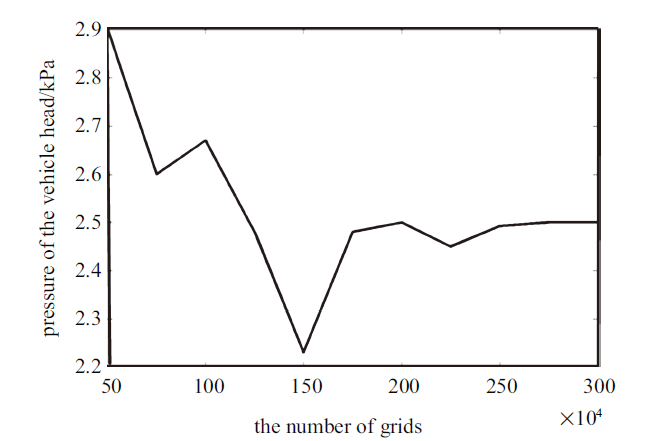新窗口打开|下载原图ZIP|生成PPT
图2不同网格数量下航行体头部压力

Fig.2Pressure of the vehicle head with different grid numbers

2 数值方法以及有效性验证

本文的数值仿真采用基于有限体积法求解N-S方程的方式进行, 多相流模型采用隐式VOF, 水平集法, 设置气相为主相, 水相为副相(定义$\alpha $表示相体积分数, $\alpha =1$表示纯气相, $\alpha =0$表示纯水相), 湍流模型选用RNG $k$-$\varepsilon $模型^[22], 压力速度耦合方法选用PISO算法, 时间离散格式选择二阶. 为方便叙述, 定义"YC"表示有槽航行体, "WC"表示无槽航行体. 部分文中无量纲参数包括通气率$Q_{i}$, 弗劳德数$Fr$, 无量纲时间$\bar{{T}}$, 无量纲压力$\bar{{P}}$定义如下

$\begin{eqnarray*} Q_{i} =\frac{Q_{iv} }{UD^{2}}, \quad Fr=\frac{U}{\sqrt {gD} }, \quad \bar{{T}}=\frac{tU}{D}, \quad \bar{{P}}=\frac{p}{\rho U^{2}} \end{eqnarray*}$

其中, $Q_{iv}$表示通气量, $U$表示航行体速度, $p$表示壁面监测点压力.

为验证数值方法的有效性, 针对无槽航行体出水排气过程进行数值仿真和缩尺实验, 其中缩尺实验在哈尔滨工程大学小尺度减压实验系统中进行, 实验工况为$Fr=4.79$, $Q_{i}=0.025$. 图3给出了实验与仿真得到的气泡无量纲长度$l/L$ (气孔到泡尾部闭合区距离为泡长$l$,航行体长度为$L)$的时变曲线, 对比发现二者吻合程度良好, 表明本文选用的数值方法可以较好地模拟航行体出水非定常排气过程.

图3

新窗口打开|下载原图ZIP|生成PPT
图3实验与仿真空泡无量纲长度曲线

Fig.3Experiment and simulation cavity length

3 环形槽作用机理及结果分析

3.1 环形槽促进空泡融合的作用机制

为了研究环形槽对气泡周向融合的影响, 本文对单排孔方案有槽、无槽航行体出水排气的结果进行对比研究. 图4给出了$Fr=7.94$, $Q_{i}=0.020$条件下各特征时刻空泡形态, 根据气泡发展特点, 可以将通气空泡的融合过程分为以下三个阶段:

(1) 通气空泡以未融合的辫状形态沿壁面轴向推进的空泡初生阶段 (如图4(a)中$\bar{{T}}=1.25$$\sim$4.375);

(2) 通气空泡轴向发展受阻, 以周向融合为主的空泡周向发展阶段 (如图4(a)中$\bar{{T}}=4.375$$\sim$6.25);

(3) 通气空泡周向融合后以融合空泡的形态轴向发展的融合增长阶段 (如图4(a)中$\bar{{T}}=6.25$$\sim$22.5).

图4

新窗口打开|下载原图ZIP|生成PPT
图4$Fr=7.94$, $Q_{i}=0.020$三维泡型

Fig.43D cavity shape at $Fr=7.94$, $Q_{i}=0.020$

其中空泡初生阶段较短, 图5(a)给出了$\bar{{T}}=2.5$时刻有、无槽航行体通气空泡初生阶段的泡内流线. 对于带槽航行体, 来流的贴壁边界层经过形状突变的台阶状凹槽上缘时, 发生流动膨胀^[30], 继而产生流动分离, 形成流速不同的内外边界层. 流速大的外侧自由边界层随来流向下游发展, 流速低的内侧边界层受外侧边界层的剪切影响在槽内形成大尺度的旋转涡. 图5(b)给出了$\bar{{T}}=2.5$时刻的空泡形态, 通气空泡流出通气孔后受来流冲击向下流动, 并被来流分隔不容易融合, 贴壁向下发展经过凹槽后, 凹槽诱导产生的旋涡将通气空泡卷吸进槽内, 空泡在槽内挤压破碎并在槽内实现周向融合. 由于高速来流冲刷, 且通气量比较少, 因此槽内的融合气泡难以溢出, 初生空泡依旧以辫状形态向下发展. 图5(a)虚线圈中的流线显示, 环形槽的卷吸作用使通气空泡在凹槽下游比较靠上的位置就开始了贴壁逆向流动, 卷吸作用促进了通气空泡的轴向流动分离, 阻滞了通气空泡的轴向推进. 来流穿过相邻两股通气空泡, 其边界层对通气空泡的剪切作用使通气空泡发展过程中发生了周向流动分离, 并形成了对称的剪切层涡. 图5(c)虚线圈内流线显示, 受到环形槽的影响空泡轴向推进速度减缓, 周向扩张增强, 这就导致有槽航行体形成周向尺寸更大的对称剪切层涡涡对, 相邻辫状空泡更易周向发展融合. 有槽工况下气泡动能的损耗导致有槽航行体的空泡与水相的碰撞和扰动弱于无槽航行体, 所以其空泡含气量更高, 泡尾厚度更小, 空泡形态更加稳定.

图5

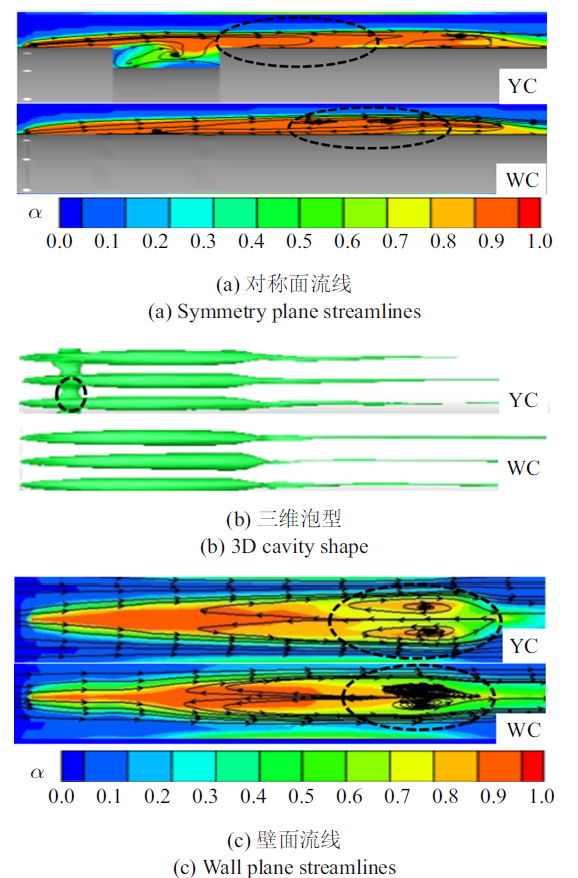新窗口打开|下载原图ZIP|生成PPT
图5$\bar{{T}}=2.5$时刻航行体表面初生空泡

Fig.5Primary cavity on the vehicle surface at $\bar{{T}}=2.5$

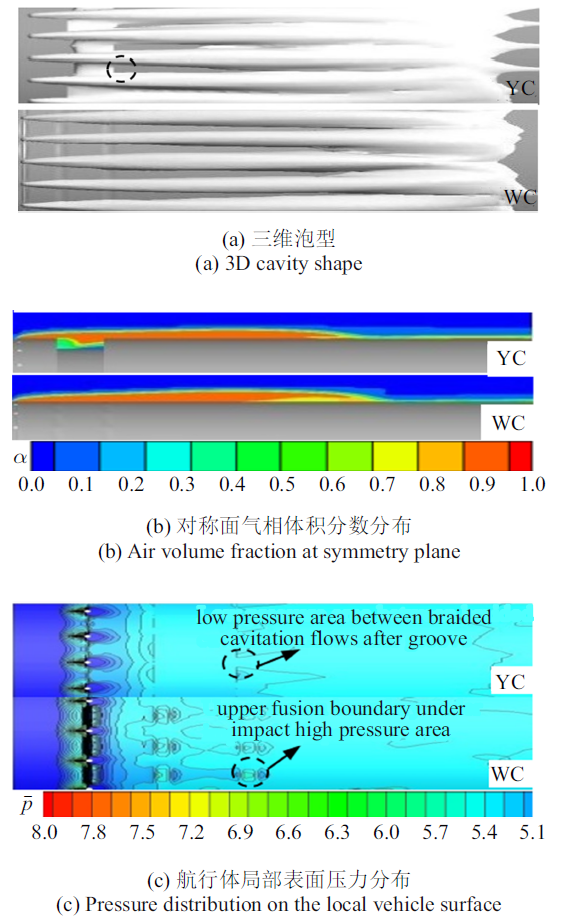
通气空泡经过初生发展阶段后进入周向融合发展阶段. 图6给出了两个特征时刻有槽、无槽航行体表面压力沿轴向分布, 对比发现, 有槽航行体空泡泡内压力梯度比无槽航行体的泡内压力梯度更大, 更大的泡内压力梯度导致有槽航行体的通气空泡轴向推进受到的阻滞作用更强, 更有利于空泡周向发展融合. 无槽航行体泡尾内外压差更大, 通气空泡内部压力梯度更小, 从而使得均压气体向航行体尾部方向较快速推进, 在剪切层涡涡对和泡尾逆向射流的作用下汇聚于泡尾局部区域. 图7给出了有、无槽方案$\bar{{T}}=6.25$时刻航行体表面三维泡型、相体积分数以及压力的分布情况, 对比发现, 开槽航行体相邻辫状空泡流过凹槽后周向尺度更大, 随着持续通气, 空泡融合上边界上移. 无槽航行体泡尾较大的内外压差导致逆向射流较大, 更大的泡内逆向射流携带更多的水射入泡内, 导致无槽航行体泡内水含量较开槽航行体更大. 由图7(c)发现, 水流流经环形凹槽下缘处时发生流动分离, 在槽下缘附近产生局部低压效应. 由于$\bar{{T}}=6.25$时凹槽已经被气体灌满, 凹槽附近辫状空泡内仍然存在的卷吸作用不断携带气体灌入凹槽, 在凹槽下缘低压区的诱导下, 多余的气体会在图7(a)虚线框所示的槽下缘与辫状空泡流交界压力梯度较高的位置溢出下泄, 增大未融合辫状空泡流的周向尺寸, 进而促使相邻两辫状空泡流完全融合.

图6

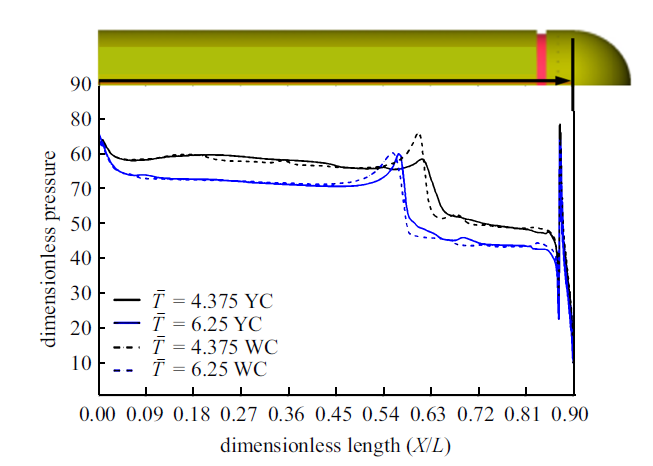新窗口打开|下载原图ZIP|生成PPT
图6对称面无量纲压力沿轴向分布

Fig.6Axial distribution of dimensionless pressure

图7

新窗口打开|下载原图ZIP|生成PPT
图7$\bar{{T}}=$6.25时刻航行体表面流场

Fig.7Flow field of the vehicle surface at $\bar{{T}}=6.25$

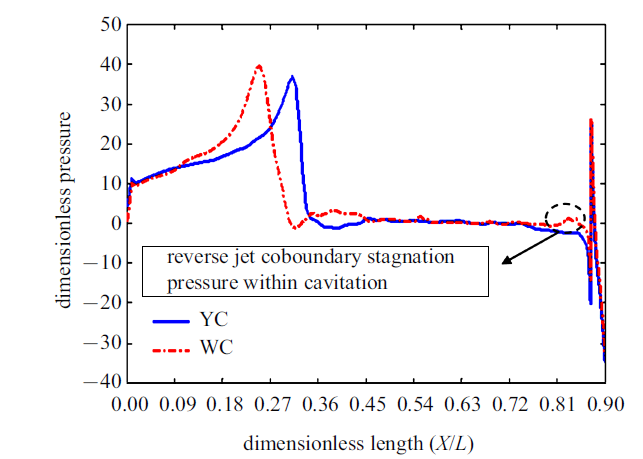
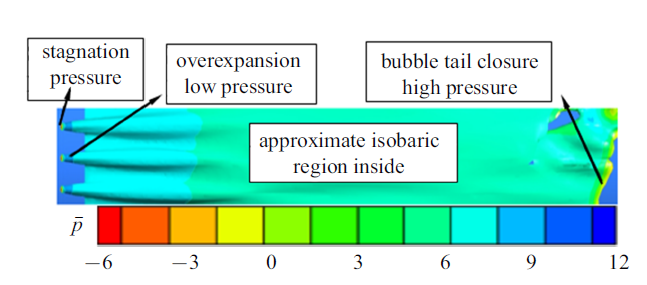
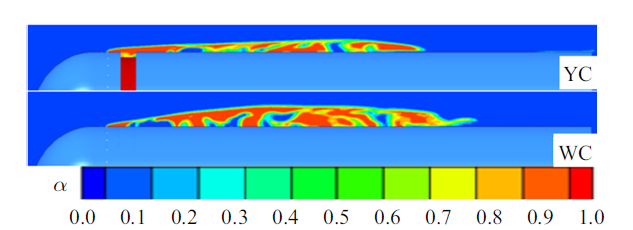
空泡经过充分周向融合后开始进入以大空泡的形态轴向发展的融合增长阶段. 图8表征了该阶段空泡轴向压力分布, 参照前文图4的特征时刻空泡形态, 无槽航行体融合空泡的融合上边界遇上游来流冲击, 难以继续向上发展, 因此通气空泡前部区域仍呈现辫状形态, 并且两相邻辫状空泡间融合上边界位置基本稳定. 凹槽内气体溢出下泄, 开槽航行体空泡融合上边界与槽内气体融合形成融合上边界为槽上缘的融合空泡. 持续注入泡内的气体将获得的动能传递给融合的大空泡, 空泡克服泡尾闭合高压和壁面冲击射流阻碍沿着航行体轴向增长. 此阶段内空泡形态基本稳定, 空泡主要表现为沿轴向拉长. 图9给出了$\bar{{T}}=22.5$时刻有槽航行体的外表面空泡形态以及压力分布, 参照图8的空泡沿轴向压力分布, 空泡按压力分布可以分为图9中的几个区域: (1)孔前气流受来流挤压形成的孔前滞止高压区; (2)来流在孔后流动分离造成的过膨胀低压区; (3)空泡周向融合充分后, 压力趋于稳定形成的近似低压区; (4)空泡泡尾闭合于壁面形成的闭合高压区. 槽的卷吸和槽上缘低压效应作用使得排气孔后凹槽前辫状空泡内气体向下游发展时有一定的加速作用, 所以开槽航行体过膨胀低压压力峰值较无槽航行体更小. 图10给出了$\bar{{T}}=22.5$时刻两种航行体对称面内的气相体积分数分布, 无槽航行体$\bar{{T}}=22.5$时泡内射流携带的水影响范围距离孔较近, 且此区域空泡形态为辫状, 所以无槽航行体泡内气体刚流过过膨胀低压区后即与逆向射流上边界相遇, 速度方向相反的逆向射流和来流气体挤压碰撞形成图8虚线框中逆向射流上边界的滞止高压. 开槽航行体逆向射流轴向影响范围更小, 射流上边界位于槽后, 此位置通气空泡已经周向融合, 所以未形成像无槽航行体那样的泡内逆向射流前端滞止高压, 从对称面气相体积分布看, 融合空泡增长阶段开槽航行体通气空泡泡厚更小, 无槽航行体泡厚更大.

图8

新窗口打开|下载原图ZIP|生成PPT
图8$\bar{{T}}=22.5$对称面无量纲压力沿轴向分布

Fig.8Axial distribution of dimensionless pressure at $\bar{{T}}=22.5$

图9

新窗口打开|下载原图ZIP|生成PPT
图9$\bar{{T}}=22.5$有槽航行体空泡外表面形态

Fig.9Out surface shape of the YC vehicle cavity at $\bar{{T}}=22.5$

图10

新窗口打开|下载原图ZIP|生成PPT
图10$\bar{{T}}=22.5$对称面气相体积分数分布

Fig.10Air volume fraction in symmetry plane at $\bar{{T}}=22.5$

3.2 不同工况下环形槽对空泡融合的作用

通气率和弗劳德数是影响垂直出水航行体空泡形态及发展过程的重要因素, 本文首先控制弗劳德数$Fr=7.94$不变, 改变通气率$Q_{i}$为0.015, 0.020, 0.025, 再控制通气率$Q_{i}=0.020$不变, 改变弗劳德数$Fr$为4.76, 6.35, 7.94, 分别针对有槽和无槽的航行体出水过程进行了仿真, 图11和图12给出了$\bar{{T}}=22.5$不同方案下空泡充分发展时刻的流场结果.

图11

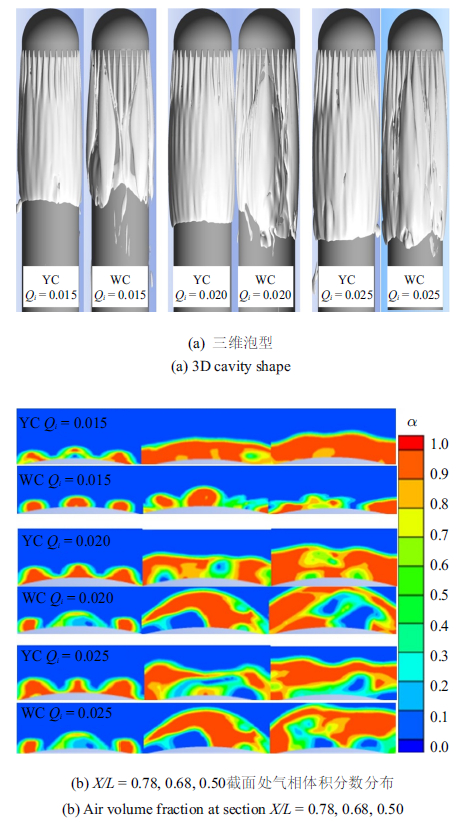新窗口打开|下载原图ZIP|生成PPT
图11$\bar{{T}}=22.5$时刻不同$Q_{i}$下有槽、无槽情况的空泡对比

Fig.11Cavity comparison between YC and WC cases at different $Q_{i}$ at $\bar{{T}}=22.5$

图12

新窗口打开|下载原图ZIP|生成PPT
图12$\bar{{T}}=22.5$时刻不同$Fr$下有槽、无槽情况的空泡对比

Fig.12Cavity comparison between YC and WC cases at different $Fr$ at $\bar{{T}}=22.5$

对比图11(a)所示的有、无槽情况下的空泡形态可以看出, 通气率$Q_{i}$较小时, 无槽航行体的通气空泡以周向分离的辫状形态沿轴向发展, 空泡融合效果较差, 未被气膜覆盖的航行体表面将暴露在水中承受流体动力冲击. 随着通气率的增大, 空泡的融合效果有一定改善, $Q_{i}=0.025$时, 已经出现了包裹住无槽航行体的大片融合空泡, 然而空泡融合的周向均匀性较差, 从图11(b)的气相体积分数分布可以看出, 随着通气率的增大, 空泡贴壁内侧出现了大片水相, 空泡变得不稳定并存在脱落的风险. 相较于无槽航行体, 有槽航行体在不同通气率下空泡外表面更加光滑, 气泡周向融合位置更靠近头部且周向分布均匀, 上下融合边界更为整齐. 参考图11(b)还可以发现, 有槽航行体在相同通气率情况下形成的空泡对航行体表面的贴附效果较好, 泡内含水量更少, 这在一定程度上确保了空泡对模型表面的保护作用. 当通气率升高时, 空泡轴向、径向尺寸明显增大, 相较无槽航行体情况空泡周向均匀性及稳定性明显改善.

带排气航行体垂直运动过程中弗劳德数的变化体现了航行体运动速度对气泡发展的影响. 在$Q_{i}$控制为0.020的情况下, 本文开展了$Fr=4.76$, 6.35, 7.94工况下的航行体出水排气仿真. 对比图12(a)和图12(b)给出的气泡形态及气相体积分数分布可以看出, 在不同$Fr$数下, 有槽航行体的空泡厚度更薄, 表面更光滑, 含气量更多, 通气空泡的贴壁效果依旧优于无槽航行体. 通过图12(a)和图12(b)还可以发现, 随着$Fr$数的增大, 在高速来流的冲击下, 两种航行体的表面空泡也随之变薄, 无槽航行体的气泡融合位置的上边界不断后移, 而有槽航行体由于槽内空泡和槽外周向融合空泡实现融合, 其上边界始终维持在凹槽上边缘.

4 结论

本文基于有限体积法数值研究了排气孔下游增加小尺度环形凹槽促进出水航行体通气空泡融合的问题, 得到以下结论:

(1)环形槽改变了航行体表面的流场分布, 其诱导产生的旋涡将通气空泡卷吸进槽内, 槽内空泡挤压破裂实现周向融合. 在空泡融合阶段, 空泡从低压处溢出下泄扩大了辫状空泡周向尺寸, 并且促进融合上边界上移.

(2)凹槽卷吸作用造成空泡动能损耗和抗剪切能力减弱, 来流边界层剪切壁面空泡, 形成周向尺寸更大的剪切层涡并沿周向扩张, 促进周向融合, 动能的损耗以及较高含气量使空泡形态更加稳定.

(3)有槽航行体融合增长的空泡因为在凹槽处已经充分融合, 所以其泡内含水相逆向射流的轴向影响范围小于无槽航行体.

(4)环形凹槽对通气空泡的发展融合具有明显改善作用. 有槽航行体形成的空泡融合覆盖面更广, 泡厚更薄, 空泡表面更光滑, 融合边界更加整齐, 空泡含气量更大, 空泡更加稳定而不易脱落. 在不同的工况下, 有槽航行体均表现出较好的融合性能.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

王一伟, 黄晨光, 杜特专等. 航行体垂直出水载荷与空泡溃灭机理分析
力学学报, 2012,41(1):39-48

[本文引用: 2]

( Wang

Yiwei

, Huang

Chenguang

, Du

Tezhuan

, et al. Mechanism analysis about cavitation collapse load of underwater vehicles in a vertical launching process
Chinese Journal of Theoretical and Applied Mechanics. 2012,44(1):39-48 (in Chinese))

[本文引用: 2]

[2]

Shao

, Balakrishna

, Yoon

. et al. Effect of mounting strut and cavitator shape on the ventilation demand for ventilated supercavitation
Experimental Thermal And Fluid Science, 2020,118:10173

[本文引用: 1]

[3]

Ludar

, Gany

. Experimental study of supercavitation bubble development over bodies in a duct flow
Journal of Marine Science and Engineering, 2020,8(1):1-11

[4]

Smith

, Venning

, Pearce

. et al. The influence of fluid-structure interaction on cloud cavitation about a stiff hydrofoil. Part 1
Journal of Fluid Mechanics, 2020,896:1-35

[5]

权晓波, 李岩, 魏海鹏等. 航行体出水过程空泡溃灭特性研究
船舶力学, 2008,12(4):545-549