李静^,*,2), 佟晓龙^?, 杨烁^?, 仇原鹰^**西安电子科技大学机电工程学院, 西安 710071
^?中航工业沈阳飞机设计研究所, 沈阳 110035

A MULTIAXIAL HIGH CYCLE FATIGUE LIFE PREDICTION MODEL CONSIDERING THE EFFECT OF MEAN STRESS FOR TENSION-TORSION LOADINGS WITH SAME FREQUENCY ¹⁾

Li Jing^,*,2), Tong Xiaolong^?, Yang Shuo^?, Qiu Yuanying^**School of Mechatronic Engineering, Xidian University, Xi'an 710071, China
^?AVIC Shenyang Aircraft Design & Research Institute, Shenyang 110035, China

通讯作者: 2)李静, 讲师, 主要研究方向: 金属材料的多轴疲劳损伤特性. E-mail:lijing02010303@163.com

收稿日期:2020-03-4接受日期:2020-03-4网络出版日期:2020-09-18

基金资助:

1)陕西省自然科学基础研究计划.2019JQ-353 中央高校基本科研业务费.JB180402 国家自然科学基金.51601221

Received:2020-03-4Accepted:2020-03-4Online:2020-09-18
作者简介 About authors


摘要
目前基于临界平面理论的高周疲劳寿命预测模型, 大都充分考虑了法向平均应力对材料疲劳寿命的影响, 但是没有有效反映剪切平均应力对疲劳寿命的影响. 通过分析7075-T651铝合金的试验数据发现, 与法向拉平均应力类似, 剪切平均应力同样对材料的疲劳寿命产生不利影响. 因此, 如果寿命预测模型中忽略剪切平均应力的影响, 存在明显剪切平均应力加载工况下, 预测寿命可能偏于危险. 由此, 本文定义具有较大法向应力的最大剪应力范围平面为临界平面, 建立了一个能够同时反映法向和剪切平均应力影响的高周疲劳寿命预测模型, 并给出了模型中材料常数的确定方法. 新模型首先将基于应变的Fatemi-Socie准则, 推广到材料的高周疲劳寿命预测, 给出了Fatemi-Socie准则的应力表述形式. 然后, 引入剪切和法向Walker因子, 反映剪切和法向平均应力对材料疲劳寿命的影响. 剪切和法向Walker因子的取值都介于0和1之间, 不同取值反映了材料对剪切和法向平均应力敏感程度的不同. 新模型适用于范围内的金属塑性材料. 利用5种材料在12种存在平均应力加载工况下的试验数据, 对所建模型进行了试验验证, 结果表明预测结果与试验结果吻合良好, 绝大多数寿命预测结果分布在3倍误差带以内.
关键词： 多轴高周疲劳;平均应力;寿命预测;临界平面;Walker因子

Abstract
The influence of normal mean stress on fatigue life prediction has been well reflected for most of the critical plane-based high cycle fatigue life prediction models, whereas the effect of shear mean stress isn't well considered in these models. It is found that the fatigue life of 7075-T651 aluminum alloy is substantially reduced due to the existing of the shear mean stress by analyzing the experimental data of this aluminum alloy, which is similar to the effect of tensile mean stress. Therefore, nonconservative predictions maybe obtained under the loading paths with substantial shear mean stresses for these life prediction models ignoring the effect of mean shear stress. In order to estimate the fatigue life better, a new critical plane-based multiaxial high cycle fatigue life prediction model is proposed to take into account the effects of both normal and shear mean stresses. In the proposed model, the strain-based Fatemi-Socie criterion is first extended to the high cycle fatigue life prediction. And then a stress-based Fatemi-Socie criterion is developed. The shear and normal Walker factors are introduced in the developed criterion to consider the effects of shear and normal mean stresses, respectively. Both the shear and normal Walker factors vary from 0 to 1, which reflects the sensitivity of the material to shear and normal mean stresses. Procedures to determine the damage parameters acting on the critical plane and to calculate the constants contained in the proposed model are all presented. The proposed model is valid for the metallic materials with the ratio ${0.5<\tau _{-1} } / {\sigma _{-1} }<0.8$. Comparisons between test results of 5 kinds of metallic materials and model predictions under 12 types of loading paths with different mean stress levels showed that the proposed model presents relatively accurate predictions. Most of the predictions are fell within a life factor of $\pm $3.
Keywords：multiaxial high cycle fatigue;mean stress;life prediction;critical plane;Walker factor


PDF (1022KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李静, 佟晓龙, 杨烁, 仇原鹰. 考虑平均应力的同频拉扭多轴高周疲劳寿命评价方法 ¹⁾. 力学学报[J], 2020, 52(5): 1409-1421 DOI:10.6052/0459-1879-20-066
Li Jing, Tong Xiaolong, Yang Shuo, Qiu Yuanying. A MULTIAXIAL HIGH CYCLE FATIGUE LIFE PREDICTION MODEL CONSIDERING THE EFFECT OF MEAN STRESS FOR TENSION-TORSION LOADINGS WITH SAME FREQUENCY ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1409-1421 DOI:10.6052/0459-1879-20-066

引言

在工程实际中, 大多数机械和工程结构都是在复杂的多轴应力状态下工作, 因此, 多轴疲劳失效在机械和结构零件中极为常见^[1-3]. 目前, 对于单轴疲劳寿命预测, 国内外已有比较成熟的方法和理论^[4]. 与之相比, 多轴疲劳寿命预测无论在力学分析, 还是物理机制方面都更为复杂, 远没有像单轴疲劳那样全面、深入^[5].

从宏观上来说, 根据材料破坏时所承受载荷循环数的多少, 可将疲劳划分为低周疲劳(low cycle fatigue, LCF)和高周疲劳(high cycle fatigue, HCF), 如航空发动机轴、轮盘等多出现LCF破坏, 而发动机叶片多出现HCF破坏. 对于LCF破坏, 通常可观察到明显的塑性损伤, 一般采用应变作为寿命预测的损伤控制参量. 对于HCF破坏, 塑性损伤通常并不明显, 一般采用应力作为寿命预测的损伤控制参量. 概括来讲, 目前常用的多轴HCF寿命预测方法主要有应力准则、细观积分法和临界平面准则3类^[6]. 早期, 各国研究者基于静强度理论, 根据试验数据提出了一系列的等效应力准则, 如Gough准则^[7], Lee准则^[8]等. 随后, 基于偏应力张量第二不变量, 各国研究者建立了一系列的应力不变量准则, 如Crossland准则^[9]、Sines准则^[10]等. 虽然应力准则形式简单、应用方便, 但是该类准则多是经验模型, 物理意义并不明确, 不能反映疲劳裂纹萌生和扩展的优先平面.

Dang Van^[11]认为在细观尺度上, 材料内部临界体积内特征滑移带上的晶粒塑性变形导致疲劳裂纹萌生, 微观剪应力和静水应力加速滑移带生成和裂纹扩展. 基于此, Papadopoulos^[12]提出了细观积分法来预测材料的HCF寿命. 典型的细观积分法还有Liu-Zenner准则^[13]、Papuga准则^[14]等. 细观积分法从细观尺度来分析疲劳裂纹萌生扩展的影响因素, 具有一定的物理意义. 但是该类方法需对所有材料平面上的剪应力进行积分, 不便于工程应用.

临界平面的概念是建立在疲劳裂纹萌生和扩展的机制上, 具有一定的物理意义, 被普遍认为是分析多轴疲劳问题的一种行之有效的方法^[5]. 在分析大量HCF数据的基础上, Findley^[15]发现临界平面上的剪应力导致疲劳裂纹萌生, 法向应力加速疲劳裂纹扩展. 基于此, Findley^[15]定义最大损伤平面为临界平面, 考虑法向平均应力影响, 以临界平面上的剪应力幅和最大法向应力的线性组合为损伤控制参量, 来预测材料的HCF寿命. 在Findley研究的基础上, Matake^[16]、McDiarmid^[17]等定义最大剪应力范围平面为临界平面, 考虑法向平均应力影响, 也以临界平面上的剪应力幅和最大法向应力的线性组合为损伤控制参量来预测材料的HCF寿命. Susmel等^[18]、张成成等^[19]、Zhang等^[20]考虑了法向平均应力影响, 定义临界平面上的剪应力幅和最大法向应力的非线性组合为损伤控制参量, 分别提出了不同的HCF寿命预测模型. Wang等^[21]考虑了平均剪应力对疲劳寿命的影响, 进一步对Zhang等^[20]构建的寿命预测模型进行了修正. Matsubara等^[22]将应力不变量与临界平面准则相结合, 建立了一个新的HCF寿命预测模型. Liu等^[23]定义最大法向应力幅平面为临界平面, 并考虑了临界平面上法向平均应力的影响, 构建了一个适用于常幅加载的多轴高周疲劳预测模型. Wei等^[24]定义最大法向损伤平面为临界平面, 将Liu准则^[23]推广应用到多轴随机加载. 常幅多轴加载下, Wei等定义的临界平面退化为Liu等定义最大法向应力幅平面^[24]. 同大多数基于临界平面理论的HCF寿命预测模型一样, 不管是Matsubara准则还是Liu准则都没有充分考虑剪切平均应力对疲劳寿命的影响.

对于法向平均应力对材料疲劳寿命的影响, 各国研究者已基本取得共识, 即拉平均应力加速疲劳裂纹扩展, 对材料的疲劳寿命产生不利影响, 而压平均应力减缓疲劳裂纹扩展, 对材料的疲劳寿命产生有利影响. Marquis等^[25]针对脆性材料GRP 500钢和塑性材料C45钢, 进行了零平均应力和存在拉伸平均应力的扭转疲劳试验, 并进一步研究了最大剪应力范围平面上最大法向应力和静水应力对材料疲劳寿命的影响. 研究发现, 最大剪应力范围平面上的最大法向应力比静水应力更为显著地影响塑性材料的疲劳寿命.

本文基于临界平面理论, 首先将基于应变的Fatemi-Socie准则^[26]推广到材料的HCF寿命预测, 给出Fatemi-Socie准则的应力表述. 然后, 综合考虑法向平均应力和剪切平均应力对材料HCF寿命的影响, 将Walker因子^[27]引入到Fatemi-Socie准则的应力表述模型中, 提出一种新的多轴HCF寿命预测模型, 并给出了模型中临界平面和材料常数的确定方法. 结合剪切形式的Basquin方程, 对5种材料进行了疲劳寿命预测, 并和McDiarmid准则^[17]、张成成所建模型^[19], 考虑平均剪应力修正的Wang准则^[21], 以及Liu-Mahadevan准则^[23]进行了对比分析, 结果表明本文所建模型具有更好的HCF寿命预测精度.

1 多轴加载下光滑试件的应力分析

当光滑试件承受拉扭或弯扭加载时, 试件表面可看作是平面应力状态, 此时任意$t$时刻试件表面的应力状态可表示为

(1) $ \begin{eqnarray} \label{eq1} { \sigma }\left( t \right)=\left[ {{\begin{array}{c@{\qquad }c@{\qquad }c} {\sigma _x \left( t \right)} & {\tau _{xy} \left( t \right)} & 0 \\ {\tau _{xy} \left( t \right)} & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} }} \right] \end{eqnarray}$
式中, ${ \sigma }$为应力张量. 若加载波形为正弦波, 且为控制应力加载, 则

(2) $ \begin{eqnarray} \label{eq2} &&\sigma _x \left( t \right)=\sigma _{\rm a} \sin \left( {\omega t} \right)+\sigma _{\rm m} \end{eqnarray}$
(3) $ \begin{eqnarray} \label{eq3} \tau _{xy} \left( t \right)=\tau _{\rm a} \sin \left( {\omega t-\varphi } \right)+\tau _{\rm m} \end{eqnarray}$
式(2)和式(3)中, $\omega $为加载频率, $\sigma _{\rm a} $和$\tau _{\rm a} $分别为轴向和剪切加载应力幅, $\sigma _{\rm m} $和$\tau _{\rm m} $分别为轴向和剪切加载平均应力, $\varphi $为相位差.

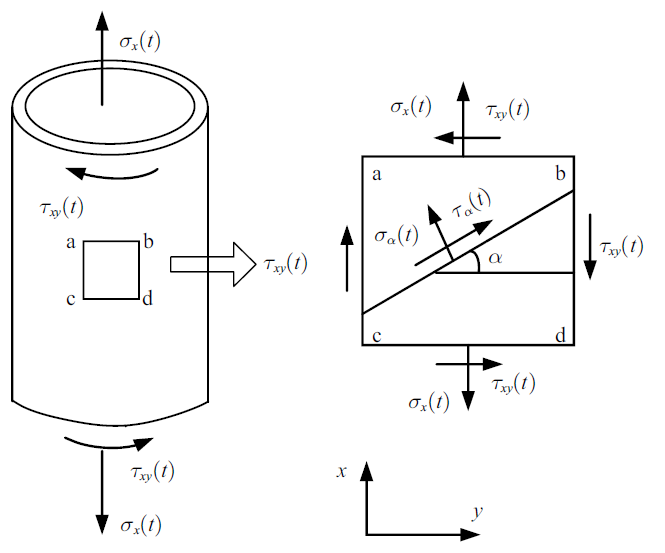
以图1所示拉扭加载为例, 由力平衡方程可得与$y$向夹角为$\alpha $的斜面上的法向和剪切应力分别为

(4) $ \begin{eqnarray} \label{eq4} &&\sigma _{\alpha } \left( t \right)=\frac{\sigma _x \left( t \right)}{2}+\frac{\sigma _x \left( t \right)}{2}\cos \left( {2\alpha} \right)+\tau _{xy} \sin \left( {2\alpha } \right) \end{eqnarray}$
(5) $ \begin{eqnarray} \tau _{\alpha }\left( t \right)=\frac{\sigma _x \left( t \right)}{2}\sin \left( {2\alpha } \right)-\tau _{xy} \left( t \right)\cos \left( {2\alpha } \right) \end{eqnarray}$

图 1

新窗口打开|下载原图ZIP|生成PPT
图 1拉扭状态下光滑试件表面的应力状态

Fig. 1Stress state of the plain specimen under axial-torsional loading



由于一个加载周期内, 最大剪应力范围平面并不唯一, 为了确定唯一的临界平面, 本文定义具有较大法向应力的最大剪应力范围平面为临界平面. 利用式(2)~式(5), 确定临界平面方位和临界平面上各疲劳破坏参数的步骤如下:

(1) 在一个加载周期内, 用微小的时间步$\Delta t$将$\sigma _x $和$\tau _{xy} $进行离散.

(2) 不同时刻下, 利用式(4)和式(5)分别计算第$i$个斜面($\alpha_{i})$上的法向应力和剪切应力

(6) $ \begin{eqnarray} \label{eq6} &&\sigma _{n,\alpha_{i}} \left( j \right)=\left[ \sigma_{\rm a} \sin \left( {j\Delta t} \right)+\sigma _{\rm m} \right]\cos^2\alpha _{i}+ \\&&\qquad\left[ {\tau _{\rm a} \sin \left( {j\Delta t-\varphi } \right)+\tau _{\rm m}} \right]\sin \left( {2\alpha_{i} } \right) \end{eqnarray}$
(7) $ \begin{eqnarray} \tau _{\alpha_{i}} \left( j \right)=\frac{1}{2}\left[ {\sigma _{\rm a} \sin \left( {j\Delta t} \right)+\sigma _{\rm m} } \right]\sin\left( {2\alpha _{i} } \right)- && \\ \qquad \left[ {\tau _{\rm a} \sin \left( {j\Delta t-\varphi } \right)+\tau _{\rm m} } \right]\cos \left( {2\alpha _{i} } \right) \end{eqnarray}$
式中, $q$为一个加载周期中离散的子步数.

(3) 分别计算第$i$个斜面($\alpha_{i})$上的剪应力范围、剪切平均应力、法向应力范围和最大法向应力

(8) $ \begin{eqnarray} \label{eq8} &&\Delta \tau _{\alpha_{i}} =\max \left( {\tau _{\alpha_{i}} \left( j \right)} \right)-\min \left( {\tau _{\alpha_{i}} \left( j \right)} \right) \end{eqnarray}$
(9) $ \begin{eqnarray} \label{eq9} \tau _{m,\alpha_{i}} ={\left[ {\max \left( {\tau _{\alpha_{i}} \left( j \right)} \right)+\min \left( {\tau _{\alpha_{i}} \left( j \right)} \right)} \right]} / 2 \end{eqnarray}$
(10) $ \begin{eqnarray} \label{eq10} \Delta \sigma _{n,\alpha_{i}} =\max \left( {\sigma _{n,\alpha_{i}} \left( j \right)} \right)-\min \left( {\sigma _{n,\alpha_{i}} \left( j \right)} \right) \end{eqnarray}$
(11) $ \begin{eqnarray} \sigma _{n,\max ,\alpha_{i}} =\max \left( {\sigma _{n,\alpha_{i}} \left( j \right)} \right) \end{eqnarray}$
(4) 在[0$^\circ$, 180$^\circ$)内, $i$以步长0.1$^\circ$变化, 计算不同斜面上的剪应力范围和最大法向应力, 并比较其大小, 从而确定临界平面的方位角$\alpha _{\rm cr}$.

(5) 将$\alpha_{\rm cr}$代入式(8)~式(11), 确定临界平面上其他疲劳破坏参数的值.

2 多轴高周疲劳寿命预测模型

2.1 模型建立

Fatemi等^[26]定义最大剪应变范围平面为临界平面, 将临界平面上的最大法向应力引入到材料的多轴疲劳寿命预测中, 构建了如下基于应变的疲劳寿命预测模型(FS)

(12) $ \begin{eqnarray} \label{eq12} \gamma _{{\rm a,max}} \left( {1+k\frac{\sigma _{n,\max } }{\sigma _{\rm y}}} \right)=f\left( {N_{\rm f} } \right) \end{eqnarray}$
式中, $\gamma _{{\rm a},\max } $和$\sigma _{n,\max } $分别为临界平面上的最大剪应变幅和最大法向应力, $\sigma _{\rm y}$为屈服强度, $k$为材料常数, $N_{\rm f}$为疲劳寿命. FS模型中引入的$\sigma _{n,\max } $可以较好地反映材料的非比例附加强化效应, 该模型在预测材料的应变疲劳寿命方面应用较为广泛^[28].

预测材料的HCF寿命时, 通常将应力作为损伤控制参量. 鉴于FS模型在预测材料应变疲劳寿命方面取得较好的预测效果, 在预测宏观上主要是线弹性变形的HCF寿命时, 定义具有较大法向应力的最大剪应力范围平面为临界平面, 建立如下HCF寿命预测模型

(13) $ \begin{eqnarray} \label{eq13} \tau _{{\rm a},\max} \left( {1+k_{\rm H} \frac{\sigma _{n,\max } }{\sigma _{\rm y} }} \right)=f\left( {N_{\rm f} } \right) \end{eqnarray}$
式中, $\tau _{{\rm a},\max} $为临界平面上的最大剪应力幅, $k_{\rm H}$为材料常数. 需要说明的是, 虽然式(13)中的$k_{\rm H}$与式(12)中的$k$物理意义相同, 但确定方法不同. $k$需要借助材料的拉压和扭转应变疲劳试验数据确定, 而$k_{\rm H}$需要借助材料的拉压和扭转应力疲劳试验数据确定.

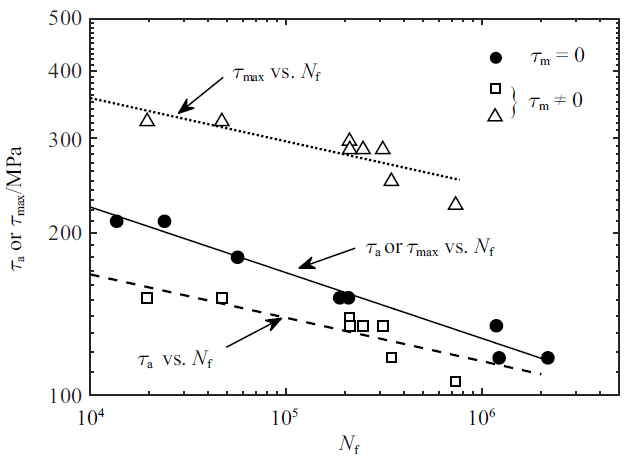
同大多数基于临界平面法的HCF寿命预测模型类似, 式(13)也只考虑了法向平均应力对疲劳寿命的影响, 没有充分考虑剪切平均应力对疲劳寿命的影响. 以7075-T651铝合金为例^[21], 图2所示为不同剪切平均应力加载下, 剪应力幅与疲劳寿命之间的关系. 由图2可见, 剪切平均应力对7075-T651铝合金的疲劳寿命具有明显的影响. 相同加载剪应力幅下, 剪切平均应力存在时, 材料的疲劳寿命明显降低. 不同剪切平均应力加载下, 7075-T651铝合金最大剪应力与疲劳寿命之间的关系也见图2. 由图可见, 在平均剪切应力为零与不为零两种工况下, 最大剪应力与疲劳寿命之间并没有很好的一致性. 换句话说, 最大剪应力并不能很好地反映不同剪切平均应力对材料平均应力的影响.

图 2

新窗口打开|下载原图ZIP|生成PPT
图 27075-T651铝合金剪切平均应力对疲劳寿命的影响^[21]

Fig. 2The influence of shear mean stress on the fatigue life for 7075-T651 aluminum alloy^[21]



大量试验数据表明, 拉伸平均应力加速材料的疲劳裂纹扩展, 而压缩平均应力减缓材料的疲劳裂纹扩展. 与最大剪应力类似, 在法向平均应力为零与不为零两种工况下, 7075-T651铝合金的最大法向应力与疲劳寿命之间也没有很好的一致性^[21]. 原因在于, 不管是最大剪应力还是最大法向应力, 用来表征材料的疲劳寿命时, 都没有考虑材料对平均应力敏感程度的不同. 因此, 考虑到不同材料对剪切和法向平均应力的敏感度, 引入剪切和法向Walker因子^[27], 将式(13)修正为

(14) $ \begin{eqnarray} \label{eq14} &&\tau _{{\rm a},\max}^{{w}_{\tau} } \left( {\tau _{{\rm a},\max} +\left| {\tau _{{{m},\alpha }_{{\rm cr}} } } \right|} \right)^{1-{w}_{\tau} }\left( {1+k_{\rm H} \frac{\sigma _{n,{\rm a}}^{{w}_{\sigma} } \sigma _{{n},\max }^{1-{w}_{\sigma} } }{\sigma _{\rm y} }} \right)= \\&&\qquad f\left( {N_{\rm f} } \right) \end{eqnarray}$
式中, $\sigma _{n,{\rm a}} $是临界平面上的法向应力幅. $w_{\tau}$和$w_{\sigma}$分别为剪切和法向Walker因子, 反映了材料对剪切和法向平均应力的敏感程度. $w_{\tau} $和$w_{\sigma} $的取值都介于0和1之间, 取值越小表明材料对平均应力越敏感. $\tau _{{\rm m,\alpha }_{{\rm cr}}}$是临界平面上的剪切平均应力, 式(14)中利用$\tau _{{{\rm m},\alpha }_{{\rm cr}}}$绝对值来反映剪切平均应力对疲劳寿命影响的原因在于, 相同等效应力下, 不管是正的还是负的剪切平均应力, 都会降低材料的疲劳寿命^[21,29-30].

在纯扭转对称循环加载下

(15) $ \begin{eqnarray} \label{eq15} \tau _{{\rm a},\max} =\tau _{\rm a} , \quad \tau _{{{\rm m},\alpha }_{{\rm cr}} } =0, \quad \sigma _{n,{\rm a}} =\sigma _{n,\max } =0 \end{eqnarray}$
将式(15)代入式(14)可得

(16) $ \begin{eqnarray} \label{eq16} \tau _{\rm a} =f\left( {N_{\rm f} } \right) \end{eqnarray}$
即在纯扭转对称循环加载下, 式(14)的左端退化为加载剪应力幅. 因此, 将式(14)与剪切形式的Basquin方程相联系, 得到如下多轴HCF寿命预测模型

(17) $ \begin{eqnarray} \label{eq17} &&\tau _{{\rm a,max}}^{{w}_{\tau} } \left( {\tau _{{\rm a},\max} +\left| {\tau _{{{\rm m},\alpha }_{{\rm cr}} } } \right|} \right)^{1-{w}_{\tau} }\left( {1+k_{\rm H} \frac{\sigma _{n,{\rm a}}^{{w}_{\sigma} } \sigma _{n,\max }^{1-{w}_{\sigma} } }{\sigma _{\rm y} }} \right)= \\&&\qquad{\tau }'_{\rm f} \left( {2N_{\rm f} } \right)^{{b}_{\rm o} } \end{eqnarray}$
式中, ${\tau}'_{\rm f} $为剪切疲劳强度系数, $b_{\rm o}$为剪切疲劳强度指数.

2.2 材料常数$k_{\rm H}$的确定

利用零平均应力工况下单轴拉压和纯扭转应力疲劳试验数据确定材料常数$k_{\rm H}$的步骤如下:

(1) 利用纯扭转疲劳试验数据计算剪切疲劳强度系数${\tau }'_{\rm f} $和剪切疲劳强度指数$b_{\rm o}$.

(2) 利用式(13)计算单轴拉压加载下本文定义的损伤控制参量$\tau _{{\rm a,eq}}$

(18) $ \begin{eqnarray} \label{eq18} \tau _{{\rm a,eq}} =\frac{\sigma _{\rm a} }{2}\left( {1+k_{\rm H} \frac{\sigma _{\rm a} }{2\sigma _{\rm y} }} \right) \end{eqnarray}$
式中, $\sigma _{\rm a} $为单轴拉压加载应力幅.

(3) 基于最小二乘法原理, 定义参数$L_{\rm FP}$为

(19) $ \begin{eqnarray} \label{eq19} L_{{\rm FP}} =\sum\limits_{i=1}^{m_{{\rm FP}} } {\left\{ {{\tau }'_{\rm f} \left( {2N_{i} } \right)^{b_{\rm o} }-\left[ {\frac{\sigma _{{\rm a},i} }{2}\left( {1+k_{\rm H} \frac{\sigma _{{\rm a},i} }{2\sigma _{\rm y} }} \right)} \right]} \right\}} ^2 \end{eqnarray}$
式中, $m_{{\rm FP}} $为纯扭转疲劳试验数据点的个数. 当$L_{\rm FP}$取最小值时, 对应$k_{\rm H}$的值即为所求材料常数.

另外, 由式(16)和式(18)可知, 当单轴拉压加载应力幅等于拉压疲劳极限$\sigma_{-1} $时, 可得

(20) $ \begin{eqnarray} \label{eq20} \tau _{{\rm a,eq}} =\frac{\sigma _{-1} }{2}\left( {1+k_{\rm H} \frac{\sigma _{-1} }{2\sigma _{\rm y} }} \right)=\tau _{-1} \end{eqnarray}$
式中, $\tau _{-1} $为剪切疲劳极限. 由式(20)可得

(21) $ \begin{eqnarray} \label{eq21} k_{\rm H} =\frac{2\sigma _{\rm y} }{\sigma _{-1} }\left( {\frac{2\tau _{-1} }{\sigma _{-1} }-1} \right) \end{eqnarray}$
因此, 当缺少疲劳试验数据时, 可利用式(21)计算材料常数$k_{\rm H}$. 由式(21)可知, 若保证$k_{\rm H}$大于零, 则有${\tau _{-1} } / {\sigma _{-1} }>0.5$. Marquis等^[25]研究表明, 脆性金属材料的HCF失效平面通常未发生在最大剪应力范围平面, 因此本文提出的HCF寿命预测模型并不适用于该类材料. Papadopoulos等^[31]研究发现, 大多数脆性金属材料的${\tau _{-1} } / {\sigma _{-1} }\geqslant 0.8$. 因此, 本文所提模型的材料适用范围在${0.5<\tau _{-1}} / {\sigma _{-1} }<0.8$.

2.3 Walker因子$w_{\tau }$和$w_{\sigma}$的确定

对于扭转疲劳试验, 当加载的剪切平均应力大于零时, 由式(17)可得

(22) $ \begin{eqnarray} \tau _{\rm a}^{w_\tau } \tau _{\max }^{1-{w}_{\tau} } ={\tau }'_{\rm f} \left( {2N_{\rm f} } \right)^{{b}_{\rm o} } \end{eqnarray}$
式中, $\tau _{\rm a} $和$\tau _{\max } $分别为加载剪应力幅和最大剪应力. 将式(22)左右两端分别取对数, 可得

(23) $ \begin{eqnarray} \label{eq23} \lg(2N_{\rm f}) =\frac{1}{b_{\rm o} }\lg \tau _{\max } +\frac{w_{\tau} }{b_{\rm o} }\lg \frac{\tau _{\rm a} }{\tau _{\max } }-\frac{1}{b_{\rm o} }\lg {\tau }'_{\rm f} \end{eqnarray}$
令

(24) $ \begin{eqnarray} \left. \begin{array}{ll} y=\lg 2N_{\rm f} , \ \ x_1 =\lg \tau _{\max } , \ \ x_2 =\lg \dfrac{\tau _{\rm a} }{\tau _{\max } }\\ p_1 =\dfrac{1}{b_{\rm o} }, \ \ p_2 =\dfrac{w_{\tau} }{b_{\rm o} }, \ \ p_3 =-\dfrac{1}{b_{\rm o} }\lg {\tau }'_{\rm f} \end{array} \right\} \end{eqnarray}$
可将式(23)变形为

(25) $ \begin{eqnarray} \label{eq25} y=p_1 x_1 +p_2 x_2 +p_3 \end{eqnarray}$
由式(25)可知, 利用多元线性回归的方法即可确定$w_{\tau} $的值.

对于单轴疲劳试验, 当加载的法向平均应力不为零时, 由Walker方程^[27]可得

(26) $ \begin{eqnarray} \label{eq26} \sigma _{\rm a}^{{w}_{\sigma} } \sigma _{\max }^{1-{w}_{\sigma} } ={\sigma }'_{\rm f} \left( {2N_{\rm f} }\right)^{b} \end{eqnarray}$
式中, ${\sigma }'_{\rm f} $为疲劳强度系数, $b$为疲劳强度指数.

对比式(22)和式(26)可知, 基于非零平均应力下的单轴疲劳试验数据, 利用和确定$w_{\tau} $值相类似的方法, 即可确定$w_{\sigma} $的值.

对于扭转脉动加载, 当载荷峰值等于该工况下的疲劳极限$\tau _0 $时, 本文定义的损伤控制参量变为

(27) $ \begin{eqnarray} \label{eq27} \tau _{{\rm a,eq}} =2^{1-{w}_{\tau} }\frac{\tau _0 }{2}=\tau _{-1} \end{eqnarray}$
化简可得

(28) $ \begin{eqnarray} \label{eq28} w_{\tau} =\log _2 \frac{\tau _0 }{\tau _{-1} } \end{eqnarray}$
因此, 当缺少疲劳试验数据时, 可利用式(28)计算$w_{\tau} $值. 但是, 通常情况下$\tau _0 $的试验值并不容易直接获取. 此时, $\tau _0$的值可利用Zenner等^[32]给出经验公式进行理论估算

(29) $ \begin{eqnarray} \label{eq29} \tau _0 =\frac{4\tau _{-1} }{2\dfrac{\sigma _{-1} }{\sigma _0 }+1} \end{eqnarray}$
相应的, 对于单轴脉动加载, 当载荷峰值等于该工况下的疲劳极限$\sigma _0 $时, 由式(26)可以推导出

(30) $ \begin{eqnarray} \label{eq30} w_{\sigma} =\log _2 \frac{\sigma _0 }{\sigma _{-1} } \end{eqnarray}$
结合式(28)~式(30), 可推导出$w_{\tau} $与$w_{\sigma}$存在如下关系

(31) $ \begin{eqnarray} \label{eq31} w_{\tau} =2-\log _2 \left( {1+2^{1-{w}_{\sigma} }} \right) \end{eqnarray}$

3 试验验证

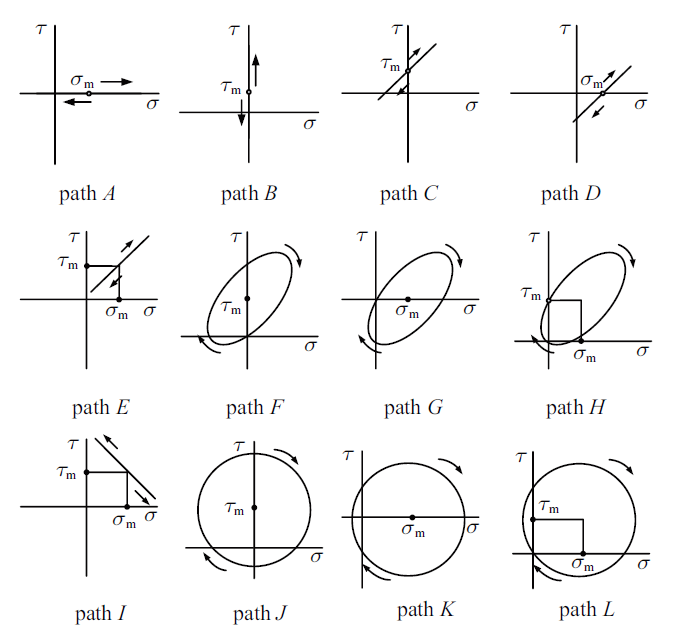
选用7075-T651铝合金^[21]、 30CrMnSiA钢^[33]、2A12-T4铝合金^[34]、 2017A-T4铝合金^[35]、 6082-T6铝合金^[35]等5种材料在不同平均应力加载下的试验数据来验证本文所提HCF寿命预测模型的正确性. 所有材料的试件形状都是光滑圆柱形试件, 加载波形都是正弦波, 加载控制方式都是控制应力加载. 前3种材料的加载方式是存在平均应力下的单轴、扭转、比例和非比例拉扭加载, 后两种材料的加载方式是存在平均应力下的弯曲、扭转和比例弯扭加载, 具体加载路径如图3所示, 其他试验情况详见文献^{[21, 33-35]}. 上述5种材料的机械性能和疲劳性能常数列于表1.

图 3

新窗口打开|下载原图ZIP|生成PPT
图 3加载路径^{[21, 33-35]}

Fig. 3Loading paths^{[21, 33-35]}



Table 1
表1
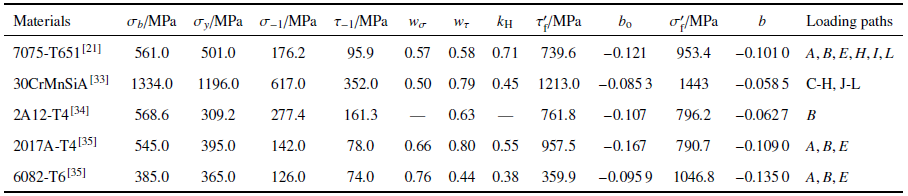
表1材料的机械性能和疲劳性能参数
Table 1Mechanical and fatigue properties of the considered materials

新窗口打开|下载CSV

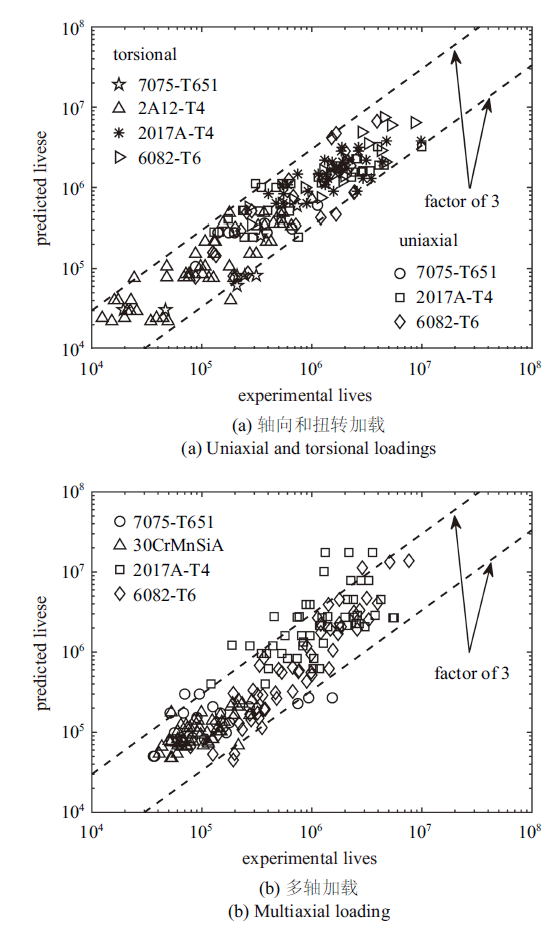
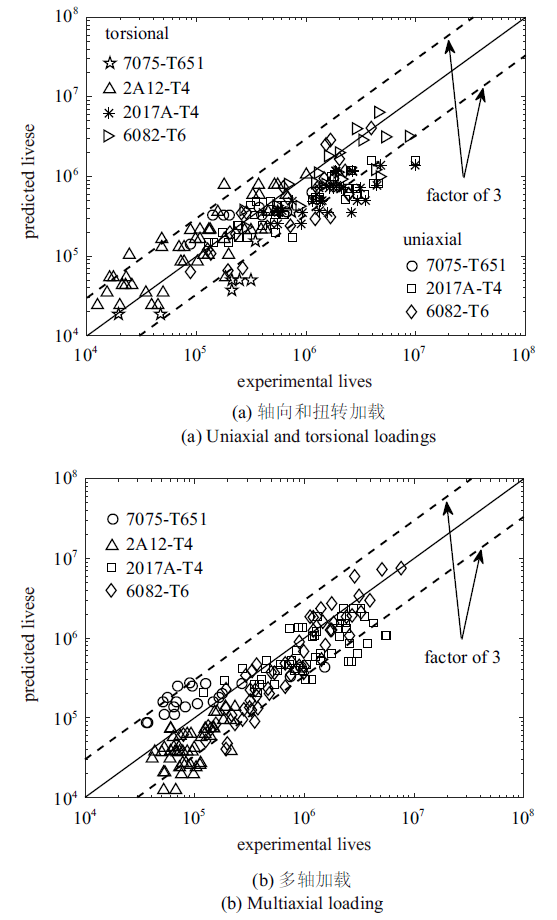
利用本文所提模型, 对表1中的5种材料在图3所示12种加载路径下的疲劳寿命进行了预测, 预测结果如图4所示. 由图4(a)可见, 在包含平均应力的轴向和扭转加载下, 绝大多数预测结果都位于3倍误差带以内. 这表明, 利用这些基础试验数据, 由前述模型参数的确定方法, 可以很好地确定所提模型中的各材料常数. 由图4(b)可见, 在包含平均应力的多轴加载下, 除了2017A-T4铝合金的个别数据点外, 其他数据点也大都位于3倍误差带以内. 由此可知, 无论是轴向加载还是扭转加载、也无论是比例加载还是非比例加载, 本文所提模型都可以很好地反映平均应力对疲劳寿命的影响.

图 4

新窗口打开|下载原图ZIP|生成PPT
图 4本文所建模型的疲劳寿命预测结果^{[21, 33-35]}

Fig. 4Fatigue life predictions of the proposed model^{[21, 33-35]}

4 讨论

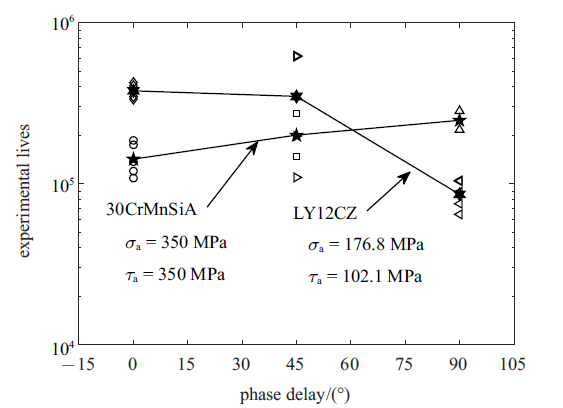
从微观角度来看, 剪切应力作用下, 滑移造成材料表面的挤入挤出, 逐渐形成驻留滑移带, 进而导致疲劳裂纹萌生. 对于高周疲劳而言, 虽然宏观上材料表现为弹性变形, 但是由于材料内部晶体存在各向异性, 位向不同的各个晶粒所受应力并不相同, 在细观尺度上部分金属晶粒仍会产生塑性变形, 从而出现滑移现象. 另外, 疲劳裂纹生长是沿着裂纹尖端剪切带的聚合过程, 裂纹面上的法向应力将使这种聚合加速. 因此, 本文定义具有较大法向应力的最大剪应力范围平面为临界平面, 以最大剪应力范围为首要的疲劳损伤控制参数, 以临界平面上的最大法向应力为辅助的疲劳损伤控制参数是合理的.

图5所示为相同加载应力幅下, 30CrMnSiA钢^[33]和LY12CZ铝合金^[36]疲劳寿命与相位差之间的关系. 由图5可见, 30CrMnSiA钢的疲劳寿命随着相位差的增大而增大, 但是LY12CZ铝合金的疲劳寿命却随着相位差的增大而减小. 由此可知, 多轴HCF中, 相位差影响材料的疲劳失效, 但具体影响程度依据材料而不同, 该结果与Papadopoulos等^[31]的研究结论相一致.

图 5

新窗口打开|下载原图ZIP|生成PPT
图 530CrMnSiA钢^[33]和LY12CZ铝合金^[36]疲劳寿命与相位差之间的关系

Fig. 5Relationships between experimental lives and phase delay for 30CrMnSiA steel^[33] and LY12CZ aluminum^[36]



以30CrMnSiA钢^[33]为例, 图6显示了拉扭加载下, 轴向和剪切加载应力幅都为350 MPa时, 临界平面位置、剪切应力范围和最大法向应力与相位差之间的关系. 由图6可见, 当相位差由0$^\circ$增大到90$^\circ$时, 临界平面位置由103$^\circ$变化到90$^\circ$, 临界平面上的剪切应力范围减小、最大法向应力增大. 由此可知, 在拉扭异相加载下, 相位差一方面影响了临界平面的位置, 另一方面也影响临界平面上损伤参量的大小.

图 6

新窗口打开|下载原图ZIP|生成PPT
图 6临界平面位置与相位差之间的关系

Fig. 6Relationships between the orientation of the critical plane and phase delay



对于剪切平均应力, Sines^[10]和Susmel等^[37]认为, 只要最大剪应力不超过材料的剪切屈服强度, 剪切平均应力就对材料的疲劳寿命没有影响. 以7075-T651铝合金^[21]为例, 该材料的剪切屈服强度为369 MPa, 由图2可见, 对于7075-T651铝合金而言, 即便最大剪应力材料低于材料的剪切屈服强度, 剪切平均应力仍然显著影响材料的疲劳寿命. 该结果与Wang等^[30]和Erickson等^[38]观察到的试验现象相一致. 由此可知, 不同材料对剪切平均应力的敏感程度并不相同. 因此, 本文引入剪切Walker因子, 来反映不同材料对剪切平均应力敏感程度的不同是合理的.

将式(2)和式(3)代入式(4), 化简可得夹角为$\alpha $的斜面上的法向平均应力$\sigma_{n,{\rm m,\alpha }} $为

(32) $ \begin{eqnarray} \label{eq32} \sigma _{n,{\rm m,\alpha }} =\sigma _{\rm m} \cos ^2\alpha +\tau _{\rm m} \sin \left( {2\alpha } \right) \end{eqnarray}$
由式(32)可见, 法向平均应力包含了轴向和剪切加载平均应力, 在一定程度上可以反映剪切平均应力对疲劳寿命的影响. 大多数基于临界平面法的HCF寿命预测模型, 如Matake模型^[16]、McDiarmid模型^[17]、Susmel^[18]模型、Zhang模型^[20]等, 都是用最大法向应力来反映平均应力对疲劳寿命的影响.

对于存在加载剪切平均应力的扭转循环加载

(33) $ \begin{eqnarray} \label{eq33} \sigma _{\rm a} =\sigma _{\rm m} =0, \ \ \tau _{\rm a} \ne 0, \ \ \tau _{\rm m} \ne 0 \end{eqnarray}$
将式(2)、式(3)和式(33)代入式(5), 化简可得

(34) $ \begin{eqnarray} \label{eq34} \tau _{\alpha } \left( t \right)=-\tau _{\rm a} \cos \left( {2\alpha } \right)\sin \left( {\omega t} \right)-\tau _{\rm m} \cos \left( {2\alpha } \right) \end{eqnarray}$
由上式可得, 夹角为$\alpha $的斜面上的剪应力范围为

(35) $ \begin{eqnarray} \label{eq35} \Delta \tau _{\alpha } =2\tau _{\rm a} \cos \left( {2\alpha } \right) \end{eqnarray}$
对式(35)进行求导, 并令其导数等于0, 可得临界平面的方位角$\alpha_{\rm cr}$等于0$^\circ$. 将$\alpha_{\rm cr} = 0^\circ$代入式(32)可知, 在该加载工况下, 无论加载剪切平均应力等于多少, 临界平面上的法向平均应力恒为0. 因此, 仅仅利用法向平均应力并不能很好地反映加载剪切平均应力对疲劳寿命的影响.

在众多临界平面模型中, McDiarmid模型较为常用且已被MCS.Fatigue等商业软件收录. 该模型定义最大剪应力范围平面为临界平面, 其数学表达式为^[17]

(36) $ \begin{eqnarray} \label{eq36} \tau _{{\rm a},\max} +\frac{\tau _{-1} }{2\sigma _{\rm b} }\sigma _{n,\max } ={\tau }'_{\rm f} \left( {2N_{\rm f} } \right)^{{b}_{\rm o} } \end{eqnarray}$
式中, $\sigma _{\rm b} $为抗拉强度.

张成成等^[19]为了更好地反映平均对材料疲劳寿命的影响, 利用Goodman平均应力修正公式, 对最大剪应力平面上的法向平均应力进行了修正, 提出如下模型(ZCC模型)

(37) $ \begin{eqnarray} \label{eq37} &&\sqrt {\tau _{{\rm a},\max}^2 -\tau _{{\rm a},\max} \sigma _{n,\max }^\ast +\frac{\tau _{-1}^2 }{\sigma _{-1}^2 }\left( {\sigma _{-1} +2\tau _{{\rm a},\max} } \right)\sigma _{n,\max }^\ast } = \\&&\qquad {\tau }'_{\rm f} \left( {2N_{\rm f} } \right)^{{b}_{\rm o} } \end{eqnarray}$
其中

(38) $ \begin{eqnarray} \label{eq38} \sigma _{n,\max }^\ast =\frac{\sigma _{n,{\rm a}} }{1-{\sigma _{n,{\rm m}} } / {\sigma _{\rm b} }} \end{eqnarray}$
式中, $\sigma _{n,{\rm a}} $和$\sigma _{n,{\rm m}} $分别为最大剪应力范围平面上的法向应力幅和法向平均应力.

Wang等^[21]进一步考虑了剪切平均应力对疲劳寿命的影响, 提出如下寿命预测模型

(39) $ \begin{eqnarray} \label{eq39} &&\Bigg\{ \left( {\tau _{{\rm a},\max} +0.207\left| {\tau _{{{\rm m},\alpha }_{{\rm cr}} } } \right|} \right)^2+ \\&&\qquad \frac{1}{3}\left[ {\sigma _{n,{\rm a}} +\left( {\sqrt {24{\tau _{-1}^2 }/{\sigma _{-1}^2 }-4.371} -1} \right)\sigma _{n,{\rm m}} } \right]^2\Bigg\}^{1/2} = \\&&\qquad {\tau }'_{\rm f} \left( {2N_{\rm f} } \right)^{{\rm b}_{\rm o} } \end{eqnarray}$
Liu等^[23]定义最大法向应力幅平面为临界平面, 考虑法向平均应力的影响, 提出如下疲劳寿命预测模型

(40) $ \begin{eqnarray} \label{eq40} &&\frac{{\rm 1}}{\beta _{{\rm LM}} }\sqrt {\left[ {\sigma _{{\rm a,c}} \left( {1+\eta \frac{\sigma _{{{\rm m},c}} }{\sigma _{-1} }} \right)} \right]^2+\left( {\frac{\sigma _{-1} }{\tau _{-1} }} \right)^2\left( {\tau _{{\rm a,c}} } \right)^2} = \\&&\qquad{\sigma }'_{\rm f} \left( {2N_{\rm f} } \right)^{b} \end{eqnarray}$
其中

(41) $ \begin{eqnarray} \label{eq41} &&\eta =\frac{3}{4}+\frac{1}{4}\left( {\frac{\sqrt 3 -\frac{\sigma _{-1} }{\tau _{-1} }}{\sqrt 3 -1}} \right) \end{eqnarray}$
(42) $ \begin{eqnarray} \label{eq42} \beta _{{\rm LM}} =\sqrt {\cos ^2\left( {2\theta } \right)\left[ {\left( {\frac{\tau _{-1} }{\sigma _{-1} }} \right)^2-{\rm 1}} \right]+{\rm 1}} \end{eqnarray}$
(43) $ \begin{eqnarray} \cos \left( {2\theta } \right)=\left\{-2+\left\{4-4\left[ {\left( {\frac{\sigma _{-1} }{\tau _{-1} }} \right)^2-3} \right]\left[ 5-\left( {\frac{\sigma _{-1} }{\tau _{-1} }} \right)^2- \\ \qquad 4\left( {\frac{\tau _{-1} }{\sigma _{-1} }} \right)^2 \right] \right\}^{1/2} \right\}\Bigg/\left\{2\left[ {5-\left( {\frac{\sigma _{-1} }{\tau _{-1} }} \right)^2-4\left( {\frac{\tau _{-1} }{\sigma _{-1} }} \right)^2} \right] \right\} \end{eqnarray}$
式(40)中, ${\sigma }'_{\rm f} $为疲劳强度系数, $b$为疲劳强度指数. $\sigma _{{\rm a,c}} $、$\sigma _{{{\rm m},c}} $和$\tau _{{\rm a,c}}$分别为最大法向应力幅平面上的法向应力幅、法向平均应力和剪切应力幅.

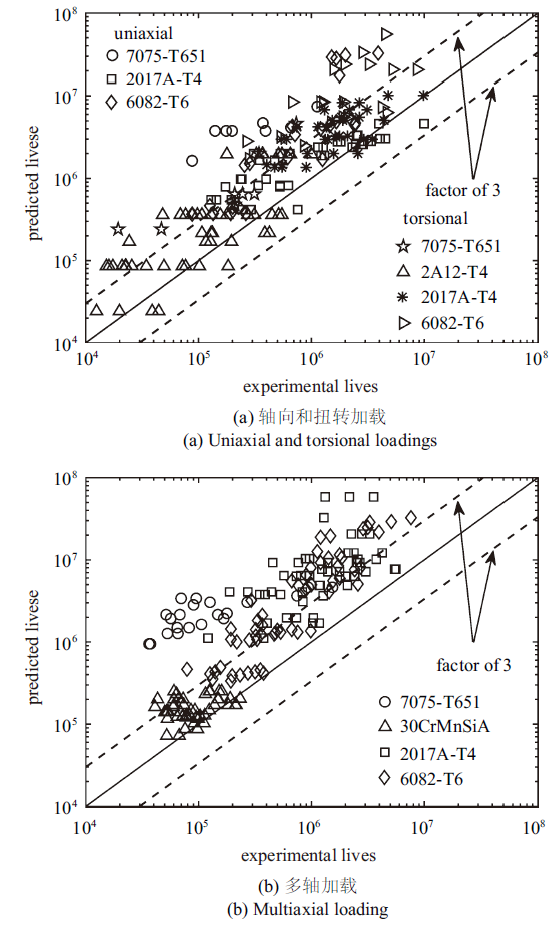
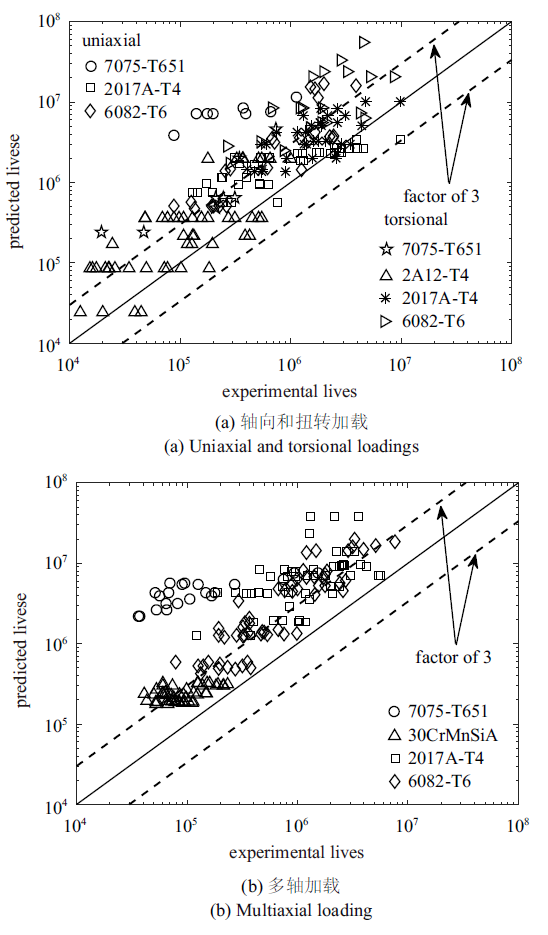
利用表1中5种材料存在平均应力工况下的HCF试验数据, 采用上述4种模型与本文所建模型进行对比, 以比较各模型的正确性和预测精度. 图7~图10分别表示McDiarmid模型、ZCC模型、Wang模型和Liu模型对表1中所列材料的疲劳寿命预测结果. 由图7和图8可见, 不管是轴向加载、扭转加载, 还是多轴加载, 存在平均应力的加载工况下, McDiarmid模型和ZCC模型的绝大多数预测结果都偏于危险. 与之相比, 由图9可见Wang模型的预测结果较为理想, 大多数预测结果位于3倍误差带以内. 原因在于, Wang模型考虑了剪切平均应力的影响, 在一定程度上提高了模型的预测精度. 但是, 在轴向和扭转加载下, 除2A12-T4铝合金外, Wang模型的大多数预测结果偏于保守. 在多轴加载下, 除7075-T651铝合金外, Wang模型的大多数预测结果也偏于保守. 原因在于, 虽然Wang模型考虑了剪切平均应力的影响, 但是该模型未考虑不同材料对剪切平均应力敏感度的不同, 从而导致某些材料预测结果偏于保守. 另外, 由式(37)可见, Wang模型中法向平均应力权重系数与${\tau _{-1} } / {\sigma _{{\rm -1}} }$成正比. 但是对于某些材料, 如6082-T6铝合金, 虽然Wang模型计算得到的法向平均应力权重系数较大, 但该材料本身对法向平均应力敏感度并不高, 从而也会导致模型的预测结果偏于保守. 由图10可见, 与上述3种模型相比, Liu模型的预测结果最为分散, Liu模型一方面高估了材料的扭转疲劳寿命, 另一方面又低估了材料的轴向疲劳寿命. 原因在于, 本文所验证的5种材料都属于典型的塑性材料, 影响材料疲劳裂纹萌生的首要因素在于材料所承受的剪切应力^[39], 而Liu等^[23]定义临界平面为最大法向应力幅平面, 认为控制材料疲劳裂纹萌生的首要因素在于法向应力, 由此导致Liu模型预测结果比较分散. 与之相比, 由图4可见, 对于图3所示的12种加载路径, 除了2017A-T4铝合金的个别数据点外, 所建模型的绝大多数预测结果都位于3倍误差带以内, 在所验证的5种模型中, 预测精度最高. 原因在于, 所建模型不但考虑了法向平均应力对材料高周疲劳寿命的影响, 而且还考虑了剪切平均应力的影响, 并且通过引入Walker因子有效地反映了不同材料对平均应力敏感程度的不同. 虽然Wang模型在修正Zhang^[20]模型时也考虑了平均剪应力的影响, 但是与所建模型相比, Wang模型忽略了不同材料对平均应力敏感程度的不同, 从而导致Wang模型的预测结果并不理想.

图 7

新窗口打开|下载原图ZIP|生成PPT
图 7McDiarmid模型的疲劳寿命预测结果^{[21, 33-35]}

Fig. 7The fatigue life predictions of the McDiarmid model^{[21, 33-35]}

图 8

新窗口打开|下载原图ZIP|生成PPT
图 8ZCC模型的疲劳寿命预测结果^{[21, 33-35]}

Fig. 8The fatigue life predictions of the ZCC model^{[21, 33-35]}

图 9

新窗口打开|下载原图ZIP|生成PPT
图 9Wang模型的疲劳寿命预测结果^{[21, 33-35]}

Fig. 9The fatigue life predictions of the Wang model^{[21, 33-35]}

图 10

新窗口打开|下载原图ZIP|生成PPT
图 10Liu模型的疲劳寿命预测结果^{[21, 33-35]}

Fig. 10The fatigue life predictions of the Liu model^{[21, 33-35]}



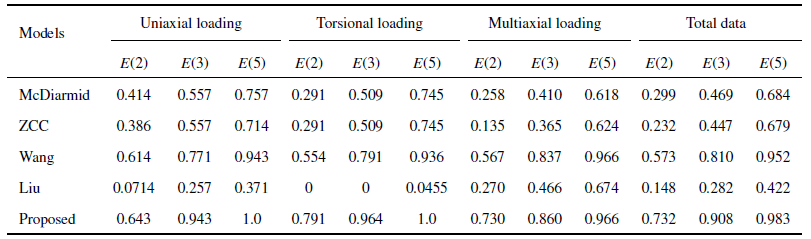
为了定量描述各种预测模型的预测精度, 定义误差因子^[40] $E(s)$为分布在${1}/{s}\leqslant {N_{\rm P}}/{N_{\rm T}}\leqslant s$带内的试验点个数与试验点的总个数的比值. 其中, $N_{\rm P} $是预测寿命, $N_{\rm T} $是试验寿命. 各种模型在不同加载工况下的误差因子见表2. 由表中数据可以看出, 不论何种加载工况, 所建模型都有最好的预测精度.

Table 2
表2
表2HCF疲劳寿命预测模型预测误差比较
Table 2Comparison of the HCF life prediction models using the error criterion

新窗口打开|下载CSV

为进一步描述不同模型的可靠性, 利用正态分布函数对表2中5种模型的疲劳寿命预测精度进行了对比分析^{[1, 41]}. 正态分布的概率密度函数为

(44) $ \begin{eqnarray} \label{eq44} f\left( x \right)=\frac{1}{\sqrt {2\pi} \sigma }{\rm e}^{-\frac{\left( {x-\mu }\right)^2}{2\sigma ^2}} \end{eqnarray}$
式中, $\mu $和$\sigma $分别为均值和标准差.

表2中所列5种模型$\lg \left( {{N_{\rm P} } / {N_{\rm T} }}\right)$值的正态分布如图11所示. 若$\lg \left( {{N_{\rm P} } / {N_{\rm T} }} \right)$值大于0表示预测结果偏于危险, 反之表示预测结果偏于保守. 由图11可见, McDiarmid模型和ZCC模型的预测精度类似, $\mu $值均大于零, 表明预测寿命均趋于危险一侧. 两种模型的$\sigma $值均较大, 表明预测结果都比较分散. Wang模型的$\mu $值小于零, $\sigma $值较小, 表明模型预测寿命偏于保守, 但预测寿命的分布较为集中. 相比较而言, Wang模型预测结果好于McDiarmid模型和ZCC模型, 其主要原因在于Wang模型更好地反映了剪切平均应力对疲劳寿命的影响. Liu模型的$\mu $值大于零, 且$\mu $值和$\sigma $值都较大, 这表明Liu模型的预测结果不但整体偏于危险, 而且最为分散. 整体来看, 本文所建模型的$\lg \left( {{N_{\rm P} } / {N_{\rm T} }} \right)$值正态分布曲线均值基本为0, 且标准差最小. 因此, 相比其他4种模型, 所建模型的预测结果分布更集中, 精度更高, 也更可靠.

图 11

新窗口打开|下载原图ZIP|生成PPT
图 11寿命比$N_{\rm P}/N_{\rm T}$的概率密度函数

Fig. 11Probability density functions of the $N_{\rm P}/N_{\rm T}$

5 结论

(1) 对于大多数金属材料而言, 高周疲劳寿命的影响因素不仅包括轴向平均应力, 还包括扭转平均应力, 扭转平均应力对疲劳寿命产生不利影响.

(2) 不同金属材料对平均应力的敏感程度不同, 疲劳寿命预测过程中应考虑不同金属材料对平均应力的敏感度.

(3) 基于临界平面理论, 构建了一个新的多轴高周疲劳寿命预测模型, 并给出了临界平面和模型参数的确定方法. 新模型通过引入Walker因子来反映不同材料对平均应力敏感程度的不同, 适用于${0.5<\tau _{-1} } / {\sigma _{-1} }<0.8$范围内的金属塑性材料.

(4) 利用五种材料的试验数据, 对所建模型和其他四种高周疲劳寿命预测模型进行对比验证后发现, Wang模型预测结果普遍偏于保守, 而McDiarmid模型和ZCC模型的预测结果则普遍偏于危险, Liu模型预测结果最为分散. 与之相比, 所建模型预测结果更为合理, 绝大多数预测结果分布在3倍误差带以内.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 崔向阳, 洪克城. 一种考虑非比例附加损伤的多轴低周疲劳模型
力学学报, 2019,51(3):863-872
[本文引用: 2]

( Cui Xiangyang, Hong Kecheng. A multiaxial low-cycle fatigue model considering non-proportional additional damage
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):863-872 (in Chinese))
[本文引用: 2]

[2] 李亚波, 宋清源, 杨凯 等. 试样疲劳性能尺度效应的概率控制体积方法
力学学报, 51(5):1363-1371


( Li Yabo, Song Qingyuan, Yang Kai, et al. Probabilistic control volume method for the size effect of specimen fatigue performance
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(5):1363-1371 (in Chinese))


[3] 张志杰, 蔡力勋, 陈辉 等. 金属材料的强度与应力--应变关系的球压入测试方法
力学学报, 2019,51(1):159-169
[本文引用: 1]

( Zhang Zhijie, Cai Lixun, Chen Hui, et al. Spherical indentation method to determine stress-strain relations and tensile strength of metallic materials
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(1):159-169 (in Chinese))
[本文引用: 1]

[4] 洪友士, 孙成奇, 刘小龙. 合金材料超高周疲劳的机理与模型综述
力学进展, 2018,48(1):201801-201801
[本文引用: 1]

( Hong Youshi, Sun Chengqi, Liu Xiaolong. A review on mechanisms and models for very-high-cycle fatigue of metallic materials
Advances in Mechanics, 2018,48(1):201801-201801 (in Chinese))
[本文引用: 1]

[5] Socie DF, Marquis G. Multiaxial Fatigue. Society of Automotive Engineers Inc, Warrendale, PA
2000
[本文引用: 2]

[6] 朱正宇, 何国求, 陈成澍 等. 多轴非比例加载高周疲劳研究进展
同济大学学报(自然科学版), 2006,34(9):1221-1226
[本文引用: 1]

( Zhu Zhengyu, He Guoqiu, Chen Chengshu, et al. Recent advances of multiaxial high cycle fatigue under nonproportional loading
Journal of Tongji University $($Natural Science$)$, 2006,34(9):1221-1226 (in Chinese))
[本文引用: 1]

[7] Gough HG, Pollard HV. The strength of metals under combined alternating stress
Proceedings of the Institution of Mechanical Engineers, 1935,131(1):3-103
DOIURL [本文引用: 1]

[8] Lee SB. A criterion for fully reversed out of phase torsion and bending
In: Brown WN, Miller KJ, editors. Advances in multiaxial fatigue, ASTM STP-853, 1985: 553-568
[本文引用: 1]

[9] Crosslang B. Effect of large hydrostatic pressures on the torsional fatigue strength of an alloy steel
// Proc Int Conf on Fatigue of Metals. Institution of Mechanical Engineers, London, 1956: 184-194
[本文引用: 1]

[10] Sines G. Behavior of metals under complex static and alternating stresses
In: Sines G, Waisman JL, editors. Metal Fatigue. McGraw-Hill, New York, 1959: 145-169
[本文引用: 2]

[11] Dang Van K. Macro-micro approach in high-cycle multiaxial fatigue
In: McDowell DL, Ellis R, editors. Advances in multiaxial fatigue, ASTM STP 1191, 1993: 120-130
[本文引用: 1]

[12] Papadopoulos IV. A high cycle fatigue criterion applied in biaxial and triaxial out-of-phase stress conditions
Fatigue and Fracture of Engineering Materials and Structures, 1995,18(1):79-91
DOIURL [本文引用: 1]

[13] Zenner H, Simburger A, Liu J. On the fatigue limits of ductile metals under complex multiaxial loading
International Journal of Fatigue, 2000,22(2):137-145
DOIURL [本文引用: 1]

[14] Papuga J, Milan R. Two new multiaxial criteria for high cycle fatigue computation
International Journal of Fatigue, 2008,30(1):58-66
DOIURL [本文引用: 1]

Abstract

Two new high cycle multiaxial criteria are proposed on the basis of previous tests on other published criteria. One of the new criteria searches for a critical plane, while the second one integrates a fatigue parameter over all planes. The two criteria use a similar hybrid fatigue parameter, and these emphasize the effect of shear stress in comparison to normal stress. They both lead to a much better prediction than that achieved by other tested criteria. The experiments used for the comparisons were gathered from other published papers. There were a total of 119 experiments, so a statistical comparison of all results was necessary.

[15] Findley WN. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending
Journal of Engineering Industry, 1959,81:301-306
DOIURL [本文引用: 2]

[16] Matake T. An explanation on fatigue limit under combined stress
Bulletin of the Japan Society of Mechanical Engineers, 1977,20(141):257-263
DOIURL [本文引用: 2]

[17] McDiarmid D. A shear stress based critical plane criterion of multiaxial fatigue failure for design and life prediction
Fatigue and Fracture of Engineering Materials and Structures, 1994,17(12):1475-1484
DOIURL [本文引用: 4]

[18] Susmel L, Lazzarin P. A bi-parametric Wohler curve for high cycle multiaxial fatigue assessment
Fatigue and Fracture of Engineering Materials and Structures, 2002,25(1):63-78
DOIURL [本文引用: 2]

[19] 张成成, 姚卫星. 一种新的多轴高周疲劳寿命预测模型
力学学报, 2010,42(6):1225-1230
URL [本文引用: 3]
分析和讨论3种典型载荷(单轴拉压、纯扭及90^\circ非比例)情况下的5组损伤控制参数,提出了一种以临界面上最大剪切应力幅和最大法向应力的非线性组合作为损伤控制参数的多轴高周疲劳寿命预测模型, 该模型考虑了平均应力对疲劳寿命的影响, 比现有的疲劳预测模型具有更宽的金属材料适用范围. 两种不同类型材料下的多轴非比例试验的预测结果表明,模型的预测结果与试验符合较好.
( Zhang Chengcheng, Yao Weixing. A new model for life prediction of multiaxial high cycle fatigue
Chinese Journal of Theoretical and Applied Mechanics, 2010,42(6):1225-1230 (in Chinese))
URL [本文引用: 3]
分析和讨论3种典型载荷(单轴拉压、纯扭及90^\circ非比例)情况下的5组损伤控制参数,提出了一种以临界面上最大剪切应力幅和最大法向应力的非线性组合作为损伤控制参数的多轴高周疲劳寿命预测模型, 该模型考虑了平均应力对疲劳寿命的影响, 比现有的疲劳预测模型具有更宽的金属材料适用范围. 两种不同类型材料下的多轴非比例试验的预测结果表明,模型的预测结果与试验符合较好.

[20] Zhang JL, Shang DG, Sun YJ, et al. Multiaxial high-cycle fatigue life prediction model based on the critical plane approach considering mean stress effects
International Journal of Damage Mechanics, 2018,27(1):32-46
DOIURL [本文引用: 4]

[21] Wang XW, Shang DG, Sun YJ, et al. Multiaxial high-cycle fatigue life prediction model considering mean shear stress effect under constant and variable amplitude loading
Theoretical and Applied Fracture Mechanics, 2018,96:676-687
DOIURL [本文引用: 23]

[22] Matsubara G, Hayashida A, Kano D. Predicting the multiaxial fatigue limit and the multiaxial high-cycle fatigue life based on the unified equivalent shear stress from axial strength characteristics with various waveforms
International Journal of Fatigue, 2018,112:52-62
DOIURL [本文引用: 1]

[23] Liu Y, Mahadevan S. Multiaxial high cycle fatigue criterion and life prediction for metals
International Journal of Fatigue, 2005,27(7):790-800
[本文引用: 5]

[24] Wei H, Carrion P, Chen J, et al. Multiaxial high-cycle fatigue life prediction under random spectrum loadings
International Journal of Fatigue, 2019, doi: https://doi.org/10.1016/j.ijfatigue.2019.105462
URLPMID [本文引用: 2]

[25] Marquis G, Socie DF. Long life torsion fatigue with normal mean stresses
Fatigue and Fracture of Engineering Materials and Structures, 2000,23(4):293-300
[本文引用: 2]

[26] Fatemi A, Socie DF. A critical plane to multiaxial fatigue damage including out of phase loading
Fatigue and Fracture of Engineering Materials and Structures, 1988,11(3):149-165
[本文引用: 2]

[27] Walker EK. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum
In: Rosenfeld M, editor. Effects of environment and complex load history on fatigue life, ASTM STP-462, 1970: 1-14
[本文引用: 3]

[28] Fatemi A, Shamsaei N. Multiaxial fatigue: An overview and some approximation models for life estimation
International Journal of Fatigue, 2011,33(8):948-958
[本文引用: 1]

[29] 陈亚军, 刘波, 刘辰辰 等. 2A12航空铝合金多轴疲劳试验及应力准则寿命预测模型研究
中国机械工程, 2017,28(9):1092-1096
[本文引用: 1]

( Chen Yajun, Liu Bo, Liu Chenchen, et al. Multiaxial fatigue test of aeronautical aluminum alloys 2A12 and research on stress criterion life predictive model
China Mechanical Engineering, 2017,28(9):1092-1096 (in Chinese))
[本文引用: 1]

[30] Wang CH, Miller KJ. The effect of mean shear stress on torsional fatigue behavior
Fatigue and Fracture of Engineering Materials and Structures, 2000,14(2):293-307
[本文引用: 2]

[31] Papadopoulos IV, Davoli P, Gorla C, et al. A comparative study of multiaxial high cycle fatigue criteria for metals
International Journal of Fatigue, 1997,19(3):219-235
[本文引用: 2]

[32] Zenner H, Simburger A, Liu J. On the fatigue limit of ductile metals under complex multiaxial loading
International Journal of Fatigue, 2000,22(2):137-145
[本文引用: 1]

[33] Liu TQ, Shi XH, Zhang JY, et al. Multiaxial high-cycle fatigue failure of 30CrMnSiA steel with mean tension stress and mean shear stress
International Journal of Fatigue, 2019,129:105219
[本文引用: 18]

[34] Zhang JY, Xiao QS, Shi XH, et al. Effect of mean shear stress on torsion fatigue failure behavior of 2A12-T4 aluminum alloy
International Journal of Fatigue, 2014,67:173-182
[本文引用: 1]

[35] Kluger K. Fatigue life estimation for 2017A-T4 and 6082-T6 aluminum alloys subjected to bending-torsion with mean stress
International Journal of Fatigue, 2014,80:22-29
[本文引用: 15]

[36] Wang YY, Yao WX. A multiaxial fatigue criterion for various metallic materials under proportional and nonproportional loading
International Journal of Fatigue, 2006,28(4):401-408
[本文引用: 3]

[37] Susmel L, Tovo R, Lazzarin P. The mean stress effect on the high cycle fatigue strength from a multiaxial fatigue point of view
International Journal of Fatigue, 2005,27(8):928-943
[本文引用: 1]

[38] Erickson M, Kallmeyer AR, Stone RHV, et al. Development of a multiaxial fatigue damage model for high strength alloy using a critical plane methodology
Journal of Engineering Materials and Technology, 2008,130(4):041008
[本文引用: 1]

[39] McClaflim D, Fatemi A. Torsional deformation and fatigue of hardened steel including mean stress and stress gradient effects
International Journal of Fatigue, 2004,26(7):733-784
[本文引用: 1]

[40] Li J, Zhang ZP, Sun Q, et al. Multiaxial fatigue life prediction for various metallic materials based on the critical plane approach
International Journal of Fatigue, 2011,33(1):90-101
[本文引用: 1]

[41] Ma S, Markert B, Yuan H. Multiaxial fatigue life assessment of sintered porous iron under proportional and non-proportional loadings
International Journal of Fatigue, 2017,97:214-226
[本文引用: 1]