具有刚性间隙约束输流管的碰撞振动 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

王乙坤^,^*^,^?^,²⁾, 王琳^,^?^,³⁾, 倪樵^?, 杨沫^*, 刘德政^*, 秦涛^*

^*湖北文理学院机械工程学院,湖北襄阳 441053

^?华中科技大学力学系,武汉 430074

VIBRO-IMPACT DYNAMICS OF PIPE CONVEYING FLUID SUBJECTED TO RIGID CLEARANCE CONSTRAINT ¹⁾

Wang Yikun^,^*^,^?^,²⁾, Wang Lin^,^?^,³⁾, Ni Qiao^?, Yang Mo^*, Liu Dezheng^*, Qin Tao^*

^*School of Mechanical Engineering,Hubei University of Arts and Science,Xiangyang 441053,Hubei,China

^?Department of Mechanics,Huazhong University of Science and Technology,Wuhan 430074,China

通讯作者: 2)王乙坤, 讲师, 主要研究方向: 非线性动力学, 动力学与控制. E-mail:wangyikun18@hbuas.edu.cn;3)王琳, 教授, 主要研究方向: 非线性动力学, 动力学与控制. E-mail:wanglindds@hust.edu.cn

收稿日期:2020-04-7接受日期:2020-04-7网络出版日期:2020-09-18

基金资助:

1)国家自然科学基金.11902112
国家自然科学基金.11972167
“机电汽车”湖北省优势特色学科群开放基金.XKQ2019008

Received:2020-04-7Accepted:2020-04-7Online:2020-09-18
作者简介 About authors

摘要
管道与间隙约束间的碰撞振动是工程输流管结构的一个重要动力学现象. 迄今,人们通常采用光滑的非线性弹簧来模拟管道与间隙约束之间的碰撞力,但这种光滑的碰撞力无法真实反映碰撞前后管道状态向量的非光滑传递特征. 本文基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型,利用 Galerkin 法离散了无穷维的管道模型, 并引入恢复系数构造了碰撞前后管道各处状态向量的传递矩阵,运用四阶龙格库塔法分析了脉动内流激励下管道与刚性间隙约束的非光滑碰撞振动现象,着重讨论了刚性间隙约束参数对管道动态响应随流速脉动频率变化的影响规律,特别是碰撞振动的周期性运动规律. 研究结果表明,刚性约束间隙值对管道碰撞振动行为的影响较大,在某些脉动频率下管道会出现多周期和非周期性的运动形态,还可出现非光滑系统特有的黏滑现象. 此外,碰撞恢复系数对管道振动的影响也比较显著,较小的恢复系数值更容易使管道在大范围脉动频率区间出现复杂的非周期碰撞振动.
关键词： 输流管;刚性间隙约束;碰撞振动;分岔;黏滑运动

Abstract
The vibro-impact dynamics due to loose constraints have become one of the key scientific problems in the dynamical system of pipes conveying fluid. The impact force modeled by smoothed nonlinear springs varies continuously with time and displacement of the vibrating pipe, which cannot exactly capture the non-smooth characteristics of the saltation of state vectors for the pipes before and after an impact. In this paper, a non-smooth mathematical model of simply supported pipes conveying pulsating fluid, subjected to a rigid constraint somewhere along the pipe length is established, with consideration of the effect of the values of clearance and coefficient of restitution of the constraint. Especially, the periodic and aperiodic oscillations are investigated under various pulsating frequencies of the internal fluid. The transition matrices of the displacement and velocity of all nodes along the pipe before and after impact were derived based on a Galerkin's approach. The nonlinear equations of motion are solved via a fourth-order Runge-Kutta method, by applying the impact boundary conditions. Results show that the pipe is capable of displaying interesting vibro-impact behaviors in the presence of the rigid clearance constraint with the variation of pulsating frequency of the flowing fluid. With a clearance close to the maximum displacement of the pipe without constraint, periodic vibro-impact behaviors are observed with multiple impacts. The vibration velocities before the pipe impacts on the edge of the rigid clearance constraint decrease to zero gradually with the displacement invariant, which is called a dynamical stick-slip motion, also known as a typical non-smooth phenomenon. By decreasing the value of coefficient of restitution, the responses of the pipe may change from periodic vibrations to chaotic ones. This work provides an attractive strategy for further understanding of the nonlinear impact dynamics of pipes conveying fluid subjected to rigid clearance constraint based on non-smooth theories.
Keywords：pipe conveying fluid;rigid clearance constraint;vibro-impact;bifurcation;sticking motion

PDF (16691KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
王乙坤, 王琳, 倪樵, 杨沫, 刘德政, 秦涛. 具有刚性间隙约束输流管的碰撞振动 ¹⁾. 力学学报[J], 2020, 52(5): 1498-1508 DOI:10.6052/0459-1879-20-137
Wang Yikun, Wang Lin, Ni Qiao, Yang Mo, Liu Dezheng, Qin Tao. VIBRO-IMPACT DYNAMICS OF PIPE CONVEYING FLUID SUBJECTED TO RIGID CLEARANCE CONSTRAINT ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1498-1508 DOI:10.6052/0459-1879-20-137

引言

输流管的振动与可靠性一直是核工业、航空航天和石油化工等行业密切关注的重要工程问题. 输流管也被认为是最简单的流固耦合系统, 在流体的激励下管道可发生丰富的流致振动现象^[1-4]. 为了提高系统的稳定性, 通常会在管道某些位置安装弹性或刚性约束; 在长时间服役后, 管道振动可能导致约束发生松动, 从而在管道和约束之间形成间隙. 在某些情形下, 因技术需求或装配需要, 管道与约束之间可能还预留了一定的间隙. 当管道振动的位移达到间隙约束边缘时, 二者就会发生碰撞. 这种非线性碰撞可能降低管道系统的可靠性, 大幅缩短结构的使用寿命. 现有关于输流管碰撞振动的研究工作均采用非线性弹簧力来近似描述这种间隙约束力, 只能用于模拟管道与间隙之间的柔性碰撞, 无法真实地描述刚性碰撞振动的非光滑特征. 因此, 很有必要针对输流管的非光滑碰撞振动开展相应的研究工作.

Paidoussis 教授是输流管动力学领域的集大成者, 早期在输流管数学模型的建立和稳定性问题上做了大量开创性的工作^[5-7], 在具有间隙约束管道的弹性碰撞振动问题上也有较多突破性的研究成果^[8-10]. Paidoussis 教授先后提出了立方非线性弹簧和修正的三线性弹簧来描述管道与间隙约束之间的碰撞力, 他的研究结果表明这两类模型在管道的柔性碰撞振动方面具有较好的适应性, 且理论解和实验结果在定性上吻合较好^{[8, 11]}. Sadath 等^[12]基于立方非线性弹簧和分段三线性弹簧计算了横向流激励下具有多处松动约束悬臂输流管的非线性碰撞振动行为, 分析了弹簧刚度对管道振动分岔行为的影响, 揭示了系统经由分岔通往混沌的路径. Hassan 等^[13]提出了一种能描述管道与约束接触长度和形态的碰撞力模型, 可更真实地描述单点接触时管道与约束之间碰撞力的分布情况. Hassan 等^[14-15]利用线性弹簧和阻尼器建立了U型管与支撑板的碰撞模型, 分析了管道发生流体弹性失稳时的碰撞振动响应, 探讨了约束间隙对碰撞力和接触率的影响规律. Azizian^[16]系统地研究了输流管与多种约束模型之间的接触形式, 考虑碰撞中摩擦力的影响, 根据实验测试和工程经验提出了一种能更准确描述碰撞约束力的模型. 张艳雷等^[17]分析了脉动内流激励下悬臂输流管在立方非线性弹簧约束下的分岔行为和混沌运动, 表明大的柔性变形系数可以消除随流速变化的混沌区域;在不同流速下,振荡频率的分岔情况会有复杂的间歇性混沌的发生. 王乙坤等^[18]分析了悬臂输流管与松动约束发生三维碰撞振动的平面和非平面运动, 研究结果表明在平行板约束下管道可出现直线型、椭圆型和瞬变型 3 种运动形态^[19-20]. Geng 等^[21]采用基于赫兹接触力模型的碰撞阻尼器分析了悬臂梁发生多模态共振时共振峰和共振幅值随碰撞参数的变化规律,发现大质量的碰撞球能较好地抑制悬臂梁的多模态共振现象, 而碰撞间隙的影响则与各阶模态有关, 且存在一个抑制多模态共振的最优间隙值.

上述关于输流管的碰撞振动研究均是基于非线性弹簧力的光滑性碰撞模型. 由于碰撞过程中弹簧要经历压缩和释放的过程, 故这类碰撞力随时间是连续变化的, 反映的是光滑性的作用过程. 碰撞是一种常见的强非线性现象, 碰撞前后存在某些状态向量 (如位移、速度和加速度等) 的突变使系统的响应曲线存在间断点. 因此, 刚硬结构之间的碰撞则是一种典型的非光滑现象^[22-26]. 罗冠炜和谢建华^[27-28]从非光滑的角度研究了有限自由度碰振系统的周期运动和分岔现象, 给出了碰振系统周期解的存在性和稳定性的一般分析方法. Yue 等^[29]从理论上分析了两自由度碰振系统的 Pitchfork 分岔和 Hopf 分岔, 给出了碰撞振动的 Poincare 映射, 揭示了对称和反对称不动点的演化路径. Li 等^[30-31]探讨了两自由度碰振系统的周期运动和分岔规律, 并计算了相应的 Lyapunov 指数, 给出了系统在某参数下会出现混沌运动的理论依据. 在连续体系统的碰撞振动方面, Wagg 等^[32]建立了悬臂梁与单点约束的非光滑碰撞振动模型, 运用 Galerkin 离散, 构造系统的碰撞恢复系数矩阵, 推导了梁单元在碰撞前后速度的传递规律, 其理论预测与实验结果在定性上具有较好的一致性.

本文将针对脉动内流激励下简支输流管与刚性间隙约束的碰撞振动问题, 提出其非光滑动力学数学模型, 依据碰撞判别条件和碰撞恢复系数来构建输流管与刚性约束发生碰撞前后速度和位移的传递矩阵; 在此基础上, 重点分析管道的刚性碰撞振动响应行为, 并探究刚性间隙约束参数对输流管碰振行为的影响机制.

1 数学模型

1.1 输流管理论模型

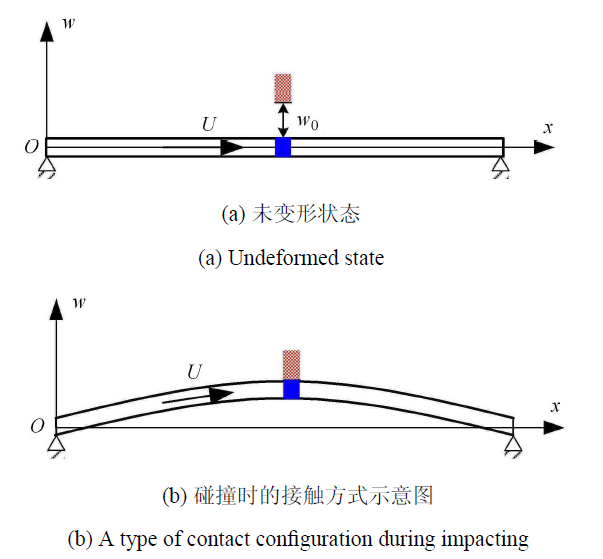
考虑如图 1 所示的简支输流管的刚性间隙约束模型. 当横向位移较大时, 固定在弹性管道中点的刚性套环 (蓝色) 与刚性约束 (红色) 会发生刚性碰撞. 本文主要探讨管道与刚性约束的正碰撞问题,因此管道被限制在 $wox$ 平面内运动. 图 1(a) 为管道未变形的初始状态,图 1(b) 为管道与约束发生碰撞接触的示意图. 图 1 中 $x$ 为沿管道长度方向的位置坐标,$w\left( {x,t} \right)$ 为管道的横向振动位移,$w_0 $ 为初始的间隙值. 管道原长为 $L$, 弯曲刚度为 $EI$,材料黏弹性系数为 $E^\ast $,密度为 $\rho _{\rm p} $,外径为 $d_{\rm o }$, 内径为 $d_{\rm i}$,横截面积为 $A$,单位长度的质量为 $m = \rho _{\rm p} A$. 管内不可压缩流体的密度为 $\rho _{\rm f}$,单位长度的质量为 $M = {\rho _{\rm f} \pi d_{\rm i}^2 } / 4$,流速为 $U$,且随时间做周期性变化.

图 1

新窗口打开|下载原图ZIP|生成PPT
图 1简支输流管单点碰撞振动示意图

Fig. 1Schematic of a simply supported pipe subjected to a point impact

根据 Euler-Bernoulli 细长梁理论, 考虑管道振动时轴线发生变形引起的几何非线性因素, 可将脉动内流激励下简支输流管的无量纲振动微分方程描述如下^[33-34]

(1) $ \begin{array}{l} \alpha \dfrac{\partial ^5\eta }{\partial \tau \partial \xi ^4} + \dfrac{\partial ^4\eta }{\partial \xi ^4} + \left[ {u^2 + \sqrt \beta \dot {u}\left( {1 - \xi } \right)} \right]\dfrac{\partial ^2\eta }{\partial \xi ^2} +\\ \qquad 2\sqrt \beta u\dfrac{\partial ^2\eta }{\partial \tau \partial \xi } + \dfrac{\partial ^2\eta }{\partial \tau ^2} - \kappa \dfrac{\partial ^2\eta }{\partial \xi ^2}\int_0^1 {\left( {\dfrac{\partial \eta }{\partial \xi }} \right)^2 d\xi } - \\ \qquad 2\alpha \kappa \dfrac{\partial ^2\eta }{\partial \xi ^2}\int_0^1 {\dfrac{\partial \eta }{\partial \xi }\dfrac{\partial ^2\eta }{\partial \tau \partial \xi } d\xi } = 0 \end{array} $

式中, 无量纲参数定义为

$$ \begin{array}{l} \eta \left( {\xi ,\tau } \right) = {w\left( {x,t} \right)}/L , \ \ \xi = x /L , \ \ d = {w_0 } /L \\ \tau = \sqrt {{EI}/{m + M}} t /{L^2} , \ \ u = \sqrt {M /{EI}} LU\\ \alpha = \sqrt {{EI} / {m + M}} {E^\ast }/ {L^2} , \ \ \beta = M /{\left( {m + M} \right)} \\ \kappa = {AL^2}/{(2I)} \end{array} $$

管内流体的无量纲脉动流速 $u$ 定义为 $u = u_0 \left( {1 + \sigma \sin \omega \tau } \right)$, 其中 $u_0 $ 为脉动流的平均流速, $\sigma $ 为脉动流的脉动幅值, $\omega $ 为脉动流的脉动频率. 下面采用 Galerkin 法对方程 (1) 进行离散化, 即

(2) $ \begin{array}{l} \left( {\xi ,\tau } \right) = \sum_{i = 1}^N {\varphi _i \left( \xi \right)q_i \left( \tau \right)} = {\pmb \varphi }\left( \xi \right){\pmb q} \left( \tau \right)\end{array} $

式中,$N$ 为模态截断数,$q_i \left( \tau \right)$ 为广义坐标,且 ${\pmb q}\left( \tau \right) = \left[ {q_1 ,q_2 , \cdots ,q_N } \right]^{\rm T}$;$\varphi _i \left( \xi \right)$ 为简支梁的模态函数,${ \pmb \varphi }\left( \xi \right) = \left[ {\varphi _1 ,\varphi _2 , \cdots ,\varphi _N } \right]$, $\varphi _i \left( \xi \right) = \sin (\lambda _i \xi) $ 且 $\lambda _i = i\pi ( i = 1$, $2, 3, \cdots )$ 为简支梁的固有频率. 经过 Galerkin 法处理后, 方程 (1) 可整理成如下形式

(3) $ \ddot{\pmb q} + {\pmb C}\dot {\pmb q} + {\pmb K\pmb q} + {\pmb g}\left( {{\pmb q}, \dot{\pmb q}} \right) = {\bf 0} $

式中,${\pmb C}$ 为系统的阻尼矩阵, ${\pmb K}$ 为刚度矩阵, ${\pmb g}\left( {{\pmb q},\dot{\pmb q}} \right)$ 为非线性向量. 各矩阵和向量的元素可由下式计算

(4) $ \left. \begin{array}{l} C_{ij} = \alpha \lambda _i^4 \delta _{ij} + 2\sqrt \beta u_0 \left[ {1 + \sigma \sin (\omega \tau) } \right]\int_0^1 {\varphi _i {\phi }'_j d\xi } \\ K_{ij} = \lambda _i^4 \delta _{ij} - u_0^2 \left( {1 + \sigma \sin \omega \tau } \right)^2\lambda _i^2 \delta _{ij} +\\ \qquad \sqrt \beta u_0 \sigma \omega \cos (\omega \tau )\int_0^1 {\left( {1 - \xi } \right)\varphi _i {\varphi }"_j d\xi } \\ g_i = \left( {q_j q_k q_l + q_j q_k \dot {q}_l } \right)\int_0^1 {\varphi _i {\varphi }"_j \int_0^1 {{\varphi }'_k {\varphi }'_l d\xi } d\xi } \end{array} \!\! \right\} $

1.2 碰撞传递关系

考虑刚性碰撞的强非线性和瞬时性, 本文将忽略管道与刚性约束发生碰撞过程所经历的时间^{[28, 32]}, 故可将碰撞前后管道上各点处节点的位移和速度传递关系写成如下形式

(5a)$ \eta \left( {\xi _{\rm b},\tau ^ + } \right) = d $

(5b)$ \dot {\eta }\left( {\xi _{\rm b},\tau ^ + } \right) = - r\dot {\eta }\left( {\xi _{\rm b},\tau ^ - } \right) $

(6a)$ \eta \left( {\xi ,\tau ^ + } \right) = \eta \left( {\xi ,\tau ^- } \right) , \quad \xi \ne \xi _{\rm b} $

(6b)$ \dot {\eta }\left( {\xi ,\tau ^ + } \right) = \dot {\eta }\left( {\xi ,\tau ^ - } \right) , \quad \xi \ne \xi _{\rm b} $

其中, $\xi _{\rm b}$ 为刚性间隙约束在管道长度方向上的作用位置; $\tau ^ - $ 表示碰撞前一时刻, $\tau ^ + $ 表示碰撞后一时刻; $r$为刚性间隙约束的碰撞恢复系数, 用于描述系统非光滑过程的参数. 式 (5) 表示碰撞前后 $\xi = \xi _{\rm b} $ 处碰撞节点的位移和速度传递关系, 式 (6) 表示碰撞前后 $\xi \ne \xi _{\rm b} $ 处各非碰撞节点的位移和速度关系; 从式 (5b) 可知, 碰撞前后管道在碰撞点的速度存在跳跃间断点, 这是一种典型的非光滑现象.

对式 (4) 进行数值积分时, 需将管道划分为 $P$ 个单元, 总节点数为 $Q = P + 1$. 将这些节点从左到右依次编号为 $1,2, \cdots ,Q$. 由于间隙约束位于管道中点 $\xi _{\rm b} = 1 /2$ 处, 为了应用状态向量的传递关系 (5) 和 (6), 管道中点处须有一个节点. 考虑到所划分节点和单元的对称性, 单元数 $P$ 须为偶数, 相应的总节点数 $Q$ 为奇数, 且 $\xi _{\rm b}= 1 /2$ 处节点的编号为 ${\left( {Q + 1} \right)} / 2$. 简支输流管在节点 $1$ 和节点 $Q$ 将应用简支梁的边界条件, 则管道上实际发生振动的自由节点数为 $Q - 2$, 自由节点的编号分别为 $2,3, \cdots ,Q - 1$. 对管道上参与振动的节点分别应用 Galerkin 法离散格式 (2), 可将刚性间隙约束下管道状态向量的关系式 (5) 和 (6) 写成如下格式

(7a)$ {\pmb \varphi }\left( {\xi _{\rm b} } \right){\pmb q}\left( {\tau ^ + } \right) = d $

(7b)$ {\pmb \varphi }\left( {\xi _{\rm b} } \right) \dot{\pmb q}\left( {\tau ^ + } \right) = - r{\pmb \varphi }\left( {\xi _{\rm b} } \right){\pmb q}\left( {\tau ^ - } \right) $

(8a)$ {\pmb \varphi }\left( \xi \right){\pmb q}\left( {\tau ^ + } \right) = \eta \left( {\xi ,\tau ^ + } \right) , \ \ \xi \ne \xi _{\rm b} $

(8b)$ {\pmb \varphi }\left( \xi \right) \dot{\pmb q}\left( {\tau ^ + } \right) = {\pmb \varphi }\left( \xi \right) \dot{\pmb q}\left( {\tau ^ - } \right) , \ \ \xi \ne \xi _{\rm b} $

为使碰撞节点 $\xi = \xi _{\rm b}$ 处管道的位移在碰撞瞬间为间隙值 $d$, 碰撞后速度变为碰撞前速度的 $ - r$ 倍, 且 $\xi \ne \xi _{\rm b} $ 处的单元和节点由于系统的惯性, 在管道发生横向振动方向上的位移和速度仍维持碰撞前的状态不变. 联立方程 (7a) 和 (8a), 并按 Galerkin 法展开如下

(9) $ \left[\!\!\begin{array}{ccccc} {\varphi _1 \left( {\xi _2 } \right)} \!&\! \!&\! {\varphi _i \left( {\xi _2 } \right)} \!&\! \!&\! {\varphi _N \left( {\xi _2 } \right)} \\ \!&\! \ddots \!&\! \!&\! \!&\! \\ {\varphi _1 \left( {\xi _j } \right)} \!&\! \!&\! {\varphi _i \left( {\xi _j } \right)} \!&\! \!&\! {\varphi _N \left( {\xi _j } \right)} \\ \!&\! \!&\! \!&\! \ddots \!&\! \\ {\varphi _1 \left( {\xi _{Q - 1} } \right)} \!&\! \!&\! {\varphi _i \left( {\xi _{Q - 1} } \right)} \!&\! \!&\! {\varphi _N \left( {\xi _{Q - 1} } \right)} \end{array} \!\! \right]_{\left( {Q - 2} \right)\times N} \cdot \\ \qquad \left(\!\! \begin{array}{c} {q_1 \left( {\tau ^ + } \right)} \\ \vdots \\ {q_i \left( {\tau ^ + } \right)} \\ \vdots \\ {q_N \left( {\tau ^ + } \right)} \end{array} \!\! \right)_{N\times 1} = \left(\!\! \begin{array}{c} {\eta \left( {\xi _2 ,\tau ^ + } \right)} \\ \vdots \\ d \\ \vdots \\ {\eta \left( {\xi _{Q - 1} ,\tau ^ + } \right)} \end{array} \!\! \right)_{\left( {Q - 2} \right)\times 1} $

式中, $i = 1,2, \cdots ,N$ 为模态编号, $j = {\left( {Q + 1} \right)} /2$ 为管道中点的碰撞节点编号. 式 (9) 描述了管道在碰撞前后的广义位移的传递关系, 该方程左边系数矩阵由模态函数和自由节点的坐标构成, 方程右边表示管道在发生碰撞瞬间各点的位移. 方程 (9) 的解即为碰撞发生后 $\tau ^ + $ 时刻管道的广义位移. 式 (9) 是 $N$ 元一次线性方程组, 其独立方程的数量为 $Q - 2$, 该方程组有唯一解的条件之一是系数矩阵为方阵, 故 $N = Q - 2$. 令

(10) $ {\pmb \varPhi } = \left[ \!\! \begin{array}{ccccc} {\varphi _1 \left( {\xi _2 } \right)} & & {\varphi _i \left( {\xi _2 } \right)} & & {\varphi _N \left( {\xi _2 } \right)} \\ & \ddots & & & \\ {\varphi _1 \left( {\xi _j } \right)} & & {\varphi _i \left( {\xi _j } \right)} & & {\varphi _N \left( {\xi _j } \right)} \\ & & & \ddots & \\ {\varphi _1 \left( {\xi _{Q - 1} } \right)} & & {\varphi _i \left( {\xi _{Q - 1} } \right)} & & {\varphi _N \left( {\xi _{Q - 1} } \right)} \end{array} \!\! \right]_{\left( {Q - 2} \right)\times N} \\ {\pmb Y} = \left(\!\! \begin{array}{c} {\eta \left( {\xi _2 ,\tau ^ + } \right)} \\ \vdots \\ d \\ \vdots \\ {\eta \left( {\xi _{Q - 1} ,\tau ^ + } \right)} \end{array} \!\! \right)_{\left( {Q - 2} \right)\times 1} $

则碰撞前后管道广义位移的传递关系可改写为

(11) $ {\pmb q}\left( {\tau ^ + } \right) = {\pmb \varPhi }^{ - 1}{\pmb Y} = {\pmb \varGamma \pmb Y} $

式中, ${\pmb \varGamma } = {\pmb \varPhi }^{ - 1}$ 为碰撞前后位移的传递矩阵. 为得到碰撞前后广义速度的传递关系, 联立方程 (7b) 和 (8b), 应用上述 $N = Q - 2$ 的推论, 将这两个方程按 Galerkin 法展开如下

(12) $ \left[ \!\! \begin{array}{ccccc} {\varphi _1 \left( {\xi _2 } \right)} & & {\varphi _i \left( {\xi _2 } \right)} & & {\varphi _N \left( {\xi _2 } \right)} \\ & \ddots & & & \\ {\varphi _1 \left( {\xi _j } \right)} & & {\varphi _i \left( {\xi _j } \right)} & & {\varphi _N \left( {\xi _j } \right)} \\ & & & \ddots & \\ {\varphi _1 \left( {\xi _{Q - 1} } \right)} & & {\varphi _i \left( {\xi _{Q - 1} } \right)} & & {\varphi _N \left( {\xi _{Q - 1} } \right)} \end{array} \!\! \right]_{\left( {Q - 2} \right)\times N}\cdot \\ \qquad \left(\!\! \begin{array}{c} {\dot {q}_1 \left( {\tau ^ + } \right)} \\ \vdots \\ {\dot {q}_i \left( {\tau ^ + } \right)} \\ \vdots \\ {\dot {q}_N \left( {\tau ^ + } \right)} \end{array} \!\! \right)_{N\times 1} = \left[\!\! \begin{array}{ccccc} 1 & & 0 & & 0 \\ & \ddots & & & \\ 0 & & { - r} & & 0 \\ & & & \ddots & \\ 0 & & 0 & & 1 \end{array} \!\! \right]_{N\times \left( {Q - 2} \right)} \cdot \\ \qquad \left[\!\! \begin{array}{ccccc} {\varphi _1 \left( {\xi _2 } \right)} & & {\varphi _i \left( {\xi _2 } \right)} & & {\varphi _N \left( {\xi _2 } \right)} \\ & \ddots & & & \\ {\varphi _1 \left( {\xi _j } \right)} & & {\varphi _i \left( {\xi _j } \right)} & & {\varphi _N \left( {\xi _j } \right)} \\ & & & \ddots & \\ {\varphi _1 \left( {\xi _{Q - 1} } \right)} & & {\varphi _i \left( {\xi _{Q - 1} } \right)} & & {\varphi _N \left( {\xi _{Q - 1} } \right)} \end{array} \!\! \right]_{\left( {Q - 2} \right)\times N} \cdot \\ \qquad \left( \!\! \begin{array}{c} {\dot {q}_1 \left( {\tau ^ - } \right)} \\ \vdots \\ {\dot {q}_i \left( {\tau ^ - } \right)} \\ \vdots \\ {\dot {q}_N \left( {\tau ^ - } \right)} \end{array} \!\! \right)_{N\times 1} $

其中, 恢复系数 $r$ 作用在碰撞节点 $j = {\left( {Q + 1} \right)} / 2$ 处. 令

(13) $ {\pmb R} = \left[\!\! \begin{array}{ccccc} 1 & & 0 & & 0 \\ & \ddots & & & \\ 0 & & { - r} & & 0 \\ & & & \ddots & \\ 0 & & 0 & & 1 \end{array}\!\! \right]_{N\times \left( {Q - 2} \right)} $

则方程 (12) 可写成如下形式

(14) $ {\pmb \varPhi} \dot {\pmb q}\left( {\tau ^ + } \right) = {\pmb R}{\pmb\varPhi} \dot {\pmb q}\left( {\tau ^ - } \right) $

在方程 (14) 中,$\dot{\pmb q}\left( {\tau ^ + } \right)$ 的解满足碰撞前后管道广义速度的传递关系,即

(15) $ \dot{\pmb q}\left( {\tau ^ + } \right) = {\pmb \varPhi}^{ - 1}{\pmb R}{\pmb\varPhi} \dot {\pmb q}\left( {\tau ^ - } \right) = {\pmb \varLambda} \dot {\pmb q}\left( {\tau ^ - } \right) $

式中, ${\pmb \varLambda } = {\pmb \varPhi }^{ - 1}{\pmb R}{\pmb\varPhi}$ 表示碰撞前后系统速度的传递关系,亦即碰撞恢复系数矩阵. 联立式 (11) 和式 (15), 运用四阶龙格库塔法对方程 (3) 进行积分即可得到输流管非光滑碰撞振动的动力学响应.

值得一提的是, 本文关于碰撞振动状态向量的传递关系式 (11) 和式 (15) 适用于 Galerkin 法分析管和梁等结构的非光滑碰撞动力学行为. 应用时仅需根据结构的特点 (对称、反对称) 和约束所在的位置, 适当地划分单元, 使得间隙约束作用某一节点上, 但须满足实际发生振动的自由节点数等于应用 Galerkin 法时所取模态截断数的条件. 下面将利用式 (11) 和式 (15) 研究脉动内流激励下简支输流管与单侧刚性间隙约束的碰撞动力学行为, 着重讨论间隙约束参数对管道非线性碰撞振动响应的影响.

2 无间隙约束时输流管的流致振动

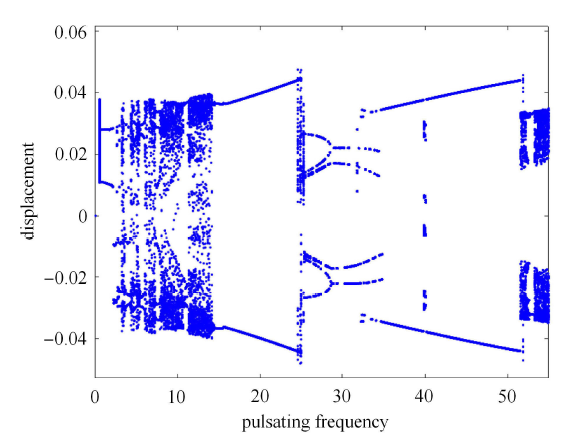
为验证本文算法的有效性, 并为后文间隙大小的取值提供依据, 选取计算参数为: $N = 5$, $u = 4.5$,$\alpha = 0.005$,$\beta = 0.64$,$\kappa = 5000$,$\sigma = 0.2$. 经数值计算, 得到在没有间隙约束时管道中点无量纲位移随无量纲流速脉动频率的分岔图, 如图 2 所示. 该位移分岔图的计算法则定义为: 当管道中点的速度发生反向时, 记录速度反向前一时刻的位移. 若采用 $N = 2$ 和 $\sigma = 0.4$ 作进一步计算, 所得管道的动态响应分岔图与 Wang 等^[35]的计算结果完全吻合, 这表明本文关于无约束两端支承输流管的动态响应问题的算法是正确的. 从计算结果来看, 在脉动频率约为 $0 \leqslant \omega \leqslant 55$ 时, 管道位移的最大值约为 $0.046$, 且只在极少数脉动频率能达到最大值; 在大部分脉动频率范围内, 管道的位移均小于 $0.038$. 此外,结合文献^[35] 的分析结果可知,在 $4 < \omega < 14$ 频率范围内管道主要表现为复杂的非周期运动. 由于两端支承管在定常流速下的失稳方式为静态屈曲,故在更高频率值的范围内管道易出现对称和反对称的周期运动,其分岔图中还可能包含有多周期运动的窗口.

图 2

新窗口打开|下载原图ZIP|生成PPT
图 2无间隙约束时管道中点位移随流速脉动频率变化的分岔图

Fig. 2Bifurcation diagram of the mid-point displacement of the supported pipe without rigid constraint under various pulsating frequencies

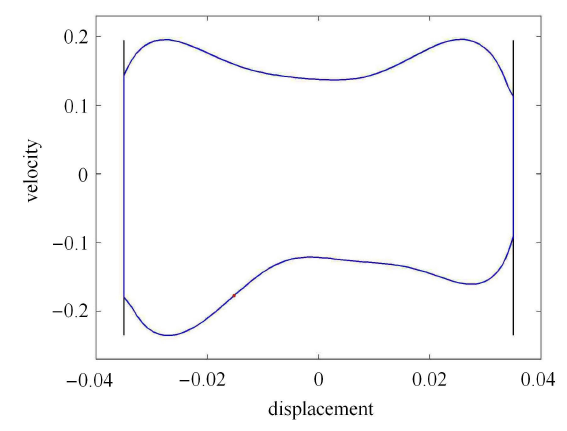
在进行 Galerkin 法离散化时, 若单元数 $P = 2$、总节点数 $Q = 3$, 则系统的自由节点数为 $Q - 2 = 1$, 此时两端支承输流管动力学模型可以简化成一个单自由度的碰撞振动系统. 本文采用罗冠炜和谢建华等的方法^[27]对该单自由度输流管系统进行碰撞振动分析, 发现在 $\omega = 14$,$R = 0.8$ 和 $d = 0.035$ 时管道在双侧对称刚性约束下出现了典型的 $2 / 1$ 碰振响应 (图 3), 这在定性上与文献^[27] 的结论是一致的, 表明本文关于碰撞前后状态向量传递关系的描述是正确的.

图 3

新窗口打开|下载原图ZIP|生成PPT
图 3$\omega =14$, $R=0.8$, $d=0.035$ 时管道单自由度系统的碰撞振动响应

Fig. 3Vibro-impact response of a single-degree-of-freedom system of the pipe with $\omega =14$, $R=0.8$ and $d=0.035$

3 刚性约束间隙值的影响

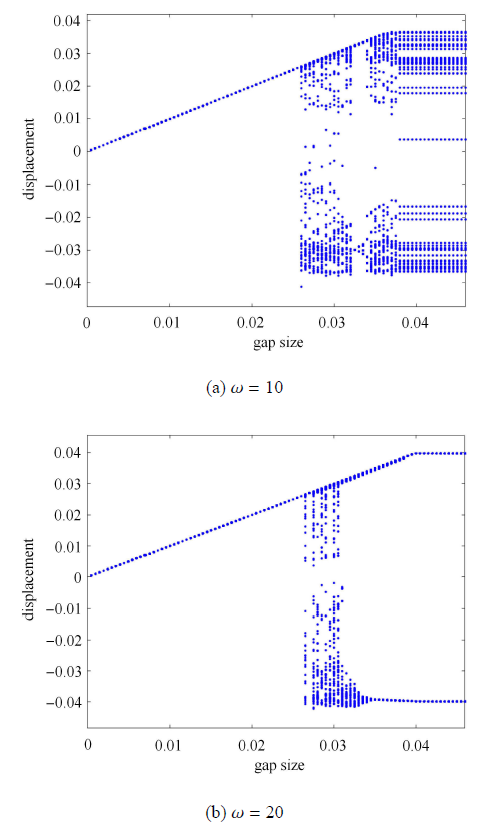
从图 2 结果可知, 当 $\omega = 10$ 时管道的响应处于非周期运动状态, 当 $\omega = 20$ 时管道处于周期运动状态. 因此, 本文选择性地取这两种典型运动状态下的频率值来初步分析约束间隙对管道动力学响应的影响规律. 典型的计算结果如图 4 所示, 其中恢复系数 $r = 0.9$.

图 4

新窗口打开|下载原图ZIP|生成PPT
图 4管道中点位移随间隙值变化的分岔图

Fig. 4Bifurcation diagrams of the mid-point displacement of the supported pipe under various gap distances

计算结果显示, 当 $\omega = 10$ 时, 较小的间隙值 ($0 \leqslant d \leqslant 0.025)$ 会抑制管道原有的振动, 此时管道可能粘连在刚性约束上; 随着间隙值的增大 ($0.026 \leqslant d \leqslant 0.046)$, 管道可发生复杂的振动行为, 故在分岔图中显示为密集的散点. 当间隙值取为 $0.038 \leqslant d \leqslant 0.046$ 范围时, 因管道位移最大值约为 $0.038$, 故管道与刚性约束之间的碰撞很弱或不再发生接触. 当 $\omega = 20$ 时, 较小的间隙值如 $0 \leqslant d \leqslant 0.027$ 仍可使管道粘贴在刚性约束上而不出现振动; 当间隙值在 $0.028 \leqslant d \leqslant 0.035$ 范围时, 管道会发生复杂的振动行为, 并在更大的间隙值时逐渐演化为周期 1 运动形态; 在 $0.036 \leqslant d \leqslant 0.04$ 范围内, 管道将维持周期 1 碰撞振动; 当间隙值继续增大到 $0.04 \leqslant d \leqslant 0.046$ 范围时, 因间隙值较大, 管道将不再与刚性约束发生碰撞. 上述列出的各种动力学现象表明, 约束间隙值对管道的动态响应行为影响十分明显, 较小的约束间隙值可抑制管道的振动, 中等大小的间隙值会导致复杂的运动形态, 较大的间隙值则不会发生碰撞.

基于图 4 的计算结果, 选取两个间隙值 ( $d = 0.03$ 和 $d = 0.035)$ 来分析管道的刚性碰撞振动行为随脉动频率的变化情况, 以进一步揭示间隙值对管道动力学响应的影响规律. 图 5 和图 6 分别给出了这两种间隙值下管道中点的位移和速度随管内流体脉动频率变化的分岔图. 其中, 速度分岔图的计算法则为: 当管道与约束发生碰撞时 $\eta \left( {\xi _{\rm b},\tau ^ + } \right) = d$, 记录碰撞前一时刻的速度 $\dot {\eta }\left( {\xi _{\rm b} ,\tau ^ - } \right)$. 从该计算法则可知, 速度分岔图主要反映管道与刚性约束间发生碰撞的次数, 从而反映出管道与约束的周期和非周期性的碰撞振动行为.

图 5

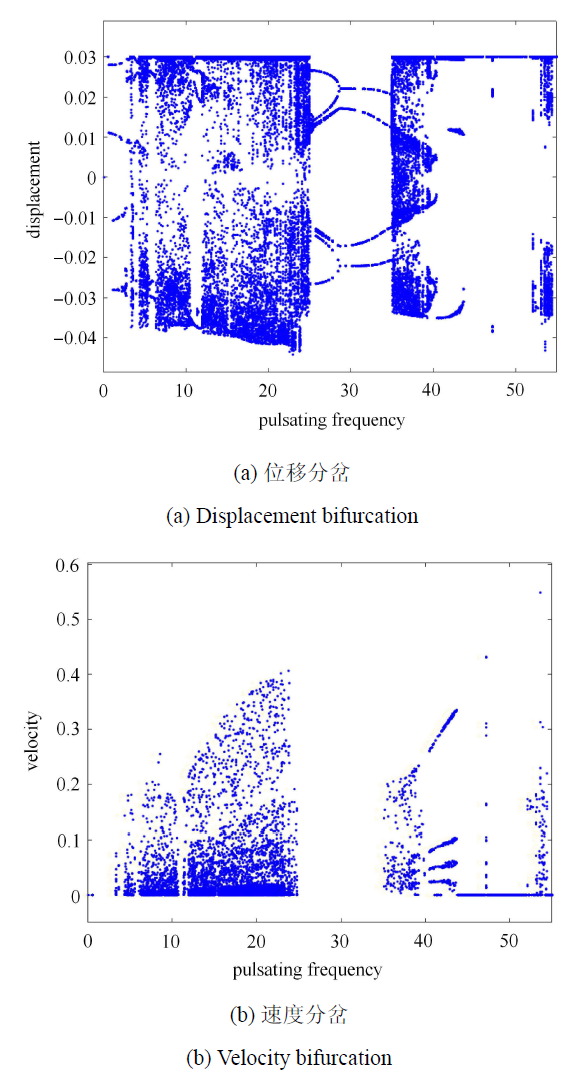
新窗口打开|下载原图ZIP|生成PPT
图 5管道中点位移和速度随脉动频率变化的分岔图, $d =0.03$

Fig. 5Bifurcation diagrams of the mid-point displacement and velocity of the supported pipe under various pulsating frequencies, for $d =0.03$

图 6

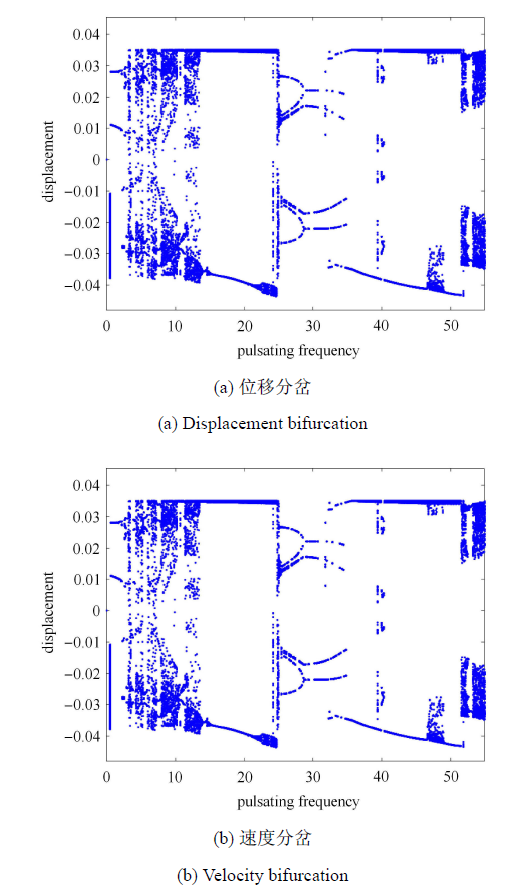
新窗口打开|下载原图ZIP|生成PPT
图 6管道中点位移和速度随脉动频率变化的分岔图, $d =0.035$

Fig. 6Bifurcation diagrams of the mid-point displacement and velocity of the supported pipe under various pulsating frequencies, for $d =0.035$

从图 5 的管道中点位移和速度分岔图可知, $d = 0.03$ 时在较宽的脉动频率范围内, 即 $3 \leqslant \omega \leqslant 24.6$,$35.1 \leqslant \omega \leqslant 40.4$,$52.1 \leqslant \omega \leqslant 54.4$, 管道均处于非周期运动状, 表现为一种无序的碰撞振动状态; 在 $24.7 \leqslant \omega \leqslant 35$ 范围里, 管道振动行为与无间隙约束时保持一致 (见图 2), 速度分岔图则显示此时管道与约束不发生接触; 在较高脉动频率值区域内 ($43.8 \leqslant \omega \leqslant 52)$, 管道与间隙约束仍可粘连在一起而不发生振动. 不过, 在某些较高脉动频率值的参数范围 (如 $40.5 \leqslant \omega \leqslant 43.7)$ 里, 管道在一个运动周期内可出现多次碰撞振动的情形. 从图 6 可发现, 当 $d = 0.035$ 时, 管道发生非周期性碰撞振动的频率区间比 $d = 0.03$ 的要窄, 而发生周期性多次碰撞振动的脉动频率范围显著增宽 (如 $15.3 \leqslant \omega \leqslant 20.5$ 和 $35.6 \leqslant \omega \leqslant 46.3)$; 当 $20.6 \leqslant \omega \leqslant 24.6$ 或 $46.7 \leqslant \omega \leqslant 49.1$ 时, 管道与约束发生复杂的多次碰撞. 从上述关于图 5 和图 6 的分析可知, 若一个振动周期内出现多次碰撞, 其碰撞振动次数通常会随着脉动频率的增大而逐渐增多. 当运动管道遇到固定的刚性约束时, 加速度方向保持不变, 碰撞前的速度经由多次碰撞逐渐减小到零 (如图 6 中 $20.4 \leqslant \omega \leqslant 24.7$ 的情形), 此时管道发生了黏滑运动^[36]. 这种黏滑运动是非光滑系统不同于光滑系统的动力学现象之一.

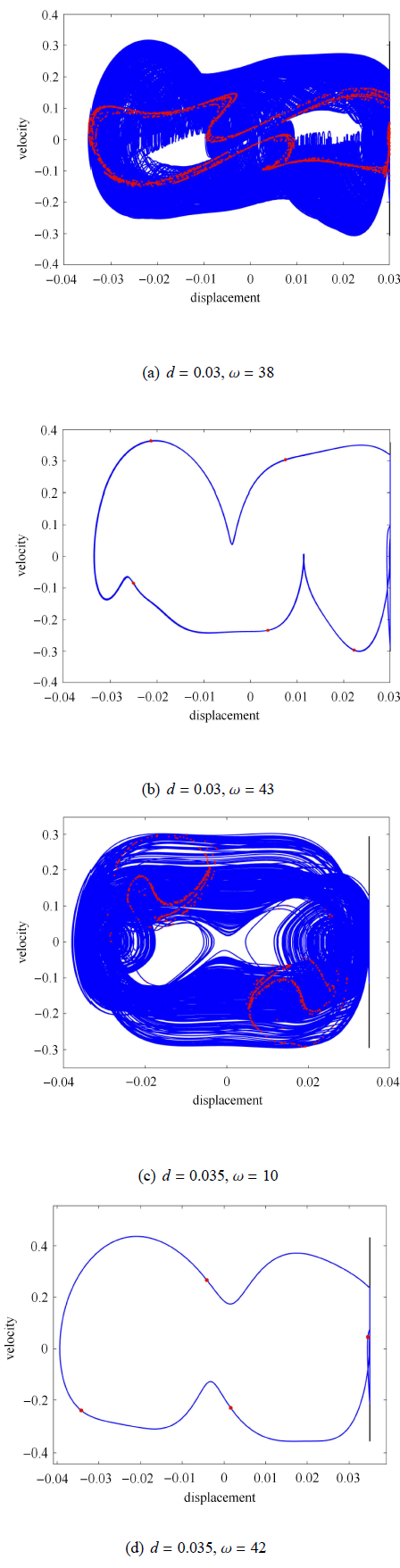
为了更直观地观察管道在某些脉动频率激励下的动态响应, 图 7 描绘了 4 种不同脉动频率取值时管道振动的相图和 Poincare 映射图. 其中,Poincare 映射的法则为: 每经历一个脉动激励周期, 记录当前时刻管道中点的位移和速度. 根据 Poincare 映射点的分布形态可以判断此时管道的运动状态 (如周期, 概周期和混沌等). 图 7(a)和图 7(c) 分别给出了 $d = 0.03$,$\omega = 38$ 和 $d = 0.035$,$\omega = 10$ 时管道的动态响应, 此时的 Poincare 映射图为一系列离散点构成且具有分形结构的奇异吸引子, 表明此时管道的非周期碰撞振动状态是混沌运动. 图 7(b) 和图 7(d) 分别显示了 $d = 0.03$, $\omega = 43$ 和 $d = 0.035$,$\omega = 42$ 时管道的动态响应, 此时管道处于周期1运动状态. 从图 7(b) 的 Poincare 映射图可看到 5 个映射点, 而图 7(d) 中则只有 4 个映射点; 从映射法则可知, 映射点的数量代表经历的脉动周期数, 故二者是不同类型的周期性碰撞振动. 由图 5(b) 和图 6(b) 的速度分岔图可知, 在这两个脉动频率下, 管道与刚性约束均发生了 4 次碰撞. 由文献^[27] 可进一步发现, 图 7(b) 是 $4/5$ 的周期碰撞振动, 而图 7(d) 是 $4 /4$ 的周期碰撞振动, 这也是非光滑碰振系统特有的现象之一.

图 7

新窗口打开|下载原图ZIP|生成PPT
图 7管道中点运动的相图 (蓝色线) 和 Poincare 映射 (红色点)

Fig. 7Phase portrait (blue line) and Poincare map (red point) of the mid-point of the pipe

4 碰撞恢复系数的影响

为了探究恢复系数对管道碰撞振动行为的影响, 约束间隙值取为 $d = 0.035$, 其他参数值保持不变. 图 8 给出了恢复系数 $r = 0.8$,$r = 0.7$ 和 $r = 0.6$ 时管道中点位移和速度的响应随脉动频率变化的分岔图. 与图 6 中 $r = 0.9$ 的分岔图对比可看出, 随着恢复系数的降低, 复杂的非周期碰撞振动所对应的脉动频率区间显著增大, 周期性碰撞振动的脉动频率范围大幅缩小. 由此可见, 对本文所研究的碰撞振动系统, 较小的恢复系数极大地增加了系统出现不规则碰撞振动现象的可能性, 而较大的恢复系数有助于使系统在较宽的频率范围内处于周期性碰撞振动状态, 可一定程度上抑制混沌运动的出现.

图 8

新窗口打开|下载原图ZIP|生成PPT
图 8管道中点位移和速度随脉动频率变化的分岔图

Fig. 8Bifurcation diagrams of the mid-point displacement and velocity of the supported pipe under various pulsating frequencies

5 结论

本文基于非光滑理论建立了简支输流管与刚性间隙约束的碰撞振动模型, 构造了碰撞前后系统状态向量的传递矩阵, 分析了在脉动内流激励下管道与刚性间隙约束的碰撞振动行为, 讨论了间隙约束间隙值和碰撞恢复系数对管道动态响应的影响. 研究结果表明, 较小的约束间隙值会使管道粘连在刚性约束上, 即不出现振动; 较大的约束间隙值可使管道随流速脉动频率的变化而演化出规律的多周期运动和复杂的非周期碰撞振动; 约束间隙值的大小还会显著影响出现非周期性碰撞振动的流速脉动频率范围. 碰撞恢复系数对管道周期和非周期性碰撞振动的影响也十分显著, 较高的恢复系数值有利于使管道处于周期性碰撞振动状态, 而较小的恢复系数值则容易使系统在更宽的脉动频率范围内出现非周期性的碰撞振动. 此外, 本文研究工作还观察到输流管刚性碰撞时的黏滑现象, 这是有别于以往输流管弹性碰撞振动研究结果的新的非光滑动力学特征.

作者信息：

王乙坤, 讲师, 湖北文理学院机械工程学院, 湖北省襄阳市隆中路296号, 441053; 华中科技大学力学系, 湖北省武汉市洪山区珞喻路1037号, 430074; wangyikun18@hbuas.edu.cn

王琳, 教授,华中科技大学力学系, 湖北省武汉市洪山区珞喻路1037号, 430074; wanglindds@hust.edu.cn

倪樵, 教授,华中科技大学力学系, 湖北省武汉市洪山区珞喻路1037号, 430074; niqiao@hust.edu.cn

杨沫, 讲师,湖北文理学院机械工程学院, 湖北省襄阳市隆中路296号, 441053; ym901116@163. com

刘德政, 副教授,湖北文理学院机械工程学院, 湖北省襄阳市隆中路296号, 441053; liudezheng126@126.com

秦涛, 副教授,湖北文理学院机械工程学院, 湖北省襄阳市隆中路296号, 441053; heu_qt@163.com

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

徐鉴, 杨前彪. 输液管模型及其非线性动力学近期研究进展
力学进展, 2004,34(2):182-194

URL [本文引用: 1]

综述了输液管系统的各类物理模型及其相应的数学模型,在流体满足基本假设条件下,对于管道内径远远小于管道长度的直管和曲管,详细叙述了梁模型管动力学数学模型的建模过程以及建模方法,针对在水动压力作用下以及管道短而且薄的情形,综述了壳模型的输液管道的动力学方程.在此基础上,概述了近几年来输液管道的非线性振动、稳定性、分岔与混沌、特别是管道控制的研究现状,并对今后的发展趋势作了分析和预测.综观非线性动力学理论的发展历程可以发现选取研究对象和典型的数学模型是至关重要的.对于低维的非线性系统,常常选用van der Pol、Duffing、Mathieu、Lorenz等典型系统来进行研究工作的.通过本文可以看出,对于研究高维非线性系统动力学,流诱发输液管的动力学问题是非常典型的模型之一,它有着容易理解的工程背景、包含了梁和壳的振动问题,并且它的数学模型相对简单,然而却能包含非常复杂的非线性动力学现象,同时容易解释数学方法得到的结果易对应到工程中的实际现象.本文希望通过对输液管动力学模型及其非线性动力学和控制研究现状的综述,建立高维非线性动力学的分析模型,以便发展高维非线性动力学的分岔与混沌理论,同时建立相应的控制理论基础.

( Xu

Jian

, Yang

Qianbiao

. Recent development on models and nonlinear dynamics of pipes conveying fluid
Advances in Mechamics, 2004,34(2):182-194 (in Chinese))

URL [本文引用: 1]

徐鉴, 王琳. 输流管动力学分析和控制. 北京: 科学出版社, 2015

( Xu

Jian

, Wang

Lin

. Dynamics and Control of Fluid-Conveying Pipe Systems. Beijing, Science Press, 2015 (in Chinese))

[3]

金基铎, 邹光胜, 张宇飞. 悬臂输流管道的运动分岔现象和混沌运动
力学学报, 2002,34(6):863-873

( Jin

Jiduo

, Zou

Guangsheng

, Zhang

Yufei

. Bifurcations and chaotic motions of a cantilevered pipe conveying fluid
Chinese Journal of Theoretical and Applied Mechanics, 2002,34(6):863-873 (in Chinese))

[4]

王乙坤, 王琳. 分布式运动约束下悬臂输液管的参数共振研究
力学学报, 2019,51(2):558-568

[本文引用: 1]

( Wang

Yikun

, Wang

Lin

. Parametric resonance of a cantilevered pipe conveying fluid subjected to distributed motion constraints
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):558-568 (in Chinese))

[本文引用: 1]

[5]

Modarres-Sadeghi

, Paidoussis

, Semler

. Three-dimensional oscillations of a cantilever pipe conveying fluid
International Journal of Non-Linear Mechanics, 2008,43(1):18-25

DOI URL [本文引用: 1]

Abstract

The aim of the study described in this paper is to investigate the two-dimensional (2-D) and three-dimensional (3-D) flutter of cantilevered pipes conveying fluid. Specifically, by means of a complete set of non-linear equations of motion, two questions are addressed: (i) whether for a system losing stability by either 2-D or 3-D flutter the motion remains of the same type as the flow velocity is increased substantially beyond the Hopf bifurcation precipitating the flutter; (ii) whether the bifurcational behaviour of a horizontal system and a vertical one (sufficiently long for gravity to have an important effect on the dynamics) are substantially similar. Stability maps and tables are used to delineate areas in a flow velocity versus mass parameter plane where 2-D or 3-D motions occur, and limit-cycle motions are illustrated by phase–plane plots, PSDs and cross-sectional diagrams showing whether the motion is circular (3-D) or planar (2-D).

[6]

Modarres-Sadeghi

, Paidoussis

. Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends
Journal of Fluids and Structures, 2009,25(3):535-543

DOI URL

Abstract

In this paper, the post-divergence behaviour of extensible fluid-conveying pipes supported at both ends is studied using the weakly nonlinear equations of motion of Semler, Li and Païdoussis. The two coupled nonlinear partial differential equations are discretized via Galerkin's method and the resulting set of ordinary differential equations is solved either by Houbolt's finite difference method or via AUTO. Typically, the pipe is stable at its original static equilibrium position up to the flow velocity where it loses stability by static divergence via a supercritical pitchfork bifurcation. The amplitude of the resultant buckling increases with increasing flow, but no secondary instability occurs beyond the pitchfork bifurcation. The effects of the system parameters on pipe behaviour as well as the possibility of a subcritical pitchfork bifurcation have also been studied.

[7]

Paidoussis

. Fluid-Structure Interactions: Slender Structures and Axial Flow. 2 ed. San Diego: Elsevier Academic Press, 2014

[本文引用: 1]

[8]

Paidoussis

, Semler

. Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid: A full nonlinear analysis
Nonlinear Dynamics, 1993,4(6):655-670

DOI URL [本文引用: 2]

[9]

Ghayesh

, Paidoussis

. Three-dimensional dynamics of a cantilevered pipe conveying fluid, additionally supported by an intermediate spring array
International Journal of Non-Linear Mechanics, 2010,45(5):507-524

[10]

Ghayesh

, Pa$\check{i}$doussis

, Modarres-Sadeghi

. Three-dimensional dynamics of a fluid-conveying cantilevered pipe fitted with an additional spring-support and an end-mass
Journal of Sound and Vibration, 2011,330(12):2869-2899

[本文引用: 1]

[11]

Paidoussis

, Li

, Moon

. Chaotic oscillations of the autonomous system of a constrained pipe conveying fluid
Journal of Sound and Vibration, 1989,135(1):1-19

[本文引用: 1]

[12]

Sadath

, Dixit

, Vyasarayani

. Dynamics of cross-flow heat exchanger tubes with multiple loose supports
Journal of Pressure Vessel Technology, 2016,138(5):051303

[本文引用: 1]

[13]

Hassan

, Weaver

, Dokainish

. A new tube/support impact model for heat exchanger tubes
Journal of Fluids and Structures, 2005,21(5-7):561-577

[本文引用: 1]

[14]

Hassan

, Mohany

. Fluidelastic instability modeling of loosely supported multispan U-tubes in nuclear steam generators
Journal of Pressure Vessel Technology, 2013,135(1):011306

[本文引用: 1]

[15]

Hassan

, Weaver

, Dokainish

. The effects of support geometry on the turbulence response of loosely supported heat exchanger tubes
Journal of Fluids and Structures, 2003,18(5):529-554

[本文引用: 1]

[16]

Azizian

. Dynamic Modeling of Tube-Support Interaction in Heat Exchangers
école Polytechnique de Montréal, 2012

[本文引用: 1]

[17]

张艳雷, 黄慧春, 陈立群. 振荡流作用下受约束的悬臂输流管的分岔特性
噪声与振动控制, 2012,32(5):46-48

[本文引用: 1]

( Zhang

Yanlei

, Huang

Huichun

, Chen

Liqun

. Bifurcation analysis of a constrained cantilevered pipe conveying fluid under the harmonic parametric excitations
Noise and Vibration Control, 2012,32(5):46-48 (in Chinese))

[本文引用: 1]

[18]

王乙坤, 倪樵, 王琳等. 具有松动约束悬臂输液管的三维非线性振动
科学通报, 2017,62(36):4270-4277

[本文引用: 1]

( Wang

Yikun

, Ni

Qiao

, Wang

Lin

, et al. Three-dimensional nonlinear dynamics of a cantilevered pipe conveying fluid subjected to loose constraints
Chinese Science Bulletin, 2017,62(36):4270-4277 (in Chinese))

[本文引用: 1]

[19]

Yang

, An

, Qian

, et al. A comparative analysis of modal motions for the gyroscopic and non-gyroscopic two degree-of-freedom conservative systems
Journal of Sound and Vibration, 2016,385:300-309

[本文引用: 1]

[20]

Yang

, An

, Qian

, et al. Elliptic motions and control of rotors suspending in active magnetic bearings
ASME Journal of Computational and Nonlinear Dynamics, 2016,11(5):054503

[本文引用: 1]

[21]

Geng

, Ding

, Wei

, et al. Suppression of multiple modal resonances of a cantilever beam by an impact damper
Applied Mathematics and Mechanics, 2020,41(3):383-400

[本文引用: 1]

[22]

Budd

, Dux

, Cliffe

. The effect of frequency and clearance variations on single-degree-of-freedom impact oscillators
Journal of Sound & Vibration, 1995,183(4):475-502

[本文引用: 1]

[23]

金栋平, 胡海岩. 碰撞振动及其典型现象
力学进展, 1999,29(2):155-163

( Jin

Dongping

, Hu

Haiyan

. Vibro-impacts and their typical behaviors of mechanical systems
Advances in Mechanics, 1999,29(2):155-163 (in Chinese))

[24]

, Tan

. Lyapunov exponent calculation of a two-degree-of-freedom vibro-impact system with symmetrical rigid stops
Chinese Physics B, 2011,20(4):123-131

[25]

Guo

, Zhang

, Tian

. Periodic solution of a non-smooth double pendulum with unilateral rigid constrain
Symmetry, 2019,11(7):886

[26]

秦志英, 李群宏. 一类非光滑映射的边界碰撞分岔
力学学报, 2013,45(1):25-29.

[本文引用: 1]

( Qin

Zhiying

, Li

Qunhong

. Border-collision bifurcation in a kind of non-smooth maps
Chinese Journal of Theoretical and Applied Mechanics, 2013,45(1):25-29 (in Chinese))

[本文引用: 1]

[27]

罗冠炜, 谢建华. 碰撞振动系统的周期运动和分岔. 北京: 科学出版社, 2004

[本文引用: 4]

( Luo

Guanwei

, Xie

Jianhua

. Periodic motions and bifurcations of vibrio-impact systems. Beijing: Science Press, 2004 (in Chinese))

[本文引用: 4]

[28]

Luo

, Xie

, Zhu

, et al. Periodic motions and bifurcations of a vibro-impact system
Chaos, Solitons & Fractals, 2008,36(5):1340-1347

[本文引用: 2]

[29]

Yue

, Xie

. Symmetry and bifurcations of a two-degree-of-freedom vibro-impact system
Journal of Sound and Vibration, 2008,314(1-2):228-245

[本文引用: 1]

[30]

, Chen

, Wei

, et al. The analysis of the spectrum of Lyapunov exponents in a two-degree-of-freedom vibro-impact system
International Journal of Non-Linear Mechanics, 2011,46(1):197-203

[本文引用: 1]

[31]

李群宏, 陈玉明. 双侧约束对碰系统 Lyapunov 指数分析
振动与冲击, 2012,31(7):148-152

[本文引用: 1]

( Li

Qunhong

, Chen

Yuming

. Analysis of the Lyapunov exponential spectrum in a vibro-impact system with two-sided rigid stops
Journal of Vibration and Shock, 2012,31(7):148-152 (in Chinese))

[本文引用: 1]

[32]

Wagg

, Bishop

. Application of non-smooth modelling techniques to the dynamics of a flexible impacting beam
Journal of Sound and Vibration, 2002,256(5):803-820

DOI URL [本文引用: 2]

[33]

Jin

, Song

. Parametric resonances of supported pipes conveying pulsating fluid
Journal of Fluids and Structures, 2005,20(6):763-783

[本文引用: 1]

[34]

Panda

, Kar

. Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances
Journal of Sound and Vibration, 2008,309(3-5):375-406

[本文引用: 1]

[35]

Wang

. A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid
International Journal of Non-Linear Mechanics, 2009,44(1):115-121

[本文引用: 2]

[36]

, Xu

, Wang

, et al. Impulsive control of sticking motion in van der Pol one-sided constraint system
Applied Mathematics and Computation, 2014,248:363-370

[本文引用: 1]