, 李溢铭FINTE SUBDOMAIN RADIAL BASIS COLLOCATION METHOD FOR THE LARGE DEFORMATION ANALYSIS1)
WangLihua, LiYiming中图分类号:O34
文献标识码:A
通讯作者:
收稿日期:2018-01-4
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (5440KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
无网格法通过点来离散求解区域, 不需要划分网格, 因此不会发生网格畸变问题,使得其广泛应用于大变形和一些复杂问题[1-9].无网格法构建方程的模式主要包括两大类：基于Galerkin法的积分弱形式[1, 6, 10-13]和基于直接配点法的强形式[14-18]. 配点型无网格法由于不需要积分, 能够获得比有限元法更高的效率[19-21], 因此逐渐获得了更多的关注[22], 高效配点型无网格法已广泛应用于声子晶体[23]、优化[24]、结构振动[25]、环境工程[26]等方面. 径向基函数配点法(radial basis collocation method, RBCM)是一种典型的强形式无网格法,这种方法具有完全不需要任何网格、求解过程简单、精度高、收敛性好以及易于扩展到高维空间等优点[27-28]. 其在分析大变形问题时, 具有不存在网格畸变等优势,但是由于其采用全域的形函数, 在求解高梯度问题时会存在精度较低和无法很好地反应局部特性的缺点[29-30].为有效改善传统径向基函数配点法存在的问题,本文引入分区径向基函数配点法(finite subdomain radial basis collocationmethod, FSRBCM)[31]来求解局部存在高梯度的大变形问题.这种方法首先将求解域根据其几何特点或材料性质等划分成若干个子(区)域,在子域内构建径向基函数插值. 在界面上施加所有的界面连续条件,在不同的子域内可以根据局域特性选用不同的形状参数,构建统一的配点方程并一次求解. 与传统区域分解法(domain decompositionmethod)[32]不同的是,区域分解法在子域边界上需要大量的迭代计算, 有时候还会存在不收敛的问题.而分区配点法的界面连续条件不需要迭代求解, 计算效率高.该方法仍然保持超收敛性, 且将原来的满阵转化成了稀疏矩阵,降低了条件数和存储空间, 提高了计算效率.也为求解大规模科学计算问题打下了基础.
本文从强形式控制方程出发,基于分区径向基函数配点法建立了大变形问题的求解格式.通过牛顿迭代法对非线性方程进行线性化, 采用完全拉格朗日格式,得到了用于分析大变形问题的增量模式, 在每个迭代步内,采用分区径向基函数配点法一次求解.数值算例表明分区径向基函数配点法能够很好地反应问题的局部高梯度特性.
1 径向基函数近似
径向基函数(radial basis function, RBF)是一类函数值取决于计算点${\pmb x}$与源点${\pmb x}_I$之间距离的实值函数$^{[28, 33]}$.常见的径向基函数有Multiquadrics(MQ)径向基函数、高斯径向基函数和薄板样条径向基函数等.由于MQ径向基函数具有较高的精度和收敛率, 本文采用MQ进行求解分析, 其表达式如下$$ g_I \left( {\pmb x} \right) = \left( {r_I^2 + c^2} \right)^{\vartheta - \tfrac{3}{2}} (1) $$
式中,$r_I = \left\| {{\pmb x} - {\pmb x}_I } \right\|_2 $表示计算点与源点的距离, 形状参数$c$是大于0的常数,$\vartheta $的取值不同表示不同类型的MQ径向基函数, 本文中取$\vartheta = 1$.
2 大变形分析
2.1 基本方程
某弹性力学问题的求解域为$\varOmega $, Neumann边界为$\varGamma $,Dirichlet边界为$\varPi $, 边界$\partial \varOmega = \varGamma \cup \varPi $, 区域$\bar{\varOmega } = \varOmega \cup \partial \varOmega $. 初始构形用坐标$X$表示,变形之后的现时构形用坐标$x$表示.采用Kirchhoff应力$S$表示的初始位形空间描述的平衡方程表示如下$$ \left.\begin{array}{ll} \left( {S_{kj} F_{ik} } \right)_{,j} + b_i = {0} \,, & {\rm in} \ \varOmega S_{jk} F_{ij} N_k = h_i & {\rm on} \ \varGamma u_i = g_i\,, & {\rm on} \ \varPi \end{array} \right \} (2) $$
其中, $F_{ik} = {\partial x_i } /{\partial X_k }$为变形梯度, $b_i $体力, $h_i $是 Neumann边界$\varGamma $上的表面力, $N_k$是曲面法线, $g_i $是 Dirichlet边界$\varPi $上的已知位移. 对于线弹性材料
$$S_{ij} = D_{ijkl} \varepsilon _{kl} (3)$$
其中
$$\varepsilon _{ij} = \dfrac{1}{2}\left( {\dfrac{\partial u_i }{\partial X_j } + \dfrac{\partial u_j }{\partial X_i } + \dfrac{\partial u_k }{\partial X_i}\dfrac{\partial u_k }{\partial X_j }} \right) (4)$$
式中,$D_{ijkl}$为常数.
将求解区域分成$m$个互不重叠的子域 $\varOmega = \varOmega ^1 \cup \varOmega ^2 \cup\cdots \cup \varOmega ^m$. 对于任一子域$\alpha , \beta = 1,2, \cdots ,m$,其中$\varOmega ^\alpha \cap \varOmega ^\beta = \emptyset \,\left( {\alpha \ne\beta } \right)$, $\partial \varOmega ^\alpha \cap \partial \varOmega ^\beta =\emptyset \,\left( {\alpha \ne \beta } \right)$, $\varLambda _{\alpha \beta } =\bar {\varOmega }^\alpha \cap \bar {\varOmega }^\beta $任一子域的控制方程可表示如下
$$ \left.\begin{array}{ll} \left( {S_{kj}^\alpha F_{ik}^\alpha } \right)_{,j} + b_i^\alpha = {0}\,, & {\rm in} \ \varOmega ^\alpha S_{jk}^\alpha F_{ij}^\alpha N_k^\alpha = h_i^\alpha \,, & {\rm in} \ \varGamma ^\alpha u_i^\alpha = g_i^\alpha \,, & {\rm in} \ \varPi ^\alpha \end{array} \right \} (5) $$
界面连续条件为
$$ \left.\begin{array}{l} S_{jk}^\alpha F_{ij}^\alpha N_k^\alpha + S_{jk}^\beta F_{ij}^\beta N_k^\beta = 0 u_i ^\alpha = u_i ^\beta \end{array} \right\} \quad {\rm in} \ \varLambda _{\alpha \beta } (6) $$
2.2 近似函数
子域中的未知量可以采用该子域内的径向基函数近似表示为$$ \left( {u^\alpha \left( {\pmb X} \right)} \right)^h = \sum_{I = 1}^{\xi ^\alpha } {g_I^\alpha \left( {\pmb X} \right)a_I } ,\quad X \in \bar {\varOmega }^\alpha (7) $$
其中,$\xi ^\alpha $为$\alpha $子域中源点的个数. 方程(7)可以写成如下的一般形式
$$\left( {{u}_i^\alpha } \right)^h = \left( {{\pmb \varPhi }^\alpha } \right)^{\rm T}{\pmb a} (8)$$
其中
$$ \left( {{\pmb \varPhi }^\alpha } \right)^{\rm T} = \left[ {{\pmb g}_1^\alpha ,{\pmb g}_{2}^\alpha , \cdots ,{\pmb g}_{N^\alpha }^\alpha } \right]\,,\quad {\pmb g}_I^\alpha = g_I^\alpha {\pmb I} (9) $$
式中,$g_I^\alpha $是子域中源点${\pmb x}_I \in \bar {\varOmega }^\alpha $的径向基函数近似,${\pmb I}$是单位矩阵.在每个子域及其边界和界面上定义如下的配点集合
$$ \left.\!\! {\pmb P}^\alpha = \{{\pmb p}_I \}_{I = 1}^{\zeta _p^\alpha } \subseteq \varOmega ^\alpha \,,\quad {\pmb Q}^\alpha = \{{\pmb q}_I \}_{I = 1}^{\zeta _q^\alpha } \subseteq \varGamma ^\alpha {\pmb R}^\alpha = \{{\pmb r}_I \}_{I = 1}^{\zeta _r^\alpha } \subseteq \varPi ^\alpha ,\quad {\pmb Z}_{\alpha \beta } = \{{\pmb z}_I \}_{I = 1}^{\zeta _{\alpha \beta } } \subseteq \varLambda _{\alpha \beta } \!\!\right\} (10) $$
其中,$\zeta _p^\alpha $,$\zeta _q^\alpha $,$\zeta _r^\alpha $, $\zeta _{\alpha \beta } $分别表示$\alpha$子域中域内、Neumann边界、Dirichlet边界和与$\alpha $子域相邻界面上的配点个数. 通常情况下,子域内选取的配点个数大于源点个数.
2.3 大变形问题求解
根据牛顿迭代原理, 其增量迭代格式可以表示为$$ \left.\!\!\begin{array}{ll} \Delta \left[ {\left( {S_{kj}^\alpha F_{ik}^\alpha } \right)_{,j} + b_i^\alpha } \right]_{v + 1}^n = - \left[ {\left( {S_{kj}^\alpha F_{ik}^\alpha } \right)_{,j} + b_i^\alpha } \right]_v^n \,, & {\rm in} \ \varOmega ^\alpha \Delta \left( {S_{kj}^\alpha F_{ik}^\alpha N_j^\alpha } \right)_{v + 1}^n = \left( {h_i^\alpha } \right)^n - \left( {S_{kj}^\alpha F_{ik}^\alpha N_j^\alpha } \right)_v^n \,, & {\rm in} \ \varGamma ^\alpha \Delta \left( {u_i^\alpha } \right)_{v + 1}^n = \left( {g_i^\alpha } \right)^n - \left( {u_i^\alpha } \right)_v^n \,, & {\rm in} \ \varPi ^\alpha \end{array} \!\! \right \} (11) $$
其中$n$和$v$分别表示载荷步和迭代步. 在第$n$载荷步上进一步展开得到
$\left( {F_{ik,j}^\alpha } \right)_v \left( {\Delta S_{kj}^\alpha } \right)_{v + 1} + \left( {S_{kj}^\alpha } \right)_v \left( {\Delta F_{ik,j}^\alpha } \right)_{v + 1} + \left( {F_{ik}^\alpha } \right)_v \left( {\Delta S_{kj,j}^\alpha } \right)_{v + 1} + \left( {S_{kj,j}^\alpha } \right)_v \left( {\Delta F_{ik}^\alpha } \right)_{v + 1}= b_i^\alpha - \left( {F_{ik,j}^\alpha S_{kj}^\alpha + F_{ik}^\alpha S_{kj,j}^\alpha } \right)_v \,, \ \ {\rm in} \ \varOmega ^\alpha (12)$
$ \left( {S_{kj}^\alpha N_k^\alpha } \right)_v \left( {\Delta F_{ik}^\alpha } \right)_{v + 1} + \left( {F_{ik}^\alpha N_j^\alpha } \right)_v \left( {\Delta S_{kj}^\alpha } \right)_{v + 1} = h_i^\alpha - \left( {S_{kj}^\alpha F_{ik}^\alpha N_j^\alpha } \right)_v \,, \ \ {\rm in} \ \varGamma ^\alpha (13)$
$ \left( {\Delta u_i^\alpha } \right)_{v + 1} = g_i^\alpha - \left( {u_i^\alpha } \right)_v \,, \ \ {\rm in} \ \varPi ^\alpha (14)$
对于相邻公共边界上的连续条件式(6), 也可以利用牛顿迭代法得到如下的增量迭代格式
$ \left( {S_{kj}^\alpha N_j^\alpha } \right)_v \left( {\Delta F_{ik}^\alpha } \right)_{v + 1} + \left( {F_{ik}^\alpha N_j^\alpha } \right)_v \left( {\Delta S_{kj}^\alpha } \right)_{v + 1} +$
$\qquad \left( {S_{kj}^\beta N_j^\beta } \right)_v \left( {\Delta F_{ik}^\beta } \right)_{v + 1} + \left( {F_{ik}^\beta N_j^\beta } \right)_v \left( {\Delta S_{kj}^\beta } \right)_{v + 1} =$
$\qquad - \left( {S_{kj}^\alpha F_{ik}^\alpha N_j^\alpha } \right)_v - \left( {S_{kj}^\beta F_{ik}^\beta N_j^\beta } \right)_v \,, \ \ {\rm in} \ \varLambda _{\alpha \beta } (15)$
$\left( {\Delta u_i^\alpha } \right)_{v + 1} - \left( {\Delta u_i^\beta } \right)_{v + 1} = \left( {u_i^\beta } \right)_v - \left( {u_i^\alpha } \right)_v \,, \ \ {\rm in} \ \varLambda _{\alpha \beta } (16)$
将径向基函数近似式(7)代入增量方程(12) $\sim$ (16), 即可得到在所有子域$\varOmega$、边界$\partial \varOmega $和相邻界面$\varLambda $上增量迭代格式的离散形式, 用矩阵表示为
$${\pmb K} \Delta {\pmb a} = {\pmb f} (17)$$
其中矩阵定义为
$ {\pmb K} = \left[\!\!\begin{array}{c} {{\pmb K}^1} {{\pmb K}^2} \vdots {{\pmb K}^m} \end{array} \!\!\right]\,,\ {\pmb K}^\alpha = \left[ \!\!\begin{array}{c} {{\pmb K}_L^\alpha } {{\pmb K}_h^\alpha } {{\pmb K}_g^\alpha } {{\pmb K}_{\Lambda _h }^\alpha } {{\pmb K}_{\Lambda _g }^\alpha } \end{array} \!\! \right]\,, \ {\pmb f} = \left[\!\!\begin{array}{c} {{\pmb f}^1} {{\pmb f}^2} \vdots {{\pmb f}^m} \end{array} \!\! \right]\,,\ {\pmb f}^\alpha = \left[ \!\!\begin{array}{c} {{\pmb f}_L^\alpha } {{\pmb f}_h^\alpha } {{\pmb f}_g^\alpha } {{\pmb f}_{\Lambda _h }^\alpha } {{\pmb f}_{\Lambda _g }^\alpha } \end{array} \!\! \right] (18)$
${\pmb K}_L^\alpha = {\pmb K}_L^\alpha = {\pmb L \pmb D}_1 {\pmb B}_1 + \left( {{\pmb L}_2 {\pmb D}_2 {\pmb A}_3 + {\pmb S}_1 } \right){\pmb B}_2 +$
$\qquad \left( {{\pmb L\pmb D}_1 {\pmb A}_1 + {\pmb L}_2 {\pmb D}_2 {\pmb A}_2 + {\pmb T}_1 + {\pmb T}_2 } \right){\pmb B}_3 (19)$
${\pmb K}_h^\alpha = {\pmb K}_{\Lambda _h }^\alpha = {\pmb L}_2 {\pmb N}_1 {\pmb D}_1 ({\pmb B}_1 + {\pmb A}_1 {\pmb B}_3 ) + {\pmb N}_2 {\pmb S}_2 {\pmb B}_3 (20)$
${\pmb K}_g^\alpha = {\pmb K}_{\varLambda _g }^\alpha = \left[ \!\!\begin{array}{cc} \left( {{\pmb \varPhi }^\alpha } \right)^{\rm T} & {\bf 0} {\bf 0} & \left( {{\pmb \varPhi }^\alpha } \right)^{\rm T} \end{array} \!\! \right] (21)$
${\pmb f}_L^\alpha = {\pmb b} - {\pmb L\pmb S} - {\pmb L}_2 \left( {{\pmb T}_3 + {\pmb T}_4 } \right) (22)$
${\pmb f}_h^\alpha = {\pmb h} - {\pmb N}_2 {\pmb L}_3 {\pmb S} (23)$
${\pmb f}_g^\alpha = {\pmb g} - {\pmb u} (24)$
${\pmb f}_{\varLambda _h }^\alpha = {\pmb f}_{\varLambda _g }^\alpha = {\bf 0} (25)$
在矩阵${\pmb f}_L^\alpha $和${\pmb f}_L^\alpha $中${\pmb \varPhi }^\alpha = {\pmb \varPhi }^\alpha \left( {{\pmb p}^\alpha } \right)$, 矩阵${\pmb K}_h^\alpha $和${\pmb f}_h^\alpha $中${\pmb \varPhi }^\alpha = {\pmb \varPhi }^\alpha \left( {{\pmb q}^\alpha } \right)$, 矩阵$ {\pmb K}_g^\alpha $和${\pmb f}_g^\alpha $中${\pmb \varPhi }^\alpha = {\pmb \varPhi }^\alpha \left( {{\pmb r}^\alpha } \right)$, 矩阵${\pmb K}_{\varLambda _h }^\alpha $和${\pmb K}_{\varLambda _g }^\alpha $中$ {\pmb \varPhi }^\alpha = {\pmb \varPhi }^\alpha \left( {{\pmb z}^\alpha } \right)$. 方程(19)$\sim$(23)各矩阵的详细表达式见附录.
由于子域内部、边界以及界面上的误差由于计算数据大小的差异在数值计算中会出现不平衡的问题, 在边界和界面上需施加合适的权重以获得最优的精度和收敛率[31]. 方程(17)的加权形式表示如下
$${\pmb W \pmb K} \Delta {\pmb a} = {\pmb W \pmb f} (26)$$
$$ {\pmb W} = \left[\!\!\begin{array}{c} {{\pmb W}^1} {{\pmb W}^2} \vdots {{\pmb W}^m} \end{array} \!\! \right]\,\,,\quad {\pmb W}^\alpha = \left[\!\! \begin{array}{c} {\pmb 1} {{\pmb W}_h^\alpha } {{\pmb W}_g^\alpha } {{\pmb W}_{\varLambda _h }^\alpha } {{\pmb W}_{\varLambda _g }^\alpha } \end{array}\!\! \right] (27) $$
其中应力边界和位移边界的权重取值如下
$$ \left. w_h^\alpha \approx O\left( {\theta ^\alpha } \right)\,, \ \ w_g^\alpha \approx O\left( {\kappa ^\alpha \xi ^\alpha } \right) w_{\Lambda _h }^{\alpha \beta } \approx O\left( 1 \right)\,, \ \ w_{\Lambda _g }^{\alpha \beta } \approx O\left( {\kappa ^{\alpha \beta }\xi ^{\alpha \beta }} \right) \!\!\right\} (28) $$
a其中,$\kappa ^\alpha = \max \left( {\lambda ^\alpha ,\mu ^\alpha } \right)$, $\kappa ^{\alpha \beta } = \max(\kappa ^\alpha ,\kappa ^\beta )$, $\theta ^\alpha = \kappa ^{\alpha \beta } / \kappa ^\alpha $, $\xi^{\alpha \beta } = \max (\xi ^\alpha ,\xi ^\beta )$, $\xi ^\alpha $和 $\xi ^\beta $即对应$\alpha $和$\beta$两个子域内选取的源点数目, $\lambda ^\alpha $和$\mu ^\alpha $为$\alpha $子域中材料的拉梅常数.超定方程(27)通常可以采用最小二乘法、截断奇异值分解法等方法进行求解.
2.4 程序设计
对于弹性大变形问题, 受到静力载荷作用, 基于完全拉格朗日格式(total Lagrangian), 具体的程序设计和求解步骤如下：(1)确定初始构型, 区域划分模式,子域个数以及域内、边界和界面上的源点和配点分布, 设置载荷增量.
(2)在第一个载荷步中(在第$n$个载荷步中), 取第一个迭代步的初始近似值${\pmb a}_0 $.
(3)计算得到${\pmb u}_0 = {\pmb \varPhi \pmb a}_0 $(${\pmb u}_v = {\pmb \varPhi \pmb a}_v $). 根据式(19) $\sim$式(25)和${\pmb u}_0 $ (${\pmb u}_v $)计算出每个子域上的${\pmb K}_L $, ${\pmb K}_h $, ${\pmb K}_g $, ${\pmb K}_{\varLambda _h } $, ${\pmb K}_{\varLambda _g } $, ${\pmb f}_L $, ${\pmb f}_h$, ${\pmb f}_g $, ${\pmb f}_{\varLambda _h } $, ${\pmb f}_{\varLambda _h }$, 组装成整体矩阵${\pmb K}$和${\pmb f}$, 通过方程(17)求出增量$\Delta {\pmb a}_1 $ ($\Delta {\pmb a}_v $).
(4)判断$\Delta {\pmb u}_1 = {\pmb \varPhi }\Delta {\pmb a}_1 $ ($\Delta {\pmb u}_v = {\pmb \varPhi }\Delta {\pmb a}_v $)是否满足下式
$$\left\| {\Delta {\pmb u}} \right\| \leqslant e (29)$$
其中,$e$为人工设置的误差界限. 如果满足, 则进入式(5). 如果不满足,取新的近似值为
$${\pmb a}_1 = {\pmb a}_0 + \Delta {\pmb a}_1 \;\left( { {\pmb a}_{v + 1} = {\pmb a}_v + \Delta {\pmb a}_{v + 1} } \right) (30)$$
然后返回式(3)继续迭代求解.
(5)在载荷中增加载荷增量进入下一个分析步.然后依据式(2) $\sim$式(4)的过程循环求解, 直至载荷步全部计算结束.
3 数值算例
3.1 受均布载荷作用的悬臂梁
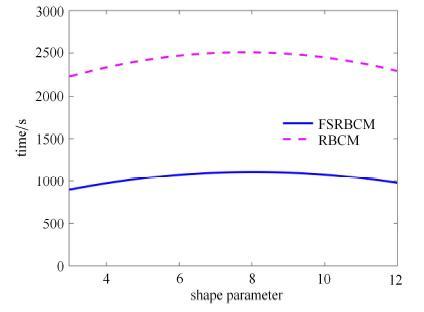
如图1所示, 悬臂梁在上下表面受到均布载荷作用, 材料参数为：弹性模量$E = 12$\,kPa, 泊松比$\nu = 0.2$.梁的长度和宽度分别为$L = 10$,m, $H = 1$,m. 载荷为$q = 5$,N/m, 载荷步为150步. 总源点个数 $\xi = 9\times51$, 源点分布如图2所示, 在分区径向基函数配点法中将整体区域划分成2个子域.边界和界面上所取的权重为：$w_h^\alpha = 10$, $w_g^\alpha = 1\times 10^3$, $w_{\varLambda _h }^{\alpha \beta }= 100$, $ w_{\varLambda _g }^{\alpha \beta } = 1\times 10^4$ ($\alpha = 1,2$; $\beta = 1,2$). 梁端挠度、横向位移随载荷的变化和柯西应力如图3和\linebreak 图4所示(位移解析解参见文献[34]), 结果表明,对于局部存在高 梯度的问题,分区径向基函数配点法能比径向基函数配点法获得更高的精度;有限元法求解的位移精度较低,而且在局部高梯度区域会出现应力波动.图5所示的挠度和横向位移收敛图表明分区径向基函数配点法在求解这类问题时仍能获得高收敛率.由于分区后形成了稀疏矩阵, 如图6所示, 分区径向基函数配点法会比径向基函数配点法节约大约一半的计算时间,显著地提高了计算效率.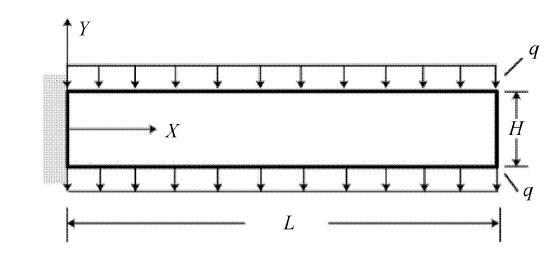
显示原图|下载原图ZIP|生成PPT图1受均布载荷作用的悬臂梁
-->Fig. 1Cantivilever beam under uniform load
-->
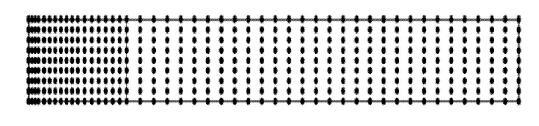显示原图|下载原图ZIP|生成PPT图2悬臂梁源点分布图
-->Fig. 2Distribution of source points for cantivilever beam
-->
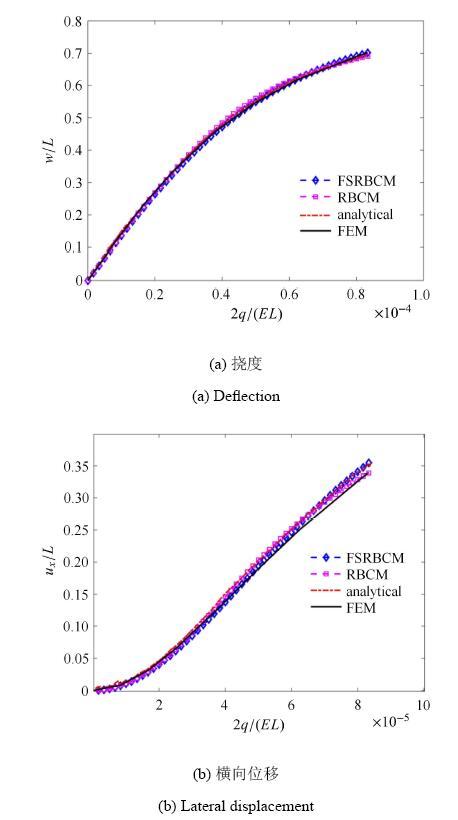显示原图|下载原图ZIP|生成PPT图3悬臂梁梁端挠度、横向位移和载荷的关系图
-->Fig. 3Deflection and lateral displacement of the end point of cantilever beam
-->
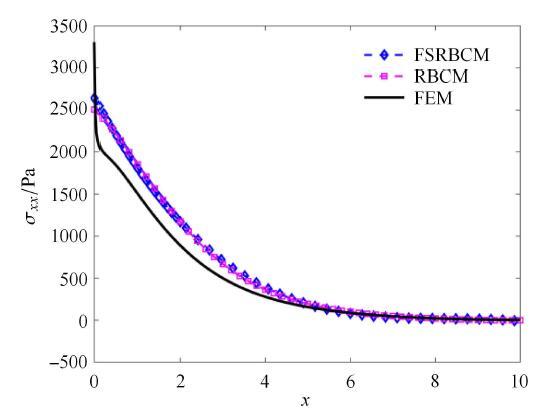显示原图|下载原图ZIP|生成PPT图4悬 臂梁上表面的柯西应力图
-->Fig. 4Cauchy stress on the upper surface of cantilever beam
-->
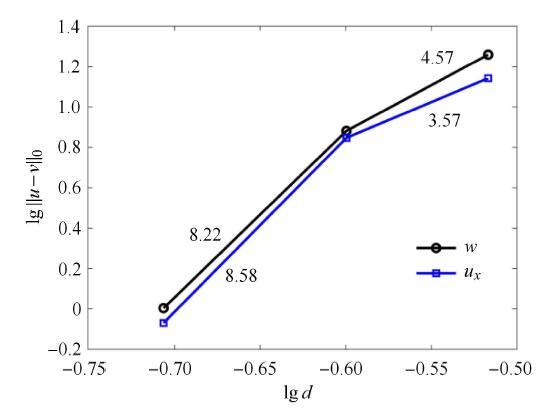
显示原图|下载原图ZIP|生成PPT图5悬臂梁挠度和横向位移收敛图
-->Fig. 5Convergence of the deflection and lateral displacement for cantilever beam
-->
显示原图|下载原图ZIP|生成PPT图 6悬臂梁计算时间对比
-->Fig. 6Comparison of the CPU time for cantilever beam
-->
3.2 纯弯曲悬臂梁
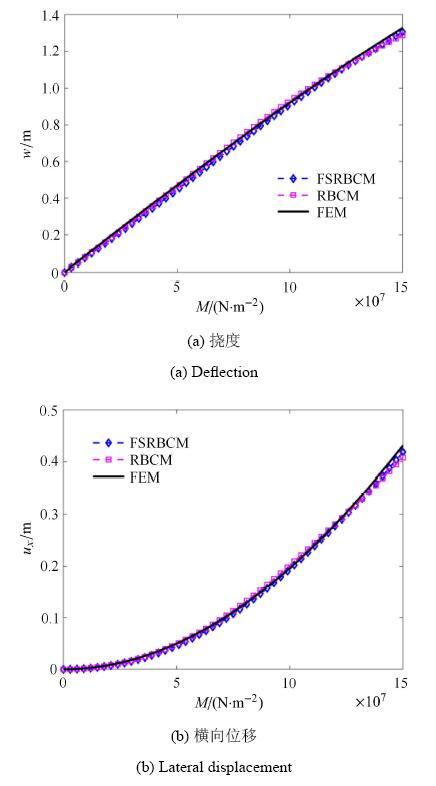
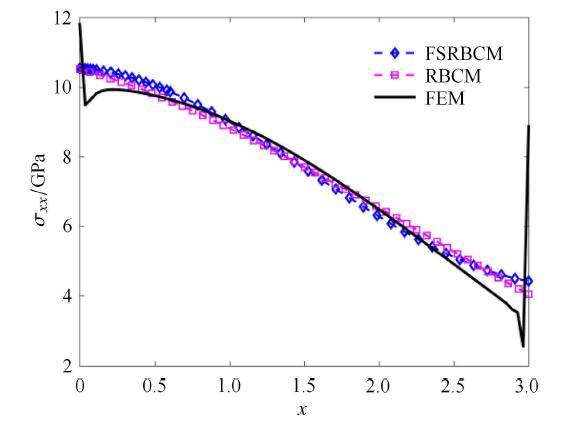
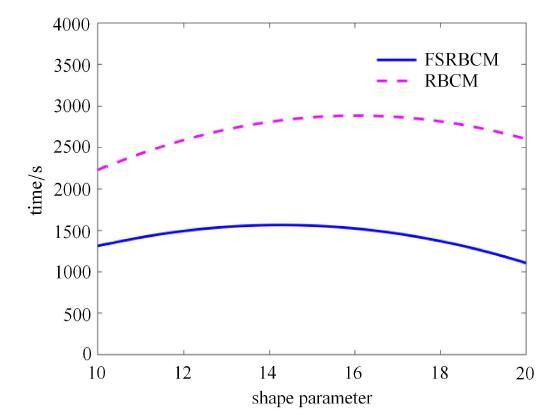
在右端部受纯弯曲载荷作用的悬臂梁如图7所示, 材料参数为：$E = 210$\,GPa, $\nu = 0.3$, 梁的尺寸为：长$L = 3$\,m,宽$H = 0.3$\,m. 载荷为$M = 0.15$\,GN$\cdot$m, 载荷步为150步. 源点分布如图8所示, 源点个数为$\xi = 9\times 45$,在分区径向基函数配点法中整体区域划分成了3个子域. 施加在边界和界面上的权重为：$w_h^\alpha = 10$, $w_g^\alpha =2\times 10^{10}$, $w_{\varLambda _h }^{\alpha \beta } = 10$, $w_{\varLambda _g }^{\alpha \beta } = 2\times10^{10}$ ($\alpha = 1,2,3$; $\beta = 1,2,3$). 图9和图10中的挠度、横向位移和柯西应力分布再次表明分区径向基函数配点法在求解局部高梯度问题中具有优势, 传统径向基函数配点法的求解精度较低, 而有限元法在求解应力时容易在局部高梯度区域出现应力波动.图11表明在求解这类问题时分区径向基函数配点法能够显著提高计算效率.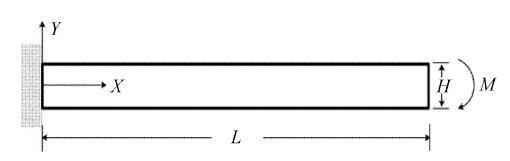
显示原图|下载原图ZIP|生成PPT图 7纯弯曲作用下的悬臂梁
-->Fig. 7Cantivilever beam under bending
-->
显示原图|下载原图ZIP|生成PPT图 8纯弯曲梁源点分布图
-->Fig. 8Distribution of source points for pure bending beam
-->
显示原图|下载原图ZIP|生成PPT图9纯弯曲梁端挠度、横向位移和载荷的关系图
-->Fig. 9Deflection and lateral displacement of the end point of pure bending beam
-->
显示原图|下载原图ZIP|生成PPT图10纯弯曲梁上表面的柯西应力图
-->Fig. 10Cauchy stress on the upper surface of pure bending beam
-->
显示原图|下载原图ZIP|生成PPT图11纯弯曲梁计算时间对比
-->Fig. 11Comparison of CPU time for pure bending beam
-->
3.3 拉伸作用下的带孔板
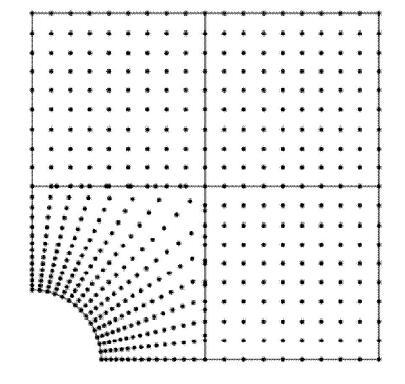
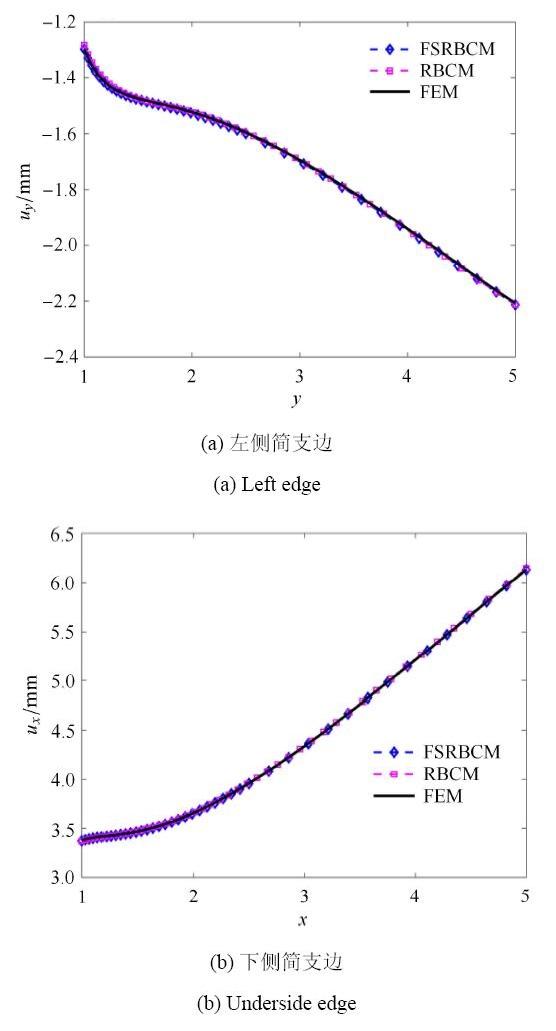
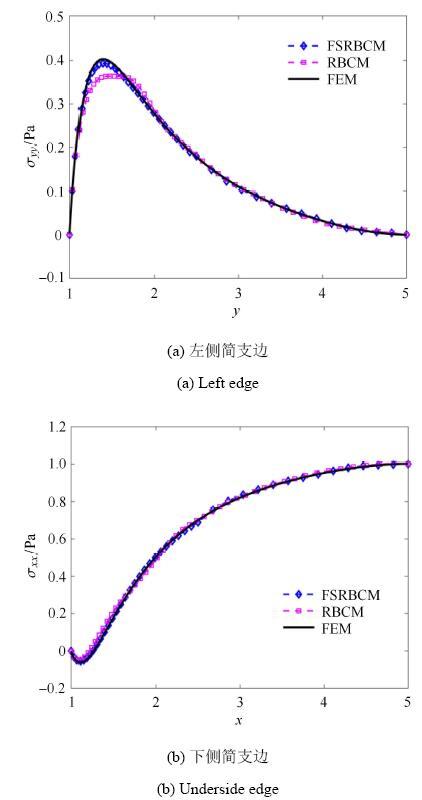
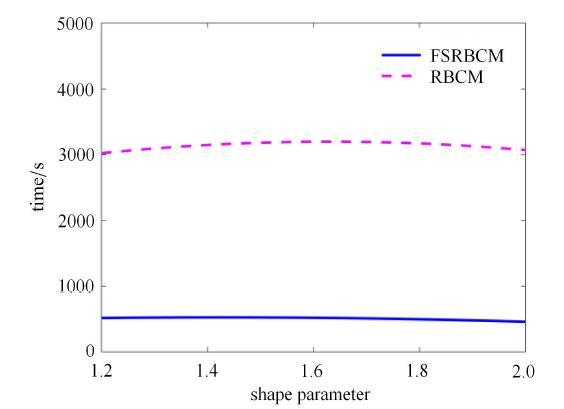
受拉伸作用的正方形板中央带圆孔如下图12所示, $a = 1$,m, 右侧受拉伸均布荷载$q = 1$,N/m, 材料参数为：$E =1\times 10^3$\,Pa, $\nu = 0.3$. 取1/4进行分析, 源点个数 $\xi = 25\times 25$, 源点分布如图13所示,将区域划分为4个子域, 取载荷步为200步. 边界和界面上的权重为：$w_h^\alpha = 10$, $w_g^\alpha = 1\times 10^3$,$w_{\Lambda _h }^{\alpha \beta } = 100$, $w_{\varLambda _g }^{\alpha \beta } = 1\times 10^4$ ($\alpha =1,2,3,4$; $\beta = 1,2,3,4$).左侧简支边界的$y$方向的位移结果分布图和下侧简支边界$x$方向的位移结果分布图如图14所示.图15给出了左侧简支边界和下侧简支边界上$x$方向的应力分布. 结果表明,分区径向基函数配点法能够比径向基函数配点法获得更好的精度(以稠密单元的有限元解作为参考解).相对于受均布载荷作用和纯弯曲作用的悬臂梁算例, 带孔板的局部梯度变化较小, 所以有限元法也获得了比较好的数值结果,没有出现明显的应力波动. 图16表明相比于全域的径向基函数配点法, 分区形式能够显著提高计算效率.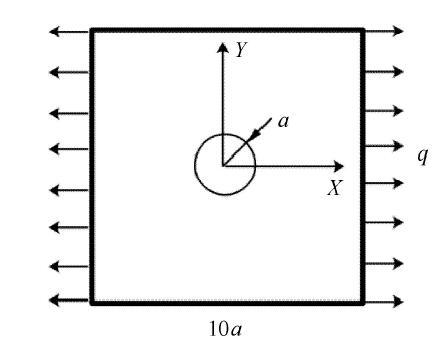
显示原图|下载原图ZIP|生成PPT图12受拉伸作用的带孔板
-->Fig. 12Plate with hole under tension
-->
显示原图|下载原图ZIP|生成PPT图13带孔板源点分布图
-->Fig. 13Distribution of source points for plate with hole
-->
显示原图|下载原图ZIP|生成PPT图14带孔板边界位移分布
-->Fig. 14Displacement of the simply supported boundary of plate with hole
-->
显示原图|下载原图ZIP|生成PPT图15带 孔板边界应力分布
-->Fig. 15Cauchy stress of the simply supported boundary of plate with hole
-->
显示原图|下载原图ZIP|生成PPT图 16带孔板计算时间对比
-->Fig. 16Comparison of CPU time for plate with hole
-->
4 结 论
由于传统径向基函数配点法在求解高梯度问题时往往会存在精度低和收敛率低的问题,本文引入分区径向基函数配点法求解了局部存在高梯度的弹性大变形问题.基于完全拉格朗日格式和牛顿迭代原理,建立了弹性大变形问题分区配点模式的增量迭代格式. 数值分析表明,相比较于传统径向基函数配点法,分区径向基函数配点法在求解高梯度大变形问题中不仅能够获得较高的精度和收敛率,而且能够显著提高计算效率. 相比较于有限元法, 其得到的应力数值结果比较光滑,能够避免传统有限元法在求解高梯度问题时出现的应力波动问题. 因此,分区径向基函数配点法在求解复杂的大变形问题中具有较好的应用前景.附录
式(19) $\sim$式(23)中的矩阵表达式如下
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . Meshless approximations based on moving least-squares, kernels, and partitions of unity are examined. It is shown that the three methods are in most cases identical except for the important fact that partitions of unity enable p -adaptivity to be achieved. Methods for constructing discontinuous approximations and approximations with discontinuous derivatives are also described. Next, several issues in implementation are reviewed: discretization (collocation and Galerkin), quadrature in Galerkin and fast ways of constructing consistent moving least-square approximations. The paper concludes with some sample calculations. |
| [3] | . |
| [4] | . 详细论述了近年来迅速发展的无网格法的理论基础及其在各个领域内的应 用. 无网格法网格依赖性弱, 避免了传统的有限元、边界元等基于网格的数值方法 中可能出现的网格畸变和扭曲, 在一些有限元、边界元等方法难以较好处理的领域体现 出独特的优势. 以加权余量法为主线归纳了已有的30多种无网格法, 各类 无网格法的主要区别在于使用了不同的加权余量法和近似函数. 详尽介绍 了各种无网格近似方案(包括移动最小二乘近似、核近似和重构核近似、单位分 解近似、径向基函数近似、点插值近似、自然邻接点插值近似等)和无网格法 中常用的各类加权余量法(伽辽金格式、配点格式、局部弱形式、加权最小二乘 格式和边界积分格式等), 并讨论了数值积分方法和边界条件的处理等问题. 在 此基础上较系统地总结了无网格法在冲击爆炸、裂纹传播、超大变形、结 构优化、流固耦合、生物力学和微纳米力学等领域的应用, 展示了无网格法相 对于传统数值方法的优势. . 详细论述了近年来迅速发展的无网格法的理论基础及其在各个领域内的应 用. 无网格法网格依赖性弱, 避免了传统的有限元、边界元等基于网格的数值方法 中可能出现的网格畸变和扭曲, 在一些有限元、边界元等方法难以较好处理的领域体现 出独特的优势. 以加权余量法为主线归纳了已有的30多种无网格法, 各类 无网格法的主要区别在于使用了不同的加权余量法和近似函数. 详尽介绍 了各种无网格近似方案(包括移动最小二乘近似、核近似和重构核近似、单位分 解近似、径向基函数近似、点插值近似、自然邻接点插值近似等)和无网格法 中常用的各类加权余量法(伽辽金格式、配点格式、局部弱形式、加权最小二乘 格式和边界积分格式等), 并讨论了数值积分方法和边界条件的处理等问题. 在 此基础上较系统地总结了无网格法在冲击爆炸、裂纹传播、超大变形、结 构优化、流固耦合、生物力学和微纳米力学等领域的应用, 展示了无网格法相 对于传统数值方法的优势. |
| [5] | . |
| [6] | . Large deformation analysis of non-linear elastic and inelastic structures based on Reproducing Kernel Particle Methods (RKPM) is presented. The method requires no explicit mesh in computation and therefore avoids mesh distortion difficulties in large deformation analysis. The current formulation considers hyperelastic and elasto-plastic materials since they represent path-independent and path-dependent material behaviors, respectively. In this paper, a material kernel function and an RKPM material shape function are introduced for large deformation analysis. The support of the RKPM material shape function covers the same set of particles during material deformation and hence no tension instability is encountered in the large deformation computation. The essential boundary conditions are introduced by the use of a transformation method. The transformation matrix is formed only once at the initial stage if the RKPM material shape functions are employed. The appropriate integration procedures for the moment matrix and its derivative are studied from the standpoint of reproducing conditions. In transient problems with an explicit time integration method, the lumped mass matrices are constructed at nodal coordinate so that masses are lumped at the particles. Several hyperelasticity and elasto-plasticity problems are studied to demonstrate the effectiveness of the method. The numerical results indicated that RKPM handles large material distortion more effectively than finite elements due to its smoother shape functions and, consequently, provides a higher solution accuracy under large deformation. Unlike the conventional finite element approach, the nodal spacing irregularity in RKPM does not lead to irregular mesh shape that significantly deteriorates solution accuracy. No volumetric locking is observed when applying non-linear RKPM to nearly incompressible hyperelasticity and perfect plasticity problems. Further, model adaptivity in RKPM can be accomplished simply by adding more points in the highly deformed areas without remeshing. |
| [7] | . 在移动最小二乘法的基础上，提出了复变量移动最小二乘法.复变量移动最小二乘法的优点是采用一维基函数建立二维问题的逼近函数，所形成的无网格方法计算量小.然后，将复变量移动最小二乘法应用于弹性力学的无网格方法，提出了复变量无网格方法，推导了复变量无网格方法的公式.与传统的无网格方法相比，复变量无网格方法具有计算量小、精度高的优点.最后给出了数值算例. . 在移动最小二乘法的基础上，提出了复变量移动最小二乘法.复变量移动最小二乘法的优点是采用一维基函数建立二维问题的逼近函数，所形成的无网格方法计算量小.然后，将复变量移动最小二乘法应用于弹性力学的无网格方法，提出了复变量无网格方法，推导了复变量无网格方法的公式.与传统的无网格方法相比，复变量无网格方法具有计算量小、精度高的优点.最后给出了数值算例. |
| [8] | . Smoothed particle hydrodynamics (SPH) is a meshfree particle method based on Lagrangian formulation, and has been widely applied to different areas in engineering and science. This paper presents an overview on the SPH method and its recent developments, including (1)02the need for meshfree particle methods, and advantages of SPH, (2)02approximation schemes of the conventional SPH method and numerical techniques for deriving SPH formulations for partial differential equations such as the Navier-Stokes (N-S) equations, (3)02the role of the smoothing kernel functions and a general approach to construct smoothing kernel functions, (4)02kernel and particle consistency for the SPH method, and approaches for restoring particle consistency, (5)02several important numerical aspects, and (6)02some recent applications of SPH. The paper ends with some concluding remarks. |
| [9] | . . |
| [10] | . |
| [11] | . The cause of shear locking in Mindlin–Reissner plate formulation is due to the inability of the numerical formulation in representing pure bending mode without producing parasitic shear deformation (lack of Kirchhoff mode). To resolve shear locking in meshfree formulation of Mindlin–Reissner plates, the following two issues are addressed: (1) construction of approximation functions capable of reproducing Kirchhoff modes, and (2) formulation of domain integration of Galerkin weak form capable of producing exact solution under pure bending condition. In this study, we first identify the Kirchhoff mode reproducing conditions (KMRC), and show that the employment of a second order monomial basis in the reproducing kernel or moving least-square approximation of translational and rotational degrees of freedom is an effective means to meet KMRC. Next, the integration constraints that fulfill bending exactness (BE) in the Galerkin meshfree discretization of Mindlin–Reissner plate are derived. A nodal integration with curvature smoothing stabilization that fulfills BE is then formulated for Mindlin–Reissner plate. The curvature smoothing stabilization is introduced in the nodally integrated Galerkin weak form. The resulting meshfree formulation is stable and free of shear locking in the limit of thin plate. Both computational efficiency and accuracy are achieved in the proposed meshfree Mindlin–Reissner plate formulation. |
| [12] | . S-R(strain-rotation)和分解定理克服了经典有限变形理论的一些缺点, 使其可以为几何非线性数值分析提供可靠的理论基础. 对于大变形问题, 由于无网格法(element-free method)避免了对单元网格的依赖, 从而从根本上避免了有限单元法(finite element method, FEM)的单元畸变问题, 保证了求解精度. 因此, 将无网格法和S-R和分解定理结合起来势必能建立一套更加合理可靠的几何非线性数值计算方法. 目前基于S-R 定理的无网格数值方法研究较少并且只能用于二维平面问题的求解, 但实际上绝大多数问题都必须以三维模型来进行处理, 因此建立适用于三维情况的S-R无网格法是非常有必要的. 本文给出了适用于三维情况的S-R 无网格法: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱式的无网格Galerkin 法(EFG)得到了用于求解三维空间问题的离散格式. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值结果与已有文献进行了比较, 验证了本文的三维S-R无网格数值算法的合理性、有效性和准确性. 本文的三维S-R无网格数值算法可以作为一种可靠的三维几何非线性数值分析方法. . S-R(strain-rotation)和分解定理克服了经典有限变形理论的一些缺点, 使其可以为几何非线性数值分析提供可靠的理论基础. 对于大变形问题, 由于无网格法(element-free method)避免了对单元网格的依赖, 从而从根本上避免了有限单元法(finite element method, FEM)的单元畸变问题, 保证了求解精度. 因此, 将无网格法和S-R和分解定理结合起来势必能建立一套更加合理可靠的几何非线性数值计算方法. 目前基于S-R 定理的无网格数值方法研究较少并且只能用于二维平面问题的求解, 但实际上绝大多数问题都必须以三维模型来进行处理, 因此建立适用于三维情况的S-R无网格法是非常有必要的. 本文给出了适用于三维情况的S-R 无网格法: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱式的无网格Galerkin 法(EFG)得到了用于求解三维空间问题的离散格式. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值结果与已有文献进行了比较, 验证了本文的三维S-R无网格数值算法的合理性、有效性和准确性. 本文的三维S-R无网格数值算法可以作为一种可靠的三维几何非线性数值分析方法. |
| [13] | . 计算效率低的问题长期阻碍着无网格伽辽金法(element-free Galerkin method,EFGM)的深入发展.为了提高EFGM的计算速度,本文提出一种求解二维弹性力学问题的光滑无网格伽辽金法.该方法在问题域内采用滑动最小二乘法(moving least square,MLS)近似、在域边界上采用线性插值建立位移场函数;基于广义梯度光滑算子得到两层嵌套光滑三角形背景网格上的光滑应变,根据广义光滑伽辽金弱形式建立系统离散方程.两层嵌套光滑三角形网格是由三角形背景网格本身以及四个等面积三角形子网格组成.为了提高方法的精度,由Richardson外推法确定两层光滑网格上的最优光滑应变.几个数值算例验证了该方法的精度和计算效率.数值结果表明,随着光滑积分网格数目的增加,光滑无网格伽辽金法的计算精度逐步接近EFGM的,但计算效率要远远高于EFGM的.另外,光滑无网格伽辽金法的边界条件可以像有限元那样直接施加.从计算精度和效率综合考虑,光滑无网格伽辽金法比EFGM具有更好的数值表现,具有十分广阔的发展空间. . 计算效率低的问题长期阻碍着无网格伽辽金法(element-free Galerkin method,EFGM)的深入发展.为了提高EFGM的计算速度,本文提出一种求解二维弹性力学问题的光滑无网格伽辽金法.该方法在问题域内采用滑动最小二乘法(moving least square,MLS)近似、在域边界上采用线性插值建立位移场函数;基于广义梯度光滑算子得到两层嵌套光滑三角形背景网格上的光滑应变,根据广义光滑伽辽金弱形式建立系统离散方程.两层嵌套光滑三角形网格是由三角形背景网格本身以及四个等面积三角形子网格组成.为了提高方法的精度,由Richardson外推法确定两层光滑网格上的最优光滑应变.几个数值算例验证了该方法的精度和计算效率.数值结果表明,随着光滑积分网格数目的增加,光滑无网格伽辽金法的计算精度逐步接近EFGM的,但计算效率要远远高于EFGM的.另外,光滑无网格伽辽金法的边界条件可以像有限元那样直接施加.从计算精度和效率综合考虑,光滑无网格伽辽金法比EFGM具有更好的数值表现,具有十分广阔的发展空间. |
| [14] | . |
| [15] | . |
| [16] | . This work introduces the weighted radial basis collocation method for boundary value problems. We first show that the employment of least-squares functional with quadrature rules constitutes an approximation of the direct collocation method. Standard radial basis collocation method, however, yields a larger solution error near boundaries. The residuals in the least-squares functional associated with domain and boundary can be better balanced if the boundary collocation equations are properly weighted. The error analysis shows unbalanced errors between domain, Neumann boundary, and Dirichlet boundary least-squares terms. A weighted least-squares functional and the corresponding weighted radial basis collocation method are then proposed for correction of unbalanced errors. It is shown that the proposed method with properly selected weights significantly enhances the numerical solution accuracy and convergence rates. Copyright 漏 2006 John Wiley & Sons, Ltd. |
| [17] | . A stable and highly accurate meshfree scheme based on strong form collocation associated with radial basis functions and explicit time integration is proposed to solve ill-posed inverse wave propagation problems. Tikhonov regularization technique and the L-curve criterion are employed to deal with the noise measurement data before solving the governing equation to get a stable solution. Appropriate weights are first derived for imposing boundary conditions and known conditions from the measurement data to yield the optimal convergence for inverse problems. Compared to the required iterative procedures in common methods, no iteration is needed in the proposed method which leads to the time-saving computation and avoids the instability resulting from the iterative methods. Dispersion analysis describes that this method has much less dispersion error than the classical finite element method(FEM) and popular weak form meshfree methods, and stability analysis is performed to predict the critical time step for the explicit time integration. Another outstanding advantage of this method is it's effortless to extend the solution scheme of one-dimensional inverse problem to high-dimensional inverse problems. Furthermore, the influences of the high noise into measurement data are evaluated, which demonstrate that even handling with very high noise in the input data the proposed algorithm can achieve stable and high-accuracy solutions. |
| [18] | . 采用径向基函数配点法分析考虑剪切效应的梁板弯曲问题,该方法利用径向基函数作为近似函数,基于配点法离散方程,通过最小二乘法求解.径向基函数配点法在离散和计算过程中不需要划分任何形式的网格,是一种真正的无网格法;径向基函数可以用一元函数来描述多元函数,存在明显的储存和运算简单的特点;而基于配点法求解不需要积分,提高了计算效率.分析考虑剪切效应的薄梁板问题时,传统的有限元法或无网格法求解均会存在剪切锁闭问题,而径向基函数在全域内存在无限连续性,能够准确地满足Kirchhoff约束条件,因此径向基函数配点法能够消除剪切锁闭现象,而且不会出现应力波动.该方法的优势在于,其不仅易于离散、精度高,而且具有指数收敛率,计算效率高.数值算例验证了上述结论和该方法的稳定性. . 采用径向基函数配点法分析考虑剪切效应的梁板弯曲问题,该方法利用径向基函数作为近似函数,基于配点法离散方程,通过最小二乘法求解.径向基函数配点法在离散和计算过程中不需要划分任何形式的网格,是一种真正的无网格法;径向基函数可以用一元函数来描述多元函数,存在明显的储存和运算简单的特点;而基于配点法求解不需要积分,提高了计算效率.分析考虑剪切效应的薄梁板问题时,传统的有限元法或无网格法求解均会存在剪切锁闭问题,而径向基函数在全域内存在无限连续性,能够准确地满足Kirchhoff约束条件,因此径向基函数配点法能够消除剪切锁闭现象,而且不会出现应力波动.该方法的优势在于,其不仅易于离散、精度高,而且具有指数收敛率,计算效率高.数值算例验证了上述结论和该方法的稳定性. |
| [19] | . In this paper, we demonstrate the efficiency and accuracy of the multiquadric collocation method as compared to the finite element method. When used as interpolants, the multiquadric (MQ) radial basis function has the property of exponential convergence with respect to a shape parameter, according to a proof by Madych and Nelson. Although the optimal choice of shape parameter is still an unsettled issue, we demonstrate by three examples that the accuracy achieved by the MQ solution cannot be rivaled by the FEM. |
| [20] | . A superconvergent meshfree collocation method with smoothed nodal gradients is presented. In this method, the first order smoothed gradients of meshfree shape function are constructed through a meshfree interpolation of the standard derivatives of meshfree shape function, while the second order smoothed gradients are computed through directly differentiating the first order smoothed gradients. It is noted that the second order smoothed gradients evaluated at meshfree nodes can be conveniently expressed as two successive first order gradient smoothing operations on the meshfree shape function, which facilitates a trivial numerical implementation. Subsequently, an employment of the second order smoothed gradients in the strong form of a given problem leads to the gradient smoothing meshfree collocation method purely using nodes as the collocation points. Based upon a local truncation error analysis, it is systematically shown that the proposed meshfree collocation method yields superconvergent solutions for odd degree basis functions. A key ingredient attributed to this superconvergence property is that the second order smoothed gradients meet the consistency conditions which go one order beyond the original basis degree of meshfree approximation. Another interesting fact is that the present formulation enables a convergent collocation scheme when the linear basis function is used in meshfree approximation, which is non-feasible in the conventional collocation formulation. The effectiveness of the proposed methodology is validated by numerical examples for both potential and elasticity problems. Numerical results well demonstrate the superconvergence and higher efficiency of the present gradient smoothing meshfree collocation method. |
| [21] | . |
| [22] | . |
| [23] | . In this paper, a meshfree or meshless local radial basis function (RBF) collocation method is proposed to calculate the band structures of two-dimensional (2D) anti-plane transverse elastic waves in phononic crystals. Three new techniques are developed for calculating the normal derivative of the field quantity required by the treatment of the boundary conditions, which improve the stability of the local RBF collocation method significantly. The general form of the local RBF collocation method for a unit-cell with periodic boundary conditions is proposed, where the continuity conditions on the interface between the matrix and the scatterer are taken into account. The band structures or dispersion relations can be obtained by solving the eigenvalue problem and sweeping the boundary of the irreducible first Brillouin zone. The proposed local RBF collocation method is verified by using the corresponding results obtained with the finite element method. For different acoustic impedance ratios, various scatterer shapes, scatterer arrangements (lattice forms) and material properties, numerical examples are presented and discussed to show the performance and the efficiency of the developed local RBF collocation method compared to the FEM for computing the band structures of 2D phononic crystals. |
| [24] | . Here we propose a new simulation-optimization model (S-O) for aquifer parameter estimation by coupling radial point collocation meshfree method (RPCM) with cat swarm optimization (CSO). The decision and state variables are zonewise transmissivity values and hydraulic heads at the predefined locations, respectively. The hydraulic head values obtained using RPCM acts as input for the CSO model. The RPCM-CSO model minimize sum of the weighted squared difference of simulated and observed hydraulic heads for different realization of transmissivity values. Further for comparison, RPCM model is coupled with particle swarm optimization (PSO) and elitist-mutated PSO (EMPSO). The RPCM-CSO model has been applied to estimate the zonal transmissivity values of a synthetic aquifer for validation and to a field problem. For synthetic problem, the transmissivity values are compared with available results. The RPCM-CSO model is more accurate than other models based on the genetic algorithm (GA) and PSO. For the field problem, average percentage error in parameter estimation using RPCM-CSO modelis 1.555%, for RPCM-PSOis 3.145% and for RPCM-EMPSO is 2.270%. Further a reliability analysis carried out showed that RPCM-CSO model is accurate and efficient to estimate the transmissivity values. This study showed the effectiveness of RPCM-CSO model for aquifer parameter estimation. |
| [25] | |
| [26] | . In this study, a meshfree radial point collocation method is used to model the contaminant transport through confined aquifer. The discretization of the governing equations is done by a point collocation method and radial basis functions (RBF) are used as the interpolation function. For comparative study, two widely used radial basis functions namely multi-quadrics and exponential RBF are used. A local circular support domain is employed to construct the shape functions. In the model, no information on nodal inter-relationship is required for shape function construction except the nodal coordinates, unlike in finite-difference (FDM) or finite-element (FEM) based methods. The developed model is validated through benchmark problems in one and two dimensions. Further, application of the model for advective transport with high Peclet number has been studied and the model has been found to be effective in handling the instability of high Peclet problems. For the field problem considered, the results obtained from the model have been compared with the FEM solution and was found to be satisfactory. This method is relatively easy to implement and offers better accuracy with acceptable computational time. Considering the significant advantages offered by this method, it can serve as a good alternative to the conventional methods. |
| [27] | . |
| [28] | . We present in this paper comparisons on the performances among five typical radial basis functions methods, namely radial basis collocation method (RBCM), radial basis Galerkin method (RBGM), compactly supported radial basis collocation method (CSRBCM), compactly supported radial basis Galerkin method (CSRBGM), and finite subdomain radial basis collocation method (FSRBCM), for solving problems arising from engineering industries and applied sciences. Numerical comparison results demonstrate that the RBCM and FSRBCM possess high accuracy and superior convergence rates in which the FSRBCM particularly attains higher accuracy for problems with large gradients. The FSRBCM, CSRBCM and RBCM are computationally efficient while the CSRBCM, CSRBGM and FSRBCM can greatly improve the ill-conditioning of the resultant matrix. In conclusion, its advantages on high accuracy; exponential convergence; well-conditioning; and effective computation make the FSRBCM a first-choice among the five radial basis functions methods. |
| [29] | . Strong form collocation in conjunction with radial basis approximation functions offer implementation simplicity and exponential convergence in solving partial differential equations. However, the smoothness and nonlocality of radial basis functions pose considerable difficulties in solving problems with local features and heterogeneity. In this work, we propose a simple subdomain strong form collocation method, in which the approximation in each subdomain is constructed separately. Proper interface conditions are then imposed on the interface. Under the subdomain strong form collocation construction, it is shown that both Neumann and Dirichlet boundary conditions should be imposed on the interface to achieve the optimum convergence. Error analysis and numerical tests consistently confirm the need to impose the optimal interface conditions. The performance of the proposed methods in dealing with heterogeneous media is also validated. Copyright 漏 2009 John Wiley & Sons, Ltd. |
| [30] | . The direct approximation of strong form using radial basis functions (RBFs), commonly called the radial basis collocation method (RBCM), has been recognized as an effective means for solving boundary value problems. Nevertheless, the non-compactness of the RBFs precludes its application to problems with local features, such as fracture problems, among others. This work attempts to apply RBCM to fracture mechanics by introducing a domain decomposition technique with proper interface conditions. The proposed method allows (1) natural representation of discontinuity across the crack surfaces and (2) enrichment of crack-tip solution in a local subdomain. With the proper domain decomposition and interface conditions, exponential convergence rate can be achieved while keeping the discrete system well-conditioned. The analytical prediction and numerical results demonstrate that an optimal dimension of the near-tip subdomain exists. The effectiveness of the proposed method is justified by the mathematical analysis and demonstrated by the numerical examples. Copyright 漏 2010 John Wiley & Sons, Ltd. |
| [31] | . Radial basis collocation method has easy implementation and exponential convergence. However, generally, the resultant collocation matrix is full and ill-conditioned and it鈥檚 hard to represent the local properties in solutions. Therefore, a finite subdomain collocation method with radial basis approximation is proposed. The approximation in subdomain is established within the subdomain and continuity conditions are imposed on all the interfaces in strong form. Consequently, the original full matrix can be transformed into a sparse matrix. Variant shape parameters can be used in different subdomains considering the need of solution representation in each subdomain. It can not only well alleviate the ill-condition and improve the solution accuracy, but also possess exponential convergence. Furthermore, CPU time can be markedly reduced. Error analysis and proper domain decomposition are also investigated. Numerical results show that this method has good performance for problems with high-gradient and singular problems which are prominent for their local characteristics. |
| [32] | . This paper discusses the application of the multizone decomposition technique with multiquadric scheme for the numerical solutions of a time-dependent problem. The construction of the multizone algorithm is based on a domain decomposition technique to subdivide the global region into a number of finite subdomains. The reduction of ill-conditioning and the improvement of the computational efficiency can be achieved with a smaller resulting matrix on each subdomain. The proposed scheme is applied to a hypothetical linear two-dimensional hydrodynamic model as well as a real-life nonlinear two-dimensional hydrodynamic model in the Tolo Harbour of Hong Kong to simulate the water flow circulation patterns. To illustrate the computational efficiency and accuracy of the technique, the numerical results are compared with those solutions obtained from the same problem using a single domain multiquadric scheme. The computational efficiency of the multizone technique is improved substantially with faster convergence without significant degradation in accuracy. |
| [33] | . 本文是关于函数的径向表示的综述性文章．基于我们对这方面的研究工作的了解，介绍了国际上近年来这方面主要的有关研究结果以及在一些领域中应用的情况．文后附有主要的参考文献以便感兴趣的读者查阅． . 本文是关于函数的径向表示的综述性文章．基于我们对这方面的研究工作的了解，介绍了国际上近年来这方面主要的有关研究结果以及在一些领域中应用的情况．文后附有主要的参考文献以便感兴趣的读者查阅． |
| [34] | . The numerical solution of three problems of finite deflection of uniform beams using the Euler-Bernoulli law of bending are presented. The problems are the uniformly loaded cantilever, the uniformly loaded simply supported beam and the column under axial loading. |
