NUMERICAL ANALYSIS OF THREE-DIMENSIONAL ELECTRO-CONVECTION OF DIELECTRIC LIQUIDS IN A CUBICAL CAVITY1)
WuJian中图分类号:O351.2
文献标识码:A
收稿日期:2018-09-9
接受日期:2018-09-9
网络出版日期:2018-11-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (14106KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
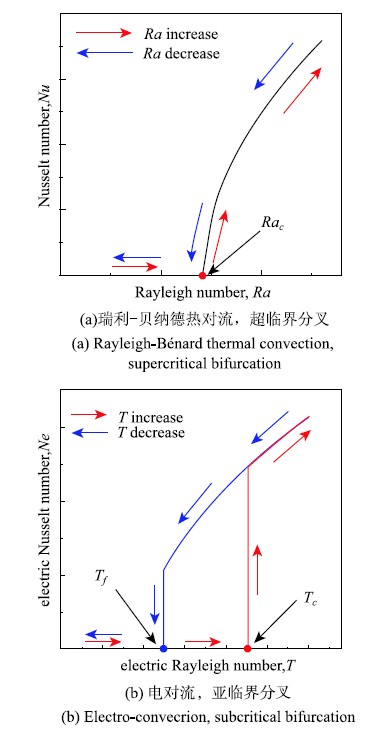
电流体动力学(electrohydrodynamics,EHD)主要研究电场与不同流体介质(包括液体、气体和晶体等)相互作用[1].与磁流体力学一样(magnetohydrodynamics,MHD),电流体动力学属于流体力学与经典电磁场理论相互交叉的一门学科.电流体动力学既是理解一系列经典物理现象(如电流动、离子风、电黏性、电流变效应等)的基本原理,又是许多实际应用(如强化传热传质、电除尘、电纺丝和喷雾、等离子流动控制、电绝缘等)的理论基础[2-5].从能量转换角度上看,电流体动力学现象涉及电能和流体动能的直接转换,这为能量的高效和智能利用提供了基础.基于电场驱动的流动技术因其具有无需运动部件、智能控制、低能耗、低噪音振动、空间跨尺度的良好适应性等特性,在微电子机械系统和低重力空间等特殊环境下有广阔应用前景[6-9].单极电荷注入(unipolar chargeinjection)引起的平行平板间介电液体电对流(electro-convection)是电流体动力学的一个经典模型问题[10].该问题对理解介电液体中电荷输运过程及其与电场、流场的非线性相互作用有重要意义.与经典的瑞利--贝纳德热对流(Rayleigh--Bénardconvection,RBC)系统一样,介电液体电对流也是一个典型的非线性耗散系统.通过连续增大电极间的电势差,电场力强度也会逐渐增大从而驱动系统依次经历静止态、稳态对流(呈现规则的流型)、非稳态流动(周期流和准周期流)和湍流.最早,Schneider等和Atten利用经典的模态分解方法对该简化模型的线性稳定性进行了理论分析,阐述了其失稳机理[11-12].众所周知,RBC系统的线性分叉类型为超临界(supercritical),如图1(a)所示.也就是说,随着驱动参数瑞利数$Ra$ (Rayleighnumber)增大,系统会连续地从静止态过渡到流动态.而电对流系统的线性分叉类型为亚临界(subcritical),如图1(b)所示.该类分叉存在两个典型特征：(1) 随着驱动参数电瑞利数$T$ (electricRayleighnumber)增大,系统一旦线性失稳将从静止状态跳变至有一定强度的流动状态;(2)要想从该流动状态回归到静止状态,驱动参数需要调整到比线性临界值小的另一个非线性临界值,即这两个临界值之间存在一个迟滞回线(hysteresisloop). Atten和Lacroix[13]对该类电对流的非线性稳定性进行了分析,给出了临界值的预估值,并理论上证明了电对流线性失稳后六角形晶胞(hexagonalcells)流型的形成. Atten等[14-16]利用在金属电极表面附加一层离子交换膜(ion exchangemembrane)实现了稳定且可重复的单极注入,并进行了大量介电液体电对流实验研究.他们的物理实验确认了电对流的亚临界线性分叉特性,但实验得到的线性和非线性临界值与理论预测均有较大差距.2015年,张蒙齐等[17]首次将非模态稳定性理论(non-modal stabilitytheory)应用于该类电流动的研究,尝试去解释实验测得的线性稳定性临界值与理论预测值不一致的问题.2016年,张蒙齐[18]使用多尺度展开方法(multiple-scale expansionmethod)对该问题的弱非线性稳定性进行了深入研究.这些理论分析都是假定无限大平板,即液体层在水平面上无限延伸,其流动不受侧壁影响,可以充分发展.为了减小侧壁的影响,电对流稳定性实验研究往往采用圆形电极且控制电极半经和电极间厚度比(称为径宽比$\varGamma)$为较大值.
显示原图|下载原图ZIP|生成PPT图1两种典型线性稳定性分叉类型
-->Fig.1Two typical types of linear bifurcation
-->
近年来,介电液体电对流的数值模拟工作取得了很大的进展.电荷密度方程的强对流特性是电对流数值求解的一个主要难点[19].研究人员发展了一些新方法和离散格式来克服该难点,主要包括粒子方法(particle-in-cellmethod, PIC) [20]、通量校正传输格式(flux corrected transportscheme, FCT) [21]、全逆差递减格式(total variation diminishingscheme, TVD) [22-23]、间断有限元法(discontinuous Galerkinmethod, DGM) [24]和格子--玻尔兹曼法(lattice-Boltzmannmethod, LBM) [25]等.这些算法的有效性和精度一般是通过二维电对流问题来验证和确定.二维计算结果确认了线性稳定性分析的预测,并揭示了非线性稳定性分析中引入的一些假设会影响非线性临界值的预测[26].2012年,Kourmatzis和Shrimpton[27]首次对三维电对流进行了数值模拟.近期,罗康等[28-29]首次在数值解中观察到了该类流动的正六边形晶胞流型,并给出了该流型对应的非线性临界值的数值预测.这些数值计算均是通过在侧壁设置对称或者周期性边界条件来模拟无限大平板情况下的电对流,从而可以和稳定性分析的结果进行对比讨论.
尽管实际物理问题中都存在侧壁面的限制,但目前只有少量研究工作关注有限空间区域内电对流问题.最早,Malraison和Atten [16, 30]对径宽比$\varGamma \approx1$的圆柱腔体内电对流进行了实验研究.Chicón等[31]对$\varGamma \approx1$圆柱腔体内电对流进行了三维数值模拟.对于该几何结构,他们的结果显示流动仍然为亚临界分叉,只是线性和非线性临界值与无限大区域情况有较大差别.为了减小计算量,他们采用采用了半解析公式代替求解Navier-Stokes方程组来获取流场,而这种解耦处理有可能会显著改变流场结构及流动分岔特性[32].在最近的两篇论文中,作者利用直接数值模拟和稳定性分析方法对二维方腔内电对流的线性稳定性进行了系统研究[33-34].他们发现在小长宽比时,侧壁对流动稳定性临界值及流场结构有重要影响,尤其是线性分叉类型会随着长宽比呈现亚临界和超临界的交叉过渡.我们拟将前述研究拓展到更接近真实物理场景的三维封闭腔体.作为第一步,本文将通过直接数值模拟方法来研究三维立方腔体内的电对流,重点分析侧壁对流动稳定性及流场结构的影响.
1 物理问题及数学模型
考虑如图2所示的三维封闭方腔体内的介电液体电对流问题.采用笛卡尔坐标系$(x, y, z)$,立方体的边长为$L$.上、下壁面为平板电极,4个侧面为电绝缘壁面. 上板接地,电压$V_0 =0$;下板外接直流电源,$V = V_1 > 0$.由于在大多数情况下,电子总是会很快被液体分子俘获,液体中的电荷载子(chargecarriers)是正负离子.一般而言,介电液体中自由电荷(离子)产生机制主要包括中性电解质的解离(分解机制)和液体--电极表面电化学反应产生的电荷注入(注入机制)[1].这两种机制都与电场强度、电解质种类、电导率、电极材料及结构布置等因素有密切且复杂的关系.为了简化问题,我们假定液体完全绝缘,自由电荷只来源于下平板的注入过程,即单极电荷注入.并且,电荷注入密度在整个下电极板上保持均匀不变,即$q = q_0 > 0$.之前的实验研究中,这些假设是通过对介电液体进行纯化把电导率降低到极小值同时在电极表面覆盖离子交换膜来实现[14-16].电场作用在这些离子上会施加给流体一个库伦体积力(Coulombforce),从而驱动产生对流,即电对流.
显示原图|下载原图ZIP|生成PPT图2三维封闭方腔内介电液体电对流示意图
-->Fig.2Sketch of the electro-convection of dielectric liquids confined within a cubical cavity
-->
电对流问题的控制方程包括简化的Maxwell方程组和Navier-Stokes方程组.由于电对流系统中的电流强度小,磁场效应可以忽略,Maxwell方程组退化到准静电学(electro-quasistatics)范畴[1].对于牛顿型不可压缩等温流体电对流,完整控制方程可写成如下形式[1,17,34]
$$\nabla \cdot u = 0 (1)$$$$\rho \frac{\partial u}{\partial t} + \rho \left( u \cdot\nabla \right) u = - \nabla p + \mu \Delta u + f_{\rm e} (2a)$$$$ f _{\rm e} = q E - \frac{1}{2} E ^2\nabla \varepsilon+ \nabla \left( \frac{ E ^2}{2}\rho \frac{\partial\varepsilon }{\partial \rho } \right) (2b)$$$$\frac{\partial q}{\partial t} + \nabla \cdot j = 0 (3a)$$$$ j = K E q + u q - D\nabla q (3b)$$$$\nabla ^2V = - \frac{q}{\varepsilon } (4)$$$$ E = - \nabla V (5)$$
式中,$ u \equiv \left[{u,v,w} \right]$为流体速度矢量,$ E \equiv \left[ {E_x ,E_y,E_z } \right]$为电场矢量,$ j $为电流密度,$ f _{\rm e}$为电场力;标量$\rho$,$p$,$V$,$q$分别表示流体密度、动态压力、电势和电荷密度;参数$\mu$,$\varepsilon$,$K$,$D$分别表示动力黏度、介电常数、离子迁移速率和电荷扩散系数.
如式(2)所示,电场力$ f_{\rm e} $包括三部分：库仑力$q E$,束缚电荷作用力(也称介电力)$ - E^2\nabla\varepsilon/2$和电致伸缩力$\nabla \left(\dfrac{1}{2} E ^2\rho{\partial \varepsilon }/{\partial \rho }\right)$.对于等温均质流体,介电常数不随空间变化,因此束缚电荷作用力为零.电致伸缩力可表示为一个标量的梯度,因此可以与流体压力项耦合[10].本文只考虑库仑力驱动流体流动.如式(3b)所示,自由电荷存在3种输运方式：在电场作用下的迁移,随着流场的流动以及扩散.在介电液体电流动中,离子迁移速率$K E $与流场速度$ u$为同一数量级,均远大于离子扩散速度.因此,电荷输运方程(3a)是一个强对流占优的非稳态对流--扩散方程.
引入一系列特征标度(长度$L$、电势$\Delta V = V_1 - V_0$、速度$K\Delta V/L$、电荷密度$q_{0}$、压力$\varepsilon \Delta V^2/L^2$),将控制方程转换成以下无量纲形式
$$\nabla \cdot u = 0 (6)$$$$\frac{\partial u}{\partial t} + \left( u \cdot \nabla\right) u = - \nabla \tilde {p} + \frac{M^2}{T}\Delta u +CM^2q E (7)$$$$\frac{\partial q}{\partial t} + \nabla \cdot \left[ q\left( u + E \right) \right] = \alpha \nabla ^2q (8)$$$$\nabla ^2V = - Cq (9)$$$$ E = - \nabla V (10)$$
无量形式的边界条件包括
$$y = 0: \quad V = 1, \quad q = 1, \quad u = v = w = 0 \\ y = 1: \quad V = 0, \quad \partial q/\partial y = 0, \quad u = v= w = 0 \\ x = 0,1: \quad \partial V/\partial x = 0, \quad \partial q/\partial x = 0, \quad u = v = w = 0 \\ z = 0,1: \quad \partial V/\partial z = 0, \quad \partial q/\partial z = 0, \quad u = v = w = 0$$
其中,电荷密度的诺伊曼边界条件是基于开口边界的假定[35],侧壁电势的诺伊曼边界条件是根据实验分析做的假设[36],而流体速度在所有的边界均为无滑移.
在以上控制方程及边界条件中出现的无量纲参数包括
$$T = \frac{\varepsilon \Delta V}{\mu K}, \quad C = \frac{q_0L^2}{\varepsilon \Delta V}, \quad M = \frac{1}{K}\left({\frac{\varepsilon }{\rho }} \right)^{1 / 2}, \quad \alpha =\frac{D}{K\Delta V}$$
其中,电瑞利数$T$定义为库仑力与流体黏性力之比,其与外加电势差成正比,是系统的主驱动参数.$C$表示电荷注入强度.根据$C$的值可以把注入程度分成三种情况：强注入$(5<C)$、中等注入$(0.2<C<5)$和弱注入($C<0.2)$~[37].$M$表示无量纲离子迁移率,其值由离子和流体的物性参数决定.对于介电液体,$ M \ge 3$ [10]. $\alpha$为无量纲电荷扩散系数,其典型取值范围为$[10^{ - 4}$,$10^{ - 3}]$[35].另外,对于封闭腔体,还需要考虑坐标$x$和$z$方向的长宽比：$A_{x}=L_{x}/L$和$A_{z}=L_{z}/L$,其中$L_{x}$和$L_{z}$分别是$x$和$z$方向的板间距.对于立方体,$A_{x}=A_{z}=1$.
2 数值方法及验证
2.1 数值方法
基于有限体积法发展了一种在时间和空间维度上均为二阶精度的算法来求解式(6)$\sim$式(10)及边界条件.由于该算法已在求解二维电场--电荷耦合问题[23]和电热对流问题[38]工作中进行了详细阐述,这里仅做简要介绍.空间离散采用非均匀笛卡尔网格,所有的变量均存储于控制容积中心,即采用同位网格布置.为了研究流场的演变过程,我们采用时间步进求解策略,在一个时间步长内依次求解静电模块和流场模块.对于Navier-Stokes方程,二阶中心差分格式用于对流和扩散项的离散,时间离散采用二阶半隐三层格式,SIMPLE格式[39]用于速度--压力的解耦,动量插值采用Rhie-Chow格式[40].文献[23]详细阐述了利用有限体积法求解静电场方程组(8)$\sim$(10)的方法,简要介绍如下.首先,我们可以把式(8)和式(9)改写成以下通用对流--扩散型方程的形式[41]
$$\frac{\partial \left( {\xi \psi }\right)}{\partial t} + \nabla \cdot \left( U\psi \right) =\nabla \cdot \left( {\zeta \psi } \right) + S\left( \psi\right)\tag11$$
其中,通用变量$\psi $可代表$q$和$V$,而$\xi$,$ U$,$\zeta $,$S(\psi )$为控制参数或者名义系数.对于式(11),开发一个高效率、高精度的通用求解器.在每个时间步内,通过连续调用该求解器来求解式(8)和式(9).该求解器的时间和扩散项离散格式与求解Navier-Stokes方程一样,而对流项离散采用全逆差递减(TVD)格式来避免电荷密度解中出现非物理震荡.TVD格式来自于计算空气动力学中的激波捕获[42],其核心思想包括两点：首先,利用一个平滑度指标(smoothnessindicator)来标记出拟求解场中的平滑区和大梯度或跳跃区;第二,通过一个以平滑度指标为自变量的限制函数(limiterfunction)实现在平滑区利用高阶格式和在大梯度或跳跃区用低阶格式求解的自动过渡.文献[43]对多种限制函数进行了总结和对比.在大量测试基础上,本文选用Gaskell和Lau提出的SMART格式[44].在完成电荷密度和电势计算之后,利用二阶中心差分格式计算式(10)获得电场,然后把新的库仑力用于下一个时间步的流场计算.以上求解策略的优点在于简化了程序开发过程,并且可直接拓展用于电热对流以及多种电荷电对流等更复杂模型.对于这些问题,我们只需要再次调用通用求解器来求解温度方程或其它电荷的传输方程.
本文的主要结果均通过最近发展的一种求解电对流问题的统一格子-Boltzmann方法[25,28]进行了验证.
2.2 验证
利用顶盖驱动三维方腔流动问题验证自编程序的流场计算模块.对于该问题,雷诺数定义为$Re=\rho U_{0}L/\mu$,其中$U_{0}$为顶盖驱动速度.图3给出了$Re=1 000$时$y$方向和$x$方向中线上的速度分布并与文献[45]的结果进行比较.从图中可知,本文结果与参考结果非常吻合.特别地,采用非均匀网格获得的结果更准确,这说明自编程序的流场模块的准确性.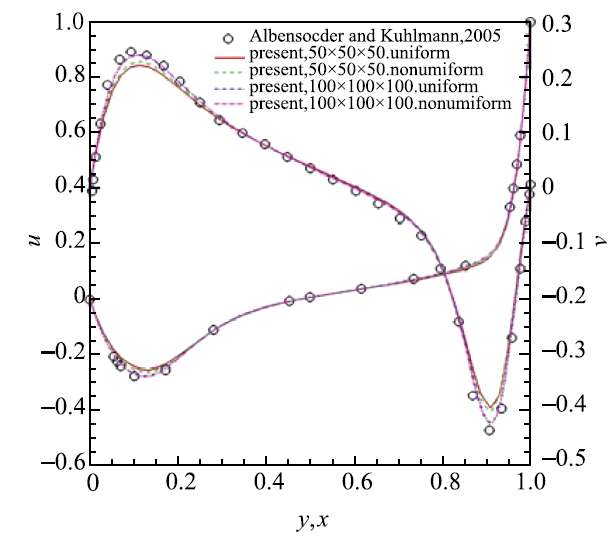
显示原图|下载原图ZIP|生成PPT图3顶盖驱动三维方腔流$Re=1000$时中线上的速度分布及与文献[
-->Fig.3Comparison of the centerlinevelocity with the lid-driven flow in cubical box at Re =1000 with the results from Ref.[
-->
通过求解式(8)$\sim$\!式(10)来验证静电场计算模块.假定空间电荷初始分布为零,在电场作用下,正离子从下电极板注入,通过迁移和扩散机制进行输运.空间电荷的存在会影响电场,从而改变离子迁移速度.最后,系统会达到一个动态平衡状态,对应的解称为流体静力学解(hydrsotatic solution).当电荷扩散系数为零时,流体静力学解存在如下显式表达式[20,26]
$$q(y) = \frac{a}{2C\sqrt {y+ b} }, \quad E_y (y) = a\sqrt {y + b} (12)$$
式中,$a$,$b$为与电荷注入强度$C$相关的参数. $C = 10$时,$a =1.488 2$,$b = 5.539\times 10^{ - 3}$.对于非零电荷扩散系数,流体静力学解的显式解析解表达式很难获得.在文献[17,18]中,作者通过对一个四阶常微分方程积分,获得了含扩散过程的流体静力学解的数值解.
图4给出了两种情况下获得的电荷密度和电场$y$方向分量沿$y$轴分布的数值结果与其他结果的比较.算例1,图4(a)对应算例参数为$C=10$和$\alpha=0$,数值结果与式解析解式(12)相比较;算例2,图4(b)对应算例参数为$C=40$和$\alpha =1.0\times 10^{ -4}$,我们的数值结果与利用数值积分方法获得的结果[17]相比较.由于电荷密度在靠近注入电极($y=0$)区域内的剧烈变化程度不一：$C$值越大,电荷密度梯度也越大.图4(a)和图4(b)中的数值结果是基于在$y$方向上分别用了100和250个控制容积的离散.通过对比可以发现,对于这两个算例,本文数值结果与参考结果都吻合得非常好.对于电荷密度,利用TVD格式获得了高精度光滑无振荡的解.算例1和2的数值结果与参考结果的最大误差分别小于2.0%和2.2%.
显示原图|下载原图ZIP|生成PPT图4流体静力学解的比较,其中(a)为与式(12)比较,而(b)为与文献[
-->Fig.4Comparison of the hydrostatic solution,our numerical results in case (a) are compared with Eqn. (12), and case (b) compared with the results from Ref. [
-->
3 结果与讨论
本文考虑$C=10$的强注入情况.由于该注入强度值可认为是实验中易实现的空间电荷限制注入(space-chargelimited injection, SCL,$C \to \infty)$的良好近似,因此它在以往的数值模拟和理论分析中广泛使用.另外,$M$和$\alpha $分别设置为60和$1.0\times 10^{ -4}$这两个典型代表值.重点考虑系统随着主驱动参数$T$的变化,尤其是侧壁对流动稳定性及流场结构的影响.经过网格无关性测试后,所有的结果都是基于一套100$\times $120$\times$100网格获得.这套网格在$x$方向和$z$方向为均匀分布,在$y$方向为非均匀.在$y$方向增加离散单元数以及减小靠近注入板的网格尺寸可有效提高电荷密度以及整体的求解的精度.3.1 线性稳定性及流场结构
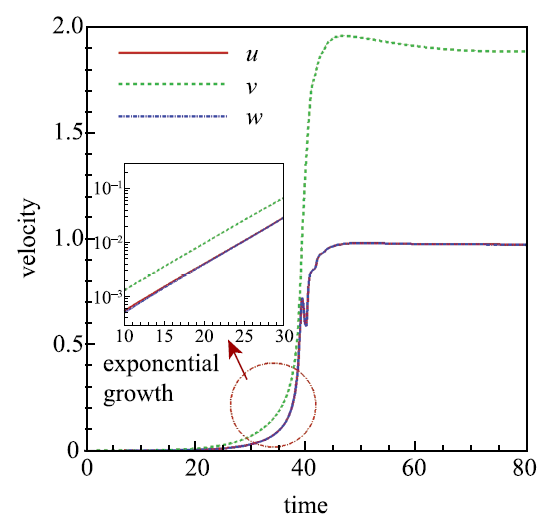
以前述流体静力学解为初始条件,计算从$T=0$以小幅度逐渐增大.发现电对流只有当$T$大于某一临界值(标记为$T_{ c})$时才可能发生,当$T$小于这个临界值时,系统将保持流体静力学状态.该临界值对应于稳定性分析理论中的线性稳定性临界值. 当$T<T_{c}$,库仑力不足以克服黏性效应,液体保持静止. 当$T>T_{ c}$,系统外部输入的电能足以克服黏性摩擦并维持流体运动.由于侧壁面会增强黏滞作用并且影响系统最不稳定扰动波数的选择,因此三维封闭方腔内电对流系统的$T_{\rm c}$会显著大于无穷大平板情况的线性稳定性临界值,也就是说侧壁对电对流起稳定流动作用.这类侧壁增强稳定效应在二维电对流以及二维和三维RBC流动都有体现[46].根据文献[12]的理论分析,对无限大平板情况,$C=10$,$\alpha=0$,$T_{\rm c}$及其对应的波数分别为164.1和5.113.通过初步测试,对于封闭立腔体,$250<T_{ c}<270$.需要说明的是,对于封闭腔体,各侧壁面要求必须满足显式边界条件,而且扰动波不能做分离变量的假设,这会给电对流线性稳定性理论分析带来一定困难[34].目前,我们还没有看到三维封闭腔内电对流问题的线性稳定性分析结果.图5给出了$T=270$ (稍大于$T_{\rm c})$时电对流流场中3个速度分量的最大值随时间变化曲线.从图中可以看出,系统从静止状态逐步发展,最终达到有一定强度的流动状态.这与封闭腔体内RBC热对流情况不一样,因为这类热对流在$Ra$稍大于$Ra_{\rm c}$时,流动强度非常弱[47].由于系统的初始扰动幅值很小,初期其遵循线性发展规律(即扰动大小随时间呈指数发展,见图5中插入图),随后扰动幅值因为非线性关系而达到饱和.可以观察到两个水平速度分量$u$和$w$的值非常接近,均小于垂直方向速度分量$v$.
显示原图|下载原图ZIP|生成PPT图5三维封闭方腔内电对流3个速度分量最大值随时间的发展曲线, $T =270$
-->Fig.5Time evolution of the maximum values of the three velocity components with electro-convection in the confined cubical enclosure, $T = 270$
-->
通过提取指数增长阶段的增长速率,可以对线性稳定性值进行估算[48].该方法的基本思想是：理论上线性稳定性临界值$R_{c}$对应的扰动发展速率为零,而当驱动参数$R$在$R_{c}$附近时,可以认为扰动的指数发展速率与($R-R_{c})$成正比,因此可以利用外推方法得到$R_{c}$的值.其详细介绍和具体操作过程可参考文献[26, 28,48].这种利用直接数值模拟结果间接确定线性稳定性临界值的方法,已经广泛应用于开口和封闭条件下的热对流和电对流问题,显示了良好的精度.特别地,基于该方法确定的二维封闭腔体内电对流线性稳定性值[33]与基于稳定性分析的预测结果[34]高度吻合.利用该方法,基于数值解预测的$T_{c}$临界值为259.3.
通过分析扰动的线性化方程及其需满足的边界条件,可以从理论上证明有限和开放空间电对流的线性稳定性值均与无量纲迁移速率$M$无关.为从数值结果上证明这点,对不同$M$值情况下的$T_{\rm c}$进行了预测,结果如表1所示. $T_{\rm c}$的平均值为259.7,最大偏差为$M=5$对应的1.36%.偏差主要来自于提取指数增长率时的误差.
Table 1
表1
表1三维封闭方腔电对流线型稳定性值$T_{\rm c}$与离子迁移率$M$关系
Table 1The relationship between the linear stability criterion $T_{\rm c}$ and the mobility parameter $M $ with electro-convection in the confined cubical enclosure
 |
新窗口打开
图6和图7分别展示了$T=270$时电对流最终状态的流场和电荷密度分布.从图中可以看出,流场和电荷密度的空间分布高度对称.图6展示的是两个截面上速度分量$v$的等值云图以及1/4区域内的流线.从图中可以看到,腔内存在一个大的中心环流,而且流动循环从边界处上升,从中心处下降.在对角区域的流动强度比壁面中心区域附近要高.封闭腔体内对流的一个典型特征是角涡的存在.从图6(a)我们可以粗略分辨出上下对角区域内的两个角涡,其中上角涡更明显.图6(b)给出了$[0.9, 1]\times [0.8, 1]\times [0.9,1]$这一上角落区域内的速度矢量分布.通过$v$速度的等值分布可以看出角落区域流动很微弱,但是能清楚分辨出流体速度方向的变化,并预见角涡的存在.
显示原图|下载原图ZIP|生成PPT图6三维封闭方腔内电对流的流场,$T = 270$
-->Fig.6The fluid velocity field for electro-convection in the confined cubical enclosure with $T = 270$
-->
显示原图|下载原图ZIP|生成PPT图7三维封闭方腔内电对流的电荷密度分布, $T=270$
-->Fig.7Charge density distribution for electro-convection in the confined cubical enclosure with $T = 270$
-->
如图7所示,电荷集中分布在下注入电极板附近区域.电荷从下板进入流体后主要通过电场迁移以及随着流场流动进行传输,传输通道为靠近侧壁的环形区域,如图7(a)中的水平截面. 特别注意到,在腔体中心出现一个"电荷空白区"(charge void region),该区域电荷密度趋于零($q \to 0)$.在图7(b)中,采用$q =0.05$的等值面来标记电荷空白区,该等值面将整个区域分成存在电荷区与电荷空白区.对于二维问题,等值面退化成等值线,也称为分界线(separatrix).这种电荷空白区是电对流的典型特征之一,它与电对流的亚临界线性失稳以及下面将讨论的迟滞效应密切相关.电荷空白区已在对称电极结构(如平行平板、同心圆环等)自由电对流中被广泛地讨论和研究.其形成的本质原因在于电荷的独特输运方式：对流和迁移.从图6(a)可以知,流场中部分区域向下的流体速度绝对值比向上的离子迁移速度大(由于采用离子迁移速度$K\Delta V/L$为无量纲尺度,因此离子迁移速度无量纲值为1),电荷不能进入这些区域.实际上,流场速度大于离子迁移速度是电荷空白区形成的必要条件[13].图5中时间$t =40$时,$u$和$w$存在一个拐点,此时$v$的值大约为1,即流体速度刚发展到与离子迁移速度相等的程度,从电荷分布可以看到此刻对应电荷空白区开始形成.注意到,电荷空白区并不封闭,而是在上电极板有开口.这是由于离子间存在的强烈库仑排斥作用(Coulombrepulsion)引起的[20].
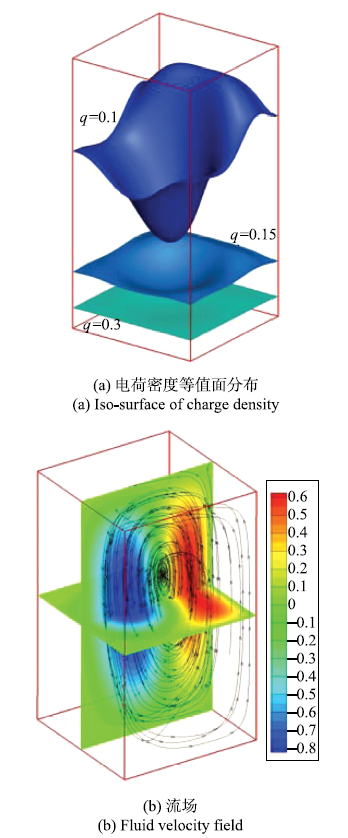
文献[33,34]对二维封闭方腔内电对流进行了研究,作者指出当腔体的长宽比小时,侧壁的无滑移引入的强附加摩擦,可能使流场强度减小到低于离子迁移速度.此时,电荷空白区不再形成,系统线性失稳类型变为超临界.图8给出了二维方腔$T=252$ (稍大于$T_{\rm c}= 240.9$[34])的最大速度随时间变化的曲线以及终态的电荷密度分布.从图中可以看出速度的终值约为0.15,电荷空白区没有形成.与二维封闭方腔相比,三维方腔内流动在$z$方向获得了发展空间,形成了电荷空白区,失稳类型是亚临界.这种情况下,侧壁面的作用体现在两方面：第一,将对流环流以及电荷空白区限制在腔体中心;第二,如图7(a)中$z=0.1$截面所示,侧壁会强烈影响其附近区域电荷分布.对小尺寸腔体$A_{x}=A_{z}=0.5$进行计算,发现此算例$T_{\rm c} \in(500,600)$.图9给出了$T=600$该小尺寸腔内电对流的电荷密度等值面分布和流场.从图中可以看出,电荷分布中没有出现电荷空白区,而且流场中向下的速度的最大值约为0.6,小于无量纲电场强度值1.0.因此,该尺寸算例对应的线性分叉类型为超临界.
显示原图|下载原图ZIP|生成PPT图8二维封闭方腔内电对流,$ T=252$
-->Fig.8Electro-convection in a two-dimensional confined square box, $T=252$
-->
显示原图|下载原图ZIP|生成PPT图9三维小尺寸封闭腔内电对流,$T=600$,$A_{x}=A_{z}=0.5$
-->Fig.9Electro-convection in a small three-dimensional confined cavity, $T=600$, $A_{x}=A_{z}=0.5$
-->
3.2 非线性稳定性与分叉图
介电液体电对流的另一个特性在于非线性稳定性.以$T=270$稳态对流结果作为初始条件,逐渐减小$T$值并进行重新计算,结果发现流动强度以及电荷空白区体积也会逐渐减小.当$T$值小于另一个临界值$T_{\rm f}\approx144.0$时,流动会从一个有限强度流动状态直接跳变至静止状态.该临界值称为非线性临界值. 由于$T_{f}<T_{\rm c}$,线性和非线性临界值之间存在一个迟滞回线.在图10中,我们通过电努塞尔数$Ne$随$T$的变化给出了立方腔体内电对流亚临界分叉完整曲线图.电努塞尔数(electrical Nusselt number,$Ne$)定义为总电流与流体静止时的电流之比,其表征流体流动对电荷输运的贡献,间接反应了流场强度的大小.
显示原图|下载原图ZIP|生成PPT图10三维封闭方腔体电对流亚临界分叉$Ne$-$T$曲线及回滞环
-->Fig.10Subcritical bifurcation diagram expressed by Ne versus $T$ for the electro-convection in the confined cubical enclosure
-->
与线性临界值不同,非线性临界值与流场和电荷空白区密切相关[13,26].任何影响流场的因素,如空间维度、离子迁移率、电荷扩散系数、侧壁边界条件等,都会影响非线性临界值.对于无限大平板情况,Atten等[13]在流场模态近似假设基础上通过非线性稳定分析给出了理论预测,对$C=10$,$\alpha =0$,$M \to \infty$时二维卷型和三维正六边形晶胞流动的$T_{\rm f}$的预测值分别是125.0和111.7.对于这两种流型,基于直接数值模拟的预测值分别为109.0[26,32]和111.1 [29].对于三维封闭方腔内电对流,由于侧壁的存在改变了流场结构并对流动施加了额外的限制,因此$T_{\rm f}$值比自由流动情况更大.
图11(a)给出了当$T$靠近$T_{\rm f}$时的电荷空白区的形状.从图中可以看出,与图7(b)相比,此时电荷空白区体积大为减小,外形也更加光滑,其上部开口变成圆形.此时,如果进一步减小$T$使$T<T_{f},$流场强度将小于离子迁移速率,电转矩(electrictorque)不能再维持流体的流动,此时电荷空白区将突然消失,流动也将停止,系统回归流体静力学状态.另一方面,如果以$T=270$时稳态电对流的解为初始条件,逐步增大$T$重新计算,我们发现流动强度会逐步增强,电荷空白区体积也会逐渐增大. 当$T \ge400$,系统会发生二次不稳定分叉,从只有一个大尺度对流胞流型跳变成含有4个小尺度对流胞的流型.如继续增大$T$,系统将向湍流态过渡.确定封闭腔体内电对流从层流到湍流转捩路径以及其与其他控制参数间的关系,将是下一步工作方向.
显示原图|下载原图ZIP|生成PPT图11三维封闭方腔体电对流中$q=0.05$等值面
-->Fig.11Isosurface of the charge density ($q=0.05$) with electro-convection in the confined cubical enclosure
-->
最后,通过与一个自由边界算例进行对比来进一步讨论侧壁对电对流的影响.考虑立方体腔为计算区域,但是4个侧壁上设置为周期性边界条件.$T=280$计算结果如图12所示：图12(a)为电荷空白区;图12(b)为流场.首先,周期性边界条件不能唯一地确定电荷空白区是位于方腔中心还是边界上.图12(a)显示了一种位于边界上的电荷空白区,它的形状和图7中的无滑边界条件基本相同,但体积大很多.图12(b)显示了垂直速度场和流线.与图7的无滑移边界情况类似,在电荷空白区的中心(即方腔边界),垂直速度是向下,而在电荷空白区外部,垂直方向向上,这与Atten等的理论预测一致[13].对比图6(a)与图12(b)可见,对于同样的$T$值,自由边界电对流的流场强度明显大于封闭腔体电对流强度.
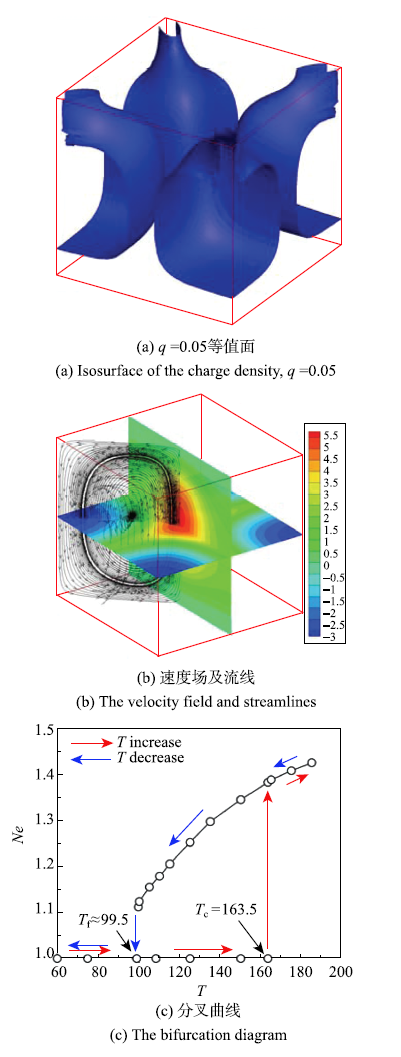显示原图|下载原图ZIP|生成PPT图12三维方腔体自由边界电对流
-->Fig.12Results for free electro-convection in a cubical enclosure with periodic condition on lateral sides
-->
并且,由于没有壁面的限制作用,在周期性边界条件的情况下,没有观察到角涡.图12(c)给出了周期性边界条件下的分叉图,从图中可以看出自由对流的线性和非线性临界$T$值都比无滑边界的要低,这进一步说明了侧壁会对流动的发展起限制作用.
4 结 论
单极电荷注入引起的平行平板电极间介电液体电对流是电流体动力学的一个经典模型问题.已有研究主要关注无限大区域自由对流情况,本文通过直接数值模拟来研究更接近真实物理场景的立方封闭腔体内的三维电对流.我们基于有限体积法发展了求解该问题的一种二阶精度算法,其中全逆差递减格式用来求解电荷密度方程.顶盖驱动三维方腔流动问题和流体静力学解被用来分别验证我们自编程序的流场和静电场计算模块.对于两个验证案例,我们的数值解与参考结果都非常吻合.数值结果表明,该问题存在线性稳定性,即只有当主驱动参数大于某临界值时,库仑力才能克服粘性效应引起流动.而且,流动的线性失稳类型为亚临界,也就是说系统线性失稳后将从静止状态跳变至一个有一定强度的对流态.只有当主驱动参数减小到另一个非线性临界值以下时,系统才能从对流态回归静止态.由于非线性临界值比线性值临界小,因此存在回滞现象.对注入强度$C=10$,电荷扩散系数$\alpha =10^{ -4}$和无量纲离子迁移速率$M=60$,我们通过数值结果确定的线性和非线性临界值分别为259.7和144.0.而且,我们数值证明了线性临界值与无量纲离子迁移速率不相关.与无限大区域中的自由电对流相比,封闭方腔内电对流线性和非线性临界参数均有明显增加.这是由于侧壁对系统施加了额外的摩擦和约束,改变了流场的结构.另外,我们揭示了封闭立方体内电对流的电荷密度和速度场的空间分布特征.其中,电荷密度分布中存在电荷空白区,流场中存在角涡.
本文获得的三维封闭方腔内电对流线性和非线性临界值的结果可为稳定性理论研究提供参考.未来,我们将分析腔体几何参数对流动线性分叉的影响以及确定电流动从层流态到湍流态的转捩路径.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . . |
| [3] | . |
| [4] | . . |
| [5] | . |
| [6] | |
| [7] | . . |
| [8] | . |
| [9] | . . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . |
| [42] | . |
| [43] | . |
| [44] | . |
| [45] | . |
| [46] | . |
| [47] | . |
| [48] | . |
