, 李明ACCURACY ANALYSIS AND IMPROVEMENT OF VISCOUS FLUX SCHEMES IN UNSTRUCTURED SECOND-ORDER FINITE-VOLUME DISCRETIZATION
WangNianhua, LiMing中图分类号:V211.3
文献标识码:A
通讯作者:
收稿日期:2018-02-8
接受日期:2018-03-27
网络出版日期:2018-06-10
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (9712KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
1 引言
随着计算流体力学(computational fluid dynamics, CFD)的发展,非结构网格生成技术及非结构网格算法得到了广泛的研究和应用. 非结构网格在处理复杂外形上具有极大的灵活性及高效性,网格生成自动化程度高,同时又能较为方便地实现网格自适应. 尽管与结构网格相比,非结构网格存在上述诸多优势,但是非结构网格及算法在计算效率和精度方面仍存在一些不足. 如今,名义上二阶精度的非结构有限体积方法已经广泛应用于CFD工程实践中,然而有限体积离散的实际精度却一直是CFD研究者关注的问题,提高有限体积离散的实际精度具有十分重要的现实意义.早在20世纪90年代,Roe[1]和Giles[2]就对Euler方程的有限体积格点型Jameson格式和Ni格式进行了数学分析和数值精度测试,并且揭示了截断误差收敛性和离散误差收敛性之间的关系.
针对非结构网格二阶精度有限体积迎风格式,已经有研究者在单元梯度重构精度[3,4,5,6,7,8,9]、无黏通量与黏性通量格式计算精度[9,10,11,12,13,14,15,16]、网格类型/网格质量对计算精度的影响[17,18]等方面进行了较多的研究工作.
比如,通过比较不同格式在不同网格上的精度高低,掌握了不同单元梯度重构方法的精度特性[3,4,5,6,7,8,9],确定了单元梯度重构达到至少一阶精度的条件[8]及计算精度较高的单元梯度重构方法
但是这些研究或是孤立地研究单元梯度重 构[4,7,9],或是仅仅通过模型方程或者Euler方程研究流动模拟精度的高低[3,8-13],而较少在实际流动的RANS(Reynolds averaged Navier-Stokes)数值模拟中对各种方法和格式进行精度测试和验证. 因此在复杂外形流动的RANS数值模拟中仍然难以有效提高有限体积离散方法的计算精度,即便采用高阶精度有限体积格式[24]. 一些改进方法离实际的CFD工程应用还有较大的距离,这也体现出对有限体积离散格式的理解仍需进一步加深,对离散格式的改进仍然需要在实际流动模拟中进行更多应用与验证.
对于实际流动模拟精度的验证与确认问题,目前更多地是采用网格收敛性测试并与风洞实验结果进行对比确认. 如用于湍流数值模拟验证与确认的美国宇航局湍流模型验证与确认数据库(turbulence modeling resource, TMR) [25,26,27],以及对实际复杂外形升阻力预测精度验证与确认的阻力预测研讨会(Drag Prediction Workshop) [28,29,30]和高升力预测研讨会(High Lift Workshop) [31,32]等.
本文针对黏性流动数值模拟问题,从梯度重构方法、黏性通量中的界面梯度计算方法两个方面考察二阶精度格心型有限体积格式的黏性流动模拟精度. 采用的主要方法是基于标量扩散方程的制造解网格收敛性精度测试. 我们将首先对黏性通量离散中的“奇偶失联”问题进行分析和制造解验证;然后通过引入差分修正项以消除“奇偶失联”现象,并在几种不同类型、不同质量的网格上进行制造解精度(阶)测试,考察前述因素对扩散方程计算精度及数值精度阶的影响,得到各种方法在制造解精度测试中的表现;最后对3个实际黏性流动数值模拟算例(二维平板层流、美国宇航局TMR中的二维平板湍流和二维翼型近尾迹流动)进行网格收敛性测试,考察前述方法对实际高雷诺数黏性流动问题的模拟能力.
2 数值方法
2.1 标量扩散方程有限体积离散
本文采用标量扩散方程作为模型方程研究黏性通量计算精度,标量扩散方程采用二阶精度格心型有限体积方法离散.扩散方程的微分形式为
$\dfrac{\partial \phi }{\partial t} = \dfrac{\partial ^2\phi }{\partial x^2} + \dfrac{\partial ^2\phi }{\partial y^2} + \dfrac{\partial ^2\phi }{\partial z^2} (1)$
上式中为了便于时间推进求解,在方程左端引入了(虚拟的)时间微分项.
为了便于有限体积方法离散求解,将方程(1)写成积分形式
$\dfrac{\partial }{\partial t}\int_\varOmega \phi d\varOmega = \int_{\partial \varOmega } {\pmb F}_{\rm v} \cdot {\pmb n} S (2) $
因此,黏性通量矢量为
$F_{v} = ( \frac{\partial \phi }{\partial x},\frac{\partial \phi }{\partial y},\frac{\partial \phi }{\partial z} ) (3)$
由式(3)可见,黏性通量矢量由单元界面梯度组成,因此在非结构二阶有限体积法中,界面梯度计算方法决定了黏性通量计算格式.
2.2 NS方程的有限体积离散
本文在3个实际黏性流动问题中(二维平板层流、二维平板湍流和二维翼型近尾迹流动)进行网格收敛性测试,实际流动的 控制方程为积分形式的Navier-Stokes (N-S)方程$\dfrac{\partial }{\partial t}\int_\varOmega {\pmb W} d\varOmega + \oint\limits_{\partial \varOmega } \left({ {\pmb F}_{\rm c} - {\pmb F}_{\rm v} } \right) dS = \int_\varOmega {\pmb Q} d\varOmega (4)$
式中
方程采用格心型非结构二阶精度有限体积法进行离散. 无黏通量离散采用Roe格式[33],求解雷诺平均N-S 方程时,选用SA一方程湍流模型[33]. 单元梯度重构有多种选择,在文献[4, 8, 34]中已做了详细的分类和测试,本文将以文献的结论作为参考,主要考察GG-Cell,LSQ-basic和WLSQ-basic单元梯度重构方法. 为排除限制器对计算精度的影响,所有算例均不采用限制器. 除此之外,黏性通量计算需要先求得相邻单元交界面的梯度值,下文将介绍界面梯度计算方法.
2.3 界面梯度计算方法
根据单元梯度值的加权方式、界面值是否连续、以及是否引入差分修正项,界面梯度的计算方法分为很多种[13]. 本文主要对4种典型格式进行测试和验证.(1)平均梯度法(average method) [14],即左右单元梯度直接平均
$\left( {\nabla \phi } \right)_{\rm f} = \left( {\overline {\nabla \phi } } \right)_{ij} = \dfrac{\left({\nabla \phi } \right)_i + \left( {\nabla \phi } \right)_j }{2} (5)$
式中
(2)差分修正法(edge correction method) [14],即平均梯度的基础上,在界面左右单元格心连线(edge)方向上用界面相邻单元的差分进行修正
$\left( {\nabla \phi } \right)_{\rm f} = \left( {\overline {\nabla \phi } } \right)_{ij} - \left[{\left( {\overline {\nabla \phi } } \right)_{ij} \cdot {\pmb e}_{ij} - \left( {\dfrac{\partial \phi }{\partial l}} \right)_{ij} } \right]{\pmb e}_{ij} (6)$
$\left( {\dfrac{\partial \phi }{\partial l}} \right)_{ij} = \dfrac{\phi _j - \phi _i }{l_{ij} } ,\quad {\pmb e }_{ij}= \dfrac{{\pmb r}_{ ij}}{l_{ij} } (7)$
式中
(3)法向导数法(face normal difference method) [35], 即构造界面中垂线上的距离界面左右单元格心最近的两个点,以此两点之差分作为界面梯度的法向分量,而界面梯度的切向分量仍直接按方法(1)取平均. 界面梯度的法向分量为
$ \ \ \left( {\dfrac{\partial \phi }{\partial n}} \right)_{\rm f} = \dfrac{\phi _2 -\phi _1 }{l_{12} } (8)$
$\left.\begin{matrix} \phi _1 = \phi _i + ( {\nabla \phi } )_i \cdot ( {{\pmb r}_1 - {\pmb r}_{ i} } ) \\ \phi _2 = \phi _j + ( {\nabla \phi } )_j \cdot ( {{\pmb r}_2 - {\pmb r}_j }\\\end{matrix}\right\} (9)$
(4)加权差分修正法(weighted edge correction method),即在界面左右单元格心连线(edge)方向上采用平均梯度与差分项的加权,该方法是本文作者在综合平均梯度法和差分修正法的基础上提出的一种界面梯度计算方法,其具体形式为
$ \left( {\nabla \phi } \right)_{\rm f} = \left[ {\left( {1 - \varepsilon } \right)\left( {\overline {\nabla \phi } } \right)_{ij} \cdot {\pmb e}_{ ij} + \varepsilon \left( {\dfrac{\phi _j - \phi _i }{l_{ij} }} \right)} \right]{\pmb e}_{ij} + \\ \left[ {\left( {\overline {\nabla \phi } } \right)_{ij} \cdot {\pmb e}_{ ij} ^ \bot } \right]{\pmb e}_{ ij} ^ \bot = \\ \left( {\overline {\nabla \phi } } \right)_{ij} - \varepsilon \left[ {\left( {\overline {\nabla \phi } } \right)_{ij} \cdot {\pmb e}_{ ij} - \dfrac{\phi _j - \phi _i }{l_{ij} }} \right] {\pmb e}_{ ij} (10)$
式中
显然,当加权系数
文献[14]指出,虽然平均梯度法简单易实现,不需要额外的数据存储,但是会在四边形网格或六面体网格上导致“奇偶失联”,而差分修正法则能够在四面体、三棱柱及六面体网格上形成强耦合的模板,因此大量的实践中均采用了差分修正法. 文献[35]则指出法向导数法计算精度最好. 为此,本文将对“奇偶失联”进行分析和数值验证,同时对这几种界面梯度计算方法进行精度测试和验证.
2.4 制造解方法
通常,我们需要一个精确解来测试离散格式的计算精度. 但是大多数的可压缩黏性流动的精确解都过于简单,不能完整 体现控制方 程的所有项. 为了解决这个问题,Roache等[36,37]提出了制造解方法.制造解方法的基本思路是选择任意的“制造解”代入原始的控制方程(如N-S方程、Euler方程或者标量方程等),一般来说,制造解 不能满足原始的控制方程,代入控制方程后,右端项不为零,可以把引入的右端项设为源项. 因此,制造解可以理解为带源项的修正方程的精确解
$\dfrac{\partial {\pmb Q }}{\partial t} + \nabla \cdot {\pmb F} - \nabla \cdot {\pmb F }_{\rm v} = {\pmb S}(11)$
文献[34]已经对制造解方法进行了详细的介绍,并将分量制造解方法和标量制造解方法应用于非结构网格二阶精度有限体积 离散格式的精度测试与验证.
本文将采用基于扩散方程的标量制造解方法研究网格类型/质量、单元梯度重构、界面梯度计算方法等因素对扩散方程计算精 度的影响. 由于标量扩散方程的形式与N-S方程中线性扩散项的形式相同,因此采用标量扩散方程作为模型方程,研究扩散方程的计算精 度对于研究N-S方程计算精度有一定的参考意义. 基于标量扩散方程的制造解方法在此不再详述,可以参考文献[34].
网格收敛性测试选取5套依次加密的网格,边界条件为Dirichlet边界,以消除边界条件离散的误差. 测试离散误差随网格尺 度减小时的收敛情况. 通过离散误差的
本文实现制造解精度测试及黏性流动数值模拟的平台均为作者所在课题组开发的HyperFLOW软件[38,39],这里不再详述.
3 黏性通量离散“奇偶失联”分析
2.3节指出采用平均梯度法在矩形网格或者六面体上求解界面梯度会导致“奇偶失联”. 以下对这一问题进行简要分析.在矩形网格上,由于一阶误差项的抵消,线性重构的单元梯度,如GG-Cell或者LSQ-basic等梯度重构方法[4,6,8,34],均可以达到二阶精度,也即等价于中心差分.
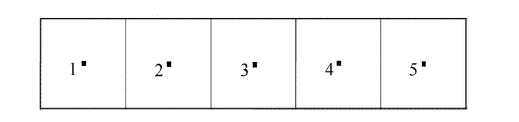
以一维笛卡尔网格(如图1所示)为例,当采用平均梯度法求解界面梯度时,那么奇数单元3的黏性通量为
$ \int_{\partial \varOmega } {\pmb F }_{\rm v} \cdot {\pmb n} S = - \left( {\nabla Q} \right)_{32} + \left( {\nabla Q} \right)_{34} = \\ - \dfrac{1}{2}\left[ {\left( {\nabla Q} \right)_2 + \left( {\nabla Q} \right)_3 } \right] + \dfrac{1}{2}\left[ {\left( {\nabla Q} \right)_3 + \left( {\nabla Q} \right)_4 } \right] = \\ - \dfrac{1}{2}\left( {\dfrac{Q_3 - Q_1 }{2\Delta x} + \dfrac{Q_4 - Q_2 }{2\Delta x}} \right) + \\ \dfrac{1}{2}\left( {\dfrac{Q_4 - Q_2 }{2\Delta x} + \dfrac{Q_5 - Q_3 }{2\Delta x}} \right) = \dfrac{Q_5 - 2Q_3 + Q_1 }{4\Delta x} (12)$
显示原图|下载原图ZIP|生成PPT图1一维矩形网格示意图
-->Fig. 1Example of one-dimensional quadrilateral grids
-->
式(12)显示,奇数单元3的黏性通量仅仅与奇数标号的单元1和单元5相关,而与相邻的偶数单元2和单元4解耦,同样也可以证明偶数单元的黏性通量只与偶数单元相关,而与奇数单元无关,即所谓的“奇偶失联”(odd-even decoupling). 在有限差分离散中,采用中心格式也会导致类似的问题,改用迎风差分或者使用交错网格可以很好的解决“奇偶失联”问题,而在有限体积法中,通过改进平均梯度法,构造强耦合的通量计算模板可以解决“奇偶失联”的问题.
正如2.3节中所提到的差分修正法和加权 差分修正法,引入相邻单元的差分项来修正平均梯度,就可以构造出强耦合的通量计算模板.
如界面梯度采用加权差分修正法,单元3的黏性通量为
$ \int_{\partial \varOmega } {\pmb F }_{v} \cdot {\pmb n} S = - \left( {\nabla Q} \right)_{32} + \left( {\nabla Q} \right)_{34} = \\ - \left( {\overline {\nabla Q} } \right)_{32} + \varepsilon \left[ {\left( {\overline {\nabla Q} } \right)_{32} \cdot {\pmb e }_{32} - \left( {\dfrac{\partial Q}{\partial l}} \right)_{32} } \right]{\pmb e }_{32} + \\ \left( {\overline {\nabla Q} } \right)_{34} - \varepsilon \left[ {\left( {\overline {\nabla Q} } \right)_{34} \cdot {\pmb e }_{34} - \left( {\dfrac{\partial Q}{\partial l}} \right)_{34} } \right]{\pmb e}_{34} = \\ - \left( {\overline {\nabla Q} } \right)_{32} - \varepsilon \left[ { - \left( {\overline {\nabla Q} } \right)_{32} - \dfrac{Q_2 - Q_3 }{\Delta x}} \right] + \left( {\overline {\nabla Q} } \right)_{34} - \\ \varepsilon \left[ {\left( {\overline {\nabla Q} } \right)_{34} - \dfrac{Q_4 - Q_3 }{\Delta x}} \right] = \\ \left( {1 - \varepsilon } \right)\left[ { - \left( {\overline {\nabla Q} } \right)_{32} + \left( {\overline {\nabla Q} } \right)_{34} } \right] + \\ \varepsilon \left( {\dfrac{Q_2 - Q_3 }{\Delta x} + \dfrac{Q_4 - Q_3 }{\Delta x}} \right) = \\ \left( {1 - \varepsilon } \right)\dfrac{Q_5 - 2Q_3 + Q_1 }{4\Delta x} + \varepsilon \dfrac{Q_4 - 2Q_3 + Q_2 }{\Delta x} (13)$
式(13)显示,加权差分修正法计算黏性通量的模板是一个加权的模板,当
以下将通过数值测试,验证黏性通量离散中的“奇偶失联”问题及其改进方法.
4 “奇偶失联”的数值验证与改进
在如图2(a)所示的矩形网格上,对扩散方程进行制造解精度测试,单元梯度重构采用GG-Cell,界面梯度计算方法分别采用平均梯度 法和加权差分修正法,其中取加权系数Table 1
表 1
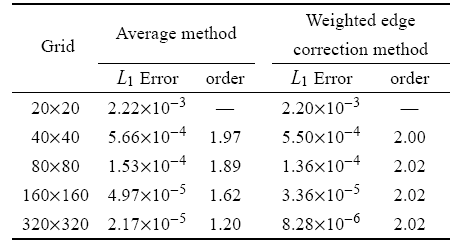
表 1两种界面梯度计算方法的计算精度
Table 1Accuracy of two interface gradient method
 |
新窗口打开
由表1可见,平均梯度法在矩形网格上,随着网格加密,格式精度阶逐渐由二阶下降到一阶. “奇偶失联”导致离散求解过程中引 入的“常数”误差项无法消除,使得格式精度阶下降. 在此甚至可以确定“奇偶失联”引入的常数项误差的量级.
假设平均梯度法离散误差由具有二阶精度的误差项和常数误差项叠加得到,即
由此,根据相邻两套网格的离散误差可得常数误差项
Table 2
表 2
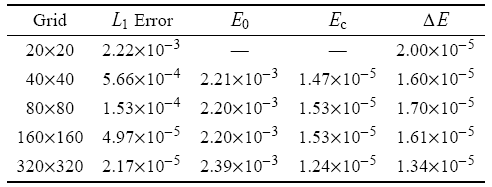
表 2“奇偶失联”数值验证结果
Table 2Verification of odd-even decoupling
 |
新窗口打开
表中
在此也要说明一点,“奇偶失联”只是影响计算精度的因素之一,且通常只在四边形或者六面体网格(笛卡尔网格)上发生,在 实际的三角形网格或者非结构/混合网格中,“奇偶失联”是较少发生的. 因此,几种界面梯度计算方法在不同类型/质量的非结构网格上的表现将在下文中进一步研究.
5 扩散方程计算精度测试与验证
本节主要在如图2所示的4种网格上通过基于扩散方程的制造解方法考察网格类型/质量、单元梯度重构方法、界面梯度计算方法对扩 散方程计算精度的影响,其中grid 1,grid 2分别为规则四边形网格和规则直角三角形网格,而grid 3,grid 4分别为引入随机扰动后的不 规则四边形网格和不规则三角形网格.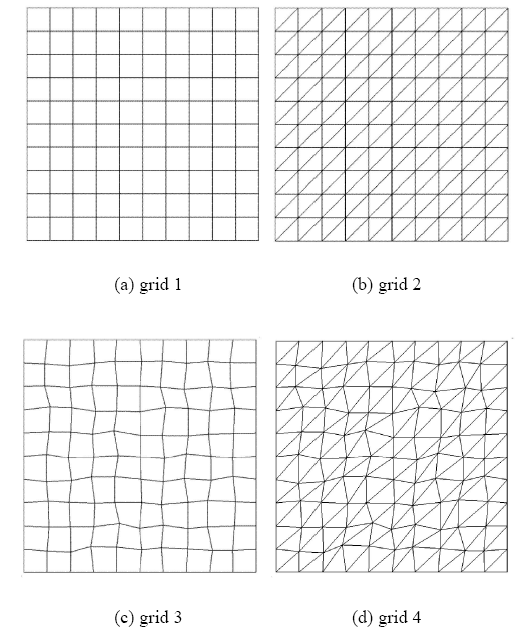
显示原图|下载原图ZIP|生成PPT图2扩散方程制造解精度测试网格
-->Fig. 2Grids for MMS accuracy tests
-->
文献[8]已经研究了GG-Cell梯度重构和LSQ-basic梯度重构方法在这4种网格上的梯度重构精度,并指出了GG-Cell发生精度降阶的现象,而LSQ-basic不仅能够保证梯度重构一阶精度,其梯度的绝对误差也更小,本节将分别考察这两种不同的单元梯度重构方法对标量扩散方程计算精度的影响.
在 2.3节中,本文作者提出了平均项与差分项加权的界面梯度计算方法加权差分修正法,并指出平均梯度法和差分修正法分别是加权系数
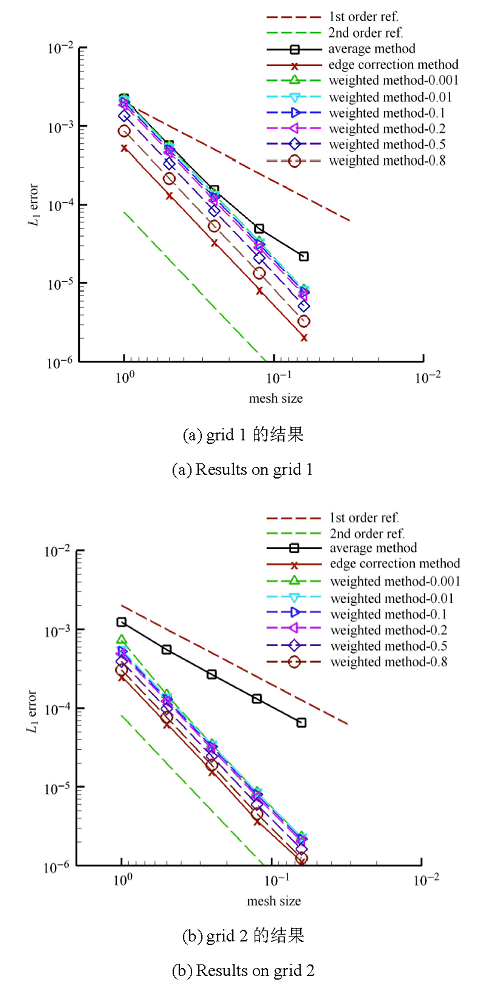
图3(a)和图3(b)分别给出了规则矩形网格grid 1和规则直角三角形网格grid 2上不同加权系数时,扩散方程的计算精度. 结果显示在两种网格上,差分项的引入均能使扩散方程恢复到二阶精度,且随着加权系数的逐渐增加,加权差分修正法计算精度逐渐提高,当加权系数为1时,计算精度达到最高,即差分修正法的计算精度最高. 因此,后文不再单独考察加权差分修正法的计算精度.
显示原图|下载原图ZIP|生成PPT图3加权系数的影响
-->Fig. 3Effects of different weights in the weighted edge correction method
-->
图4(a)和图4(b)分别给出了矩形网格、规则三角形网格上的测试结果,由于在矩形网格上GG-Cell梯度重构(图中标记为ggcell)和LSQ-basic梯度重构(图中标记为lsq)都等价于中心差分,而在规则三角形网格上,GG-Cell梯度重构也与LSQ-basic梯度重构等价,因而在两图中均只能看到GG-Cell的结果. 由结果可以看到,在矩形网格上,差分修正法和法向导数法的离散误差完全相同(曲线重叠),均能达到二阶精度,而平均梯度法计算精度随着网格加密,逐渐下降到一阶,这一现象即为本文第3节和第4节中所分析的“奇偶失联”现象导致. 而在三角形网格上,由于单元梯度重构只有一阶精度,平均梯度法只能达到一阶精度,而另外两种界面梯度方法均能达到二阶精度,且离散误差接近,误差绝对值也远小于平均梯度法.
图4(c)和图4(d)分别给出了扰动四边形、扰动三角形网格上的测试结果. 由于在扰动网格上,GG-Cell梯度重构精度下降到零阶[8],因此不管采用何种界面梯度方法,扩散方程计算精度均降阶到零阶,离散误差也不随网格加密而减小. 而LSQ-basic方法在扰动网格上仍然保持梯度重构一阶精度,除平均梯度法外,差分修正法和法向导数法两种界面梯度方法,扩散方程计算精度均恢复二阶精度,平均梯度法计算精度较差,且计算容易发散.
显示原图|下载原图ZIP|生成PPT图4不同类型网格上界面梯度的比较
-->Fig. 4Comparison of interface gradient on different meshes
-->
因此,各向同性网格上基于扩散方程的制造解精度测试表明：单元梯度重构精度和界面梯度计算方法均对扩散方程计算精度起重要作用,要使扩散方程计算精度达到二阶,单元梯度重构必须保持至少一阶精度,且界面梯度要选择合适的计算方法. 虽然在三角形网格上平均梯度法不会导致“奇偶失联”,但是其表现仍然比其他两种界面梯度计算方法差,相较而言,界面梯度计算方法差分修正法和法向导数法在计算精度阶和离散误差的绝对值上均具有较大优势.
6 实际流动计算精度测试与验证
本节将在3个实际黏性流动问题中进行网格收敛性测试,以验证第5节中的结论.6.1 层流平板算例
平板层流流动是相对简单的黏性流动,边界层方程简化为常微分方程后求解可以得到自相似的Blasius解. 全平板(长度为2$C_{\rm f} = \dfrac{1}{c}\int_0^{2c} c_{\rm f} x = \dfrac{1.8781}{\sqrt {Re_{\rm c} } } = 0.004 20(15)$
该算例的来流条件为
Table 3
表 3
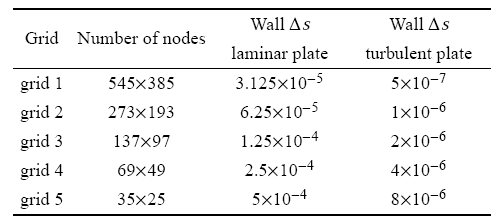
表 3平板层流及平板湍流计算网格相关参数
Table 3Parameters for laminar and turbulent flat plate grids
 |
新窗口打开
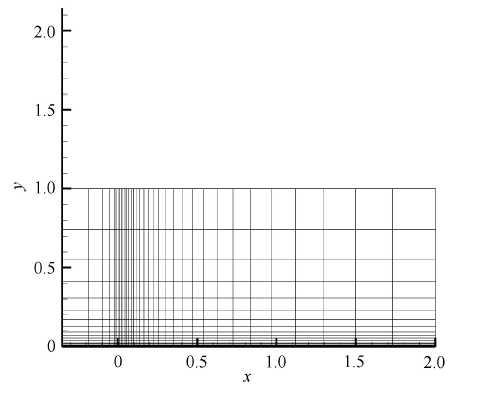显示原图|下载原图ZIP|生成PPT图5平板算例各向异性矩形网格示意图
-->Fig. 5Anisotropic quadrilateral grids of a flate plate
-->
图6给出了各向异性矩形网格上界面梯度分别采用3种不同方法时的网格收敛性测试结果. 由于网格长宽比较大, 按照文献[6]结论,引入反距离加权,提高LSQ-basic梯度重构精度,方法记为WLSQ-basic(图中标记为wlsq),同时还考 察了GG-Cell梯度重构(图中标记为ggcell)的计算精度.
显示原图|下载原图ZIP|生成PPT图6平板层流网格收敛性测试结果
-->Fig. 6Grid convergence tests of laminar flat plate
-->
首先比较3种不同界面梯度计算方法. 结果显示,对于两种单元梯度重构方法,平均梯度法误差均最大,且网格收敛性也最差,而法向导数法与差分修正法计算精度近似,结果具有较好的网格收敛性,显示出一定的优势.
其次,比较两种不同的单元梯度重构方法. 结果显示除在采用平均梯度法时,粗网格上GG-Cell和WLSQ-basic的结果存在较大差异外,在其他情况下,两种梯度重构方法流动模拟精度差异不大,这与各向同性网格上制造解精度测试结论存在一定差异.
在各向同性网格上,由于WLSQ-basic方法能在任意非结构网格上保持梯度重构一阶精度,流动模拟保持二阶精度,比无法保证流动模拟二阶精度的GG-Cell方法更有优势.
而在长细比较大、网格间距不均匀的各向异性网格上,这种优势并没有体现出来,文献[6]也发现了类似现象,也即,使用梯度精度较差的方法同样得到了较好的流动模拟精度,文献[6]将其原因归结于边界层内流动方向与网格方向相匹配,但是在各向异性网格上,单元梯度重构精度与黏性流动模拟精度的关系还需要进一步的理论分析和数值研究.
6.2 湍流平板算例
湍流平板算例是美国宇航局TMR[25,26,27]验证与确认算例库中较为基础的算例之一.计算条件为：
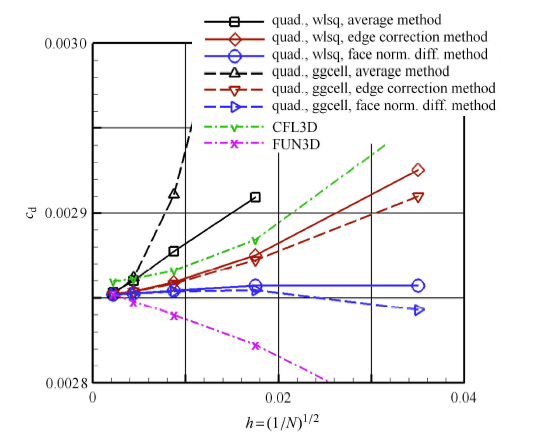
图7所示为各向异性矩形网格上的网格收敛性测试结果以及CFL3D和FUN3D的结果[36,37,38].
显示原图|下载原图ZIP|生成PPT图7矩形网格平板湍流网格收敛性测试结果
-->Fig. 7Grid convergence tests of turbulent flat plate
-->
同样,首先比较3种不同界面梯度计算方法. 结果显示,随着网格加密,几种界面梯度计算方法的均能收敛到与非结构解算 器FUN3D相同的网格收敛解. 但是在粗网格上,平均梯度法计算误差最大,法向导数法计算误差最小,差分修正法的计算误差与法向导数法接近,网格收敛性较好.
其次,比较两种不同的单元梯度重构方法. 除了在采用平均梯度法时WLSQ-basic计算精度优于GG-Cell外,在采用其他两种界 面梯度时,两种单元梯度重构方法流动模拟精度差异不大,也即,采用WLSQ-basic并未使流动模拟精度提高,这一结果与层流 平板类似,再次证明各向异性网格上,单元梯度重构精度对黏性流动模拟精度的影响还需进一步研究.
6.3 二维翼型近尾迹流动算例
二维翼型近尾迹流动(2D Airfoil Near-Wake,ANW)算例也是美国宇航局TMR验证与确认算例库中的基础算例之一. 翼型DSMA661(MODEL A) [25]前缘有一定的曲率变化,而且翼型上下表面曲率不同,可以用于各向异性弯曲网格的测试.计算条件为：
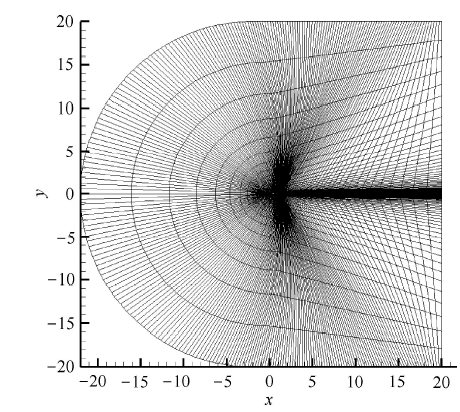显示原图|下载原图ZIP|生成PPT图82D ANW算例各向异性四边形网格示意图
-->Fig. 8Anisotropic quadrilateral grids of the 2D ANW case
-->
图9(a)、图9(b)、图9(c)分别给出了各向异性四边形网格上2D ANW翼型升力系数、压差阻力和摩阻系数的网格收敛性精度测试结果.
从图9可以看出：3种界面梯度计算方法的升力系数和压差阻力计算精度相当,均收敛到与CFL3D和FUN3D相同的网格无关解. 但是,3种界面梯度计算方法得到的摩阻系数存在一定差异,其中平均梯度法计算精度和网格收敛性均相对较差,而差分修正法 和法向导数法具有较好的计算精度和网格收敛性,在实际黏性流动数值模拟中具有一定的优势,这也证实了基于扩散方程的制造 解精度测试得到的结论.
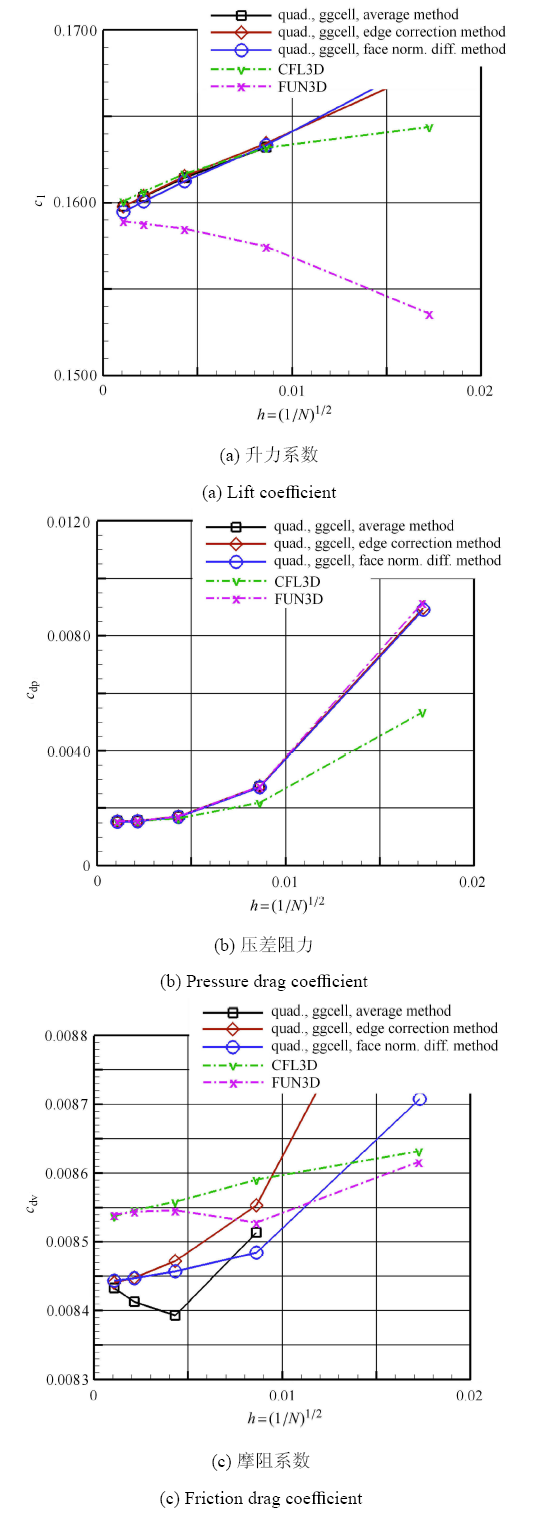显示原图|下载原图ZIP|生成PPT图92D ANW网格收敛性测试结果
-->Fig. 9Grid convergence tests of 2D ANW
-->
7 结 论
本文首先介绍了二阶精度有限体积方法中黏性项离散的几种常见界面梯度方法,分析了中心型离散(平均梯度法)在矩形笛卡尔网格上存在的“奇偶失联”问题,导致常数误差项无法消除,从而计算精度阶下降,离散误差增大. 通过基于扩散方程的制造解精度测试,验证了“奇偶失联”的存在,并通过在相邻单元连线方向上引入差分加权项,消除了“奇偶失联”引入的常数误差项,提高了扩散方程计算精度.进一步,通过基于扩散方程的制造解精度测试,在几种不同的各向同性网格上研究了不同单元梯度重构方法、不同界面梯度计算方法对扩散方程计算精度的影响,结果表明扩散方程计算精度由单元梯度重构和界面梯度重构方法共同决定,要使扩散方程计算精度达到二阶,单元梯度必须保持至少一阶精度,且界面梯度要选择合适的计算方法.
最后,本文通过3个实际黏性流动问题(层流平板、湍流平板和二维翼型近尾迹流动)的网格收敛性测试考核了单元梯度重构方法及界面梯度计算方法对实际黏性流动模拟精度的影响,并初步验证了制造解精度测试的结果.
结果证实了制造解精度测试结论：差分修正法和法向导数法在计算精度、网格收敛性和计算稳定性上均有较大优势. 但是在层流平板和湍流平板算例中,单元梯度重构方法GG-Cell和WLSQ-basic的流动模拟精度差异不大,这与各向同性网格上制造解精度测试的结论存在一定差异,显示出各向异性网格上单元梯度重构精度对黏性流动模拟精度的影响仍然有待深入研究.
下一步还可以在更多复杂外形流动中验证不同单元梯度重构方法和界面梯度计算方法对实际高雷诺数黏性流动模拟精度,尤其是对摩阻计算精度的影响,为提高实际复杂外形高雷诺数流动摩阻模拟精度打下基础.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | , |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . . |
| [35] | . . |
| [36] | . |
| [37] | . |
| [38] | . |
| [39] | . |
