, 马戎ACCURATE AERO-HEATING PREDICTIONS BASED ON MUL-TI-DIMENSIONAL GRADIENT RECONSTRUCTION ON HYBRID UNSTRUCTURED GRIDS1)
WanYunbo, MaRong中图分类号:V211.3
文献标识码:A
通讯作者:
收稿日期:2018-03-19
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (13411KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
近三十年来, 计算流体力学(CFD)得到了飞速发展, 并成功地应用于气动设计[1]. 但气动热环境的精确预测一直是高超声速飞行器外形和热防护系统设计的重点和难点. 近年来高超声速飞行器迅猛发展, 以X37B, X43A, X51A, HTV2等为代表的新型高超声速飞行器陆续诞生, 对气动热环境的预测精度和计算周期提出了更加严苛的要求. 虽然CFD工作者经过长期的努力, 在高质量结构网格上已能得到较好的热流计算结果, 但是生成复杂飞行器结构网格的人工成本和时间成本均很高. 随着飞行器外形日趋复杂, 生成结构网格的网格量不仅会成倍增加, 而且时间成本也会大幅度提高, 从而导致计算周期过长. 而混合网格同时结合了结构网格和非结构网格的优势, 具有很强的复杂外形适应能力, 已在复杂飞行器的气动力数值模拟应用中取得巨大成功, 其代表了网格生成技术未来的发展方向[2]. 为了缩短气动热环境数值计算的任务周期, 迫切需要开展基于非结构/混合网格的高精确气动热环境预测方法研究.近年来, 一些****在非结构网格气动热环境数值计算方面已经开展了较多的研究工作[3-8], 并取得了一些卓有成效的进展. 早期的研究发现[3-5], 热流的数值模拟对算法和网格非常敏感. 在结构化或比较规则的非结构网格上(如结构网格剖分的非结构网格)一般可以得到较好的热流计算结果, 但是在方向随机的非结构网格上往往得不到较好的结果, 尤其是在驻点区域. 其主要原因是随机的网格面与激波斜交, 微小的激波捕捉误差将导致壁面热流(温度梯度相关量)的剧烈变化. 即便是在结构网格上, 如果对网格分布进行一定的随机扰动, 也可能导致壁面热流的误差较大[6]. 因此, 激波的光滑捕捉是保证热流精确预测的前提. 为此, 有****提出利用激波装配法以提高激波的捕捉能力, 进而提高热流预测精度[7]. 这种方法对于简单外形可行, 但是对于复杂外形, 由于头激波结构复杂往往难以进行激波装配, 这相反使得非结构网格的几何灵活性优势丧失. 另一种策略是在激波区进行网格自适应[8], 采用很密的网格降低激波后物理量的误差. 这当然是一种较好的方法, 但是其并没有从本质上消除激波捕捉带来的误差, 只是使得误差量值有所降低.
事实上, 基于非结构网格的数值模拟是一种真正的多维问题, 因此需要采用多维算法才能得到较好的结果. 因此, 在后续的研究中, Gnoffo[9-12]将多维无黏通量重构(旋转迎风格式)引入热流的计算, 发现这种方法确实较"准一维''的传统通量格式更有优势, 能有效改善驻点附近的热流预测精度. 但是, 从能检索到的文献来看, 他们在复杂外形上的应用也比较有限, 对于SYS-2模型的计算也是采用的六面体剖分的四面体进行的计算[11]. 在国内, 一些****也开展了类似研究, 如原志超[13]采用旋转迎风格式, 在六面体剖分的规则四面体网格上得到了较好的热流计算结果.
从数值算法的角度来看, CFD工作者先后发展了多种多维算法, 除了前述的多维通量格式之外[9-10,13-16], 还有多维梯度重构方法[17-18]和多维限制器方法[19-21] 等. 在本文中, 通过引入多维梯度重构方法[18], 发展了基于"常规''的非结构/混合网格的高精度热流计算方法. 这里的"常规''意指在气动力计算中普遍采用的混合网格类型, 即在壁面附近采用四边形(2D)、三棱柱或六面体(3D)网格, 而在外场采用方向随机的三角形(2D)和四面体(3D)网格. 利用该多维算法对典型的高超声速Benchmark 算例(二维/三维圆柱和三维双椭球)进行了模拟, 并与气动力计算广泛采用的Green-Gauss类方法和最小二乘类方法进行了对比. 计算结果表明, 多维梯度重构方法能有效提高非结构/混合网格热流预测精度, 其鲁棒性和收敛性更好, 展现了较好的复杂外形气动热环境预测潜力.
1 数值离散方法简介
本文基于完全气体模型求解NS方程, 其积分形式为\begin{equation*}\dfrac{\partial}{\partial t}\int\limits_\varOmega Q\text d V+\oint\limits_{\partial\varOmega} F^i( Q)\text dS=\oint\limits_{\partial\varOmega} F^v( Q)\text d S\tag*{(1)}\end{equation*}
其中$ Q$为守恒变量, $ F^i$和$ F^v$分别为无黏和黏性通量. $\varOmega$为控制体, $\partial\varOmega$ 为控制体的外边界.
对于以上控制方程, 本文采用课题组自主研发的结构/非结构耦合通用计算流体力学解算器——HyperFlow[22-24]. 该软件平台的空间离散采用二阶精度"格心型''有限体积法. 时间离散格式选用该平台中的LU-SGS格式; 黏性项离散采用中心型格式. 对于无黏通量, 本文选用该平台中的Van Leer 格式[25]. 其原因是该格式数值耗散适中, 有利于计算的稳定性, 同时该格式中无自由参数, 可以避免由于自由参数的选取(如Roe格式中的熵修正系数)对计算结果的影响. 具体的计算方法细节请参见相关的文献[22,23,24].
在计算无黏通量时, 需要首先得到网格交界面上左右两侧的物理量. 这里采用如图1所示的线性重构方法, 即
\begin{equation*}\begin{split}& U_\text L= U_I+\varPhi_I(\nabla U)_I\cdot \Delta r_I\\& U_\text R= U_J+\varPhi_J(\nabla U)_J\cdot \Delta r_J\end{split}\tag*{(2)}\end{equation*}
其中, $ U$为原始变量, 下标$I$代表目标单元, 下标$J$代表单元$I$的邻居单元; 下标$ {\text L}$ 和$ {\text R}$ 分别代表交界面中点左右两侧位置. $\nabla U$为物理量的梯度, $\Delta r$ 为单元中点到交界面中心的距离矢量, 而$\varPhi$则是为了抑制数值振荡的限制器函数, 本文采用气动力计算中最常用的Venkatakrishnan限制器[26].
显示原图|下载原图ZIP|生成PPT图1界面物理量的重构示意图
-->Fig.1The reconstruction of interface variables
-->
目前, 非结构网格求解过程广泛使用的梯度重构方法是Gauss-Green和最小二乘法两类方法, 且两类方法又有不同的表现形式, 如常见的基于单元的Gauss-Green方法(GG-Cell方法), 基于格点的Gauss-Green方法(GG-Node方法), 加权最小二乘方法(WLSQ方法)和Green-Gauss与最小二乘的混合方法(GLSQ方法)[27]. 前期的研究表明[28], 这些方法在常规混合网格上的热流计算中均表现不佳, 为此这里引入了文献[18]中介绍的多维线性重构方法(MLR方法). MLR方法本质上属于Green-Gauss类方法, 其思想和GG-Node方法相同, 区别是权重系数$w_j$ 的计算方法不同.
Green-Gauss类梯度重构方法是基于Green-Gauss理论, 将封闭控制体内的梯度计算转换为面积分的计算过程
\begin{equation*}\left.\begin{split}&\int\limits_\varOmega \nabla U \text d\varOmega=\oint\limits_{\partial\varOmega} U n\text d S\\&\nabla U=\dfrac{1}{V}\oint\limits_{\partial\varOmega} U n\text d S\end{split}\right\}\tag*{(3)}\end{equation*}
其中, $ n$是面法向, $V$是控制体$\varOmega$的体积.
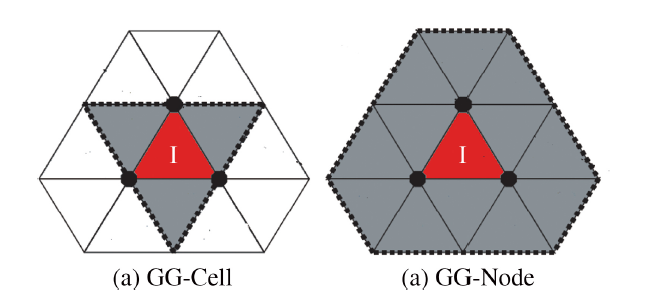
GG-Cell方法利用目标单元和相邻单元的加权平均求得每个积分面上的值(图2左为网格模板) GG-Node方法则首先加权平均求得各网格节点上的值, 然后再利用节点值插值得到积分面值(图2右为网格模板).
显示原图|下载原图ZIP|生成PPT图2GG-Cell和GG-Node方法的单元模板
-->Fig.2Grid stencils for GG-Cell and GG-Node method
-->
MLR方法与GG-Node方法类似, 但其采用pseudo-Laplacian权方法计算权系数$w_j$. 以某网格点$A$为例, pseudo-Laplacian权方法要求权系数$w_j$满足
\begin{equation*}\left.\begin{split}&L(x_n)=\sum\limits^N_{j=1}w_j(x_{c,j}-x_A)=0\\&L(y_n)=\sum\limits^N_{i=1}w_j(y_{c,j}-y_A)=0\end{split}\right\}\tag*{(4)}\end{equation*}
其中$(x_{c,j},y_{c,j})$为格点$A$周围单元$j$中心坐标值, $(x_A,y_A)$为单元节点坐标值. 将权系数$w_j$写为如下形式
\begin{equation*}w_j=1+\Delta w_j\tag*{(5)}\end{equation*}
pseudo-Laplacian权方法要求式(6)的值最小, 可以得到最优的权系数
\begin{equation*}C=\sum\limits^N_{j=1}(r_j\Delta w_j)^2\tag*{(6)}\end{equation*}
其中$r_j$为单元$j$中心到网格点$A$的距离. 通过求解式$(4)\sim$式(6)得到$\Delta w_j$的值如下
\begin{equation*}\Delta w_j=\dfrac{1}{r^2_j}\Big[\lambda_x(x_{c,j}-x_A)+\lambda_y(y_{c,j}-y_A)\Big]\end{equation*}
其中
\begin{equation*}\begin{split}&\lambda_x=\dfrac{I_{xy}R_y-I_{yy}R_x}{I_{xx}I_{yy}-I_{xy}^2},\lambda_y=\dfrac{I_{xy}R_x-I_{xx}R_y}{I_{xx}I_{yy}-I_{xy}^2}\\&R_x=\sum\limits^N_{i=1}(x_{c,j}-x_A),~R_y=\sum\limits^N_{i=1}(y_{c,j}-y_A) &I_{xx}=\sum\limits^N_{j=1}(x_{c,j}-x_A)^2/r^2_j\\&I_{yy}=\sum\limits^N_{j=1}(y_{c,j}-y_A)^2/r^2_j\\&I_{xy}=\sum\limits^N_{j=1}(x_{c,j}-x_A)(y_{c,j}-y_A)/r^2_j\end{split}\end{equation*}
Kim等[18]针对无黏、层流和湍流等流动问题, 使用各种类型的网格, 对多维梯度重构进行了验证与确认, 在流场分辨率和整体气动力计算中均有良好的表现. 在本文中将其应用于气动热环境的计算, 希望能得到较其他方法更好的结果.
2 典型二维算例各种梯度重构方法计算结果的对比
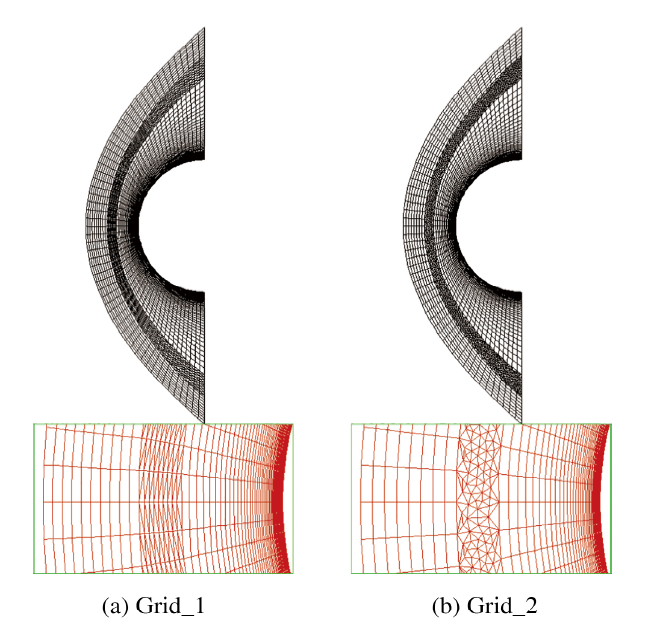
本节选取文献[3]中提及的一个"挑战性''算例——二维圆柱高超声速绕流作为基准算例进行计算结果的对比分析. 计算工况为: 马赫数$Ma=8.03$, $Re=1.835\times 10^5~\text m^{-1}$, 圆柱半径$R=1~\text m$, 来流温度取为124 K, 壁面温度为294.4 K. 由Fay-Riddell公式[29]得到的无量纲驻点热流值为0.003 5(用$\rho v^3$ 无量纲化, $\rho$为来流密度, $v$ 为来流速度). 根据工程应用经验, 驻点热流值与FR 值的误差在$\pm 10\%$范围内认为数值计算热流值的结果可以接受.本节主要就激波区域使用不同类型的网格进行计算, 对比前述4种典型梯度重构方法和MLR多维重构方法的计算结果, 重点考察这些梯度重构方法在热流计算精度、收敛性方面的表现. 采用的计算网格如图3所示, 即激波区域网格分别为各向异性(由质量较好的四边形网格剖分而成)三角形网格(grid_1)和各向同性随机三角形(grid_2), 其他区域采用结构化的网格(转化为非结构数据进行计算), 这样可以更为直接地反应激波捕捉对热流计算结果的影响.
显示原图|下载原图ZIP|生成PPT图3用于二维圆柱热流计算的不同类型混合网格
-->Fig.3Different types of hybrid grids for heat flux prediction
-->
由于激波导致了熵的变化, 虽然圆柱绕流是热流计算中最简单的算例, 但也很难定量分析流场的计算精度. 为了从定量的角度分析对比几种梯度重构方法对流场的影响, 本文对图4所示的两条特殊曲线上的物理量进行对比, 其中一条是激波后的线(line1), 另一条是流场的对称线(line2).
显示原图|下载原图ZIP|生成PPT图4对流场进行定量对比分析的两条特征线
-->Fig.4Two representative curves in the flow field for quantitative comparison
-->
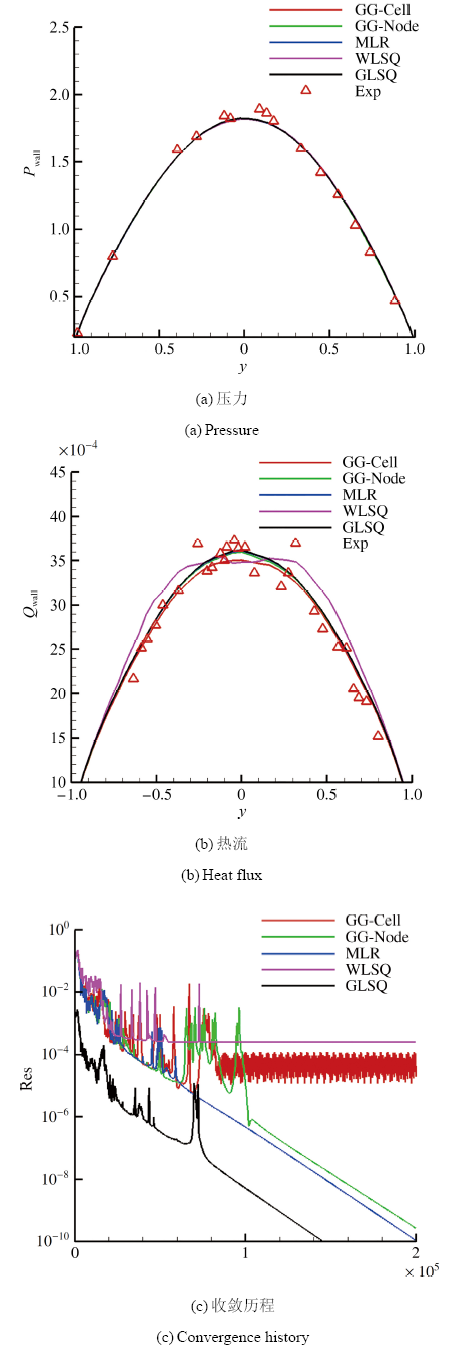
图5所示为grid_1网格上的计算结果, 可以看出使用不同的梯度重构方法时, 壁面压力的结果一致, 但是壁面热流的结果却存在较大差异. 其中MLR方法、GG-Node方法以及GLSQ方法的热流分布的对称性和光滑性较好, GG-Cell 方法在驻点区域的热流值略有下降, WLSQ方法虽然梯度计算精度较高, 但是整体计算的稳定性较差, 导致热流计算的精度低. 需要指出的是, 梯度重构方法需要和限制器配合使用, 计算过程中发现即使调整限制器的自由参数WLSQ方法也不能得到较好的热流计算结果. 从收敛历程可以看出, MLR方法、GG-Node方法和GLSQ方法收敛性均较好, 其他两种方法相对较差.
显示原图|下载原图ZIP|生成PPT图5Grid_1上各种梯度重构方法计算所得的壁面压力分布、 壁面热流分布和残差收敛历程
-->Fig.5Pressure distribution, heat flux distribution and convergence history on grid_1 with different gra-dient reconstruction methods
-->
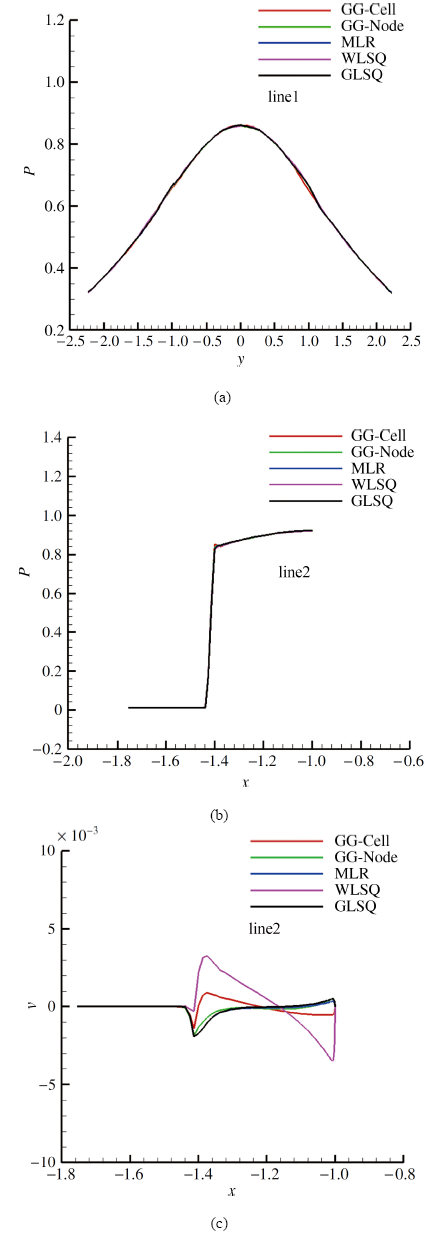
为了从定量的角度分析几种梯度重构方法的性能, 图6依次给出了line1上的压力、line2上的压力和法向速度$v$ 分布. 几种梯度重构方法在两条线上的压力分布基本一致, 实际上两条线上的密度和温度分布也基本一致(由于篇幅限制这里没有给出), 但是line2上的法向速度$v$却存在较大差异. 由于line2是对称线, 理论上法向速度$v$的值严格为0, 但实际计算中存在数值振荡导致$v$很难等于0, 所以$v$沿line2的分布规律可以在一定程度上反映流场的计算精度. 从法向速度$v$的分布可以看出WLSQ方法的振荡明显高于其他几种方法, 而其他几种方法的振荡程度基本相当, 且均处于较低的范围. 上述计算结果说明在激波区域使用各向异性三角形网格时Green-Gauss类方法以及GLSQ方法在热流结果以及流场精度方面基本相当, 而WLSQ方法由于稳定性问题以及在拉伸比的网格上精度降低的原因, 并没能得到较好的热流和流场计算结果.
显示原图|下载原图ZIP|生成PPT图6Line1上的压力、line2上的压力和$y$方向速度分布规律(grid_1)
-->Fig.6Pressure distribution on line1, pressure distribution and velocity in $y$ direction on line2 (grid_1)
-->
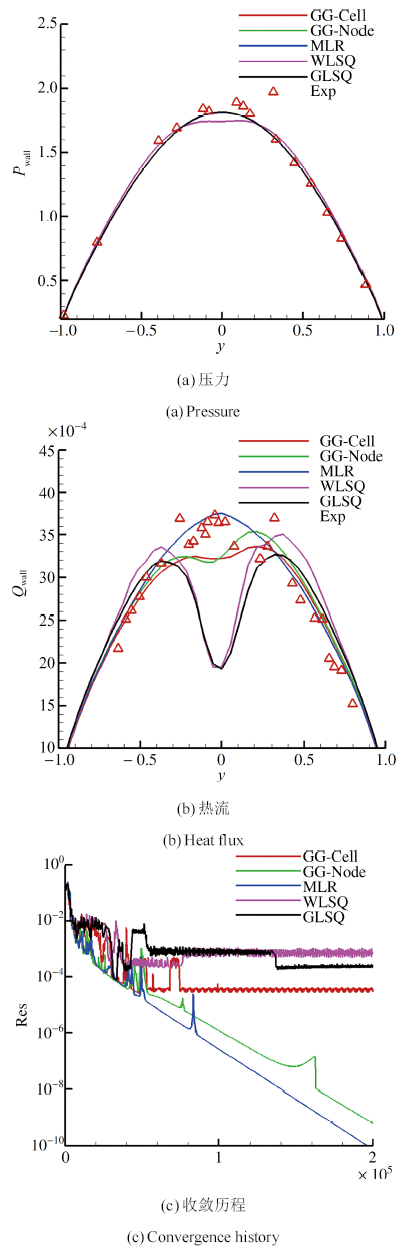
在grid_2网格上的计算结果如图7所示. 可以看出压力结果基本一致, 只有WLSQ方法在驻点区域的压力结果变差. 在热流结果方面, 只有MLR方法的驻点值以及分布是在误差范围内的, 其他方法均得到了畸形的热流分布. 从收敛历程可以看出, MLR方法和GG-Node方法收敛性较好, 其他3种方法都较差.
显示原图|下载原图ZIP|生成PPT图7grid_2上各种梯度重构方法计算所得的壁面压力分布、壁面热流分布和残差收敛历程
-->Fig.7Pressure distribution, heat flux distribution and convergence history on grid_2 with Different gradient reconstruction methods
-->
对比line1和line2上的压力分布(图8(a) $\sim$图8(b)), 几种方法的压力结果基本一致, MLR方法的结果较其他几种方法略有改善. 但是从法向速度$v$的分布(图8(c))可以看出, WLSQ方法的振荡最高, MLR方法的振荡最小, 再次说明WLSQ 方法在热流计算中表现较差, 而MLR方法在抑制振荡以及流场精度方面面具有明显优势.
显示原图|下载原图ZIP|生成PPT图8line1上的压力、line2上的压力和$y$方向速度分布规律(grid_2)
-->Fig.8Pressure distribution on line1, pressure distribution and velocity in $y$ direction on line2 (grid_2)}
-->
通过上面的结果对比说明, 针对二维圆柱高超声速绕流这一Benchmark经典算例, MLR方法在流场和热流精度以及收敛性方面要明显优于其他几种梯度重构方法. 其本质原因正是其能光滑地捕捉激波, 激波后的物理量误差更小.
3 多维梯度重构方法的应用
3.1 三维圆柱绕流
为了推进混合网格在复杂外形热流预测方面的工程应用, 需要在前述的"常规''混合网格上得到较好的热流计算结果. 为此, 参考文献[3]中的做法, 特意将前节的二维圆柱展向拓展为三维, 计算工况与前节相同, 计算网格如图9所示, 边界层区域是六面体网格, 空间为各向同性随机四面体网格. 非结构网格容易导致流场不对称, 三维圆柱绕流问题又多出一个展向, 更难得到好的热流计算结果[3].
显示原图|下载原图ZIP|生成PPT图9三维圆柱计算混合网格
-->Fig.9Hybrid grids over the 3D cylinder
-->
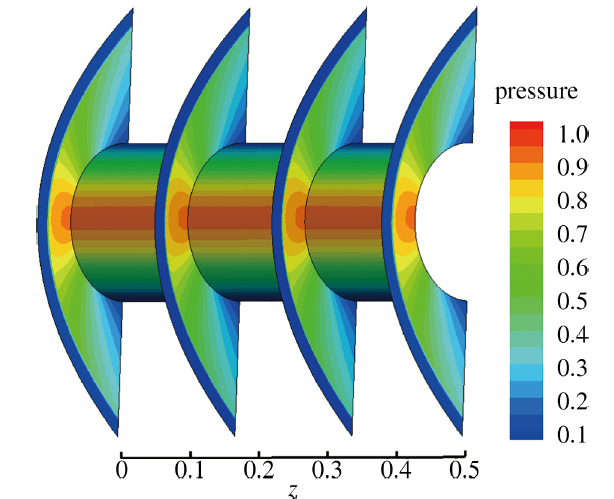
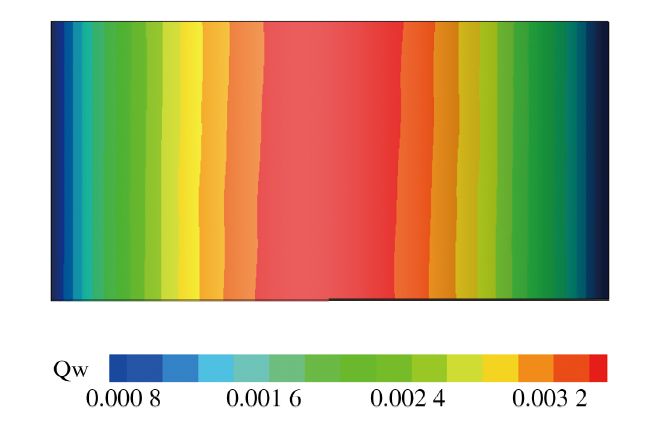
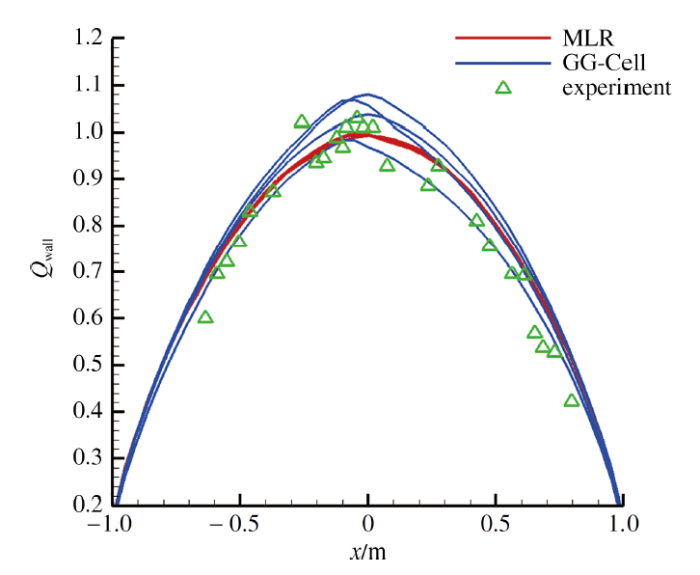
图10是4个截面和物面上的压力分布云图, 可以看出较清晰地分辨了流场和激波结构, 4个截面上的压力云图基本没有差异, 也未出现所谓的"红玉''现象. 热流的计算结果如图11所示, 具有较好的对称性和光滑性, 其中驻点热流为0.003 7, 在FR公式合理误差范围内. 4个典型截面上的归一化热流(以驻点热流为基准)如图12所示, 可以看到MLR方法(图12中的红色线)与实验值[30]吻合较好, 且截面间的差异很小, 而常用的GG-Cell方法(图12中的蓝色线)给出的各截面热流误差较大.
显示原图|下载原图ZIP|生成PPT图104个截面和物面压力分布
-->Fig.10Pressure contours on four cross-sections and solid wall
-->
显示原图|下载原图ZIP|生成PPT图11物面热流分布
-->Fig.11Heat flux distribution on the solid wall
-->
显示原图|下载原图ZIP|生成PPT图12四个典型截面上的热流分布及实验结果
-->Fig.12Heat flux distributions on four cross-sections and experimental results
-->
3.2 双椭球绕流
双椭球是研究高超声速大气再入问题的标准算例之一, 可以考察混合网格对相对复杂外形的气动热预测能力, 因此本文对0°和20°攻角的双椭球高超声速绕流进行了数值模拟. 计算来流条件为: $Ma=10.02$, $Re=2.2\times 10^6/\text m^{-1}$, 总压$P_0=6.9~\text{MPa}$, 总温$T_0=1457~\text K$[31]. 计算网格如图13 所示, 边界层区域是三棱柱网格, 壁面法向第一层网格$Re$数为1, 空间网格是四面体网格, 正是常用的混合网格, 在激波处的网格是方向随机的四面体.
显示原图|下载原图ZIP|生成PPT图13双椭球模型计算网格
-->Fig.13Hybrid grid over double ellipsoid configuration
-->
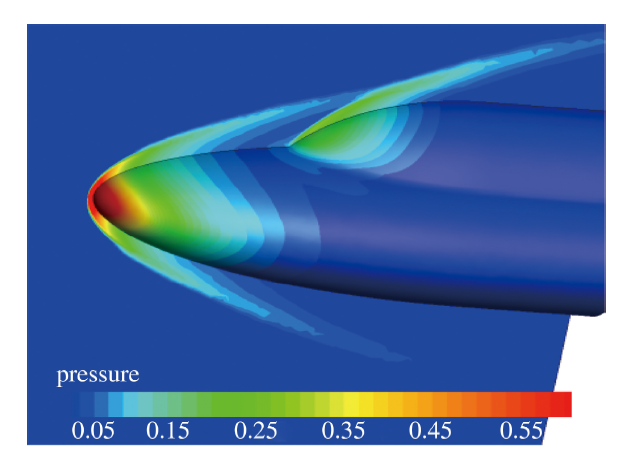
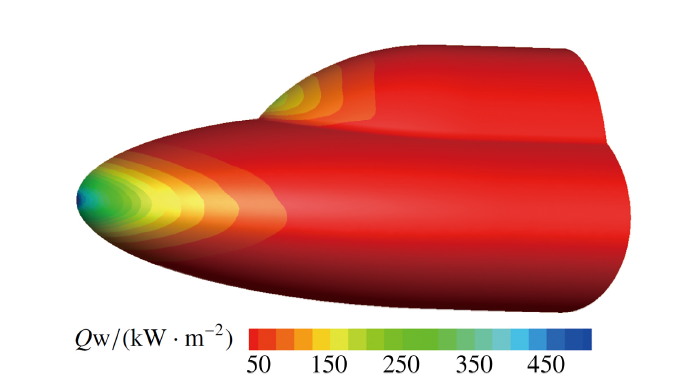
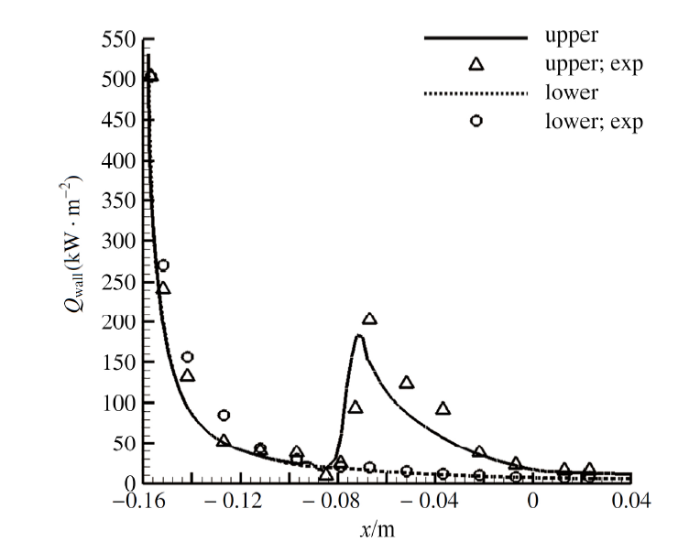
图14是$0^\circ$攻角时对称面和物面上的压力云图, 可以看到其捕捉到清晰的激波结构; 图15给出了相应的流线图, 清楚地模拟出了二次分离现象. 图16为$0^\circ$攻角时壁面热流分布云图, 其具有较好的光滑性. 图17和图18分别给出了$0^\circ$和$20^\circ$攻角时上下两条子午线上热流分布, 其与实验值吻合较好, 能够准确模拟出二次分离对热流分布的影响.
显示原图|下载原图ZIP|生成PPT图14$0^\circ$度攻角时对称面和物面压力云图
-->Fig.14Pressure contours on symmetry plane and solid wall(angle of attack is $0^\circ$)
-->
显示原图|下载原图ZIP|生成PPT图15对称面和物面流线图
-->Fig.15Streamlines on symmetry plane and solid wall
-->
显示原图|下载原图ZIP|生成PPT图16壁面热流云图
-->Fig.16Heat flux contours on solid wall
-->
显示原图|下载原图ZIP|生成PPT图17上下子午线上的热流分布($0^\circ$攻角)
-->Fig.17Heat flux distributions of upper and lower symmetric lines (angle of attack is $0^\circ$)
-->
显示原图|下载原图ZIP|生成PPT图18上下子午线上的热流分布($20^\circ$攻角)
-->Fig.18Heat flux distributions of upper and lower symmetric lines (angle of attack is $20^\circ$)
-->
4 结束语
本文通过引入多维梯度重构方法, 发展了一种适应于非结构混合网格、具有较高精度的热流预测方法. 典型高速声速算例表明具有多维特性的MLR方法能光滑捕捉激波, 在各向同性随机非结构网格上, 较其他常用梯度重构方法具有更好的热流预测能力, 在鲁棒性和收敛性方面也表现更好. 下一步将把该方法推广应用于实际复杂外形的热流数值模拟.需要指出的是, 仅仅依靠MLR方法不足以彻底解决非结构/混合网格对复杂外形气动热数值模拟精度较低的问题. 梯度重构方法需要与限制器等密切配合才能发挥更好的作用, 下一步将对此开展更加深入的研究. 此外, 多维方法为什么能提高热流预测精度, 其理论基础是什么, 尚不清楚, 这方面也需要开展深入的研究, 以便弄清机理从而发展更好的数值方法.
另一方面, 根据本文的计算结果, 在与激波正交的规则网格上, 一般能得到较好的热流计算结果, 为此, 将在未来发展各向异性的网格自适应技术, 根据流动特征自动调整激波区的网格分布和形态, 使激波区的网格尽可能与激波正交, 希望通过这些技术的综合应用进一步改善非结构/混合网格上气动热环境预测的精度、鲁棒性和收敛性.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . [博士论文] . [PhD Thesis]. |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . . |
| [23] | . |
| [24] | . . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . . |
| [29] | . |
| [30] | . |
| [31] |
