1.上海师范大学建筑工程学院,上海 201418
A PARTITIONED STRONG COUPLING ALGORITH FOR FLUID-STRUCTURE INTERACTION USING ARBITRARY LAGRANGIAN-EULERIAN FINITE ELEENT FORULATION
HeTao中图分类号:O357.1
收稿日期:2017-05-3
接受日期:2018-01-4
网络出版日期:2018-04-16
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (492KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
流固耦合广泛存在于土木工程、机械工程、海洋工程、航空航天工程和生物医学工程等众多工程领域[1-9]. 以土木工程为例,超高层建筑、高耸结构、空间结构、大跨桥梁及长径线缆等钝体结构在强风作用下风致振动是典型流固耦合现象. 此类结构具有质量轻、柔性大、阻尼小和自振频率低等特点,流固耦合效应突出,风损风毁现象已屡见不鲜. 例如,1940年11月7日美国华盛顿州塔科马窄桥在较低风速(约为设计风速的50%)下发生颤振失稳、进而垮塌. 因此,准确考虑流固耦合作用对保障工程结构安全意义重大.由于两相介质在交界面处存在耦合作用,一方变化会激发另一方的强烈响应,故解析求解流固耦合异常困难,目前多需依赖数值计算. 流固耦合数值仿真已成为当前工程计算与设计中的重要需求,引起****和工程师的广泛关注. 一般而言,分区弱耦合算法效率较高,常用于气动弹性问题[6]. 然而,分区弱耦合算法难以克服强附加质量效应,易导致数值失稳,故多用于高质量比刚体流致振动[10]. 对于低质量比、大位移或柔性体等复杂情形,可采用分区强耦合算法进行求解.
分区强耦合算法在每时间步内依次迭代计算各单场方程直至收敛,具备良好的物理守恒性和程序模块性[11],因而备受青睐. 其中,固定点法是一种广泛运用的强耦合方法. Le Tallec和ouro[1]提出了固定点法的预条件最速下降松弛技术,兼具数值稳定与能量守恒,已用于复杂工业问题. Küttler和Wall[13]根据界面位移构造Aitken动态松弛因子加速固定点迭代,极大扩展了该技术的应用范围. Bai 等[14]利用ANSYS-CFX 软件实施固定点迭代计算湍流下三维桥梁断面颤振问题. 由于优化了网格运动,该方案具有工程应用潜力. Sun等[15]也基于分区强耦合的模块化优势,运用商业软件计算桥梁结构风致振动问题. 笔者及其合作者提出新型混合界面耦合条件,采用固定点法数值模拟各类钝体流致振动问题[16-18]. 有关流固耦合数值方法的最新研究进展可参考文献[19]. 需指出,笔者提出一种部分强耦合迭代算法,进一步提升计算效率[17].
本文基于任意拉格朗日--欧拉(arbitrary Lagran- gian-Eulerian, ALE)有限元方法,灵活选择不同物理模型及单场求解手段,提出一种精确高效的分区强耦合算法,数值模拟大位移流固耦合问题,并揭示相关流致振动现象,为流固耦合数值仿真研究提供新思路.
1 流体模型
1.1 控制方程
考虑移动网格情形,不可压缩黏性流体的质量守恒律和动量守恒律可写为ALE描述下的无量纲化Navier-Stokes(NS)方程$\nabla \cdot {\pb u} = {\bf 0} $(1)
$\dfrac{\partial {\pb u }}{\partial t} + {\pb c } \cdot \nabla {\r {\bf u}} +\nabla \cdot {\pb \siga }^{\r F} - {\pb f }^{\r F} = {\bf 0}$ (2)
式中,$\nabla $为梯度算子,${\pb u}$和$p$为流体速度和压力,对流速度${\pb c}={\pb u } - {\pbw }$,${\pb w}$为网格速度,${\pb \siga }^{\r F}$为流体应力张量,${\pb f}^{\r F}$为流体体力项. 流体本构方程表述为
$ {\pb \siga }^{\r F} = - p{\pb I} + \dfrac{1}{Re}\left( {\nabla {\pb u} + \left( {\nabla {\pb u} } \right)^{\r T} } \right) $ (3)
式中,${\pb I}$为单位矩阵,雷诺数${Re} = \rho^{\r F} UD/\u $,$\rho^{\r F}$为流体密度,$U$和$D$分别为来流特征速度和特征长度,$\u $为流体黏度,上标T表示转置.
初始条件和边界条件指定如下
${\pb u} = {\pb u }^0 \,, \ \ p = p^0$ (4)
${\pb u} = {\pb g }^{\r F} \,,{\pb \siga }^{\r F} \cdot {\pb n} = {\pb h }^{\r F}$ (5)
1.2求解过程
运用半隐式特征线分裂(characteristic-based split, CBS)算法[0]求解NS方程(1)和(),主要步骤说明如下:(a) 计算辅助速度场
$\babl {\pb u }^ * - {\pb u }^n = \Delta t\Bigg \{ - {\pb c } \cdot \nabla {\pb u } + \dfrac{1}{Re}\nabla^{\pb u } + \[] \qquad \dfrac{\Delta t}{}\left[ {{\pb c} \cdot \nabla \left( {{\pb c} \cdot \nabla{\pb u}} \right)} \right]\Bigg \}^n \eal\eqno(6)$
(b) 更新压力场
$\nabla ^p^{n + 1} = \dfrac{1}{\Delta t}\nabla \cdot {\pb u}^ * \eqno(7)$
(c) 修正速度场
${\pb u}^{n + 1} - {\pb u}^ * = \Delta t\left[ {\nabla p^{n + 1} -\dfrac{\Delta t}{}\left( {{\pb c } \cdot \nabla ^p} \right)^n} \right] \eqno(8) $
CBS算法的稳定系数为$(\Delta t)^{} /$,与单元尺寸无关,故动网格计算略为省时. 半隐式CBS方法的稳定性较好且对时间步$\Delta t$限制较小. 因CBS算法可对速度和压力采用等阶/低阶插值,选用三节点三角形(T3)单元进行有限元离散.
2 固体模型
2.1 刚体动力学
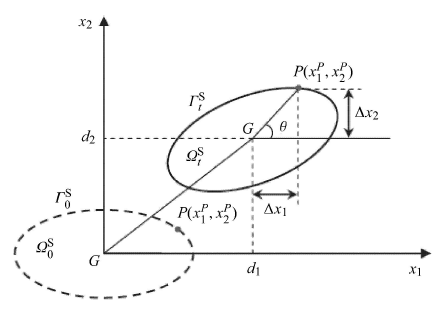
刚体位移记为${\pb d} = \{ d_{1}, d_{}, \theta \}^{\r T}$,其中$d_{i}$ ($i= 1, $)和 $\theta $ 分别表示平动和转动分量,如图1所示. 假定每个方向自由度相互解耦,则刚体运动方程的无量纲分量形式可写为$ \ddot {d}_1 + 4\pi f_{{\r R}1} \zeta _1 \dot {d}_1 + \left( {\pi f_{{\r R}1} }\right)^d_1 = \dfrac{C_{\r D} }{_1^ * } (9)$
$ \ddot {d}_ + 4\pi f_{{\r R}} \zeta _ \dot {d}_ + \left( {\pi f_{{\r R}} }\right)^d_ = \dfrac{C_{\r L} }{_^ * } (10)$
$ \ddot {\theta } + 4\pi f_{{\r R}\theta } \zeta _\theta \dot {\theta } + \left( {\pi f_{{\r R}\theta } } \right)^\theta = \dfrac{C_{\r } }{_\theta ^ * } (11)$
式中,换算频率$f_{{\r R}i} = f_{{\r N}i} D / U$,转动换算频率$f_{{\r R}\theta } = f_{{\r N}\theta } D / U$,自然频率$f_{{\r N}i} = \sqrt { k_i / _i } / (\pi) $,转动自然频率$f_{N\theta } =\sqrt {k_\theta / I_\theta } / (\pi )$,阻尼比$\zeta _i = {c_i } / ( \sqrt {_i k_i })$,转动阻尼比$\zeta _\theta = {c_\theta } / (\sqrt {I_\theta k_\theta } ) $,质量比$_i^\ast = {_i } /(\rho ^FD^)$和 $_\theta ^\ast = {I_\theta } /(\rho ^{\r F}D^4)$,$_i $, $c_i $和$k_i$分别为平动方向的质量、阻尼和刚度,$I_\theta $, $c_\theta $和$k_\theta$分别为扭转方向的惯性矩、阻尼和刚度,$C_{\r D} $, $C_{\r L} $和$C_{\r }$为流体阻力系数、升力系数和冲量矩系数.
刚体平面运动还应满足协调条件[1]. 该条件阐述了边界位移、速度和加速度与重心变量之间的几何关系(参见图1).
显示原图|下载原图ZIP|生成PPT图1一般刚体平面运动
-->Fig. 1Scheatic view of generalized planar rigid-body otion
-->
2.2. 弹性动力学
几何非线性固体的无量纲运动方程可写为如下形式$\ddot{\pb d} - \dfrac{1}{^ * }\nabla \cdot {\pb \siga}^{\r S} - {\pb f }^{\r S} = {\bf 0 } \eqno(12)$
式中,位移${\pb d} = \{d_{1}, d_{}\}^{\r T}$,质量比$^{\ast } =\rho^{\r S}/ \rho^{\r F}$,${\pb \siga}^{\r S}$为Cauchy应力,${\pb f}^{\r S}$为结构体力项. St. Venant-Kirchhoff材料本构关系可写为
${\pb S} = {\pb C}:{\pb E}\,,{\pb E} = {\pb F}^{\r T}{\pb F} - {\pb I} \eqno(13)$
式中,${\pb S}$是第二Piola-Kirchhoff应力,${\pb C}$为弹性本构张量,${\pb E}$表示Green-Lagrangian应变,${\pb F}$为变形梯度. 第二Piola-Kirchhoff应力经构形转换可表示为Cauchy应力
${\pb S} = J{\pb F}^{ - 1}{\pb \siga }^{\r S}{\pb F}^{ - {\r T}} \eqno(14)$
其中,$J ={\r det} ({\pb F})$. 初始条件和边界条件如下
${\pb d} = {\pb d }^0\,,\dot{\pb d} = \dot{\pb d}^0\,, {\pb \siga }^{\r S} \cdot {\pb n} = {\pb h}^{\r S} \eqno(15)$
本文基于总体拉格朗日格式运用修正牛顿$\!$-$\!$-$\!$拉普森法[
2 .3 光滑有限元法
传统有限元法组装的结构刚度矩阵偏刚. 为此,这里采用光滑有限元方法[3-4]求解式(1)线性化后的增量方程. 光滑处理能有效“软化”刚度矩阵,令有限元解更接近理论解,亦未引入新自由度,其基本原理叙述如下.根据梯度光滑运算,任意场变量
$\tilde {\nabla }X\left( {{\pb x}_{\r C} } \right) = \dint_{\varOega _{\r C} } {\nabla X\left( {\pb x}\right)} \Phi \left( {{\pb x} - {\pb x}_{\r C} } \right){\r d}\varOega \eqno(16)$
式中,${\pb x}$代表空间坐标,$\varOega_{\r C}$为光滑域,$\varPhi $为Heaviside型光滑核函数.
由高斯散度定理可知,式(16)可进一步写为
$\babl \tilde {\nabla }X\left( {{\pb x}_{\r C} } \right) = \dint_{\varGaa _{\r C} } {X\left( {\pb x} \right)} {\pb n}\left( {\pb x} \right)\varPhi \left( {{\pb x} - {\pb x}_{\r C} } \right){\r d}\varGaa - \[] \qquad \dint_{\varOega _{\r C} } {X\left( {\pb x} \right)} \nabla \varPhi \left( {{\pb x} - {\pb x}_{\r C} } \right){\r d}\varOega \end{array}\eqno(17) $
其中,$\varGaa_{C}$为$\varOega_{C}$边界,${\pb n}$是$\varGaa _{C}$外法向. 根据非负性和归一性要求,光滑核函数$\varPhi $可定义为
$\varPhi \left( {{\pb x} - {\pb x}_{\r C} } \right) = \left\{ \!\! \begin{array}{lc} {0,} & {\pb x} \notin \varOega _{\r C} \[] 1 / A_{\r C} \,, & {\pb x} \in \varOega _{\r C} \end{array} \right. \eqno(18)$
式中,$A_{\r C}$为光滑域面积.
将式(18)代入式(17)中并注意到常数导数为零,则标量$X$的梯度可写为
$\tilde {\nabla }X\left( {{\pb x}_{\r C} } \right) =\dfrac{1}{A_{\r C} }\dint_{\varGaa _{\r C} } {X\left( {\pb x}\right)} {\pb n}\left( {\pb x} \right){\r d}\varGaa \eqno(19)$
用一点高斯积分即可准确计算上述线积分
$\tilde {\nabla }X\left( {{\pb x}_{\r C} } \right) = \dsu_{i = 1}^{ nsd} \dfrac{1}{A_{{\r C}i} }X\left({{\pb x}_i^{{\r GP}} } \right){\pb n}\left( { {\pb x}_i^{{\r GP}} } \right) l_i \eqno(20)$
其中,${nsd}$为每单元内光滑域个数,${\pb x}^{\r GP}$为高斯点坐标,$l_{i}$为边长.
光滑域构造及其形函数值见后文.
2.4 时间积分
结构运动方程可写为如下一般形式${\pb }\ddot {\pb d} + {\pb C}\dot {\pb d} + {\pb K \pb d} = {\pb F}_{{\r EX}} \eqno(21)$
式中,${\pb }$, ${\pb C}$和${\pb K}$分别表示结构质量矩阵、阻尼矩阵和刚度矩阵,${\pb F}_{\r EX}$为外力向量. 时间积 分方案选用复合隐式时间积分法[5-7],其基本思想是：将一时间步分为两子步,分别运用Newark-$\beta $法[8]和三点向后欧拉差分.
主要原理简述如下.
记$[t, t+\Delta t] =\Delta t[n, n + 1] = \Delta t[n,n +\alpha ] \cup \Delta t[n + \alpha $, $n + 1]$,其中0＜a＜1. 在第一个子步内将结构运动方程于 tn+α
${\pb }\ddot {\pb d}^{n + \alpha } + {\pb C}\dot {\pb d}^{n + \alpha } +
{\pb K \pb d}^{n + \alpha } = {\pb F}_{{\r EX}}^{n + \alpha } \eqno(22)$
对上式应用Newark-$\beta $法,可得
$\dot{\pb d}^{n + \alpha } = \dot{\pb d}^n + \left( {1 - \gaa } \right) \alpha \Delta t \ddot{\pb d}^{n + \alpha } (23)$
$ {\pb d }^{n + \alpha } = {\pb d }^n + \alpha \Delta t \dot{\pb d}^n + \left({1 / - \beta } \right)\left( {\alpha \Delta t} \right)^\ddot{\pb d}^n + \beta \left( {\alpha \Delta t} \right)^\ddot{\pb d}^{n + \alpha } (24)$
其中, $\beta \geqslant 1/4$, $\gaa \geqslant 1/$. 由式(4)可得加速度
$\ddot{\pb d}^{n + \alpha } = \dfrac{1}{\beta \left( {\alpha \Delta t} \right)^}\left( {{\pb d }^{n - \alpha } - {\pb d }^n} \right) - \dfrac{1}{\beta \alpha \Delta t } \dot{\pb d}^n -\left( {\dfrac{1}{\beta } - 1} \right) \ddot{\pb d}^n (25)$
将式(3) $\si$式(5)代入式(),那么
$\left( {\dfrac{1}{\beta \left( {\alpha \Delta t} \right)^}{\pb } +\dfrac{\gaa }{\beta \alpha \Delta t }{\pb C} +{\pb K }} \right){\pb d }^{n + \alpha } = {\pb F }_{{\r EX}}^{n + \alpha } + {\pb }\left[ {\dfrac{1}{\beta \left( {\alpha \Delta t} \right)^} {\pb d}^n + \dfrac{1}{\beta \alpha \Delta t }\dot{\pb d}^n + \left( {\dfrac{1}{\beta } - 1} \right) \ddot{\pb d}^n}\right] + {\pb C }\left[ {\dfrac{\gaa }{\beta \left( {\alpha \Delta t} \right)^}{\pb d }^n + \left( {\dfrac{\gaa }{\beta } - 1} \right) \dot {\pb d}^n + \left( {\dfrac{\gaa }{\beta } - 1} \right) {\alpha \Delta t} \ddot{\pb d}^n} \right] (26)$
同理,在第二个子步内将结构运动方程于$t^{n + 1}$时刻离散
${\pmb M}\ddot{\pmb d }^{n + 1} + {\pmb C}\dot{\pmb d }^{n + 1} + {\pmb K}{\pmb d }^{n + 1} = {\pmb F }_{{\rm EX}}^{n + 1} \eqno(27)$
因任意变量的时间导数$\dot {Q}^{n + 1}$可根据$Q^n$, $Q^{n + \alpha }$和$Q^{n + 1}$近似获得 [29]
$\ddot {Q}^{n + 1} = c_1 Q^n + c_2 Q^{n + \alpha } + c_3 Q^{n + 1} \eqno(28)$
其中,$c_1 = \dfrac{1 - \alpha }{\alpha \Delta t}$,$c_2 = \dfrac{1}{\left( {1 - \alpha } \right)\alpha \Delta t}$和$c_2 = \dfrac{2 - \alpha }{\left( {1 - \alpha } \right)\Delta t}$. 由式(28)可知
$\dot{\pmb d }^{n + 1} = c_1 {\pmb d }^n + c_2 {\pmb d }^{n + \alpha } + c_3 {\pmb d }^{n + 1} \hfill (29)$
$ \ddot{\pmb d }^{n + 1} = c_1 \dot{\pmb d }^n + c_2 \dot{\pmb d} ^{n + \alpha } + c_3\dot {\pmb d }^{n + 1} \hfill (30)$
将式(29)和式(30)代入式(27)中,可得
$ \babl \left( {c_3 c_3 {\pmb M} + c_3 {\pmb C} + {\pmb K}} \right){\pmb d}^{n + \alpha } = {\pmb F}_{{\rm EX}}^{n + \alpha } -{\pmb M}\left( {c_1 c_3 {\pmb d}^n + c_2 c_3 {\pmb d}^{n + \alpha } + c_1 \dot{\pmb d }^n +c_2 \dot{\pmb d }^{n + \alpha }} \right) + {\pmb C}\left( {c_1 {\pmb d}^n + c_2 {\pmb d}^{n + \alpha }} \right) \end{array}\eqno(31) $
式中, $\beta = 1/4$, $\gamma = 1/2$和 $\alpha = 1/2$. $n + \alpha $ 时刻外力由$n$和$n +1$时刻值线性插值获得; 弹性体的${\pmb K}^{n + \alpha }$由文献[30]所建议方法获得.
表面上,复合隐式时间积分法的计算时间近两倍于Newmark-$\beta $法,但它能适应更大时间步,故总耗时并未显著延长 [25].
一般而言,结构时间步大于流体时间步,上述特性也将更利于流体子循环 [31].
3 网格更新
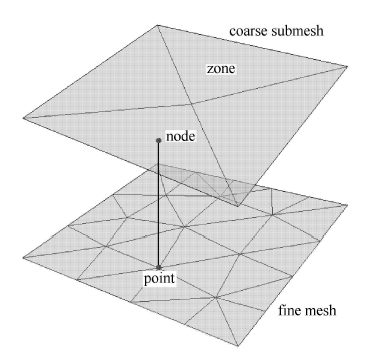
这里采用简单高效的子块移动技术[3]结合正交-半扭转弹簧近似法[33]更新流体动网格,其基本思想是通过粗糙背 景网格(即子块)运动插值获得精细网格的节点坐标,如图所示. 相比单纯使用弹簧近似法,该手段可大幅提高网格更新效率,具体过程描述如下:(a) 提取粗、细两层网格信息;
(b) 确定每个子块内的细网格节点数;
(c) 计算每个动网格节点的插值系数;
(d) 由结构运动更新界面节点位置;
(e) 如粗网格有内部节点则调用正交-半扭转弹簧近似法,否则跳过此步;
(f) 对子块位置进行插值获得细网格新位置;
(g) 检查两层网格质量.
显示原图|下载原图ZIP|生成PPT图2子块移动技术示意图
-->Fig.2Diagraatic sketch of the MSA technique
-->
同时,为满足几何守恒律,将一质量源项 [34]引入压力泊松方程(7)可得
$\nabla ^2p^{n + 1} = \dfrac{1}{\Delta t}\nabla \cdot {\pmb u}^ * +S_{{\rm MST}}^{n + 1} \eqno(32)$
其中
$S_{{\rm MST}}^{n + 1} = \dfrac{1}{2A_{\rm e}^{n + 1} }\left( \left| \begin{array}{cc} {w_1^2 - w_1^1 } & {w_2^2 - w_2^1 } {w_1^3 - w_1^1 } & {w_2^3 - w_2^1 }\end{array} \right| \right)^{n + 1} \eqno(33) $
式中,$A_{\rm e}$为单元面积,网格速度上标表示局部节点编号,下标表示坐标轴方向. 由式(33)易知质量源项在欧拉网格上退化为零. 引入质量源项可避免构造复杂的网格速度格式 [35].
4 分区强耦合算法
4.1 界面条件
在流固交界面$\Sigma $处须满足速度连续性和应力平衡性,即${\pmb u} = {\pmb d }\,, \ \ {\pmb t }^{\rm F} = {\pmb t}^{\rm S} \eqno(34)$
其中,流体拖拽力和结构拖拽力写为
$ {\pmb t}^{\rm F} = {\pmb \sigma }^{\rm F} \cdot {\pmb n}^{\rm S}$,${\pmb t}^{\rm S} = {\pmb \sigma }^{\rm S} \cdot {\pmb n}^{\rm S} $ (35)
式中,${\pmb n}^{\rm S}$为界面法向向量,其方向由结构域指向流体域. 此外,还需保障界面处的几何连续性
${\pmb x} = {\pmb d} \,, \ \ {\pmb w} = \dot {\pmb d} \eqno(36)$
上述界面条件可通过构建高阶速度增量和高阶应力增量 [16-18,36-38]进行修正,在此不再赘述.
4.2 强耦合算法
固定点法配合Aitken's $\Delta ^{2}$松弛 [13]易实施、精度与效率较为理想,已见诸于各类流固耦合问题模拟.本文采用此手段耦合各场,主要步骤描述如下:
(a) 预测界面位移 [39]
$\hat{\pmb d }_{\Sigma ,k}^{n + 1} = {\pmb d }_\Sigma ^n + \Delta t\left( {1.5 \dot{\pmb d }_\Sigma ^n - 0.5 \dot{\pmb d }_\Sigma ^{n - 1} } \right) \eqno(37) $
(b) 开始迭代并令$k \leftarrow k + 1$;
(c) 更新流体动网格并计算网格速度
${\pmb w}_k^{n + 1} = \dfrac{\hat {\pmb d}_k^{n + 1} - {\pmb d}^n}{\Delta t} \eqno(38) $
(d) 计算质量源项;
(e) 求解流体NS方程并获得流体激力;
(f) 求解结构运动方程;
(g) 计算界面残差,检查是否收敛, 若收敛则进入下一时间步,否则进行第(h)步;
(h) 重新计算Aitken因子 [9],并松弛界面位移
$\hat{\pmb d }_{\Sigma ,k}^{n + 1} = \lambda _k^{n + 1} {\pmb d}_{\Sigma ,k}^{n + 1} + \left( {1 - \lambda _k^{n + 1} } \right) \hat{\pmb d }_{\Sigma ,k - 1}^{n + 1} \eqno(39)$
(i) 返回至第(b)步.
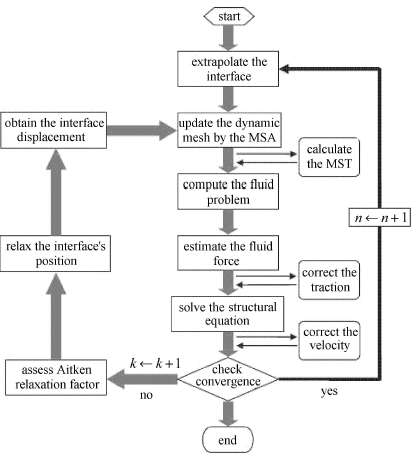
上述分区强耦合算法的流程图如图3所示.
显示原图|下载原图ZIP|生成PPT图3分区强耦合算法
-->Fig. 3Flowchart of partitioned strong coupling algorith
-->
4.3 Aitken加速技术
在每一迭代步中,动态松弛因子按以下递归公式计算 [13]$\lambda _k^{n + 1} = \left\{ \!\! \begin{array}{ll} {\max \left( {\lambda _{{\rm MAX}} ,\lambda ^n} \right) }\,, & {k = 1} \lambda _{k - 1}^{n + 1} \dfrac{{ \pmb e\pmb r \pmb r }_k^{\rm T} \left( { {\pmb e\pmb r \pmb r }_{k - 1} - { \pmb e\pmb r \pmb r }_k } \right)}{\left| { {\pmb e\pmb r \pmb r }_k - {\pmb e\pmb r \pmb r}_{k - 1} } \right|} \,, & {k \geqslant 2} \end{array} \!\! \right.$ (40)
式中,$k$代表迭代步,${\pmb e\pmb r \pmb r} $是界面位移残差, $\lambda _{\rm MAX} = 0.1$和 $\lambda_{0} =0.5$.
5 数值算例
5.1 桥梁截面颤振
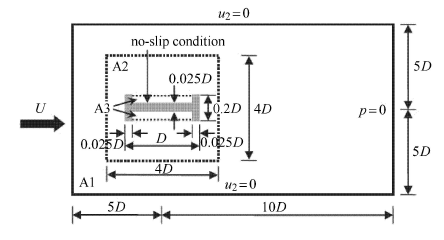
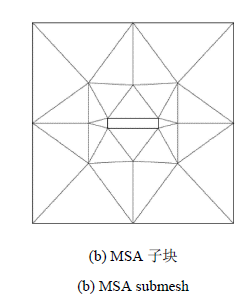
H型桥梁截面在均匀来流下经历竖向平动和转动,如图4所示. 相关参数设置如下 [40]：流体密度$\rho^{\rm F} =1.25$, 流体黏性$\mu = 0.1$,结构质量$m_{2} = 3\,000$,阻尼因子$c_{2} = 100$,弹簧刚度$k_{2} =2\,000$,转动惯量$I_{\theta } = 25\,300$,转动阻尼因子$c_{\theta } = 2\,200$,转动弹簧刚度$k_{\theta } =40\,000$,入口速度$U = 10$,特征长度$D = 12$和雷诺数${Re} = 1\,500$.在图4中动网格域限定为A2. 网格划分和子块划分如图5所示,其中计算域包含6\,486个T3单元和3\,329个节点. 时间步长取$\Delta t = 0.02$.
显示原图|下载原图ZIP|生成PPT图4桥梁截面问题描述 ^(a)流场 (b) SA子块
-->Fig. 4Proble description of the oscillating deck ^ (a) Fluid field (b) SA subesh
-->
显示原图|下载原图ZIP|生成PPT图5问题网格划分
-->Fig. 5esh and subesh for the proble
-->
验网格无关性,选用1(6 486个T3单元和3 39个节点)和(11 714个T3单元和5 953个节点)进行对比计算,结果列 于表1. 由表1可知,两组结果相差很小,故本文方法不受网格影响. 综合考虑效率与精度,选取1进行后续模拟.
Table 2
表1
表1计算结果对比
Table 2Coparison between two sets of results
| Mesh | $d_{MAX2}$ | $f_{O2}$ | $d_{MAX\theta }$ | $f_{O\theta }$ |
|---|---|---|---|---|
| M1 | 0.040 7 | 0.214 | 0.385 | 0.215 |
| M2 | 0.0421 | 0.211 | 0.393 | 0.211 |
新窗口打开
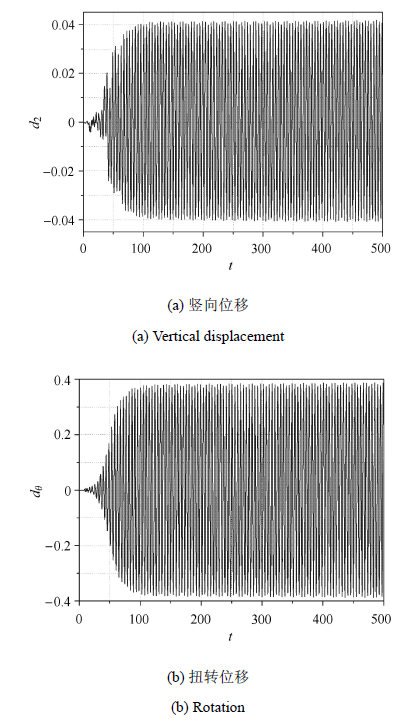
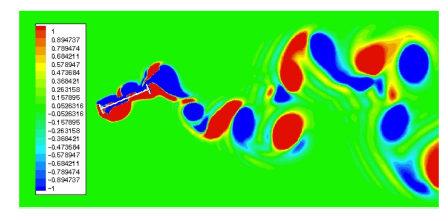
两方向振幅与振动频率列于表. 由表可知,本文结果稍大于文献[40]结果;桥梁截面经历较大 扭转振动且两方向振 动频率相同. 图6所示为两方向位移时程. 由该图可知,本文位移时程曲线相当平滑,而文献[41]的位移曲线则略有起伏,说明本文方法表现稳定. 综合表1和图6可知,结构振动频率非常接近其转动自然频率($f_{\rm N\theta } =0.200\,1$),截面扭转强烈而竖向平动微弱. 此时结构运动由扭转振动控 制,出现明显扭转颤振现象. 图7进一步给出某典型时刻涡量场.
Table 2
表2
表2计算结果对比
Table 2Coparison between the existing and present data
| $d_{MAX2}$ | $f_{O2}$ | $d_{MAX\theta }$ | $f_{O\theta }$ | |
|---|---|---|---|---|
| Ref.[40] | 0.0325$\sim$0.035 | - | 0.271 | - |
| Present | 0.0407 | 0.214 | 0.385 | 0.215 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图6桥梁截面位移时程
-->Fig. 6Tie history of the deck displaceent
-->
显示原图|下载原图ZIP|生成PPT图7涡量云图
-->Fig. 7Vorticity contour of the oscillating bridge deck
-->
5.2 节流阀瓣涡激振动
在均匀流动下,槽道内节流阀瓣发生涡激振动,问题定义如图8所示. 系统参数设定为 [42]：流体密度 $\rho^{F} = 1.0$,流体黏性$\mu = 0.001$,结构密度$\rho^{S} = 1000$ (Case A)和$\rho ^{S} = 62.5$ (Case B),杨氏模量$E = 60\,000$,泊松比$\upsilon = 0.45$,入口速度$U = 1$,立杆高度$D = 1$和雷诺数${Re} = 1000$.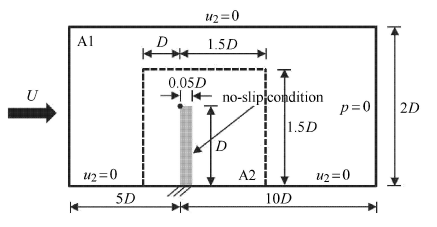
显示原图|下载原图ZIP|生成PPT图8节流阀瓣问题描述
-->Fig. 8Problem description of the restrictor flap in a channel
-->
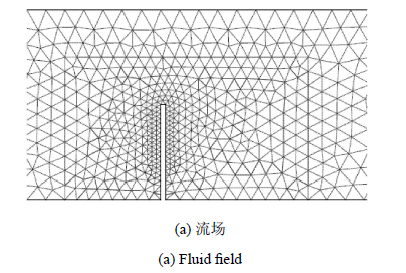
动网格域取为非对称域A2,测点置于立杆左上角,见图8. 流体域划分为2\,786个T3单元和1\,523个节点,固体域 则均匀划分为40 × 2个Q4单元. 流场网格和子块划分如图9所示. 由稳定性条件 [23],将一个Q4单元分为4个光滑子域,形函数构造如图10所示. 时间步长取为$\Delta t = 0.005$.
显示原图|下载原图ZIP|生成PPT图9问题网格划分
-->Fig. 9Mesh and subesh for the problem
-->
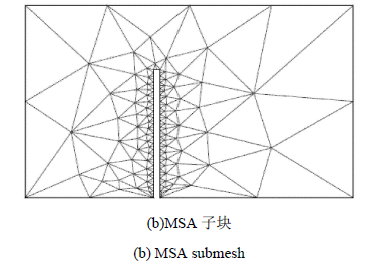显示原图|下载原图ZIP|生成PPT-->Fig.9-1esh and subesh for the problem (continued)
-->
显示原图|下载原图ZIP|生成PPT图10光滑域与形函数构造
-->Fig. 10Construction of soothing doain and shape functions
-->
两组不同流体网格验证算法的网格敏感性,即1( 786个T3单元和1 53个节点)和(5 006个T3单元和 644个节点). 两种工况下测点最大水平位移列于表3. 可见,两组网格结果相差较小,再次验证了本文算法不受网格划分影响. 下文计算均基于1网格.
Table 3
表3
表3计算结果对比
Table 3Coparison between two sets of results
| Mesh | Case A | Case B |
|---|---|---|
| M1 | 0.641 | 0.575 |
| M2 | 0.652 | 0.593 |
新窗口打开
图11给出两种工况下测点水平位移时程曲线,并与文献[42]进行对比.
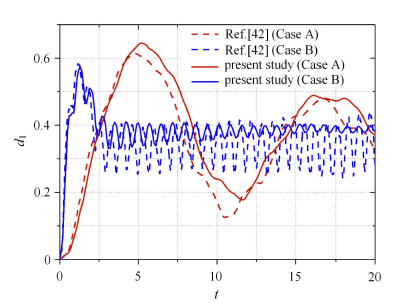显示原图|下载原图ZIP|生成PPT图11测点水平位移时程由该图可知,两种工况下最大振幅均为0.6左右,与已有 结果相符. 进一步观察可知,Case A与文献[
-->Fig. 11Time history of horizontal displacement of the measuring point
-->
解释如下：结构密度较大时,结构在黏性流体中的振动主要受惯性影响,流体作用相当于阻尼振子,逐渐消耗结构动能.
Case A中结构振动的衰减特征正说明了这点. 在Case B中,文献[42]的时程曲线仍可维持相当振幅,而本文结构振动则衰减相当迅速. 文献[43]同样报道了这一现象.
系统参数与数值方法的不同导致了计算结果的差异. 为清楚说明涡激振动现象,图12给出Case A中某典型时刻水平速度与压力云图.
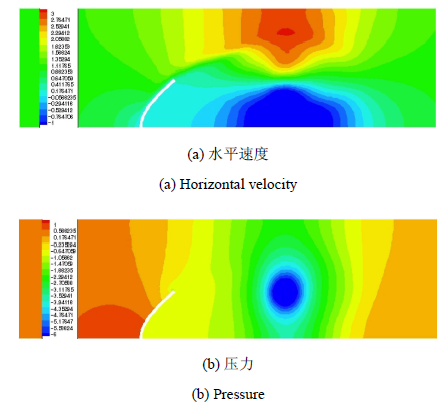显示原图|下载原图ZIP|生成PPT图12Case A中水平速度与压力云图
-->Fig. 12Horizontal velocity and pressure contours in Case A
-->
6 结论
本文基于ALE有限元公式提出一种分区强耦合方法,数值模拟了大位移流固耦合问题. 采用半隐式CBS算法求解不可压缩NS方程, 可进行速度--压力等阶插值且省时;运用新颖的复合隐式时间积分法对结构方程进行时间积分,能选取较大时间步. 针对几何非线性,选用精确高效的光滑有限元法计算结构增量方程. 动网格更新采用子块移动技术高效结合正交--半扭转弹簧近似法,同时引入质量源项保证流体分步算法满足几何守恒律. 多场耦合经固定点迭代配以Aitken加速技术,简单高效. 本文强耦合算法能灵活选取不同单场技术,兼具程序模块性、精度与效率优点. 从原理看,较高的效率主要源于流场计算、网格更新和耦合迭代等. 数值算例表明,计算结果与已有数据吻合较好,成功揭示了典型流致振动现象.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . . |
| [3] | . . |
| [4] | . . |
| [5] | . |
| [6] | . . |
| [7] | . . |
| [8] | . . |
| [9] | . . |
| [10] | . . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | 99: |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . |
| [39] | . |
| [40] | |
| [41] | . |
| [42] | |
| [43] | . |
