, 邹丽NUMERICAL STUDY OF RESPONSE PERFORMANCE OF VORTEX-INDUCED VIBRATION ON A FLEXIBLE CYLINDER WITH PINNED-PINNED BOUNDARY CONDITION
GaoYun, ZouLi中图分类号:O357
文献标识码:A
通讯作者:
收稿日期:2017-10-11
接受日期:2017-12-20
网络出版日期:2017-12-21
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (33168KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
当流体流过圆柱体时,在一定的雷诺数下,会在圆柱体两侧形成交替脱落的漩涡. 周期性的漩涡脱落会引起结构产生周期性的振动,称为涡激振动(vortex induced vibration, VIV)[1]. 当漩涡脱落频率接近圆柱体固有频率时,便会发生锁定. 锁定区域内,圆柱体会发生大幅的、危险的涡激振动响应,这种响应会对结构带来很大的疲劳损伤.关于圆柱体涡激振动响应问题,在过去的几十年中,有诸多****对其展开了大量研究. 早期的研究主要集中在刚性圆柱体[2-5], 通过对刚性圆柱体的研究,****们发现了一些非常重要的涡激振动响应特性,如锁定特性[6] 以及迟滞特性[7] 等. 但随着海洋工程的快速发展,伴随着大量细长柔性圆柱结构(如立管以及锚链等) 的出现,近些年针对细长柔性圆柱体的涡激振动响 应研究得到了越来越广泛的关注. 细长柔性圆柱体涡激振动响应的研究方法包括实验方法[8-14]、计算流体动力学(computational fluid dynamics, CFD) 方法[15-17] 以及经验模型方法[18-20].
实验方法本身虽存在很多优点(如分析数据可靠、分析现象直观等),但实验方法通常研究成本较高. 而CFD 方法在分析细长柔性圆柱体时则存在一定的局限性,主要是由于较大的结构轴向尺寸会导致在整个流场区域内展开全尺度涡激振动响应时域模拟非常困难,且CFD 研究方法的计算时间较长. 因此有必要建立一种能够快速预报细长柔性圆柱体涡激响应的经验模型方法,这种方法可以模拟出细长柔性圆柱体涡激振动响应的一些主要特征. 尾流振子方法则正是近些年应用较为广泛的一种经验模型方法. CFD 方法与经验模型方法的本质区别在于如何获取结构上的流体力：CFD 方法通过直接求解Navier-Stokes 方程得到圆柱体上的流体力;而经验模型方法则是基于实验数据建立经验模型得到流体力.
由过去大量的研究可以看出：柔性圆柱体涡激振动响应具备一些刚性圆柱体所没有的特性,包括驻波响应特性、行波响应特性、多模态振动 特性、时间共享特性以及频率随时间变化的特性等. 其中,驻波响应特性以及行波响应特性是柔性圆柱体涡激振动响应区别于刚性圆柱体的两个重要特征,它们反应的是柔性圆柱体涡激振动 响应沿着圆柱体轴线方向是发生变化的. 通常对于刚性圆柱体来说,当涡激振动响应达到稳定时, 横流方向振动位移$y$ 可近似地表示为$y(t)=y_{0}\cos(\omega t)$,其中$y_{0}$ 为振动幅值, $\omega $ 为振动圆频率,$t$ 为时间[7],该表达式意味着刚性圆柱体的涡激振动位移响应沿着圆柱体轴线方向是保持不变的. 但对于柔性圆柱体,涡激振动位移响应沿着圆柱体轴线方向是发生变化的,因此表达式要更为复杂. 柔性圆柱体涡激振动位移响应$y$ 的表达式通常可分为两类：当振动响应为驻波时,$y(z,t) = y_{0}\sin(2\pi z /\lambda )\sin \omega t$;当振动响应为行波时,$y(z, t)=y_{0}\sin(2 \pi z / \lambda - \omega t )$,其中 $\lambda $ 为波长[9]. 针对柔性圆柱体涡激振动响应,目前尚存在很多问题有待进一步的展开研究. 比如：在线性剪切来流中,两端铰接的柔性圆柱体的涡激振动位移响应特性(振动幅值以及振动波长) 以及频率响应特性(主导频率、频率带宽以及频率随时间变化的特性) 随着剪切剖面的变化将会发生怎样的变化?
基于以上问题,本文基于尾流振子模型对剪切来流中两端铰接的柔性圆柱体涡激振动响应特性展开了数值研究. 具体研究内容如下： 在第2 部分建立了柔性圆柱体结构振子以及尾流振子之间的耦合模型. 在3.1 部分基于二阶精度中心差分格式对耦合模型先离散后迭代进行求解. 在3.2 部分通过与他人直接数值模拟(direct numerical simulation, DNS) 方法分析结果进行对比验证本文数值模型的可靠性. 在4.1 部分以及4.2 部分分别对不同剪切参数下柔性圆柱体的涡激振动位移响应特性以及频率响应特性展开了研究.
1 分析模型
如图1 所示,考虑一长度为$L$、直径为$D$ 的细长柔性圆柱体在线性剪切来流作用下引起的横流方向涡激振动响应问题. 圆柱体两端采用铰接边界条件,取坐标原点$O$ 为圆柱体的下端,$X$ 方向为顺流方向,$Z$ 方向为铅直方向,$Y$ 方向则是横向振动方向,$X$,$Y$ 以及$Z$ 三个方向形成右手直角坐标系. 柔性圆柱体上受到的张力为 $\varTheta $,柔性圆柱体的弯曲刚度为$EI$,来流大小为$U(Z)$. 本文通过改变剪切参数$\beta $ 来反应不同的剪切流剖面,如图1 所示,假设线性剪切流剖面的平均流速为$U_{\rm ref}$,剪切参数 $\beta =(U_{\max}- U_{\min})/U_{\rm ref}$. 由于$U_{\rm ref} =(U_{\max}+U_{\min})/2$,因此,$U_{\max}=U_{\rm ref} (1+ \beta /2)$;$U_{\min}=U_{\rm ref}(1- \beta /2)$,任意点$Z$ 处的流速$U(Z)=U_{\min}+(U_{\max} - U_{\min})Z/L$.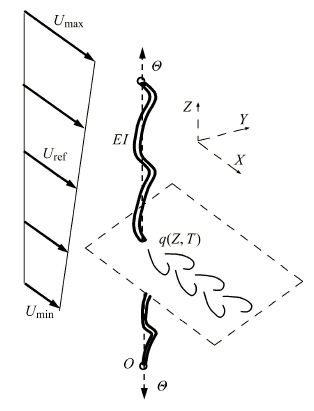
显示原图|下载原图ZIP|生成PPT图1线性剪切流中两端铰接的细长柔性圆柱体模型
-->Fig. 1A flexible cylinder with pinned-pinned boundary condition subjected to a linearly sheared flow
-->
将图1 中的细长柔性圆柱体看作细长张力梁模型,建立如下振动方程
$m\dfrac{\partial ^2Y(Z,T)}{\partial T^2} + R\dfrac{\partial Y(Z,T)}{\partial T} -\varTheta \dfrac{\partial Y^2(Z,T)}{\partial Z^2} + EI\dfrac{\partial Y^4(Z,T)}{\partial Z^4} = p(Z,T) $ (1)
式中$T$ 为时间,$p(Z,T)$ 为升力,可写作[7]$p(Z,T) = \dfrac{1}{4}\rho U^{2}\left( Z \right)DC_{\rm L0} q(Z,T) $ (2)
式中,$q(Z,T)$ 表示尾流振子的运动,$C_{\rm L0}$ 为横向升力系数. 式(1) 中柔性圆柱体单位长度质量$m$ 包括结构质量$m_{\rm s}$ 和附加流体质量$m_{\rm f}$,可表示为
$m = m_{\rm s} + m_{\rm f}, \ \ m_{\rm f} = C_{\rm M} \rho {D^2\pi } /4$ (3)
式中$\rho $ 表示流体密度,$C_{\rm M}$ 表示附加质量系数,对于圆柱体,$C_{\rm M} =1.0$. 式(1) 中阻尼$R$ 包括结构阻尼$R_{\rm s}$ 和流体阻尼$R_{\rm f}$,可表示如下
$R = R_{\rm s} + R_{\rm f}, \ \ R_{\rm f} = \gamma {\varOmega }_{\rm f} \rho D^2$ (4)
式中$\gamma $ 为黏滞力系数,与流体阻尼系数$C_{\rm D}$ 的关系式为：$\gamma = C_{D}/(4\pi St)$,${St}$ 数为斯脱哈尔数[7]. 由于结构阻尼通常与流体阻尼相比较小,尤其在低质量阻尼比介质(如水) 中,结构阻尼可以忽略. 因此,本文中忽略了结构阻尼,只考虑了流体阻尼的影响. 式(4) 中$\varOmega_{\rm f}$ 为根据斯脱哈尔关系式计算得到的局部斯脱哈尔漩涡泄放频率,可表示为
$ {\varOmega }_{\rm f} = \dfrac{2\pi \cdot St \cdot U\left( Z \right)}{D}$ (5)
采用改进的Van der pol 方程来满足尾流振子的非线性特性,表达式如下[22]
$\dfrac{\partial ^2q(Z,T)}{\partial T^2} + \varepsilon {\varOmega }_{\rm f} (q^2(Z,T) - 1)\dfrac{\partial q(Z,T)}{\partial T} + {\varOmega }_{\rm f}^2 q(Z,T)= \dfrac{A}{D}\dfrac{\partial ^2Y(Z,T)}{\partial T^2}$ (6)
式中$\varepsilon $ 为非线性项中的小参数,$A$ 为结构对流体的耦合动力参数.
将方程(1) 和(6) 转换成无量纲形式,令
$y = Y/D, \ \ z = Z / D, \ \ t = T \cdot {\varOmega }_{\rm ref} $ (7)
式中,$\varOmega_{\rm ref}$ 为依据平均流速$U_{\rm ref}$ 计算得到的斯脱哈尔漩涡发放频率, $\varOmega_{\rm ref}=2\pi StU_{\rm ref}/D$. 将式(7) 三个等式分别代入 方程(1) 和(6) 中,整理得到无量纲方程为
$\dfrac{\partial ^2y\left( {z,t} \right)}{\partial t^2} + \omega _{\rm f} \left( z \right) \cdot \dfrac{\gamma }{\mu }\dfrac{\partial y\left( {z,t} \right)}{\partial t} - c^2\dfrac{\partial ^2y\left( {z,t} \right)}{\partial z^2} + b^2\dfrac{\partial^{4}y\left( {z,t} \right)}{\partial z^4} =\omega _{\rm f} ^2\left(z \right)Mq \\ \dfrac{\partial ^2q\left( {z,t} \right)}{\partial t^2} + \omega _{\rm f} \left( z \right) \cdot \varepsilon \left( {q\left( {z,t} \right)^2 - 1} \right)\dfrac{\partial q\left( {z,t} \right)}{\partial t} + \omega _{\rm f}^{2}\left( z \right) \cdot q\left( {z,t} \right) = A\dfrac{\partial ^2y\left( {z,t} \right)}{\partial t^2} $ (8)
式中, $\omega_{\rm f} (z)=U(z)/U_{\rm ref} =1-\beta /2+\beta z/(L/D)$, $\mu $ 为质量比,可表 示为$\mu=m/(\rho D^{2})$,无量纲参数$M$ 表示如下
$M=\dfrac{C_{\rm L0}}{16\pi^2 St^2 \mu}$ (9)
式中$c$ 为无量纲张力,表示为$c=\sqrt{\varTheta/m}/(\varOmega_{\rm ref}D)$;$b$ 为无量纲弯曲刚度,表示为$b=\sqrt{EI/m}/(\varOmega_{\rm ref}D^2)$.
2 数值方法以及数值模型验证
2.1 数值方法
在空间和时间上均采用二阶精度中心差分格式对方程式(8) 先离散后迭代进行求解. 假设柔性圆柱体无量纲总长度$L/D$ 可划分为$M$ 段;计算无量纲总时间$t_{\rm total}$ 可划分为$N$ 段. 那么,计算空间步长为$\Delta z=L /(D M)$;计算时间步长$\Delta t=t_{\rm total}$/$N$. 被离散后的$M +1$ 个空间点可表示为：$z=z_{i }$ ($i =0$, 1, 2, $\cdots$, $M$);被离散后的$N$+1 时间点可表示为：$t=t_{j}$ ($j =0$, 1, 2, $\cdots$, $N$). 假设$t_{n}$ 时刻$z_{m}$ 位置处对应的无量纲参数$y$ 和$q$ 可表示为$y_n^m $ 以及$q_n^m $,那么式(8) 中各偏导数项的二阶精度差分格式可表示为$\begin{equation} \left. \begin{aligned} {\dfrac{\partial y}{\partial t}}|_{t = t_n ,z= z_m } = \dfrac{y_{n + 1}^m - y_{n - 1}^m }{2\Delta t} \\ \left. {\left( {\dfrac{\partial^2y}{\partial t^2}} \right)} \right|_{t = t_n ,z = z_m } = \dfrac{y_{n + 1}^m + y_{n - 1}^m - 2y_n^m }{\Delta t^2} \\ \dfrac{\partial q}{\partial t}|_{t = t_n ,z= z_m } = \dfrac{q_{n + 1}^m - q_{n - 1}^m }{2\Delta t} \\ \dfrac{\partial ^2q}{\partial t^2}|_{t = t_n ,z = z_m } = \dfrac{q_{n + 1}^m + q_{n - 1}^m- 2q_n^m }{\Delta t^2} \\ \dfrac{\partial ^2y}{\partial z^2}|_{t =t_n ,z = z_m } = \dfrac{y_n^{m + 1} + y_n^{m - 1} - 2y_n^m }{\Delta z^2} \\ \dfrac{\partial ^4y}{\partial z^4}|_{t = t_n ,z = z_m } = \dfrac{y_n^{m + 2} -4y_n^{m + 1} + 6y_n^m - 4y_n^{m - 1} + y_n^{m - 2} }{\Delta z^4} \end{aligned} \right\} \end{equation}$ (10)
将式(10) 代入方程(8) 整理得到
$\begin{equation} \left. \begin{aligned} ( \dfrac{1}{\Delta t^2} + \omega _{f}(z_m)\dfrac{\gamma}{2\mu \Delta t})y_{n + 1}^m = \omega_{f}^2(z_m) Mq_n^m +(\dfrac{2}{\Delta t^2} - \dfrac{2c^2}{\Delta z^2}- \dfrac{6b^2}{\Delta z^4})y_n^m +(\omega_{f}(z_m)\dfrac{\gamma }{2\mu \Delta t} - \dfrac{1}{\Delta t^2})y_{n - 1}^m +\\ y_n^{m + 1}(\dfrac{c^2}{\Delta z^2} + \dfrac{4b^2}{\Delta z^4}) + y_n^{m - 1} (\dfrac{c^2}{\Delta z^2} + \dfrac{4b^2}{\Delta z^4})-\dfrac{b^2}{\Delta z^4}(y_n^{m + 2}+ y_n^{m - 2}) \\ \{\dfrac{1}{\Delta t^2} + \omega _{\rm f}(z_m) \cdot \dfrac{\varepsilon \left[ {\left( {q_n^m} \right)^2 - 1} \right]}{2\Delta t} q_{n+1}^m = A\dfrac{y_{n + 1}^m + y_{n - 1}^m - 2y_n^m}{\Delta t^2} +(\dfrac{2}{\Delta t^2} - \omega _{\rm f}^2(z_m))q_n^m -\dfrac{1}{\Delta t^2}q_{n - 1}^m + \\ \omega _{\rm f}\left( {z_m } \right) \cdot\varepsilon \left( {\dfrac{\left( {q_n^m } \right)^2 - 1}{2\Delta t}} \right)q_{n - 1}^m \end{aligned} \right\} \end{equation}$ (11)
$y$ 的初始条件设为 $y =0$ 以及$\partial y / \partial t=0$;$q$ 的初始条件设为：$q$ 为一个波数的微幅扰动以及$\partial q/\partial t=0$. 边界条件为铰接边界条件,即柔性圆柱体两个端点处位移以及弯矩均为0,可表示为
$\begin{equation} \left. \begin{aligned} y(0,t) = y(L/D,t) = 0\\ \dfrac{\partial ^2y (0,t)}{\partial z^2} = \dfrac{\partial ^2y(L/D,t)}{\partial z^2} = 0 \end{aligned} \right\} \end{equation}$ (12)
由式(11) 可以看出：当$ 2 ≤ m ≤ M -2$ 时$y$ 可直接使用式(11) 进行求解;当$m =0$ 以及$m=M$ 时,则需要使用位移为0 的边界条件,$y$ 表示如下
$y_{n + 1}^0 = y_{n + 1}^M = 0 $ (13)
当$m=1$ 以及$m=M-1$ 时,则需要使用弯矩为0 的边界条件,由$m=0$ 以及$m=M$ 时弯矩为0 得到
$y_n^{ - 1} = - y_n^1 , \ \ y_n^{M + 1} = - y_n^{M - 1}$ (14)
联合式(14) 以及式(11) 得到$m=1$ 以及$m=M-1$ 时$y$ 的表达式如下
$\begin{equation} \left. \begin{aligned} (\dfrac{1}{\Delta t^2} + \dfrac{\omega _{f}(z_1)\cdot \gamma}{2\mu \Delta t})y_{n + 1}^1 = \omega_{f}^2(z_1) Mq_n^1 +(\dfrac{2}{\Delta t^2} -\dfrac{2c^2}{\Delta z^2} - \dfrac{6b^2}{\Delta z^4})y_n^1 +\dfrac{\omega _{f}(z_1)\gamma}{2\mu \Delta t}- \dfrac{1}{\Delta t^2}y_{n - 1}^1 +\\y_n^2 (\dfrac{c^2}{\Delta z^2} + \dfrac{4b^2}{\Delta z^4})+ y_n^0(\dfrac{c^2}{\Delta z^2} + \dfrac{4b^2}{\Delta z^4}) - \dfrac{b^2}{\Delta z^4}(y_n^3 - y_n^1)\\(\dfrac{1}{\Delta t^2} + \omega _f (z_{M - 1}) \dfrac{\gamma}{2\mu \Delta t})y_{n + 1}^{M - 1} = \omega _{\rm f}^2 (z_{M - 1}) Mq_n^{M - 1} + (\dfrac{2}{\Delta t^2} -\dfrac{2c^2}{\Delta z^2} - \dfrac{6b^2}{\Delta z^4})y_n^{M - 1} +\\(\omega _{f}(z_{M - 1}) \dfrac{\gamma }{2\mu \Delta t} - \dfrac{1}{\Delta t^2})y_{n-1}^{M-1}+\\y_n^M(\dfrac{c^2}{\Delta z^2} + \dfrac{4b^2}{\Delta z^4})+y_n^{M - 2}(\dfrac{c^2}{\Delta z^2} +\dfrac{4b^2}{\Delta z^4}) - \dfrac{b^2}{\Delta z^4}(-y_n^{M -1} + y_n^{M - 3})\end{aligned} \right\} \end{equation}$ (15)
当$t_{n + 1}$ 时刻$z_{m}$ 处的$y$ 已知,便可依据式(11) 的第2 个表达式求得$t_{n +1}$ 时刻$z_{m}$ 处的$q$,依此类推对式(11) 进行迭代求解.
2.2 数值模型验证
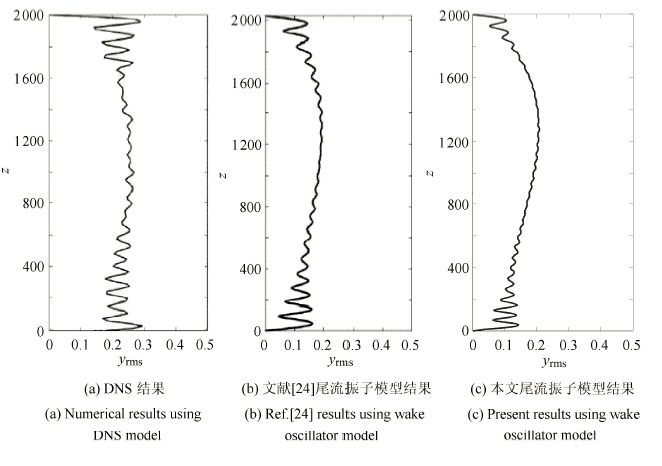
为了验证本文尾流振子模型的可靠性,这里对其进行了数值验证. 验证过程中选取的所有参数与文献[23] 相同,$C_{D}=1.2$,$C_{\rm L0} =0.3$,$St =0.20$, $\mu =2.785$,$c =23.6$,$b =303$,$L/D =2000$. 来流为线性剪切来流,流剖面中最大流速$U_{\max}$ 和最大小流速$U_{\min}$ 满足：($U_{\max}- U_{\min})/U_{\max} =0.7$,$U_{\rm ref} =(U_{\max}+U_{\min})/2=1.0$. 验证计算时空间步长$\Delta z$ 以及时间步长$\Delta t$ 分别取为：$\Delta z =1$;$\Delta t =0.001$,计算总时间$t_{\rm total}$ 取为600 个无量纲时间.图2给出了文献[23]DNS 方法、文献[24] 尾流振子模型 以及本文尾流振子模型计算得到的两端铰接的柔性圆柱体涡激振动位移响应均方 根值沿
显示原图|下载原图ZIP|生成PPT图2涡激振动位移均方根值对比
-->Fig. 2Comparison of RMS values of VIV displacement
-->
3 分析与讨论
对四种不同剪切参数$\beta $ (0.5, 1.0, 1.5 以及2.0) 下两端铰接的细长圆柱体涡激振动响应特性展开了研究,研究过程中选取的所有参数与文献[16] 相同,$C_{\rm D}=1.2$,$C_{\rm L0}=0.3$,${St}=0.20$,$\mu =6$,$c=4.55$, $b=9.09$,$L/D=200$. 计算时空间步长$\Delta z$ 以及时间步长$\Delta t$ 分别取为：$\Delta z=0.1$;$\Delta t=0.01$,计算总时间$t_{\rm total}$ 取为600 个无量纲时间.3.1 圆柱体涡激振动位移响应分析
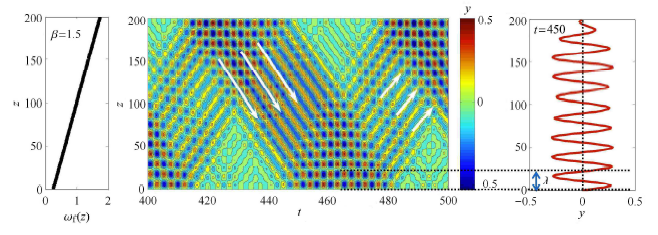
图3给出了不同剪切参数$\beta $下圆柱体振动无量纲位移随时间与空间的变化云图. 由图3 可以看出：结构振动位移响应由驻波以 及行波混合组成. 在圆柱体两端附近,结构振动位移响应呈现明显的驻波占主导的特性;而在圆柱体中间段附近,结构振动位移响应则呈现明显的行 波占主导的特性.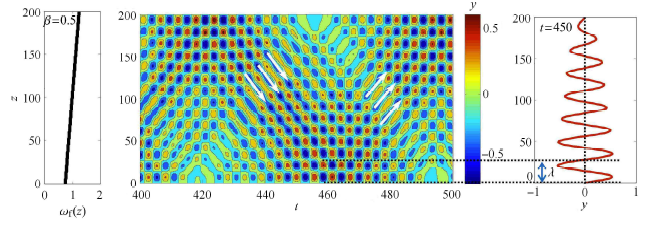
显示原图|下载原图ZIP|生成PPT图3-a不同剪切参数下圆柱体的位移响应变化云图以及$t =450$时振动位移随空间的瞬时变化特性 (a) $\beta=0.5$
-->Fig. 3-aEvolution of cylinder vibration displacement versus time and span and the instantaneous displacement along the span at $t =450$ for different shear parameters(a) $\beta=0.5$
-->
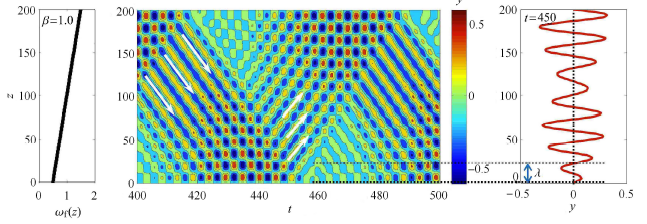
显示原图|下载原图ZIP|生成PPT图3-b不同剪切参数下圆柱体的位移响应变化云图以及$t =450$时振动位移随空间的瞬时变化特性 (b) $\beta=1.0$
-->Fig. 3-bEvolution of cylinder vibration displacement versus time and span and the instantaneous displacement along the span at $t =450$ for different shear parameters (b) $\beta=1.0$
-->
显示原图|下载原图ZIP|生成PPT图3-c不同剪切参数下圆柱体的位移响应变化云图以及$t =450$时振动位移随空间的瞬时变化特性 (c) $\beta=1.5$
-->Fig. 3-cEvolution of cylinder vibration displacement versus time and span and the instantaneous displacement along the span at $t =450$ for different shear parameters(c) $\beta=1.5$
-->
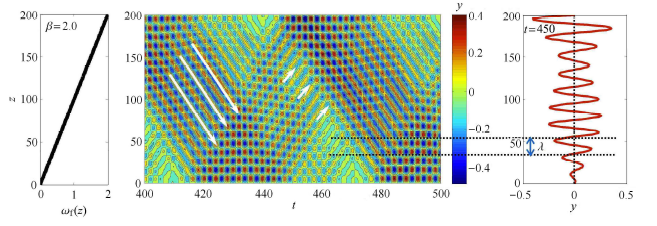
显示原图|下载原图ZIP|生成PPT图3-d不同剪切参数下圆柱体的位移响应变化云图以及$t =450$时振动位移随空间的瞬时变化特性 (d) $\beta=2.0$
-->Fig. 3-dEvolution of cylinder vibration displacement versus time and span and the instantaneous displacement along the span at $t =450$ for different shear parameters(d) $\beta=2.0$
-->
行波按照其传播方向可分为两种：从高流速区向低流速区进行传播(即沿$z$ 轴负方向) 以及从低流速区向高流速区进行传播(即沿$z$ 轴正方向). 当 $\beta =0.5$ 时,从高流速区向低流速区传播时行波占主导的区间与从低流速区向高流速区传播时行波占主导的区间大小相当. 但随着剪切参数 $\beta $ 的增大,从高流速区向低流速区传播时行波占主导的区间在逐渐增大,而从低流速区向高流速区传播时行波占主导的区间在逐渐减小. 当 $\beta $ 增大到2.0 时,从高流速区向低流速区传播时行波占主导的区间要明显大于从低流速区向高流速区传播时行波占主导的区间. 换句话说：随着剪切系数 $\beta $ 的增大,行波更倾向于从高流速区向低流速区进行传播.
为了确定圆柱体涡激振动位移响应的振动波长,图3 进一步给出了不同剪切参数 $\beta $ 下某一时刻($t =450$) 振动位移随空间变化的瞬时特性. 当 $\beta $ 为0.5, 1.0, 1.5 以及2.0 时,圆柱体轴线长度($L/D =200$) 上分别存在7, 7.5, 9 以及10 个波长 $\lambda $,得到对应的波长 $\lambda $ 分别为：28.6, 26.7, 22.2 以及20.0. 可以看出：圆柱体涡激振动响应的振动波长随着剪切参数 $\beta $ 的增大而呈下降趋势.
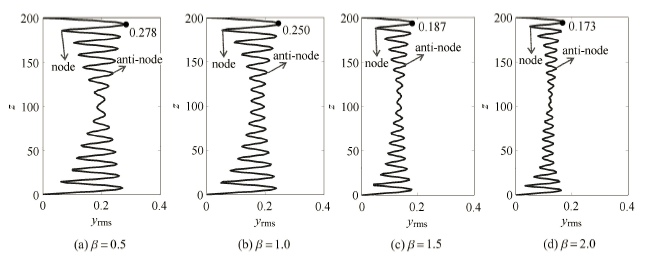
图4给出了不同剪切参数$\beta $下圆柱体振动位移的均方根值沿$z$变化的特性. 由图4 的圆柱体涡激振动位移均方根值同样可以看 出图3 中的圆柱体涡激振动位移响应特性,即结构振动位移响应由驻波和行波共同组成. 由图4 可以看出：圆柱体振动均方根位移沿$z$方向分布着若干个波谷(位移响应极小值) 以及波峰(位移响应极大值),波谷以及波峰对 应的位置分别称之为节点(node) 以及腹点(anti-node). 沿整个轴线上节点以及腹点的存在说明：在整个圆柱体长度区间上涡激振动位移响应均具有驻波特性. 而每一个节点处的位移均方根值又都大于0 说明：在整个圆柱体长度区间内,涡激振动位移响应同样具备行波特性. 当$z$处于圆柱体两端附近处,节点与腹点处的位移响应存在明显的区别,说明此时圆柱体振动位移呈现出驻波占主导的特性;当$z$处于圆柱体中间段附近处,圆柱体节点以及腹点处的位移响应值非常接近,说明此时圆柱体振动位移呈现出行波占主导的特性.
显示原图|下载原图ZIP|生成PPT图4不同剪切参数下圆柱体振动位移均方根值
-->Fig. 4RMS values of cylinder vibration displacement along the span for different shear parameters
-->
此外,由图4 可以得到涡激振动位移响应中行波占主导的区间随着剪切参数 $\beta $的增大而逐渐变大,且圆柱体位移均方根值沿圆 柱体中点处呈对称分布. 当 $\beta $ 为0.5, 1.0, 1.5 以及2.0 时,圆柱体位移均方根最大值分别为0.278, 0.250,0.187 以及0.173,可以看出结构位移均方根值最大值随着剪切参数 $\beta $ 的增大呈下降趋势. 图5 给出了不同剪切参数$\beta $ 下圆柱体振动位移最大值沿$z$ 方向的变化特性. 由图5 可以看出圆柱体振动位移最大值沿圆柱体中点处不呈对称分布：高流速区的圆柱体位移响应最大值要略大于低流速区的圆柱体位移响应最大值. 当 $\beta $ 为0.5, 1.0, 1.5 以及2.0 时,整个$z$ 方向的圆柱体振动位移最大值分别为0.771, 0.688, 0.527 以及0.491,得到圆柱体振动位移最大值同样随着剪切参数 $\beta $ 的增大而逐渐减小.
3.2 圆柱体涡激振动频率响应分析
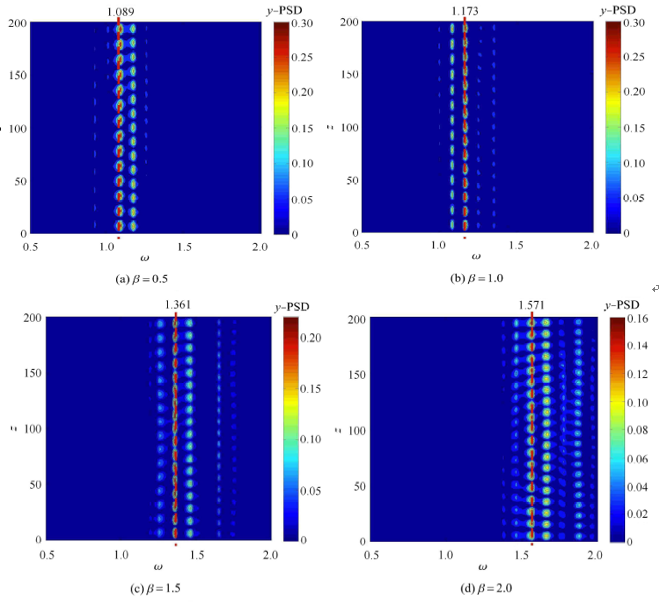
图6给出了不同剪切参数 $\beta $ 下圆柱体沿$z$ 方向的振动位移频率响应特性. 由图6 可以看出剪切来流下的圆柱体涡激振动位移频 率响应呈现明显的多频分布特性：即位移响应存在若干个峰值频率. 当$\beta $ 为0.5, 1.0, 1.5 以及2.0 时,位移响应分别存在5, 5, 6 以及7 个峰值频率,峰值频率的个数随着剪切参数$\beta $的增大逐渐变大. 当$\beta $为0.5, 1.0, 1.5 以及2.0 时,圆柱体振动位移响应主导频率(图中红色虚线) 分别为1.089, 1.173, 1.361 以及1.571,即：位移响应主导频率随着剪切参数$\beta $的增大呈上升趋势. 随着剪切系数$\beta $的增大,响应频率分布带宽同样逐渐增大。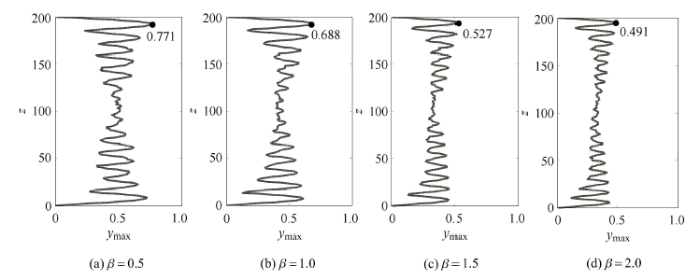
显示原图|下载原图ZIP|生成PPT图5不同剪切参数下圆柱体振动位移最大值
-->Fig. 5Maximum values of cylinder vibration displacement along the span for different shear parameters
-->
显示原图|下载原图ZIP|生成PPT图6不同剪切参数下圆柱体振动位移谱分析
-->Fig. 6Temporal spectral analysis of cylinder vibration displacement for different shear parameters
-->
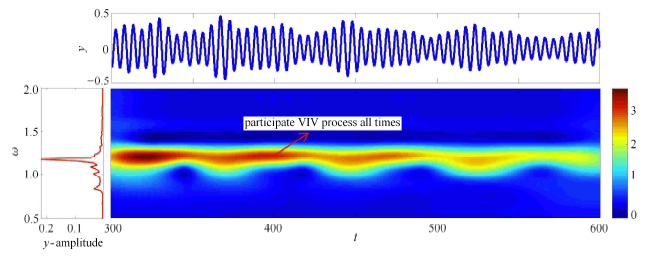
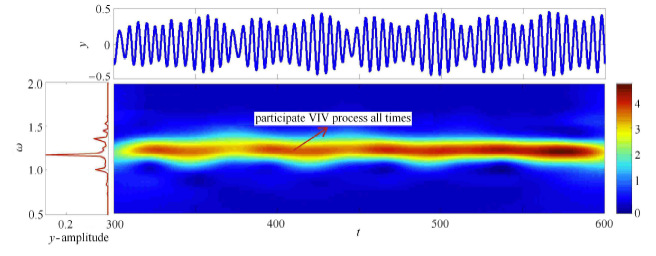
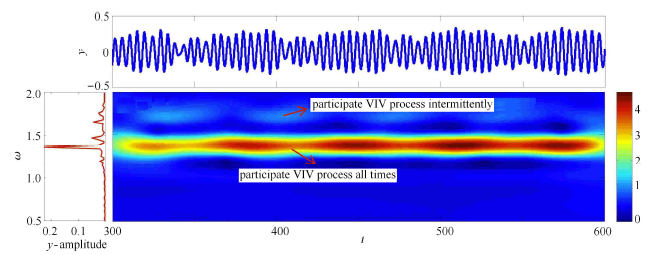
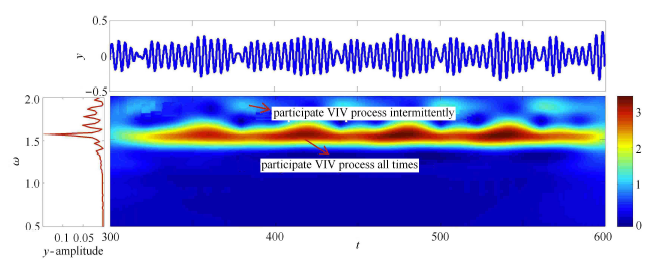
为了进一步研究圆柱体涡激振动频率响应随时间变化的特性,图7 进一步给出了不同剪切参数$\beta $ 下圆柱体中间点处($z=100$) 涡激振动响应频率随时间变化的特性. 由图7 可以看出：随着剪切系数$\beta$ 的增大,圆柱体的涡激振动响应主导频率呈上升趋势. 当剪切系数 $\beta $ 较小时($\beta=0.5$ 和1.0),涡激振动响应频率能量较为集中,且响应频率会全程参加涡激振动响应过程. 但随着剪切系数 $\beta $的增大,当 $\beta $为1.5 以及2.0 时,涡激振动响应频率能量变得更为发散,此时主导频率仍然会全程参加涡激振动响应,但较大的非主导峰值频率则在时历上断断续续地分布,意味着较大的非主导峰值频率不会全程而是间歇性地参加涡激振动.
3.3 综合讨论
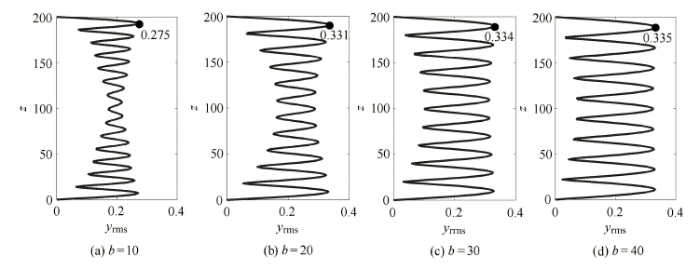
在4.1 和4.2 部分依次对不同剪切参数$\beta $下柔性圆柱体涡激振动的位移响应以及频率响应特性进行了分析,这两部分内容均属 于流场的参数敏感性分析,而对于圆柱体的涡激振动响应问题来说,结构的参数敏感性分析同样非常重要,这里针对结构的一个重要参数(弯曲刚度) 的参数敏感性进行了分析. 分析过程中,流剖面剪切参数$\beta=0.5$,$C_{\rm D} =1.2$,$C_{\rm L0} =0.3$,$St =0.20$, $\mu =6$,$c =4.55$,$L/D =200$,对4 种不同无量纲弯曲刚度$b$ (10, 20, 30 以及40) 下两端铰接的细长圆柱体涡激振动响应特性展开了研究. 计算时空间步长$\Delta z$ 以及时间步长$\Delta t$ 分别取为：$\Delta z =0.1$;$\Delta t =0.01$,计算总时间$t_{\rm total}$ 取为600 个无量纲时间.图8给出了不同无量纲弯曲刚度$b$ 下圆柱体振动位移均方根值沿$z$ 变化的特性. 当$b$ 为10, 20, 30 以及40 时,圆柱体位移均方根值最 大值分别为0.275, 0.331, 0.334 以及0.335,可以看出结构位移均方根值最大值随着无量纲弯曲刚度$b$ 的增大呈上升趋势. 当无量纲弯曲刚度$b$ 较小时( 10 和20),在圆柱体两端附近,驻波占主导;而在圆柱体中间段附近,行波占主导. 随着无量纲弯曲刚度$b$ 的增大,行波占主导的区间在逐渐减小,与此同时驻波占主导的区间在逐渐增大,当无量纲弯曲刚度增大到30 以及40 时,行波占主导的区间已完全消失,此时在整个圆柱体长度区间上均为驻波占主导. 图8 给出了不同无量纲弯曲刚度$b$下圆柱体振动位移均方根值沿$z$变化的特性. 当$b$为10, 20, 30 以及40 时,圆柱体位移均方根值最 大值分别为0.275, 0.331, 0.334 以及0.335,可以看出结构位移均方根值最大值随着无量纲弯曲刚度$b$的增大呈上升趋势. 当无量纲弯曲刚度$b$较小时( 10 和20),在圆柱体两端附近,驻波占主导;而在圆柱体中间段附近,行波占主导. 随着无量纲弯曲刚度$b$的增大,行波占主导的区间在逐渐减小,与此同时驻波占主导的区间在逐渐增大,当无量纲弯曲刚度 增大到30 以及40 时,行波占主导的区间已完全消失,此时在整个圆柱体长度区间上均为驻波占主导.
显示原图|下载原图ZIP|生成PPT图7-a不同剪切参数下中间点处涡激振动位移响应频率时间特性分析 (a) $\beta=0.5$
-->Fig. 7-aTime-frequency analysis of VIV displacement response at mid-point for different shear parameters (a) $\beta=0.5$
-->
显示原图|下载原图ZIP|生成PPT图7-b不同剪切参数下中间点处涡激振动位移响应频率时间特性分析 (b) $\beta=1.0$
-->Fig. 7-bTime-frequency analysis of VIV displacement response at mid-point for different shear parameters (b) $\beta=1.0$
-->
显示原图|下载原图ZIP|生成PPT图7-c不同剪切参数下中间点处涡激振动位移响应频率时间特性分析 (c) $\beta=1.5$
-->Fig. 7-cTime-frequency analysis of VIV displacement response at mid-point for different shear parameters (c) $\beta=1.5$
-->
显示原图|下载原图ZIP|生成PPT图7-d不同剪切参数下中间点处涡激振动位移响应频率时间特性分析 (d) $\beta=2.0$
-->Fig. 7-dTime-frequency analysis of VIV displacement response at mid-point for different shear parameters (d) $\beta=2.0$
-->
显示原图|下载原图ZIP|生成PPT图8不同无量纲弯曲刚度下圆柱体振动位移均方根值
-->Fig. 8RMS values of cylinder vibration displacement along the span for different dimensionless bending stiffness
-->
由前面部分的分析可以看出：尾流振子模型可以很好地模拟出线性剪切来流下两端铰接的细长柔性圆柱体的涡激振动响应特性. 这里对尾流振子模型的优缺点进行简要阐述. 与CFD 方法和实验方法相比,尾流振子模型最大的优点在于计算时间短、消耗成本低,本文所有工况的计算时间均在一个小时内完成. 因此尾流振子模型更适用于计算实际海洋工程中细长柔性圆柱体涡激振动响应的多工况问题. 但是鉴于模型自身的简化性,尾流振子模型同样存在不足之处,其中最大的不足便是计算精度问题. 由于尾流振子模型是基于试验参数的一种半经验模型方法,其计算精度受到很多因素制约,如：尾部非线性振子的模拟、水动力系数的选 取以及经验参数($A$ 和$\varepsilon $)的选取等都会影响到最终的计算结果. 如何提高尾流振子模型的计算精度使其更好地适用于实际海洋工程中?这是一个非常具有实际工程价值的问题,也会在后续的工作中对 该问题展开更为深入地研究.
4 结论
本文先是针对线性剪切来流下两端铰接的细长柔性圆柱体涡激振动响应问题建立了互为耦合的结构振子以及尾流振子模型,随后使用具备二阶精度的有限差分格式对耦合方程先离散后迭代进行求解,并系统地对不同剪切参数下圆柱体的涡激振动响应特性进行了研究,通过研究可得到如下结论：(1) 圆柱体的涡激振动位移响应同时具备驻波以及行波特性. 当无量纲弯曲刚度较小时,在圆柱体两端附近,结构位移响应为驻波特性占主导;而在圆柱体中间段附近,结构位移响应则为行波特性占主导. 当无量纲弯曲刚度较大时,在圆柱体整个长度上均为驻波占主导.
(2) 随着剪切参数的增大,圆柱体涡激振动响应的振动波长以及振动位移响应均逐渐变小;而圆柱体涡激振动响应主导频率以及频率分布带宽均逐渐增大.
(3) 随着剪切参数的增大,圆柱体的涡激振动响应频率能量分布逐渐发散但主导频率会全程参加涡激振动响应. 当剪切参数较大时,具有较大值的非主导峰值频率不会全程而是间歇性地参加涡激振动响应过程.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | |
| [2] | [Master Thesis]. |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . . |
| [13] | . . |
| [14] | . . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
