Chuanxin Zhu ^1,
, Jia Wang ^2,
, Li Jiang ^1,
, Pu Zheng ^1,
, 1.Institute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Sichuan 621900, China
2.Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
Received Date:2019-10-10
Accepted Date:2019-12-14
Available Online:2020-03-01
Abstract:The cross-section data of the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction have been measured with the neutron energies of 12 MeV to 19.8 MeV using the activation technique and the relative method. The ⁸⁵Rb samples were irradiated on the surface of a two-ring orientation assembly with neutrons produced from the ³H(d, n)⁴He reaction at the 5SDH-2 1.7-MV Tandem accelerator in China. Theoretical model calculations were performed with the TALYS-1.9 code. The present data were compared with previously obtained experimental data and the available evaluated data.

HTML

--> --> -->

The ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section constitutes important data in nuclear engineering designs, applications, and researches in the reaction mechanism. Several measurements for this (n, 2n) reaction cross-section have been carried out by numerous nuclear institutes in the past. Prestwood and Bayhurst [1] measured the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section for neutron energies from 12.2 MeV to 19.8 MeV, based on measuring the $ {\beta} $ particle with the ²⁷Al(n, $ {\alpha} $)²⁴Na reaction as the neutron flux monitor. The experimental uncertainties were between 5% and 10%. Bormann [2], Ghorai [3], Erlandsson [4], Yuan Xialin [5], Konno [6] measured the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section for neutron energies around 12.6 to 19.6 MeV by measuring $ {\gamma} $-rays with the ²⁷Al(n, $ {\alpha} $)²⁴Na reaction as the neutron flux monitor. The experimental uncertainties were between 3% and 13%. Our previous measurement [7] of the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section data for neutron energies of 13.4 MeV to 14.8 MeV were measured using the same method, where the experimental uncertainties were about 4%.
There is above 40% disagreement between measuring the $ {\beta} $ particle and $ {\gamma} $-rays, and the tendency of measurements by two methods is quite different, especially in the high energy region. In contrast, there is above 15% disagreement in the results by the same method for $ {\gamma} $-ray measurement. Therefore, there are obvious discrepancies in the experimental data in the literature. The discrepancies are also shown in the data from the evaluated nuclear reaction data libraries. To date, measurements are thus needed to clarify the discrepancies between the existing and guide evaluations.
The precision measurement of the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section is a difficult task because of the long half-life of the products, the low neutron flux, variety of neutron fluxes in the sample position, and the effect of neutron scattering. A two-ring orientation assembly had been designed and successfully used to measure the (n, 2n) reaction cross-section data for several nuclei [7]. To obtain the precision sample positions to reduce the uncertainty of neutron energies by the sample positions, two improvements were achieved in the present work. First, the two-ring orientation assembly was fixed with the target tube using a stainless steel sleeve to avoid the moving of the two-ring orientation assembly during irradiation. Second, two center orientation poles were added in the two-ring orientation assembly to obtain a precision angle of each sample.
The neutron flux was monitored by the BF$ _3 $ detector. The radioactivity of products was measured using a Ge detector (GEM60P type) with high resolution and efficiency (relative efficiency of 60%). The cross-section measurements were all carried out relative to the ⁹³Nb(n, 2n)$ {^{92{\rm m}}}{\rm{Nb}}$ reaction cross-section [8]. The method of the activation technique is the same as Refs. [9, 10]. The cross-section data for the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction were measured within the neutron energies of 12 MeV to 19.8 MeV and compared with the previous experimental data and available evaluated data. Model calculations were performed with the TALYS-1.9 code.

2

-->

2.1.Irradiation field

The 12–20 MeV neutrons were produced by the D-T reaction on the target assembly at 5SDH-2 1.7MV Tandem accelerator in the China Institute of Atomic Energy. The incident deuteron beam energy and intensity were 3.276 MeV and about 7 μA, respectively. To reduce the scattered neutrons caused by target assembly, the neutron source target is a titanium-tritide (TiT) foil with 12-mm diameter, and mounted on the end of a tube, which is 21 mm in diameter, 1-mm wall thickness, and 50-cm length. The target is cooled by an air-cooled device. The TiT target is 3 m from the ground and 5 m from the wall and ceiling. The arrangement of the TiT target and the samples for the reaction cross-section measurement are shown in Fig. 1 and Fig. 2. Each sample is 5 cm from the center of the TiT target.
Figure1. Sample position.

Figure2. (color online) Photograph of TiT target and sample arrangement.

Each sample was sandwiched between two niobium foils with a thickness of 0.5 mm. The same diameter was machined for the RbCl sample and niobium foils, such that the neutron flux of the RbCl sample position was equal to that of niobium foils. The samples are placed at the angles of 0°, 29°, 48°, 64°, 79°, 94°, 110°, 129°, and 161° with respect to the deuteron beam direction and TiT target center. The neutron energy of angles ranging from 0° to 161° were: 19.8, 19.2, 18.2, 17.2, 16.1, 15.0, 14.0, 13.0, and 12.0 MeV, such that simultaneous irradiations could be fulfilled in the neutron range of 12–19.8 MeV.
After deducting the beam energy loss in the half-target, the energy was calculated based on the high voltage of the accelerator and the thickness of the TiT target. The neutron energy and energy resolution of the 0° direction were calculated by the TARGET program based on the geometry parameter of the target tube in this experiment. The neutron energy-angle distribution from the 0° to 180° direction with 5-cm distance from the titanium-tritide target to sample was calculated by the NEUYIE program in the DROSG-200 program package. The calculated results of the neutron energy-angle distribution from the 0° to 180° direction are shown in Fig. 3.
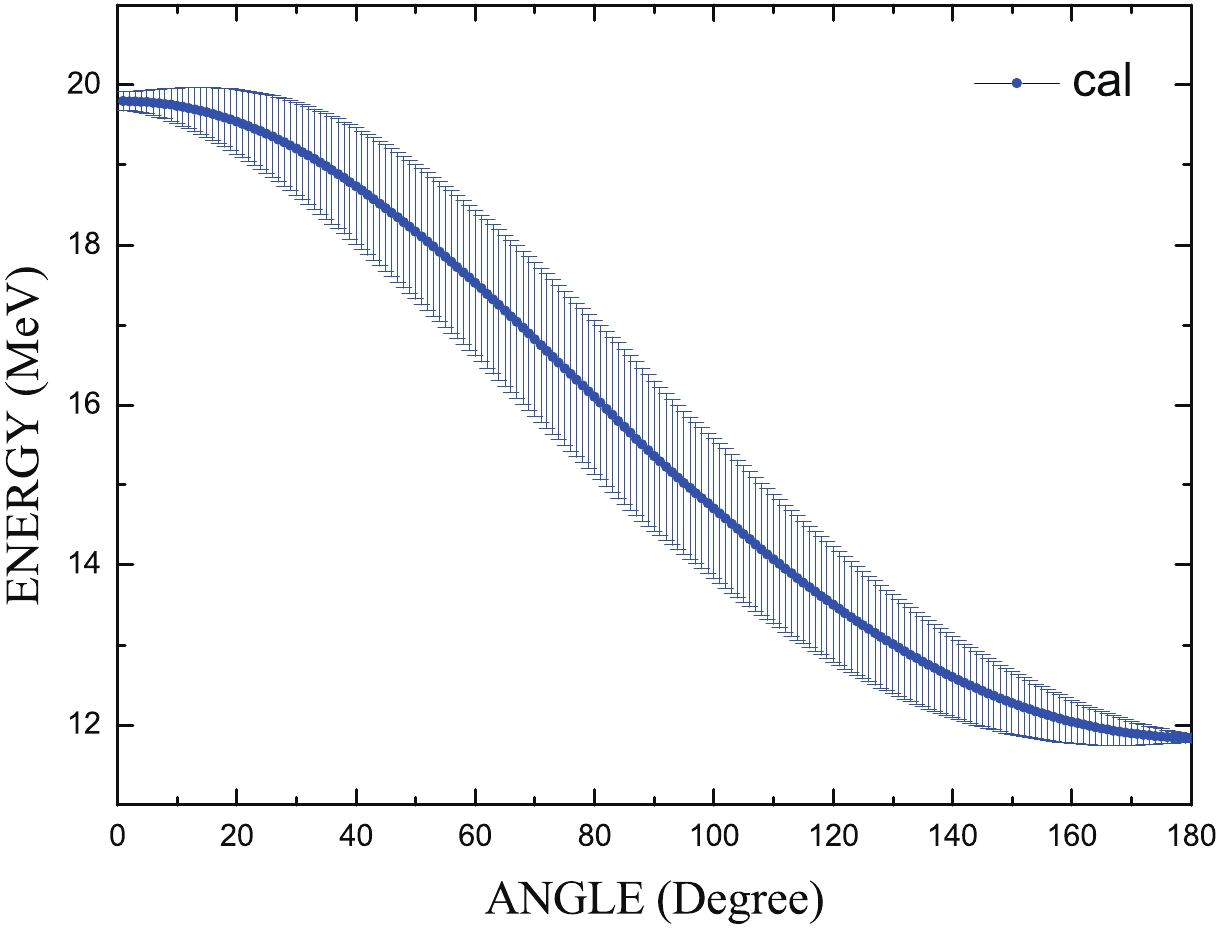Figure3. (color online) Neutron energy-angle distribution.

The neutron flux was obtained by monitoring neutrons with the BF₃ detector located in the direction of 0° and at about 5-m distance. The irradiation time was about 107 h. The irradiation history can be divided into any number of separate parts, each with a relative neutron flux given by the counts. The total neutron flux, as measured by the ⁹³Nb(n, 2n)$ {^{92{\rm m}}}{\rm{Nb}}$ monitor reaction, is apportioned into each irradiation step.
2 -->

2.2.Sample preparation

Samples were procured from Beijing General Research Institute for Nonferrous Metals. The niobium purity was 99.999%. The RbCl sample with thickness of 1 mm was made by pressing RbCl powder with purity of 99.5%. Table 1 lists the purity, isotopic composition, thickness, and diameter for each sample [11].

sample	purity (%)	isotopic composition (%)	thickness /mm	diameter /mm
Niobium	99.999	100 (93Nb)	0.5	20
Rubidium	99.50	72.17 (85RbCl)	1.0	20
		27.83 (87RbCl)

Table1.Sample characteristics.

2 -->

2.3.Radioactivity measurements

After irradiation, a high resolution Ge detector (type: ORTEC GEM60P) with high efficiency (relative efficiency of 60%) was used to measure the radioactivity of the sample. The details of these measurements are given in Table 2 [12]. The efficiency calibration of Ge has been done carefully with a set of standard $ {\gamma} $-ray sources including ¹⁵²Eu, ²²⁶Ra, ¹³³Ba, and ⁶⁰Co procured by England Aeatechnology. The detector efficiency for 1332 keV is 0.00482. Corrections were made for self-absorption in the sample.

nucleus	half-life /d	$E_{\gamma}$ /keV	$I_{\gamma}$ (%)
${^{92m}}{\rm{Nb}}$	10.15	934.44	0.9915
84Rb	32.82	881.60	0.689

Table2.Details of radioactivity constants used in analysis of experimental data.

2

-->

3.1.Reaction cross-section calculation

The measured cross-section is given by:

$ \begin{split} \sigma_{\rm X} = & \frac{\lambda_{\rm X}N_{\rm X}A_{\rm X}}{\lambda_{\rm Nb}N_{\rm Nb}A_{\rm Nb}}\frac{W_{\rm Nb}P_{\rm Nb}}{W_{\rm X}P_{\rm X}} \frac{\eta_{\rm Nb}f_{s{\rm Nb}}f_{\rm Nb}\varepsilon_{\rm Nb}}{\eta_{\rm X}f_{s{\rm X}}f_{\rm X}\varepsilon_{\rm X}}\\ &\times kF_{\phi}\frac{1-{\rm e}^{-\lambda_{\rm Nb}t_{m{\rm Nb}}}}{1-{\rm e}^{-\lambda_{\rm X}t_{m{\rm X}}}}\sigma_{\rm Nb}, \end{split} $

(1)

where the subscripts of X and Nb indicate the RbCl sample and niobium nucleus, respectively. $ \sigma $ is the cross-section, $ \lambda $ is the decay constant of the activity, N is $ {\gamma} $-ray peak count, A is atomic weight of the target nucleus, W is the weight of the sample, P is the purity of the sample, $ \eta $ is abundance of the target nucleus, $ f_{s} $ is $ {\gamma} $-ray self-absorption correction factor, f is the branch ratio of $ {\gamma} $-ray, $ \varepsilon $ is the Ge detector $ {\gamma} $-ray efficiency, k is difference correction factor of the point source and plane source, $ F_{\phi} $ is correction factor for the neutron flux fluctuation during the irradiation, and $ t_{m} $ is the duration of $ {\gamma} $-ray counting.
It is assumed that the induced radioactivities are uniformly distributed in a sample. Since the distance between the sample and the detector is about 8.2 cm, and the thickness of the sample is at most 0.5–1.0 mm, the one-dimensional treatment is reasonably accepted. The $ {\gamma} $-ray self-absorption correction factor $ f_{s} $ is given by

$ f_{s} = \frac{1-{\rm e}^{-{\mu}t}}{{\mu}t}, $

(2)

where t is the sample thickness (mm), and $ \mu $ is the absorption coefficient (mm^?1), $ F_{\phi} $ is given by

$ F_{\phi} = \frac{\displaystyle\sum\limits_{i = 1}^l N_{{\phi}i}{(1-{\rm e}^{-\lambda_{\rm Nb}T_{i}})}{\rm e}^{-{\lambda_{\rm Nb}}t_{i}}} {\displaystyle\sum\limits_{i = 1}^l N_{{\phi}i}{(1-{\rm e}^{-\lambda_{\rm X}T_{i}})}{\rm e}^{-{\lambda_{\rm X}}t_{i}}}, $

(3)

where $ N_{{\phi}i} $ is the relative neutron number within the ith irradiation time-interval, $ T_{i} $ is the time of the ith time-interval, $ t_{i} $ is the cooling time of the ith irradiation, l is total number of time bins.
The used standard cross-section data of ⁹³Nb(n, 2n)$ {^{92{\rm m}}}{\rm{Nb}}$ reaction were conducted from reference [8] by the interpolation method.
2 -->

3.2.Uncertainty estimation

The main uncertainty sources were due to the $ {\gamma} $-ray detector efficiency, counting statistics, and standard cross-section. The efficiency uncertainty for $ {\gamma} $-ray of energy was assigned to be 3.0%. The statistical uncertainty of $ {\gamma} $-ray depended mainly on activity levels and $ {\gamma} $-ray emission probabilities, which is about 1.0%–2.0%. The uncertainty of the standard reaction cross-section ⁹³Nb(n, 2n)$ {^{92{\rm m}}}{\rm{Nb}}$ reaction is about 0.7%–1.5% for the entire energy range from 12.0 to 20.0 MeV. The self-absorption correction factor was calculated, and its uncertainty is about 1%. The data for the half-life and $ {\gamma} $-ray emission probability quoted in Table 2 were taken from the internet nuclear data [12]. The detector efficiency of the point source is different from the column source as a sample. In present work, we made a photon transport model including Ge detector, point source, and column source by their real sizes and materials with a sample-detector distance of 8.2 cm. The calculation of detector efficiency was performed with the MCNP code to correct the difference.

The theoretical calculations of the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section were performed with the TALYS-1.9 code [13]. TALYS is a nuclear reaction program, which can be used to simulate nuclear reactions induced by neutron, photon, proton, deuteron, triton, ³He and alpha-particle, in the 1 keV–200 MeV energy range and for target nuclide of mass 12 and heavier. In the TALYS-1.9 code, all optical models and models of direct reactions calculations are performed by the ECIS06 code [14]. All open reaction channels can be calculated consistently in the fast energy region using the nuclear reaction models for direct, pre-equilibrium, and compound mechanisms.
The cross-section values were calculated using the default nuclear reaction models and parameters as well as various models for the level density. For the optical model potential, the local parameterization of Koning and Delaroche [15] was used. Since ⁸⁵Rb is an odd-A nucleus, to take into account direct inelastic scattering, the distorted wave born approximation and the weak coupling model were implemented. Meanwhile, the two-component exciton model for pre-equilibrium processes [16] and the Hauser-Feshebach theory with the Moldauer model for width fluctuation corrections [17, 18] for compound processes were performed. Six different models of the level density were tested. These are the constant temperature and the Fermi gas model [19], the back-shifted Fermi gas model [20], the generalized superfluid model [21, 22], and the other three microscopic models [23-25]. In these level density models, the optimal global and local parameters are based on the mean resonance spacings $ D_{0} $ and discrete levels [26]. Usually, $ D_{0} $ is obtained from the available experimental set of s-wave resonances.
The results of calculations are compared with the present cross-section data in Fig. 4. The calculated ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section values using different level density models have significant differences between each other, and none of these can reproduce the present data within experimental uncertainties in the entire energy region. At 12 MeV, the microscopic model based on temperature-dependent Hartree-Fock-Bogolyubov calculations using the Gogny force [25] efficiently describes the cross-section. At 13–16 MeV, the calculated data from the back-shifted Fermi gas model and the microscopic model based on Hartree-Fock calculations using the Skyrme force [23] are in good agreement with the present data. At 17–20 MeV, the calculated data from the constant temperature and Fermi gas model are consistent within the experimental uncertainty with the present data. The cross-section data are overestimated below 15 MeV and underestimated above 15 MeV by the microscopic model based on the combinatorial model [24].
Figure4. (color online) Comparison of theoretically calculated ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section with present data (six level density models).

From the calculations, it is evident that the (n, 2n) reaction is in competition with all other open reaction channels, as shown in Fig. 5. For ⁸⁵Rb, the inelastic scattering is the main competitive channel at the energy range from the (n, 2n) reaction threshold up to 20 MeV. Therefore, the calculated ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-section values are related to the calculated values of total, elastic scattering, and inelastic scattering cross-sections. The models and parameters of the optical model and level density are crucial for a reliable theoretical calculation. Further, numbers of the discrete level, deformation parameters, and pre-equilibrium strength are important. Since there are not sufficient experimental data for ⁸⁵Rb, in particular the experimental cross-section data of total, elastic, and inelastic and experimental angular distributions of scattering, as well as the experimental $ D_{0} $ of ⁸⁵Rb and ⁸⁴Rb, it is difficult to optimize the nuclear structure parameters, which are the primordial components for a simulation of nuclear reactions, to obtain accurate calculated cross-sections of neutron induced reactions on ⁸⁵Rb.
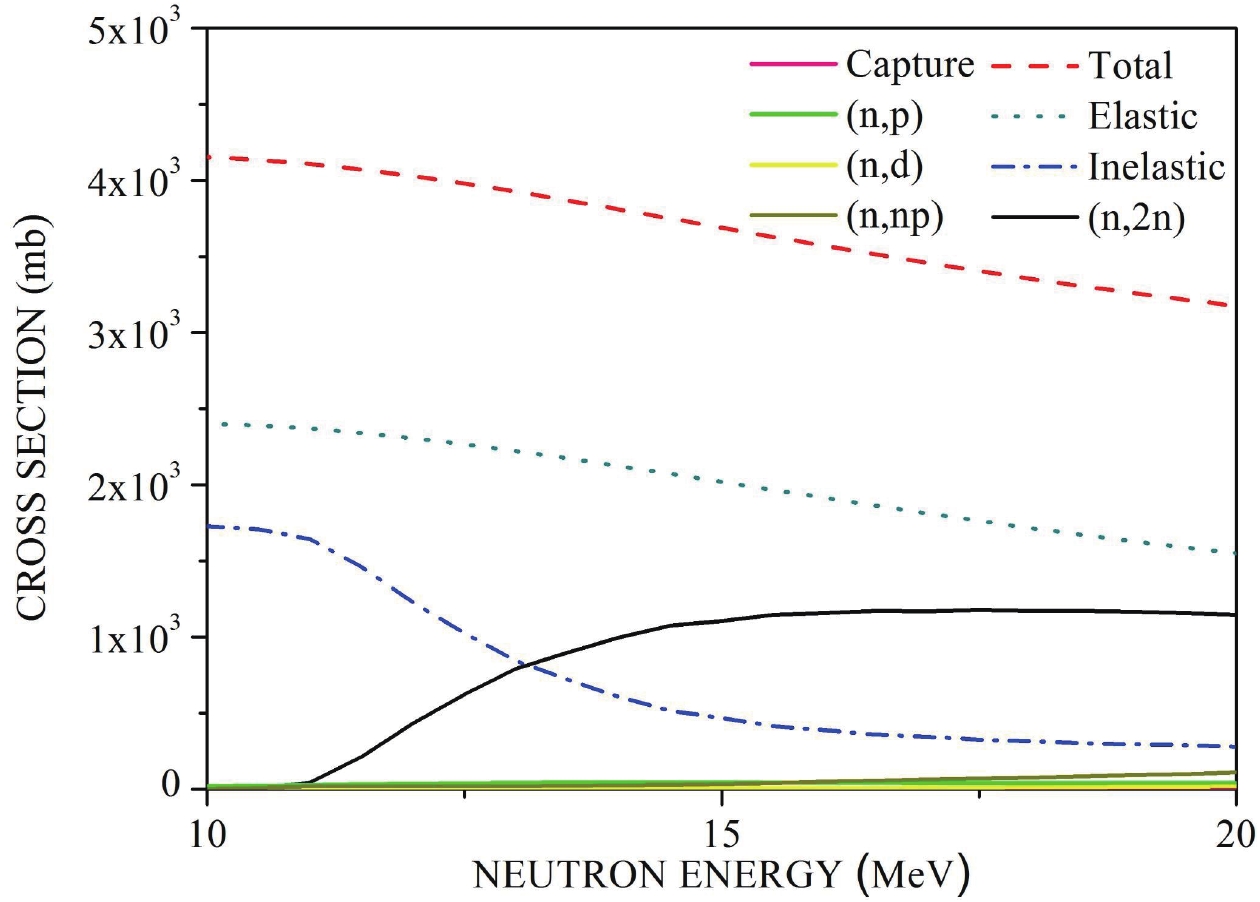Figure5. (color online) Theoretically calculated values of open channels for neutron induced ⁸⁵Rb reaction.

The values of the cross-sections measured in the present study are given in Table 3. Figure 6 shows the experimental ⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-sections from this work along with the existing measurements and the available evaluated data from ENDF/B-VIII.0 [27], JENDL4.0 [28], and CENDL3.1 [29].

energy /MeV	uncertainty /MeV	$\sigma$ /mb	uncertainty /mb
12.0	0.23	336	18
13.0	0.62	785	41
14.0	0.81	991	51
15.0	0.89	1126	58
16.1	0.96	1214	62
17.2	0.94	1279	66
18.2	0.83	1296	66
19.2	0.58	1295	65
19.8	0.12	1300	67

Table3.⁸⁵Rb(n, 2n)⁸⁴Rb reaction cross-sections from this work.

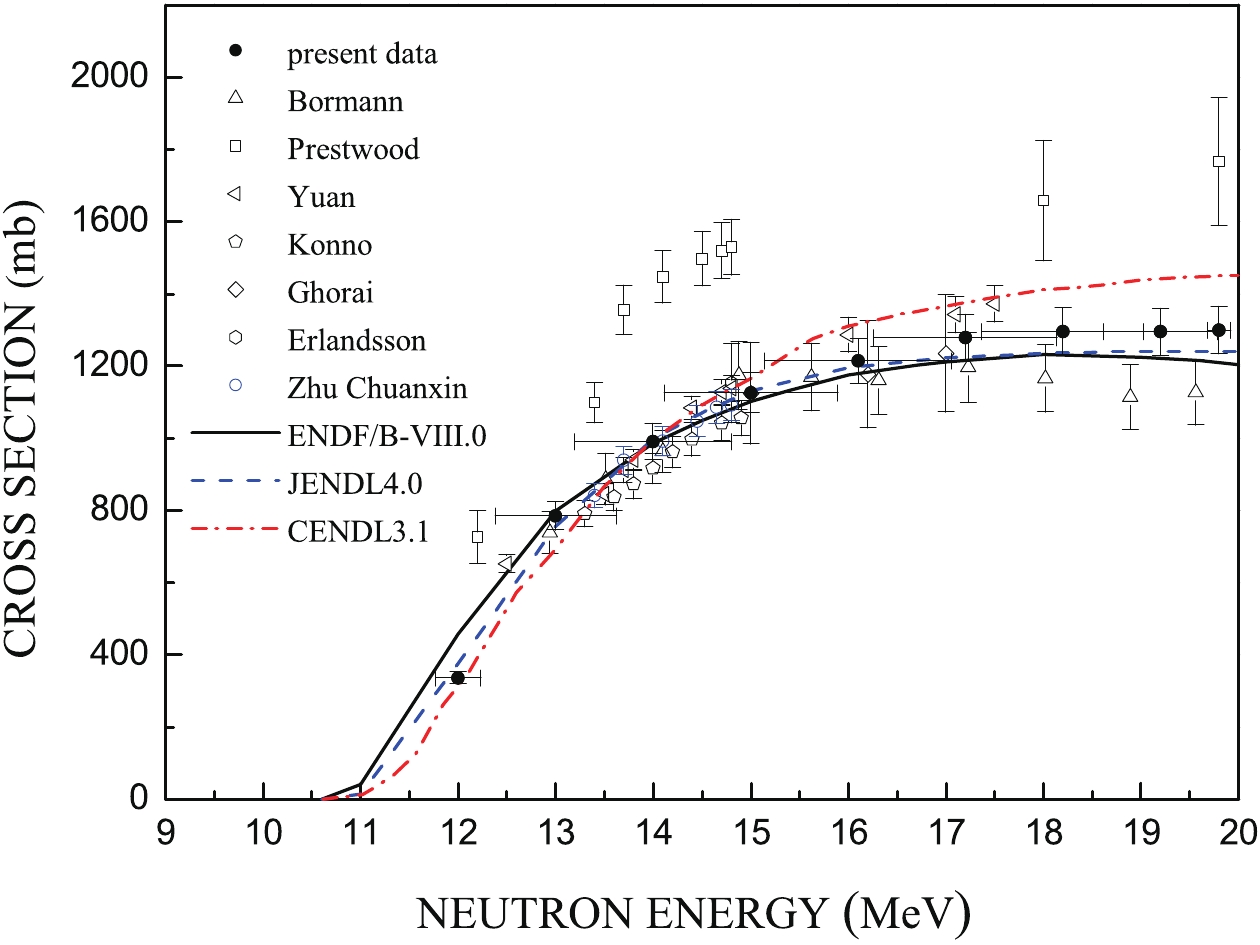Figure6. (color online) Comparison of cross-section for ⁸⁵Rb(n, 2n)⁸⁴Rb reaction.

The experimental data of Ref. [1] are about 40% higher than the ones reported in the present work at 12–20 MeV. The experimental data of Refs. [3, 4, 6, 7] are in agreement with the present work. The experimental data of Ref. [5] are about 3%–6% higher than the ones reported in the present work at 15–17 MeV. The experimental data of Ref. [2] are in good agreement with the present work at 13–15 MeV, and they are about 7%–13% lower than the ones reported in the present work at 15–20 MeV.
The evaluated data from ENDF/B-VIII.0 overestimate the present data at 12 MeV by about 36% and underestimate the present data at 17–20 MeV by 4%–8%. Good agreements are observed between the ENDF/B-VIII.0 data and the present data at 13–16 MeV. The evaluated data from JENDL4.0 are consistent within experimental uncertainty with the present data at 12–16 MeV and underestimate the present data at 17–20 MeV by 4%–8%. The evaluated data from CENDL3.1 are in good agreement with the present data only at 12 MeV and 14 MeV, underestimate the present data at 13 MeV by about 12% and overestimate the present data at 15–20 MeV by 3%–12%. Notably, the total cross-sections from the above mentioned evaluated data libraries are inconsistent. To obtain the evaluated (n, 2n) reaction cross-sections, the level density parameters had to be adjusted according to different experimental data in each evaluation.

Cross-sections for the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction were measured at the neutron energies from 12 MeV to 19.8 MeV based on the activation technique and relative to the ⁹³Nb(n, 2n)$ {^{92{\rm m}}}{\rm{Nb}}$ reaction. An improved two-ring orientation assembly was used to reduce both the effect of neutron scattering and the uncertainty of neutron energies by the sample positions. The theoretical calculation of reaction cross-sections were performed with the TALYS-1.9 code. In the case of ⁸⁵Rb, the inelastic scattering is the main competitive channel to the (n, 2n) reaction from the threshold up to 20 MeV, and the calculation is sensitive to the parameters of the optical model and level density. Therefore, the precise measurements for these values are necessary in the future. The measured results were compared with previously acquired experimental data and current evaluated data, and the discrepancies were revealed. Current evaluations were shown to have some problems, such as large discrepancies of 30%–40% between the present data and the evaluated data from ENDF/B-VIII.0 near the threshold for the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction. There are moreover different discrepancies in the other energy region. The present experimental data of the ⁸⁵Rb(n, 2n)⁸⁴Rb reaction can be used to improve the future evaluation, especially for the neutron energy region of 12.0–19.8 MeV.
The authors are indebted to the accelerator staff, Zhiqiang Wang, Hailong Luo, and Yina Liu for the deuteron beam at the 5SDH-2 1.7MeV Tandem accelerator.