Long Zhu
, Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082, China
Received Date:2019-08-02
Available Online:2019-12-01
Abstract:The multinucleon transfer (MNT) process has been proposed as a promising approach to produce neutron-rich superheavy nuclei (SHN). MNT reactions based on the radioactive targets ²⁴⁹Cf, ²⁵⁴Es, and ²⁵⁷Fm are investigated within the framework of the improved version of a dinuclear system (DNS-sysu) model. The MNT reaction ²³⁸U + ²³⁸U was studied extensively as a promising candidate for producing SHN. However, based on the calculated cross-sections, it was found that there is little possibility to produce SHN in the reaction ²³⁸U + ²³⁸U. In turn, the production of SHN in reactions with radioactive targets is likely.

HTML

--> --> -->

Early calculations predicted that the nucleus $ Z = 114 $ and $ N = 184 $ is the double magic nucleus and that it is at the center of the island of stability [1–4]. The production of neutron-rich superheavy nuclei (SHN) around the island of stability and superheavy elements with $ Z>118 $ is one of the most challenging topics in nuclear physics [5, 6].
Because of the limiting number of combinations for producing neutron-rich SHN in the stable beam-induced fusion reactions, many approaches were proposed in recent years to attain the island of stability. (i) Radioactive beam-induced fusion reactions could be candidates for producing neutron-rich SHN [7–9]. In present facilities, the intensities of radioactive beams are very low [10], which strongly suppresses the production rates. (ii) Stable beam-induced hot fusion reactions in charged particle evaporation channels are also investigated as a possible approach [11]. The disadvantage is that the Coulomb barrier prevents the charged particle evaporation in the cooling process. In our previous study [9], we compared the two approaches. It is shown that the production rates in the radioactive beam-induced reactions are comparable to those in stable beam-induced reactions in the charged particle evaporation channels. (iii) The multinucleon transfer (MNT) process is also suggested for the production of SHN [12–14]. To elucidate the mechanism of the MNT process and produce SHN, the reaction ²³⁸U + ²³⁸U has been investigated in many studies [15–21]. In Ref. [14], several low-energy collisions of heavy nuclei for producing SHN were studied based on multidimensional Langevin equations. The production of long-lived neutron-rich SHN in collisions of transuranium ions seems likely.
Recently, Wuenschel et al. attempted to produce SHN based on the MNT process [22]. Some promising results were presented. However, no direct evidence indicating that SHN are produced in the collisions of ²³⁸U + ²³²Th is shown. The reason is probably that the charge number of the target is not sufficiently high. The favorable combinations are always essential for producing unknown nuclei [23, 24]. In Ref. [25], one improved version of the DNS model (DNS-sysu) is introduced in detail. The DNS-sysu model can provide a reasonable description of MNT reactions for producing SHN. The reactions based on the ²³⁸U target are investigated in Ref. [25]. The production cross-sections decrease strongly with the increasing charge number of products, and the heavy projectiles are favorable for the production of trans-target nuclei. Based on the Langevin-type approach, several ²³⁸U induced MNT reactions, including with the target ²⁵⁴Es, are studied in Ref. [26]. It was shown that several actinide nuclei can be produced with the cross-sections larger than 1 μb.
The cross-sections of produced SHN in MNT reactions, based on targets with large charge number, are worth estimating. In this study, the MNT reactions based on radioactive targets ²⁴⁹Cf, ²⁵⁴Es, and ²⁵⁷Fm are investigated within the DNS-sysu model. The prospects of the radioactive projectile ²³⁹Pu for producing SHN are also investigated. In Section 2, the DNS-sysu model is described briefly. The results and discussion are presented in Section 3. Finally, I summarize the main results in Section 4.

In Ref. [25], detailed descriptions on the DNS-sysu model were presented. Here, the brief introductions regarding the model are presented. The master equation in the DNS-sysu model can be written as [25, 27].

$ \begin{split} \frac{{\rm d}P(Z_{1},N_{1},\beta_{2},t)}{{\rm d}t} =& \sum\limits_{Z_{1}^{'}}W_{Z_{1},N_{1},\beta_{2};Z_{1}^{'},N_{1},\beta_{2}}(t)[d_{Z_{1},N_{1},\beta_{2}}P(Z_{1}^{'},N_{1},\beta_{2},t)-d_{Z_{1}^{'},N_{1},\beta_{2}}P(Z_{1},N_{1},\beta_{2},t)]\\& +\sum\limits_{N_{1}^{'}}W_{Z_{1},N_{1},\beta_{2};Z_{1},N_{1}^{'},\beta_{2}}(t)[d_{Z_{1},N_{1},\beta_{2}}P(Z_{1},N_{1}^{'},\beta_{2},t) -d_{Z_{1},N_{1}^{'},\beta_{2}}P(Z_{1},N_{1},\beta_{2},t)]\\& +\sum\limits_{\beta_{2}^{'}}W_{Z_{1},N_{1},\beta_{2};Z_{1},N_{1},\beta_{2}^{'}}(t)[d_{Z_{1},N_{1},\beta_{2}}P(Z_{1},N_{1},\beta_{2}^{'},t) -d_{Z_{1},N_{1},\beta_{2}^{'}}P(Z_{1},N_{1},\beta_{2},t)].\end{split} $

(1)

Here, $ P(Z_{1},N_{1},\beta_{2},t) $ is the probability distribution function for the fragment 1 with proton number $ Z_{1} $ and neutron number $ N_{1} $ at time t. $ \beta_{2} $ is the dynamical deformation parameter of the DNS. $ W_{Z_{1},N_{1},\beta_{2};Z_{1}^{'},N_{1},\beta_{2}} $, $ W_{Z_{1},N_{1},\beta_{2};Z_{1},N_{1}^{'},\beta_{2}} $, and $ W_{Z_{1},N_{1},\beta_{2};Z_{1},N_{1},\beta_{2}^{'}} $ denote the mean transition probabilities from the channels ($ Z_{1} $, $ N_{1} $, $ \beta_{2} $) to ($ Z_{1}^{'} $, $ N_{1} $, $ \beta_{2} $), ($ Z_{1} $, $ N_{1} $, $ \beta_{2} $) to ($ Z_{1} $, $ N_{1}^{'} $, $ \beta_{2} $), and ($ Z_{1} $, $ N_{1} $, $ \beta_{2} $) to ($ Z_{1} $, $ N_{1} $, $ \beta_{2}^{'} $), respectively. $ d_{Z_{1},N_{1},\beta_{2}} $ is the microscopic dimension (the number of channels) corresponding to the macroscopic state ($ Z_{1} $, $ N_{1} $, $ \beta_{2} $) [28]. For the degrees of freedom of the charge and neutron number, the sum is taken over all possible proton and neutron numbers that fragment 1 may take, however only one nucleon transfer is considered in the model ($ Z_{1}^{'} = Z_{1}\pm1 $; $ N_{1}^{'} = N_{1}\pm1 $). For $ \beta_{2} $, we assume the range –$ 0.5 \sim 0.5 $. The evolution step length is 0.01. The transition probability is related to the local excitation energy [27, 29].
The PES is defined as

$ \begin{split}U(Z_{1}, N_{1}, \beta_{2}, R_{ \rm{cont}}) =& \Delta(Z_{1}, N_{1})+\Delta(Z_{2}, N_{2})\\ &+V_{ \rm{cont}}(Z_{1}, N_{1}, \beta_{2}, R_{ \rm{cont}})\\ &+\frac{1}{2}C_{1}(\beta_{2}^{1}-\beta_{2}^{ \rm{p}})^{2}+\frac{1}{2}C_{2}(\beta_{2}^{2}-\beta_{2}^{ \rm{t}})^{2}, \end{split}$

(2)

where $ \Delta(Z_{i}, N_{i}) $ ($ i = 1 $, 2) is mass excess of the fragment i. $ V_{ \rm{cont}}(Z_{1}, N_{1},\beta_{2}, R_{ \rm{cont}}) $ is the effective nucleus-nucleus interaction potential. The last two terms in the right side of the equation are deformation energies. The detailed description of each term is provided in Ref. [25] and the references therein.
The cross-sections of the primary products can be calculated as

$ \begin{split}{{\sigma _{{\rm{pr}}}}({Z_1},{N_1},{E_{{\rm{c}}.{\rm{m}}.}})} =& {\frac{{\pi {\hbar ^2}}}{{2\mu {E_{{\rm{c}}.{\rm{m}}.}}}}\sum\limits_{J = 0}^{{J_{{\rm{max}}}}} {(2J + 1)} {T_{{\rm{cap}}}}(J,{E_{{\rm{c}}.{\rm{m}}.}})}\\&{\times \sum\limits_{{\beta _2}} P ({Z_1},{N_1},{\beta _2},{E_{{\rm{c}}.{\rm{m}}.}}).}\end{split} $

(3)

Clear signatures were observed for the formation of DNS in heavy collision systems, such as ²³⁸U + ²³⁸U [30]. For heavy systems without a potential pocket, there is no capture. I consider that the DNS is formed when incident energy is higher than the interaction potential at the contact position. The contact positions are near the relatively flat parts of interaction potential curves [23]. From the diffusion point of view, the strength of diffusion strongly depends on the interaction time, which is reflected from the probability distribution function $ P(Z_{1},N_{1},\beta_{2},E_{ \rm{c.m.}}) $. Therefore, it is reasonable to consider $ T_{ \rm{cap}} $ as 1.
In the DNS-sysu model, with consideration of the deformation evolution, the excitation energy of primary products can be calculated with following equation [25].

$ \begin{split}E^{*}_{Z_{i},N_{i},J} =& \frac{Z_{i}+N_{i}}{A_{ \rm{tot}}}\\&\times\! \frac{\sum\limits_{\beta_{2}}[ P(Z_{i},N_{i},\beta_{2},J,t\!=\! \tau_{ \rm{int}}) E^{*}_{ \rm{DNS}}(Z_{i},N_{i},\beta_{2},J,t \!=\! \tau_{ \rm{int}})]}{\sum\limits_{\beta_{2}} P(Z_{i},N_{i},\beta_{2},t = \tau_{ \rm{int}})}. \end{split}$

(4)

Here, $ E^{*}_{\rm DNS} $ is the local excitation energy of the system [25].
The total kinetic energy loss (TKEL) for the configuration (Z₁, N₁, β₂) calculated in the DNS-sysu model as shown in Ref. [27] can be written as

${\rm{TKEL}}=E_{\rm{diss}}+V_{\rm{cont}}(Z_{\rm p}, N_{\rm p},R_{\rm{cont}})-V_{\rm{cont}}(Z_1,N_1,\beta_2,R_{\rm{cont}} ). $

(5)

Here, Z_p and N_p are the charge number and neutron number of the projectile, which denotes the configuration in the entrance channel. The detailed description of E_diss can be seen in Ref. [25].
In the cooling process, the statistical model is applied with the Monte Carlo method [25]. In the ith de-excitation step, the probability of the s event can be written as

$ P_{\rm s}(E^{*}_{i}) = \frac{\Gamma_{\rm s}(E^{*}_{i})}{\Gamma_{ \rm{tot}}(E^{*}_{i})}, $

(6)

where, $ {\rm s} = $ n, p, $ \alpha $, $ \gamma $, and fission. $ E_{i}^{*} $ is the excitation energy before ith decay step, which can be calculated from the equation $ E^{*}_{i+1} = E^{*}_{i}-B_{i} $. $ B_{i} $ is the separation energy of particle or energy assumed by the $ \gamma $ ray in the ith step. $ \Gamma_{\rm tot} = \Gamma_{\rm n}+\Gamma_{\rm f}+\Gamma_{\rm p}+\Gamma_{\alpha}+\Gamma_{\gamma} $. Detailed descriptions of the decay width in each decay channel are provided in Ref. [25] and the references therein. Here, I would like to emphasize that the parameters in the DNS-sysu model are usually fixed.

MNT reactions ²³⁸U + ²⁴⁸Cm and ²³⁸U + ²³⁸U for producing trans-target isotopes are compared in Fig. 1. From the available experimental data, the reaction ²³⁸U + ²⁴⁸Cm exhibits at least two orders of magnitude larger cross-sections than the ones ²³⁸U + ²³⁸U. The calculations in the DNS-sysu model are also presented. According to the experiments, the incident energies of $ E_{\rm c.m.} = 800 $ and 892 MeV are used in calculations for the reactions ²³⁸U + ²⁴⁸Cm and ²³⁸U + ²³⁸U, respectively. Good agreement with experimental data is noted. The main reason for the increase in cross-sections in the reaction ²³⁸U + ²⁴⁸Cm is that ²⁴⁸Cm is heavier than ²³⁸U.
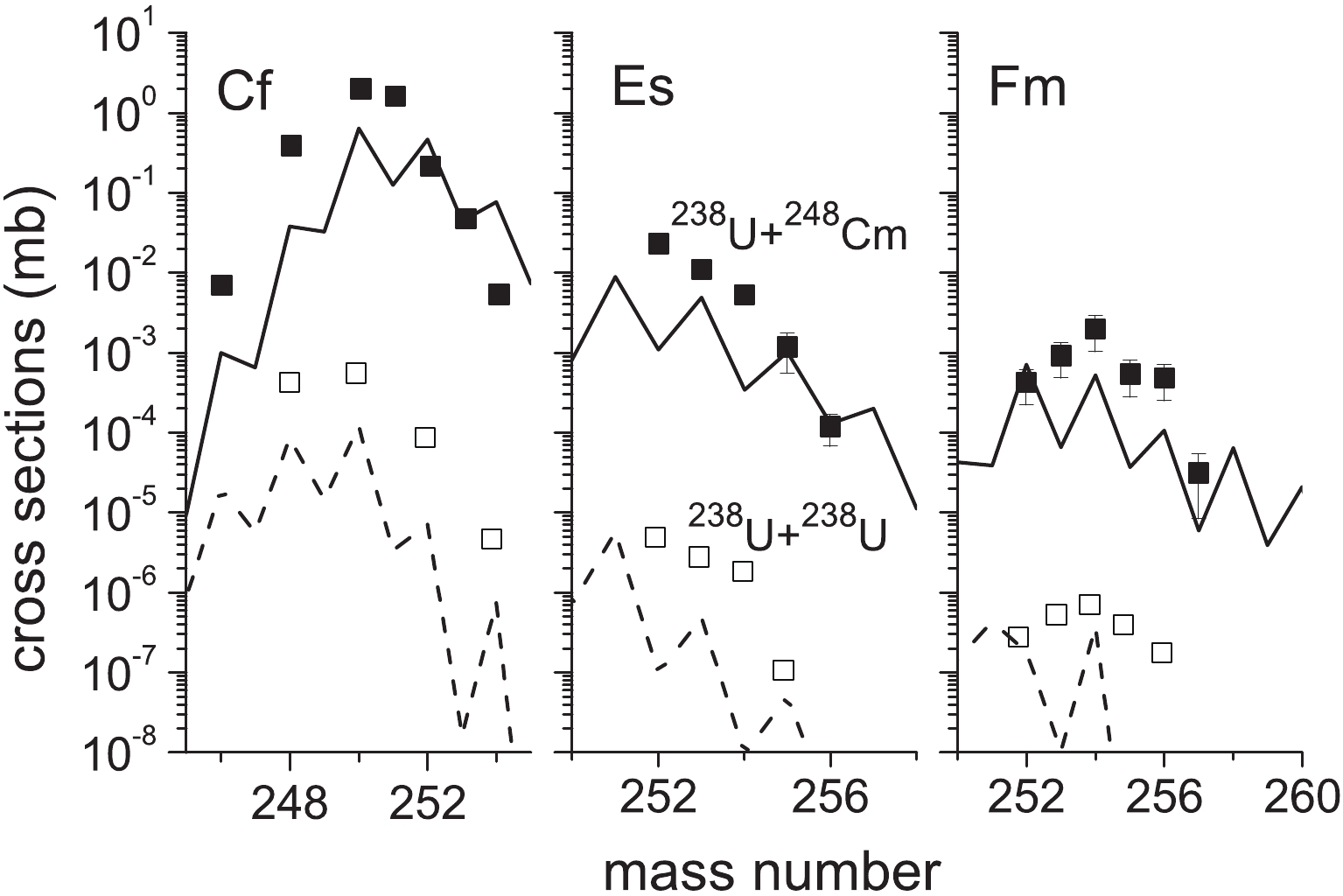Figure1. Yields of isotopes produced in MNT reactions ²³⁸U + ²⁴⁸Cm [31] and ²³⁸U + ²³⁸U [32]. Curves show calculations of DNS-sysu model.

The above behavior encouraged me to explore the possibilities of producing SHN in the MNT reactions based on radioactive targets. Figure 2 shows the calculated producted cross-sections of isotopes with $ Z = 100-109 $ in MNT reactions with the radioactive targets ²⁴⁹Cf, ²⁵⁴Es, and ²⁵⁷Fm. The half-lives of ²⁵⁴Es and ²⁵⁷Fm are hundreds of days. The two projectiles ²³⁸U and ²³⁹Pu with a different charge number and neutron-proton ratio are applied. As expected, the produced cross-sections decrease significantly with the increasing charge number of products for all of these reactions. The target effects on produced cross-sections are obvious. Although there is only one proton more in the ²⁵⁷Fm target in comparison to ²⁵⁴Es, the production yields are much higher in the reaction based on the ²⁵⁷Fm target. By comparing the reactions ²³⁸U + ²⁴⁹Cf, ²³⁸U + ²⁵⁴Es, and ²³⁸U + ²⁵⁷Fm, the advantages of cross-sections in the reaction based on the ²⁵⁷Fm target are gradually faded away with an increasing transferred number of protons, which is due to the decrease of the yield contribution from quasi-elastic events.
Figure2. (color online) Predictions of cross-sections for produced isotopes with Z = 100–109 in MNT reactions ²³⁸U + ²⁵⁴Es, ²³⁸U + ²⁵⁷Fm, ²³⁹Pu + ²⁵⁴Es, ²³⁹Pu + ²⁵⁷Fm, ²³⁸U + ²⁴⁹Cf, and ²³⁸U + ²³⁸U, the corresponding incident energies are 962, 970, 982, 991, 950, and 902 MeV, respectively. Circles on curves denote unknown SHN.

Moreover, the ²³⁹Pu projectile can remarkably enhance the production yields in the neutron-deficient region, because of the high proton richness in ²³⁹Pu. However, to produce neutron-rich isotopes, the cross-sections in the ²³⁹Pu induced reactions have little advantage over those in the ²³⁸U induced reactions. I also show the calculated results of the reaction ²³⁸U + ²³⁸U. Based on the calculated cross-sections, there is little chance to produce SHN by the ²³⁸U + ²³⁸U reaction.
Based on the calculated cross-sections, the reaction ²³⁹Pu + ²⁵⁷Fm is more likely to produce SHN. As shown in Ref. [14, 25], the production cross-sections of SHN are strongly dependent on the incident energy. Indeed, although in same reaction, to produce different objective nuclei, the optimal incident energies are usually different [33]. Therefore, the incident energies for producing specific nuclei should be chosen carefully. Here, I only estimate the possibilities of producing SHN in MNT reactions. The incident energy of 1.3V$ _{ \rm{cont}} $ for each reaction is used. In Fig. 2, the circles denote unknown SHN with cross-sections larger than 1 pb. Several neutron-rich SHN can be produced in the reaction ²³⁹Pu + ²⁵⁷Fm. Moreover, to produce Mt isotopes, the calculated cross-sections of several nuclei are above the level of pb. However, the enrichments of radioactive targets ²⁵⁴Es and ²⁵⁷Fm are very low, and they are usually produced in the neutron capture process. Therefore, if sufficient ²⁵⁴Es and ²⁵⁷Fm can be collected to make a target, multinucleon transfer reactions will be encouraging for the production of SHN. In turn, to produce nuclei located at the island of stability, neutron-rich radioactive beams would be promising.

The DNS-sysu model has been developed and tested to investigate MNT reactions with the aim of producing SHN. Because of the significant decrease of cross-sections in produced SHN with increasing transferred protons in MNT reactions, it seems unlikely that SHN are produced in the reaction ²³⁸U + ²³⁸U. Further, the reactions with radioactive targets ²⁴⁹Cf, ²⁵⁴Es, and ²⁵⁷Fm are investigated. The production cross-sections of SHN up to $ Z = 109 $ can reach tens of pb in the reactions based on the radioactive targets ²⁴⁹Cf, ²⁵⁴Es, and ²⁵⁷Fm. From the point of view of cross-sections, the radioactive combinations with ²⁵⁴Es and ²⁵⁷Fm targets are promising for the production of SHN. However, further experiments should be performed to constrain the theoretical models for better predictions.