Chun-Wang Ma ^1,2,,
, Dan Peng ^2,
, Hui-Ling Wei ^2,
, Zhong-Ming Niu ^3,
, Yu-Ting Wang ^2,
, R. Wada ^4,
,

Corresponding author: Chun-Wang Ma, machunwang@126.com

1.Institute of Particle and Nuclear Physics, Henan Normal University, Xinxiang 453007, China
2.School of Physics, Henan Normal University, Xinxiang 453007, China
3.School of Physics and Materials Science, Anhui University, Hefei 230601, China
4.Institute of Cyclotron, Texas A&M Univ, College Stn, TX 77843, USA
Received Date:2019-07-18
Accepted Date:2019-10-28
Available Online:2020-01-01
Abstract:The Bayesian neural network (BNN) method is proposed to predict the isotopic cross-sections in proton induced spallation reactions. Learning from more than 4000 data sets of isotopic cross-sections from 19 experimental measurements and 5 theoretical predictions with the SPACS parametrization, in which the mass of the spallation system ranges from 36 to 238, and the incident energy from 200 MeV/u to 1500 MeV/u, it is demonstrated that the BNN method can provide good predictions of the residue fragment cross-sections in spallation reactions.

HTML

--> --> -->

The spallation reaction is a high-energy nuclear reaction in which a target nucleus is struck by a light particle (for example, $ p, n $, and $ \alpha $) with an incident energy above 50 MeV/u, from which numerous lighter particles (neutrons, protons, or various composite particles) are ejected and form residues lighter than the target nucleus. It occurs in Nature in cosmic radiation and artificially in particle accelerators. Due to the various applications in aeronautics and astronautics testing [1], nuclear waste disposal [2, 3], proton therapy [4, 5] and the experiments based on the third generation of radioactive ion beam facilities [6, 7], the study of spallation reactions has attracted considerable interest.
Driven by the demands of disposal of nuclear waste and the design of accelerator driven subcritical system (ADS), systematic experimental measurements of spallation reactions have been performed at the FRagment Separator (FRS), GSI, Darmstadt, which cover a broad range of incident energies (from 200 MeV/u to 1500 MeV/u) and spallation nuclei from ⁵⁶Fe to ²³⁸U. At Lawrence Berkeley Laboratory (LBL), the spallation reactions of relatively small systems, ^{36, 40}Ar and ⁴⁰Ca were measured [8, 9]. Besides many experimental studies, different theoretical models have been developed for nuclear spallation reactions, in which the prediction of fragment production is of great interest. The traditional methods deal with the spallation reaction as a two-stage processes, in which the first (fast) stage is described by quasi-free nucleon-nucleon collisions and intranuclear cascades, and the second stage by de-excitation or fission of the excited compound nuclei. A number of codes have been developed to treat the first stage, for example, ISABEL [10], INCL++ [11–13] and the CRISP code [14]. Models based on microscopic quantum molecular dynamics have also been developed [15–19], which usually combine statistical de-excitation simulations with the binary decay code GEMINI [20], or the evaporation-fission code ABRA07 [21]. To deal with the compound nucleus formed at low energies, or its evolution through multi-fragmentation at high energies, the statistical multi-fragmentation model (SMM) has been adopted in Refs. [22–24]. Methods based on empirical parametrizations have also been proposed, for example, the SPACS parametrization [25], and the semi-empirical parametrizations by Silberberg and Tsao [26], Webber et al. [27], Waddington et al. [28], or by using the empirical formula based on the scaling phenomena in spallation reactions [29]. Difficulties still exist in predicting the yields of residue fragments because spallation reactions occur in a wide range of incident energies and incident species, from medium nuclei to heavy nuclei. Furthermore, the residue fragments are distributed over a large range of mass and charge numbers.
Neural network methods are a powerful tool for predicting behavior because they have a strong ability to learn from known data. They have been widely used in various areas, such as pattern recognition and machine learning [30, 31]. Neural network methods have also been used in nuclear physics, for example for prediction of nuclear masses [32, 33], nuclear charge radii [34], nuclear $ \beta $-decay half-lives [35] and fission product yields [36], and have achieved considerable success. In these methods, hundreds or even thousands of parameters are used to achieve a better prediction, which may lead to the problem of over-fitting. The introduction of the vague prior for the hyper-parameters can control the complexities in simulations and avoid the over-fitting problem in the Bayesian neural network (BNN) methods [37, 38]. In this article, the BNN method is introduced to predict the cross-sections of residue fragments in proton induced spallation reactions. Comparing with the measured cross-sections of residue fragments in various reactions, it is shown that the BNN method is a useful tool for studying the residue fragments from spallation reactions.

The principle of Bayes' rule is to establish a posterior distribution from all unknown parameters trained by a given data sample [38]. The process of BNN starts by defining a prior distribution $ p(w) $, which is a probability distribution for the model parameter w. A set of data $ D = \{(x_1,t_1),(x_2,t_2),\cdots,(x_n,t_n)\} $ is prepared, where $ x_{k} $ (k = 1,2,···,n) are the input data, which may consist of a group of parameters. $ t_{k} $ (k = 1,2,···,n) are the output data, which in this work represent the fragment cross-sections, and n is the number of training data. The posterior distribution is updated as,

$ p(w/D) = p(D/w)p(w)/p(D), $

(1)

in which the prior probability $ p(w) $ denotes the trial distribution based on the background knowledge. In the case of insufficient information, $ p(w) $ changes little and determines the final predictions. The impact of $ p(w) $ is gradually weakened as the number of input data sets is increased. $ p(w/D) $ is the posterior distribution. $ p(D) $ is a normalized constant, which ensures that the posterior distribution is a valid probability density and integrates to one. $ p(D/w) $ is the likelihood function, and it can influence the prior probability after examining the training data. In this work, the prior probability of each model parameter is a Gaussian distribution with zero mean. The precision (the inverse of the variance) of a Gaussian distribution is the gamma distribution, as in Ref. [35], which can make the precision vary over a large range. Optimal precision is automatically found during the sampling process. In this work, the likelihood function $ p(D/w) $ is a Gaussian distribution exp$ (-\chi^{2}/2) $. $ \chi^{2} $ is given by

$ \chi^{2} = \sum\limits_{n = 1}^{N}\left(\frac{t_{n}-S(x,w)}{\Delta{t_{n}}}\right)^{2}, $

(2)

where $ \Delta{t_{n}} $ is the standard deviation, which denotes the noise error of the n?th observable [35]. $ S(x,w) $ is the functional equation of the feed-forward neural network, which is written as,

$ S(x,w) = a+\sum\limits_{j = 1}^{H}b_j {\rm tanh}\bigg\{c_j+\sum\limits_{i = 1}^{I} d_{ji} x_i \bigg\}, $

(3)

where w defines all model parameters a (bias of output layers), $ b_j $ are the weights of output layers, $ c_j $ bias of hidden layers, and $ d_{ji} $ weights of hidden layers. H and I are the numbers of neurons in the hidden layer and the number of input variables, respectively. A schematic diagram of a neural network with a single hidden layer, three hidden neurons (H=3), and two input variables (I=2) is shown in Fig. 1.
Figure1. (color online) A schematic diagram of a neural network with a single hidden layer, three hidden neurons (H = 3) and two input variables (I = 2).

In this work, for the case of spallation reactions $ X + p $, the bombarding energy E (in MeV/u), the mass number ($ A_{\rm proj} $) and charge number ($ Z_{\rm proj} $) of the projectile nucleus and the mass number A, charge number Z, neutron excess $ N-Z $ and pairing effect $ B_p $ [39, 40] of the fragments are considered as input, i.e. $ x_{i} $ = ($ A_{\rm proj} $, $ Z_{\rm proj} $, E, A, Z, $ N-Z $, $ B_p $). The output $ t_k $ (k = 1,2,···,n) is in the form of lg$ {\sigma_{k}} $, where $ \sigma_{k} $ are the cross-sections. $ B_p $ has a simple form

$ B_p = [(-1)^Z+(-1)^N]\cdot A^{-1/2}. $

(4)

After determining the prior distribution and the model structure, the posterior distribution of the model parameters can be obtained from the Bayesian principle, after taking into account the new data D. In the Bayesian neutral network, the quantity of interest is the model prediction that corresponds to the new input data, rather than the posterior probability distribution of the neural network weights. To predict the new output $ \langle S^{\rm new}\rangle $ corresponding to the new input $ x^{\rm new} $, the Markov Chain Monte Carlo (MCMC) method is used to approximate the mathematical expectation as,

$ \langle S^{\rm new}\rangle = \int S(x,w)p(w/D) = \frac{1}{K} \sum\limits_{k = 1}^{K}S(x^{\rm new},w_k). $

(5)

The uncertainty is estimated as $ \Delta{S^{\rm new}} $ = $ \sqrt {\langle {S^{\rm new}}^2\rangle \!-\! \langle S^{\rm new} \rangle ^2} $.

In the past decades, many spallation reaction systems, with the incident energy ranging from a few hundreds MeV/u to above GeV/u, and the mass of the spallation nucleus from A=36 to above 200, have been experimentally measured, as listed in Table 1. A recent parametrization, called SPACS [25], was proposed to predict the cross-sections of residue fragments. To complement the experimental data, SPACS was used for some reaction systems where no measured data is available (1166 data sets for 5 reaction systems are produced by SPACS, see Table 2). It should be noted that in spallation reactions, fission and multi-fragmentation are the two most important mechanisms for forming residue fragments. Since the formation of fissile fragments is quite different from the multi-fragmentation process, the fissile fragments are not considered in this work.

$ ^{A}X $ + p	E/(MeV/u)	Numbers	Charge Range	Reference
36Ar + p	361	42	9-17	[8]
	546	42	9-17
	765	38	9-17
40Ar + p	352	45	9-17	[8]
40Ca + p	356	48	10-20	[9]
	565	54	10-20
	763	54	10-20
56Fe + p	300	128	10-27	[41]
	500	136	10-27
	750	148	8-27
	1000	152	8-26
	1500	157	8-27
136Xe + p	200	96	48-55	[42]
	500	271	41-56	[43]
	1000	604	3-56	[44]
197Au + p	800	352	60-80	[45]
208Pb + p	500	249	69-83	[46]
	1000	459	61-82	[47]
238U + p	1000	364	74-92	[48]

Table1.The number of measured fragments in 19 measured $X $+ p spallation reactions.

$ ^{A}X $ + p	E/(MeV/u)	Numbers	Charge Range
103Rh + p	800	40	36-41
150Nd + p	700	333	40-60
169Tm + p	600	239	53-69
181Ta + p	800	375	55-74
208Pb+p	600	179	76-82

Table2.The number of fragments in spallation reactions predicted using the SPACS parametrization.

The data for 23 reactions listed in Tables 1 and 2 were chosen as the learning set (LS), and the remaining ones as the testing set (TS) for the reliability of the BNN method. Two different data sets were selected as TS, i.e. TS1 for the 800 MeV/u ¹⁹⁷Au + p reaction [45], TS2 for the 500 MeV/u ⁵⁶Fe + p reaction [41]. Different number of hidden nodes, from 34 to 36, were used to find the optimal hidden nodes.
In Fig. 2 to Fig. 4, the BNN predictions are shown for 800 MeV/u ¹⁹⁷Au + p with different hidden nodes H from 34 to 36. In the experiments, only the cross-sections for fragments with $ Z \geqslant 60$ have been measured. It is observed that BNN with H = 34 significantly overestimates the neutron-deficient fragments for $ Z \leqslant 62$, as shown in Fig. 2, and underestimates those for $ Z\geqslant 67$, Fig. 3 and Fig. 4. BNN with H = 36 underestimates the yields of the neutron-rich fragments for $ Z \leqslant 61$, Fig. 2, and overestimates those for Z = 75 and 76, Fig. 4. BNN with H = 35 predicts best the overall yields, without significant deviation from the experimental data. When Z of the fragments is larger than the projectile Z, the cross-sections for the very neutron-rich isotopes are significantly overestimated.
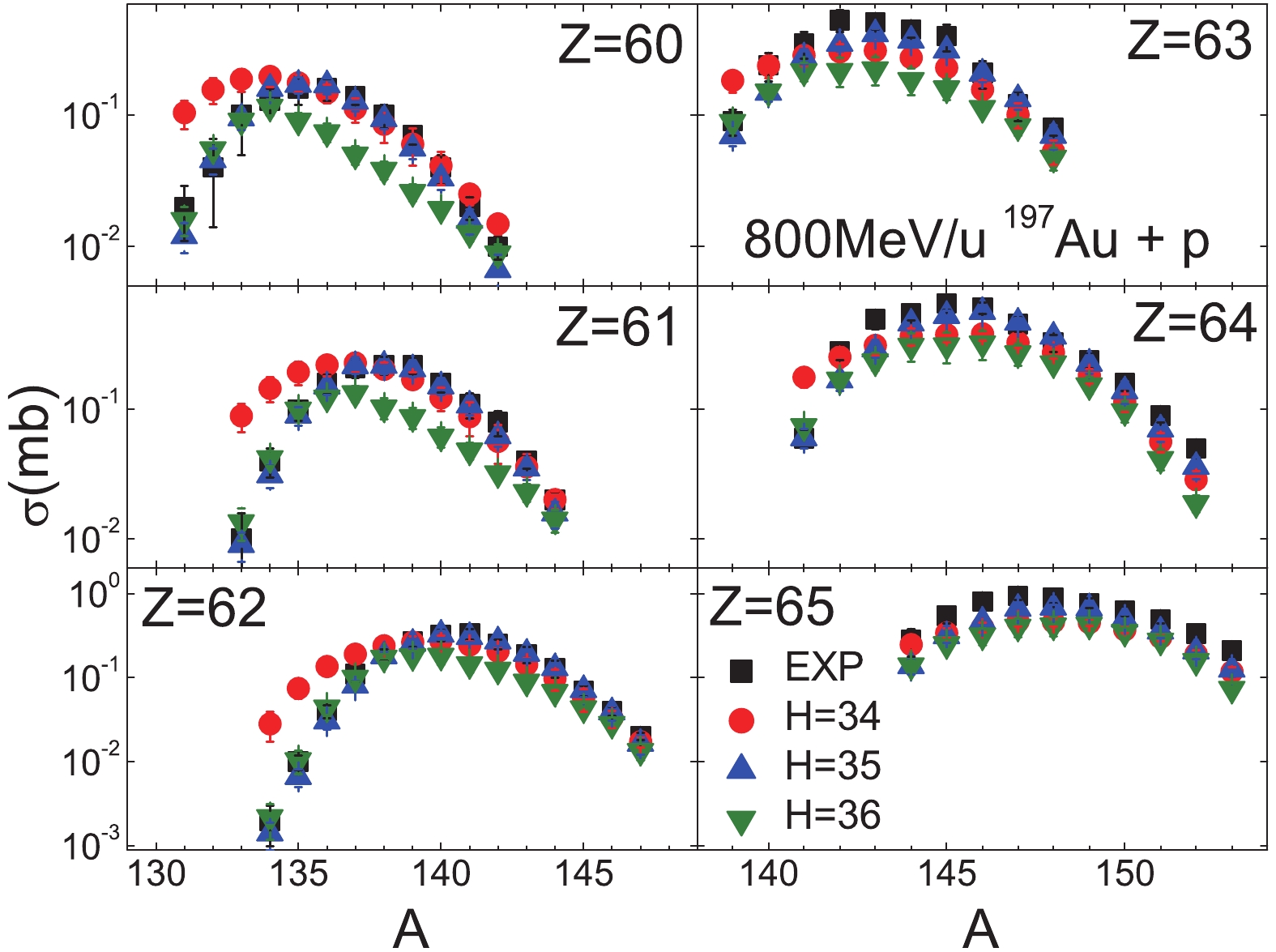Figure2. (color online) BNN predictions for selected residue fragments with Z=60 to 65 in the 800 MeV/u ¹⁹⁷Au + p spallation reaction. Three different numbers of hidden nodes are tested, H = 34 (circles), 35 (triangles), 36 (triangles). The measured results are shown as black squares.

Figure4. (color online) Similar as Fig. 2, but for Z=75 to 80.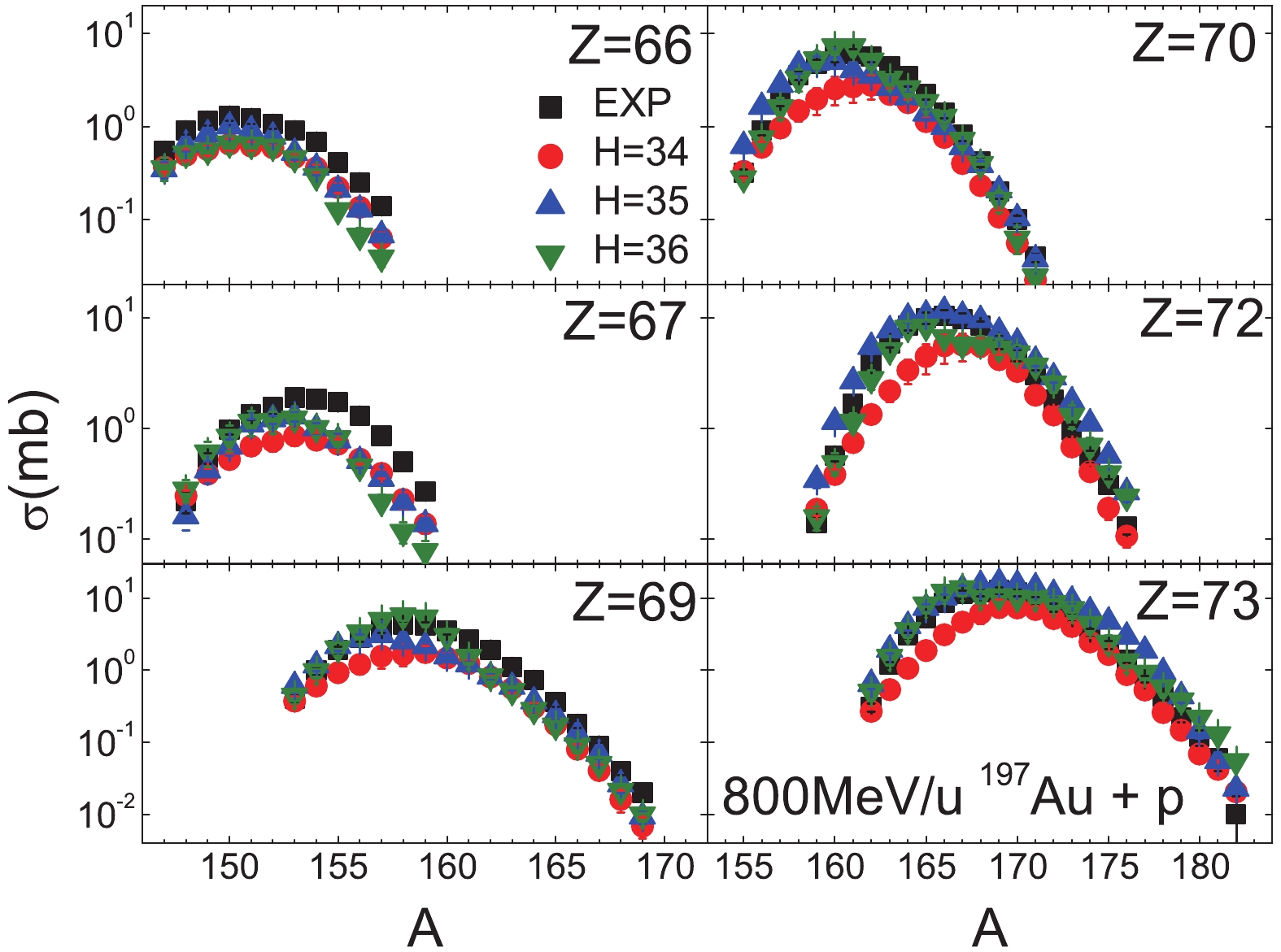

Figure3. (color online) Similar as Fig. 2, but for Z=66 to 73.

In Figs. 5 to 7, the BNN predictions for TS2 (500 MeV/u ⁵⁶Fe + p ) with H = 34, 35 and 36 are seen to be in good agreement with the experimental data, except for $ Z > 23 $. The cross-sections of the very neutron-rich isotopes are over-predicted by about one order of magnitude. For all five incident energies 300, 500, 750, 1000 and 1500 MeV/u, the change of one or two hidden nodes influences the results very slightly.
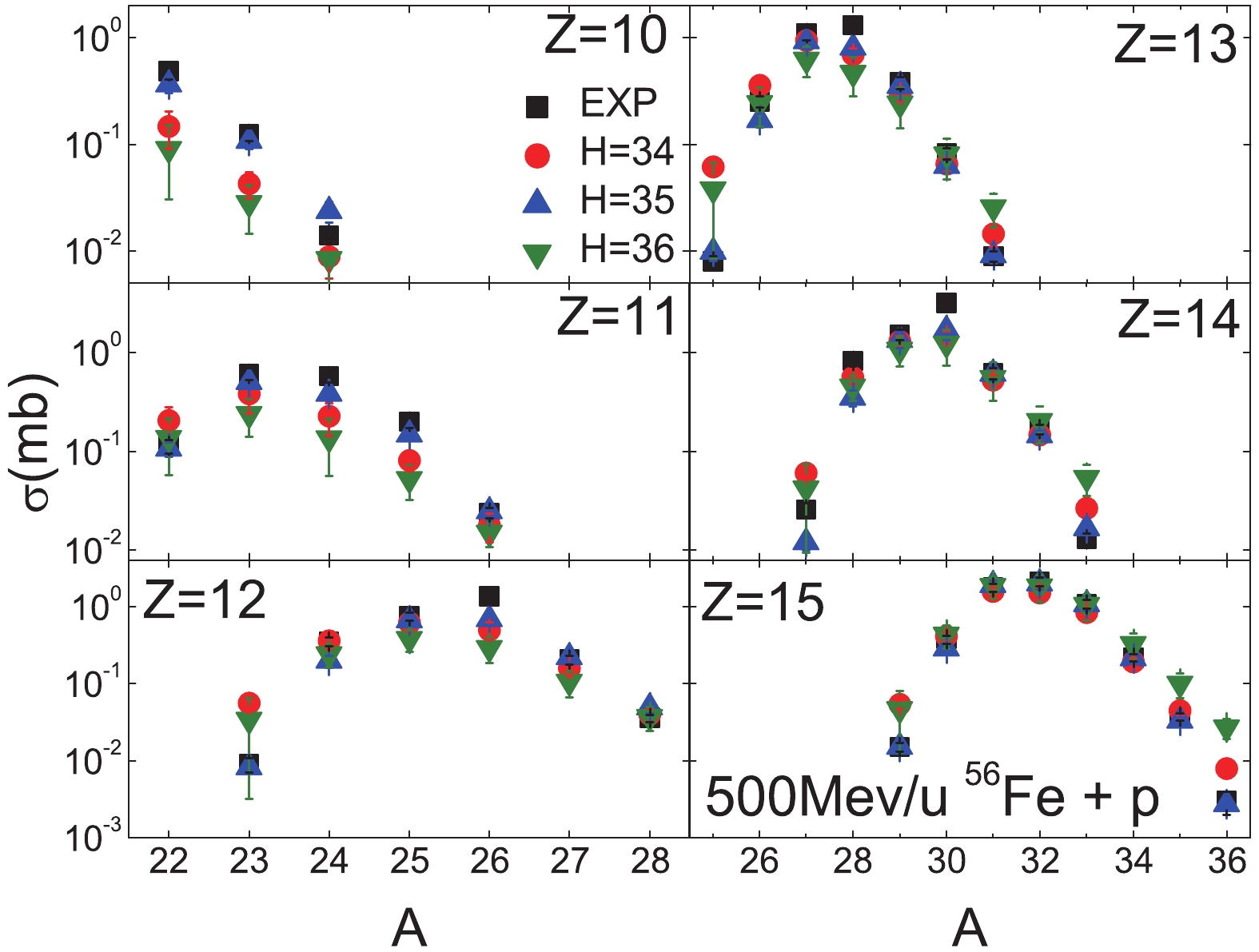Figure5. (color online) BNN predictions for the 500 MeV/u ⁵⁶Fe + p reaction with H = 34, 35 and 36. The results for the selected residues Z=10 to 15 are compared to the measured residue fragments [41]. The symbols are the same as in Fig. 2.

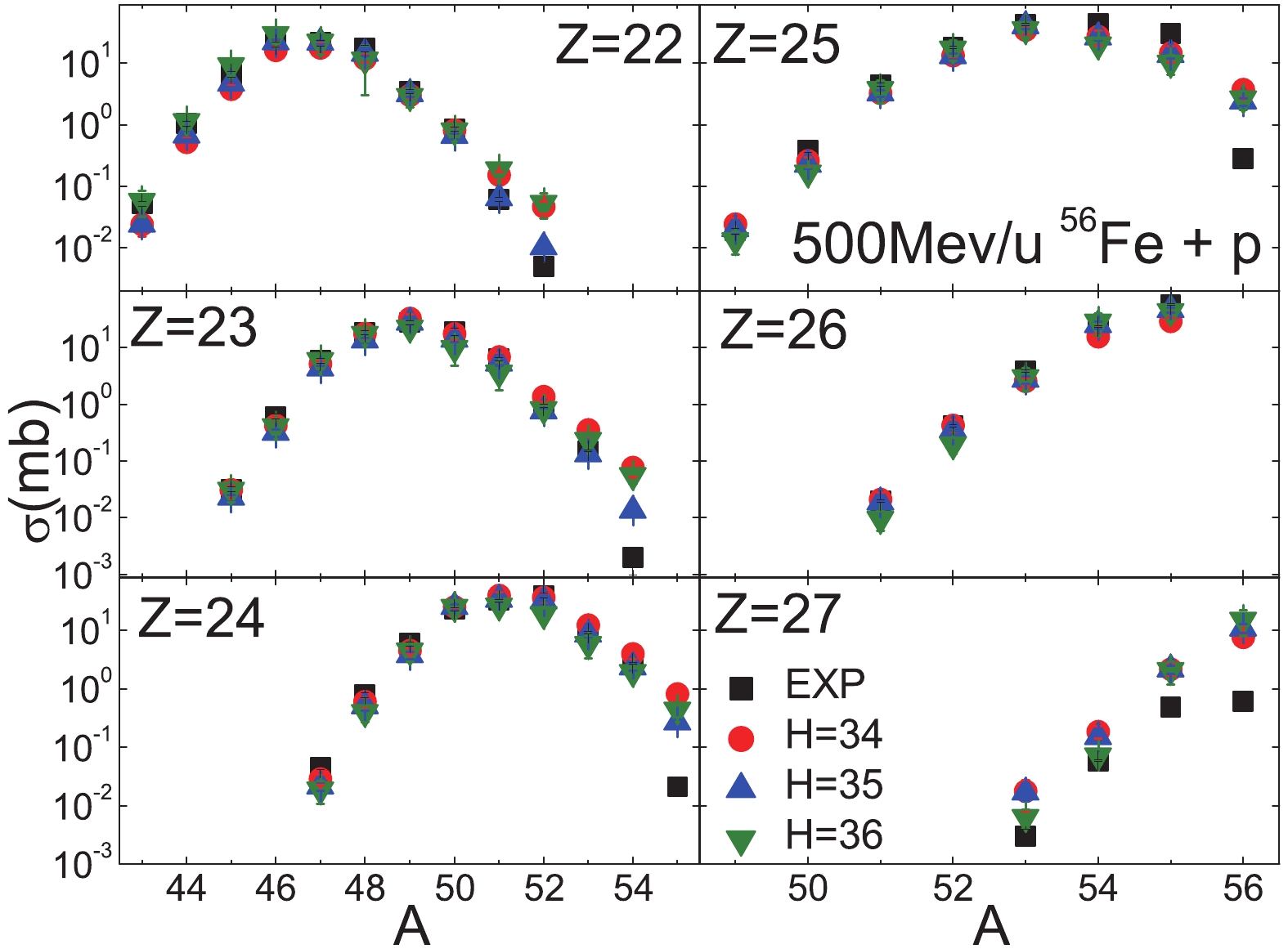Figure7. (color online) Similar as Fig. 5, but for Z = 22 to 27.

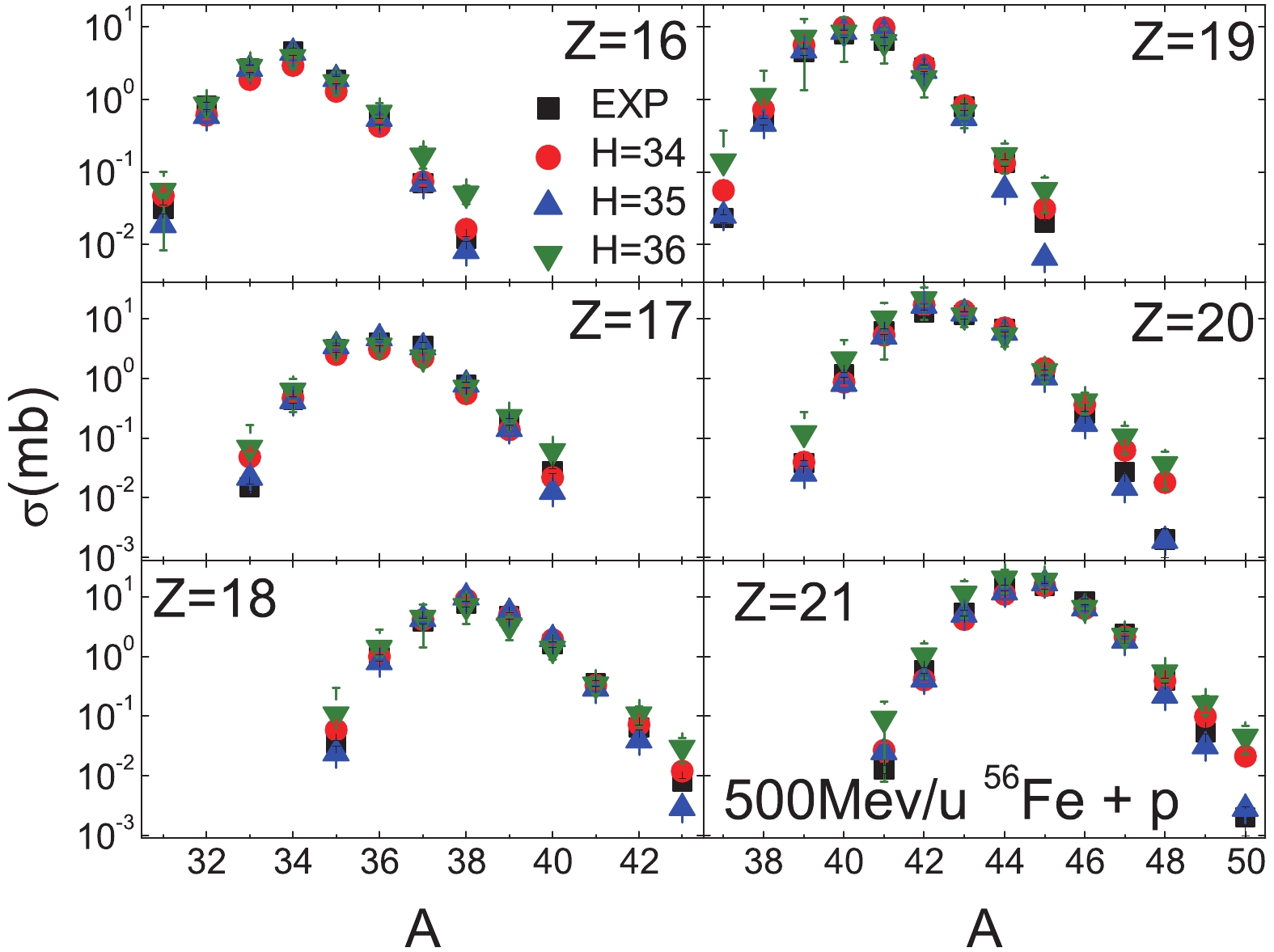Figure6. (color online) Similar as Fig. 5, but for Z = 16 to 21.

Based on the above analysis of a relatively large spallation system, ¹⁹⁷Au, and a medium one, ⁵⁶Fe, the BNN method with H = 35 hidden nodes provides the best results, and is selected in this work as the optimal number of hidden nodes. The trained parameter sets with H = 35 and TS1 are used for predictions of the unknown fragment cross-sections in four reaction systems, ¹³⁶Xe + p at 1000 MeV/u, ²³⁸U + p at 1000 MeV/u, ⁴⁰Ca + p at 763 MeV/u, and ³⁶Ar + p at 361 MeV/u. The predictions with the BNN method are also compared with the SPACS results and the experimental data, when available.
In Figs. 8 and 9, the results for the residue fragments in the 1000 MeV/u ¹³⁶Xe + p spallation reaction are shown. The measured fragment cross-sections cover a wide range of charge numbers, from Z = 3 to Z = 56, but a limited isotope range. The BNN results are in good agreement with the experimental data for light to heavy isotopes, where the experimental data are available. The predictions of the SPACS parametrization for the light fragments are significantly lower, by about 4 (Z = 8) to 5 (Z = 3) orders of magnitude, for medium masses they are lower by about 2 (Z = 22) to 3 (Z = 17) orders of magnitude, but are in good agreement with the experimental data for heavy residues. There is a good agreement between BNN and SPACS for $ Z > 36$, except that the BNN predictions are larger than SPACS for neutron-deficient and very neutron-rich isotopes.
Figure8. (color online) BNN predictions (with TS1 and H = 35) (circles) for selected fragments with Z = 3 to 22 in the 1000 MeV/u ¹³⁶Xe + p spallation reaction, compared to the experimental data (squares, from [44]) and the SPACS results (triangles, from [25]. The experimental and BNN error bars are smaller than the symbols.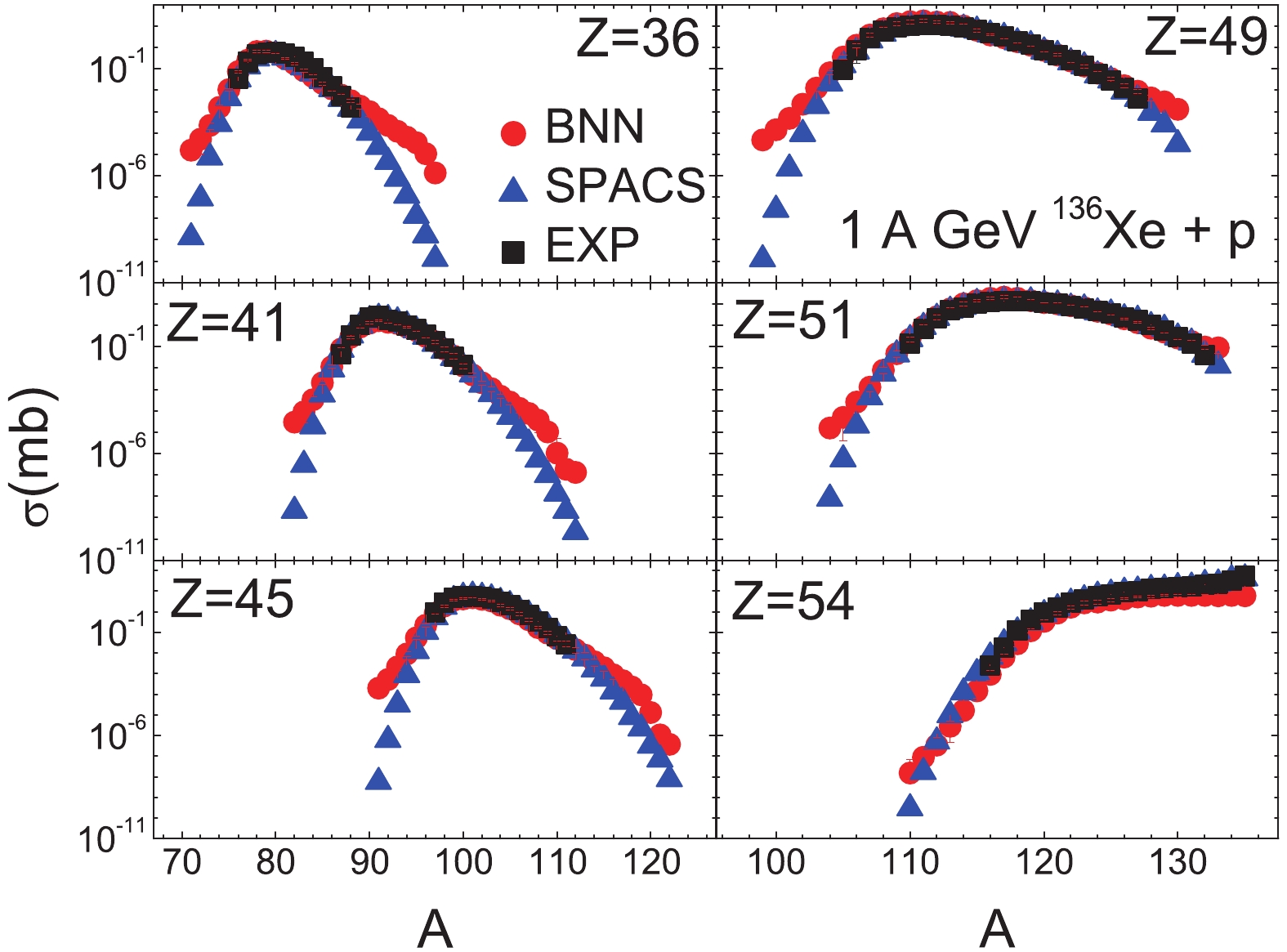

Figure9. (color online) Similar as Fig. 8, but for Z = 36 to 54.

In Figs. 10 and 11, the predicted isotopic cross-sections for the 1000 MeV/u ²³⁸U + p reaction are shown. In [48], only the isotopic cross-sections for the $ Z \geqslant $ 74 fragments are reported. It can be seen that the BNN results reproduce the measured data well, while SPACS provides good predictions only for the residues with Z = 74 to 83, and significantly overestimates those with $ Z\geqslant $ 86 on the neutron deficient side. For the fragments with Z = 54 to 70, BNN predicts a reduction of the peak of the isotopic cross-section which is much slower than the overall drop. The shapes of the isotope distributions predicted by BNN and SPACS are also different. BNN predicts much higher cross-sections for the neutron-rich isotopes. This was also seen in the ¹³⁶Xe system in Fig. 8, which reflects the lack of cross-section data for neutron-rich isotopes in the present BNN learning set.
Figure10. (color online) Predictions of isotopic distributions by BNN (squares) and SPACS (circles) for the 1000 MeV/u ²³⁸U + p spallation reaction for Z = 54 to 70 [48]. Experimental distributions are not available for $ Z < 74 $. The BNN error bars are smaller than the symbol size.

Figure11. (color online) Similar as Fig. 8, but for 1000 MeV/u ²³⁸U + p and for Z = 74 to 92.

In Fig. 12, the isotopic cross-sections for the 763 MeV/u ⁴⁰Ca + p reaction are shown. Compared to the measured cross-sections, BNN and SPACS reproduce the experimental data well. For the very neutron-rich fragments with no measured data available, the BNN and SPACS predictions show a large difference. As mentioned above, this difference is due to the lack of data for neutron-rich isotope cross-sections in the BNN method .
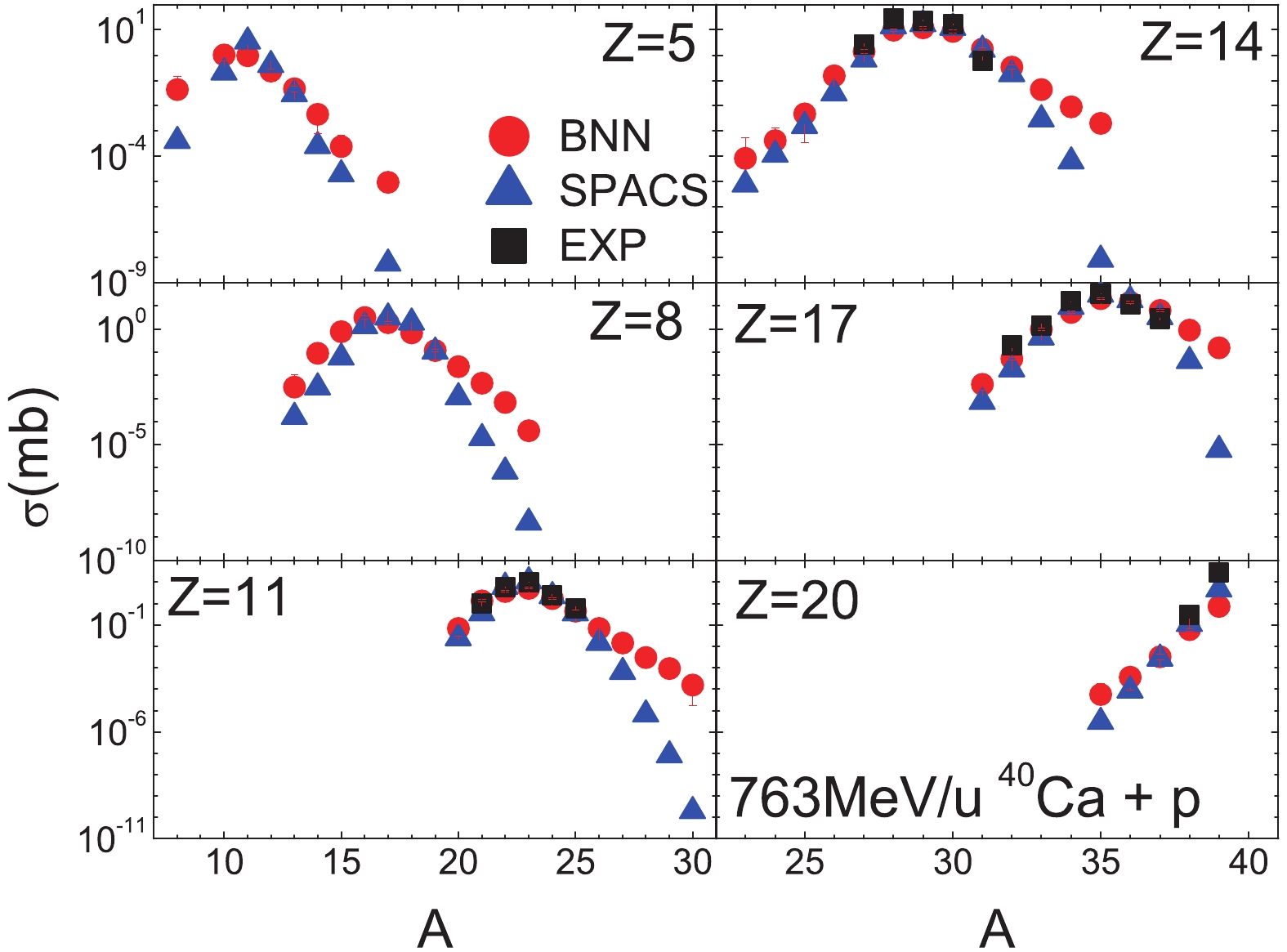Figure12. (color online) Similar as Fig. 8, but for the 763 MeV/u ⁴⁰Ca + p spallation reaction [9]. Experimental data are not available for fragments with $ Z < 10 $.

In Fig. 13, the isotopic cross-sections for the 361 MeV/u ³⁶Ar + p reaction are shown. ³⁶Ar is the smallest projectile in the training data. A similar result as for the 763 MeV/u ⁴⁰Ca + p reaction is seen, that is both the BNN and SPACS methods reproduce the measured data well, whereas for very neutron-rich fragments the BNN predictions are slightly larger than the SPACS results.
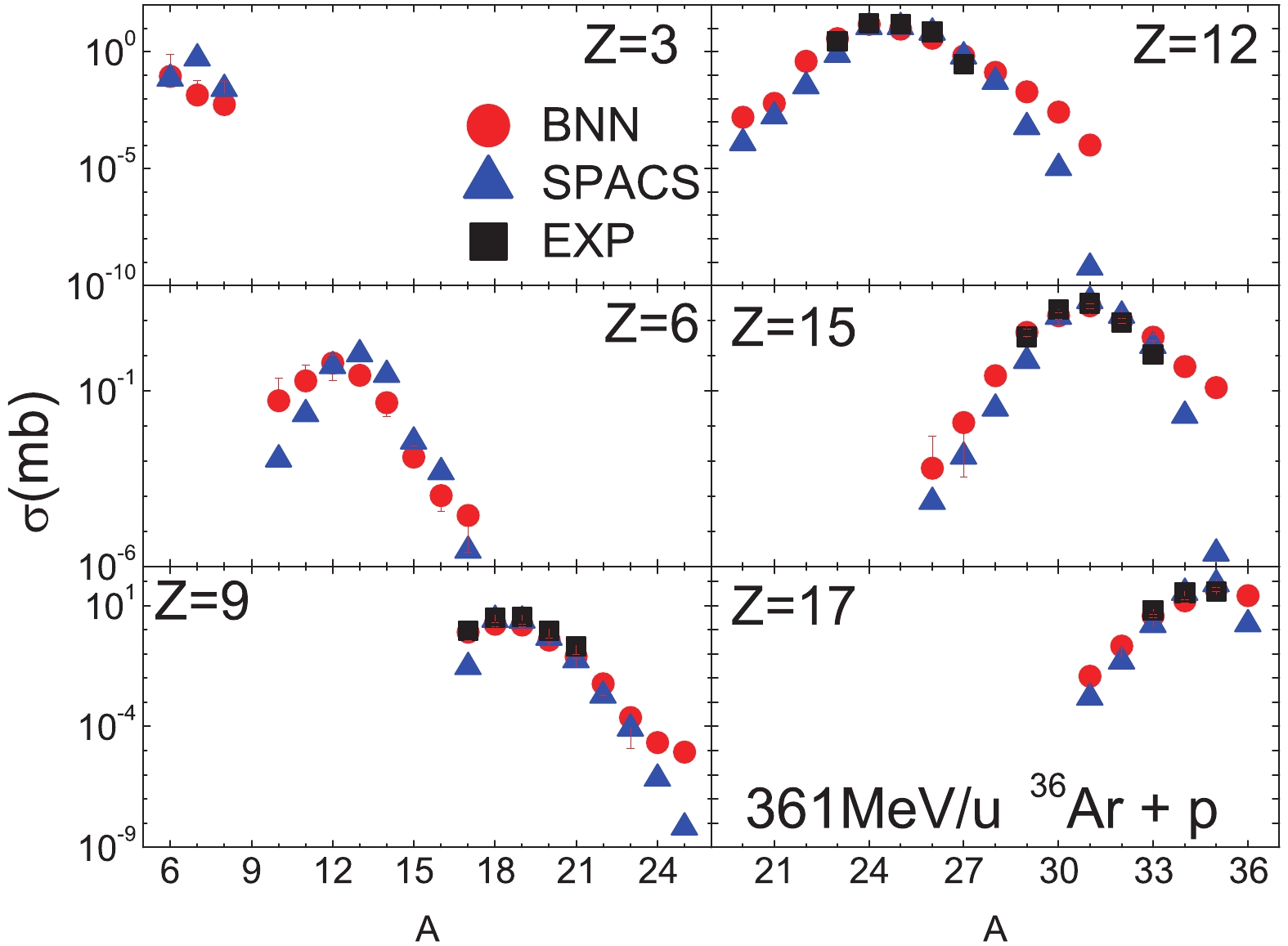Figure13. (color online) Similar as Fig. 8, but for the 361 MeV/u ³⁶Ar + p reaction with Z = 3 to 17 [8].

From the BNN predictions for the ³⁶Ar, ⁴⁰Ca, ¹³⁶Xe, and ²³⁸U spallation reactions, it may be concluded that the BNN method provides good predictions for the cross-sections of fragments, except for those that are far from the measured data. Additional experimental measurements should reduce the effect of the prior distribution error and improve the prediction ability of BNN. For simulated reactions in a wide range of masses from ³⁶Ar to ²³⁸U and incident energies, it is demonstrated that the BNN method has a good ability to predict the fragment production cross-section in spallation reactions.
In most cases, it is seen that the BNN predictions for neutron-rich fragments are higher than SPACS. To check these predictions, in particular when there is a large difference, the empirical relation between the isotopic cross-section and the average binding energy ($ B' $) is introduced

$ \sigma = C {\rm exp}[(B' - 8)/\tau], $

(6)

where C and $ \tau $ are free parameters. $ B' = (B - \varepsilon_{p})/A $ denotes the average binding energy per nucleon of the fragment. $ \varepsilon_{p} $ is the correction due to the pairing energy

$ \varepsilon_{p} = 0.5[(-1)^N + (-1)^Z]\varepsilon_{0}\cdot A^{-3/4}, $

(7)

Based on the canonical ensemble theory, this empirical formula was shown to be reasonable for fragment production in multi-fragmentation reactions [49]. Evidence that this formula is obeyed by both the neutron-deficient and neutron-rich fragments was given in [50–53]. The correlation between the BNN and SPACS isotopic cross-sections and $ B' $ for isotopes with Z = 8, 17, and 41 in the 1 A GeV ¹³⁶Xe + p reaction, and for Z = 11 in the 763 A MeV ⁴⁰Ca + p reaction, are plotted in Fig. 14. The nucleus binding energy was taken from AME16 [54], and $ \varepsilon_{0} = $ 30 MeV was chosen following Ref. [49]. The linear fit of the correlation between the measured cross-sections and $ B' $ of the fragments is shown by the solid line.
Figure14. (color online) Correlation between the isotopic cross-sections and the average binding energy B'. The squares, triangles, and circles denote the measured data, BNN predictions, and SPACS predictions, respectively. The lines denote the linear fit of the correlation between $ \sigma $ and B'.

For the ¹³⁶Xe + p reaction, it is seen that the BNN predictions obey well the formula in Eq. (6) when Z is relatively small, while for the neutron-rich fragments of the Z = 41 isotope, the BNN predictions are above the empirical formula. The SPACS predictions obey well the empirical formula for the Z = 41 fragments. It is not possible to conclude if the BNN and the SPACS predictions obey the empirical formula for the Z = 11 fragments, as there are only two points. In general, the BNN predictions are closer to the measured data, which suggests that they obey the empirical formula better than SPACS. Based on this analysis, we conclude that the BNN predictions are satisfactory for fragments with relatively small charge numbers, while the SPACS predictions are better for fragments with relatively large charge numbers.
It is worth mentioning that other spallation systems have also been simulated using the BNN and SPACS parametrization methods (not shown in this article), and that similar results were obtained for the ¹³⁶Xe + p, ²³⁸U + p, ⁴⁰Ca + p and ³⁶Ar + p reactions. From the BNN predictions for the ³⁶Ar + p, ⁴⁰Ca + p, ¹³⁶Xe + p and ²³⁸U + p spallation reactions, it was shown that the BNN method provides good predictions for the fragment cross-sections, although improvements should be made for the very neutron-rich isotopes in the case of the ²³⁸U system. Further experimental measurements for the very neutron-rich isotopes would help to improve the quality of BNN predictions. It can be concluded that for a wide mass range, from ⁴⁰Ca to ²³⁸U, and a wide incident energy range, from 200 MeV/u to 1500 MeV/u, the BNN method has a good ability to predict fragment production in spallation reactions.

The BNN method was applied to predict the isotopic cross-sections in proton induced spallation reactions with incident energies from 200 MeV/u to 1500 MeV/u. Using about 4600 isotopic cross-section data, the number of optimal hidden nodes in the BNN method was determined as H = 35. The input for BNN includes the incident energy, the mass and charge numbers of the projectile nucleus, the mass and charge numbers of the fragment, the neutron-excess and the pairing effect in the fragment. Comparing with the experimental data, it was demonstrated that the BNN method provides a good prediction of the isotopic cross-sections in proton induced spallation reactions, in particular for fragments with small charge number. It is suggested that the BNN method provides a new tool for predicting the cross-sections of fragments in spallation reactions, and may contribute to the related research in nuclear physics, proton therapy, and nuclear technology.
RW thanks for the support of visiting professorship from the Henan province.