城市空间增长与人口密度变化之间的关联关系

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-29

赵睿¹^,², 焦利民^,¹^,², 许刚³^,⁴, 徐智邦¹^,², 董婷¹^,²1. 武汉大学资源与环境科学学院,武汉 430079
2. 武汉大学地理信息系统教育部重点实验室,武汉 430079
3. 武汉大学遥感信息工程学院,武汉 430079
4. 自然资源部城市国土资源监测与仿真重点实验室,深圳 518034

The relationship between urban spatial growth and population density change

ZHAO Rui¹^,², JIAO Limin^,¹^,², XU Gang³^,⁴, XU Zhibang¹^,², DONG Ting¹^,²1. School of Resource and Environmental Sciences, Wuhan University, Wuhan 430079, China
2. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China
3. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
4. Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Natural Resources, Shenzhen 518043, China

通讯作者: 焦利民(1977-), 男, 河南安阳人, 教授, 博士生导师, 研究方向为城市化与国土空间优化、地理空间分析与建模等。E-mail: lmjiao@whu.edu.cn

收稿日期:2018-12-5修回日期:2019-12-20网络出版日期:2020-04-25

基金资助:

国家自然科学基金项目.41971368
国家重点研发计划.2017YFA0604404
自然资源部城市国土资源监测与仿真重点实验室开放基金资助课题.KF-2019-04-036

Received:2018-12-5Revised:2019-12-20Online:2020-04-25

Fund supported:

National Natural Science Foundation of China.41971368
National Key Research and Development Program of China.2017YFA0604404
Open Fund of Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Natural Resources.KF-2019-04-036

作者简介 About authors
赵睿(1995-),女,贵州安顺人,硕士生,研究方向为城市土地扩张E-mail:ZhaoRui27@whu.edu.cn。

摘要
探究城市空间增长与人口密度变化之间的关联关系是城市可持续发展研究的基础,对制定有效的土地政策、促进城市紧凑发展具有重要意义。选取中国和欧洲23个人口100万以上城市作为研究样本,采用1990年、2000年和2014年3期土地利用数据和人口数据,计算各时段样本城市空间增长速率,建立城市紧凑度指标,并将城市空间增长方式划分为紧凑型、保持型和蔓延型,进一步探讨了样本城市的空间增长特征、人口密度变化特征及两者之间的关系。主要结论为：① 人口密度降低这一现象普遍存在于中国和欧洲城市,中国城市人口密度相对较高且降低速率较快,欧洲城市人口密度相对较低且降低速率较慢;1990—2014年中国城市半径的增长速率明显快于欧洲城市半径的增长速率。城市空间增长速率与人口密度变化速率呈现强负相关关系（Pearson相关系数为-0.693）;② 1990—2000年中欧城市主要以紧凑型方式增长。2000—2014年中国城市主要以蔓延型方式增长,且人口密度随时间下降的速率加快;欧洲城市主要以紧凑型和保持型方式增长,人口密度降低速率减小;③ 紧凑型的空间增长方式并不一定会带来人口密度的升高,但会减缓人口密度下降的速率。中欧城市对比分析表明,城市维持紧凑型空间增长方式,则城市人口密度随时间下降速率减慢;而空间增长方式由紧凑型转为蔓延型,将加剧城市人口密度随时间下降。
关键词： 城市空间增长;人口密度;反S函数;中国;欧洲

Abstract

Exploring the relationship between urban spatial growth and population density change is the basis of urban sustainable development research, which is of great significance for formulating effective land policies to promote urban compact development. The research selected 23 cities with a population of more than 1 million in China and Europe as the study areas. Based on the land use and population data in the study areas in 1990, 2000, and 2014, the research calculated the growth rate of sample urban space during each period, and the urban compactness index was then established to divide the urban spatial growth mode into compact type, maintenance type and spread type. The characteristics of spatial growth, population density change, and their relationship were further discussed. The results are as follows: (1) Population density decline is widespread in cities of China and Europe. Population density in cities of China is relatively high, and the rate of decline is fast, whereas population density in cities of Europe is relatively low and the rate of decline is slow. From 1990 to 2014, the growth rate of urban spatial radius in China was significantly higher than that in Europe. There is a strong negative correlation between the growth rate of urban space and the change rate of population density (with a Pearson's r of -0.693). (2) From 1990 to 2000, most of the sample cities' spatial growth mode were compact. From 2000 to 2014, most Chinese cities' spatial growth mode transformed into spread type and rate of population density decline increased. By contrast, European cities' spatial growth mode maintained to be compact or transformed into maintenance, and the rate of population density decline decreased. (3) Compact spatial growth does not necessarily lead to an increase in population density, but it tends to lower the rate of population density decline, relative to spread spatial growth. The comparative analysis of Chinese and European cities shows that if cities maintain a compact spatial growth mode, the rate of population density will be lowered. If cities' spatial growth mode transforms from compact to spread, it will intensify the decline of urban population density over time.

Keywords：urban spatial growth;population density;inverse S-shaped function;China;Europe

PDF (4990KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
赵睿, 焦利民, 许刚, 徐智邦, 董婷. 城市空间增长与人口密度变化之间的关联关系. 地理学报[J], 2020, 75(4): 695-707 doi:10.11821/dlxb202004003
ZHAO Rui. The relationship between urban spatial growth and population density change. Acta Geographica Sinice[J], 2020, 75(4): 695-707 doi:10.11821/dlxb202004003

1 引言

随着全球范围内城市人口的不断增加,城市土地持续的向外扩张,城市土地扩张快于城市人口增长的现象已十分普遍,进而导致城市人口密度随时间下降^[1,2,3]。城市人口密度是衡量城市的重要属性,诸多城市要素均与人口密度紧密关联。已有研究发现城市能源使用效率随人口密度上升而提高,人均碳排放量随人口密度上升而减少。在城市增长过程中,城市人口密度随时间下降的现象将加剧城市蔓延,进而给城市及其周边耕地资源和生态环境带来巨大压力,严重阻碍区域可持续发展。中国正经历快速城镇化阶段,未来仍将有数亿人口转移至城市,而受土地资源特别是耕地资源限制,城市土地扩展的空间有限。研究城市空间增长方式与人口密度变化之间的关系是科学规划城市空间发展和布局的基础,对于科学划定城市边界、实现城市紧凑集约可持续发展具有重要意义。

现有关于城市空间增长的研究大多侧重于对其时空特征及演化的分析,主要包括：城市空间增长的规模、要素、结构和形态研究^[4];城市空间增长的方式、机制和测度方法的探讨^[5,6,7];使用分形理论或借助城市土地密度对城市空间增长特征的研究^{[8,9,10,11,12,13,14]};构建城市扩张自由度、紧凑度、蔓延度等指标对城市空间增长过程进行综合度量等^[15,16]。针对城市人口密度,现有研究多集中在以下几个方面：① 城市人口密度的空间分布格局,包括全国尺度、省域尺度的城市人口密度空间分布格局及模型研究^[17,18,19];② 城市人口密度的时空变化,主要从全球视角和城市市辖区的角度研究人口密度变化趋势和影响因素^[20,21,22]。

尽管国内外****对城市空间增长和人口密度展开了大量的研究,但是缺乏城市空间增长与人口密度变化两者之间关联的研究。紧凑的空间增长是否会提高人口密度?该效应在中国和欧洲城市之间有何区别?城市空间增长与人口密度变化之间的关联关系至今并不清楚,而两者之间的关系却是城市可持续发展研究的基础,对于今后城市规划决策和土地政策制定具有指导意义与参考价值。

本文以进入城市化稳定阶段的欧洲和快速城市化的中国为研究区,选取23个人口在100万以上的城市作为样本,根据研究区1990年、2000年和2014年3期土地利用数据计算城市土地密度。利用圈层分析和反S函数对城市土地密度进行拟合,通过拟合的参数计算各时段城市空间增长速率,建立刻画城市空间增长的紧凑度指标,最后探讨城市空间增长与人口密度之间的关联关系,为今后的土地政策和城市规划提供参考和决策支持。

2 数据来源及方法

2.1 研究区与数据来源

本文选取中国和欧洲23个城市作为研究区,土地利用数据和人口密度数据来源于纽约大学、联合国人居署和林肯土地政策研究中心联合研究的城市扩张项目所公布的数据集（The Atlas of Urban Expansion（2016 Edition））^[23]。本文选用该数据原因如下：① 数据集内200个城市的数据处理规则统一、处理过程清晰明确。该数据集包含了全球代表性的200个样本城市在1990年、2000年和2014年的人口和土地利用数据。土地利用数据来源于空间分辨率为30 m的Landsat影像,通过非监督分类方法（ISODATA）解译遥感影像得到城市用地、开放空间和水体3种城市土地利用类型^[24]。通过Google Earth高空间分辨率遥感影像对非监督分类结果进行验证和评估,结果显示城市用地的用户精度为91%,生产者精度为89.3%^[23]。在城市范围和城市用地的界定上,以遥感影像解译得到的城市用地和开放空间作为城市组团,面积最大的城市组团界定为主城区。对主城区以外的组团建立面积为该组团自身面积1/4的缓冲区,如果缓冲区与主城区相交,则该组团与主城区共同构成城市范围。本研究涉及的中国和欧洲样本城市的范围统一界定为数据集中的组团连同主城区构成的城市范围,建成区面积为遥感影像解译得到的城市用地面积;城市人口数据来源于各城市的人口普查数据,来源途径包括：哥伦比亚大学国际地球科学信息中心（http://www.ciesin.org）,WorldPop网站（www.citypopulation.de）,中国科学院以及各国家的人口统计局网站^[23]。通过统计所界定的城市用地范围内的人口,计算出相应的建成区人口密度。② 数据集内的数据及其结论得到多位****的应用,其适应性和合理性得到验证。在东南亚3个特大城市扩张的宏观模式和微观动态的研究^[25],以及全球120个城市建成区与夜间灯光指数之间关系的研究中^[26],****均采用该数据集内的土地利用数据和人口数据,该数据集的适用性和在全球不同城市之间的可比性均予以验证。

本文从数据集中选取人口100万以上的23个中国和欧洲城市作为研究样本,其中包括13个欧洲城市：伦敦、巴黎、莫斯科、圣彼得堡、柏林、曼彻斯特、米兰、马德里、华沙、布达佩斯、维也纳、安特卫普、谢菲尔德;10个中国城市：北京、上海、广州、常州、成都、海口、济南、唐山、天津、郑州（研究样本空间分布如图1所示）。土地利用数据和人口数据的研究时点为3个时间点（1990年、2000年、2014年）,3种土地利用类型为：城市用地（建成区）、开放空间和水体。

图1

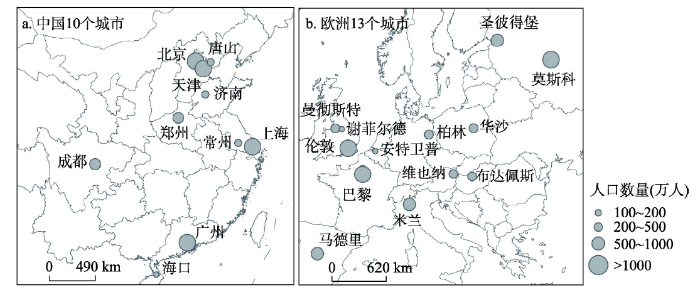
新窗口打开|下载原图ZIP|生成PPT
图1中国和欧洲23个研究城市空间分布及其2014年人口数量

Fig. 1The spatial distribution of 23 sample cities in China and Europe (a. 10 cities of China; b. 13 cities of Europe)

本文选取的样本城市具有代表性和可比性。中欧处于不同的经济发展背景,欧洲经济发展水平居各大洲之首,绝大多数国家都是发达国家,具有较高的城市化率;中国是世界上最大的发展中国家,近40年来经济保持稳步高速增长,中国的城市处于快速城市化阶段。欧洲是最早进入城市化的地区,随着工业革命的发展和深入,在1950年城市化率已达51.3%^[27],当今欧洲大部分地区,城市化率已超过80%并稳定在80%~90%之间^[28]。就城市形态而言,“紧凑型城市”的特征是高密度和相对较短的通勤距离^[29],欧洲的城市常被看作是紧凑的^[30]。欧洲南部的城市最为紧凑,中欧和北欧相比南欧和西欧城市密度较低^[31],其城市结构较松散不连续,人口密度相对于其他区域较低^[28]。当今中国正处在与20世纪50年代欧洲同样的快速城镇化阶段,在2013年中国城市化率达到53.73%^[27]。城市化快速发展的进程中,每年将有大量新增人口涌入城市,为满足人们的生活生产需求,中国的城市用地呈不断扩张的趋势。主要大城市在1990—2010年间经历了快速低密度扩张的过程,城市建设用地人口密度平均每年下降3%~4%^[32]。样本城市之间的基础设施较为完善,整体上呈紧凑型发展,人口密度较高;在私家车持有率不断上升的情况下,中欧城市的居民出行大部分依赖于公共交通;样本城市在2014年人口均达到100万以上,属于大城市。将不同发展阶段的样本城市对比分析,研究结论对快速城市化地区的城市发展决策更具有参考价值。

2.2 研究方法

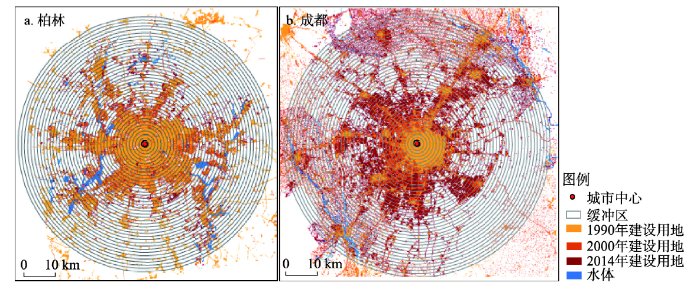
2.2.1 圈层分析法研究选用圈层法来探究各圈层内城市土地密度的空间梯度变化。以The Atlas of Urban Expansion数据集^[23]提供的各城市1990年CBD中心的经纬度,结合高分辨率互联网地图和道路网数据进行检验和核查,最终确定城市中心。以城市中心每隔1 km向外做缓冲区,直至最外圈层覆盖2014年的城市土地范围为止（图2）。在形成的圈层结构基础上,分别计算各圈层内的城市土地密度。城市土地的圈层密度（Density）计算公式为：

（1）

Density = \frac{S_{built - up}}{S_{ring} - S_{water}}

式中：S_built-up为缓冲区内各圆环的建设用地面积;S_ring为缓冲区内各圆环的面积;S_water为缓冲区内各圆环的水体面积。

图2

新窗口打开|下载原图ZIP|生成PPT
图23期土地利用数据以及缓冲区

Fig. 2The buffer areas and urban land area at three time points in Berlin (a) and Chengdu (b)

2.2.2 反S函数 Jiao以2015年中国28个主要城市为样本,研究不透水表面密度到城市中心距离的递减规律,提出了反S函数对这种不透水表面密度的分布进行拟合^[33]。本文运用该反S函数对23个样本城市的土地圈层密度分布进行拟合分析,根据拟合结果得到每个城市基于土地密度的城市形态。反S函数如下：

（2）

f (r) = \frac{1 - c}{1 + e^{α ((\frac{2 r}{D}) - 1)}} + c

式中：

f (r)

表示城市密度;r表示到城市中心的距离;e是欧拉数;α、c和D是参数;α值是控制反S函数曲线斜率的参数;c值表示城市腹地建设用地密度的背景值;D值表示主要城市区域半径的拟合估计值。

根据反S函数拟合的参数,按公式（3）计算每个研究时点的紧凑度,即函数拟合得到的内城区与城区半径的比值。紧凑度K_P值与参数α互为反比,若后一时点相对于前一时点K_P值减小,则表征研究期内城市往紧凑方向发展。紧凑度（K_P）计算公式如下^[33]：

（3）

K_{P} = \frac{r_{2} - r_{1}}{D} = \frac{1.316957}{α}

式中：

r_{2} - r

为内城区范围;D为城市半径;α为控制反S函数曲线斜率的参数。

反S函数拟合得到的参数

D

是主城区的半径估计值,通过对参数

D

值变化的考察,可比较每个城市空间增长的速度,用城市半径

D

值的增长率表征城市空间增长速率（V）,计算公式如下：

（4）

V = \sqrt[n]{(\frac{D_{t}}{D_{0}})} - 1

式中：D_t为研究期末城市半径;D₀为研究期初城市半径;n为研究时段。

3 结果与分析

3.1 人口密度变化

本文采用的人口密度数据为数据集所提供的数据,计算的人口密度为总体城市人口密度,定义为城市常住人口和建成区面积之比。样本城市3个研究时点的人口密度总体变化情况如图3所示。

图3

新窗口打开|下载原图ZIP|生成PPT
图3样本城市人口密度(a)和中欧人口密度变化对比图(b)

Fig. 3Temporal variations of population density (a) and comparison of population density changes in China and Europe (b)

所有城市在3个时点的总人口数和建成区面积都呈一个持续上升的状态。在3个不同研究时段,样本城市的人口密度除伦敦、曼彻斯特、谢菲尔德和上海在2000—2014年内人口密度上升外,几乎都呈下降状态,但这4个城市人口密度上升速率也仅为0.64%、0.50%、0.21%、0.36%。对比中欧的样本城市,中国城市人口密度总体较欧洲城市人口密度高,在1990年中国城市平均人口密度为146.86人/hm²,欧洲城市平均人口密度为87.51人/hm²,但中国城市人口密度降低速率相对较快,2014年欧洲人口密度降低为55.23人/hm²,中国人口密度却降低为68.36人/hm²。对比分析可发现,人口密度降低普遍存在于中国和欧洲城市中,中国城市具有人口密度高、降低速率快的特点,欧洲城市虽然总体人口密度较中国城市低,但降低速率较慢。

3.2 城市空间增长

运用公式（1）计算各个城市相应的圈层土地密度值,根据公式（2）在Matlab 2014软件中采用非线性最小二乘法拟合23个城市土地密度,得到城市土地密度分布反S函数的拟合参数结果如表1所示,23个城市的土地密度函数空间衰减模式及拟合曲线如图4所示。

Tab. 1
表1
表1反S函数拟合参数
Tab. 1The parameters of fitted inverse S-shaped functions in 23 sample cities

城市	1990年				2000年				2014年
城市	ɑ	c	D	R²	ɑ	c	D	R²	ɑ	c	D	R²
北京	4.578	0.116	25.98	0.995	5.336	0.152	29.06	0.994	4.663	0.259	35.55	0.988
上海	1.791	0.117	25.17	0.966	2.784	0.111	44.57	0.984	4.259	0.086	64.51	0.990
广州	1.561	0.047	8.51	0.980	1.512	0.133	22.14	0.956	1.453	0.248	30.43	0.965
天津	3.828	0.067	15.59	0.995	3.850	0.076	16.93	0.994	3.554	0.247	23.82	0.990
成都	3.403	0.022	11.70	0.996	5.615	0.080	18.58	0.995	3.922	0.159	29.78	0.976
常州	4.191	0.047	7.49	0.999	5.039	0.134	13.13	0.997	4.708	0.261	18.05	0.995
郑州	4.202	0.087	12.14	0.995	5.965	0.134	15.26	0.996	4.263	0.172	27.25	0.991
济南	3.852	0.101	13.56	0.993	3.760	0.126	15.36	0.992	3.465	0.171	19.15	0.994
唐山	2.613	0.113	8.00	0.979	3.115	0.148	9.42	0.976	2.737	0.259	12.18	0.967
海口	1.935	0.041	5.10	0.970	2.344	-0.181	9.06	0.965	3.236	-1.015	18.19	0.956
伦敦	2.652	0.047	35.22	0.983	2.996	0.092	37.29	0.984	3.319	0.113	38.25	0.986
巴黎	2.980	0.091	33.89	0.989	3.880	0.157	36.29	0.991	4.436	0.246	37.92	0.990
柏林	2.190	0.053	14.78	0.996	2.571	0.041	20.85	0.998	2.716	0.098	22.76	0.997
莫斯科	2.231	0.124	24.32	0.987	2.631	0.172	28.20	0.987	2.537	0.212	30.04	0.981
马德里	3.395	0.070	12.93	0.989	3.161	0.094	14.89	0.988	3.057	0.134	18.27	0.985
维也纳	2.742	0.054	12.95	0.997	3.105	0.069	16.39	0.998	3.403	0.088	17.41	0.997
米兰	2.851	0.155	14.19	0.957	2.846	0.202	15.52	0.956	2.854	0.279	19.28	0.955
华沙	1.950	0.055	12.38	0.978	2.408	0.081	15.13	0.983	2.662	0.125	17.89	0.981
圣彼得堡	3.513	0.083	21.38	0.987	3.623	0.122	22.01	0.985	3.658	0.149	24.34	0.987
布达佩斯	3.218	0.098	15.74	0.983	3.266	0.116	16.01	0.981	3.334	0.183	17.82	0.971
曼彻斯特	2.092	0.004	19.92	0.973	2.205	0.033	21.41	0.975	2.248	0.017	22.20	0.975
谢菲尔德	2.551	0.067	10.30	0.987	2.733	0.078	10.80	0.986	2.749	0.081	10.91	0.987
安特卫普	1.944	0.106	10.39	0.974	1.953	0.151	10.14	0.971	2.102	0.191	10.28	0.968

新窗口打开|下载CSV

图4

新窗口打开|下载原图ZIP|生成PPT
图4不同圈层内城市不透水表面密度随到城市中心的空间变化及反S函数拟合曲线

Fig. 4The spatial variation of impervious surface density in different circles with the distance to city center and the curve fitted by inverse S function

由表1可以看出,函数拟合效果均很好,R²基本在0.9以上;① α值反映城市形态的紧凑程度,α值越大城市越紧凑,样本城市在3个时点α值的取值范围在1.453~5.965之间;② c值是城市边缘腹地的土地密度值,样本城市在3个时点c值的取值范围在-1.015~0.279之间。一般c值都小于0.1,若出现比较大的数值,如米兰达到0.279,这是大都市区的大城市几乎连续性的连接到周边城市的特点;③ D值代表城市半径,每个城市的城市半径随着时间的推移都在逐渐增大,但增长速率有所差异。1990年城市半径最小和最大的城市分别为海口和伦敦,2014年城市半径最小和最大的城市分别为安特卫普和上海。

曲线形态反映城市扩张情况,紧凑城市的曲线在接近城市中心的位置较平缓,中部快速下降呈陡峭的形状,而快速扩张的城市曲线大幅度向后右偏移。总体上看,中国样本城市在1990年较紧凑,尤其郑州、天津、常州、成都、北京等城市紧凑程度明显。2000年后中国样本城市便开始快速扩张,并且第二个时段扩张的幅度大于第一个时段,例如济南、唐山、天津、郑州、成都、北京,而广州和常州在两个研究时段城市扩张幅度都较大;欧洲的样本城市相对于中国样本城市来说,在1990年相对松散,从曲线可以明显看出柏林、莫斯科、曼彻斯特等城市的曲线向右后偏移,城市处于较松散的状态,而1990年后,除柏林在整个研究时段内扩张程度较大外,其他欧洲城市紧凑程度变化没有中国城市明显。

3.3 城市空间增长与人口密度变化的关系

3.3.1 空间增长速率与人口密度变化的关系根据反S函数拟合得到城市半径估计值D,以城市半径的变化表征城市空间增长速率的变化。通过公式（4）计算每个城市3个时段的城市空间增长速率（图5a）,并对应相同时段的人口密度变化速率做相关性分析（图5b）。

图5

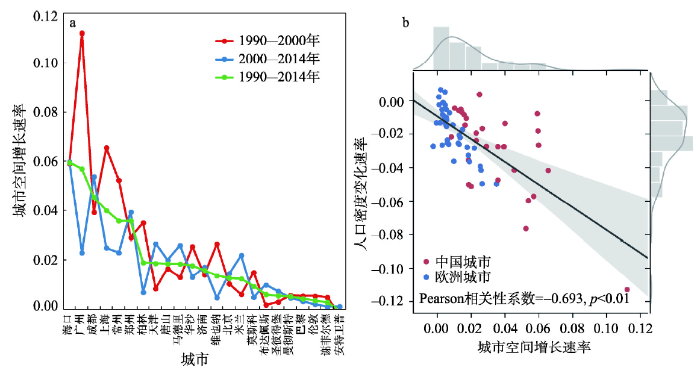
新窗口打开|下载原图ZIP|生成PPT
图5不同时段样本城市空间增长速率(a)与城市空间增长速率和人口密度变化速率相关性(b)

Fig. 5Urban spatial growth rate of sample cities in different periods (a) and correlation between urban spatial growth rate and population density change rate (b)

在1990—2014年整个研究时段内样本城市空间增长速率在0.00~0.11之间,海口、广州、成都、上海等中国城市空间增长速率较高在0.04以上,而安特卫普、谢菲尔德、伦敦、巴黎等欧洲城市空间增长速率较低在0.01以下;2000—2014年相对于1990—2000年城市空间增长速率减小的城市共11个,其中3个中国城市、8个欧洲城市;2000—2014年相对于1990—2000年城市空间增长速率增大的城市共12个,其中7个中国城市,5个欧洲城市。由此看出,研究期内欧洲大部分城市空间增长速率在降低,中国大部分城市空间增长速率在增大。计算Pearson相关系数研究城市空间增长速率与人口密度变化速率之间的相关关系,得到相关系数为-0.693,两者呈强负相关关系。

3.3.2 空间增长方式与人口密度变化的关系通过缓冲区分析计算各圈层内土地密度,由反S函数拟合得到各参数,并计算紧凑度K_P值。紧凑度表征的是某一时点土地密度快速下降的范围占整个城市半径的比值,可刻画某一时点城市形态特征;K_P值越小城市形态越紧凑,反之越松散。两个时点K_P值的变化可描述这段研究期内城市紧凑度的变化,利用两个时点K_P值的差值来刻画研究期内城市空间增长方式。本文定义若城市后一个时点相对于前一个时点K_P值增大,该城市空间增长方式为蔓延型;若K_P值减小,该城市空间增长方式为紧凑型;若K_P值不变（前后两个时点K_P的差值小于0.01）,该城市空间增长方式为保持型。不同时期均采用这一标准进行分类^[33]。计算3个时点样本城市的紧凑度K_P值（图6a）,根据两个时点紧凑度K_P值的差值来表征1990—2000年、2000—2014年两个时段的城市空间增长方式（图6b）。

图6

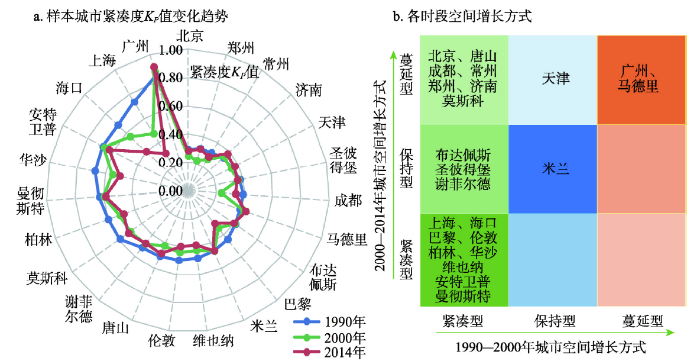
新窗口打开|下载原图ZIP|生成PPT
图6各时点样本城市紧凑度K_P值变化趋势(a)及各时段空间增长方式(b)

Fig. 6The trend of urban compactness $K_{P}$ changes at each time point (a) and the land growth modes of sample cities during each research period (b)

研究结果表明,大部分样本城市K_P值在0.3~0.6之间。1990年中国大部分城市为紧凑城市,欧洲城市相对而言较松散。1990—2000年这一研究时段大部分样本城市空间增长方式为紧凑型,2000—2014年大部分中国城市空间增长方式演变为蔓延型,欧洲一部分城市空间增长方式演变成保持型,另一部分城市依旧维持紧凑型。中国城市在2000年后进入工业化中高级阶段,快速的经济增长和城镇化促使土地需求增大,城市转变为蔓延型空间增长。

计算不同时段样本城市紧凑型、蔓延型和保持型3种不同城市空间增长方式所对应的城市人口密度几何增长率（图7）,将城市空间增长方式与人口密度变化速率结合分析（图8）,研究两者之间的关联关系,得到以下结果：

图7

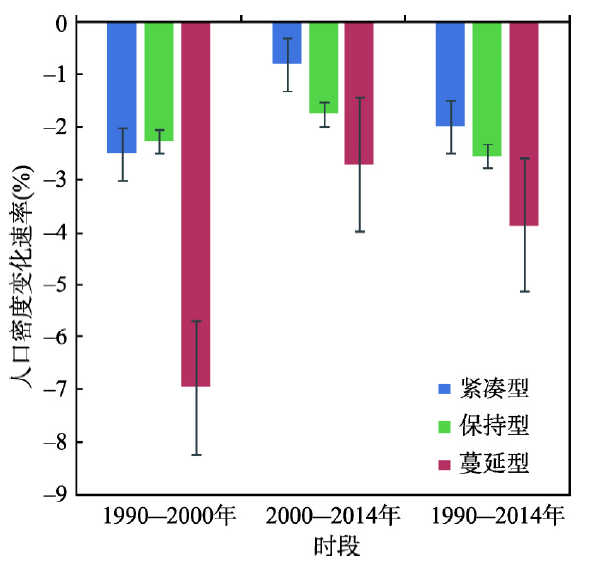新窗口打开|下载原图ZIP|生成PPT
图7不同空间增长方式的城市在各研究时段的平均人口密度降低速率

Fig. 7The population density decline rate of sample cities with different land growth modes in each research period

图8

新窗口打开|下载原图ZIP|生成PPT
图8不同城市空间增长方式对应的人口密度变化速率

Fig. 8Population density change rate of sample cities with different land growth modes

（1）紧凑型的空间增长不一定会带来人口密度的升高,但可以减缓人口密度降低的速率。样本城市中,除伦敦、曼彻斯特、谢菲尔德和上海这4个城市在2000年人口密度升高,其余城市人口密度都呈下降的状态。以紧凑型方式增长的城市,人口密度并没有升高,而是相对于蔓延型城市来说,人口密度降低速率减小。3个研究时段中,蔓延型空间增长城市的平均人口密度降低速率都远大于紧凑型空间增长城市的人口密度降低速率。因此,紧凑型的空间增长并不一定会带来人口密度的升高,但倾向于减缓城市人口密度下降的速率。

（2）当城市连续两个时段以紧凑型方式增长,第二时段人口密度降低速率减小;当第二时段以蔓延型方式增长时,则人口密度降低速率增大。1990—2000年这一研究时段内,样本城市以紧凑型作为主要空间增长方式,其中有19个城市为紧凑型空间增长;2000—2014年,若城市继续以紧凑型方式增长,则人口密度下降速率较上一时段减小,若城市转变为蔓延型空间增长方式,则人口密度降低速率较上一时段增大。若城市本身为蔓延城市,两个研究时段依旧以蔓延型增长方式扩展的话,第二个时段人口密度降低速率会小于第一个时段人口密度降低速率。

（3）第一时段中国和欧州城市几乎都以紧凑方式增长,人口密度降低速率差异不大;第二时段中国城市以蔓延型方式增长,人口密度降低速率增大。欧洲以紧凑型和保持型方式增长,人口密度降低速率减小。1990—2000年这一时段中欧城市大部分以紧凑型空间增长方式进行扩展,两个研究区城市的平均人口密度降低速率没有较大差异;2000—2014年这一时段中国处于快速城镇化阶段,城市转变为蔓延型空间增长方式,进而导致人口密度降低速率增大。而欧洲城市已达到较高城市化率水平,除莫斯科和马德里外其余城市空间增长方式继续以紧凑型方式增长或转变为保持型空间增长方式,人口密度降低速率减小。

4 结论与讨论

4.1 结论

本文采用定量方法刻画城市形态并划分城市空间增长方式（紧凑型、保持型和蔓延型）。在此基础上,本文首次探讨城市空间增长与城市人口密度随时间变化的关联关系,并对比分析了中国和欧洲城市空间增长及其与人口密度变化关联关系的差异。具体结论如下：

（1）中欧城市人口密度普遍随时间降低,中国城市人口密度相对较高且降低速率较快,欧洲城市人口密度相对较低且降低速率较慢;1990—2014年中国城市半径的增长速率明显快于欧洲城市半径的增长速率。城市空间增长速率与人口密度变化速率呈现强负相关关系（Pearson相关系数为-0.693）。

（2）1990—2000年中欧城市几乎都以紧凑型方式增长。2000—2014年中国城市以蔓延型方式增长,且人口密度随时间下降的速率加快;欧洲城市以紧凑型和保持型方式增长,人口密度降低速率减小。

（3）紧凑型的空间增长方式并不一定会带来人口密度的升高,但会减缓人口密度下降的速率。中欧城市对比分析表明城市维持紧凑型空间增长方式,则城市人口密度随时间下降速率减慢;而由紧凑型转为蔓延型空间增长方式,将加剧城市人口密度随时间下降。

4.2 讨论

中国当前正处于城镇化快速发展阶段,推进城镇化又好又快发展需要统筹协调城市空间增长和城市人口增长。研究城市空间增长与人口密度变化的关联关系,并对比分析处于不同发展阶段的世界其他地区的城市化进程对中国未来城市化决策具有重要借鉴价值。现有研究表明城市人口密度随时间下降是一种全球普遍现象和长期历史趋势^[22],本研究的中欧典型城市分析也进一步验证了这一趋势。城市人口密度随时间下降反映出人均建设用地面积增加,这将提高人口城镇化的土地成本。城市人口密度下降在中国快速城市化进程中也具有普遍性,结合中国“人多地少”的基本国情,我们认为亟需采取有效措施减缓或抑制城市人口密度下降趋势。值得警惕的是,即使在欧洲高度城市化的发达国家,城市人口密度仍然呈现下降趋势。这提示我们,抑制城市人口密度下降需要长期持续关注并采取有效措施。在城市化进程中,节约集约利用土地、提高土地利用效率、提高城市综合承载力必须作为长期坚持的基本方针,才能应对人均土地资源消耗惯性增加的巨大挑战,这对于保障中国耕地安全、生态安全和可持续发展都具有重大意义。

本研究证明了紧凑型空间增长方式可以有效减缓城市人口密度随时间下降的速度。该发现既对紧凑城市研究具有理论价值,又对城市规划的实践具有指导意义。面向可持续发展目标,中国城市应充分考虑城市人口密度下降的风险,采取紧凑型空间增长战略,可采用的措施包括但不限于：划定城市增长边界（Urban Growth Boundary, UGB）;优先发展公共交通,鼓励城市土地混合利用,提高土地利用效率;实施城市更新和低效用地再开发,维持和提高中心城区的吸引力等。

城市空间增长与城市人口密度变化是一个长期动态过程。受限于数据可获得性,本文只探讨了1990年以来中国和欧洲主要城市的城市空间增长与人口密度变化的差异。在未来研究中,横向上要加强中国城市与美国、日本等发达国家城市的对比,探究不同国家城市的发展差异;纵向上要深入城市内部,探究更细尺度的空间增长与人口密度变化的关联机制。此外,随着海量新兴数据的不断涌现,结合多源数据感知不同类别人口的密度变化将有助于进一步深入理解城市空间增长和城市人口密度变化的微观机制。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Brueckner

. Urban sprawl: Diagnosis and remedies
International Regional Science Review, 2000,23(2):160-171.

DOI:10.1177/016001700761012710 URL [本文引用: 1]

[2]

Angel

, Parent

, Civco D

, et al. The dimensions of global urban expansion: Estimates and projections for all countries, 2000-2050
Progress in Planning, 2011,75(2):53-107.

DOI:10.1016/j.progress.2011.04.001 URL [本文引用: 1]

[3]

Angel

, Parent

, Civco D

, et al. Making Room for a Planet of Cities
Washington D C: Targeted News Service, 2011.

[本文引用: 1]

[4]

Zhou

Chunshan

, Ye

Changdong

. Features and causes of urban spatial growth in Chinese metropolises
Acta Geographica Sinica, 2013,68(6):728-738.