How to teach genetic drift
Chunming Wang, Changjun Lin, Huyuan FengSchool of Life Sciences, Lanzhou University, Lanzhou 730000, China编委: 陈德富
收稿日期:2020-09-24修回日期:2020-11-29网络出版日期:2020-12-20
| 基金资助: |
Received:2020-09-24Revised:2020-11-29Online:2020-12-20
| Fund supported: |
作者简介 About authors
王春明,博士,副教授,硕士生导师,研究方向:细胞遗传学。E-mail:

摘要
遗传漂变是影响群体遗传平衡的4个重要因素之一。因为它的作用形式不如突变、选择、迁移这3个因素那么直观易懂,所以在理解和掌握上存在较大的困难。尤其目前国内外教材中关于遗传漂变内容的介绍系统性不足,要么过于粗略,要么完全忽视了二项式定理这样的数学基础,造成了遗传漂变学习长期不到位的困难局面。本文总结得出遗传漂变的5个基本属性,即固有性、普遍性、随机性、无方向性、有规律性。进而从遗传漂变的遗传基础是雌雄配子的自由组合出发,指出抽样误差属性是遗传漂变固有的本质特征,并循序渐进地从N = 1这样仅仅由1个个体组成的极端小群体出发,推演出遗传漂变随着群体变大而影响减弱的性质,通过二项式定理数学模型、二项分布的特点、以及计算机模拟结果,形象直观地展示遗传漂变的作用,助力遗传漂变教学。
关键词:
Abstract
Genetic drift is one of the four important factors affecting population genetic balance. Because its form of action is not as apparent as mutation, selection, and migration, which are intuitive and easy to understand, there are potential difficulties in understanding and mastering genetic drift. A particularly prominent problem is that the current introduction of genetic drift contents in textbooks is systematically insufficient. They are either even too rough, or completely neglecting the mathematical foundation such as the binomial theorem, resulting in long-term inadequate learning of genetic drift. In this paper, we summarize the five basic attributes of genetic drift, namely inherent, universal, random, non-directional, and regular features. Based on the concept that the genetic basis of genetic drift is the free combination of male and female gametes, we pointed out that the attribute of random sampling error is the inherent essential feature of genetic drift. Then step by step, from an extremely small population consisting of only one individual (N = 1), we deduced that the effect of genetic drift decreased while population size increased. Through introducing the mathematical model of the binomial theorem, the characteristics of the binomial distribution, and the results of computer simulations, the effect of genetic drift is visually and intuitively displayed to help the teaching the concept of genetic drift.
Keywords:
PDF (662KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
王春明, 林昌俊, 冯虎元. 遗传漂变教学方法刍议. 遗传[J], 2020, 42(12): 1211-1220 doi:10.16288/j.yczz.20-310
Chunming Wang.
群体遗传平衡是指群体的基因频率和基因型频率在平衡群体中世代不变的现象。其中,基因频率世代不变是群体遗传平衡的本质属性,只要基因频率不变,基因型频率自然也保持不变。因此,影响群体遗传平衡的因素可以理解为影响基因频率的因素,这样的因素主要有4个,分别是:突变、选择、迁移、遗传漂变。前3者的作用方式比较直观,容易理解。比如,假设群体中有一对等位基因,分别为A和a。突变的作用可以理解为,A正向突变成a,导致a基因增多;或者a反向突变成A,导致A基因增多;只要正反突变的结果不能相互抵消,就会导致二者的基因频率发生变化而影响遗传平衡。选择的作用可举例为,当选择对aa个体不利时,那么a基因的频率在群体中就会减少。迁移的作用可举例为,A迁出群体,使A基因减少;或者a迁入群体,使a基因增加;不平衡的迁出和迁入都可以造成群体基因频率的不平衡。这3个因素对群体遗传平衡的影响通过简单而直观的分析就可以理解,而遗传漂变的作用方式就没有这么直观易懂了。
笔者曾撰文探讨如何理解遗传漂变定义中的抽样误差概念;[1];,指出所谓抽样误差导致的群体基因频率的随机波动,是指由于雌雄配子形成合子的过程是随机的,这个过程就“相当于”从亲代产生的配子库(gene pool,基因池)中“随机抽样”的过程,因此可以用抽样误差规律来表征遗传漂变的作用规律。该文澄清了遗传漂变定义中抽样误差的概念,给出了更易被理解的建议。但是,文中对于如何具体安排遗传漂变的讲授内容着墨不多,未能从根本上彻底解决遗传漂变的教学问题,这也正是撰写本文的初衷。
本科遗传学对影响群体遗传平衡的4个主要因素的介绍都相对简明,这是由本科教学目的所决定的。通过学习本科遗传学课程,为学生打下遗传学的知识基础,而不是要培养遗传学科某一具体方向的专门人才。因此,在群体遗传平衡这部分的内容安排上尽量简化模型,规范条件,以期达到易于理解和掌握各因素作用规律和作用结果的目的。比如,突变的影响通常以一对等位基因A/a为例,正反向突变率世代不变;选择的作用通常针对aa个体的完全选择和不完全选择;迁移条件的设定则更加严格地限制在“迁移发生在群体生殖之前,迁出者不在群体中生殖,迁入者在群体内生殖,每代的迁移率保持不变”。这些条件的限制都是为了在普通遗传学中尽量将相关知识点介绍得清楚易懂这一教学目的。实际上,突变、选择、迁移、遗传漂变等因素对群体遗传平衡的影响是非常复杂的,相应的研究成果也非常丰富,很难在本科教材中用一章篇幅完整地呈现。这方面有群体遗传学和统计遗传学等教材和专著详尽介绍;[2,3];。本文对遗传漂变教学方法的建议同样尽量简化模型,限定前提条件为:群体中的个体生殖力相同;随机交配;雌雄配子数目无限大;不存在突变、选择、迁移等因素影响;世代不重叠且大小维持不变;且针对二倍体的一对等位基因A/a,在基因频率相等的前提条件下(p = q = 1/2),介绍遗传漂变的作用在不同大小群体中的变化规律,力求循序渐进地加深学生对遗传漂变规律的认知、理解和掌握。
1 遗传漂变的作用在大小群体中都存在
遗传漂变对群体遗传平衡的影响在所有群体中都存在,这是由有性生殖雌雄配子自由组合形成合子(后代个体)这一基本规律所决定的。我们知道,群体世代传递的基础是后代个体的产生,这一过程是雌雄配子随机自由组合的结果。这个自由组合的过程,就类似于从群体的雌雄配子库中随机抽取一个配子,与另外一个随机抽取的异性配子结合成合子,即后代个体。这个过程类似于抽样的过程。因此,可以用抽样的性质来研究。正是因为抽样误差存在的固有属性,决定了遗传漂变对群体遗传平衡的影响是不可避免的,在群体中普遍存在。基于此,遗传漂变的性质可归纳为如下5点:固有性、普遍性、随机性、无方向性、有规律性。
固有性:遗传漂变的存在是由其固有的内在因素(合子形成)决定的,与突变、选择、迁移这些可以发生扰动的因素不同,如果群体不发生突变、选择和迁移,则不会影响遗传平衡,而遗传漂变是群体无法避免的固有存在。因此,也可概括为:内因决定。
普遍性:遗传漂变的遗传基础是雌雄配子自由组合形成合子,这一过程在群体中普遍存在,因此遗传漂变的存在也具有普遍性。尤其在生活中常见的有限群体中,遗传漂变普遍具有显著作用。因此,可概括为:普遍存在。
随机性:遗传漂变对群体遗传平衡影响程度的大小是随机的,不能准确预测,这可用二项分布的规律来说明(见本文第3节)。因此,可概括为:大小随机。
无方向性:遗传漂变对基因频率变化方向的影响是不确定的,到底是A增加还是a增加,是无法预见的,只有等到后代群体产生后,才知道确切的结果。因此,可概括为:方向不定。
有规律性:遗传漂变的作用符合抽样误差的变化规律,因此又是有规律可循的。就如核外电子的分布一样,虽然我们不知道某一时刻电子的确切位置,但我们知道电子在核外的可能分布区域。遗传漂变也一样,我们不能确切知道下一代具体会发生多大的遗传漂变,会有什么方向的影响,但是遗传漂变的作用是可以用抽样误差规律来表征的。因此,可概括为:符合抽样误差规律。
可见,固有性、普遍性、随机性、无方向性、有规律性,这五个属性还可以理解和表述为“内因决定,普遍存在,大小随机,方向不确定,符合抽样误差规律”。
这些性质的根本基础是群体后代形成是类似抽样的过程,因此可用抽样误差的变化规律来衡量遗传漂变的作用规律。而抽样误差与群体大小密切相关,小群体中抽样误差大,大群体中抽样误差小。因此,遗传漂变在大小群体中的影响也呈现在小群体中影响大、在大群体中影响小的特点。下面从极端小群体(N = 1)开始,循序渐进地加以介绍。
2 遗传漂变在小群体中影响大,在大群体中影响小
我们以群体中一对等位基因A/a为例,来说明群体平衡的情况。假设A/a的基因频率分别为p和q,且二者频率相等p = q = 1/2。平衡群体世代间基因频率保持不变,下一代的A/a基因的频率也仍然是p = q = 1/2。如果p和q值发生变化,则说明群体平衡受到了影响。在极端情况下,有可能p = 1, q = 0,表明后代群体里全部是A基因,没有了a基因,我们称这种情况为A基因被固定,而a基因被丢失。反之亦然。由1个个体组成的群体是最小的群体,N = 1。在现实情况下,这种群体可以由自花授粉的植物来实现,但是所结的种子也必须假定为只有1粒。假设第1代群体基因型为Aa,群体的大小保持不变,第2代仍然是N = 1,也就是说每代都仅结一颗种子,如果群体平衡,则这1粒种子的基因型应该是Aa,p = q = 1/2。那么这个群体的第2代保持平衡状态的概率是多少呢?在没有突变、选择、迁移等因素的影响下,仅仅是由于形成合子时的“抽样”误差的作用,第2代这1个个体的基因型就有3种可能,AA、Aa、aa,它们的比例为1/4、1/2、1/4。可见,在第2代中,群体的基因型只有1/2的可能性是Aa,即与第1代保持平衡;而另外1/2的概率是不平衡群体,其中有1/4的可能性是AA,此时A基因被固定,a基因丢失,还有1/4的可能性是aa,此时A基因丢失,a基因固定。后面这两种基因型为AA或aa的情况下,群体都失去了平衡,分别实现了A和a基因的固定,相应的丢失了它们的等位基因。这就是遗传漂变(随机抽样)导致的群体基因频率的随机变化作用,完全是由于雌雄配子随机结合造成的,不受其它因素的影响,是所有群体内在的性质。总的来看,在N = 1的群体中,经过1代的随机交配,第2代有1/2的几率出现基因固定的现象。可见,在小群体中发生基因丢失或固定现象的概率非常大,这不是任何外来因素造成的,而是完全随机的事件,这就是随机遗传漂变作用的体现。
让我们增加群体的大小,看看在N = 2的群体中遗传漂变的作用。第1代群体产生的配子基因频率依然假设为p = q = 1/2,即A基因和a基因各占1/2。那么,第1代的2个初始个体的基因型就可能都是Aa,或者AA和aa各1个,只要满足群体A和a基因频率相等即可。这2个个体组成的群体实现遗传平衡时,其第2代群体的2个个体的基因型也可能都是Aa,或者AA和aa各1个;不平衡群体的组成情况包括都是AA或aa,或者1个AA、1个Aa,或者1个Aa、1个aa等情况,只要A和a的频率不再为1/2,就表示群体失去了平衡。我们在这里延续N = 1的分析方式,仅仅考察极端的情况,也就是基因被固定或丢失的情况(2个AA或2个aa)。后代不同基因型个体出现的概率仍然是AA、Aa、aa对应1/4、1/2、1/4的比例。可计算得到基因固定于A或a的比例分别为1/4 × 1/4 = 1/16,整个固定发生的总概率为1/16 + 1/16 = 1/8。可见,N值仅增加1,基因固定发生的概率就从N =1群体的1/2迅速降低为N = 2群体的1/8。也就是说,随着群体的增大,遗传漂变造成的基因固定现象发生的概率迅速降低,从这个极端情况说明遗传漂变的作用大小与群体规模大小关系密切。
同理:N = 3时AAAAAA和aaaaaa两类固定发生的总概率为1/32;N = 4时AAAAAAAA和aaaaaaaa两类固定发生的总概率1/128。N值每增加1,两类固定发生的概率减少(1/2);2;。表1总结了不同大小群体中,基因被固定概率的变化情况,其中群体大小为N时出现第2代群体的基因被固定的概率为 (1/2);2;;N;;-1; (表1)。
表1群体繁殖一代后,基因被固定或丢失的概率
Table 1
Table 1Probability of allele loss or fixation after one generation
| 群体大小 | 基因固定类型 | 每类固定发生概率 | 固定发生总概率 |
|---|---|---|---|
| 1 | AA;aa | 1/4 = (1/2);2; | 1/2 |
| 2 | AAAA;aaaa | (1/4);2; = (1/2);4; | (1/2);3; |
| 3 | AAAAAA;aaaaaa | (1/4);3; = (1/2);6; | (1/2);5; |
| ┇ | ┇ | ┇ | ┇ |
| N | N•AA;N•aa | (1/4);N; = (1/2);2;;N; | (1/2);2;;N;;-1; |
新窗口打开|下载CSV
表1可见,遗传漂变对群体遗传平衡的影响与群体大小密切相关。遗传漂变在小群体中的作用大,而在大群体中的作用小。而这仅仅是通过基因被固定这一极端情况发生的概率角度进行的简单分析。实际上,遗传不平衡的情况当然不仅仅是上述极端情况,而是还有许多中间过渡形式。以N = 3群体为例,第2代的3个后代个体基因型依据A或a基因的数目不同一共可组成7种群体,分别是:AAAAAA, AAAAAa, AAAAaa (AAAaAa), AAAaaa (AaAaAa), AAaaaa (AaAaaa), Aaaaaa, aaaaaa。上述各组群体书写的规律是A基因逐渐减少,a基因逐渐增加;括号内容表示在A和a数目不变情况下,具体还可能有其他类型基因型的组合。其中,仅有AAAaaa群体是平衡群体,其余群体都存在不同程度的不平衡,这就是遗传漂变的具体表现,完全是随机抽样导致的结果。不同大小群体基因型分布及平衡群体占比情况总结于表2。
Table 2
表2
表2群体基因型分布及绝对平衡群体占比
Table 2
| 群体大小 | 群体类型分布 | 群体类型系数 | 类型数 | 平衡群体占比 |
|---|---|---|---|---|
| 1 | AA, Aa, aa | 1 2 1 | 3 | 2/4 |
| 2 | AAAA, AAAa, AAaa (AaAa), Aaaa, aaaa | 1 4 6 4 1 | 5 | 6/16 |
| 3 | AAAAAA, AAAAAa, AAAAaa (AAAaAa), AAAaaa<break/>(AaAaAa), AAaaaa (AaAaaa), Aaaaaa, aaaaaa | 1 6 15 20 15 6 1 | 7 | 20/64 |
| ┇ | ┇ | ┇ | ┇ | ┇ |
| N | A;2;;N;, A;2;;N;;-1;a, A;2;;N;;-2;a;2;, ∙∙∙, A;2;a;2;;N;;-2;, Aa;2;;N;;-1;, a;2;;N; | C;0;2NC;1;2NC;2;2N…C;2N-2;2NC;2N-1;2NC;2N;2N | 2N+1 | C;N;2Np;N;q;N; |
新窗口打开|下载CSV
表2展示的群体类型分布中,当N = 1, 2, 3等较小数值时,我们直接用个体的基因型表示群体的组成。在通项N行,我们无法再一一罗列出所有可能的基因型组合,因此,用群体类型中包含多少A和a来表示。如某类型群体包含x个A,y个a,则表示为A;x;a;y;。因为讨论的是二倍体,所以在含有N个个体的群体中,等位基因共有2N个,如果全部都是A,则表示为A;2;;N;a;0;即A;2;;N;;接下来A少一个,a多一个,表示为A;2;;N;;-1;a;1;即A;2;;N;;-1;a;其余各项依此类推。
N = 1时,群体类型有AAAaaa三种,可用二项式(A + a);2;的展开式导出,系数(比例)为1 2 1。N = 2 时,群体类型有AAAA, AAAa, AAaa (AaAa), Aaaa, aaaa五种,其中AAaa (AaAa)依据A和a数目相等可归为一类;同样可通过二项式(A + a);4;的展开式导出,系数为1 4 6 4 1。N = 3时的群体类型情况同样可通过(A + a);6;的展开式导出。可见,群体类型的分布规律及其相对比例符合二项式展开式的规律。
表2可见,绝对平衡的群体(p = q = 1/2)在所有可能观察到的群体中所占比例从2/4迅速减少,其余类型群体或多或少存在的不平衡现象都不是外界因素影响造成的,而是后代形成过程本身存在的固有性质。正如前述,这是雌雄配子自由组合形成后代个体的固有属性,其分布规律符合随机抽样原理。实际上,遗传漂变对群体遗传平衡的影响确实可以用二项式定理和二项展开式来完美诠释。
3遗传漂变的作用方式可以用二项式定理及二项展开式来表征
3.1 群体类型分布规律与标准二项式中n为偶数的二项式展开式的情况相符
把表2中的A和a分别用它们的基因频率p和q代替,更能直观反映出表中内容与二项式定理和二项展开式之间的关系(表3)。表3中“群体类型分布”用基因频率p和q代替了表2中等位基因A和a的组合。例如,N = 1群体后代AAAaaa分别用p;2;pgq;2;代替。这样的表述在N> 1以上的群体后代类型表示中优势特别明显,比如N = 2群体中用p;4;代替了AAAA,用p;2;q;2;代替了AAaa和AaAa。如此表述的优点有4:(1)使得群体类型的描述更为简洁;(2)用基因频率表示群体类型也与基因频率是决定群体遗传结构的本质因素这一特性相一致;(3)便于计算某类型群体出现的概率;(4)如此表述在形式上与二项分布规律更为一致。
表4是二项式及其展开式,与表3比较可以发现群体类型分布规律与标准二项式中n为偶数的二项式展开式的情况相符。这是由每个二倍体含有1对等位基因的性质所决定的。也就是说,每个个体含有2个等位基因,因此等位基因在群体中是成对增加的,群体大小每增加一个个体就相当于增加了1对(2个)等位基因(例如本文讨论的A/a)。因此,N个个体的群体就含有2N个等位基因,n = 2N,它们之间的组合就符合二项式(p + q);2;;N;展开式的分布规律。
表4所示二项式定理及其展开式是高中阶段的学习内容,将其应用到大学《遗传学》的学习过程中,做到温故知新,学以致用,把数学理论应到鲜活的遗传学规律之中。
二项式展开式:
二项式展开式通项:
相应的,遗传漂变作用下的群体类型分布也可归类总结为二项展开式和通项。根据遗传学的习惯和字母在遗传学中的意义,我们用p和q分别代替a和b,用k代替r。得到如下公式:
展开式:
通项:
上面这个通项的含义是,在N个个体组成的群体繁殖后代中,有k个a基因和2N-k个A基因这样的后代群体出现的可能性(几率)。
我们在进行遗传分析的时候,习惯于针对A基因进行分析。故可将上述通项形式修改为以A基因个数为考察的目标。即后代群体中A的数目为k个,相应的a基因数目为2N-k个,这样的后代群体出现的可能性通式为:
表3群体类型分布规律
Table 3
Table 3Distribution of population types
| 群体大小 | 群体类型分布 | 群体类型系数 | 群体类型数 | 公式 |
|---|---|---|---|---|
| 1 | p;2;pqq;2; | 1 2 1 | 3 | (p + q);2; |
| 2 | p;4;p;3;qp;2;q;2;pq;3;q;4; | 1 4 6 4 1 | 5 | (p + q);4; |
| 3 | p;6;p;5;qp;4;q;2;p;3;q;3;p;2;q;4;pq;5;q;6; | 1 6 15 20 15 6 1 | 7 | (p + q);6; |
| ┇ | ┇ | ┇ | ┇ | ┇ |
| N | p;2;;N;p;2;;N;;-1;q ∙∙∙ pq;2;;N;;-1;q;2;;N; | C;0;2NC;1;2N…C;2N-1;2NC;2N;2N | 2N+1 | (p + q);2;;N; |
新窗口打开|下载CSV
Table 4
表4
表4二项式定理及其展开式(a + b);n;
Table 4
| n | 项 | 各项系数 | 项数 | 公式 |
|---|---|---|---|---|
| 1 | a b | 1 1 | 2 | (a + b);1; |
| 2 | a;2;abb;2; | 1 2 1 | 3 | (a + b);2; |
| 3 | a;3;a;2;bab;2;b;3; | 1 3 3 1 | 4 | (a + b);3; |
| 4 | a;4;a;3;ba;2;b;2;ab;3;b;4; | 1 4 6 4 1 | 5 | (a + b);4; |
| 5 | a;5;a;4;ba;3;b;2;a;2;b;3;ab;4;b;5; | 1 5 10 10 5 1 | 6 | (a + b);5; |
| 6 | a;6;a;5;ba;4;b;2;a;3;b;3;a;2;b;4;ab;5;b;6; | 1 6 15 20 15 6 1 | 7 | (a + b);6; |
| ┇ | ┇ | ┇ | ┇ | ┇ |
| n | a;n;a;n-;;1;b a;n-;;2;b;2; ∙∙∙ a;2;b;n-;;2;ab;n-;;1;b;n; | C;0;nC;1;nC;2;n…C;2n-2;2NC;2n-1;C;n;n | n+1 | (a + b);n; |
新窗口打开|下载CSV
3.2 群体类型分布随N值增加而接近正态分布(p = q = 1/2)
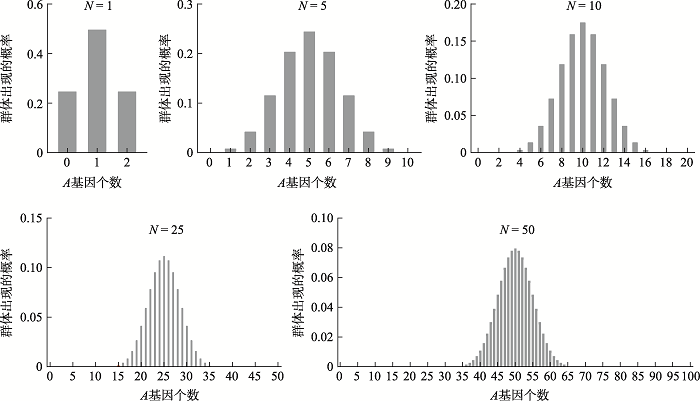
上述用于表示群体类型分布的二项展开式(公式3)各项的实际意义是,表征后代群体可能的基因比例。以通项(公式5)为例,其代表的是后代群体中含有k个A和2N-k个a的群体出现的可能概率。如果把有限群体各项出现的概率对应所含A基因的个数作图,就可以得到群体类型分布图(图1),即二项分布图。该图可直观显示仅仅由于遗传漂变(抽样误差)作用,就可导致后代群体在基因频率方面的差异变化情况,也就是后代群体遗传平衡的差异。图1具体列出了N = 1, 5, 10, 25, 50这5种不同大小群体繁殖一代后可能出现的基因组合分布图,这些都是依据表3中各项分布规律计算的结果。各图的横坐标代表A基因数,表示群体中各个个体所含A基因从0到2N个;纵坐标是这些群体类型在后代群体中出现的概率。各图中N个A的群体类型所含A和a基因个数相等(p = q = 1/2),属于平衡群体,此类群体在图中所占比例依次为0.5000, 0.2461, 0.1762, 0.1123, 0.0796。可见,初始基因频率为p = q = 1/2的平衡群体,其繁殖一代后得到的新群体中,严格意义上的p = q = 1/2(A基因数 = a基因数)后代群体的概率也随着群体所含个体增加而迅速减小。其余绝大多数情况下得到的群体都或多或少存在着A和a基因数不相同的情况。这是抽样误差存在的客观规律,也是遗传漂变发挥作用的客观表现。
我们还应该看到,图1中各图的纵坐标数值随着群体增大而迅速减小,说明后代群体多样性增加,各具体群体类型出现的概率减小。图1直观地展示了随着群体的增大,绝对平衡的群体在后代中出现的概率迅速降低,而不平衡群体出现的概率则持续增加,这也说明遗传漂变对大群体同样会表现出作用。
二项分布的均数公式μ (mu) = np。图1中均数μ = np = 2N × 0.5 = N,这与图中所示N个A的群体类型所含A和a基因个数相等(p = q = 1/2,属于平衡群体)是一致的。均数处代表的群体类型频率也是最高的。
图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1不同大小群体繁衍后形成的群体类型分布
N = 1, 5, 10, 25, 50。等位基因A, a; p = q = 1/2。
Fig. 1Population type distribution of different sizes of population after one generation
二项分布是离散分布,其计算有时候非常繁琐,因此在实际应用中常常进行近似操作。比如,在np> 5和n(1-p) > 5时,二项分布就非常接近正态分布,可以用正态分布近似;[4];,这是一个常用的规则。也有文献报道,当np> 10且n(1-p) > 10时,用正态分布对二项分布作近似计算;[5];。可见,不同研究者对二项分布的正态分布近似条件略有不同,但共同点在于都强调需要相对较大规模的群体才适合应用正态分布规律作近似分析。以本文p = q = 1/2的假设条件来推断,上述群体规模要求分别为n> 10和n> 20。从图1可见,N = 25, 50这两组图形无疑更接近正态分布。
正态分布是连续分布,是概率论中最常见、也是最重要的概率分布,它在理论上和应用中都占有头等重要的地位。对于以频率表示的资料,正态分布数据分析的标准差计算公式为:$\text{ }\!\!\sigma\!\!\text{ }=\sqrt{\frac{pq}{n}}$;该公式可用来衡量抽样误差与样本大小(n)的关系。由于遗传群体中n = 2N,因此在用于评价遗传漂变作用与群体大小(N)关系时,该公式即转换为:$\text{ }\!\!\sigma\!\!\text{ }=\sqrt{\frac{pq}{2N}}$。这就是教材中该公式的来源,公式具体应用详见教材中的叙述;[6];,此处不再赘述。
图1各群体中,仅仅A = N的群体是绝对平衡的(p = q = 1/2),其余群体都存在或多或少的差异,这就是遗传漂变(随机抽样)对群体平衡的影响。如果认为其余群体都是不平衡的,显然是过于严苛、不符合实际的。那么,我们如何判断群体是否平衡呢?如何认定哪些类型的群体是平衡的呢?如果仅仅考察一代的世代交替,图1展示的群体出现的概率可以人为地规定某个范围的群体是平衡的。比如,用95%置信区间的方法。但是,这样的思考其实是没有必要的。因为,群体的遗传不是一代的问题,基因频率在这一代发生了偏差,在遗传漂变的作用下,在下一代还有可能调整过来,也有可能继续发生大的偏离,这就需要考察多个世代交替,然后才能评价群体遗传是否稳定,是否平衡,这样才有意义。因此,仅仅从图1呈现的各个群体类型的概率分布去考察群体是否平衡是不充分的,也是不必要的。可以用计算机模拟的方法,展示不同大小群体在经过多个世代交替后的基因频率变化,以此反映遗传漂变对群体遗传平衡的作用。
3.3计算机模拟结果显示随着群体增大,遗传漂变作用减小
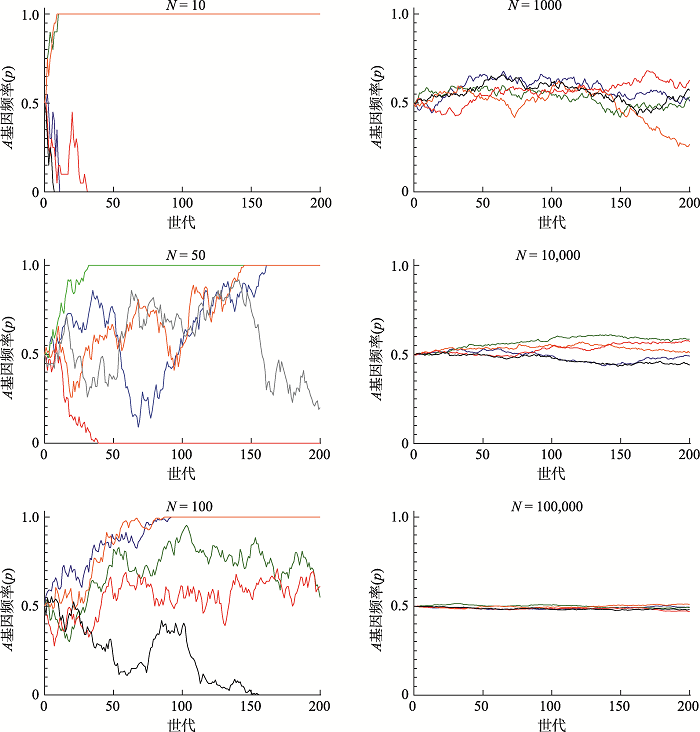
应用Excel软件模拟了5组不同大小群体世代交替200代后,基因频率变化情况(图2)。Excel软件模拟遗传漂变方法见丁建华等文献;[7];。计算机模拟是正确理解遗传漂变作用的重要手段。图2针对不同大小群体,各模拟了5组群体传递200代过程中,群体基因频率变化的情况。各组起始基因频率均为p = q = 1/2。图中N = 10的5个群体在30代之前均已固定,其中2个群体基因频率固定为1(p = 1, q = 0),3个群体固定为0(p = 0, q = 1)。N = 50的5个群体中有3个群体的基因频率固定为1,1个固定为0,仍有1个在200代时仍未固定,但已严重偏离初始基因频率1/2。N = 100的5个群体中有2个固定为1,1个固定为0,其余2个在200代时仍存在,且变化幅度较N = 50的要小。这些都说明,在比较小的群体中,遗传漂变的作用非常明显。如果继续比较N = 1 000, 10 000, 100 000这3组较大群体的情况,可以明显发现与前面的3组较小群体的差别,它们都没有发生基因频率的固定。而且,基因频率的变化幅度随群体增大明显减少,到N = 100 000这组群体时,基因频率的变化幅度已非常微小,几乎呈一束紧密的直线。可见,随着群体的增大,遗传漂变的作用明显减弱,且在大群体中的影响微乎其微。如果像平衡群体定义中强调的“无限大的群体”,则遗传漂变的作用就可以忽略不计了。总之,图2直观展现了遗传漂变与群体大小的关系,非常有利于对遗传漂变影响的理解和掌握。需要指出的是,图2展示的各组模拟结果不是固定不变的,而仅仅是一次由计算机随机模拟生成的结果,可以随着每次的随机模拟而有所改变。
图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2计算机模拟5组不同大小群体世代交替200代过程中A基因频率(p)的变化情况
条不同颜色的线代
Fig. 2Computer simulations of random genetic drift over 200 generations. Each coloured line represents a simulated population5
4 讨论与总结
专注本科教育,提高教学质量,一直是高校教师的职业追求。在遗传学教学方面,也涌现出多方探索成果。近期就有将较为尖端的遗传学研究技术引入实验教学;[8,9];,也有针对传统教学内容进行的素材挖掘和扩展;[10];,还有针对教学方法的实践探索;[11];。笔者执教本科遗传学十几年来,特别执着于教学内容的思考,曾撰文探讨遗传漂变概念;[1];,也曾就粗糙脉孢菌顺序四分子分析独有的7种子囊型归类问题进行过探究;[12];。本文则进一步针对遗传漂变教学的具体方法和内容提出建议。遗传漂变无论是在概念上,还是在具体内容方面,都很难准确及简洁地介绍清楚。因此,在中外相关教材中都存在着或多或少的不足。以国外遗传学教材“Introduction to Genetic Analysis”和“Principles of Genetics”为例。前者内容较为详实,但对二项分布介绍不足,且缺乏与正态分布关系的讨论;[13];;后者则内容过于简略单薄;[14];;二者均无法满足对遗传漂变准确理解和把握的要求。这与国内教材的情况是一致的。原因可能与遗传漂变属于群体遗传学范畴、内容丰富、数学知识要求相对较高有关,导致很难在普通遗传学中用有限篇幅达到通透的效果,进而造成了多年来很难透彻理解和准确把握的窘境。本文据此整理了相关资料,从最小群体(N = 1)出发,通过二项式定理数学模型、二项分布的特点、以及计算机模拟结果,形象直观地展示遗传漂变的作用。
简单总结如下:
1. 遗传漂变对群体遗传平衡的影响具有5个基本性质:固有性、普遍性、随机性、无方向性、有规律性。
2. 遗传漂变作用对小群体影响大,对大群体影响小。
3. 遗传漂变作用导致的后代群体基因频率分布特点符合二项分布,当群体大于10(或20),可用正态分布近似计算,用抽样误差$\text{ }\!\!\sigma\!\!\text{ }=\sqrt{\frac{pq}{2N}}$评价遗传漂变作用与群体大小的关系。
4. 计算机模拟是理解遗传漂变作用的直观手段,需要经过多个世代交替才能反映出遗传漂变对群体遗传平衡的影响。
需要指出的是,本文介绍的内容并非遗传漂变的全部,而仅仅是以现有教材为基础,属于Wright-Fisher模型的部分内容;[1];。实际上,遗传漂变相关研究成果颇丰,远非本文所能涵盖。本文写作目的仅是利用简单且符合逻辑的论述,帮助读者理解和掌握相关知识,形成正确的观念。
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 3]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
.
[本文引用: 1]
[本文引用: 1]
.
[本文引用: 1]
