,1,*, 赵平2, 赵秀华2, 张锦秀1, 朱丽薇2, 欧阳磊2, 张笑颜1Impact of environmental factors on the decoupling coefficient and the estimation of canopy stomatal conductance for ever-green broad-leaved tree species
ZHANG Zhen-Zhen,1,*, ZHAO Ping2, ZHAO Xiu-Hua2, ZHANG Jin-Xiu1, ZHU Li-Wei2, OUYANG Lei2, ZHANG Xiao-Yan1通讯作者:
编委: 周广胜
责任编辑: 李敏
收稿日期:2018-07-30修回日期:2018-10-23网络出版日期:2018-12-20
| 基金资助: |
Received:2018-07-30Revised:2018-10-23Online:2018-12-20
| Fund supported: |
摘要
关键词：
Abstract
Keywords：
PDF (1703KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张振振, 赵平, 赵秀华, 张锦秀, 朱丽薇, 欧阳磊, 张笑颜. 环境因子对常绿阔叶树种脱耦联系数及冠层气孔导度估算的影响. 植物生态学报[J], 2018, 42(12): 1179-1191 doi:10.17521/cjpe.2018.0176
ZHANG Zhen-Zhen.
植物蒸腾作为森林维持流域和区域水资源平衡的重要功能, 对社会和经济发展具有重要的生态意义(Anton et al., 2008; Little et al., 2009)。人类活动引起的环境变化可能会迫使森林蒸腾发生改变, 从而影响区域水资源平衡。
环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(Martin et al., 1997; Cienciala et al., 2000; Kumagai et al., 2004, 2008; Barradas et al., 2005)。冠层上方的水汽导度(GT)可以分为两个部分: 森林冠层气孔导度(GS)和空气动力学导度(ga), 两者都与叶片生理、冠层结构以及冠层上方和内部的气象条件有关(Jones, 1992; Kumagai et al., 2004)。而两者对于GT的贡献目前仍存在争议。有研究认为当ga/GS > 10时, 蒸腾主要受GS控制(Herbst, 1995; Law et al., 2001; Komatsu, 2003; Komatsu et al., 2012)。同时也有研究发现, 风速(u)的增加可以通过引起ga的变化显著促进冠层蒸腾(Taylor et al., 2001; Bladon et al., 2006)。事实上, ga对水汽运动的贡献随森林类型及其生境的变化而变化(Dixon & Grace, 1984; Gutiérrez et al., 1994; Campbell-Clause, 1998)。冠层脱耦联系数(Ω)的提出为评估ga和GS对冠层水分传输的影响提供了可能。尽管已有大量关于土壤-植物-大气连续体(SPAC)的水分运动与环境条件之间的关系的研究(Jarvis, 1976; Jarvis & McNaughton, 1986; Granier & Loustau, 1994; Martin et al., 1997), 却很少有****关注Ω的大小对于冠层水汽通量计算的影响。
以往的研究中, 在不考虑边界层阻力的影响时, GS通常被认为等同于GT (Wullschleger et al., 2000)。而其中最常用的就是基于树干液流的K?stner公式计算的GS。其计算如下:
其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(Magnani et al., 1998; Oren et al., 1998; Kim et al., 2008)。该方法由于参数较少, 计算简单, 因此被广泛采用。但是有研究认为, 只有满足以下条件, 这种方法才能够使用: (1)植物储存水对蒸腾作用贡献较小;2)在冠层内部没有垂直水汽压梯度变化;(3)叶片边界层导度远高于气孔导度(Aphalo & Jarvis, 1991; Cienciala et al., 1998; Sch?fer et al., 2000)。Sch?fer等(2000)指出, 这种方法对于Ω较小的林分来说计算较为精确, 如针叶林。然而事实上, 在亚热带常绿阔叶林中, 以上这些条件都无法得到满足(Motzer et al., 2005; 赵平等, 2006)。尽管如此, 这一方法仍被用于一些阔叶林分蒸腾的研究(Ewers et al., 2007; Whitley et al., 2009), 但其所带来的误差并未得到评估。而基于Penman-Monteith公式(Monteith & Unsworth, 2007)计算的冠层气孔导度则通过整合植物生理性状和微气象因子, 综合考虑了冠层气孔阻力和空气动力学阻力对冠层水汽通量的影响, 因此也就能够更精确定量冠层蒸腾过程(Lu et al., 2003)。本研究将通过与基于Penman- Monteith公式计算的GS进行对比, 分析利用K?stner公式计算阔叶树种GS的可行性。
1 材料和方法
1.1 研究区概况
本研究在乡土种木荷(Schima superba)和外来种尾叶桉(Eucalyptus urophylla)人工林中进行。前者位于广州市中国科学院华南植物园(23.18° N, 113.36° E, 海拔41 m)。所在地为典型的南亚热带季风气候, 年降水量1 612-1 909 mm, 年平均气温21.4-21.9 ℃。雨季从4月持续至9月, 旱季从9月持续到次年3月(Zhu et al., 2012)。坡向为东北向, 坡度为11.7°, 土壤pH值为4.0, 有机质含量为2.3%, 总氮含量为0.07%。从2011年1月到12月, 对21株木荷进行了树干液流的测定。尾叶桉林位于中国广西桂林黄冕林场(24.78° N, 109.87° E), 所在地坡向朝南(坡度28°), 为南亚热带和中亚热带过渡地带, 降水丰沛(1 750-2 000 mm), 年平均气温19 ℃。土壤以红砂岩和红壤为主, pH值为3.5, 有机质含量为2.8%, 总氮含量为0.1%。雨季是3月至8月, 其余月份为旱季。从2012年6月至2013年5月对15株树木进行了树干液流测定。两个林分中均建有一座观测塔(木荷林塔高18 m, 尾叶桉林塔高23.5 m), 用于冠层结构和生理参数及气象参数的测定。木荷林年平均叶面积指数(LAI)为4.33, 尾叶桉林为1.53 (表1)。Table 1
表1
表1木荷和为尾叶桉林区参数
Table 1
| 树种 Species | 密度 Density | n | DBH | H | As | LAI | l | Al | Ac |
|---|---|---|---|---|---|---|---|---|---|
| 木荷 S. superba | 603 | 21 | 15.5 (1.3)a | 12.7 (0.5)a | 0.018 (0.002)a | 4.3 (0.1)a | 9.1 (0.4)a | 66.6 (10.2)a | 20.7 (2.9)a |
| 尾叶桉 E. urophylla | 1 375 | 15 | 10.1 (0.6)b | 11.5 (0.8)a | 0.007 (0.001)b | 1.5 (0.1)b | 10.9 (0.2)b | 21.0 (2.7)b | 4.0 (0.2)b |
新窗口打开|下载CSV
1.2 树干液流监测
采用热消散探针法(TDP)测定树液通量密度 (Fd, g·H2O·m-2·s-1)。具体测定方法参见Granier (1987)的研究。探针长度为20 mm, 数据每30 s读取一次, 并用数据记录器(DL2e, Delta-T Devices, Cambridge, UK)平均每10 min记录一次。1.3 环境因子监测
实验期间在塔顶安装AV-S3型温度和相对湿度探头, 测量冠层空气温度(T, ℃)和相对湿度(RH, %), 计算大气水汽压亏缺(D, kPa), 安装净辐射传感器(NR2-07, AVALON, London, UK)监测冠层净辐射(Rn, W·m-2), 并将3块土壤热通量板(HFP01, HUKSEFLUX, Delftechpark, Netherlands)埋入土壤表面下2 cm, 测量土壤热通量(G, W·m-2)。冠层上方的光合有效辐射(PAR, μmol·m-2·s-1)用光量子传感器(SKP 215, QT SYSTEM, London, UK)进行监测;冠层上方的风速(u, m·s-1)则利用风速计(AN4-05, Omega, Norwalk, USA)来记录。土壤含水量(SWC, m3·m-3)用3个埋入地表下30 cm的土壤水分传感器(SM300, Delta T device, Cambridge, UK)进行监测。以上所有的参数每30 s记录一次, 每10 min取平均值存储于数据采集仪(DL2, Delta T device, Cambridge, UK)中。1.4 林分参数测定
实验期间, 在每月月初用LI-COR 2000植物冠层分析仪(LI-COR, Lincoln, USA)测定冠层LAI。样树的胸径(DBH)和树高(H)则分别用胸径尺和测高仪(SI-121, Sunto Tandem, Rotterdam, Netherlands)测定, 每年一月份开展一次。同时在样地外围用生长锥获取树木树芯, 并根据树芯上的颜色差异测定边材的深度及树皮厚度。样本的总叶面积可以根据2009年(木荷)和2012年(尾叶桉)样地附近树木DBH与总叶面积之间的异速生长关系获得。两个样地的林分参数如表1所示, 除树高外, 所有参数都有显著差异(p > 0.05), 尤其是LAI。1.5 冠层蒸腾
利用样地外围样树树芯分别获取木荷和尾叶桉的边材面积(AS)和DBH的异速生长关系:冠层叶片蒸腾速率(El, g H2O·m-2·s-1)可以通过树液通量密度Fd、叶面积和AS的计算获得。前人研究发现, 木荷40-60 mm深度的树液通量密度显著低于外部20 mm处的树液通量密度, 而0-20和20-40 mm处的树液通量密度没有显著差异(梅婷婷等, 2010; Zhu et al., 2012)。因此, 可以通过使用Zhu等(2012)得出的等式来计算木荷的El, 其中包括了液流的径向分布(式4)。但由于尾叶桉边材深度(d)为(2.13 ± 0.40) cm, 接近TDP探针的长度, 即探针实际已经基本覆盖了整个边材部分, 因此不需要考虑液流在边材中的径向变化, 所以使用式5估计El的数值。
其中, As40为d > 40 mm的边材面积, As0-40为0 < d < 40 mm的边材面积, Al为总叶面积。
1.6 冠层气孔导度(GS)
根据式1计算简化的冠层气孔导度(GS1) , 根据Penman-Monteith公式的逆形式(公式6)计算GS2 (Wallace et al., 1990; Kelliher et al., 1993; Zeppel & Eamus, 2008)。由于其考虑了冠层阻力的影响, 因此也就能够更加精确的模拟冠层气孔导度。其计算公式如下:其中, Δ为饱和水气压随温度的变化曲线(kPa·℃-1), Rn为冠层净辐射(MJ·m-2·h-1), G为地面土壤热通量(MJ·m-2·h-1), ρ为干燥空气密度(kg·m-3), cp为恒压干燥空气的比热(MJ·kg-1·℃-1), D为蒸气压差(kPa), ga为空气动力学导度(m·s-1), GS2为冠层气孔导度(mmol·m-2 s-1), λ为水汽化潜热(MJ·kg-1), γ为干湿表系数(kPa·℃-1), ga根据风速估算为:
其中, z0为表面粗糙度(约0.1 h), h为平均树高, d0为零平面位移(约0.75 h), k为冯卡门常数, u (m·s-1)为
在z0水平下的风速。根据前人的研究, 当D < 100 Pa时, 叶片表面的边界层阻力远远大于气孔阻力, 而此时植物气孔导度的大小主要受到PAR的影响, 因此当D < 100 Pa时, GS的计算会存在极大的误差, 因此本研究中, GS是在排除D < 100 Pa时间段的数据后进行计算的(Sch?fer et al., 2000)。
1.7 冠层脱耦联系数Ω
冠层与大气解耦程度可用无量纲系数Ω来描述 (McNaughton, 1983):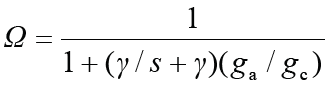
其中, s是饱和水汽压的变化...率; γ是干湿表系数(Pa·℃-1); gc是冠层导度, 为GS与LAI的乘积。Ω被分为6个等级(0-0.05、0.05-0.10、0.10-0.15、0.15-.0.20、0.20-0.25、0.25-0.30), 以量化大气解耦对气孔调节的影响。此外, 本研究中应用边界线分析来确定Ω与单因素气象条件和气孔导度(PAR, D, u, GS)之间的关系。
1.8 GS对D的敏感度
Oren等(1999b)通过边界线分析发现, 当土壤湿度不受限制时, GS和D之间的关系可以表示为:其中, GSiref是参比气孔导度(即在D = 1 kPa时GS的值), -m是回归拟合方程的斜率, 表示气孔导度对D的变化的敏感性(即GS随lnD的变化率dGS/dlnD)。通过边界线分析, 我们利用所得边界线数据分析利用这两种方法模拟的不同树种的GS对D响应的差异性。该方法已在多因素作用下的GS响应研究中得到应用(Dye & Olbrich, 1993; Granier et al., 1996; Oren et al., 2001)。
1.9 统计分析
我们采用SAS 9.2对GS及Ω进行ANOVA统计分析。同时对气象因子及Ω进行主成分分析以确定环境因子对Ω的影响程度及相关性。为了分析每个环境因子对Ω的定量关系, 我们在Excel 2010中进行边界线分析。分析结果使用Origin 8.6进行绘图。另外, 为了研究不同时间尺度两个树种的Ω和GS的特征, 我们分别计算了Ω的日均值, 月均值和年均值, 并选择1、4、7、10月分别代表一年中的4个季节, 对两个树种进行配对t检验, 来比较它们的大小。2 结果
2.1 林分气象条件
2012年6月至2013年5月尾叶桉林和2011年1月至12月木荷林的数据表明尾叶桉林和木荷林的平均气温分别为22.18和22.54 ℃, 且年变化相似(图1C, 配对t检验, p = 0.53)。两个林分PAR和D都有明显的季节性差异(图1A)。木荷林日平均D ((1.04 ± 0.64) kPa)显著高于尾叶桉林((0.74 ± 0.55) kPa), 表明了更强的蒸腾需求(配对t检验, p < 0.01)。尾叶桉林 的年平均SWC ((0.33 ± 0.06) m3·m-3)高于木荷林((0.28 ± 0.07) m3·m-3), 而生长在山坡上的尾叶桉林风速((1.36 ± 0.67) m·s-1)比木荷林的大((0.91 ± 0.54) m·s-1, p < 0.01)。图1
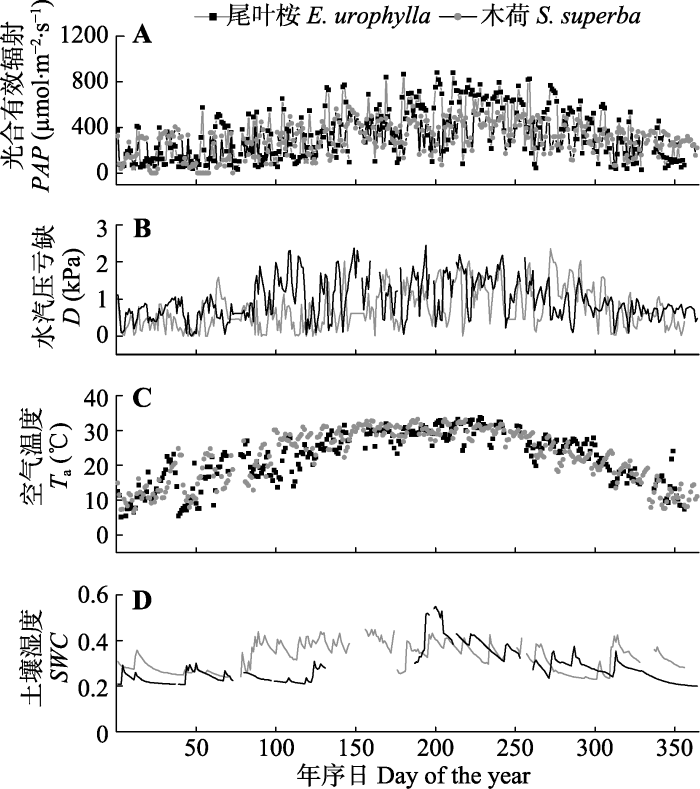新窗口打开|下载原图ZIP|生成PPT图1研究期间的气象条件。A, 光合有效辐射(PAR)。B, 水汽压亏缺(D)。C, 空气温度(Ta)。D, 土壤含水量(SWC)。
Fig. 1Meteorological conditions during study periods. A, Photosynthetic photon flux density (PAR). B, Vapor pressure deficit (D). C, Daily mean air temperature (Ta). D, Soil water content (SWC).
2.2 不同时间尺度下解耦系数(Ω)的变异性
根据公式(8), 我们使用GS2计算了Ω值, 来量化森林冠层蒸腾与大气气象因子的耦合度。木荷的Ω年均值为0.17 ± 0.03, 显著高于尾叶桉林(Ω = 0.10 ± 0.03, p = 0.000 1)。两个观测站之间Ω的差异则可能与LAI代表的冠层郁闭度的差异有关(表1)。另外由于环境条件的变化(图1, 图3A-3D), Ω也存在着显著的季节动态(图2)。而尾叶桉林Ω的季节变化幅度相对较大(从1月份的0.06 ± 0.02上升至7月份的0.15 ± 0.02, p <0.01), 明显高于木荷林(从1月份的0.17 ± 0.06到4月份的0.20 ± 0.04, p = 0.09)。另外Ω也存在显著的日变化(图3E、3F)。木荷林Ω的日变化呈明显的单峰曲线, 而尾叶桉林的Ω日变化呈逐渐增加的趋势。两个林分Ω值的最小值和最大值分别出现在10月的上午和4月的下午, 这可能与10月份较高的D和PAR (DOY 210-240, 图1)和华南地区4月份较高的降水量有关。此外, 由于清晨低风速和高湿度有利于在叶面和冠层表面形成厚的边界层, 从而导致较高的Ω值(Motzer et al., 2005)。图2
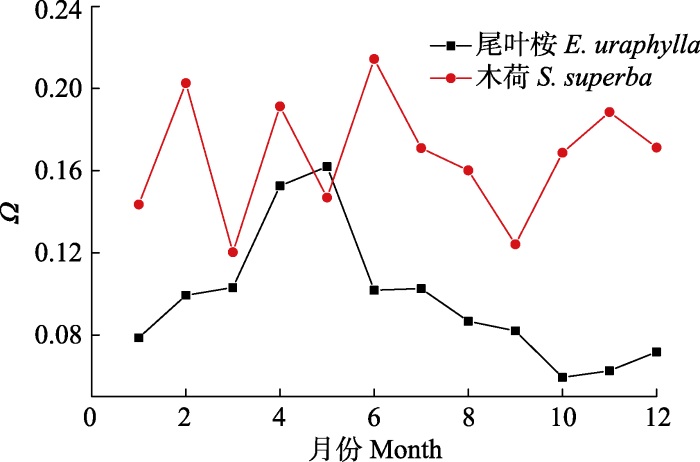新窗口打开|下载原图ZIP|生成PPT图2尾叶桉林和木荷林每月脱耦联系数(Ω)。
Fig. 2Monthly decoupling coefficients (Ω) of Eucalyptus urophylla and Schima superba stands.
图3
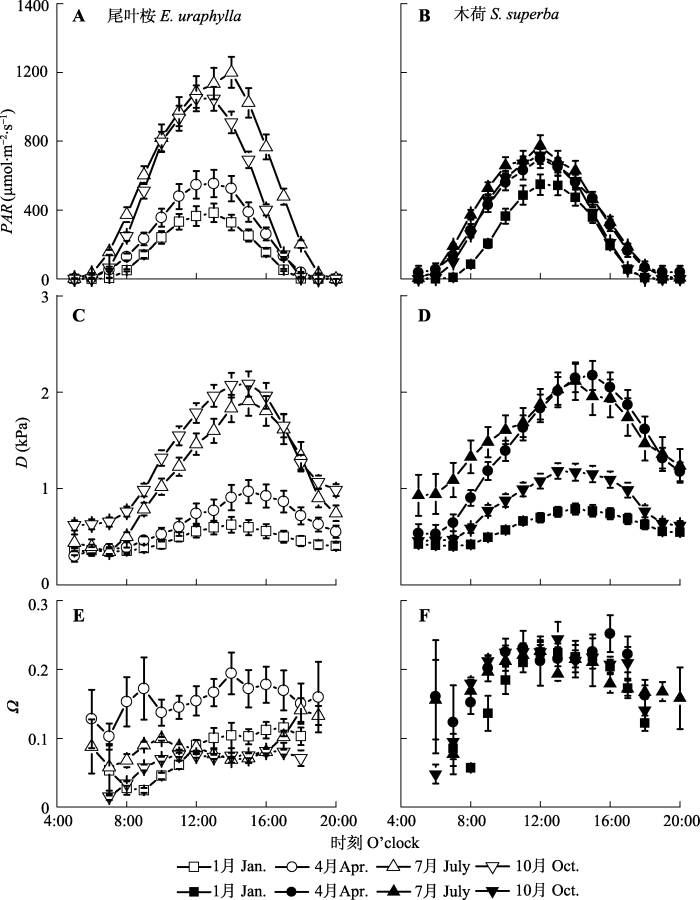新窗口打开|下载原图ZIP|生成PPT图3尾叶桉林和木荷林光合有效辐射(PAR)、水汽压亏缺(D)和脱耦联系数(Ω)日变化(平均值±标准误差)。
Fig. 3Diurnal course of photosynthetically active radiation (PAR, μmol m-2·s-1) (A, B), vapor pressure deficit (D, kPa) (C, D), and decoupling coefficient (Ω) (E, F) for Eucalyptus urophylla and Schima superba stands (mean ± SE) respectively.
2.3 环境因子和气孔调控对Ω的影响
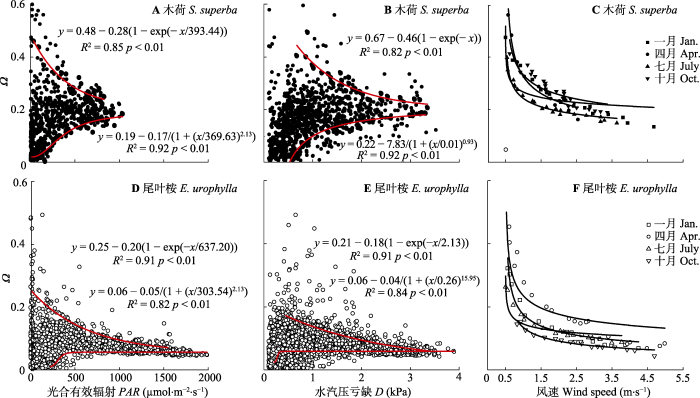
我们对大气气象因子以及GS与Ω进行主成分分析, 结果前3个主成分分别占Ω变异的75.1% (尾叶桉)和76.4% (木荷)。其中以D和PAR为主的第一主成分可解释Ω变异的45.9% (尾叶桉)和43.2% (木荷)。尽管如此, 当考虑单一因素时, 各因子与Ω之间的相关性并不显著。Ω与尾叶桉的PAR (r = -0.07)和D (r = -0.10)呈负相关关系。然而, Ω与木荷的PAR和D呈正相关关系。另外风会极大地改变叶片边界层阻力, 因此可能对叶和冠层表面与蒸腾产生解耦作用。然而事实上, Ω与u之间相关性较弱(尾叶桉和木荷的r分别为-0.30和-0.20)。我们对D和PAR与Ω之间的关系进行了边界线分析(图4A、4B、4D、4E)。结果发现Ω均存在上下边界线, 分别代表多重环境影响下的最大值和最小值。上边界线与D或PAR呈负相关关系, 而下边界线与D或PAR呈正相关关系。当PAR或D进一步增加时, Ω都接近恒定值(木荷-0.2, 尾叶桉-0.05)。我们对Ω与u以及GS之间的关系也进行了边界线分析(图4C、4F), 结果Ω作为u的函数也具有上边界线, 但没有显著的下边界线(图4C、4F)。两个树种Ω随着u的增加呈幂指数下降。并且Ω值也趋近恒定值(即0.20 (木荷)和0.05 (尾叶桉))。我们对GS与Ω之间的关系也进行了边界线分析(图5), 结果Ω与GS2间也存在上下边界, 且呈线性相关关系, 但尾叶桉和木荷的Ω值对GS响应的敏感性存在差异(斜率分别为0.001 86和0.003 56)。
图4
新窗口打开|下载原图ZIP|生成PPT图4尾叶桉林和木荷林中脱耦联系数(Ω)和光合有效辐射(PAR)(A, D)、水汽压亏缺(D) (B, E)及风速(C, F)之间的关系。图中仅显示了边界线数据区域。
Fig. 4Relationships between decoupling coefficient (Ω) and (A, D) photosynthetically active radiation (PAR,) as well as (B, E) vapor pressure deficit (D), (C, F) wind speed in Eucalyptus urophylla and Schima superba stands. Only boundary line data area shown in the figure.
图5
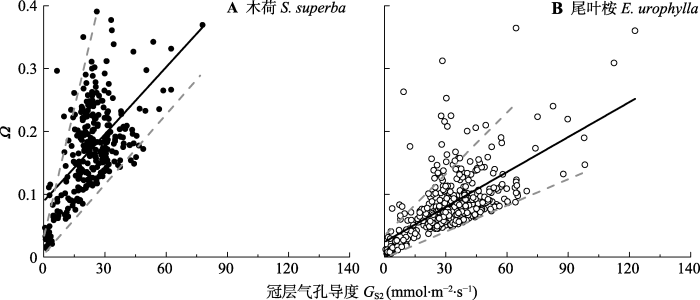新窗口打开|下载原图ZIP|生成PPT图5使用修订的Penman-Monteith公式估算的冠层气孔导度及相关的脱耦联系数(Ω)。
Fig. 5Decoupling coefficient (Ω) in relation to canopy stomatal conductance estimated with the inverse Penman-Monteith equation (GS2).
2.4 不同时间尺度下两个树种冠层气孔导度(GS)的变化
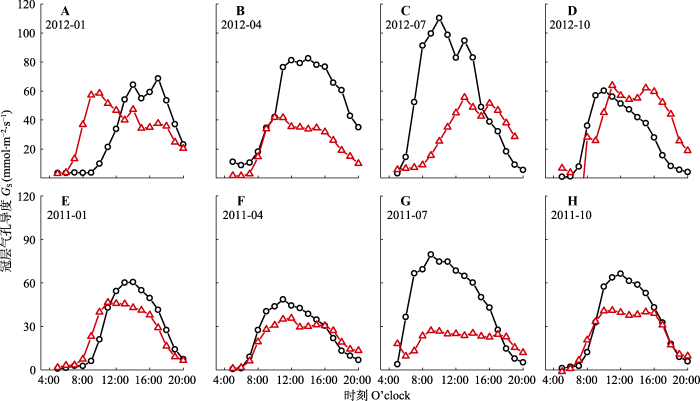
不同季节, 两种树种的GS日变化相似, 均随PAR的增加而迅速增加, 并在中午达到顶峰, 然后逐渐下降(图6)。尾叶桉和木荷的GS1年平均值分别为(42.55 ± 14.69)和(33.43 ± 9.40) mmol·m-2·s-1 , GS2年平均值分别为(33.42 ± 9.37)和(23.40 ± 2.03) mmol·m-2·s-1, 表明公式(1)不考虑冠层阻力可能导致GS偏大。另外, 两个树种相比, 尾叶桉在雨季(5-9月)和旱季(10月-翌年4月)平均GS1值分别为(48.96 ± 42.32)和(33.48 ± 16.95) mmol·m-2·s-1, 而木荷的平均值为(24.1 ± 17.36)和(28.88 ± 21.95) mmol·m-2·s-1。另外与木荷不同, 尾叶桉GS1的季节动态与大气气象条件的变化相一致(图1)。图6
新窗口打开|下载原图ZIP|生成PPT图6根据K?stner公式(GS1, ○)和Penman-Monteith逆公式(GS2, △)估计的尾叶桉林(A-D)和木荷林(E-H)冠层气孔导度(GS)的日变化。
Fig. 6Daily variation of canopy stomatal conductance (GS) estimated from the K?stner equation (GS1, ○) and the inverse Penman-?Monteith equation (GS2, △) for Eucalyptus urophylla (A-D) and Schima superba (E-H).
2.5 不同方法下GS值的比较
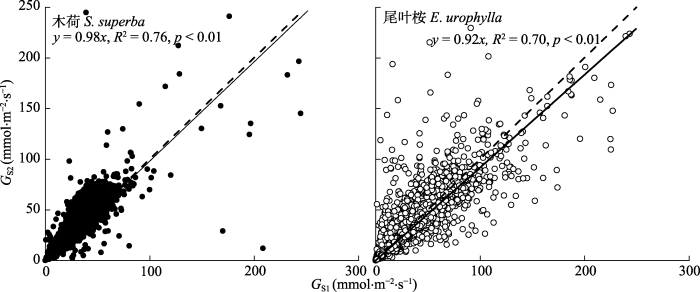
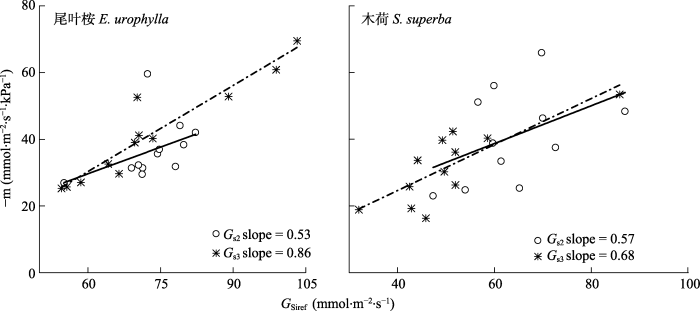
我们对两个树种的GS1和GS2进行线性分析,尽管大多数数据点在1:1的两侧分布(图7), 但总体来看, 无论是木荷还是尾叶桉, GS2往往低于GS1 (p < 0.01)。并且木荷的拟合效果比尾叶桉更好(R2更高, 图7)。我们对木荷和尾叶桉的GS响应D的敏感性-m以及参比气孔导度GSiref进行了计算, 结果表明, 木荷的-m与GSiref的比例平均值为0.64 ± 0.20 (GS1)和0.63 ± 0.14 (GS2), 尾叶桉的分别为0.50 ± 0.11 (GS1)和0.56 ± 0.09 (GS2)。在此基础上, 我们进行GSiref与m之间的线性拟合分析(图8)。两种树种dGSi/dlnD和GSiref之间的关系都达到显著水平(p < 0.001)。图7
新窗口打开|下载原图ZIP|生成PPT图7尾叶桉和木荷利用K?stner法计算的气孔导度(GS1)和利用Penman-Monteith公式计算的气孔导度(GS2)之间的关系。
Fig. 7Relationship between stomatal conductance estimated from the K?stner equation (GS1) and the inverse Penman-Monteith equation (GS2) for Eucalyptus urophylla and Schima superba.
图8
新窗口打开|下载原图ZIP|生成PPT图8冠层气孔导度(GS)对水汽压亏缺的敏感性(-m)与水汽压亏缺(D) = 1 kPa时的GS (GSref)之间的比例变化。数值来自一个月数据子集的边界线拟合。对于每种方法组合, 线是最小二乘拟合(p < 0.001)。GS1: 直线和空心圆, GS2: 点划线和星号。
Fig. 8Proportional increase of sensitivity of tree crown-level stomatal conductance (GS) to vapor pressure deficit (-m) with the conductance at vapor pressure deficit (D) = 1 kPa (GSref). Values are from boundary line fits of one month subsets of data. Lines are the least-square fit (p < 0.001) for each method combination. GS1, line and open circle; GS2, dash dot and asterisk
3 讨论
3.1 阔叶林分间Ω值的差异性
研究认为, 随着LAI的增加, 冠层GS随之增加(Granier et al., 1996, 2000; Katsoulas et al., 2007)。然而, 另一方面, 冠层叶面积的增加可能会阻碍空气流动, 降低ga (Kim et al., 2014), 这将导致阔叶树种Ω变化的不确定性。我们的研究结果表明, LAI相对较高的木荷Ω值更大。但与其他阔叶树种相比, 两个树种的Ω相对较小(尾叶桉和木荷1-4月的Ω值分别为0.10和0.17), 明显低于Meinzer等(1997)的研究(1-3月平均Ω = 0.75)和Wallace等(1990)的研究(林下树木, 干季平均Ω = 0.78), Kumagai等(2004)(年平均值0.4)及Motzer等(2005)(0.25-0.43, 11月至次年3月)在南美的热带雨林研究。事实上, 我们的结果更加接近于针叶树种的数值大小(0.05-0.2)(Jarvis & McNaughton, 1986; Zeppel & Eamus, 2008)。许多****对世界各地的尾叶桉进行了较为充分的研究(Forrester et al., 2010), 并指出即使在蓝桉(Eucalyptus globulus)和金合欢(Acacia farnesiana)混交的人工林中, 尾叶桉的Ω值也在0.1-0.2之间变化。然而Cabral等(2010)则发现尾叶桉杂交种(E. globulus × E. urophylla)在夏季和冬季的平均Ω分别为0.6 ± 0.08和0.13 ± 0.07, 尽管其密度(1 370 ind.·hm-2)与本研究中的尾叶桉林相似。这些结果的差异表明, 阔叶树种的Ω值不仅取决于各自的林分特征, 同时还与其所处的大气环境条件紧密相关。3.2 不同林分Ω季节变化的差异性
除了种间差异, Ω的季节变化很大(Zeppel & Eamus, 2008; Forrester et al., 2010)。 Hutley等(2001)发现, Ω值在雨季(D较低, SWC较高)较高, 在旱季(D较高, SWC较低)较低, 尾叶桉的Ω变化模式与之类似(图1)。而同样的结果也在巴西巨桉(Eucalyptus grandis)中观测到(Mielke et al., 1999)。但这种显著的Ω季节性变化并没有在木荷林中观测到(图2)。然而, 我们同时也发现木荷Ω的日变化与D和PAR的变化模式相一致, 甚至比尾叶桉的更为匹配(图3)。根据公式8, Ω的变化受ga和gc (GS × LAI)的制约, 前者与给定树高处的风速相关(Daudet et al., 1999), 而后者主要受D和PAR的影响(Maruyama & Kuwagata, 2008; Nicolás et al., 2008)。即Ω是受大气直接和间接控制的(通过对GS的影响)。另外, 不同时间尺度和不同物种Ω变化的不一致表明, 单因素的直接影响在本研究中较弱。相反, 两个林分(图1F,图2, 图4)的Ω和GS2季节变化则存在较好的一致性。因此可以认为, 在气象因子的作用下, 木荷自身的生理活动可能会起主导作用。而植物与冠层大气之间的脱耦联也很大程度上受到自身生理调节的反馈抑制。3.3 Ω与大气条件之间的关系
大气对Ω的影响是各种环境因子的综合作用, 因此任何个体效应都可能被其他因素影响所掩盖。通常风速被认为会引起Ω的波动。例如, Wei等(2013)认为, 风速会增加冠层脱耦联程度。Mielke等(1999)也观察到u与Ω之间存在显著正相关关系, 且中度水分亏缺会促进这种相关性。然而, 在我们的研究中没有发现这种正效应(尾叶桉和木荷的相关系数分别为-0.30和-0.20)。相反, 边界线分析显示Ω随u呈指数下降(图4)。这说明u也并非仅仅是直接引起Ω的变化。同样D和PAR与Ω之间也存在相似的结果。另外, 当D和PAR不受限制时, Ω趋近于一个特定值。 图4中的边界线分析表明D和PAR的增加导致Ω在较高D和PAR处趋近收敛。而这种定值的种间变异(木荷为0.20, 尾叶桉为0.05)揭示了尾叶桉和木荷在碳水平衡调节策略上的差异性。3.4 Ω对两种方法计算GS的影响
尽管尾叶桉和木荷Ω的平均值相对较小(分别为0.1和0.17), 表明两个林分与大气环境存在部分脱耦联, 即不满足“引言”中提出的用于估算GS1的条件(3)。本研究中, 尾叶桉和木荷的GS2:GS1分别为0.92和0.98, 表明GS1相对偏大(p < 0.01)。这表明即使具有良好大气耦合条件的森林, 在估算GS时边界层阻力也不可忽略。另外, 两种方法估算的GS对大气D的响应的差异性表明, GS1在描述植物生理响应时也存在一些偏差。研究发现-m和GSiref之间0.6的比例是为防止植物木质部的过度空穴化, 维持最小叶水势(ΨL)而产生(Oren et al., 1999b; Ewers et al., 2005)。而在以下条件下这个比例值会出现实质性偏差: (1)非等水植物允许最小ΨL随着D的增加而下降; (2) D的变化范围极大; (3)边界层导度与GS的比值较低(Oren et al., 1999a)。前两个条件导致-m与GSiref的比值Pi小于0.6, 而条件3则导致Pi大于0.6 (Oren et al., 1999a)。尾叶桉和木荷GS1的Pi分别为0.53和0.57, 两者均略低于标准值0.6。与GS1相比, 尾叶桉和木荷GS2的Pi分别为0.86和0.68, 远高于0.6, 故可推测这种偏差可能是较低的边界层导度引起的。这说明边界层阻力足够大时, 如阔叶树种, 简化公式所得的GS可能偏低, 并且无法反映真实的GS对环境因子的响应。为了更加详细地评估边界层阻力对GS计算的影响, 我们用所有观测数据计算了每个Ω水平的Pi值(每个水平4-5个重复)(表3)。在0.05-0.15的范围内, 尾叶桉Pi与标准值0.6相当(p > 0.05)。一旦边界层较厚(Ω > 0.15), Pi高于0.6, Ω甚至可以达到0.3。Blanken等(1997)研究毛白杨(Populus tomentosa)林时选择Ω = 0.5作为界定粗糙表面森林的标准, 我们的结果则对这种标准提出了质疑。相比之下, 木荷的最佳Ω范围(Pi与0.6差异不显著)在0.1-0.2之间。因此可以认为对尾叶桉和木荷估计的Ω的最佳区间范围分别为0.05-0.15和0.10-0.20。
Table 2
表2
表2文中常用变量及其缩写
Table 2
| 变量 Variables | 缩写 Abbreviations | 单位 Units |
|---|---|---|
| 冠层气孔导度 Canopy stomatal conductance | GS | mmol·m-2·s-1 |
| 冠层脱耦联系数 Canopy decoupling coefficient | Ω | 无纲量 No dimension |
| 光合有效辐射 Photosynthetically active radiation | PAR | μmol·m-2·s-1 |
| 水汽压亏缺 Water vapor deficit | D | kPa |
| 风速 Wind speed | u | m·s-1 |
| 水汽导度 Water vapor conductance | GT | mmol·m-2·s-1 |
| 冠层导度 Canopy conductance | gc | mmol·m-2·s-1 |
| 空气动力学导度 Aerodynamic conductance | ga | mmol·m-2·s-1 |
| 树木蒸腾速率 Tree transpiration rates | E | g·m-2·s-1 |
| 叶面积指数 Leaf area index | LAI | m2·m-2 |
| 胸径 Diameter at breast height | DBH | cm |
| 树高 Tree height | H | m |
| 边材面积 Sap wood area | AS | m2 |
| 总叶面积 Total leaf area | Al | m2 |
| 气动阻力 Stomatal resistance | ra | s·m-1 |
| 土壤含水量 Soil water content | SWC | m3·m-3 |
新窗口打开|下载CSV
Table 3
表3
表3不同冠层脱耦联系数(Ω)区间范围尾叶桉和木荷的冠层气孔导度对水汽压亏缺的敏感性(-m)和参比气孔导度(GSiref)之间的比例(Pi)
Table 3
| 树种 Species | Ω区间 Ω interval | Pi |
|---|---|---|
| 0.00-0.05 | - | |
| 0.05-0.10 | 0.57 (0.06) | |
| 尾叶桉 E. urophylla | 0.10-0.15 | 0.58 (0.06) |
| 0.15-0.20 | 1.04 (0.16)** | |
| 0.20-0.25 | 8.32 (7.62)** | |
| 0.25-0.3 | 1.43(5.02)** | |
| 0.00-0.05 | - | |
| 0.05-0.10 | 0.75 (0.13)** | |
| 木荷 S. superba | 0.10-0.15 | 0.61 (0.10) |
| 0.15-0.20 | 0.58 (0.08) | |
| 0.20-0.25 | 0.70 (0.13)** | |
| 0.25-0.30 | 1.21 (0.40)** |
新窗口打开|下载CSV
由于Ω具有较大的年变化和日变化(图2, 图3), 有必要量化GS数据最佳区间的百分比, 这样用简化的公式来估算GS更为合理。根据计算, 尾叶桉和木荷各自落在最佳区间范围的GS数据量分别为83.1%和47.8%, 因此可以认为一年中尾叶桉和木荷有83.1%和47.8%的Ω条件下适合利用简化公式计算GS。
4 结论
尾叶桉林和木荷林的Ω分别为0.10 ± 0.03和0.17 ± 0.03, 表明森林冠层与大气之间具有较高的耦合度。而林分Ω的季节变化不仅受到气象条件的影响, 同时也与植物生理调节作用紧密相关。因此Ω的动态变化是各种环境因子综合相互作用的结果, 任何单因素效应都可能被其他影响所掩盖。这是导致不同地区、不同林分, 森林Ω变异的主要原因。另外尽管两个林分Ω值均相对较小, 但与GS2相比, GS1值仍然偏大(尾叶桉斜率为0.92, 木荷斜率为0.98), 而GS对D的敏感性分析也表明, 简化公式计算的GS可能无法反映真实的气孔响应。这说明K?stner公式估算的阔叶树种的GS可能存在较大误差。尽管如此, 我们的结果也认为并非所有的GS值均不可信, 通过对GS1合理范围的分析, 以及相应数据量的统计, 我们发现, 当K?stner公式应用于GS的计算时, 尾叶桉和木荷林各自有83.1%和47.8%的数据是相对可靠的。因此, 我们的这些结果可以为更加精确的区域水量平衡的估算提供参考。致谢 感谢中国科学院华南植物园赵培强、周娟、 孙振伟和高建国在现场工作中的帮助。
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
DOI:10.1111/j.1365-3040.1991.tb01379.xURL [本文引用: 1]
Abstract. The objective of the work reported was to answer the following questions: (1) Do stomata respond to both humidity and temperature? (2) Do these responses interact in such a way that relative humidity at the leaf surface is a more appropriate variable than water vapour saturation deficit at the leaf surface and yields a simpler description of the compound response? To answer these questions, we measured the response of leaf conductance to humidity under constant leaf temperature, and the response to increasing leaf temperature under constant relative humidity and under constant water vapour saturation deficit. We found that, in Hedera helix subsp. canariensis (Willd.) Coutinho, there was a reversible response to humidity under constant temperature, and that there was also a response to temperature under constant relative humidity. The relationship between leaf conductance and relative humidity was different when measured at the same temperature rather than at different temperatures. An inversely proportional response was consistently obtained when stomatal conductance was expressed in relation to water vapour saturation deficit. The interaction between the effects of leaf temperature and water vapour saturation deficit was not compatible with a mechanism of response to humidity and temperature based solely on relative humidity. From these data, we conclude that water vapour saturation deficit is a more appropriate variable for describing stomatal responses to humidity.
DOI:10.1016/j.agwat.2004.09.035URL [本文引用: 1]
Water use and canopy conductance were monitored in 2-year-old apricot ( Prunus armenica L.) trees growing in 70-L plastic pots. The experiment was carried out in a research field near Murcia, Spain, over a 3-week period between September 26 and October 16, 2000. Eight trees were used in the experiment, four of which were placed under a rectangular shading net, while the other four were maintained in the open air. Trees were irrigated adequately until October 5 (day 279); later the water was withheld in all trees for five days. The estimation of transpiration from sap flow measurements was done under both radiation conditions along the experiment, recording a significant decrease of transpiration in shaded trees with respect to the exposed trees. The mild water stress affected the exposed and shaded plants in a similar manner. In both cases, the water deficit induced a significant reduction of transpiration after two days of water withholding. Total conductance was obtained from daily measurements of transpiration and vapor pressure deficit between September 28 and October 10, and was similar to canopy conductance. Maximum canopy conductance showed the lowest values at the end of mild water stress (October 10) (0.0017 and 0.0012 m s 鈭1, shaded and sunny, respectively), and the highest values on September 28 when the trees were in well-irrigated condition (0.0024 and 0.0018 m s 鈭1, shaded and sunny, respectively). Finally, the decoupling coefficient reached the highest values in the shaded trees and the lowest in sun-exposed trees. The results showed that water vapor exchange was strongly dominated by vapor pressure deficit and controlled by leaf conductance. It was also noticeable that trees under shade were more decoupled from the atmosphere than those fully exposed to the sun, meaning that exposed trees resulted in a better control of water loss. We think that net shading could be extended to apricot culture in many areas in which irrigation water is scarce and insolation is high, because the water use clearly decreased in shaded trees with respect to the exposed ones.
DOI:10.1016/j.agrformet.2006.03.015URL [本文引用: 1]
We compared the change in microclimate and tree water relations between a boreal mixedwood, variable retention (VR), partially harvested stand and an adjacent, unharvested control stand. A nearly three-fold increase in potential evapotranspiration (ET P) at the crown level in the VR site was approximately proportional to a 2.8-fold increase in wind speed ( u), along with subsidiary increases in net radiation ( Q *) and vapour pressure deficit ( D) after harvesting. Soil volumetric moisture content ( v) also increased, while there were negligible changes in air temperature ( T a) and relative humidity (RH) after partial harvesting. Whole-tree sap flow response to cutting was measured in white spruce ( Picea glauca), balsam poplar ( Populus balsamifera) and paper birch ( Betula papyrifera) with thermal-dissipation sap flow sensors. After partial harvesting, transpiration per unit leaf area ( Q l) in all three species began earlier in the morning and extended later in the day in VR trees than control trees. Mean maximum sap flow rates per leaf area ( Q l-max) during mid-day for P. glauca in the VR site were about 2.5 times greater than in the control trees, while B. papyrifera Q l-max was approximately 1.6 times higher in the VR site. For P. balsamifera, however, Q l-max was only marginally greater in the VR site than in the control. This suggests stomatal closure by the P. balsamifera and B. papyrifera residual trees likely occurred to prevent excessive xylem cavitation. Xylem pressure potential ( x) measurements of twigs also indicated water stress in both P. balsamifera and B. papyrifera in the VR stand, but not for P. glauca. However, similarity of sapwood hydraulic conductivity ( K ) between the two sites, for all three species, showed that xylem cavitation of the main stems was insignificant following VR harvesting. Decoupling coefficients ( ) indicated that all three species were more coupled to the atmosphere in the VR site than in the control. Species differences in susceptibility to atmospheric moisture-stress induced cavitation, combined with differences in stress-coping mechanisms and physiology, appeared to influence the response in transpiration to increased ET P following VR harvesting. Species susceptibility to atmospheric moisture-stress due to increased ET P following partial harvesting can be ranked as: P. balsamifera > B. papyrifera > P. glauca.
DOI:10.1029/97JD00193URL [本文引用: 1]
The energy balance components were measured throughout most of 1994 in and above a southern boreal aspen (Populus tremuloides Michx.) forest (53.62900°N 106.20000°W) with a hazelnut (Corylus cornuta Marsh.) understory as part of the Boreal Ecosystem-Atmosphere Study. The turbulent fluxes were measured at both levels using the eddy-covariance technique. After rejection of suspect data due to instationarity or inhomogeneity, occasional erratic behavior in turbulent fluxes and lack of energy balance closure led to a recalculation of the fluxes of sensible and latent heat using their ratio and the available energy. The seasonal development in leaf area was reflected in a strong seasonal pattern of the energy balance. Leaf growth began during the third week of May with a maximum forest leaf area index of 5.6 m2 m0908082 reached by mid-July. During the full-leaf period, aspen and hazelnut accounted for approximately 40 and 60% of the forest leaf area, respectively. Sensible heat was the dominant consumer of forest net radiation during the preleaf period, while latent heat accounted for the majority of forest net radiation during the leafed period. Hazelnut transpiration accounted for 25% of the forest transpiration during the summer months. During the full-leaf period (June 1 to September 7) daytime dry-canopy mean aspen and hazelnut canopy conductances were 330 mmol m0908082 s0908081 (8.4 mm s0908081) (70% of the total forest conductance) and 113 mmol m0908082 s0908081 (2.9 mm s0908081) (24% of the total forest conductance), respectively. Maximum aspen and hazelnut canopy conductances were 1200 mmol m0908082 s0908081 (30 mm s0908081) and 910 mmol m0908082 s0908081 (23 mm s0908081 ), respectively, and maximum stomatal conductances were 490 mmol m0908082 s0908081 (12.5 mm s0908081) and 280 mmol m0908082 s0908081 (7 m s0908081), aspen and hazelnut, respectively. Both species showed a decrease in canopy conductance as the saturation deficit increased and both showed an increase in canopy conductance as the photosynthetic active radiation increased. There was a linear relationship between forest leaf area index and forest canopy conductance. The timing, duration, and maximum leaf area of this deciduous boreal forest was found to be an important control on transpiration at both levels of the canopy. The full-leaf hazelnut daytime mean Priestley and Taylor [1972] coefficient of 1.22 indicated transpiration was largely energy controlled and the quantity of energy received at the hazelnut surface was a function of aspen leaf area. The full-leaf aspen daytime mean of 0.91 indicated some stomatal control on transpiration, with a directly proportional relationship between forest leaf area and forest canopy conductance, varying during much of the season through a range very sensitive to regional scale transpiration and surface-convective boundary layer feedbacks.
DOI:10.1016/j.jhydrol.2010.04.041 [本文引用: 1]
The eddy covariance method was used to measure energy and water balance of a plantation of Eucalyptus ( grandis × urophylla) hybrids over a 2 year period. The average daily evaporation rates were 5.4 (±2.0) mm day 611 in summer, but fell to 1.2 (±0.3) mm day 611 in winter. In contrast, the sensible heat flux was relatively low in summer but dominated the energy balance in winter. Evaporation accounted for 80% and 26% of the available energy, in summer and winter respectively. The annual evaporation was 82% (1124 mm) and 96% (1235 mm) of the annual rainfall recorded during the first and second year, respectively. Daily average canopy and aerodynamic conductance to water vapour were in the summer 51.9 (±38.4) mm s 611 and 84.1 (±25.6) mm s 611, respectively; and in the winter 6.0 (±10.5) mm s 611 and 111.6 (±24.6) mm s 611, respectively.
DOI:10.1071/EA91220URL [本文引用: 1]
DOI:10.1016/S0022-1694(00)00291-2URLPMID:2617573 [本文引用: 1]
Water use of Acacia mangium trees grown in plantations was measured by a heat balance method in two stands that largely differed in tree density. Tree sap flow was closely coupled to climatic drivers and responded with minimal time delay. Using no time shift, sap flow rate could be tightly fitted to a simple equation that combined a parabolic response to radiation and an inverse linear response to air humidity. On the contrary, the analysis of canopy conductance showed no meaningful response to either individual or combined microclimatic variables. No indication of water deficit was observed, though the measurement period was during the dry period of the year. The measurements indicate a minimal diurnal use of water stored in plant tissues. The difference in tree water use from the two studied stands was effectively scaled by tree sapwood area. Canopy transpiration of the densest stand reached in average 3.9 mm d 611 compared with 2.7 mm d 611 for the stand representing the average conditions in the catchment.
DOI:10.1051/forest:19980104URL [本文引用: 1]
DOI:10.1016/S0168-1923(99)00079-9URL [本文引用: 1]
DOI:10.1093/oxfordjournals.aob.a086751URL [本文引用: 1]
[本文引用: 1]
DOI:10.1111/j.1365-3040.2005.01312.xURL [本文引用: 1]
We quantified the effect of stand age and tree species composition on canopy transpiration ( E C ) by analysing transpiration per unit leaf area ( E L ) and canopy stomatal conductance ( G S ) for boreal trees comprising a five stand wildfire chronosequence. A total of 196 sap flux sensors were used on 90 trees consisting of Betula papyrifera Marsh (paper birch; present in the youngest stand), Populus tremuloides Michx (quaking aspen), Pinus banksiana Lamb. (jack pine), and Picea mariana (Mill.) (black spruce). While fine roots were positively correlated with stand E C ; leaf area index, basal area, and sapwood area were not. Stands less than 70 years old were dominated by Populus tremuloides and Pinus banksiana and stands greater than 70 years old were composed almost entirely of Picea mariana. As Populus tremuloides and Pinus banksiana increased in size and age, they displayed an increasing sapwood to leaf area ratio ( A S : A L ), a constant minimum leaf water potential (Ψ L ), and a constant proportionality between G S at low vapour pressure deficit ( Dj G Sref ) and the sensitivity of G S to D (– δ ). In contrast, A S : A L , minimum Ψ L , and the proportionally between – δ and G Sref decreased with height and age in Picea mariana . A G S model that included the effects of D , A S : A L , tree height, and for Picea mariana an increasing soil to leaf water potential gradient with stand age, was able to capture the effects of contrasting hydraulic properties of Picea mariana , Populus tremuloides and Pinus banksiana during stand development after wildfire.
DOI:10.1093/treephys/27.1.11URLPMID:17169902 [本文引用: 1]
We investigated interannual variability of canopy transpiration per unit ground area (E(C)) and per unit leaf area (E(L)) across seven tree species in northern Wisconsin over two years. These species have previously been shown to be sufficient to upscale stand-level transpiration to the landscape level during one growing season. Our objective was to test whether a simple plant hydraulic model could capture interannual variation in transpiration. Three species, wetland balsam fir (Abies balsamea (L.) Mill), basswood (Tilia Americana L.) and speckled alder (Alnus rugosa (DuRoi) Spreng), had no change in E(C) or E(L) between 2000 and 2001. Red pine (Pinus resinosa Air) had a 57 and 19% increase in E(C) and E(L), respectively, and sugar maple (Acer saccharum Marsh) had an 83 and 41 % increase in E(C) and EL, respectively, from 2000 to 2001. Quaking aspen (Populus tremuloides Michx) had a 50 and 21 % decrease in E(C) and E(L), respectively, from 2000 to 2001 in response to complete defoliation by forest tent caterpillar (Malascoma district Huber) and subsequent lower total leaf area index of the reflushed foliage. White cedar (Thuja occidentalis L.) had a 20% decrease in both E(C) and E(L) caused by lowered surface water in wetlands in 2001 because of lower precipitation and wetland flow management. Upland A. balsamea increased E(L) and E(C) by 55 and 53 %, respectively, as a result of release from light competition of the defoliated, overstory P. tremuloides. We hypothesized that regardless of different drivers of interannual variability in E(C) and E(L), minimum leaf water potential would be regulated at the same value. Minimum midday water potentials were consistent over the two years within each of the seven species despite large changes in transpiration between years. This regulation was independently verified by the exponential saturation between daily E(C) and vapor pressure deficit (D) and the tradeoff between a reference canopy stomatal conductance (G(S)) and the sensitivity of G(S) to D, indicating that trees with high G(S) must decrease G(S) in response to atmospheric drought faster than trees with low G(S). Our results show that models of forest canopy transpiration can be simplified by incorporating G(S) regulation of minimum leaf water potential for isohydric species.
[本文引用: 2]
DOI:10.1093/treephys/3.4.309URLPMID:14975915 [本文引用: 1]
Abstract Transpiration of a Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) stand was evaluated by sap flow measurements during a 4-month period. Between-tree variation in sap flow depended on crown class. On a sunny day, total transpiration was 1.6, 8.0 and 22.0 liters day(-1) for suppressed, codominant and dominant trees, respectively. Transpiration estimated by sap flow fell below potential evapotranspiration when available soil water decreased below 30% of its maximum value. Sap flow measurements gave transpiration values similar to those obtained by the water balance method.
DOI:10.1111/gcb.1996.2.issue-3URL [本文引用: 2]
DOI:10.1016/0168-1923(94)90100-7URL [本文引用: 1]
ABSTRACT The transpiration of a maritime pine canopy was determined from sap-flow measurements obtained from three experiments carried out at two sites in the Landes de Gascogne Forest, southwest France. From these data, the canopy stomatal conductance was estimated by inverting the Penman-Monteith equation, and a canopy conductance model which included the effects of air vapour pressure deficit, soil moisture deficit and irradiance was tested. Values of canopy transpiration simulated by the model for the three sites were compared with field data. The canopy stomatal conductance was decreasingly sensitive to air vapour pressure deficit, soil moisture deficit and global irradiance. There was better agreement between predicted and actual data for transpiration (R2 = 0.83–0.87) than for canopy stomatal conductance (R2 = 0.50–0.78). Values of daily transpiration simulated by the model were in good agreement with field data (R2 = 0.85–0.93).
DOI:10.1051/forest:2000158URL [本文引用: 1]
DOI:10.1111/j.1365-3040.1994.tb00532.xURL [本文引用: 1]
Stomatal regulation of transpiration was studied in hedgerow coffee ( Coffea arabica L.) at different stages of canopy development encompassing a range of leaf area indices ( L ) from 0 7 to 6 7. Stomatal ( g s ) and crown ( g c ) conductance attained maximum values early during the day and then declined as both leaf-to-bulk air water vapour mole fraction difference ( V a ) and photosynthetically active photon flux density ( I ) continued to increase. Covariation of environmental variables during the day, particularly V, I , and wind speed ( u ), obscured stomatal responses to individual variables. This also caused diurnal hysteresis in the relationship between g c and individual variables. Normalization of g s and g c by I removed the hysteresis and revealed a strong stomatal response to humidity. At the crown scale, transpiration ( E ) increased linearly with net radiation ( R n ) and seemed to increase with increasing wind speed. Increasing wind speed imposed higher leaf interior to leaf surface water vapour mole fraction differences ( V s ) at given levels of V a . However, strong relationships between declining g c and E and increasing wind speed were obtained when g c and E were normalized by I and R n , respectively, without invoking additional potential interactions involving temperature or CO 2 concentration at the leaf surface. Apparent stomatal responses to wind were thus at least partially a reflection of the stomatal response to humidity.
DOI:10.1111/j.1365-3040.1995.tb00611.xURL [本文引用: 1]
On the basis of measurements or stand transpiration and microclimate, the bulk stomatal or bulk leaf conductance ( g L ) of a beech forest in northern Germany was calculated for periods in which leaves were fully expanded and the canopy was dry. This conductance depends strongly on light and humidity conditions above the forest. During periods with photosynthetic photon flux densities Q > 1200 μmol m 612 s 611 , g L was reduced from 1500mmol m 612 s 611 at a vapour pressure deficit D = 0.5kPa to 500 mmol m 612 s 611 at D = 2kPa. Light saturation of g L was not reached until Q = 1200 μmol m 612 s 611 at low D , or until even higher Q at higher D . The dependence of g L , on Q and D was described mathematically by a non-linear equation that requires two empirical parameters. Values for g L as simulated by this equation provided a satisfactory agreement with independent porometer data collected on single leaves and scaled up to the canopy. A comparison of stomatal and aerodynamic conductances showed a strong coupling between the forest canopy and the atmosphere, indicating that transpiration of the beech forest is controlled mainly by the stomata.
DOI:10.1007/s004420000539URLPMID:28547459 [本文引用: 1]
Data from savannas of northern Australia are presented for net radiation, latent and sensible heat, ecosystem surface conductance (Gs) and stand water use for sites covering a latitudinal range of 5掳 or 700 km. Measurements were made at three locations of increasing distance from the northern coastline and represent high- (1,750 mm), medium- (890 mm) and low- (520 mm) rainfall sites. This rainfall gradient arises from the weakened monsoonal influence with distance inland. Data were coupled to seasonal estimates of leaf area index (LAI) for the tree and understorey strata. All parameters were measured at the seasonal extremes of late wet and dry seasons. During the wet season, daily rates of evapotranspiration were 3.1-3.6 mm day-1and were similar for all sites along the rainfall gradient and did not reflect site differences in annual rainfall. During the dry season, site differences were very apparent with evapotranspiration 2-18 times lower than wet season rates, the seasonal differences increasing with distance from coast and reduced annual rainfall. Due to low overstorey LAI, more than 80% of water vapour flux was attributed to the understorey. Seasonal differences in evapotranspiration were mostly due to reductions in understorey leaf area during the dry season. Water use of individual trees did not differ between the wet and dry seasons at any of the sites and stand water use was a simple function of tree density. Gsdeclined markedly during the dry season at all sites, and we conclude that the savanna water (and carbon) balance is largely determined by Gsand its response to atmospheric and soil water content and by seasonal adjustments to canopy leaf area.
DOI:10.1098/rstb.1976.0035URL [本文引用: 1]
DOI:10.1016/S0065-2504(08)60119-1URL [本文引用: 2]
[本文引用: 1]
DOI:10.1016/j.agrformet.2007.03.003URL [本文引用: 1]
Improving the design, control and management of greenhouse ventilation systems requires a better insight into the coupling and feedback mechanisms between the crop, the internal atmosphere and the outside atmosphere. The objective of this work was to characterize the leaf boundary-layer conductance ( g b) in highly ventilated greenhouse conditions and to study its dependence on the ventilation conductance ( g v) and outside conditions. For this purpose, measurements of g b were carried out in a greenhouse cultivated with rose plants, using rose leaf replicas consisting of a pair of artificial leaves, one being heated and the other unheated. The relation between g b and g v was established and quantified, and further generalised to the case of large greenhouses. By implementing the relation into the expression of the canopy aerodynamic conductance, the influence of the leaf area index (LAI) on the total greenhouse conductance was addressed. It was shown that LAI plays a major role in determining the degree of coupling between the greenhouse canopy and the outside atmosphere. The results underline the importance of integrating estimates of the canopy aerodynamic conductance in greenhouse climate control algorithms.
DOI:10.1007/BF00323485URLPMID:28312937 [本文引用: 1]
Canopy-scale evaporation rate (E) and derived surface and aerodynamic conductances for the transfer of water vapour ($\text{g}_{\text{s}}$and$\text{g}_{\text{a}}$, respectively) are reviewed for coniferous forests and grasslands. Despite the extremes of canopy structure, the two vegetation types have similar maximum hourly evaporation rates (Emax) and maximum surface conductances ($\text{g}_{\text{smax}}$) (medians = 0.46 mm h-1and 22 mm s-1). However, on a daily basis, median Emaxof coniferous forest (4.0 mm d-1) is significantly lower than that of grassland (4.6 mm d-1). Additionally, a representative value of$\text{g}_{\text{a}}$for coniferous forest (200 mm s-1) is an order of magnitude more than the corresponding value for grassland (25 mm s-1). The proportional sensitivity of E, calculated by the Penman-Monteith equation, to changes in$\text{g}_{\text{s}}$is >0.7 for coniferous forest, but as low as 0.3 for grassland. The proportional sensitivity of E to changes in$\text{g}_{\text{a}}$is generally 卤0.15 or less. Boundary-line relationships between$\text{g}_{\text{s}}$and light and air saturation deficit (D) vary considerably. Attainment of$\text{g}_{\text{smax}}$occurs at a much lower irradiance for coniferous forest than for grassland (15 versus about 45% of full sunlight). Relationships between$\text{g}_{\text{s}}$and D measured above the canopy appear to be fairly uniform for coniferous forest, but are variable for grassland. More uniform relationships may be found for surfaces with relatively small$\text{g}_{\text{a}}$, like grassland, by using D at the evaporating surface ($\text{D}_{\text{o}}$) as the independent variable rather than D at a reference point above the surface. An analytical expression is given for determining$\text{D}_{\text{o}}$from measurable quantities. Evaporation rate also depends on the availability of water in the root zone. Below a critical value of soil water storage, the ratio of evaporation rate to the available energy tends to decrease sharply and linearly with decreasing soil water content. At the lowest value of soil water content, this ratio declines by up to a factor of 4 from the non-soil-water-limiting plateau. Knowledge about functional rooting depth of different plant species remains rather limited. Ignorance of this important variable makes it generally difficult to obtain accurate estimates of seasonal evaporation from terrestrial ecosystems.
DOI:10.1016/j.agrformet.2013.11.013URL [本文引用: 1]
Wind velocity (U) within and above forest canopies can alter the coupling between the vapor-saturated sub-stomatal airspace and the drier atmosphere aloft, thereby influencing transpiration rates. In practice, however, the actual increase in transpiration with increasing U depends on the aerodynamic resistance (RA) to vapor transfer compared to canopy resistance to water vapor flux out of leaves (RC, dominated by stomatal resistance, Rstom), and the rate at which RA decreases with increasing U. We investigated the effect of U on transpiration at the canopy scale using filtered meteorological data and sap flux measurements gathered from six diverse species of a mature broadleaved deciduous forest. Only under high light conditions, stand transpiration (EC) increased slightly (6.5%) with increasing U ranging from 650.7 to 654.7ms611. Under other conditions, sap flux density (Js) and EC responded weakly or did not change with U. RA, estimated from Monin–Obukhov similarity theory, decreased with increasing U, but this decline was offset by increasing RC, estimated from a rearranged Penman–Monteith equation, due to a concurrent increase in vapor pressure deficit (D). The increase of RC with D over the observed range of U was consistent with increased Rstom by 6540% based on hydraulic theory. Except for very rare half-hourly values, the proportion of RA to total resistance (RT) remained <15% over the observed range of conditions. These results suggest that in similar forests and conditions, the direct effect of U reducing RA and thus increasing transpiration is negligible. However, the observed U–D relationship and its effect on Rstom must be considered when modeling canopy photosynthesis.
DOI:10.1016/j.agrformet.2013.11.013URL
Wind velocity (U) within and above forest canopies can alter the coupling between the vapor-saturated sub-stomatal airspace and the drier atmosphere aloft, thereby influencing transpiration rates. In practice, however, the actual increase in transpiration with increasing U depends on the aerodynamic resistance (RA) to vapor transfer compared to canopy resistance to water vapor flux out of leaves (RC, dominated by stomatal resistance, Rstom), and the rate at which RA decreases with increasing U. We investigated the effect of U on transpiration at the canopy scale using filtered meteorological data and sap flux measurements gathered from six diverse species of a mature broadleaved deciduous forest. Only under high light conditions, stand transpiration (EC) increased slightly (6.5%) with increasing U ranging from 650.7 to 654.7ms611. Under other conditions, sap flux density (Js) and EC responded weakly or did not change with U. RA, estimated from Monin–Obukhov similarity theory, decreased with increasing U, but this decline was offset by increasing RC, estimated from a rearranged Penman–Monteith equation, due to a concurrent increase in vapor pressure deficit (D). The increase of RC with D over the observed range of U was consistent with increased Rstom by 6540% based on hydraulic theory. Except for very rare half-hourly values, the proportion of RA to total resistance (RT) remained <15% over the observed range of conditions. These results suggest that in similar forests and conditions, the direct effect of U reducing RA and thus increasing transpiration is negligible. However, the observed U–D relationship and its effect on Rstom must be considered when modeling canopy photosynthesis.
DOI:10.1093/treephys/28.4.559URLPMID:18244943 [本文引用: 1]
Abstract We examined the tradeoffs between stand-level water use and carbon uptake that result when biomass production of trees in plantations is maximized by removing nutrient and water limitations. A Populus trichocarpa Torr. x P. deltoides Bartr. & Marsh. plantation was irrigated and received frequent additions of nutrients to optimize biomass production. Sap flux density was measured continuously over four of the six growing-season months, supplemented with periodic measurements of leaf gas exchange and water potential. Measurements of tree diameter and height were used to estimate leaf area and biomass production based on allometric relationships. Sap flux was converted to canopy conductance and analyzed with an empirical model to isolate the effects of water limitation. Actual and soil-water-unlimited potential CO(2) uptakes were estimated with a canopy conductance constrained carbon assimilation (4C-A) scheme, which couples actual or potential canopy conductance with vertical gradients of light distribution, leaf-level conductance, maximum Rubisco capacity and maximum electron transport. Net primary production (NPP) was about 43% of gross primary production (GPP); when estimated for individual trees, this ratio was independent of tree size. Based on the NPP/GPP ratio, we found that current irrigation reduced growth by about 18% compared with growth with no water limitation. To achieve maximum growth, however, would require 70% more water for transpiration, and would reduce water-use efficiency by 27%, from 1.57 to 1.15 g stem wood C kg(-1) water. Given the economic and social values of water, plantation managers appear to have optimized water use.
DOI:10.3178/jjshwr.16.423URL [本文引用: 1]
[本文引用: 1]
DOI:10.1016/j.jhydrol.2003.10.002URL [本文引用: 3]
DOI:10.1016/j.agrformet.2008.04.010URL [本文引用: 1]
Plant–soil system patterns and processes along a slope are among the greatest causes of uncertainty in estimating watershed-scale transpiration ( E). Tree-to-tree and radial variations in xylem sap flux density ( F d), in addition to tree biometrics, were measured over a 2-year period (2005–2006) in two slope stand positions. The areas of interest consisted of an upper slope plot (UP) and a lower slope plot (LP) in a Japanese cedar ( Cryptomeria japonica D. Don) forest watershed and the environmental controls of stand E for each plot were compared. Canopy stand E ( E C) and canopy stomatal conductance ( G C) in the UP were less than those in the LP during the growing season, while those in the UP were greater than those in the LP over winter. In addition, mean stand F d ( J S) in the UP was greater than that in the LP over winter, but J S values were similar in the UP and LP except in the winter, which allows us to extrapolate watershed-scale E based on J S estimated from F d measurements of a partial stand in the watershed. However, this relationship contains a bias and differed between 2005 and 2006. Although there were significant differences in soil moisture conditions between the UP and LP in both years, a systematic relationship between the similarity in J S and soil moisture conditions was not found. The bias was due to a tendency for J S in the LP to be greater than that in the UP in 2006. This tendency was amplified because J S in the LP was greater than that in the UP around an atmospheric humidity deficit ( D) of 1–1.5 kPa and frequencies of this D range were higher in 2006 than in 2005. The greater J S in the LP at D 65 1–1.5 kPa could be explained by the difference in the response of G C to D between the UP and LP. Our results suggest this to be the cause of the similarity in J S values for the UP and LP and for the occasional abortion of its similarity. However, even when the bias or the occasional deviation is disregarded, the error in estimating stand E from a partial stand is so small that it is comparable to an F d measurement error. For example, the error when using only the LP was 6.6% for stand E.
DOI:10.1093/treephys/21.5.299URLPMID:11262921 [本文引用: 1]
Abstract We investigated key factors controlling mass and energy exchange by a young (6-year-old) ponderosa pine (Pinus ponderosa Laws.) plantation on the west side of the Sierra Nevada Mountains and an old-growth ponderosa pine forest (mix of 45- and 250-year-old trees) on the east side of the Cascade Mountains, from June through September 1997. At both sites, we operated eddy covariance systems above the canopy to measure net ecosystem exchange of carbon dioxide and water vapor, and made concurrent meteorological and ecophysiological measurements. Our objective was to understand and compare the controls on ecosystem processes in these two forests. Precipitation is much higher in the young plantation than in the old-growth forest (1660 versus 550 mm year-1), although both forests experienced decreasing soil water availability and increasing vapor pressure deficits (D) as the summer of 1997 progressed. As a result, drought stress increased at both sites during this period, and changes in D strongly influenced ecosystem conductance and net carbon uptake. Ecosystem conductance for a given D was higher in the young pine plantation than in the old-growth forest, but decreased dramatically following several days of high D in late summer, possibly because of xylem cavitation. Net CO2 exchange generally decreased with conductance at both sites, although values were roughly twice as high at the young site. Simulations with the 3-PG model, which included the effect of tree age on fluxes, suggest that, during the fall through spring period, milder temperatures and ample water availability at the young site provide better conditions for photosynthesis than at the old pine site. Thus, over the long-term, the young site can carry more leaf area, and the climatic conditions between fall and spring offset the more severe limitations imposed by summer drought.
DOI:10.1016/j.jhydrol.2009.06.011URL [本文引用: 1]
Land-use and forest cover change play important roles in socio-economic processes and have been linked with water supply and other ecosystem services in various regions of the world. Water yield from watersheds is a major ecosystem service for human activities but has been dramatically altered by landscape management superimposed on climatic variability and change. Many studies from different regions of the world have documented that in small watersheds (<100 ha) fast-growing forest plantations reduce water yield. Nevertheless, these effects have not been adequately documented in large watersheds >10,000 ha. In this paper, we examine the temporal variation of the residuals between best-fit precipitation–runoff relationships and instrumental streamflow records for two large watersheds (Purapel en Nirivilo, PNN and Cauquenes en el Arrayán, CQA) located in the Mediterranean-climate coastal range of South-Central Chile. In these watersheds, high resolution satellite imagery shows a decline in native forest cover from 52.3% to 14.2% for PPN and 36.1% to 8.1% in CQA, between 1975 and 2000. Conversely, in the same period the percentage area covered by forest plantations, mainly Pinus radiata, increased from 12% to 55% in PPN, and 4.7% to 42% in CQA. We observed a decreasing trend in summer runoff residuals regressed against annual precipitation in the same period, with slopes significantly different from zero for PPN ( p = 0.035) and CQA ( p = 0.008). We interpreted this pattern as an evidence of change in the hydrological regime in these watersheds as a consequence of forest cover and land-use changes. From a reanalysis of the observed data we estimate a decrease in runoff from 13.1 to 7.5 mm/summer for PPN and from 7.3 to 5 mm/summer for CQA, refer to the period 1991–2000 compared to 1981–1990. Multiple regression analyses of annual and seasonal flows show that besides precipitation, percentage-cover of forest plantations is a statistically significant predictor of summer flow with a partial negative correlation of 610.45 and 610.44 for PPN and CQA, respectively, p < 0.05. This study clearly shows the important effect that land-use change can have on water yield and to our knowledge this is the first study documenting the decrease in summer runoff in a landscape where native forest cover has dramatically declined and forest exotic plantations have expanded. Similar methods could be used elsewhere to inform policy and decision-making regarding forest and land-use planning.
DOI:10.1071/FP02181URL [本文引用: 1]
Whole-vine transpiration was estimated for well-watered nine-year-old Sultana grapevines (Vitis vinifera L. cv. Sultana) from xylem sap flow measured with Granier's heat-dissipation probes. Canopy conductance of the grapevine was calculated by inverting the Penman Monteith equation. Transpiration from grapevine canopies was strongly controlled by the canopy conductance. Canopy conductance decreased exponentially with increasing vapour pressure deficit (VPD) except in the morning when solar radiation was less than 200 W m^2 and the canopy conductance was predominantly limited by the solar radiation. A non-linear model of canopy conductance as a function of the solar radiation and VPD explained > 90% of the variation observed in canopy conductance. Under contrasting VPD conditions (daytime maximum of 3 kPa vs 8 kPa), grapevines were able to regulate their canopy conductance from 0.006 to 0.001 m s-1 to maintain a near constant transpiration. Whole-canopy transpiration calculated from modelled canopy conductance using the PenmanMonteith equation was highly correlated with the measured transpiration (sap flow) values over the range of 0-0.20 mm h-1 (R2 > 0.85). Cross-validation shows that these mechanistic models based on solar radiation and VPD provide good predictions of canopy conductance and transpiration under the conditions of the study.
DOI:10.1046/j.1365-3040.1998.00328.xURL [本文引用: 1]
The transpiration of a mature beech ( Fagus sylvatica L.) forest was measured over a whole season by the heat pulse velocity technique and the results analysed in terms of a new analytical canopy conductance model, which takes into account the effects of partial decoupling from the atmosphere on the local humidity environment experienced by the canopy. Stand daily transpiration ranged from 0·62 to 2·97 mm d –1 , with a seasonal mean value of 1·97 mm d –1 . Maximum canopy conductance was 18·5 mm s –1 , with a mean estimated value of 5·0 mm s –1 ; computed values were little affected by the assumption of neutral atmospheric conditions. The decoupling coefficient Ω varied greatly on a daily and seasonal basis, with an average value of 0·28. As a result of partial decoupling, the estimated vapour pressure deficit at the notional canopy surface exceeded the values measured above the canopy by 380 Pa on average. When correctly expressed in terms of humidity at the canopy surface, the model explained 80% of the variance in half-hourly transpiration measurements. Upon cross-validation it still explained 72% of the variance, as compared to only 40% when correction for partial decoupling was not introduced. A baseline canopy conductance of 0·7 mm s –1 , not modulated by the environment, was estimated. The implications of the model are discussed for the representation of canopy conductance and transpiration of broad-leaf forests.
[本文引用: 2]
DOI:10.1016/j.agrformet.2008.03.001URL [本文引用: 1]
Bulk stomatal conductance (g(S)) is an important factor that expresses the effect of stomatal movements on water transfer between the plant and atmosphere at the canopy scale and is widely used as a parameter in many micrometeorological models. Diurnal and seasonal variations in gs of the rice canopy were determined using a heat transfer model based on heat flux measurements in irrigated rice fields. Season-long observations from transplanting to maturation of rice plants were conducted to obtain heat flux data in a humid temperate climate at three experimental sites with widely differing cropping seasons in Japan. A double source model was used as the heat transfer model to calculate gs. Seasonal variations in heat fluxes differed for sensible heat and latent heat. Sensible heat flux was smaller and relatively constant within the range -50 to So W m(-2), whereas latent heat flux showed large variations from 0 to 250 W m(-2) throughout the growth period. It was suggested that this would be a common pattern for paddy rice fields in all cropping seasons. Diurnal variation in g(s). showed a common trend in all growth periods with lower values in the morning and evening, and higher values during the midday because of its dependence on solar radiation. The relationship between absorbed solar radiation (S-abs) and g(s) was determined using a Jarvis-type model for each growth period. Maximum values of bulk stomatal conductance (g(Smax)) for saturated S-abs, rapidly decreased from 0.06 to 0.02 m s(-1) between the active tillering and panicle formation stages, and moderately decreased from 0.02 to 0.01 m s(-1) during the ripening stage. This was considered to be due to the change in leaf chlorophyll concentration. Seasonal variation in q(Smax) can be commonly expressed for all cropping seasons using the function of developmental stage (P-S). Using this function, the gs value can be obtained easily at a given developmental stage, which makes it possible to use micrometeorological models in relation to rice phenological development for evaluating important factors, such as water temperature and transpiration, that affect rice production. (C) 2008 Elsevier B.V. All rights reserved.
[本文引用: 1]
URL [本文引用: 1]
基于液流格型特征值-偏度和峰度分析了不同胸径荷木在水分利用方面的差异,并利用标准化的方法消除强影响 因子(光合有效辐射,PAR)对液流的影响,研究了弱影响因子(土壤湿度)与液流的关系.结果表明:荷木胸径越大,偏度越小,液流密度峰值越靠后,相应的 液流峰值越大,蒸腾量也越大.与旱季相比,荷木大树在湿季偏度较小,液流密度到达峰值时间靠后,峰值大,蒸腾量也大;而小树偏度在旱、湿季的差异不明显, 蒸腾量差异也不大.用PAR峰值对荷木个体蒸腾和土壤湿度进行标准化后,荷木个体蒸腾与土壤湿度呈更明显的正相关关系.在土壤湿度较大的季节,荷木大树的 蒸腾量随土壤湿度增加而上升的速率基本稳定;而中等木和小树的某些个体则明显下降,说明这些树木的蒸腾和吸收土壤水分的能力可能接近极限.
URL [本文引用: 1]
基于液流格型特征值-偏度和峰度分析了不同胸径荷木在水分利用方面的差异,并利用标准化的方法消除强影响 因子(光合有效辐射,PAR)对液流的影响,研究了弱影响因子(土壤湿度)与液流的关系.结果表明:荷木胸径越大,偏度越小,液流密度峰值越靠后,相应的 液流峰值越大,蒸腾量也越大.与旱季相比,荷木大树在湿季偏度较小,液流密度到达峰值时间靠后,峰值大,蒸腾量也大;而小树偏度在旱、湿季的差异不明显, 蒸腾量差异也不大.用PAR峰值对荷木个体蒸腾和土壤湿度进行标准化后,荷木个体蒸腾与土壤湿度呈更明显的正相关关系.在土壤湿度较大的季节,荷木大树的 蒸腾量随土壤湿度增加而上升的速率基本稳定;而中等木和小树的某些个体则明显下降,说明这些树木的蒸腾和吸收土壤水分的能力可能接近极限.
[本文引用: 1]
DOI:10.1007/PL00009746URL [本文引用: 2]
Predawn leaf water potential, stomatal conductance and microclimatic variables were measured on 13 sampling days from November 1995 through August 1996 to determine how environmental and physiological factors affect water use at the canopy scale in a plantation of mature clonal Eucalyptus grandis Hill ex-Maiden hybrids in the State of Espirito Santo, Brazil. The simple ”big leaf” Penman-Monteith model was used to estimate canopy transpiration. During the study period the predawn leaf water potential varied from –0.4 to –1.302MPa, with the minimum values observed in the winter months (June and August 1996), while the average estimated values for canopy conductance and canopy transpiration fell from 17.3 to 5.802mm s –1 and from 0.54 to 0.1802mm h –1 , respectively. On the basis of all measurements, the average value of the decoupling coefficient was 0.25. During continuous soil water shortage a proportional reduction was observed in predawn leaf water potential and in daily maximum values of stomatal conductance, canopy transpiration and decoupling coefficient. The results showed that water vapour exchange in this canopy is strongly dominated by the regional vapour pressure deficit and that canopy transpiration is controlled mainly by stomatal conductance. On a seasonal basis, stomatal conductance and canopy transpiration were mainly related to predawn leaf water potential and, thus, to soil moisture and rainfall. Good results were obtained with a multiplicative empirical model that uses values of photosynthetically active radiation, vapour pressure deficit and predawn leaf water potential to estimate stomatal conductance.
[本文引用: 1]
DOI:10.1093/treephys/25.10.1283URLPMID:16076777 [本文引用: 3]
Abstract We investigated tree water relations in a lower tropical montane rain forest at 1950-1975 m a.s.l. in southern Ecuador. During two field campaigns, sap flow measurements (Granier-type) were carried out on 16 trees (14 species) differing in size and position within the forest stand. Stomatal conductance (g(s)) and leaf transpiration (E(l)) were measured on five canopy trees and 10 understory plants. Atmospheric coupling of stomatal transpiration was good (decoupling coefficient Omega = 0.25-0.43), but the response of g(s) and E(l) to the atmospheric environment appeared to be weak as a result of the offsetting effects of vapor pressure deficit (VPD) and photosynthetic photon flux (PPF) on g(s). In contrast, sap flow (F) followed these atmospheric parameters more precisely. Daily F depended chiefly on PPF sums, whereas on short time scales, VPD impeded transpiration when it exceeded a value of 1-1.2 kPa. This indicates an upper limit to transpiration in the investigated trees, even when soil water supply was not limiting. Mean g(s) was 165 mmol m(-2) s(-1) for the canopy trees and about 90 mmol m(-2) s(-1) for the understory species, but leaf-to-leaf as well as tree-to-tree variation was large. Considering whole-plant water use, variation in the daily course of F was more pronounced among trees differing in size and crown status than among species. Daily F increased sharply with stem diameter and tree height, and ranged between 80 and 120 kg day(-1) for dominant canopy trees, but was typically well below 10 kg day(-1) for intermediate and suppressed trees of the forest interior.
DOI:10.1016/j.envexpbot.2007.11.007URL [本文引用: 1]
Sap flow, as a measure of transpiration, was monitored in 2-year-old lemon trees growing in pots. Eight trees were used in the experiment, four of which were placed under a rectangular shading net, while the other four were maintained in the open air. Daily averages of canopy conductance and photosynthesis were not affected by shading; however, the daily transpiration was reduced in shaded plants, which displayed an increase in water use efficiency compared with exposed trees. The decoupling coefficient was higher in the shaded trees, indicating that the transpiration of lemon trees was efficiently controlled by stomata in exposed plants, while the transpiration rate was mainly influenced by radiation in the plants growing under the net. This influence was more pronounced in the afternoon, when the whole tree transpiration was largely dominated by equilibrium transpiration in the plants under netting, and the relationship between transpiration and radiation showed a steeper slope in shaded trees. The reduction in transpiration and the maintenance of photosynthesis in shaded plants with respect to exposed trees indicated that screen structures in semi-arid and arid environments could be considered as an intermediate solution for reducing plant water stress and increasing water use efficiency.
DOI:10.1890/1051-0761(1998)008[0990:WBDTSL]2.0.CO;2URL [本文引用: 1]
To link variation in canopy conductance to soil moisture in the rooting zone, measurements of throughfall (PT), volumetric soil moisture (theta) to 0.7 m, transpiration from trees >10 mm in diameter (EC), and vapor pressure deficit (D) were made in a forest dominated by Pinus taeda. Total evapotranspiration (ET) was estimated from PT, changes in volumetric soil water content within a defined soil volume (AS), and drainage out of that volume (Q), calculated from unsaturated soil hydraulic conductivity and theta. Our calculations suggest that over 145 growing-season days, Q was negligible, and most of PT, averaging apprx2 mm/d, was partitioned between soil moisture recharge (0.4 mm/d) and ET (1.6 mm/d, not including apprx0.4 mm/d of interception, I, by canopy trees), of which EC was estimated from direct measurements at nearly 1.2 mm/d. Evapotranspiration by the subcanopy component accounted for slightly over 0.4 mm/d, about a third of ET (a fourth if I is included). Most of the water used for ET (>90%) was taken from the upper soil layer (top 0.35 m, or less). Canopy leaf conductance, calculated from EC, D, and canopy leaf area, was strongly related to theta in the upper soil layer once theta decreased below 0.22.
DOI:10.1093/treephys/19.6.337URLPMID:12651555 [本文引用: 2]
Abstract We used 20-mm-long, Granier-type sensors to quantify the effects of tree size, azimuth and radial position in the xylem on the spatial variability in xylem sap flux in 64-year-old trees of Taxodium distichum L. Rich. growing in a flooded forest. This information was used to scale flux to the stand level to investigate variations in half-hourly and daily (24-hour) sums of sap flow, transpiration per unit of leaf area, and stand transpiration in relation to vapor pressure deficit (D) and photosynthetically active radiation (Q(o)). Measurements of xylem sap flux density (J(s)) indicated that: (1) J(s) in small diameter trees was 0.70 of that in medium and large diameter trees, but the relationship between stem diameter as a continuous variable and J(s) was not significant; (2) J(s) at 20-40 mm depth in the xylem was 0.40 of that at 0-20 mm depth; and (3) J(s) on the north side of trees was 0.64 of that in directions 120 degrees from the north. Daily transpiration was linearly related to daily daytime mean D, and reached a modest value of 1.3 mm day(-1), reflecting the low leaf area index (LAI = 2.2) of the stand. Because there was no soil water limitation, half-hourly water uptake was nearly linearly related to D at D < 0.6 kPa during both night and day, increasing to saturation during daytime at higher values of D. The positive effect of Q(o) on J(s) was significant, but relatively minor. Thus, a second-order polynomial with D explained 94% of the variation in J(s) and transpiration. An approximately 40% reduction in LAI by a hurricane resulted in decreases of about 18% in J(s) and stand transpiration, indicating partial stomatal compensation.
DOI:10.1007/s004420000497URLPMID:28547434 [本文引用: 1]
We measured the xylem sap flux in 64-year-old Taxodium distichum (L.) Richard trees growing in a flooded forest using Granier-type sensors to estimate mean canopy stomatal conductance of the stand ($G_{\text{S}}$). Temporal variations in$G_{\text{S}}$were investigated in relation to variation in vapor pressure deficit (D), photosynthetic photon flux density ($Q_{\text{o}}$), and the transpiration rate per unit of leaf area ($E_{\text{L}}$), the latter variable serving as a proxy for plant water potential. We found that$G_{\text{S}}$was only weakly related to$Q_{\text{o}}$below 500 μmol m-2s-1(r2=0.29), but unrelated to$Q_{\text{o}}$above this value. Above$Q_{\text{o}}$=500 μmol m-2s-1and D=0.6 kPa,$G_{\text{S}}$decreased linearly with increasing$E_{\text{L}}$with a poor fit (r2=0.31), and linearly with lnD with a much better fit (r2=0.81). The decrease of$G_{\text{S}}$with lnD was at a rate predicted based on a simple hydraulic model in which stomata regulate the minimum leaf water potential. Based on the hydraulic model, stomatal sensitivity to D is proportional to stomatal conductance at low D. A hurricane caused an 6541% reduction in leaf area. This resulted in a 28% increase in$G_{\text{S}}$at D=1 kPa ($G_{\text{Sref}}$), indicating only partial compensation. As predicted, the increase in$G_{\text{Sref}}$after the hurricane was accompanied by a similar increase in stomatal sensitivity to D (29%). At night,$G_{\text{Sref}}$was 6520% of the daytime value under non-limiting light ($Q_{\text{o}}$>500 μmol m-2s-1). However, stomatal sensitivity to D decreased only to 6546% (both reductions referenced to prehurricane daytime values), thus having more than twice the sensitivity expected based on hydraulic considerations alone. Therefore, non-hydraulic processes must cause heightened nighttime stomatal sensitivity to D.
DOI:10.1046/j.1365-3040.1999.00513.xURL [本文引用: 2]
ABSTRACT Responses of stomatal conductance ( g s ) to increasing vapour pressure deficit ( D ) generally follow an exponential decrease described equally well by several empirical functions. However, the magnitude of the decrease – the stomatal sensitivity – varies considerably both within and between species. Here we analysed data from a variety of sources employing both porometric and sap flux estimates of g s to evaluate the hypothesis that stomatal sensitivity is proportional to the magnitude of g s at low D ( ≤ 1 kPa). To test this relationship we used the function g s = g sref – m · ln D where m is the stomatal sensitivity and g sref = g s at D = 1 kPa. Regardless of species or methodology, m was highly correlated with g sref (average r 2 = 0·75) with a slope of approximately 0·6. We demonstrate that this empirical slope is consistent with the theoretical slope derived from a simple hydraulic model that assumes stomatal regulation of leaf water potential. The theoretical slope is robust to deviations from underlying assumptions and variation in model parameters. The relationships within and among species are close to theoretical predictions, regardless of whether the analysis is based on porometric measurements of g s in relation to leaf-surface D ( D s ), or on sap flux-based stomatal conductance of whole trees ( G Si ), or stand-level stomatal conductance ( G S ) in relation to D . Thus, individuals, species, and stands with high stomatal conductance at low D show a greater sensitivity to D , as required by the role of stomata in regulating leaf water potential.
DOI:10.1046/j.1365-3040.2000.00553.xURL [本文引用: 3]
ABSTRACT Variation in stomatal conductance is typically explained in relation to environmental conditions. However, tree height may also contribute to the variability in mean stomatal conductance. Mean canopy stomatal conductance of individual tree crowns ( G Si ) was estimated using sap flux measurements in Fagus sylvatica L., and the hypothesis that G Si decreases with tree height was tested. Over 13 d of the growing season during which soil moisture was not limiting, G Si decreased linearly with the natural logarithm of vapour pressure deficit ( D ), and increased exponentially to saturation with photosynthetic photon flux density ( Q o ). Under conditions of D = 1 kPa and saturating Q o , G Si decreased by approximately 60% with 30 m increase in tree height. Over the same range in height, sapwood-to-leaf area ratio ( A S : A L ) doubled. A simple hydraulic model explained the variation in G Si based on an inverse relationship with height, and a linear relationship with A S : A L . Thus, in F. sylvatica , adjustments in A S : A L partially compensate for the negative effect of increased flow-path length on leaf conductance. Furthermore, because stomata with low conductance are less sensitive to D , gas exchange of tall trees is reduced less by high D . Despite these compensations, decreasing hydraulic conductance with tree height in F. sylvatica reduces carbon uptake through a corresponding decrease in stomatal conductance.
DOI:10.1093/treephys/21.6.403URLPMID:11282580 [本文引用: 1]
In Australia, tree planting has been widely promoted to alleviate dryland salinity and one proposed planting configuration is that of strategically placed interception belts. We conducted an experiment to determine the effect of tree position in a belt on rate. We also assessed how much the effect of tree position can be explained by advection and environmental conditions. Daily rates were determined by the heat pulse velocity technique for four edge and 12 inner trees in a 7-year-old Tasmanian () plantation in South Australia. Various climatic variables were logged automatically at one edge of the plantation. The relationship between daily sap flow and sapwood area was strongly linear for the edge trees (r2 = 0.97), but only moderately correlated for the inner trees (r2 = 0.46), suggesting an edge effect. For all trees, sap flow normalized to sapwood area (Qs) increased with potential evaporation (PE) initially and then became independent as PE increased further. There was a fairly close correlation between of the edge and inner trees, implying that availability was partially responsible for the difference between inner and edge trees. However, the ratio of edge tree to inner tree differed from unity, indicating differences in canopy conductance, which were estimated by an inverse form of the Penman-Monteith equation. When canopy conductances were less than a critical value, there was a strong linear relationship between Qs of the edge and inner trees. When canopy conductances of the edge trees were greater than the critical value, the slope of the linear relationship was steeper, indicating greater of the edge trees compared with the inner trees. This was interpreted as evidence for enhancement of of the edge trees by advection of wind energy.
DOI:10.1016/0168-1923(90)90040-DURL [本文引用: 2]
The stomatal conductances of the leaves and panicles of a sparse dryland millet crop grown at ICRISAT Sahelian Center, Sadoré, in southwest Niger were measured using a diffusion porometer and an infrared gas analyser, respectively. Leaf conductances were found to be high, up to 12 mm s 611 or 480 mmol m 612 s 611, and varied according to the leaf surface, age and position in the canopy. These data were combined with measurements of leaf area index to calculate canopy conductance. Because of the low leaf area (maximum 1.3), canopy conductances were low and varied both diurnally and seasonally. Transpiration was calculated using the above canopy conductance values using the Penman-Monteith and Shuttleworth-Wallace models. In comparison to the Shuttleworth-Wallace model, it was found that the Penman-Monteith equation underestimated transpiration when the soil was dry and overestimated it when the soil was wet. These differences in transpiration arise because of the modification of the in-canopy vapour pressure deficit caused by heat and water vapour fluxes from the soil, a mechanism which is only present in the Shuttleworth-Wallace model.
DOI:10.1007/s11434-013-5858-3URL [本文引用: 1]
Canopy resistance estimation model based on the scaling-up leaf stomatal resistance is the focus of evapotrantion research, as there is a need to select the proper scaling-up model for winter wheat in typical areas of North China. Two years of field experimental data are used for the Leuning-Ball and Jarvis stomatal model calibration and validation, canopy resistance estimation models are established based on Leuning-Ball and Jarvis stomatal models, their application effects are compared and verified. Results show that daily variation of stomatal resistance of winter wheat is higher than that of canopy resistance, and there exists scale differences between leaf and canopy scale; Leuning-Ball stomatal model can be better explicated by the response of stomatal conductance towards environmental factors; Leuning-Ball canopy resistance estimation models turn out to be an effective canopy resistance simulation, and thus can be applied to research on the scaling-up of vapor transmission resistance of winter wheat in typical areas of North China.
DOI:10.1016/j.jhydrol.2009.04.036URL [本文引用: 1]
DOI:10.1016/S0168-1923(00)00152-0URL [本文引用: 1]
There is a strong need to extend whole-tree measurements of sap flow into broad-leaved forests where characteristics of stand structure, surface roughness, leaf dimension, and aerodynamic and canopy conductance may interact to partially decouple the canopy from the atmosphere. The implications of this partial decoupling to understanding the environmental control of canopy transpiration and to the modeling of forest water use are many. Therefore, thermal dissipation probes were used over a three-month period (June through August, 1997) to quantify day-to-day and tree-to-tree variation in whole-tree sap flow ( Q) for 12 red maple ( Acer rubrum L.) trees growing in an upland oak forest of eastern Tennessee. Whole-tree Q was calculated as the product of measured sap velocity, sapwood area and the fraction of sapwood functional in water transport. Daily canopy transpiration ( E c) was calculated from whole-tree Q and projected crown area, whereas average daily conductance ( g c) was derived by inverting the Penman–Monteith equation. Maximum Q averaged 73 kg per tree per day and varied between 45 and 160 kg per day for trees that ranged in stem diameter (DBH) from 17 to 35 cm, and from 19 to 26 m in height. Canopy transpiration peaked at 3.0 mm per day in early July and averaged 1.5 mm per day over the 3-month measurement period. Tree-to-tree variability for E c was high. Maximum rates of E c varied from 1.9 mm per day for the tree with the smallest projected crown area to 5.7 mm per day for one of the largest trees. Day-to-day variation in E c was a function of daily differences in net radiation ( R n) and atmospheric humidity deficit ( δ e). Increases in daily R n and δ e led to linear increases in canopy transpiration and there was no indication that a plateau-style relationship existed between E c and average daily δ e. Mean daily g c ranged from 1.4 to 6.7 mm s 611, and averaged 3.4 mm s 611 across the 12 study trees. Some of the tree-to-tree variation observed for E c and g c was related to the fact that not all trees occupied the same vertical position within the stand. Variation in estimates of the daily decoupling coefficient (0≤Ω≤1) was also considerable and for individual trees the seasonally-averaged Ω varied from 0.12 to 0.37, and averaged 0.23 for the 12 study trees. An Ω of this magnitude indicates that red maple canopies are partially decoupled from the atmosphere and suggests that significant vertical gradients of air temperature and δ e from the canopy surface to the bulk air several meters above the canopy are possible. Model analysis of hourly data indicated that simulated surface temperatures in mid-July were 3.6–5.8°C higher than above-canopy reference temperatures, and δ e at the canopy surface was 0.3 kPa higher than that of the bulk atmosphere. These calculations were partially supported by leaf-level measurements taken on one of the trees from a 20-m canopy-access tower. The implications of this partial decoupling to understanding and modeling the environmental control of canopy transpiration are discussed.
DOI:10.1071/BT07091URL [本文引用: 3]
DOI:10.3321/j.issn:1000-0933.2006.12.018 [本文引用: 1]
利用G ran ier热消散探针在2003年10月测定了广东鹤山丘陵地马占相思林14株样树的树干液流,同时监测林冠上方的光合有效辐射、空气湿度和气温,结合树木的形态和林分的结构特征,计算马占相思的整树蒸腾(E)、林分总蒸腾(Et)以及冠层平均气孔导度(gc),分析树形特征与整树水分利用的关系、冠层气孔导度对光合有效辐射(PAR)和空气水汽压亏缺(D)的响应.结果表明,整树蒸腾与胸径(P0.0001)、边材面积(P0.0001)和冠幅(P=0.0007)以自然对数的形式、与树高(P=0.014)以幂函数的形式呈现显著正相关.冠层气孔导度最大值(gcm ax)随D的上升呈对数函数下降(P0.0001),对光合有效辐射的响应则呈双曲线函数增加(P0.0001).液流测定系统能提供连续和准确的整树和林分蒸腾速率值,经严格数学推导公式计算,最终可求出冠层气孔导度,是研究森林水分利用与环境因子相互关系的有效方法.
DOI:10.3321/j.issn:1000-0933.2006.12.018 [本文引用: 1]
利用G ran ier热消散探针在2003年10月测定了广东鹤山丘陵地马占相思林14株样树的树干液流,同时监测林冠上方的光合有效辐射、空气湿度和气温,结合树木的形态和林分的结构特征,计算马占相思的整树蒸腾(E)、林分总蒸腾(Et)以及冠层平均气孔导度(gc),分析树形特征与整树水分利用的关系、冠层气孔导度对光合有效辐射(PAR)和空气水汽压亏缺(D)的响应.结果表明,整树蒸腾与胸径(P0.0001)、边材面积(P0.0001)和冠幅(P=0.0007)以自然对数的形式、与树高(P=0.014)以幂函数的形式呈现显著正相关.冠层气孔导度最大值(gcm ax)随D的上升呈对数函数下降(P0.0001),对光合有效辐射的响应则呈双曲线函数增加(P0.0001).液流测定系统能提供连续和准确的整树和林分蒸腾速率值,经严格数学推导公式计算,最终可求出冠层气孔导度,是研究森林水分利用与环境因子相互关系的有效方法.
DOI:10.1007/s00468-011-0615-1URL [本文引用: 4]
Abstract efflux () has been estimated from a temperature-related equation, but sap flux often affects measurements of , which leads to misunderstanding real stem respiration. In order to observe the relationship between and stem temperature and to analyze the effect of sap velocity on , stem temperature, and sap flux were measured from a subtropical and sap velocity were significantly higher in July than in October. Stem temperature could explain 17–41 and 54–75% variations of in July and October, respectively. A negative relationship between and stem temperature was found during 1800–230002hours in July. The daytime was 9.2, 4.3 and 2.4% higher than the predicted for three trees in July, and this occurred only on Tree 1 in October. Sap velocity was positively correlated with for three trees in July, and the increase of with the increase of sap velocity was only observed on Tree 1 in October. These results demonstrated that the occurrence of sap flux could account for the increase of daytime , and the effect of sap velocity on varied with the seasons from the S. superba stem.
Effect of Pinus radiata plantations on water balance in Chile
1
2008
... 植物蒸腾作为森林维持流域和区域水资源平衡的重要功能, 对社会和经济发展具有重要的生态意义(
Do stomata respond to relative humidity?
1
1991
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Transpiration and canopy conductance in young apricot ( Prunus armenica L.) trees subjected to different PAR levels and water stress
1
2005
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Differential transpiration by three boreal tree species in response to increased evaporative demand after variable retention harvesting
1
2006
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Energy balance and canopy conductance of a boreal aspen forest: Partitioning overstory and understory components
1
1997
... 为了更加详细地评估边界层阻力对GS计算的影响, 我们用所有观测数据计算了每个Ω水平的Pi值(每个水平4-5个重复)(
The energy and water balance of a Eucalyptus plantation in southeast Brazil
1
2010
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Stomatal response of grapevines to wind
1
1998
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Tree sap flow and stand transpiration of two Acacia mangium plantations in Sabah, Borneo
1
2000
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Water flux in boreal forest during two hydrologically contrasting years: Species specific regulation of canopy conductance and transpiration
1
1998
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Wind speed and leaf boundary layer conductance variation within tree crown: Consequences on leaf-to-atmosphere coupling and tree functions
1
1999
... 除了种间差异, Ω的季节变化很大(
Effect of wind on the transpiration of young trees
1
1984
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Estimating transpiration from 6-year-old Eucalyptus grandis trees: Development of a canopy conductance model and comparison with independent sap flux measurements
1
1993
... 其中, GSiref是参比气孔导度(即在D = 1 kPa时GS的值), -m是回归拟合方程的斜率, 表示气孔导度对D的变化的敏感性(即GS随lnD的变化率dGS/dlnD).通过边界线分析, 我们利用所得边界线数据分析利用这两种方法模拟的不同树种的GS对D响应的差异性.该方法已在多因素作用下的GS响应研究中得到应用(
Effects of stand age and tree species on canopy transpiration and average stomatal conductance of boreal forests
1
2005
... 尽管尾叶桉和木荷Ω的平均值相对较小(分别为0.1和0.17), 表明两个林分与大气环境存在部分脱耦联, 即不满足“引言”中提出的用于估算GS1的条件(3).本研究中, 尾叶桉和木荷的GS2:GS1分别为0.92和0.98, 表明GS1相对偏大(p < 0.01).这表明即使具有良好大气耦合条件的森林, 在估算GS时边界层阻力也不可忽略.另外, 两种方法估算的GS对大气D的响应的差异性表明, GS1在描述植物生理响应时也存在一些偏差.研究发现-m和GSiref之间0.6的比例是为防止植物木质部的过度空穴化, 维持最小叶水势(ΨL)而产生(
Interannual consistency in canopy stomatal conductance control of leaf water potential across seven tree species
1
2007
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Enhanced water use efficiency in a mixed Eucalyptus globulus and Acacia mearnsii plantation
2
2010
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
... 除了种间差异, Ω的季节变化很大(
Evaluation of transpiration in a Douglas-fir stand by means of sap flow measurements
1
1987
... 采用热消散探针法(TDP)测定树液通量密度 (Fd, g·H2O·m-2·s-1).具体测定方法参见
Transpiration of trees and forest stands: Short and long-term monitoring using sap flow methods
2
1996
... 其中, GSiref是参比气孔导度(即在D = 1 kPa时GS的值), -m是回归拟合方程的斜率, 表示气孔导度对D的变化的敏感性(即GS随lnD的变化率dGS/dlnD).通过边界线分析, 我们利用所得边界线数据分析利用这两种方法模拟的不同树种的GS对D响应的差异性.该方法已在多因素作用下的GS响应研究中得到应用(
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Measuring and modelling the transpiration of a maritime pine canopy from sap-flow data
1
1994
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
A generic model of forest canopy conductance dependent on climate, soil water availability and leaf area index
1
2000
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Regulation of transpiration in coffee hedgerows: Covariation of environmental variables and apparent responses of stomata to wind and humidity
1
1994
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Stomatal behaviour in a beech canopy: An analysis of Bowen ratio measurements compared with porometer data
1
1995
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Monsoonal influences on evapotranspiration of savanna vegetation of northern Australia
1
2001
... 除了种间差异, Ω的季节变化很大(
The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field
1
1976
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Stomatal control of transpiration: Scaling up from leaf to region
2
1986
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
1
1992
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Leaf boundary layer conductance in ventilated greenhouses: An experimental approach
1
2007
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Evaporation and canopy characteristics of coniferous forests and grasslands
1
1993
... 根据式1计算简化的冠层气孔导度(GS1) , 根据Penman-Monteith公式的逆形式(公式6)计算GS2 (
Sensitivity of stand transpiration to wind velocity in a mixed broadleaved deciduous forest
1
2014
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Sensitivity of stand transpiration to wind velocity in a mixed broadleaved deciduous forest
2014
Actual and potential transpiration and carbon assimilation in an irrigated poplar plantation
1
2008
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Values of the decoupling factor observed on forest canopies
1
2003
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Canopy conductance for a Moso bamboo ( Phyllostachys pubescens) forest in western Japan.
1
2012
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Transpiration, canopy conductance and the decoupling coefficient of a lowland mixed dipterocarp forest in Sarawak, Borneo: Dry spell effects
3
2004
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
... ;
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Transpiration and canopy conductance at two slope positions in a Japanese cedar forest watershed
1
2008
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Carbon dioxide and water vapor exchange by young and old ponderosa pine ecosystems during a dry summer
1
2001
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
Revealing the impact of forest exotic plantations on water yield in large scale watersheds in South-Central Chile
1
2009
... 植物蒸腾作为森林维持流域和区域水资源平衡的重要功能, 对社会和经济发展具有重要的生态意义(
Regulation of canopy conductance and transpiration and their modelling in irrigated grapevines
1
2003
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Modelling the surface conductance of a broad-leaf canopy: Effects of partial decoupling from the atmosphere
1
1998
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Crown conductance and tree and stand transpiration in a second-growth Abies amabilis forest
2
1997
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
... ;
Diurnal and seasonal variation in bulk stomatal conductance of the rice canopy and its dependence on developmental stage
1
2008
... 除了种间差异, Ω的季节变化很大(
1
... 冠层与大气解耦程度可用无量纲系数Ω来描述 (
基于液流格型特征值和标准化方法分析胸径和土壤水分对荷木液流的影响
1
2010
... 冠层叶片蒸腾速率(El, g H2O·m-2·s-1)可以通过树液通量密度Fd、叶面积和AS的计算获得.前人研究发现, 木荷40-60 mm深度的树液通量密度显著低于外部20 mm处的树液通量密度, 而0-20和20-40 mm处的树液通量密度没有显著差异(
基于液流格型特征值和标准化方法分析胸径和土壤水分对荷木液流的影响
1
2010
... 冠层叶片蒸腾速率(El, g H2O·m-2·s-1)可以通过树液通量密度Fd、叶面积和AS的计算获得.前人研究发现, 木荷40-60 mm深度的树液通量密度显著低于外部20 mm处的树液通量密度, 而0-20和20-40 mm处的树液通量密度没有显著差异(
Control of transpiration from the upper canopy of a tropical forest: The role of stomatal, boundary layer and hydraulic architecture components.
1
1997
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Stomatal control of transpiration in the canopy of a clonal Eucalyptus grandis plantation
2
1999
... 除了种间差异, Ω的季节变化很大(
... 大气对Ω的影响是各种环境因子的综合作用, 因此任何个体效应都可能被其他因素影响所掩盖.通常风速被认为会引起Ω的波动.例如,
1
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Stomatal conductance, transpiration and sap flow of tropical montane rain forest trees in the southern Ecuadorian Andes
3
2005
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
... 根据公式(8), 我们使用GS2计算了Ω值, 来量化森林冠层蒸腾与大气气象因子的耦合度.木荷的Ω年均值为0.17 ± 0.03, 显著高于尾叶桉林(Ω = 0.10 ± 0.03, p = 0.000 1).两个观测站之间Ω的差异则可能与LAI代表的冠层郁闭度的差异有关(
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Environmental and stomatal control of transpiration, canopy conductance and decoupling coefficient in young lemon trees under shading net
1
2008
... 除了种间差异, Ω的季节变化很大(
Water balance delineates the soil layer in which moisture affects canopy conductance
1
1998
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
a). Sap-flux-scaled transpiration responses to light, vapor pressure deficit, and leaf area reduction in a flooded Taxodium distichum forest.
2
1999
... 尽管尾叶桉和木荷Ω的平均值相对较小(分别为0.1和0.17), 表明两个林分与大气环境存在部分脱耦联, 即不满足“引言”中提出的用于估算GS1的条件(3).本研究中, 尾叶桉和木荷的GS2:GS1分别为0.92和0.98, 表明GS1相对偏大(p < 0.01).这表明即使具有良好大气耦合条件的森林, 在估算GS时边界层阻力也不可忽略.另外, 两种方法估算的GS对大气D的响应的差异性表明, GS1在描述植物生理响应时也存在一些偏差.研究发现-m和GSiref之间0.6的比例是为防止植物木质部的过度空穴化, 维持最小叶水势(ΨL)而产生(
... 大于0.6 (
Sensitivity of mean canopy stomatal conductance to vapor pressure deficit in a flooded Taxodium distichum L. forest: Hydraulic and non-hydraulic effects
1
2001
... 其中, GSiref是参比气孔导度(即在D = 1 kPa时GS的值), -m是回归拟合方程的斜率, 表示气孔导度对D的变化的敏感性(即GS随lnD的变化率dGS/dlnD).通过边界线分析, 我们利用所得边界线数据分析利用这两种方法模拟的不同树种的GS对D响应的差异性.该方法已在多因素作用下的GS响应研究中得到应用(
b). Survey and synthesis of intra- and interspecific variation in stomatal sensitivity to vapour pressure deficit
2
1999
...
... 尽管尾叶桉和木荷Ω的平均值相对较小(分别为0.1和0.17), 表明两个林分与大气环境存在部分脱耦联, 即不满足“引言”中提出的用于估算GS1的条件(3).本研究中, 尾叶桉和木荷的GS2:GS1分别为0.92和0.98, 表明GS1相对偏大(p < 0.01).这表明即使具有良好大气耦合条件的森林, 在估算GS时边界层阻力也不可忽略.另外, 两种方法估算的GS对大气D的响应的差异性表明, GS1在描述植物生理响应时也存在一些偏差.研究发现-m和GSiref之间0.6的比例是为防止植物木质部的过度空穴化, 维持最小叶水势(ΨL)而产生(
The effect of tree height on crown level stomatal conductance
3
2000
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
... ).
... 在z0水平下的风速.根据前人的研究, 当D < 100 Pa时, 叶片表面的边界层阻力远远大于气孔阻力, 而此时植物气孔导度的大小主要受到PAR的影响, 因此当D < 100 Pa时, GS的计算会存在极大的误差, 因此本研究中, GS是在排除D < 100 Pa时间段的数据后进行计算的(
Enhanced transpiration in response to wind effects at the edge of a blue gum (Eucalyptus globulus) plantation.
1
2001
... 环境变化带来的森林蒸腾变化可以通过冠层水汽导度对环境因子的响应来表征(
The estimation of transpiration from sparse dryland millet using stomatal conductance and vegetation area indices
2
1990
... 根据式1计算简化的冠层气孔导度(GS1) , 根据Penman-Monteith公式的逆形式(公式6)计算GS2 (
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
Application and comparison of winter wheat canopy resistance estimation models based on the scaling-up of leaf stomatal conductance
1
2013
... 大气对Ω的影响是各种环境因子的综合作用, 因此任何个体效应都可能被其他因素影响所掩盖.通常风速被认为会引起Ω的波动.例如,
Comparing the Penman-Monteith equation and a modified Jarvis-Stewart model with an artificial neural network to estimate stand-scale transpiration and canopy conductance
1
2009
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Environmental control of whole-plant transpiration, canopy conductance and estimates of the decoupling coefficient for large red maple trees
1
2000
... 以往的研究中, 在不考虑边界层阻力的影响时, GS通常被认为等同于GT (
Coordination of leaf area, sapwood area and canopy conductance leads to species convergence of tree water use in a remnant evergreen woodland
3
2008
... 根据式1计算简化的冠层气孔导度(GS1) , 根据Penman-Monteith公式的逆形式(公式6)计算GS2 (
... 研究认为, 随着LAI的增加, 冠层GS随之增加(
... 除了种间差异, Ω的季节变化很大(
马占相思林冠层气孔导度对环境驱动因子的响应
1
2006
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
马占相思林冠层气孔导度对环境驱动因子的响应
1
2006
... 其中, GV是通用气体常数(0.462 m3·kPa·K-1·kg-1), Ta是空气温度(K), ρ是水的密度(998 kg·m-3), El是冠层叶片蒸腾速率(
Effects of sap velocity on the daytime increase of stem CO2 efflux from stems of Schima superba trees.
4
2012
... 本研究在乡土种木荷(Schima superba)和外来种尾叶桉(Eucalyptus urophylla)人工林中进行.前者位于广州市中国科学院华南植物园(23.18° N, 113.36° E, 海拔41 m).所在地为典型的南亚热带季风气候, 年降水量1 612-1 909 mm, 年平均气温21.4-21.9 ℃.雨季从4月持续至9月, 旱季从9月持续到次年3月(
... 冠层叶片蒸腾速率(El, g H2O·m-2·s-1)可以通过树液通量密度Fd、叶面积和AS的计算获得.前人研究发现, 木荷40-60 mm深度的树液通量密度显著低于外部20 mm处的树液通量密度, 而0-20和20-40 mm处的树液通量密度没有显著差异(
... ).因此, 可以通过使用
...
