Ruiheng XIE^1,2,
Aihui WANG^2,,

Corresponding author: Aihui WANG,wangaihui@mail.iap.ac.cn

1.School of Atmospheric Sciences, Chengdu University of Information Technology, Chengdu 610225, China
2.Nansen-Zhu International Research Center, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
Manuscript received: 2020-04-13
Manuscript revised: 2020-06-01
Manuscript accepted: 2020-06-18
Abstract:Potential evapotranspiration (E_PET) is usually calculated by empirical methods from surface meteorological variables, such as temperature, radiation and wind speed. The in-situ measured pan evaporation (ET_pan) can also be used as a proxy for E_PET. In this study, E_PET values computed from ten models are compared with observed ET_pan data in ten Chinese river basins for the period 1961?2013. The daily observed meteorological variables at 2267 stations are used as the input to those models, and a ranking scheme is applied to rank the statistical quantities (ratio of standard deviations, correlation coefficient, and ratio of trends) between ET_pan and modeled E_PET in different river basins. There are large deviations between the modeled E_PET and the ET_pan in both the magnitude and the annual trend at most stations. In eight of the basins (except for Southeast and Southwest China), ET_pan shows decreasing trends with magnitudes ranging between ?0.01 mm d^?1 yr^?1 and ?0.03 mm d^?1 yr^?1, while the decreasing trends in modeled E_PET are less than ?0.01 mm d^?1 yr^?1. Inter comparisons among different models in different river basins suggest that PET_Ham1 is the best model in the Pearl River basin, PET_Ham2 outperforms other models in the Huaihe River, Yangtze River and Yellow River basins, and PET_FAO is the best model for the remaining basins. Sensitivity analyses reveal that wind speed and sunshine duration are two important factors for decreasing E_PET in most basins except in Southeast and Southwest China. The increasing E_PET trend in Southeast China is mainly attributed to the reduced relative humidity.
Keywords: potential evapotranspiration model,
pan evaporation,
model comparison,
sensitivity analysis,
China
摘要:潜在蒸散(E_PET)通常是利用近地表的气象变量(如温度、辐射、风速等)借助经验公式计算得出, 站点观测的蒸发皿蒸发量(ET_pan)也常被当作E_PET的替代品. 在本文中, 我们基于2267个站点的日观测气象数据, 将十组潜在蒸散模型计算得到的E_PET与1961-2013年间中国十大流域的站点观测ET_pan进行对比分析. 紧接着我们利用一种统计评分方法, 对各流域中的ET_pan和模拟的E_PET之间的三组统计量(标准差比值, 相关系数, 趋势比值)进行了排序评分, 以此来筛选每个流域表现最好的模型. 计算得到的E_PET和ET_pan在量级和年际趋势上都有着很大的差异, 除了东南地区和西南地区以外的八个流域中, ET_pan的下降趋势都在-0.01mm d^-1 yr^-1到-0.03mm d^-1 yr^-1之间, 而E_PET的下降趋势则总是小于-0.01 mm d^-1 yr^-1. 在各流域对不同模型进行对比分析后, 我们得到了每个流域表现性最好的模型. 其中, PET_Ham1是珠江流域最适用的模型; 在淮河、长江以及黄河流域, PET_Ham2要优于其他模型; 在其它流域中, 则是以PET_FAO表现最好. 敏感性分析表明, 除了东南地区和西南地区以外, 风速和日照时数是影响E_PET减小的最重要的因子, 而E_PET在东南地区的上升趋势则主要归因于相对湿度的减小.
关键词:潜在蒸散模型,
蒸发皿蒸发,
模型比较,
敏感性分析,
中国

HTML

--> --> -->

Evapotranspiration (ET) plays an important role in both energy and hydrologic cycles at the land surface, and it consists of open water evaporation, bare soil evaporation, rainfall interception evaporation, and vegetation transpiration (Zeng et al., 2018). The release of latent heat due to evaporation affects water and heat balances near the surface, and approximately two-thirds of precipitations falling over the land is from evaporated water (Wang et al., 2012a). Furthermore, ET is of great significance for agriculture, and it is a prerequisite for irrigation planning (Paparrizos et al., 2017). In the meteorological and agricultural sciences, there are usually three different ET notations, including actual evapotranspiration (AET), potential evapotranspiration (E_PET), and pan evaporation (ET_pan). AET denotes the actual moisture evaporating from the land surface under local climate conditions, and E_PET is defined as the amount of evaporation and transpiration that would occur under certain meteorological conditions with a sufficient water supply but without advection and heating effects (Dingman, 1992; McMahon et al., 2013; Li et al., 2016). E_PET is the upper limit of AET and can be used to estimate AET (Gao et al., 2006). ET_pan is evaporation from a water pan under local climatic/environmental conditions, and to a certain extent, it can represent open water evaporation.
ET_pan can be measured at a meteorological station, and the measurement is obtained using an evaporation pan with enough water supplies at an open site. AET can also be measured by a lysimeter, the eddy covariance technique, or Bowen ratio method (Wang et al., 2012a). However, unlike routine meteorological observations, in-situ measurements of AET are not available in many regions worldwide. In practice, AET is usually calculated by empirical methods (Gao et al., 2007). E_PET cannot be directly observed and is usually estimated by empirical methods (referred to as E_PET models) using meteorological parameters as inputs.
According to the types of input variables, E_PET models can be classified as temperature-based, radiation-based, and combination models in which multiple meteorological parameters are used as the model inputs (Bormann, 2011). For instance, to estimate reference crop evapotranspiration (ET_ref), the Penman?Monteith (PM) method recommended by the Food and Agriculture Organization (FAO) is one of the combination models and is widely used to estimate E_PET. This model requires temperature, radiation and wind speed as inputs (Allen et al., 1998). Using station-observed meteorological data as inputs, E_PET computed with the FAO56 model indicates an overall downward trend in most parts of China (Gao et al., 2006; Yin et al., 2010a). Although the PM method is regarded as the most representative formula for estimating E_PET and has been widely used in many studies (Gao et al., 2006; Zhang et al., 2007; Zuo et al., 2012), this model requires multiple surface meteorological quantities and several empirical coefficients, which are usually not easily obtainable. Therefore, other E_PET models that require fewer inputs have been developed and used commonly in research. For instance, Samani and Pessarakli (1986) concluded that the temperature-based Hargreaves model can reasonably estimate E_PET in regions with Arizonian climatic conditions. The traditional Priestley?Taylor model uses only air temperature and net radiation as inputs to compute E_PET and has been adopted in various studies (Priestley and Taylor, 1972). Ding et al. (2013) incorporated the leaf area index, soil moisture and mulching fraction into the original Priestley?Taylor model and found that the modified model improved E_PET estimates in cold and arid areas. In general, the performances of different E_PET models are region dependent, and a specific model may not be suitable for all regions in China. Therefore, to obtain the most representative E_PET model in each Chinese river basin, it is necessary to perform comprehensive evaluations of their performances.
Many studies have compared or evaluated E_PET models over the past few decades (Jacobs et al., 2004; Lu et al., 2005; Douglas et al., 2009; Donohue et al., 2010; Bormann et al., 2011; Li et al., 2016; Paparrizos et al., 2017). The conclusions of these studies are quite different, and the “best” E_PET models vary across different climate regimes. In contrast to E_PET, the evaporation pan exchanges heat and moisture with the surrounding environment, which affects the water evaporation rate in the pan (ET_pan) (Zuo et al., 2016). Although ET_pan and E_PET have different physical meanings and are derived from different approaches, many studies still regard ET_pan as a surrogate for E_PET (Liu et al., 2004; Yin et al., 2010b; Han et al., 2012). In China, meteorological stations routinely measure ET_pan, which has been used to evaluate, or are regarded as, E_PET models (Zhou et al., 2006; and Weiβ and Menzel, 2008). However, most previous studies have evaluated the performances of E_PET models at only a few stations for a short time period (Xu et al., 2002; Li et al., 2016; Paparrizos et al., 2017), and the results may not be representative in large areas for a long time period. China has a vast land domain, and its climate condition varies regionally. It is necessary to investigate the applicability of different E_PET models in different climate regimes.
In the current study, ET_pan observations at 2267 stations for the period 1961?2013 are used to evaluate the performances of ten E_PET models in ten Chinese river basins. Various statistical quantities are computed and inter-compared, and subsequently, the best-performing E_PET model is obtained for each river basin. Finally, based on the best E_PET model for each river basin, sensitivity analyses are also conducted for the E_PET to the input meteorological variables.

2

-->

2.1. Meteorological data

High-quality daily observations at 2425 meteorological stations were obtained from the National Meteorological Information Center of the China Meteorological Administration (http://data.cma.cn/en). The variables used in this study include 20-cm micro-pan evaporation (ET_pan), minimum air temperature (T_min), maximum air temperature (T_max), mean air temperature (T_a), wind speed at 10 m (U₁₀), relative humidity (RH), and sunshine duration (SD) from 1961 to 2013. To ensure the long-term representation of those meteorological data stations, available records of less than 30 years are discarded, and 2267 observation stations remain in this study.
As E_PET is an important land surface hydrological element, and divisions of drainage basins are often used in hydrology research, China is divided into ten drainage basins (Fig. 1), including seven river basins [the Songhua River (143 stations), Liaohe River (89 stations), Haihe River (252 stations), Yellow River (307 stations), Huaihe River (211 stations), Yangtze River (661 stations), Pearl River (236 stations) basins] and three other drainage basins[Southeast China (SE, 110 stations), Southwest China (SW, 92 stations) and Northwest China (NW, 166 stations)]. Below, the analyses will be performed for those basins.
Figure1. Distribution of ten drainage basins and the locations of 2267 meteorological stations in China. The station number in each basin is indicated in brackets.



2 -->

2.2. E_PET models

By reviewing the literature, a set of 10 different E_PET models are adopted in our study (Table 1), and these models are widely used in various studies. They include four temperature-based models [Hargreaves (Hargreaves and Samani, 1985), Romanenko (Oudin et al., 2005), Hamon version1 (Lu et al., 2005) and Hamon version2 (Oudin et al., 2005)], four radiation-based models [Priestley?Taylor (Priestley and Taylor, 1972), Abtew (Oudin et al., 2005), Jensen?Haise (Jensen and Haise, 1963) and Makkink (Makkin, 1957)], and two combination models [Penman (Oudin et al., 2005) and FAO56 (Allen et al., 1998)]. Among those E_PET models, radiation-based models require solar radiation (R_s) and net radiation (R_n) as inputs, which are usually not available from in-situ measurements. Empirical formulae with available meteorological variables can be used to derive radiation datasets (Allen et al., 1998; Yang et al., 2006). For example, Yang et al.(2006) proposed a hybrid method in which surface radiation was a function of the sunshine duration. Then, the researchers used this method to calculate R_s in China, the USA and Saudi Arabia and found that the modeled R_s values were the most consistent with the observations when compared to those from other methods. Here, we adopted the method of Yang et al. (2006) to compute R_s:

EPET models	References
$ {\mathrm{P}\mathrm{E}\mathrm{T}}_{\mathrm{H}\mathrm{a}\mathrm{r}}=0.0023{R}_{\mathrm{a}}{\left({T}_{\max}-{T}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)}^{0.5}({T}_{\mathrm{a}}+17.8) $	(Hargraves et al., 1985)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{R}\mathrm{o}\mathrm{m} }=4.5{\left(1+\dfrac{ {T}_{\mathrm{a} } }{25}\right)}^{2}\left(1-\dfrac{ {e}_{\mathrm{a} } }{ {e}_{\mathrm{s} } }\right)$	(Oudin et al., 2005)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{H}\mathrm{a}\mathrm{m}1}=0.1651\times \dfrac{\mathrm{S}\mathrm{D} }{12}\times \dfrac{216.7\times 6.108 {\mathrm{e} }^{\dfrac{17.26939 {T}_{\mathrm{a} } }{ {T}_{\mathrm{a} }+237.3} } }{ {T}_{\mathrm{a} }+273.3}\times 1.2$	(Lu et al., 2005)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{H}\mathrm{a}\mathrm{m}2}={\left(\dfrac{\mathrm{S}\mathrm{D} }{12}\right)}^{2}{\mathrm{e} }^{\left(\frac{ {T}_{\mathrm{a} } }{16}\right)}$	(Oudin et al., 2005)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{P}\mathrm{T} }=\alpha \dfrac{\Delta }{\Delta +\mathrm{\gamma } }\dfrac{ {R}_{\mathrm{n} } }{\lambda }$	(Priestley and Taylor, 1972)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{A}\mathrm{b}\mathrm{t} }=0.53\dfrac{ {R}_{\mathrm{s} } }{\lambda }(1-\alpha)$	(Oudin et al., 2005)
$ {\mathrm{P}\mathrm{E}\mathrm{T}}_{\mathrm{J}\mathrm{e}\mathrm{n}}=0.408[0.014\left({1.8T}_{\mathrm{a}}+32\right)-0.37]{R}_{\mathrm{s}} $	(Jensen and Haise, 1963)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{m}\mathrm{a}\mathrm{k} }=0.61\left(\dfrac{ {\Delta } }{ {\Delta }+\mathrm{\gamma } }\right)\dfrac{ {R}_{\mathrm{s} } }{\mathrm{\lambda } }-0.12$	(Makkink, 1957)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{P}\mathrm{e}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{n} }=\dfrac{ {\Delta }{R}_{\mathrm{n} }+2.6\mathrm{\gamma }\left({e}_{\mathrm{s} }-{e}_{\mathrm{a} }\right)(1+0.536{U}_{2})}{\lambda \mathrm{\rho }({\Delta }+\mathrm{\gamma })}$	(Oudin et al., 2005)
${\mathrm{P}\mathrm{E}\mathrm{T} }_{\mathrm{F}\mathrm{A}\mathrm{O}56}=\dfrac{0.408{\Delta }{R}_{\mathrm{n} }+\mathrm{\gamma }\dfrac{900}{\mathrm{T}+273}{U}_{2}\left({e}_{\mathrm{s} }-{e}_{\mathrm{a} }\right)}{ {\Delta }+\mathrm{\gamma }(1+0.34{U}_{2})}$	(Allen et al., 1998)

Table1. The E_PET models used in the study. The input variables of these formulae include: T_a = mean air temperature (°C), T_max = maximum temperature (°C), T_min = minimum temperature (°C), SD = sunshine duration (h), γ = psychrometric constant (kPa °C^?1), Δ = slope of the vapor pressure curve (kPa °C^?1), λ= latent heat of vaporization (MJ kg^?1), α = surface albedo, e_s = saturation vapor pressure (kPa), e_a = actual vapor pressure (kPa), U₂ = wind speed at 2 m height (m s^?1), R_s = global solar radiation (MJ m^?2), R_a = extraterrestrial radiation (MJ m^?2), and R_n = net radiation (MJ m^?2).


where R_s is the solar radiation; R_c is the solar radiation under clear-sky conditions, which is calculated by meteorological observations, ozone absorption and turbidity coefficients; n is the measured sunshine duration; N is the maximum possible sunshine duration; and a₀, a₁ and a₂ are regression coefficients. Equation (1) has been widely applied in many studies (Yang et al., 2010; Tang et al., 2011; Wang et al., 2012b; He et al., 2018). In addition, we also adopted the coefficients of Wang et al. (2012b), in which a₀ is 0.33, a₁ is 0.70, and a₂ is ?0.02 in Eq. (1), which were derived from meteorological station variables.
According to the principle of the conservation of energy, R_n is the difference between incoming net shortwave radiation (R_ns) and the outgoing net longwave radiation[R_nl, Eq. (2)]. The FAO has also provided equations to calculate these variables (Allen et al., 1998). Moreover, Yin et al.(2008) used radiation measurements in China to calibrate the R_nl models and found that the Penman method (1948), in Eq. (4), was more accurate than the FAO24 and FAO56-PM models:
where α= 0.23 is the albedo for the reference crop, $\sigma $ is the Stefan?Boltzmann constant (4.903×10^?9 MJ K^?4 m^?2 d^?1), T_x,k (T_n,k) is the maximum (minimum) absolute temperature for 24 h (K), and e_a is the actual vapor pressure (kPa).
In the Penman and FAO models, the 2-m wind speed is needed (Table 1). Thus, we converted the 10-m wind speed to 2-m wind speed using the wind profile formula (Allen et al., 1998):
where U₂ is the wind speed at 2 m above the ground surface (m s^?1) and U_z is the measured wind speed at z m above the ground surface (m s^?1), which is 10 m in this study.
In the Hargreaves and Jensen?Haise models, the E_PET is a function of T_a and R_s. From these models (Table 1), when T_a is lower than ?17.8°C for the Hargreaves model and ?3.1°C for the Jensen?Haise model, the E_PET would be negative. These are not correct in reality. Similarly, the Priestley?Taylor method requires T_a and R_n as inputs. However, R_s occurs only in the daytime, but the R_nl is available for both daytime and nighttime. During the cold season in high latitudinal regions, the relatively short daytime SD would also reduce the R_s, leading to R_nl values greater than R_ns. Under the above two circumstances, R_n will be less than zero, and then, the E_PET from the Priestley?Taylor model would also be negative. As an important factor of agriculture, E_PET is more prominent during the crop growing seasons than in other seasons, and E_PET should be very small or even negligible in the cold seasons. To avoid appearance of a negative E_PET value due to the meteorological inputs in some E_PET models, our analyses are confined to the growing season of March to October during each year. After the above procedure, E_PET is set as the missing value if it is still less than zero.

2 -->

2.3. Sensitivity analysis

To estimate the effects of changes in various meteorological factors on modeled E_PET, sensitivity analyses are also conducted for each E_PET model. Because different E_PET models have different structures and input requirements and these input variables have diverse magnitude ranges, it is difficult to directly conduct the E_PET sensitivity analysis with different input variables (Gong et al., 2006). In this study, we adopt a dimensionless relative sensitivity coefficient (SC), which has been widely used in ET studies (McCuen, 1974; Gong et al., 2006; Yin et al., 2010a; Zuo et al., 2012):
where SC is the sensitivity coefficient, and X is one of the model input variables. SC represents the relative change in E_PET induced by the relative change in the meteorological factor X. In other words, the relative change in X multiplied by SC equals the relative change in E_PET. For example, SC=0.1 indicates that 10% of X change would cause 1% of E_PET change. A positive (negative) SC represents that changes in E_PET are consistent (inconsistent) with those in X. The higher SC is, the stronger the X effect imposed on E_PET will be. However, SC cannot fully reflect the impact of each meteorological factor on the E_PET changes. A literature review of previous studies revealed that E_PET was the most sensitive to RH in the Yangtze River basin (Gong et al., 2006) and the Weihe River basin (Zuo et al., 2012) in China. However, Yin et al. (2010b) reported that RH was only a highly sensitive but not a dominant factor of E_PET, and its insignificant trend during 1971?2008 could only induce a small change in E_PET. To further address this issue, we combined the relative change (RC) in each input variable and its SC for E_PET attribution analysis. The RC (units: %) is described as follows (Yin et al., 2010a):
where T_X is the linear trend in the annual time series for any variable X, and |X| is its absolute mean during the past 53 years. RC represents the mean percentage change in the variable X during the study period. Based on Eqs. (6) and (7), we also conducted attribution analyses below. At each station, we recalculated the E_PET with individual input meteorological variables changing from ?10% to 10% by assuming that other factors remained unchanged (Yin et al., 2010b). Then, we calculated SC using Eq. (6) and RC using Eq. (7). The product of SC and RC denotes the relative contribution (RCT) of the target meteorological variable to the E_PET change. Inter comparisons of RCTs for different meteorological factors can represent the relative importance of each metrological variable for the E_PET change.

2 -->

2.4. Ranking scheme

To quantify the differences between modeled E_PET and ET_pan, we compute three statistical quantities, including the ratio of E_PET standard deviations to that of ET_pan, the correlation coefficient, and the ratio of E_PET trends to ET_pan trends. Moreover, to evaluate the performance of E_PET models in terms of those statistical quantities in each basin, a ranking scheme is utilized. Wang et al. (2012c) applied this approach to rank four statistical quantities between reanalysis products and observations in the Tibetan Plateau to evaluate the performances of each reanalysis product. In the present study, based on each statistical quantity, the mean ranking scores from 1 to 10 are given to each E_PET model. The ranking score is computed as follows: Among all 10 E_PET models, the highest correlation coefficient is given a ranking score of 1, and the lowest one is given a score of 10. Regarding the ratio of standard deviations and the ratio of trends, 1 is given to the model with the ratio closest to 1, and 10 indicates the ratio farthest away from 1. Then, we average all ranking scores of three quantities in each basin, and the mean magnitude from the lowest to the highest represents the closest to the least close relationships between E_PET models and ET_pan.

2

-->

3.1. Spatial distribution and magnitude of the modeled E_PET

Figure 2 shows the spatial distribution of the multiple growing seasonal mean E_PET and ET_pan from 1961 to 2013. This figure shows the apparent spatial variations in E_PET. At the majority of stations, the mean ET_pan is above 4 mm d^?1. The stations with relatively low ET_pan are mainly located in the Yangtze River basin and Liaohe River basin, while large values appear in the Yellow River basin and Northwest China, where the magnitude of ET_pan is generally larger than 8 mm d^?1 at most stations. In terms of magnitudes, PET_Rom is more consistent with ET_pan than other models, with a mean E_PET above 3 mm d^?1 at 85% of stations in China and even larger than 8 mm d^?1 in Northwest China. For the distribution pattern, PET_Rom is also the closest to ET_pan, and the spatial correlation coefficient is up to 0.86. PET_FAO and PET_Abt also correlate well with ET_pan, while the spatial correlation coefficients are 0.72 and 0.74, respectively. Compared to other models and ET_pan, the E_PET values from both PET_Ham1 and PET_Ham2 are relatively low, especially for PET_Ham2, with values of less than 2 mm d^?1 at 93% of stations. In addition, for the radiation-based models, the PET_Jen produces the largest value with a magnitude larger than 4 mm d^?1 in eastern China.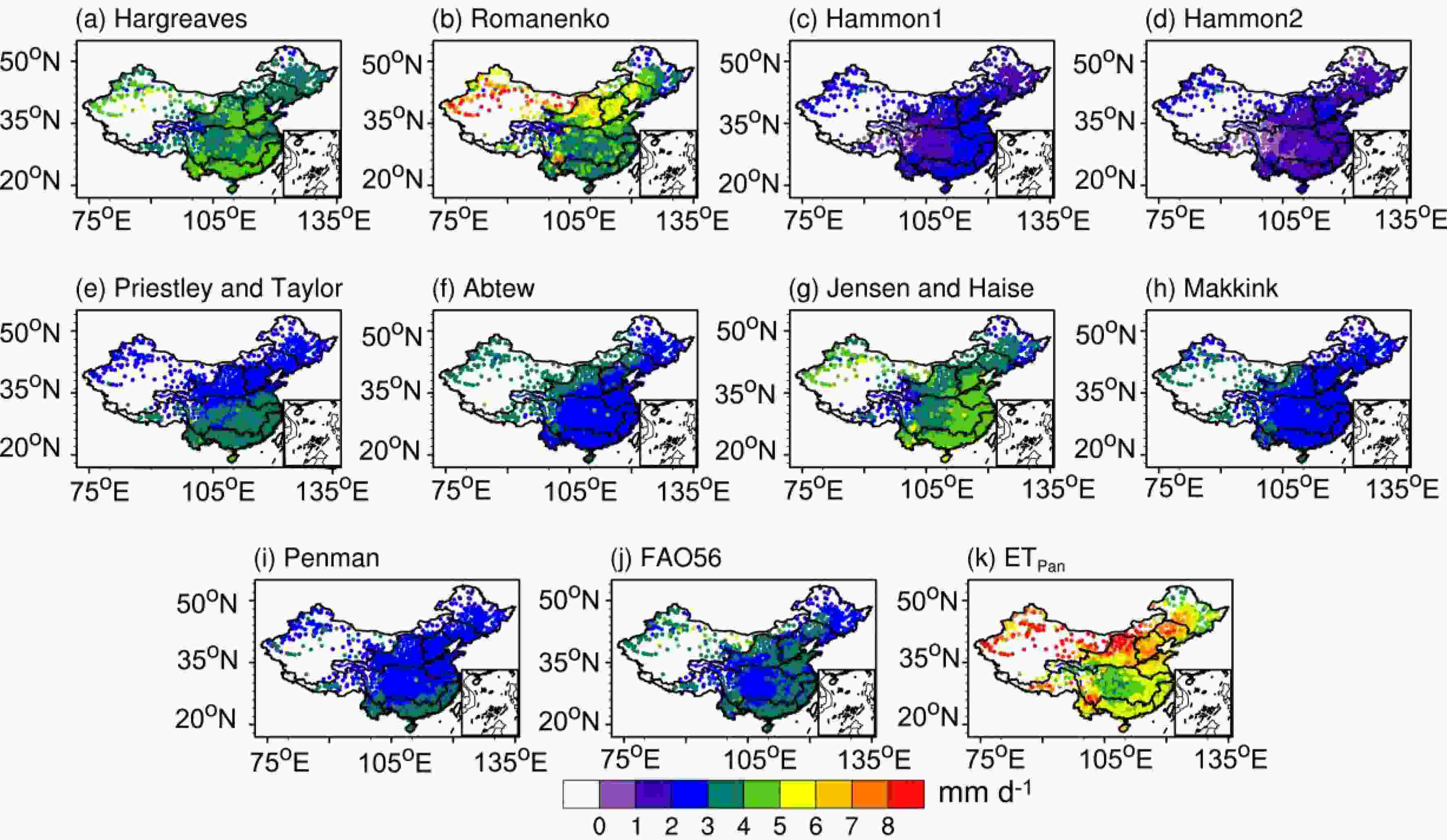
Figure2. Spatial distribution of the annual meangrowth season (Mar?Oct) pan evaporation and E_PET calculated by different models: (a) Hargreaves, (b) Romanenko, (c) Hamon version 1, (d) Hamon version 2, (e) Priestley and Taylor, (f) Abtew, (g) Jensen and Haise, (h) Makkink, (i) Penman, (j) FAO56 and (k) ET_pan.


Figure 3 shows the ranges of ET_pan and E_PET from different models from three basins: the Yangtze River basin (Fig. 3a), Yellow River basin (Fig. 3b), and Northwest China (Fig. 3c). The three basins represent the humid, semiarid and arid regions in China, respectively. By comparison, the modeled E_PET is relatively close to ET_pan in the humid Yangtze River basin; however, in arid Northwest China, they show obvious differences. This finding implies that ET_pan and E_PET are closer to each other in the humid region than in the arid region. This may be caused by the larger non-uniformity of climate conditions between the water body in the pan and the surrounding environment in the arid regions, and the non-uniformity is related to differences in surface temperature, moisture and albedo, which are also larger in arid regions (Zuo et al., 2016). Furthermore, in all three basins, no model can capture the peak values of ET_pan, and the modeled E_PET amplitudes are smaller than those of ET_pan, and the biases of their maximum values are particularly large. Except for PET_Jen, the radiation-based models show relatively small differences between the upper and lower quartile than those of the temperature-based models, which somehow indicates that the temporal and spatial variabilities in the radiation-based models (PET_PT, PET_Abt, and PET_Mak) should also be smaller than those of the temperature-based models (PET_Rom, PET_Ham1, PET_Ham2). Additionally, PET_FAO is closer in magnitude to ET_pan than PET_PM. Although both PET_FAO and PET_PM have similar structures and input requirements, PET_PM displays a narrower magnitude range than that from PET_FAO due to its lower maximum value.
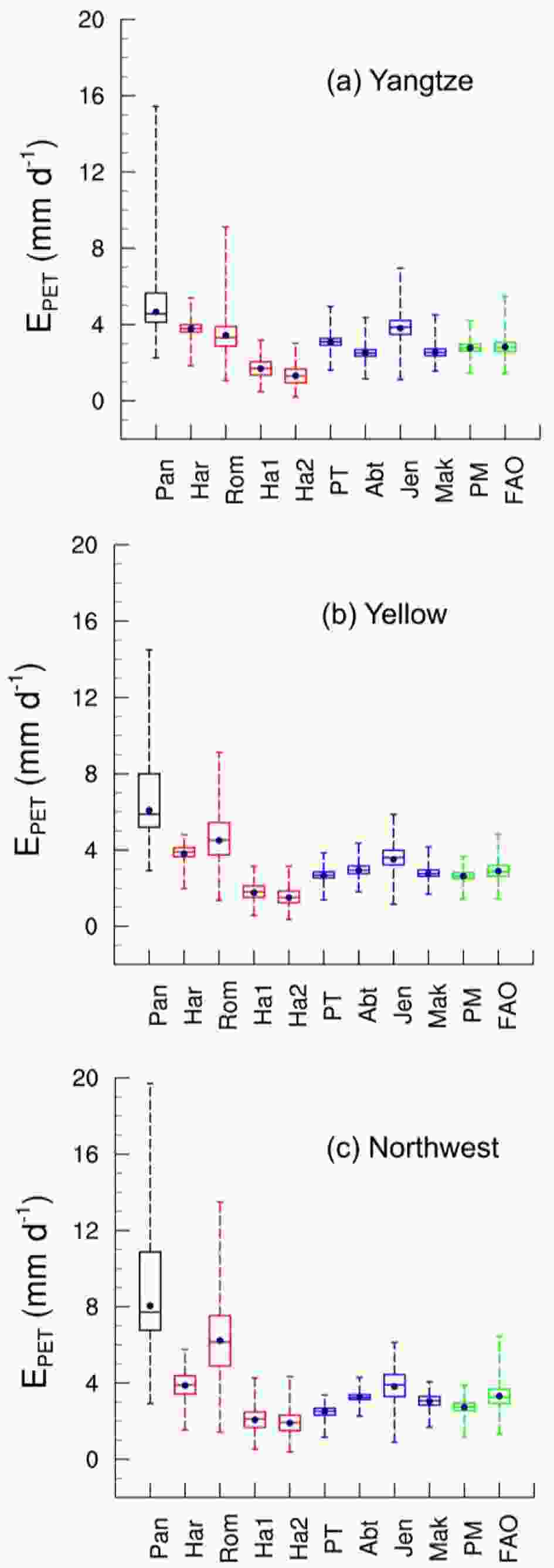Figure3. Boxplots of annual mean growth season (Mar?Oct) ET_pan and E_PET calculated from different models in three selected basins: (a) Yangtze River basin, (b) Yellow River basin, and (c) Northwest China.



2 -->

3.2. Trends and variability

Figure 4 shows the linear trends in the E_PET models and ET_pan during 1961?2013. There are apparent differences, and opposing trend signs occur in some cases. ET_pan has an upward trend in Southeast and Southwest China, while it has a downward trend in other basins. The downward trend in ET_pan ranges from ?0.01 mm d^?1 yr^?1 to ?0.03 mm d^?1 yr^?1, while the decreasing E_PET trends are always less than ?0.01 mm d^?1 yr^?1. In the Songhua River and Liaohe River basin, and Southeast and Northwest China, the trends in PET_FAO and ET_pan are the most similar, and in Northwest China, PET_FAO is the only model that can successfully capture the decreasing ET_pan trend. In Southwest China, the trend in PET_Mak is consistent with that of ET_pan, and PET_Ham2 can best capture the trend in ET_pan in the remaining basins. In addition, PET_Rom is proportional to T_a (Table 1) and its temporal variabilities are consistent with that of T_a, showing an increasing trend in all basins.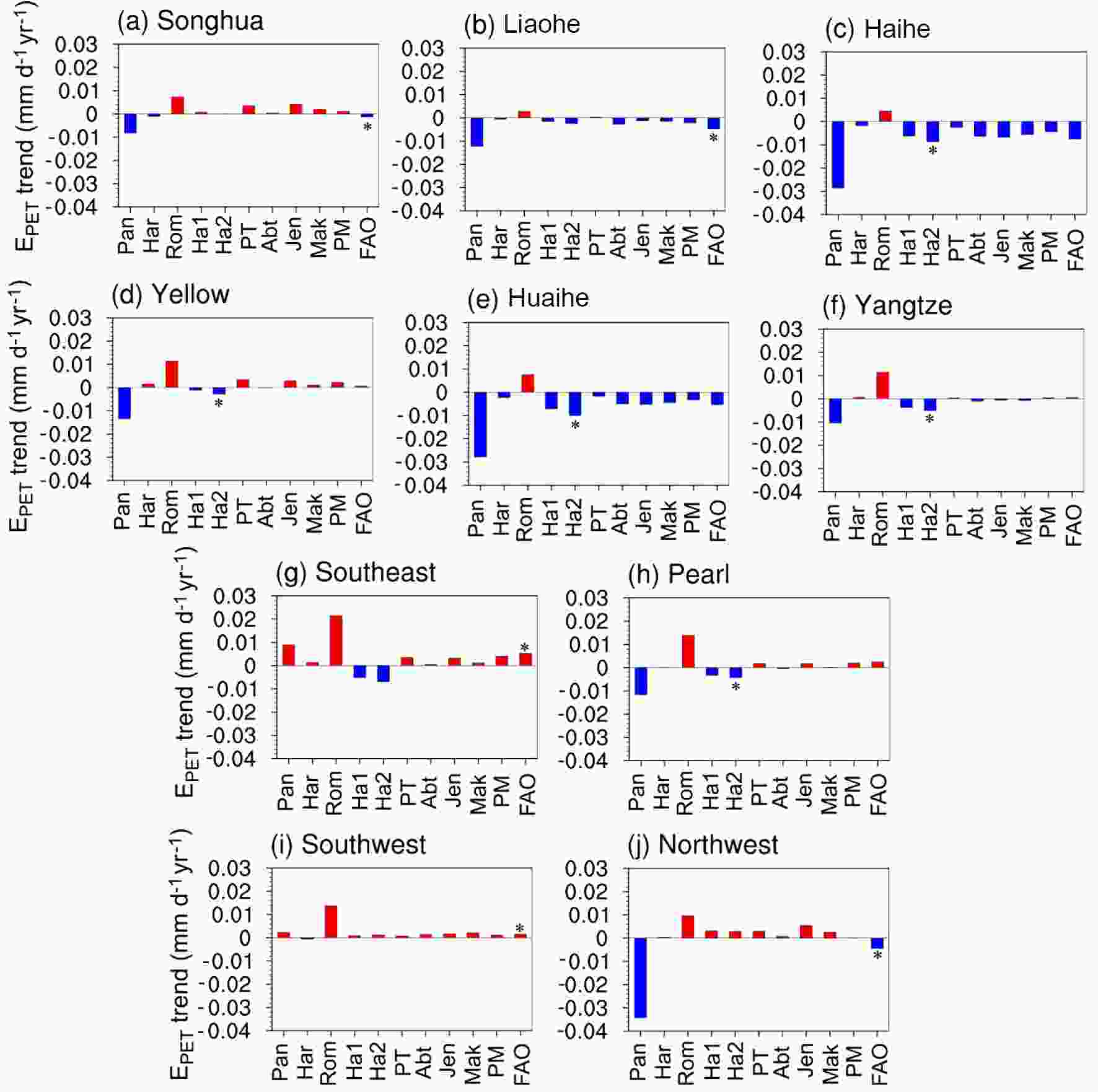
Figure4. Trends in annual growing season mean ET_pan and E_PET from 1961 to 2013 in (a) Songhua River basin, (b) Liaohe River basin, (c) Haihe River basin, (d) Yellow River basin, (e) Huaihe River basin, (f) Yangtze River basin, (g) Southeast China, (h) Pearl River basin, (i) Southwest China, and (j) Northwest China. The E_PET model with the closest trend to that in ET_pan is marked with a star (*).


We further assess the inter annual variability in the modeled E_PET and ET_pan. Figure 5 shows the growing seasonal mean anomalies of E_PET and ET_pan from 1961 to 2013 in three different drainage basins, and the corresponding anomalies of T_a and SD are also exhibited. In the Yangtze River basin (Fig. 5b), T_a shows an apparently upward trend since the 1990s, and SD shows an abrupt decline around the early 1980s. ET_pan also displays a significant downward trend, and its anomalies change from positive to negative in 1981. For most models except for PET_Rom, the inter annual variability is relatively small, and their standard deviations are no more than 0.2 mm d^?1. In terms of the temperature-based equations, PET_Rom is the most consistent with T_a and has been significantly increasing since the 1990s (Fig. 5a). Although the trend of R_s in the Yellow River basin and Northwest China is not obvious (Figs. 5d and f), the warming trend since the 1990s is still significant (p=99%). The ET_pan shows obviously decreasing trends in the Yellow River basin and Northwest China (Figs. 5c and e), and the downward trend is dramatic in Northwest China (T=?0.034 mm d^?1 yr^?1). Additionally, except for PET_Rom, the inter annual variability in the E_PET models is still small, and the standard deviations are also less than 0.2 mm d^?1 in these two basins.
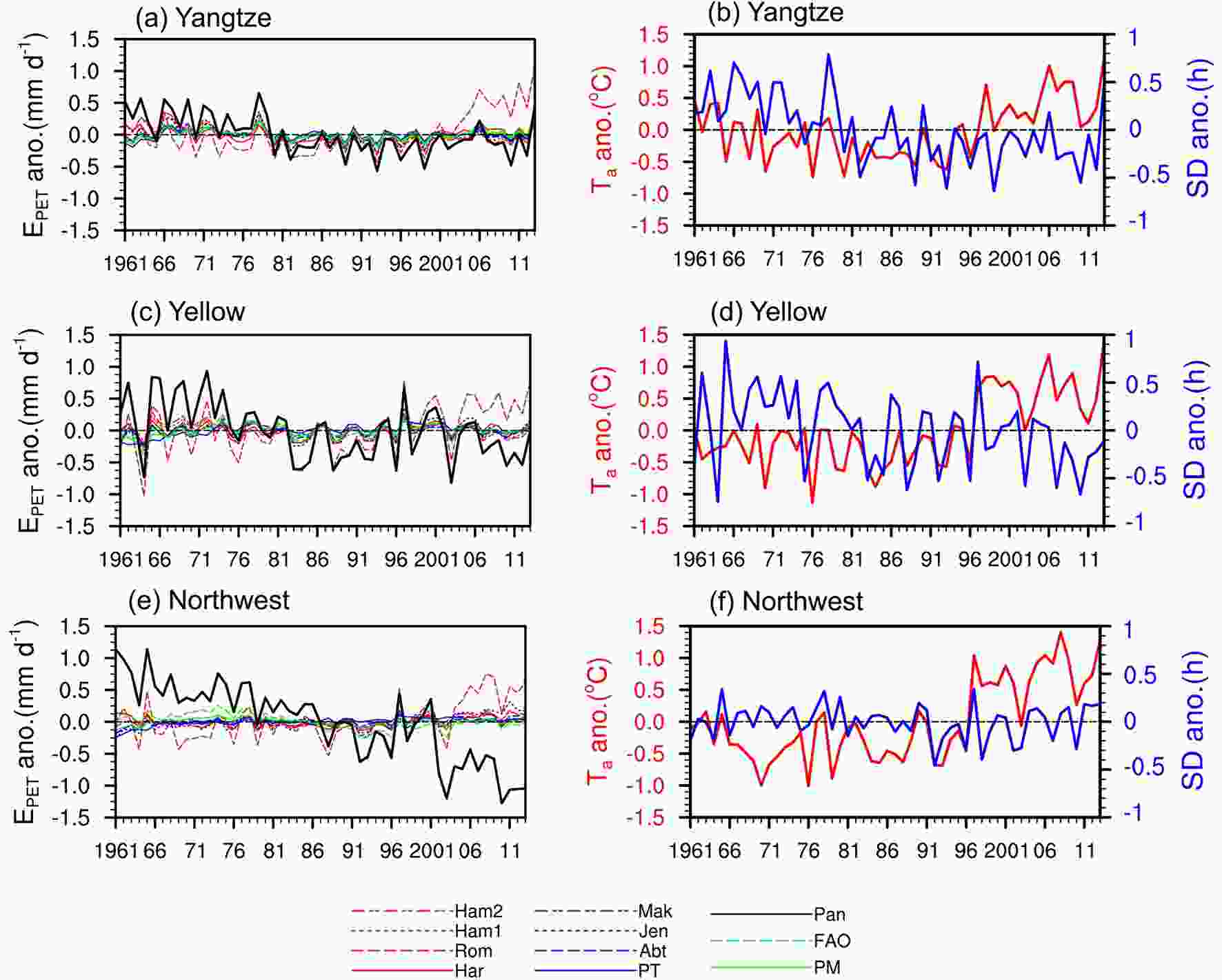Figure5. Mean E_PET anomaly in (a) the Yangtze River basin, (c) the Yellow River basin, and (e) Northwest China, and the anomalies in temperature and sunshine duration (b, d, f) averaged over the growing seasons (Mar?Oct) from 1961 to 2013. The red curve indicates the temperature anomaly (left axis), and the blue curve is the sunshine duration anomaly (right axis).


Because both ET_pan and E_PET have obvious seasonal variations, so seasonality changes of modeled E_PET are also investigated. Figure 6 exhibits the monthly trends in the E_PET models and ET_pan. ET_pan shows a decreasing trend during all months in the three basins, and the largest declining rates occur in May and June. In contrast, PET_Rom has an apparent upward trend in all months due to its highly consistent variability with that of temperature. Except for PET_Rom, the PET trends in all E_PET models in all months are synchronous in the Yangtze River basin and show downward trends from June to September (Fig.6a). Among them, the trend in PET_Ham2 is the closest to that of ET_pan. Additionally, the monthly trend of PET_Ham2 is closer to that of ET_pan than other models in the Yellow River basin (Fig.6b). However, in Northwest China (Fig.6c), the monthly trends in all models are greatly different from ET_pan. Although the declining trend in PET_FAO is consistent with that of ET_pan, the trend magnitudes of the two are very different. This is likely due to the differences in the physical processes of E_PET and ET_pan in this region, and we will discuss this further in section 4. Overall, compared to humid regions, the differences between the ET_pan and E_PET monthly trends are much greater in arid regions.
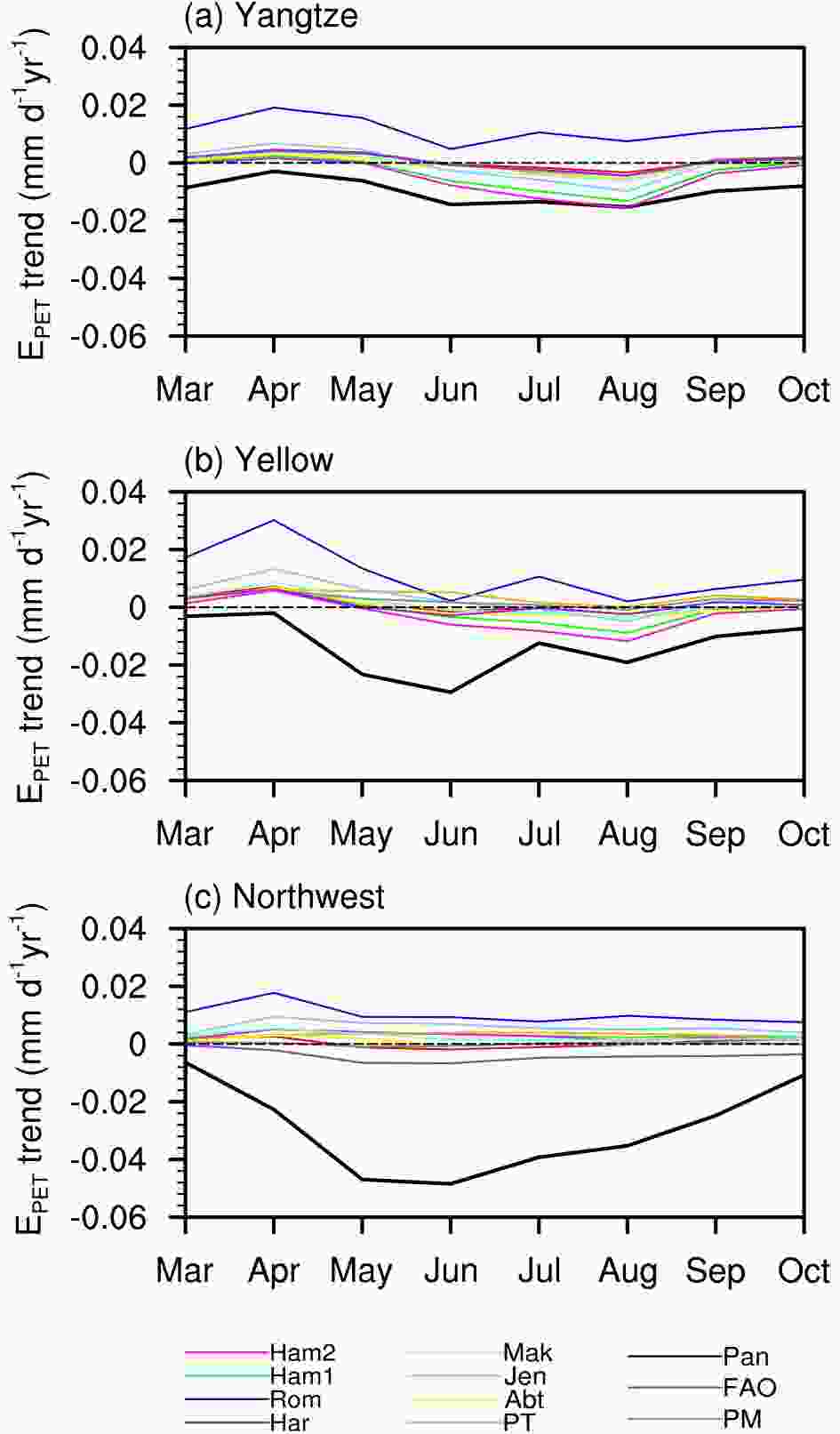Figure6. Annual trends in ET_pan and E_PET during each month in three selected basins: (a) Yangtze River basin, (b) Yellow River basin, and (c) Northwest China.



2 -->

3.3. Ranking scores

The ranking scores of the three statistical quantities are shown in Fig. 7. For the ratio of standard deviations (Fig. 7a), PET_Rom has the best performance, maintaining a value of 1 in all basins, followed by PET_Jen. The ranking scores of PET_Jen are less than 3 in most basins except for Southwest China, but the other radiation-based models do not perform well. In addition, PET_PM also has relatively high ranking scores in all basins. The above results indicate that the variabilities in ET_pan and modeled E_PET are quite different. In terms of the correlation coefficient, the PET_Rom has high scores in the Haihe River, Huaihe River, Yangtze River and Pearl River basins (Fig. 7b), and PET_PT also has poor scores in all basins. PET_FAO shows good performance in most basins except for the Yangtze River and Pearl River basins, where PET_Ham1 has the lowest score. There are nine basins with correlation coefficients greater than 0.5 between ET_pan and PET_FAO, except for the Pearl River basin, and between ET_pan and PET_Ham1/PET_Ham2, except for Northwest China. Notably, in Northwest China, several modeled E_PET are negatively correlated with ET_pan, except for PET_FAO (0.65), PET_PM (0.21) and PET_Har (0.27). This further illustrates that E_PET is very different from ET_pan, especially in the arid region. Regarding the ratio of trends (Fig. 7c), PET_Rom has positive trends and the worst scores in most basins where ET_pan shows negative trends. In summary, PET_Ham2 and PET_FAO show the best performances based on the ranking scores in all basins. In Northwest China, the ratios of trends are greater than zero only in PET_FAO and PET_PM, which are the only models that produce a negative trend as in ET_pan. Finally, we average the ranking scores of all three statistical quantities in each basin, and the model with the lowest score is selected and regarded as the best model for this basin (Fig. 8). For example, PET_Ham2 performs best in the Yellow River, Huaihe River and Yangtze River basins, while PET_Ham1 is outperformed in the Pearl River basin. For the remainder of the basins, PET_FAO is the best model.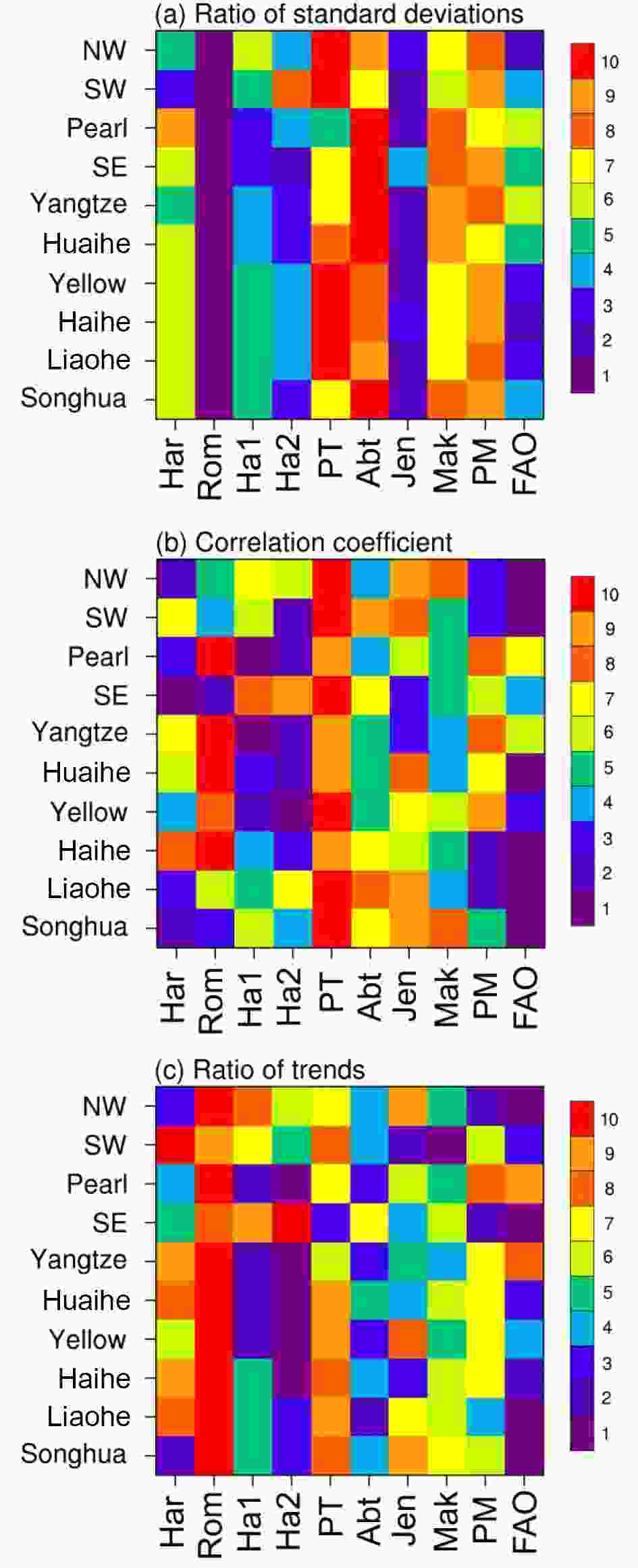
Figure7. Ranking scores of (a) the ratio of standard deviations, (b) the correlation coefficient, and (c) the ratio of trends, in different basins. The label of 1 (10) represents the best (worst) score of a modeled E_PET compared to ET_pan.


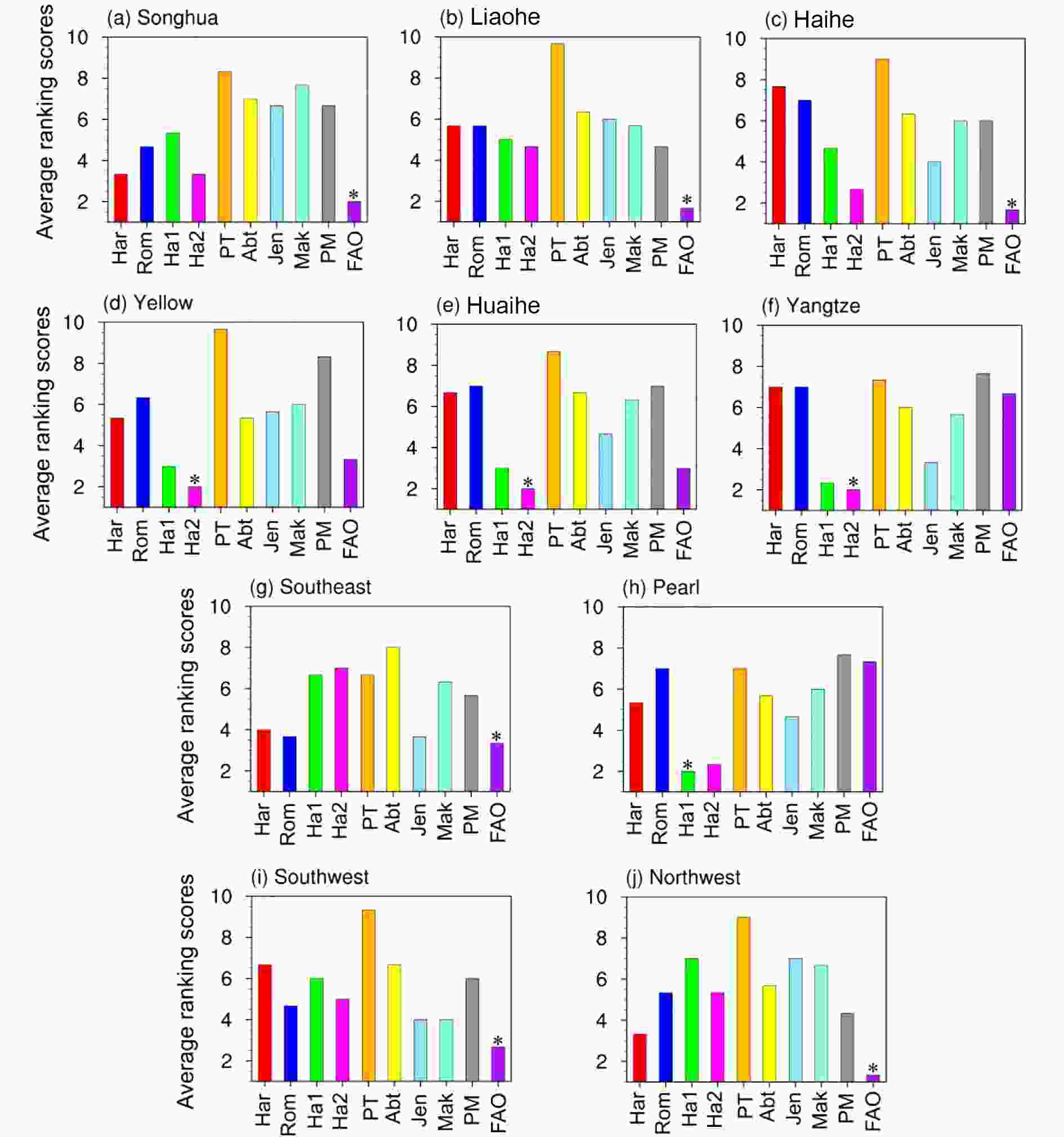Figure8. Average ranking scores of three statistical quantities in (a) Songhua River basin, (b) Liaohe River basin, (c) Haihe River basin, (d) Yellow River basin, (e) Huaihe River basin, (f) Yangtze River basin, (g) Southeast China, (h) Pearl River basin, (i) Southwest China, and (j) Northwest China. The lowest (highest) value indicates the best (worst) performance of the E_PET models,and the best model is marked with a star (*).



2 -->

3.4. Sensitivity analyses

Among the selected best models in each basin, PET_FAO considers temperature, relative humidity, wind speed and net radiation, and it is also the most commonly used E_PET model in climate research (Gao et al., 2006; Gong et al., 2006; Yin et al., 2010a; Zuo et al., 2012). Both PET_Ham1 and PET_Ham2 belong to a temperature-based model and are derived from air temperature and sunshine duration. All the best models that were selected are affected by multiple meteorological factors. To determine the RCT of each meteorological variable to E_PET changes, we apply a sensitivity analysis to the best-performing model in each basin. Because the best-performing E_PET models are not troubled by a negative value, the sensitivity analyses are conducted for the whole year instead of only the growing seasons as in the previous sections.
Table 2 shows the SC for RH is always less than zero, implying opposing variations in RH and E_PET. RH is a factor that is highly sensitive to E_PET, and the minimum of SC can reach ?1.32. However, due to the insignificant trend in RH during the study period, the RC of RH is less than 8% in the basins where the best model is PET_FAO. Thus, RH is not a determining factor of E_PET changes, and the corresponding RCTs of RH to E_PET changes are less than 2%, except for Southeast China. However, in Southeast China, RH decreases by 7.32%, which induces E_PET increases of 5.73%, and RH is the primary contributor to increasing E_PET in this basin (Table 3). In other basins where PET_FAO is selected, the wind speed at 2 m (U₂) is the most responsible factor for E_PET reductions, although it is not the most sensitive factor. The SC is greater than 0.5 in the Songhua River, Liaohe River and Haihe River basins and Northwest China. Furthermore, the reduction in U₂ in these basins is more than 40%, which leads to a more than 20% reduction in E_PET. In Southwest China, the RC of U₂ is ?27.25%, which drives E_PET reduction by 5.35%, and the RCT of U₂ to E_PET change is far less than that in other basins. Thus, the change in E_PET is affected by multiple factors in this basin, with the overall RCT of the meteorological variables to an E_PET change of 2.86% and the actual relative change in E_PET of 0.71%. The two values are very close, which further illustrates that sensitivity analyses can be used to attribute the changes in E_PET in Southwest China (Yin et al., 2010b). T_max has little effect on E_PET, which would lead to a 6.77% enhancement in E_PET in Northwest China and less than 4% in other regions. For T_min, low sensitivity appears in nearly all basins; the lowest SC (?0.01) appears in Northwest China, and the highest SC (0.21) is in Southeast China. However, it has great RC in some basins, especially in the Songhua River and Liaohe River basin, where the RC reaches 608.27% and 277.55%. This is due to the average T_min being close to zero in these basins, where a slight change in absolute value would cause a large percentage change in T_min. The RCTs of T_min to E_PET are quite different in different basins, and the value is 24.16% and 14.85% in the Songhua River and Liaohe River basin, respectively, but less than 4% in other basins. Therefore, T_min is a vitally important variable for E_PET changes in the Songhua and Liao River basins. For basins with PET_FAO as the selected best model, the SC of E_PET to SD ranges from ?0.26 (Songhua River basin) to 0.14 (Southwest China), with negative values in the Songhua River, Liaohe River and Haihe River basins and Northwest China and positive values in other basins, while the RCTs of SD to E_PET change are less than 5% in all basins. This result indicates that SD is not the primary factor for E_PET change in these basins.

Basin	Model	Ta	Tmax	Tmin	RH	U2	SD
Songhua River	FAO	?	0.08	0.04	?1.32	0.57	?0.26
Liaohe River	FAO	?	0.23	0.05	?1	0.54	?0.21
Haihe River	FAO	?	0.51	0.08	?0.83	0.5	?0.17
Yellow River	Ham2	0.61	?	?	?	?	2
Huaihe River	Ham2	0.93	?	?	?	?	2
Yangtze River	Ham2	1.11	?	?	?	?	2
SE	FAO	?	0.54	0.21	?0.77	0.15	0.12
Pearl River	Ham1	1.25	?	?	?	?	1
SW	FAO	?	0.45	0.12	?0.30	0.15	0.14
NW	FAO	?	0.47	?0.01	?0.68	0.54	?0.24

Table2. Sensitivity coefficient (SC) of the best-performing E_PET models in each basin during 1961?2013. The abbreviation of each variable name is shown in Table 1. The SC is computed from Eq. (6) in the text.

RCT (%)	Ta	Tmax	Tmin	RH	U2	SD
Songhua River	?	0.43	24.16	0.51	?26.43	2.03
Liaohe River	?	0.75	14.85	?2.1	?22.65	1.68
Haihe River	?	2.93	3.05	1.87	?24.53	3.09
Yellow River	9.8	?	?	?	?	?17.55
Huaihe River	7.51	?	?	?	?	?42.02
Yangtze River	6.57	?	?	?	?	?21.51
SE	?	3.12	1.92	5.73	?4.69	?1.39
Pearl River	4.78	?	?	?	?	?12.91
SW	?	3.15	3.57	1.33	?5.35	0.16
NW	?	6.77	?2.63	0.37	?22.12	0.6

Table3. The relative contributions (RCT = SC × RC) of each meteorological variable to E_PET changed in ten drainage basins. The meteorological variables are the required inputs of the best-performing model in each basin. The abbreviation of each variable name is shown in Table 1. SC and RC are derived from Eqs. (6) and (7), respectively.


For the basins with PET_Ham1 and PET_Ham2 as the best models, both T_a and SD are the inputs of the models. In terms of PET_Ham2, SD is more sensitive than T_a, and the SC for SD is 2 in those basins. For PET_Ham1, the SC for T_a (1.25) is higher than that of SD (1). In addition, the minimum RC for SD can reach ?21.01% in the Huaihe River basin. As a result, SD is the primary contributor to E_PET change in those basins. The RCTs to E_PET change range from ?12.91% (Pearl River basin) to ?42.02% (Huaihe River basin). Although the percentage changes in E_PET are large, the actual E_PET trend does not exceed ?0.01 mm d^?1 yr^?1. This is because the E_PET magnitudes calculated by PET_Ham1 and PET_Ham2 are too small (Fig. 2). In general, the summation of RCT from individual meteorological variables is a close approximation to the actual E_PET changes in eight basins (except for Southeast and Northwest China), where the differences are less than 5%. In both Southeast and Northwest China, the large differences in RCTs and actual E_PET change may be due to the other variables in the radiation calculation formulas, such as ozone absorption and turbidity coefficients.

2 -->

3.5. Relationship between ET_pan and E_PET

ET_pan and E_PET can be linked by regression equations, i.e., E_PET = K_panET_pan, where K_pan is the regression coefficient (Chiew and McMahon, 1992; Linacre, 1994; McMahon et al., 2013). Linacre (1994) provided a K_pan with a value of 0.7 by analyzing the data from a dozen places around the world, and this value was adopted in some studies (Weiβ and Menzel, 2008). However, many studies have reported that K_pan is dependent on the local climate conditions and should not be globally unified (McVicar et al., 2007; Zheng et al., 2009). To further understand the relationship between ET_pan and E_PET, we also calculated K_pan based on our selected E_PET model in each basin (Fig. 9). The Yangtze River basin (Fig. 9f) has the largest K_pan, with a value of 0.38, and the minimum value of K_pan (0.13) appears in Northwest China (Fig. 9j). Moreover, the determination coefficient (R²) is below 0.5 in Northwest China, further indicating that ET_pan may not be used as a E_PET proxy in the arid region.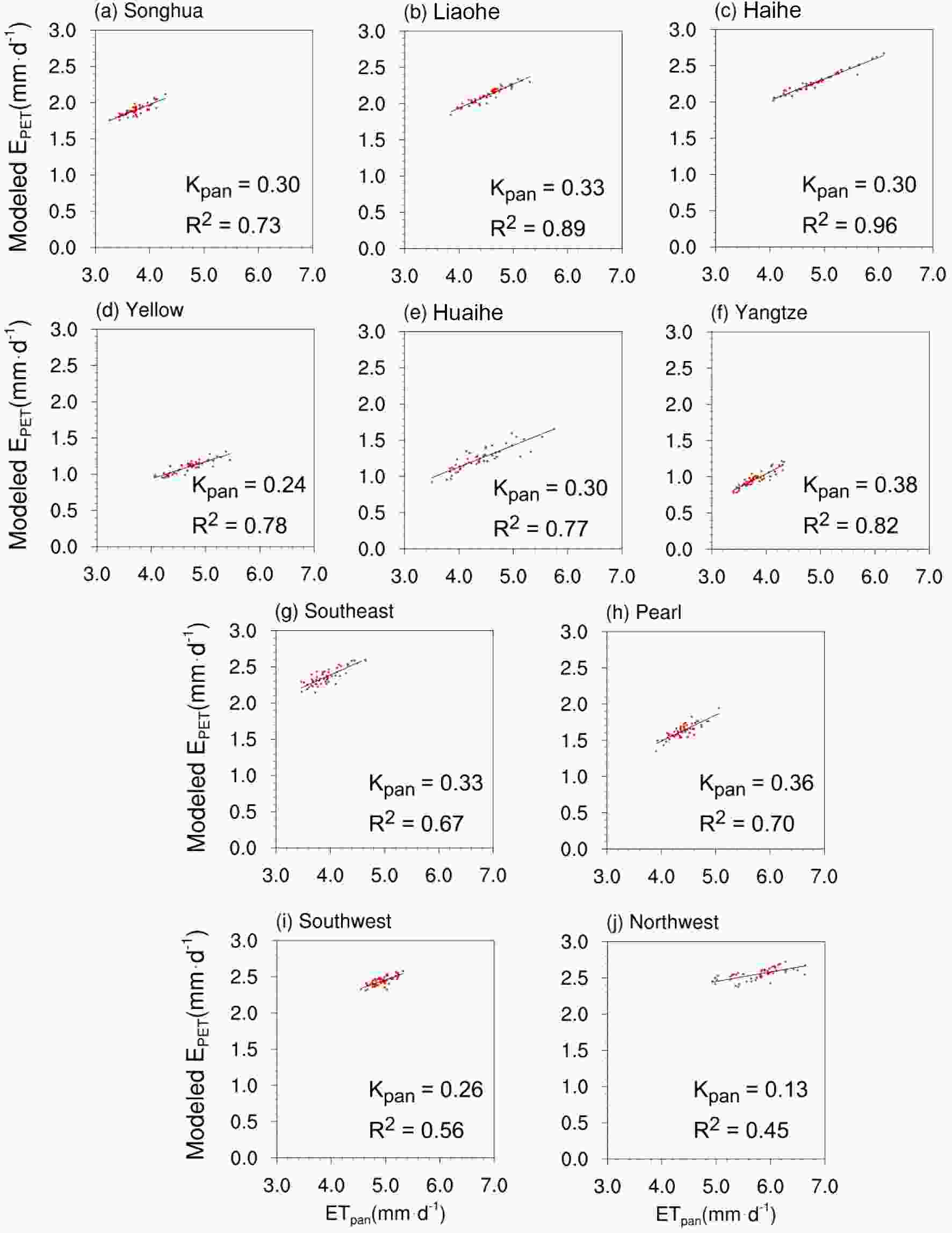
Figure9. Relationship between annual ET_pan and E_PET calculated by the best-performing model for each basin:(a) Songhua River basin, (b) Liaohe River basin, (c) Haihe River basin, (d) Yellow River basin, (e) Huaihe River basin, (f) Yangtze River basin, (g) Southeast China, (h) Pearl River basin, (i) Southwest China, and (j) Northwest China. The slope (K_pan, E_PET = K_panET_pan) and determinant coefficients (R²) are also indicated.

In the current study, ET_pan and E_PET calculated by an empirical method show differences in magnitudes, inter annual variability and trends. Some of the reasons stem from the differences in their definitions. The definition of E_PET assumes no advection and no heating effects, which means no water-advected energy and no heat storage effects (McMahon et al., 2013), while the evaporation pan has strong heat storage. In fact, the wall and bottom of the evaporation pan can receive and reflect radiation, which will influence the evaporation rate. Moreover, according to Zuo et al. (2016), the size of the evaporation pan will also affect the evaporation rate; for instance, the smaller the water body is, the greater the evaporation rate will be. When the water body in the pan is sufficiently wide, the ET_pan would be closer to the water surface evaporation. After adjusting for the energy exchange of the pan, ET_pan can be considered open-water evaporation (Dingman, 1992; McMahon et al., 2013). However, the empirical E_PET models were designed to underlie various surface and climate conditions, and they may not only represent water evaporation. For example, PET_FAO calculated the E_PET in the reference surface with an assumed crop height of 0.12 m, a fixed surface resistance of 70 s m^?1 and an albedo of 0.23 (Allen et al., 1998). PET_Mak was used to estimate grass ET under cool conditions (Makkink, 1957). In summary, there are big differences in magnitude between ET_pan and E_PET, particularly in the northwest arid region. Despite the difference in magnitude, the trend in ET_pan agrees with that of modeled E_PET in most regions (Gao et al., 2006; Zhang et al., 2007; Zheng et al., 2009; Yang and Yang, 2012). In Northwest China, there is not only a large difference in magnitude but also in the trend (Figs. 3c and 5c), and only PET_FAO can capture the negative ET_pan trend well. This is because the significantly decreasing trend in ET_pan is mainly caused by the significant downward trend in wind speed in this region (Shen et al., 2009; Yang and Yang, 2012; Wang et al., 2017), and only PET_PM and PET_FAO use wind speed as inputs. Moreover, all the E_PET models required air temperature, which exhibits a significant upward trend during the study period (Shen et al., 2009), inducing an increasing trend in E_PET in Northwest China. For PET_FAO, U₂ is the major factor of E_PET changes in this region, the SC of U₂ is 0.55, and the RC of U₂ reaches ?41.62%; therefore, PET_FAO can capture the negative trend in E_PET in Northwest China. Since most E_PET models perform poorly in Northwest China, the applicability of E_PET models in arid regions remains to be explored (Steiner et al., 1991; Li et al., 2016).
It should be noted that R_s is greatly impacted by aerosol and it usually reduces the solar irradiance arriving at the surface (Hu et al., 2017). In recent years, air pollution in China has become a serious issue, which also brings large amounts of aerosol. Current research does not consider the above effects, and thus the computed R_s based on sunshine duration only might be overestimated and affect the accuracy of E_PET results. The weight setting of the ranking scores is also worthy of further attention. We put equal weight for each of the three statistical metrics in this research. As we mentioned previously, the trend in ET_pan agrees with that of modeled E_PET in most regions, and thus it might be reasonable to give larger weight to the ratio of trends in these regions. However, it is difficult to determine weight values for each metric at the current stage. It is necessary to explore this in future research by using different weights in ranking schemes.
Despite the magnitude differences between ET_pan and E_PET in some basins, there is also a close relationship between them. Previous studies have revealed that the magnitude of ET_pan is generally greater than ET_ref (Jensen et al., 1990; Weiβ and Menzel, 2008), while ET_pan and E_PET (or ET_ref) are usually linked by the regression coefficient K_pan (Fig.9). In addition, there are different types of evaporation pan in practice. For instance, Class-A pans are used in most countries, such as the USA and Australia, while 20-cm micro-pans are popular in China. With different types of pans, the magnitudes of K_pan are also different. The pan coefficients for the Class-A pan are higher than the Chinese micro-pan coefficients, but the seasonal ranges of K_pan values for the two different pans are similar (McVicar et al., 2007; McMahon et al., 2013).
Although we characterize E_PET changes through sensitivity analyses, and conclude that wind speed and sunshine duration are the major factors affecting E_PET changes, E_PET is not affected by only these two factors. For total ET, transpiration is a very important component that is controlled by the leaf area index (LAI), surface roughness, and vegetation root distributions (Arora, 2002). Furthermore, because of the increasing CO₂ fertilization effects, climate change, and land use-land cover change, global-scale LAI shows a significant upward trend (Zhu et al., 2016), which would cause changes in transpiration. According to Zeng et al.(2018), a greening Earth would induce a significant increase in terrestrial ET. Therefore, similar to ET, E_PET is also affected by the CO₂, vegetation and land use-land cover change. ET_pan is the evaporation of the open water surface without considering the effects of transpiration or interception.

Based on meteorological observations, we calculated the E_PET of ten Chinese drainage basins using 10 different E_PET models. Then, we compared the ET_pan and E_PET to obtain the best-performing model for each basin. By comparison, large disparities exist between modeled E_PET and ET_pan. The daily ET_pan is over 4 mm d^?1 at the majority of stations, while the E_PET calculated by most models is less than 3 mm d^?1. In eight basins (except for Southeast and Southwest China), the downward annual ET_pan trends range from ?0.01 mm d^?1 yr^?1 to ?0.03 mm d^?1 yr^?1, while the decreasing E_PET trends are less than ?0.01 mm d^?1 yr^?1. Additionally, the differences are larger in arid regions than in humid regions, and the largest disparities appear in Northwest China, where only PET_FAO can successfully capture the negative trend in ET_pan.
Then, a scheme was applied to rank the three statistical quantities of ET_pan and E_PET in different basins, including the ratio of standard deviations, the correlation coefficient, and the ratio of trends. The results show that PET_Ham1 is the best model for the Pearl River basin, while PET_Ham2 is outperformed in the Huaihe River, Yangtze River and Yellow River basins. In terms of the remaining basins, PET_FAO is the best-performing model. The sensitivity analyses of the best-performing E_PET model in each basin reveal that U₂ and SD are the two factors contributing to the overall decrease in E_PET. The contributions of SD to E_PET change are always greater than 10% in the basins with selected PET_Ham1/PET_Ham2, and the contributions of U₂ are larger than 20% in the Haihe River, Songhua River and Liaohe River basins and Northwest China. In addition, in the Songhua River and Liaohe River basins, T_min also contributes considerably to the E_PET changes, and the RCT can reach 24.16% and 14.85% respectively. In Southeast China, the upward trend in E_PET is primarily controlled by the decreasing RH. Furthermore, the K_pan varies from 0.13 (Northwest China) to 0.38 (Yangtze River basin), and is larger in the humid regions than in the arid regions.
Understanding the characteristics of E_PET and its impacting factors can help us to gain insight into the hydrological process and, in particular, water resource management in an arid region. Through the current study, we have identified the best-performing E_PET models in each Chinese basin and derived long-term, high-quality daily E_PET datasets in China, which can be used as a benchmark for E_PET research in the future. Moreover, the selected model in each basin also reduces the input requirements, which is particularly practical in regions with limited availability of meteorological variables.
Acknowledgments. This paper was financially supported by the National Natural Science Foundation of China (Grant No. 41875106) and the National Key R&D Program of China (Grant No. 2016YFA0602401). We also thank the two anonymous reviewers for their constructive comments.