孙昊^1,2,3, 游勇^1,2, 柳金峰^1,2, 林雪平^1,2,3
1. 中国科学院山地灾害与地表过程重点实验室, 成都 610041;
2. 中国科学院水利部成都山地灾害与环境研究所, 成都 610041;
3. 中国科学院大学, 北京 100049
2017年4月14日 收稿; 2017年6月19日 收修改稿
基金项目: 国家科技支撑计划课题（2014BAL05B01）和中国科学院STS项目（KFJ-EW-STS-094）资助
通信作者: 游勇, E-mail:yyong@imde.ac.cn

摘要: 拦沙坝是泥石流防治中最常见和最有效的工程措施，稳定性计算是拦沙坝工程设计中的重要部分。在拦沙坝荷载组合与稳定性分析的基础上，推导空库工况和半库工况黏性泥石流过流时坝体稳定性系数的表达式，对比分析不同条件下坝体稳定性的变化规律。研究认为，在一定条件下，空库工况并不总是较危险工况，而半库工况在运行过程中表现出更不利的发展趋势；相同条件下半库工况时坝体稳定性系数随着库内淤积物厚度的增大而减小，即拦截相同来流时库内淤积越满坝体越偏于危险；研究还发现，迎水面坡比对拦沙坝稳定性的影响随着不断来流而逐渐减小，因此，建议在实际工程中可将迎水面设计为下部缓上部相对陡的折线型，以减少拦沙坝建设成本，提高工程价值。
关键词: 黏性泥石流拦沙坝荷载组合稳定性分析
Loading and stability analyses of viscous debris flow check dam
SUN Hao^1,2,3, YOU Yong^1,2, LIU Jinfeng^1,2, LIN Xueping^1,2,3
1. Key Laboratory of Mountain Hazards and Earth Surface Process, Chinese Academy of Sciences, Chengdu 610041, China;
2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China


Abstract: As a counter measure, check dam has been constructed widely because of its obvious advantages. Stability analysis is one of the most important contents in engineering designs of a check dam. Based on analysis of loading combination in this work, a mathematical expression of stability coefficient has been reduced when reservoir of check dam has or has not a deposition. The expression shows a decreasing variation in stability coefficient basically in intercepting process. Through the contrastive analyses of different working conditions of check dam, the results show that check dam having a deposition in reservoir is more dangerous than that harving no deposition, when intercepting earlier arrays of debris flow. The thicker the deposition behind check dam is the more dangerous. Finally the relationship between stability and upstream slope of check dam has been discussed. The results indicate that the effect of upstream slope of check dam decreases when intercepting debris flow continuously. Then a fold-line shaped upstream slope of check dam, which is gentle in the downside and steep in the upside, is suggested for engineering design.
Keywords: viscous debris flowcheck damloading combinationstability analysis
拦沙坝是修建在泥石流沟道内的一种横断沟床的人工建筑物，由于具有工程结构简单、防治效果好、就地取材、施工及维护方便、使用周期长、造价省等特点，是目前泥石流灾害治理中使用最为广泛的工程措施之一，尤其在城镇、矿山、公路、铁路等泥石流整治中被优先采用^[1-2]。
目前关于拦沙坝已经形成较为成熟的体系研究，但多集中于调控性能^[3-5]、坝后回淤^[6-7]、坝下冲刷^{[2, 8]}以及冲击特性^[9-11]等。此外，陈宁生等^[12]通过对西南山区15条泥石流沟的拦挡工程进行调查，对比分析泥石流拦挡工程的效益比；林雪平^[13]对比分析拦沙坝不同形状溢流口的过流能力，建立流量计算的经验计算方法，但为试验条件下得到的结论，有待在工程实践中进一步检验；李承泽^[14]采用多层土渗流原理研究不同条件下泥石流拦沙坝的坝基渗流及其渗透变形；汪惠^[15]通过渗透试验分析宽级配土中细颗粒含量与拦沙坝坝底扬压力的关系，对拦沙坝扬压力的计算具有一定的指导意义。
拦沙坝的受力及稳定性验算是工程设计中的重要环节，需在多工况或荷载组合下进行验算。王显林等^[16]推导泥石流拦沙坝抗滑稳定性与剖面参数的关系，但其仅分析了空库和满库两种工况。Lin等^[17]分析空库工况下两种不同过流形式时的坝体稳定性，但因未分析半库工况而缺乏对比性。目前工程应用中普遍一般以一次泥石流满库溢流为最危险工况，满库过流非地震工况最安全^{[2, 18]}。但野外实际工程调查发现(图 1)，大多数拦沙坝并不总是在空库工况时遭受破坏，而是在半库运行过程中被破坏或部分冲毁。
Fig. 1

	Download: JPG larger image
图 1 野外拦沙坝被冲毁的现象(镜头朝向上游) Fig. 1 Phenomenon of destroyed check dam in actual engineering (a view toward upstream) 图 1 野外拦沙坝被冲毁的现象(镜头朝向上游) Fig. 1 Phenomenon of destroyed check dam in actual engineering (a view toward upstream) -->

针对上述问题，在拦沙坝荷载组合与稳定性分析的基础上，重点探究黏性泥石流在空库和半库两种工况时拦沙坝的抗滑稳定性和抗倾覆稳定性，并分析拦沙坝在运行过程中其稳定性的演化规律和特征，旨在为拦沙坝在泥石流灾害治理工程中的应用提供科学合理的理论依据和技术支持，使其更好地为泥石流防灾减灾服务。
1 黏性泥石流拦沙坝的荷载分析1.1 坝体承受的荷载拦沙坝所受基本荷载^{[2, 18]}主要包括：坝体自重、泥石流压力、堆积物的土压力、水平水压力、扬压力、冲击力等。本文主要针对黏性泥石流，因黏性泥石流堆积物不透水，故不考虑水平水压力和坝体扬压力。
1) 坝体自重W_d
W_d取决于单宽坝体体积V_b和筑坝材料容重γ_b，即

${W_{\rm{d}}} = {V_{\rm{b}}}{\gamma _{\rm{b}}},$

(1)

一般拦沙坝采用浆砌石作为坝体材料，γ_b可取24kN/m³。
2) 土体重W_s
W_s是指拦沙坝溢流面以下垂直作用于坝体斜面上的泥石流体重量或堆积物重量。当不同深度的堆积物容重有差别时，则应作分层计算。
3) 溢流重W_f
W_f是泥石流翻越坝体时作用于坝体上的重量，其值大小与泥石流容重和泥石流在坝体顶面的溢流深度有关。
4) 黏性泥石流体水平压力F_vl
作用于拦沙坝迎水面上的黏性泥石流体水平压力F_vl，可采用朗肯土压力公式计算：

${F_{{\rm{v1}}}} = \frac{1}{2}{\gamma _{\rm{c}}}h_{\rm{c}}^2{\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right),$

(2)

式中：γ_c为黏性泥石流体容重；h_c为黏性泥石流体泥深；φ为黏性泥石流体内摩擦角，据有关资料介绍φ可为4°~10°，野外实测φ值可达8°(流体黏稠，并含有大量粒径为5~10cm的块石)。若堆积物已固结，则F_vl为堆积物的水平土压力。用式(2)作计算时，γ_c应取固结后的堆积物容重，φ值取堆积物的内摩擦角。
5) 泥石流总冲击力F_c
泥石流的冲击力一般分为两种：一种是泥石流流体压力，另一种是泥石流流体中的大石块冲击力。后者通常采用弹塑性理论公式来计算，但通常是针对单个大石块的冲击力计算方法^[19-21]，由于泥石流中大石块的冲击具有一定的随机性^[22-23]，无法确定其作用位置，因而为坝体稳定性计算带来诸多困难。为了简化计算过程，根据文献[18]中建议，本文通过式(3)计算泥石流总冲击力：

${F_{\rm{c}}} = \lambda \frac{{{\gamma _{\rm{c}}}}}{g}{v^2}\sin \theta ,$

(3)

式中：当泥石流所挟石块最大粒径D≤0.5m, λ取1.47；D=1.5m, λ取2.7；D=3.0m, λ取4.0；D＞3.0m, λ最大取8.0。可内插取值。v为泥石流断面平均流速，θ为泥石流冲击角度，其他符号同上。
1.2 黏性泥石流荷载组合及分析本文重点分析黏性泥石流空库过流和半库过流两种工况下的荷载组合情况。考虑到实际工程中，重力实体式拦沙坝坝高一般远大于泥石流泥深，即一般不会出现首阵泥石流满库过坝的情况，而多是连续流满库过流或多阵泥石流满库过坝(如图 2)。
Fig. 2

	Download: JPG larger image
图 2 泥石流空库和半库过流工况示意图 Fig. 2 Schematic of overflow for multi array debris flow when there is deposition in reservoir of check dam and there is not deposition 图 2 泥石流空库和半库过流工况示意图 Fig. 2 Schematic of overflow for multi array debris flow when there is deposition in reservoir of check dam and there is not deposition -->

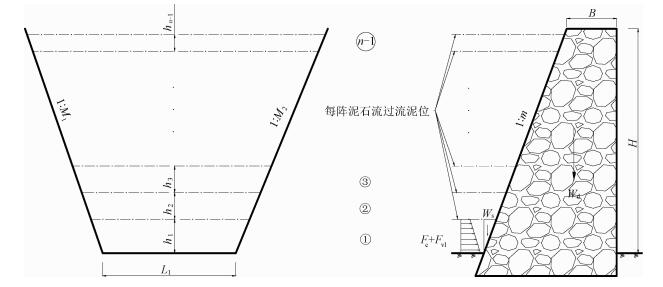
1.2.1 空库工况过流空库工况过流时荷载主要有坝体自重、拦沙坝溢流面以下作用于坝体迎水面上的黏性泥石流体重和溢流体重、黏性泥石流水平压力和冲击力(如图 3)。上述荷载均可通过式(1)~式(3)计算得到。
Fig. 3

	Download: JPG larger image
图 3 空库工况过流时坝体受力分析示意图 Fig. 3 Schematic of force analysis of overflow cross-section for multi array debris flow when there is not deposition in reservoir of check dam 图 3 空库工况过流时坝体受力分析示意图 Fig. 3 Schematic of force analysis of overflow cross-section for multi array debris flow when there is not deposition in reservoir of check dam -->

设拦沙坝坝高为H，坝顶宽为B，迎水面坡比为1：m，坡度为θ，有$ {\rm{sin}}\theta = \frac{1}{{\sqrt {1 + {m^2}} }}$，背水面近垂直，沟道底宽为L₁，沟道纵比降为I，沟床糙率为n，沟道两岸坡比分别为1：M₁和1：M₂，设第n阵来流时发生越坝过流，每阵泥石流泥深为h_i，流速为v_i。
以下对空库工况每一阵来流时坝体所承受的荷载进行分析，并计算每一阵来流时的抗滑和抗倾覆稳定性系数。计算过程如下：
步骤1)：第1阵泥石流来流时坝体受力分析及稳定性计算
坝体自重(单宽)：

${W_d} = {V_{\rm{b}}} \cdot {\gamma _{\rm{b}}} = \frac{1}{2}\left( {2B + mH} \right) \cdot H \cdot {\gamma _{\rm{b}}},$

土体重：$ {W_{{\rm{s1}}}} = \frac{1}{2}mh_1^2{\gamma _{\rm{c}}}$，
侧压力：${F_{{\rm{vl1}}}} = \frac{1}{2}{\gamma _{\rm{c}}}h_1^2{\rm{ta}}{{\rm{n}}^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right) $，
冲击力：$ {F_{{\rm{c1}}}} = \lambda \frac{{{\gamma _{\rm{c}}}}}{g}v_1^2{h_1}{\rm{sin}}\theta $，
抗滑稳定计算：

${K_{{\rm{c1}}}} = \frac{{f\sum {{W_1}} }}{{\sum {{Q_1}} }} = \frac{{\left[ {{W_{\rm{d}}} + {W_{{\rm{s1}}}}} \right]f}}{{{F_{{\rm{vl1}}}} + {F_{{\rm{cl}}}}}},$

抗倾覆稳定计算：

${K_{{\rm{y1}}}} = \frac{{\sum {{W_{{\rm{y1}}}}} }}{{\sum {{W_{{\rm{o1}}}}} }} = \frac{{{N_ * } + {W_{{\rm{s1}}}}\left( {B + mH - \frac{1}{3}m{h_1}} \right)}}{{\frac{1}{3}{F_{{\rm{vl1}}}}{h_1} + \frac{1}{2}{F_{{\rm{cl}}}}{h_1}}}.$

式中，$ {N_ * } = \frac{1}{2}m{H^2}{\gamma _{\rm{b}}}\left( {B + \frac{1}{3}mH} \right) + \frac{1}{2}{B^2}H{\gamma _{\rm{b}}}$，其他符号同上。
步骤2)：第2阵泥石流来流时坝体受力分析及稳定性计算
坝体自重(单宽)：

${W_{\rm{d}}} = {V_{\rm{b}}} \cdot {\gamma _{\rm{b}}} = \frac{1}{2}\left( {2B + mH} \right) \cdot H \cdot {\gamma _{\rm{b}}},$

土体重：${W_{{\rm{s2}}}} = \frac{1}{2}m{({h_1} + {h_2})^2}{\gamma _{\rm{c}}} $，
侧压力：

${F_{{\rm{vl2}}}} = \frac{1}{2}{\gamma _{\rm{c}}}{\left( {{h_1} + {h_2}} \right)^2}{\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right),$

冲击力：$ {F_{{\rm{c2}}}} = \lambda \frac{{{\gamma _{\rm{c}}}}}{g}v_2^2{h_2}{\rm{sin}}\theta $，
抗滑稳定计算：

${K_{{\rm{c2}}}} = \frac{{f\sum {{W_2}} }}{{\sum {{Q_2}} }} = \frac{{\left[ {{W_{\rm{d}}} + {W_{{\rm{s2}}}}} \right]f}}{{{F_{{\rm{vl2}}}} + {F_{{\rm{c2}}}}}},$

抗倾覆稳定计算：

$\begin{array}{*{20}{c}}{{K_{{\rm{y2}}}} = \frac{{\sum {{M_{{\rm{y2}}}}} }}{{\sum {{M_{{\rm{o2}}}}} }} = }\\{\frac{{{N_ * } + {W_{{\rm{s2}}}}\left( {B + mH - \frac{1}{3}m\left( {{h_1} + {h_2}} \right)} \right)}}{{\frac{1}{3}{F_{{\rm{vl2}}}}\left( {{h_1} + {h_2}} \right) + {F_{{\rm{c2}}}}\left( {\frac{1}{2}{h_2} + {h_1}} \right)}}.}\end{array}$

步骤3)：第n-1阵泥石流来流时坝体受力分析及稳定性计算
坝体自重(单宽)：

${W_{\rm{d}}} = {V_{\rm{b}}} \cdot {\gamma _{\rm{b}}} = \frac{1}{2}\left( {2B + mH} \right) \cdot H \cdot {\gamma _{\rm{b}}},$

土体重：${W_{{\rm{s(}}n - {\rm{1)}}}} = \frac{1}{2}m{\left( {\sum\limits_{i = 1}^{n - 1} {{h_i}} } \right)^2}{\gamma _{\rm{c}}} $，
侧压力：

${F_{{\rm{vl}}\left( {n - 1} \right)}} = \frac{1}{2}{\gamma _{\rm{c}}}{\left( {\sum\limits_{i = 1}^{n - 1} {{h_i}} } \right)^2}{\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right),$

冲击力：${F_{{\rm{c(}}n - 1)}} = \lambda \frac{{{\gamma _{\rm{c}}}}}{g}v_{n - 1}^2{h_{n - 1}}{\rm{sin}}\theta $，
抗滑稳定计算：

${K_{{\rm{c}}\left( {n - 1} \right)}} = \frac{{f\sum {{W_{n - 1}}} }}{{\sum {{Q_{n - 1}}} }} = \frac{{\left( {{W_{\rm{d}}} + {W_{{\rm{s}}\left( {n - 1} \right)}}} \right)f}}{{{F_{{\rm{vl}}\left( {n - 1} \right)}} + {F_{{\rm{c}}\left( {n - 1} \right)}}}},$

抗倾覆稳定计算：

$\begin{array}{l}{K_{{\rm{y}}\left( {n - 1} \right)}} = \frac{{\sum {{M_{{\rm{y}}\left( {n - 1} \right)}}} }}{{\sum {{M_{{\rm{o}}\left( {n - 1} \right)}}} }} = \\\frac{{{N_ * } + {W_{{\rm{s}}\left( {n - 1} \right)}}\left( {B + mH - \frac{1}{3}m\sum\limits_{i = 1}^{n - 1} {{h_i}} } \right)}}{{\frac{1}{3}{F_{{\rm{vl}}\left( {n - 1} \right)}}\sum\limits_{i = 1}^{n - 1} {{h_i}} + {F_{{\rm{c}}\left( {n - 1} \right)}}\left( {\sum\limits_{i = 1}^{n - 1} {{h_i}} - \frac{1}{2}{h_{n - 1}}} \right)}}.\end{array}$

1.2.2 半库工况过流半库工况过流时荷载有坝体自重、土重(分层计算)、溢流体重黏性泥石流水平压力和冲击力(如图 4)。设坝后泥石流堆积物厚度为h₀，堆积物容重为γ₀，内摩擦角为φ₀，其余参数(如坝体、沟道及泥石流来流特征等参数)与空库工况时一致，且泥石流在第n阵来流时发生越坝过流。
Fig. 4

	Download: JPG larger image
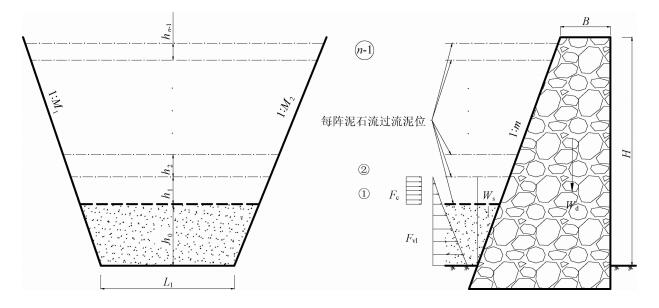
图 4 半库工况过流时坝体受力分析示意图 Fig. 4 Schematic of force analysis of overflow cross-section for multi array debris flow when there is deposition in reservoir of check dam 图 4 半库工况过流时坝体受力分析示意图 Fig. 4 Schematic of force analysis of overflow cross-section for multi array debris flow when there is deposition in reservoir of check dam -->

以下对半库工况每一阵来流时坝体所承受的荷载进行分析，并计算每一阵来流时的抗滑和抗倾覆稳定性系数。计算过程如下：
步骤1)：第1阵泥石流来流时坝体受力分析及稳定性计算
坝体自重(单宽)：

${W_{\rm{d}}} = {V_{\rm{b}}} \cdot {\gamma _{\rm{b}}} = \frac{1}{2}\left( {2B + mH} \right) \cdot H \cdot {\gamma _{\rm{b}}},$

土体重：

${W_{{\rm{s1}}}} = \frac{1}{2}m{\left( {{h_0} + {h_1}} \right)^2}{\gamma _{\rm{c}}} + \frac{1}{2}mh_0^2\left( {{\gamma _0} - {\gamma _{\rm{c}}}} \right),$

侧压力：

$\begin{array}{l}{F_{{\rm{vl1}}}} = \frac{1}{2}{\gamma _{\rm{c}}}{h_1}{\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right)\left( {{h_0} + {h_1}} \right) + \\\frac{1}{2}\left( {{\gamma _{\rm{c}}}{h_1} + {\gamma _0}{h_0}} \right){\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right){h_0},\end{array}$

冲击力：${F_{{\rm{c1}}}} = \lambda \frac{{{\gamma _{\rm{c}}}}}{g}v_1^2{h_1}{\rm{sin}}\theta $，
抗滑稳定计算：

${K_{{\rm{c1}}}} = \frac{{f\sum {{W_1}} }}{{\sum {{Q_1}} }} = \frac{{\left( {{W_{\rm{d}}} + {W_{{\rm{s}}1}}} \right)f}}{{{F_{{\rm{vl}}1}} + {F_{{\rm{c}}1}}}},$

抗倾覆稳定计算：

$\begin{array}{*{20}{c}}{{K_{{\rm{y1}}}} = \frac{{\sum {{M_{{\rm{y}}1}}} }}{{\sum {{M_{{\rm{o}}1}}} }} = }\\{\frac{{{N_ * } + \frac{1}{2}m{{\left( {{h_0} + {h_1}} \right)}^2}{\gamma _{\rm{c}}}A_1^ * + \frac{1}{2}mh_0^2\left( {{\gamma _0} - {\gamma _{\rm{c}}}} \right)A_0^ * }}{{C_1^ * + D_1^ * + E_1^ * + {F_{{\rm{c1}}}}\left( {\frac{1}{2}{h_1} + {h_0}} \right)}}.}\end{array}$

式中，$ A_n^ * = B + mH - \frac{1}{3}m\sum\limits_{i = 0}^n {{h_i}} ;$

$\begin{array}{l}C_n^ * = \frac{1}{2}{\gamma _{\rm{c}}}\left( {\sum\limits_{i = 1}^n {{h_i}} } \right){\rm{ta}}{{\rm{n}}^2}\left( {\frac{\pi }{4} - \frac{\varphi }{2}} \right)\left( {\frac{1}{3}\sum\limits_{i = 1}^n {{h_i} + {h_0}} } \right);\\D_n^ * = \frac{1}{2}{\gamma _{\rm{c}}}\sum\limits_{i = 1}^n {{h_i}} {\rm{ta}}{{\rm{n}}^2}\left( {\frac{\pi }{4} - \frac{\varphi }{2}} \right)h_0^2;\end{array}$

$ E_n^ * = \frac{1}{6}\left( {{\gamma _{\rm{c}}}\sum\limits_{i = 1}^n {{h_i} + {\gamma _0}{h_0}} } \right){\rm{ta}}{{\rm{n}}^2}\left( {\frac{\pi }{4} - \frac{\varphi }{2}} \right)h_0^2$，其他符号同上。
步骤2)：第2阵泥石流来流时坝体受力分析及稳定性计算
坝体自重(单宽)：

${W_{\rm{d}}} = {V_{\rm{d}}} \cdot {\gamma _{\rm{b}}} = \frac{1}{2}\left( {2B + mH} \right) \cdot H \cdot {\gamma _{\rm{b}}},$

土体重：

${W_{{\rm{s2}}}} = \frac{1}{2}m{\left( {{h_0} + {h_1} + {h_2}} \right)^2}{\gamma _{\rm{c}}} + \frac{1}{2}mh_0^2\left( {{\gamma _{\rm{0}}} - {\gamma _{\rm{c}}}} \right),$

侧压力：

$\begin{array}{l}{F_{{\rm{v12}}}} = \frac{1}{2}{\gamma _{\rm{c}}}\left( {{h_1} + {h_2}} \right){\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right)\left( {{h_0} + {h_1} + } \right.\\\left. {{h_2}} \right) + \frac{1}{2}\left( {{\gamma _{\rm{c}}}\left( {{h_1} + {h_2}} \right) + {\gamma _0}{h_0}} \right){\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{{{\varphi _0}}}{2}} \right){h_0},\end{array}$

冲击力：$ {F_{{\rm{c2}}}} = \lambda \frac{{{\gamma _{\rm{c}}}}}{g}v_2^2{h_2}{\rm{sin}}\theta $，
抗滑稳定计算：

${K_{{\rm{c2}}}} = \frac{{f\sum {{W_2}} }}{{\sum {{Q_2}} }} = \frac{{\left( {{W_{\rm{d}}} + {W_{{\rm{s}}2}}} \right)f}}{{{F_{{\rm{vl}}2}} + {F_{{\rm{c}}2}}}},$

抗倾覆稳定计算：

$\begin{array}{l}{K_{{\rm{y2}}}} = \frac{{\sum {{M_{{\rm{y}}2}}} }}{{\sum {{M_{{\rm{o}}2}}} }} = \\\frac{{{N_ * } + \frac{1}{2}m{{\left( {{h_0} + {h_1} + {h_2}} \right)}^2}{\gamma _{\rm{c}}}A_2^ * + \frac{1}{2}mh_0^2\left( {{\gamma _0} - {\gamma _{\rm{c}}}} \right)A_0^ * }}{{C_2^ * + D_2^ * + E_2^ * + {F_{{\rm{c2}}}}{h_2}\left( {\frac{1}{2}{h_2} + {h_0} + {h_1}} \right)}}.\end{array}$

步骤3)：第n-1阵泥石流来流时坝体受力分析及稳定性计算
坝体自重(单宽)：

${W_{\rm{d}}} = {V_{\rm{b}}} \cdot {\gamma _{\rm{b}}} = \frac{1}{2}\left( {2B + mH} \right) \cdot H \cdot {\gamma _{\rm{b}}},$

土体重：

${W_{{\rm{s}}\left( {n - 1} \right)}} = \frac{1}{2}m{\left( {\sum\limits_0^{n - 1} {{h_i}} } \right)^2}{\gamma _{\rm{c}}} + \frac{1}{2}mh_0^2\left( {{\gamma _0} - {\gamma _{\rm{c}}}} \right),$

侧压力：

$\begin{array}{l}{F_{{\rm{vl}}\left( {n - 1} \right)}} = \frac{1}{2}{\gamma _{\rm{c}}}\sum\limits_{i = 1}^{n - 1} {{h_i}{{\tan }^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right)} \sum\limits_{i = 0}^{n - 1} {{h_i}} + \\\frac{1}{2}\left( {{\gamma _{\rm{c}}}\left( {\sum\limits_{i = 1}^{n - 1} {{h_i}} } \right) + {\gamma _0}{h_0}} \right){\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{{{\varphi _0}}}{2}} \right){h_0},\end{array}$

冲击力：${F_{{\rm{c}}(n - {\rm{1)}}}} = \lambda \frac{{{\gamma _{\rm{c}}}}}{g}v_{n - 1}^2{h_{n - 1}}{\rm{sin}}\theta $，
抗滑稳定计算：

${K_{{\rm{c}}\left( {n - 1} \right)}} = \frac{{f\sum {{W_{n - 1}}} }}{{\sum {{Q_{n - 1}}} }} = \frac{{\left[ {{W_{\rm{d}}} + {W_{{\rm{s}}\left( {n - 1} \right)}}} \right]f}}{{{F_{{\rm{vl}}\left( {n - 1} \right)}} + {F_{{\rm{c}}\left( {n - 1} \right)}}}},$

抗倾覆稳定计算：

$\begin{array}{l}{K_{{\rm{y}}\left( {n - 1} \right)}} = \frac{{\sum {{M_{{\rm{y}}\left( {n - 1} \right)}}} }}{{\sum {{Q_{n - 1}}} }} = \\\frac{{{N_ * } + \frac{1}{2}m{{\left( {\sum\limits_{i = 0}^{n - 1} {{h_i}} } \right)}^2}{\gamma _{\rm{c}}}A_{n - 1}^ * + \frac{1}{2}mh_0^2\left( {{\gamma _0} - {\gamma _{\rm{c}}}} \right)A_0^ * }}{{C_{n - 1}^ * + D_{n - 1}^ * + E_{n - 1}^ * + {F_{{\rm{c}}\left( {n - 1} \right)}}\left( {\frac{1}{2}{h_{n - 1}} + \left( {\sum\limits_{i = 0}^{n - 2} {{h_i}} } \right)} \right)}}.\end{array}$

假定连续流满库过流过程中泥石流流量不变，由式Q=v_i·A_i可得v_i= $ \frac{Q}{{\left( {{L_i} + \frac{1}{2}\left( {{M_1} + {M_2}} \right){h_i}} \right){h_i}}} = \frac{Q}{{({L_i} + M{h_i}){h_i}}}$，其中$M = \frac{1}{2}({M_1} + {M_2}), i = 1, 2, \ldots , n;{L_n} = {L_1} + 2{\rm{ }}M\sum\limits_{i = 1}^{n - 1} {{h_i}} $，又$ {v_i} = \frac{1}{n}h_i^{2/3}{I^{1/2}}$，代入式中可得${h_i} = {\left( {\frac{{nQ}}{{({L_i} + M{h_i}){I^{\frac{1}{2}}}}}} \right)^{\frac{3}{5}}} $，将已知的基础参数代入，迭代计算可得每一阵来流时的泥深、过流断面形态以及流速参数等。
2 算例分析根据上述分析结果，我们以如下算例对不同工况下泥石流拦沙坝的稳定性进行分析。某泥石流拦沙坝坝体结构参数、沟道断面参数以及泥石流特征参数如表 1~表 3所示。根据文献[18]中对于基底摩擦系数f的建议取值：砂类土0.4，碎石类土和泥石流堆积0.5，软质岩0.4~0.6，硬质岩0.6~0.7，本案例取为0.5。
Table 1

表 1 坝体结构参数Table 1 Parameters of check dam 坝顶厚度 B/m 坝高H/ m 迎水面坡比 (1:m) 筑坝材料容重 γb/(t/m3) 基底摩擦系数f 3 15.5 1:0.6 2.4 0.5

表 1 坝体结构参数Table 1 Parameters of check dam

Table 2

表 2 沟道断面参数Table 2 Parameters of channel 沟道底宽 L1/m 左岸坡比 (1:M1) 右岸坡比 (1:M2) 沟道纵比降I 沟床糙率系数1/n 8 1:0.8 1:0.7 0.25 1/0.040

表 2 沟道断面参数Table 2 Parameters of channel

Table 3

表 3 泥石流特征参数Table 3 Parameters of debris flow 泥石流容重 γc/(t/m3) 泥石流流量Q/ (m3/s) 泥石流体内摩擦角?/(°) 最大颗粒粒径D/m 1.9 80 6 1.5

表 3 泥石流特征参数Table 3 Parameters of debris flow

2.1 空库工况过流分析通过式${h_i} = {\left( {\frac{{nQ}}{{({L_i} + M{h_i}){I^{\frac{1}{2}}}}}} \right)^{\frac{3}{5}}} $迭代计算出每一阵来流时的泥深和过流断面形态(底宽、面积)，并进一步得到每一阵来流的流速，最后计算得每一阵来流时坝体的抗滑稳定性系数K_c和抗倾稳定性系数K_y，计算结果列于表 4中。
根据表 4中计算结果分析，$ \sum\limits_{i = 1}^{29} {{h_i}} < H < \sum\limits_{i = 1}^{30} {{h_i}} $，即泥石流在第30阵来流时发生满库越坝过流，图 5结果表明，空库过流工况时拦砂坝的抗滑稳定性系数K_c随拦截泥石流阵数的增加呈先略有增大而后又逐渐减小的趋势，抗倾覆稳定性系数K_y则随着拦截泥石流阵数的增加而逐渐减小。
Table 4

表 4 空库工况过流时计算结果Table 4 Results of calculations when there is not deposition in reservoir of check dam 阵数 泥深/ m 底宽/ m 断面面积/ m2 流速/ (m/s) 抗滑Kc 抗倾Ky 1 0.836 8 7.212 11.093 3.076 63.107 2 0.773 9.254 7.600 10.528 3.620 25.807 3 0.724 10.413 7.936 10.081 3.962 18.415 4 0.685 11.500 8.233 9.716 4.013 15.138 5 0.653 12.528 8.502 9.410 3.780 13.176 6 0.626 13.507 8.747 9.146 3.363 11.781 7 0.602 14.446 8.973 8.915 2.885 10.677 8 0.582 15.350 9.184 8.711 2.429 9.746 … … … … … … … 21 0.437 25.143 11.121 7.194 0.416 3.692 22 0.430 25.798 11.233 7.122 0.381 3.477 23 0.424 26.443 11.343 7.053 0.350 3.282 24 0.418 27.079 11.449 6.988 0.324 3.104 25 0.412 27.706 11.552 6.925 0.301 2.941 26 0.407 28.325 11.653 6.865 0.280 2.791 27 0.402 28.935 11.751 6.808 0.262 2.654 28 0.397 29.538 11.847 6.753 0.245 2.527 29 0.392 30.134 11.940 6.700 0.231 2.410

表 4 空库工况过流时计算结果Table 4 Results of calculations when there is not deposition in reservoir of check dam

Fig. 5

	Download: JPG larger image
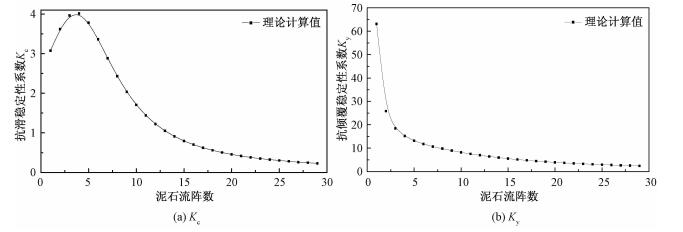
图 5 空库过流工况拦沙坝稳定性系数的变化 Fig. 5 Variation in stability coefficient with the array of debris flow when there is not deposition in reservoir of check dam 图 5 空库过流工况拦沙坝稳定性系数的变化 Fig. 5 Variation in stability coefficient with the array of debris flow when there is not deposition in reservoir of check dam -->

2.2 半库过流工况分析设实例中拦沙坝一段时间后呈半库工况下运行，坝后淤积厚度为h₀，具体拦砂坝库内淤积物特征参数见表 5所示。为便于计算，忽略半库工况时沟道糙率和纵比降的变化对来流流速的影响。本文以h₀/H表示拦砂坝半库工况运行时库内的淤积状态，记为S，并对比分析不同S时拦砂坝的抗滑和抗倾稳定性。
Table 5

表 5 拦沙坝库内堆积物特征参数Table 5 Parameters of sediment behind check dam 淤积物容重 γ0/(t/m3) 淤积厚度h0/ m h0/H 堆积体内摩擦角 ?0/(°) 2.3 3.7 0.24 16 4.9 0.33 7.6 0.49 10.1 0.65

表 5 拦沙坝库内堆积物特征参数Table 5 Parameters of sediment behind check dam

与空库工况时计算类似，不同S值时的计算结果分别列于表 6~表 9中。
Table 6

表 6 S=0.24时计算结果Table 6 Results of calculations when S=0.24 阵数 泥深/ m 底宽/m 断面面积/m2 流速/(m/s) 抗滑Kc 抗倾Ky 1 0.626 13.507 8.747 9.146 4.165 12.290 2 0.602 14.446 8.973 8.915 4.012 11.176 3 0.582 15.350 9.184 8.711 3.805 10.229 4 0.564 16.222 9.380 8.528 3.573 9.393 5 0.547 17.068 9.565 8.364 3.336 8.644 … … … … … … … 21 0.407 28.325 11.653 6.865 1.339 2.959 22 0.402 28.935 11.751 6.808 1.290 2.815 23 0.397 29.538 11.847 6.753 1.244 2.681 24 0.392 30.134 11.940 6.700 1.203 2.558

表 6 S=0.24时计算结果Table 6 Results of calculations when S=0.24

Table 7

表 7 S=0.33时计算结果Table 7 Results of calculations when S=0.33 阵数 泥深/ m 底宽/m 断面面积/m2 流速/ (m/s) 抗滑Kc 抗倾Ky 1 0.582 15.350 9.184 8.711 3.855 10.494 2 0.564 16.222 9.380 8.528 3.631 9.654 3 0.547 17.068 9.565 8.364 3.398 8.894 4 0.533 17.888 9.740 8.213 3.169 8.205 5 0.519 18.687 9.906 8.076 2.953 7.578 … … … … … … … 17 0.418 27.079 11.449 6.988 1.484 3.383 18 0.412 27.706 11.552 6.925 1.424 3.206 19 0.407 28.325 11.653 6.865 1.368 3.044 20 0.402 28.935 11.751 6.808 1.318 2.894 21 0.397 29.538 11.847 6.753 1.271 2.757 22 0.392 30.134 11.940 6.700 1.228 2.630

表 7 S=0.33时计算结果Table 7 Results of calculations when S=0.33

Table 8

表 8 S=0.49时计算结果Table 8 Results of calculations when S=0.49 阵数 泥深/m 底宽/m 断面面积/m2 流速/ (m/s) 抗滑Kc 抗倾Ky 1 0.507 19.466 10.064 7.949 2.847 7.554 2 0.496 20.227 10.215 7.831 2.667 7.008 3 0.486 20.971 10.360 7.722 2.501 6.510 4 0.476 21.699 10.498 7.620 2.350 6.056 ... … … … … … … 15 0.402 28.935 11.751 6.808 1.377 3.112 16 0.397 29.538 11.847 6.753 1.328 2.963 17 0.392 30.134 11.940 6.700 1.283 2.825

表 8 S=0.49时计算结果Table 8 Results of calculations when S=0.49

Table 9

表 9 S=0.65时计算结果Table 9 Results of calculations when S=0.65 阵数 泥深/m 底宽/m 断面面积/m2 流速/ (m/s) 抗滑Kc 抗倾Ky 1 0.459 23.114 10.760 7.435 2.144 4.058 2 0.451 23.802 10.884 7.350 2.032 3.940 3 0.444 24.478 11.004 7.270 1.930 3.815 4 0.437 25.143 11.121 7.194 1.837 3.687 … … … … … … … 9 0.407 28.325 11.653 6.865 1.480 3.060 10 0.402 28.935 11.751 6.808 1.425 2.945 11 0.397 29.538 11.847 6.753 1.374 2.835 12 0.392 30.134 11.940 6.700 1.328 2.730

表 9 S=0.65时计算结果Table 9 Results of calculations when S=0.65

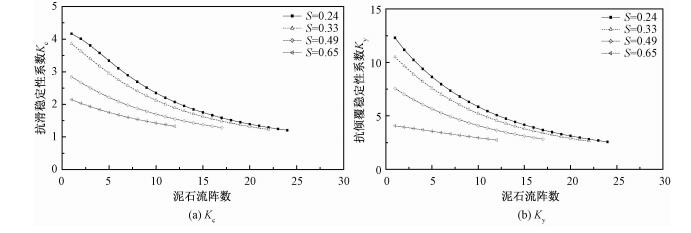
根据表 6~表 9中计算结果，S=0.24的半库工况，泥石流在第25阵来流时发生满库越坝现象；S=0.33时在第23阵发生满库越坝；S=0.49时在第18阵发生满库越坝；S=0.65时在第13阵发生满库越坝。分析结果还表明(图 6)，半库工况时拦沙坝的抗滑稳定系数K_c和抗倾稳定系数K_y均随来流阵数的增加而减小；且其他条件相同的情况下，S值越大，稳定性系数越小。因此，研究认为，在半库工况运行过程中，随着库内淤积高度的增大，拦沙坝稳定性逐渐向不利的方向发展，即拦截相同来流时更容易被损毁破坏。
Fig. 6

	Download: JPG larger image
图 6 半库过流工况拦沙坝稳定性系数的变化 Fig. 6 Variation in stability coefficients with the array of debris flow when there is deposition in reservoir of check dam 图 6 半库过流工况拦沙坝稳定性系数的变化 Fig. 6 Variation in stability coefficients with the array of debris flow when there is deposition in reservoir of check dam -->

2.3 空库和半库工况下的稳定性对比分析目前关于坝体稳定性的研究大都认为，对任一泥石流类型来说，空库过流对坝体安全最为不利，满库过流偏安全，半库过流介于二者之间。
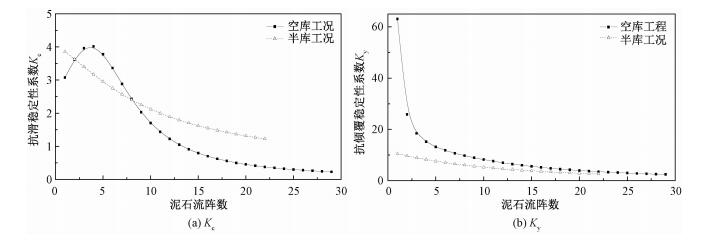
如图 7，对比分析拦砂坝空库工况和半库工况(S=0.33)运行时的稳定性演变，研究表明，在在第2阵到第9阵泥石流时，半库工况下的坝体抗滑稳定性要小于空库工况，第九阵之后，半库工况下的抗滑稳定性大于空库工况；而对于抗倾覆稳定性，半库工况下要小于空库工况。
Fig. 7

	Download: JPG larger image
图 7 空库工况和半库工况拦沙坝稳定性系数变化对比 Fig. 7 Variation in stability coefficients with the array of debris flow in different working conditions 图 7 空库工况和半库工况拦沙坝稳定性系数变化对比 Fig. 7 Variation in stability coefficients with the array of debris flow in different working conditions -->

显然，目前关于坝体稳定性的研究结论是不严谨的，只是在一定条件下适用，这也一定程度上可以解释很多泥石流拦砂坝在半库工况而不是空库工况运行时被局部冲毁破坏的现象。
2.4 拦沙坝迎水面坡比对坝体稳定性的影响拦沙坝迎水面坡比是泥石流拦沙坝的截面设计中的重要参数之一。与水工坝相反，泥石流拦沙坝的迎水面坡缓，以增大泥石流体正压力，有利于坝体安全，而背水面坡陡，以防止泥石流或泥石流中的大石块直接坠砸破坏坝体。目前泥石流防治工程设计中拦砂坝迎水面坡比一般取1:0.4~1:0.8^{[2, 21]}，根据不同拦沙坝断面形式取值有所差异。根据前文所推导的计算公式，本文验算了迎水面坡比分别为1:0.4、1:0.5、1:0.6、1:0.7、1:0.8和1:0.9时的拦沙坝抗滑和抗倾覆稳定性。
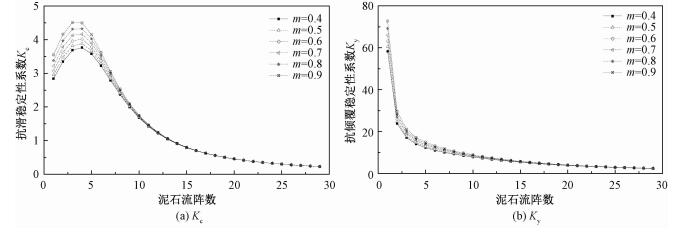
如图 8所示，拦砂坝的抗滑和抗倾覆稳定性均随着迎水面坡比1:m的增大而减小，且在泥石流的来流过程中，迎水面坡比在来流前期影响较大，而在后期随着泥石流的不断来流其影响逐渐减小。因此，在拦沙坝迎水面坡比设计中，在可保障坝体安全的前提下，可将坝体迎水面设计为下部缓上部相对陡的折线形，以减小工程建设成本，提高工程价值。
Fig. 8

	Download: JPG larger image
图 8 不同迎水面坡比时拦沙坝稳定性系数变化对比 Fig. 8 Relationship of stability coefficients of check dam with the upstream slope and the array of debris flow 图 8 不同迎水面坡比时拦沙坝稳定性系数变化对比 Fig. 8 Relationship of stability coefficients of check dam with the upstream slope and the array of debris flow -->

3 结论与讨论基于黏性泥石流过流时拦沙坝荷载分析及稳定性计算，推导拦沙坝在空库工况和半库工况运行时坝体的抗滑稳定系数和抗倾覆稳定系数的表达式，并得到如下结论：
1) 空库过流时拦沙坝抗滑稳定性随来流阵数的增加呈先略增大后逐渐减小的趋势，抗倾覆稳定性则随泥石流阵数的增加而减小。
2) 半库过流时拦沙坝抗滑稳定性和抗倾覆稳定性均随泥石流阵数的增加而减小；随坝后淤积厚度的增大而减小。
3) 对比分析空库和半库两种工况认为，空库工况并不总是较危险工况，在拦截相同来流时，初始时半库工况下的抗滑稳定系数小于空库工况，即半库工况为较危险工况，而后空库工况时抗滑稳定性系数小于半库工况；抗倾覆稳定系数则表现为半库工况总小于空库工况，即半库工况为较危险工况。
4) 对比分析空库工况下不同迎水面坡比时拦沙坝的抗滑和抗倾覆稳定性，研究发现，迎水面坡比对拦沙坝稳定性的影响随着不断来流而逐渐减小，因此，建议在实际工程中可将迎水面设计为下部缓上部相对陡的折线型，以减少拦沙坝建设成本，提高工程价值。
5) 本文是基于一定假设条件下的针对黏性泥石流拦沙坝稳定性分析的理论计算，比如，在泥石流总冲击计算方面未充分考虑泥石流中大石块的冲击压力，而是对流体冲击力进行修正，这主要是考虑到大石块冲击作用的随机性给计算带来的困难，但初步分析所得结论仍可一定程度上解释野外部分拦沙坝的运行状况，对泥石流拦沙坝的结构稳定性计算有了新认识，为泥石流拦沙坝的设计提供参考和依据，以更好地为防灾减灾服务。
参考文献

[1]	李德基. 泥石流减灾理论与实践[M]. 北京: 科学出版社, 1997.
[2]	周必凡, 李德基, 罗德富, 等. 泥石流防治指南[M]. 北京: 科学出版社, 1991.
[3]	贾世涛, 崔鹏, 陈晓清, 等. 拦沙坝调节泥石流拦挡与输移性能的试验研究[J]. 岩土力学与工程学报, 2011, 30(11): 2338-2345.
[4]	曾庆利, 岳中琦, 杨志法, 等. 谷坊在泥石流防治中的作用[J]. 岩石力学与工程学报, 2005, 24(17): 3137-3145. DOI:10.3321/j.issn:1000-6915.2005.17.022
[5]	周伟. 拦砂坝作用下的泥石流容重衰减特征及其对排导纵坡的影响[D]. 北京: 中国科学院大学, 2011.
[6]	Farouk M, Haruyuki H, Shinya I, et al. Effect of two successive check dams on debris flow deposition[R]. Padua, Italy: 5th International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, 2011. 1073-1082.
[7]	吴鑫, 马东涛, 杨敏. 粘性泥石流坝后回淤比降的实验[J]. 山地学报, 2013, 31(5): 594-600. DOI:10.3969/j.issn.1008-2786.2013.05.012
[8]	Pan H L, Wang R, Huang J C, et al. Study on the ultimate depth of scour pit downstream of debris flow sabo dam based on the energy method[J]. Engineering Geology, 2013, 160: 103-109. DOI:10.1016/j.enggeo.2013.03.026
[9]	张宇, 韦方强, 王青. 基于动量守恒的粘性泥石流冲击力计算[J]. 泥沙研究, 2006(3): 23-26. DOI:10.3321/j.issn:0468-155X.2006.03.004
[10]	陈洪凯, 唐红梅, 鲜学福, 等. 泥石流冲击特性模型试验[J]. 重庆大学学报, 2010, 33(5): 114-119.
[11]	唐金波, 胡凯衡, 周公旦, 等. 基于小波分析的泥石流冲击力信号处理[J]. 四川大学学报(工程科学版), 2013, 45(1): 8-13.
[12]	陈宁生, 周海波, 卢阳, 等. 西南山区泥石流防治工程效益浅析[J]. 成都理工大学学报(自然科学版), 2013, 40(1): 50-58. DOI:10.3969/j.issn.1671-9727.2013.01.008
[13]	林雪平. 泥石流拦砂坝溢流口过流能力实验研究[D]. 成都: 中国科学院成都山地灾害与环境研究所, 2014.
[14]	李承泽. 不同降雨量下泥石流拦挡坝坝基渗流及渗透变形研究[D]. 重庆: 重庆大学, 2013.
[15]	汪惠. 宽级配土中细颗粒含量与泥石流拦砂坝底扬压力的关系[D]. 绵阳: 西南科技大学, 2015.
[16]	王显林, 马东涛, 黄海, 等. 泥石流拦砂坝抗滑稳定性与剖面参数的关系[J]. 安全与环境学报, 2010, 10(6): 197-201. DOI:10.3969/j.issn.1009-6094.2010.06.046
[17]	Lin X, You Y, Liu J, et al. A tentative study on the stability of a check dam[J]. Advances in Earth & Environmental Sciences, 2013, 53-59.
[18]	蒋忠信. 震后山地地质灾害治理工程设计概要[M]. 成都: 西南交通大学出版社, 2013.
[19]	何思明, 吴永, 沈均. 泥石流大块石冲击力的简化计算[J]. 自然灾害学报, 2009, 18(5): 51-56. DOI:10.3969/j.issn.1004-4574.2009.05.008
[20]	何思明, 李新坡, 吴永. 考虑弹塑性变形的泥石流大块石冲击力计算[J]. 岩石力学与工程学报, 2007, 26(8): 1664-1669. DOI:10.3321/j.issn:1000-6915.2007.08.017
[21]	陈剑, 王全才, 陈颖骐, 等. 基于Hertz理论的泥石流大块石冲击力修正计算[J]. 哈尔滨工业大学学报, 2017, 49(2): 124-129.
[22]	He S, Liu W, Li X. Prediction of impact force of debris flows based on distribution and size of particles[J]. Environmental Earth Sciences, 2016, 75(4): 1-8. DOI:10.1007/s12665-015-5180-2
[23]	曾超, 苏志满, 雷雨, 等. 泥石流浆体与大颗粒冲击力特征的试验研究[J]. 岩土力学, 2015, 36(7): 1923-1930.