0 引言
【研究意义】蒸腾速率是反映作物水分状况的有效指标,蒸腾是作物与外界水分交换的重要过程,植物根部吸收水分的99%被以茎流的形式耗散,而且研究发现植物茎流速率和实际蒸腾速率具有显著相关性,可以用作物茎流来表征作物的蒸腾量[1,2]。因此阐明不同处理下,作物茎流的影响因子敏感性,以及精确预测作物茎流对估算作物蒸腾量具有重要指导意义。【前人研究进展】近年来,国内外****应用热平衡原理对玉米、枣树、叶底珠、油蒿、棉花、黄芪等植物的茎流特征进行了比较广泛的分析和研究,并得出了很多估算模型[3,4,5,6,7,8]。但由于对作物根系土壤水分状况对于蒸腾过程的影响认识局限,以往模型的精确性以及稳定性还有待进一步完善。研究表明,作物能够感受土壤水分胁迫从而产生根源信号传递到地上部分调节其蒸腾过程,根系合成的ABA可优化气孔开度进而改变蒸腾效率[9,10,11]。然而不同土层根系ABA含量差异很大,研究表明除特别干燥表皮土壤中根系外,所有根尖部分的ABA浓度与相应土层中含水量显著相关[12]。交替沟灌条件下,作物根系经历反复干湿交替对根内源ABA也会有显著影响,不同区域含水量对茎流的影响并不能单纯归结为线性关系,交替沟灌条件下,根区交替湿润效应对作物茎流的影响可能还具有复杂的非线性特点,传统的研究方法主要是通过线性回归建立的经验模型,由于涉及因素较多,参数选取较为困难,预测结果差异也较大,且经验模型中的参数适用范围小,对不同处理茎流进行估算时,需要重新进行数据分析,完成复杂的调参过程,因此在实际应用中存在很大的局限性。【本研究切入点】以往的茎流模型大多基于土壤平均含水量以及作物生长过程中的温度、辐射、风速等局地气象条件[13,14,15,16,17],并没有考虑不同土壤深度含水量对茎流的影响,这严重影响了作物茎流模型的精确度。人工神经网络模型是处理非线性系统的有力工具[18,19]。它具有较强的学习能力,与传统模型相比,省去了数据分析以及人工调参等繁琐过程,具有不可忽视的优势。【拟解决的关键问题】本文以交替沟灌玉米为研究对象,通过通径系数和互信息,比较不同处理玉米茎流与影响因素的响应差异,找出相关度较高、较为敏感的气象因子。将不同土层土壤含水量与选定的气象因子为模型输入项,采用主成分回归模型(principal component regression,PCR)和人工神经网络模型(artificial neural networks,ANN)分别建立茎流预测模型,通过误差分析和不确定性分析,对比模型优劣,评价神经网络模型在茎流估算的可行性。利用不同土层含水量对模型的响应差异找出与玉米茎流关系最密切的关键土层含水量,为深入了解玉米受旱机理和运用茎流进行植株水分亏缺诊断提供依据。1 材料与方法
1.1 试验设计与数据处理
1.1.1 试验区概况 试验于2016年7月至2016年11月在西北农林科技大学旱区农业水土工程教育部重点实验室节水灌溉试验站遮雨棚下进行,该站位于东经108°24′,北纬34°20′,海拔高度 521 m。试验站所在地区属于半湿润半干旱地区,多年平均气温12.5℃(2006—2016年),年降雨量635—665 mm,年蒸发量900—1 100 mm。1.1.2 试验设计 试验在6个规格为深(60 cm)宽(80 cm)长(100 cm)的测坑中进行,测坑内土壤取自西北农林科技大学试验田表层土壤,取土层次为 0—40 cm。土壤容重为1.35 g·cm-3,土壤类型为
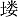
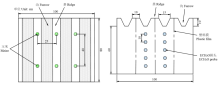
1.1.3 试验处理 试验研究对象为夏玉米,品种为西农985。试验于2016年7月10日播种,9月29日收获,整个生育期共80 d。每个测坑种植6棵玉米,行距40 cm,株距25 cm。试验设置常规灌溉处理(conventional furrow irrigation,CFI)、交替沟灌高水处理(alternate furrow irrigation,AFI1)和交替沟灌低水处理(alternate furrow irrigation,AFI2)处理,共3个处理,每个处理2个重复。土壤含水量降到70%FC时开始灌溉,灌水上限为100%FC。灌水量通过公式M=H×L×D(θFC-θ),式中,H为计划湿润层深度,苗期取30 cm,其他生育期取50 cm;L为测坑长度,取100 cm;D为玉米种植间距,取25 cm;θFC为田间持水量,经测定为31.2%(体积含水量);θ为计划湿润层深度内土壤水分平均含水量。AFI1和AFI2单次灌水量分别为CFI灌水量的2/3和1/2。当灌水侧的ECH2O测得的含水量平均值下降至土壤含水量下限(70%FC)时,开始给未灌水一侧进行灌水,以后轮流交替进行。首次灌水3个处理均灌至田间持水量,玉米长至苗期后开始控水处理。除草、施肥等其他管理措施均跟当地保持一致(图1)。
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图1试验布置示意图
-->Fig. 1Experimental arrangement diagram
-->
1.1.4 监测指标 (1)土壤含水量:利用ECH2O(Decagon,USA)土壤水分传感器监测不同土层土壤体积含水量,时间间隔为30 min。(2)气象因素:利用微型WatchDog(Spectrum Technologies Inc.,USA)系列气象站每30 min自动测定并记录一次空气温度(temperature,T)、相对湿度(relative humidity,RH)、太阳辐射(solar radiation,Ra)等。空气饱和水汽压差(vapor pressure deficit,VPD)由FAO56中修正的Penman-Monteith公式计算得到。(3)玉米茎流:采用flow-32(Dynamax Ltd,USA)包裹式茎流计测定玉米茎流。每个处理挑选一株生长状况良好,叶片茎秆无损伤的玉米植株安装一个包裹式茎流计,每30 min由数据采集器自动记录一次茎流速率。安装前将玉米底部老叶剔除,并将安装部位的茎秆清理干净,探头安装于离地面10 cm的玉米茎秆处。
1.2 模型原理与方法
1.2.1 变量间相关分析 变量间相关性主要利用通径分析和互信息来考察。互信息(MI)可用来衡量两个变量间的一致性变化以及依赖性的强弱程度。它不仅能描述变量间的线性相关关系,也能描述变量间的非线性相关关系。MI=∫∫fX,Y 1n
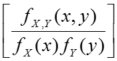
式中,fX(x)、fX(y)为变量X、Y的边际分布函数,fX,Y(x,y)是联合边际分布函数。当变量X、Y相互独立时,互信息MI=0,说明两个变量之间不存在共同信息。反之,X、Y相互依赖程度越高,MI值越大。
相关性分析数据取自8月13日至9月5日间茎流和气象数据(试验期间当地风速较小,前期分析没有太大影响,选择Ra、T、VPD对茎流影响较大的气象因子进行相关性分析),8月到9月是玉米的抽雄灌浆期,该时段玉米蒸腾耗水量大,是玉米茎流量高峰时期,也是玉米关键需水期。剔除部分时段内无效监测数据(8月13日到9月5日为玉米抽雄灌浆期,在此期间避免玉米茎秆与传感器粘连,茎流计会每5 d拆卸维护,个别时间茎流计或ECH2O未显示数据,为保证数据同步,剔除了这些日期的整日数据),最终得到样本数据为CFI样本数n=576,AFI1样本数n=408,AFI2样本数n=384。
1.2.2 模型选取 本文BP(back propagation,BP)神经网络模型计算过程如下:学习过程中信号经过正向传播通过逐层处理,算出各层神经元的输出,若输出层实际输出与期望输出不符,则将误差信号反向传播,将误差分摊给各层所有单元,通过修正各单元的权值,使误差逐渐减小到允许的精度。本文采用trainlm函数作为训练函数,传输函数选择线性函数(purelin)、S型传输函数(Logsig)和双曲线正切函数(Tansig)。通过多次试算,隐含层节点为3个时BP神经网络精度最好,BP网络拓扑结构示意图如图2所示。
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图2人工神经网络茎流模型结构示意图
-->Fig. 2Structure of the ANN model used in the prediction of sap flow
-->
选取8月13日至9月5日之间的茎流数据,剔除部分时段内无效监测数据(茎流计、ECH2O未显示数值,为保证数据同步,剔除该日数据),最终得到样本数据为CFI样本数n=576,AFI1样本数n=408,AFI2样本数n=384,所有数据均以30 min为间隔,其中每个处理2/3的数据样本用作训练样本,1/3数据作为检测样本。输入项数据分为3种类型,分别为茎流数据,气象数据和土壤含水量数据。其中气象数据包括空气温度、太阳辐射和饱和水汽压差,土壤含水量数据包括0—10,10—20,20—30,30—40,40—50 cm不同土层含水量。输出项均为玉米茎流速率。
1.3 模型的检验与评价
模型的评价指标包括决定系数R2和均方根误差(root mean square error,RMSE)2个评价指标。其中RMSE通过以下公式计算得到:RMSE=
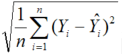
Yi、公式用到了?\(\hat{Y}_i\)分别为实测值和预测值。
RMSE用于模型的预测误差分析的优势在于其量纲与要模拟的量一致,方便不同模型间的比较。其值越小,模型的模拟效果越好。
1.4 不确定分析
本文采用d-factor指数对两种模型的不确定性进行比较以及不同土层敏感性分析。其方法是通过改变模型输入项,在原有样本数据的每一个输入项(Xi)增加与减少10%的范围内,使用matlab中的unifrnd分布函数生成连续均匀分布的随机数,将生成的新数据作为新输入项导入已建立的模型中。
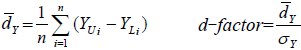
式中, \(\overline{d}_Y\)为指示性的上限(YUi)与下限(YLi)的平均距离,即95%置信区间之间的平均距离,n为样本数量,σY为茎液流实测值标准差。
2 结果
2.1 不同灌水方式与灌水量对茎流的影响
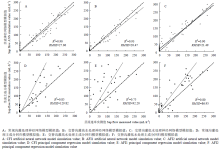
一般对于作物茎流估算模型的研究,大多是基于常规灌溉方式并且水分供应充足的条件下得到,这种估算方法对于其他水分状况下的茎流估算并不可靠,因为灌水方式和灌水量不同对于作物茎流有不同影响。选择一个灌水周期内两种典型天气下3种处理玉米茎流速率日变化过程进行分析,不同水分处理对玉米茎流速率变化影响如图3所示(晴天8月5日、多云8月6日)。从玉米茎流速率日变化来看,晴天下8:00左右3个处理玉米茎流开始快速上升,13:00左右茎流速率达到第一次峰值,CFI、AFI1和AFI2茎流峰值分别为269.93、234.88和179.65 mL·h-1,CFI处理峰值最大,交替沟灌条件下,玉米茎流峰值随着灌水量减小而减小;第二次峰值出现在17:30—18:30,分别为223.61、176.20和122.62 mL·h-1, 之后辐射持续降低,茎流速率开始下降,蒸腾停止后降至最低值。21:00—24:00之间出现微弱的茎流。与晴天相比,在多云天气下茎流速率较小。太阳辐射呈不规则变化,茎流速率随太阳辐射的波动而波动,茎流速率出现多个峰值,CFI茎流速率最大,AFI1处理次之,AFI2处理峰值则明显小于两者,这一点与晴天时茎流规律相同。不同天气下3个灌水处理日累计茎流量也有明显差异,晴天时茎流积累量明显大于阴天,但两种天气条件下茎流累积量表现出相同的规律,CFI累计茎流量最高,AFI1次之,AFI2最低。 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图3不同处理茎流速率日变化过程与日积累曲线
-->Fig. 3Diurnal variation process and diurnal accumulation curve of sap flow rate in different treatments
-->
2.2 茎流与气象因素以及不同土层含水量相关分析
为了阐明各影响因素与玉米茎流的直接影响,选择影响玉米茎流的主要气象指标与0—50 cm分层含水量进行通径分析,计算得到统计系数,结果如表1所示。CFI、AFI1处理的气象指标通径系数和互信息值均大于AFI2处理,而从土壤含水量来看,CFI与AFI1处理通径系数和互信息值均小于AFI2处理,这表明CFI与AFI1处理土壤水分灌水量较高,此时影响玉米茎流的主要是气象因素,而AFI2处理茎流对含水量的响应较强,与气象因素的关系较弱,此时影响玉米茎流的主要因素为土壤含水量。交替沟灌条件下的两个处理,除了10—20 cm、20—30 cm土层外,其余没有达到显著性水平,但其互信息值较大。表层含水量受到蒸发影响并未表现出显著相关性,10—20 cm和20—30 cm土层含水量相关性较好,达到显著性水平,深层含水量与茎流表现出负相关关系。从MI值计算结果来看,3种处理深层含水量MI值较小,这也说明深层土壤含水量变化与茎流变化协同趋势较弱。CFI与AFI1处理10—20 cm与20—30 cm土层含水量MI值较大,AFI2处理0—10、10—20和20—30 cm层含水量MI值较大,3种处理的土层敏感性不一致,对其敏感性需要进一步评价。
Table 1
表1
表1玉米茎流与影响因素的通径系数(R)与互信息(MI)结果列表
Table 1Results of the correlation analysis (R) and mutual information (MI) method
| 指标 表达不准确。Indexes | 处理 Treatment | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
|---|---|---|---|---|---|---|---|---|---|
| 通径系数 Path coefficient | CFI | 0.59** | 0.48** | -0.53** | 0.22* | 0.20** | 0.21 | -0.06* | -0.07* |
| AFI1 | 0.55** | 0.37** | -0.77** | 0.18 | 0.16* | 0.23** | -0.17** | -0.11 | |
| AFI2 | 0.51** | 0.36** | -0.18* | 0.23 | 0.18** | 0.22* | -0.20* | -0.06 | |
| 互信息值 Mutual information | CFI | 3.99 | 2.48 | 1.96 | 1.37 | 1.72 | 1.73 | 1.35 | 1.13 |
| AFI1 | 3.91 | 2.31 | 1.91 | 1.50 | 1.94 | 1.92 | 1.45 | 1.15 | |
| AFI2 | 3.90 | 2.26 | 1.89 | 1.93 | 2.26 | 2.36 | 1.56 | 1.22 |
新窗口打开
2.3 不同茎流模型模拟分析
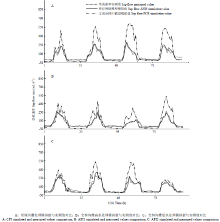
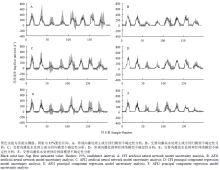
基于相关性分析结果,以训练样本数据分别建立主成分回归模型(PCR)与人工神经网络模型(ANN),经数据训练后,将检测样本分别输入到PCR模型和ANN模型,两个模型模拟结果如图4所示。从两种模型模拟效果对比来看,神经网络模型模拟值与真实值相关性更好,3组处理的神经网络模型R2值均在0.9以上,主成分回归模型R2值在0.8左右,而神经网络模型RMSE值远小于主成分回归模型,人工神经网络模型均方根误差在20—30 mL·h-1,而主成分回归模型误差则达到了77—109 mL·h-1,而实测值变化范围为0—400 mL·h-1,显然PCR模型误差值过大不能被接受。主成分回归模型对中午时段的茎流值估计过大(图5),而ANN模型则可以很好的模拟出这种强蒸腾条件下作物自身调节导致的茎流降低现象,这也是以往线性模型所不具有的优势。对夜间蒸腾为零时的作物茎流,两个模型都不能准确预测,甚至出现负值。基于以上分析,可以得出,应用人工神经网络模型模拟玉米茎流是可行的,与PCR模型相比,它不需要对不同处理再分别建立模型,所有数据分析与参数调整均由模型自动完成,很大程度上提高了效率和模拟精度。2.3.1 模型不确定性分析 模型的不确定性分析主要是考察当输入项发生变化时,模型模拟效果是否稳定,能否对新的输入项仍能达到准确的模拟效果。本研究应用不确定性分析与d-factor指数对模型稳定性进行评价,不确定性越大,说明模型模拟值落在真实值附近的范围越大,模型精度就越低,模型越不稳定。模型输出项变化范围如图6所示,图中曲线为玉米茎流的观测值,阴影部分为95%置信区间。对比两种模型,ANN模型更能合理的应对输入项的变化带来的输出值变化,它可以重新调整内部学习机制,对各层函数阈值参数做出调整,而PCR模型模拟值输出数值变化范围较大,对于输入项的变化无法做出响应,若要提高精确度还需要对变化后的输入项重新整理分析调整模型系数。结合d-factor值来看(表2),ANN模型平均值较小,不确定性小于PCR模型;模型不确定性从小到大依次为AFI1-ANN模型(0.882)<AFI2-ANN模型<CFI-ANN模型;对比3种处理,AFI1处理两种模型不确定性均低于AFI2处理,CFI处理模型不确定性最高。综上所述,人工神经网络模型拟合精度更高,模型更稳定。
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图4茎流速率实测值与模型预测值之间的对比
-->Fig. 4Comparison between the measurement and predication of sap flow rate
-->
2.3.2 关键土层敏感性判断 关键土层敏感性分析依然采用d-factor指数进行定量描述,d-factor值越大,预测值变化范围越大,说明所对应的土层含水量对模型越敏感。在每层含水量实测值增加和减少20%的范围内以Matlab中的unifrnd函数生成(连续)均匀分布的随机数,其他输入项的观测值按照增加与减少10%的范围内生成(连续)均匀分布的随机数。将生成的输入项数组导入模型,分别计算两种模型预测值d-factor指数。不同土层含水量d-factor指数计算结果如表3所示。
由表3可知,常规灌溉处理条件下,两种模型对20—30 cm土壤含水量数据变化最敏感,10—20 cm次之。交替沟灌高水处理条件下,PCR模型对输入项变化最敏感的是30—40 cm土层,其次是20—30 cm和10—20 cm土层,ANN模型则对20—30 cm土层数据变化最敏感,10—20 cm土层次之。低水处理条件下,两种模型对10—20 cm土层含水量最敏感,20—30 cm土层次之。考虑到高水处理水平下PCR模型拟合误差较大,因此认为ANN模型得到的敏感性分析结果更有参考性。
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图5不同模型模拟值与实测值对比
-->Fig. 5Comparison of measurement and different models predication of sap flow rate
-->
Table 2
表2
表2不同模型稳定性分析中的d-factor指数
Table 2Uncertainty measuring parameter (d-factor) for different models
| 模型 Model | d-factor | |||
|---|---|---|---|---|
| 常规沟灌处理 Conventional furrow irrigation treatment | 交替沟灌高水处理 Alternate furrow irrigation-high water treatment | 交替沟灌低水处理 Alternate furrow irrigation-low water treatment | 平均值 Average | |
| 主成分回归模型 PCR model | 2.206 | 1.621 | 2.147 | 1.991 |
| 人工神经网络模型 ANN model | 1.302 | 0.882 | 1.221 | 1.135 |
新窗口打开
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图6常规处理、高水处理、低水处理的神经网络模型,主成分回归模型不确定性分析
-->Fig. 6Uncertainty analysis of ANN and PCR models under different water control
-->
Table 3
表3
表3不同处理的分层含水量敏感性分析中的d-factor指数
Table 3Uncertainty measuring parameter (d-factor) for different measurements
| 土层 Soil layers | d-factor | |||||
|---|---|---|---|---|---|---|
| 常规灌溉处理 Conventional furrow irrigation treatment | 交替沟灌-高水处理 Alternate furrow irrigation-high water treatment | 交替沟灌-低水处理 Alternate furrow irrigation-low water treatment | ||||
| 主成分回归模型 PCR model | 神经网络模型 ANN model | 主成分回归模型 PCR model | 神经网络模型 ANN model | 主成分回归模型 PCR model | 神经网络模型 ANN model | |
| 0-10cm | 1.725 | 1.233 | 1.945 | 0.885 | 3.170 | 1.178 |
| 10-20cm | 2.313 | 1.299 | 2.497 | 1.316 | 3.235 | 1.220 |
| 20-30cm | 2.314 | 1.315 | 2.498 | 1.322 | 3.233 | 1.211 |
| 30-40cm | 2.305 | 1.229 | 2.581 | 1.156 | 3.207 | 1.193 |
| 40-50cm | 2.287 | 1.211 | 2.475 | 1.194 | 3.231 | 1.141 |
新窗口打开
3 讨论
作物茎流速率可以在不破坏作物的情况下获得,而且能很好的表征作物体内水分状况,因此获得了迅速的研究和推广。以往茎流经验方程尽管计算简单,但其应用存在参数无法转移的问题,即相同作物在不同试验条件下,或者不同作物在相同试验条件下参数不尽相同,这给以茎流推算作物水分状况带来了一定的局限,若直接照搬其他研究者的模拟方程必然会导致误差,因此提出一种能够在不同试验背景下都能够适用的估算方法就显得十分重要。3.1 模型误差来源分析
从图3中可以看出茎流在达到最大值后又出现第二次峰值,出现此情况是由于中午太阳辐射很强,空气温度较高,植物为了保持体内水分不被过度散失,玉米叶片气孔暂时性关闭,出现了特有的“午休”现象,即玉米的蒸腾减弱,茎流速率下降。当太阳辐射逐渐减弱,空气温度下降,玉米叶片气孔打开,蒸腾速率也出现回升。不同处理茎流对影响因子的响应存在差异,当外界因子发生变化时,所建立的PCR模型中的系数并不能随着外界因子的变化而进行调整,这就带来了模拟误差。从PCR模型模拟结果来看,采用检测样本对模型进行验证时,当中午温度和辐射增大至最大值,预测值与真实值偏差较大(图4),作物由于“午休”现象,茎流速率通过自身气孔调节作用反而降低,而PCR模型中系数固定不变使得茎流速率的模拟值随着辐射和温度的增加而严重偏大(图5)。不同试验条件下,PCR模型很难适应外界环境因素的变化,因此基于以往线性回归方法对于不同试验条件下的茎流模拟很难提出统一的算法。神经网络经过学习后会对权值进行动态调整,在茎流模拟过程中信号经过正向传播逐层处理,算出各层神经元的输出,若输出层实际输出与期望输出不符,则将误差信号反向传播,将误差分摊给各层所有单元,通过修正各单元的权值,使误差逐渐减小到允许的精度。因此对于不同背景下的试验,只要神经网络结构合理,有足够的训练数据,输入统一的计算程序,人工神经网络即可迅速完成数据分析与建模。这与常规方法相比,避免了参数无法转移的问题,也大大缩短了建模时间。本文通过matlab基于人工神经网络算法,构建了统一的茎流计算程序,将不同处理茎流训练样本分别输入程序进行训练,得到了不同处理的预测模型。本试验中,不同的灌水方式以及灌水量处理条件下,玉米茎流速率存在差异,但是观察后发现,经过样本训练后建立的神经网络模型对于3种处理茎流速率的模拟精度较高,尤其是对于中午时“午休”现象导致的茎流骤升骤降,常规模型并不能作出相应反应,人工神经网络模型有着独特的优势。3.2 大田尺度模型修正与应用
本文基于人工神经网络建立了茎流估算模型,并取得了良好的效果,但对不同试验背景下的作物实现茎流模拟还需要进一步验证。大田中外界影响因素复杂,需要在本模型的基础上考虑风速和降水量带来的影响。降水是影响大田土壤水分的主要因素,雨后浅层土壤含水量迅速升高,雨后又快速降低,含水量波动大,深层土壤含水量增大会滞后于降水,这可能对作物茎流模拟精度带来影响。不同雨强和不同历时的降水对土壤含水量也会造成影响,模型预测精度还需在今后试验中进一步验证。大田中玉米根系更发达,不同深度土壤水分对作物茎流的影响也需要进一步探究。研究提出的影响茎流变化关系最密切的关键土层的思路,可为大田中关键水分调控土层分析提供借鉴,有助于认识和理解植株茎流与分土层含水量之间的潜在联系,可以用于根区局部土壤水分调控,调节茎流的关键土层根系产生的根源信号,降低作物蒸腾作用,减少水分无效蒸发,进而提高水分利用率,实现节水优产的目的,为缓解干旱区水资源短缺和精准农业管理的实现提供理论支撑[27,28]。3.3 神经网络模型精度影响因素
人工神经网络模型在数据量越大的情况下,其训练结果及函数逼近精度也会更高,参与训练的数据量会对预测精度有一定的影响。因此在满足预测精度的情况下,要尽量使用当地易于取得的模型输入指标。本文图5中可以发现,夜间茎流出现负值,这是因为白天玉米植株茎流过大,根系在一定程度上不能满足蒸腾失水,导致植物体内水分供需平衡失调,水容下降[15,29]。夜间蒸腾停止后,根系需要继续从土壤中吸收水分以补充白天由于蒸腾导致的水分亏缺,此时水分传输的主要动力来源于根压和叶片水势较低产生的水势差[23,24,25,26],茎流与环境因子相关性弱,两个模型均未区分白天和夜间茎流,一定程度上影响了预测精度。另外,相关性分析结果表明(表1),深层含水量与茎流表现出负相关关系,这可能因为茎流速率变化与深层土壤含水量变化存在一定的时间滞后,作物茎流是典型的日变化过程[30,31],而不同土层的含水量会先后出现峰值,两者变化趋势不一致也影响了模型的预测精度[32],因此,在模型的完善及模型在实际应用等方面还需要进一步的研究。4 结论
本文研究了交替沟灌条件下夏玉米茎流变化规律常规沟灌处理、交替沟灌高水处理和低水处理玉米茎流与太阳辐射、温度和饱和差均呈正相关变化,其中太阳辐射与茎流相关性最好,温度和饱和差次之。10—20 cm和20—30 cm土层含水量相关性较好,是影响玉米茎流的主要含水层。常规处理与高水处理水平下,与茎液流变化关系最密切为20—30 cm土层,其次是10—20 cm土层;低水处理水平下,为10—20 cm土层,其次是20—30 cm土层。在对玉米茎流速率预测预报中,人工神经模型模拟精度较高且模型更稳定,可应用于玉米茎流估算。The authors have declared that no competing interests exist.
