,2, 黄明镜3, 王国芳1, 任健11 2
3
Mapping of Soil Organic Matter and Its Driving Factors Study Based on MGWRK
QIAO Lei1, ZHANG WuPing,2, HUANG MingJing3, WANG GuoFang1, REN Jian1通讯作者:
责任编辑: 李云霞
收稿日期:2019-11-14接受日期:2020-02-13网络出版日期:2020-05-16
| 基金资助: |
Received:2019-11-14Accepted:2020-02-13Online:2020-05-16
作者简介 About authors
乔磊,E-mail：qiaolei1995@126.com。
摘要
关键词：
Abstract
Keywords：
PDF (3337KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
乔磊, 张吴平, 黄明镜, 王国芳, 任健. 基于MGWRK的土壤有机质制图及驱动因素研究[J]. 中国农业科学, 2020, 53(9): 1830-1844 doi:10.3864/j.issn.0578-1752.2020.09.011
QIAO Lei, ZHANG WuPing, HUANG MingJing, WANG GuoFang, REN Jian.
0 引言
【研究意义】土壤有机质是土壤的重要组成部分[1],土壤有机质对于作物生长[2]、土壤肥力[3]、环境保护[4]等方面有着重要的作用,出于有机质的重要性,土壤有机质制图就尤为重要,土壤有机质制图对于揭示土壤有机质空间分布、农业管理以及生态环境等诸多方面都有着巨大的推动作用。对土壤有机质的空间分布及预测能够为农业管理和生态建设提供有力依据,探究土壤有机质与环境协变量之间的空间非平稳特征可以更加明确不同影响因子对土壤有机质的影响程度及空间变化。【前人研究进展】近年来利用地理加权回归方法分析土壤有机质的空间分布及空间非平稳性特征已有报道[5,6,7,8,9,10,11],吴春生等[5]利用高程、年均气温、年均降雨量以及归一化植被指数4个协变量完成地理加权回归建模,提高了有机质空间预测精度;陈琳等[6]对比了不同空间回归技术的预测精度,证实了地理加权回归克里金（GWRK）的预测精度优于普通克里金（OK）、逐步回归克里金（SWRK）;ZENG[7]等对比了混合地理加权回归方法、GWR等多种空间预测方法的模拟效果,展示了混合地理加权回归的良好应用前景。【本研究切入点】地理加权回归的应用非常广泛,涉及林业[12,13]、环境[14,15,16]、城镇化[17]、交通[18]等众多领域,但是利用多重尺度地理加权回归克里金方法分析有机质分布及空间非平稳性特征却鲜有报道。【拟解决的关键问题】本研究利用多重尺度地理加权回归克里金（multiscale geographically weighted regression kriging,MGWRK）方法选取坡向、坡度、年均降水量、年平均温度、海拔、植被年总初级生产力、年蒸散量、地形湿度指数、平面曲率、汇流动力指数、地形指数、地形粗糙指数、年平均NDVI共13个环境协变量对土壤有机质进行建模,探究不同协变量的空间非平稳性特征和尺度效应,并与普通克里金（ordinary kriging,OK）、回归克里金（regression kriging,RK）、地理加权回归克里金（geographically weighted regression kriging,GWRK）对比分析各自的预测精度与制图效果。旨在获得更高精度的有机质空间分布结果以及不同影响因素的空间非平稳性特征,为土壤管理和空间分析提供依据和参考。1 材料与方法
1.1 研究区概况
本研究选取晋中平原中平遥县的7个乡镇作为研究区域。研究区位于平遥县西北部,是山西省晋中盆地腹地位置,境内多为平川。研究区属温带大陆性半干旱季风气候,平均气温12℃,年平均相对湿度58%,年均降水量502 mm,主要分布在7—9月份。主导风向春秋冬季为西北风,夏季多为东南风,年平均风速2.1 m·s-1。种植作物以玉米为主,土壤类型以潮土为主,部分地区为盐土、褐土。1.2 土壤采样与数据来源
样品采集于2010年春季作物种植前,依据《耕地地力调查与质量评价技术规程》（NY/T 1634—2008）,用不锈钢土钻等工具,在每个田块中采用“S”法布点采样,以GPS定位点作为中心,向四周辐射多个分样点,每个混合土样取15个以上分样点,每个分样点的采土部位、深度、数量保持一致,采样深度为0—20 cm,共采集样点2 616个,采样点分布见图1。土壤有机质（SOM）采用重铬酸钾加热法[19]测定。数字高程数据（digital elevation model,DEM）来自中国科学院计算机网络信息中心地理空间数据云网站（www.gscloud.cn）,各地形因子均由DEM数据计算得出。气象数据来自国家气象信息中心中国气象数据网（http://data.cma. cn/）。研究中所用遥感数据均来自NASA网站（https://earthdata.nasa.gov/）,2009年植被年总初级生产力（gross primary productivity,GPP）数据来自MOD17数据集,2009年蒸散（evapotranspiration,ET）数据来自MOD16数据集,2009年平均NDVI数据来自MOD13数据集。环境协变量数据列于表1。图1
新窗口打开|下载原图ZIP|生成PPT图1研究区概况及样点分布
Fig. 1Study area and soil sample sites
Table 1
表1
表1环境协变量数据列表
Table 1
| 数据类型 Data type | 指标 Index |
|---|---|
| 地形因子数据 Terrain data | 坡向Aspect |
| 坡度 Slope | |
| 海拔 Height | |
| 地形湿度指数 Topographic wetness index, TWI | |
| 平面曲率 Plan curvature, PC | |
| 汇流动力指数 Stream power index, SPI | |
| 地形指数 Terrain position index, TPI | |
| 地形粗糙指数 Terrain ruggedness index, TRI | |
| 气象数据 Meteorological data | 年平均降水Annual mean precipitation, PRE |
| 年平均温度 Annual mean temperature, TEM | |
| 遥感数据 Remote sensing data | 年植被总生产量GPP (From MOD17A2) |
| 年蒸散量 ET (From MOD16A2) | |
| 年平均NDVI (来自MOD13A1,使用最大合成法求得) Annual mean NDVI (Data from MOD13A1, obtained by Maximum Value Composites method) |
新窗口打开|下载CSV
1.3 研究方法
1.3.1 普通克里金（OK） 普通克里金（ordinary kriging,OK） 基于空间自相关性和二阶平稳假设[20],依据估算误差最小和半方差函数分析,赋予一定邻域内样点不同权重后,计算样点值加权和即为插值结果。其中半变异函数公式为：式中,γ(h)为半变异函数值;N(h)为距离等于h时的点对总数;Z(xi)为区域变量在位置xi处的实测数值;Z(xi+h)为在xi+h处的实测数值。
1.3.2 回归克里金（RK） 回归克里金[21]是多元线性回归（multiple linear regression,MLR）与克里金插值方法的结合,通过多元线性回归方法获取预测模型,对预测产生的残差进行普通克里金估计,将趋势值与残差项相加得到最终预测结果。本研究使用的多元线性回归方法为普通最小二乘法（ordinary least square,OLS）,是因变量yi与自变量xi的多元线性函数：
式中,β0为常数项即斜率,βi为每个自变量的回归系数,εi为随机误差项。
回归克里金[22]的公式如下：
式中,Z为RK模型预测值,m(xi)为MLR过程的趋势值,e(xi)是利用OK法估计的MLR过程残差,后续的GWRK与MGWRK方法回归项计算均与此类似。
1.3.3 地理加权回归克里金（GWRK） GWRK[23]是地理加权回归（geographically weighted regression,GWR）模型与克里金插值方法的结合,也可视为是RK的改进,RK是全局回归模型[24],在RK中多元线性回归假设因变量与自变量的关系在空间上不随着空间位置的变化而变化,而GWRK为局部回归模型。地理加权回归[25]是众多空间回归技术应用最为广泛的一种,建立模型的过程中考虑到了各样点的空间位置以及不同位置中自变量与因变量关系的变化,揭示在空间尺度中自变量与因变量的关系。
假定共n个观测点,观测点为i∈{1, 2, ..., n},每个观测点的位置为（ui,vi）,参与建模的自变量共m个。GWR模型[26]的表达式如下：
式中,xij是i观测点的第j个自变量,βi(ui,vi)为在(ui,vi)位置上第j个自变量的回归系数,εi为随机误差项,yi为因变量。
核函数和有效带宽[26]是GWR建模过程中最重要的两项指标。核函数可用于确定空间权重,包括高斯函数、双平方函数和指数函数,核函数在运行过程中可采用不同的类型,包括固定核函数和自适应核函数[13],若观测点均匀分布时可采用固定核函数,否则选择自适应核函数,本研究使用自适应高斯函数进行空间权重确定。由于GWR是移动窗口回归方法的一种,而带宽则是核函数的重要性质之一,带宽与核函数原理详见文献[26],有效带宽的确定方法包括修正赤池信息量准则（corrected akaike information criterion,AICc）、赤池信息量准则（akaike information criterion,AIC）、贝叶斯信息准则（bayesian information criterion,BIC）等,本研究采用修正赤池信息量准则（AICc）确定模型带宽,原则是AICc最小化,以此作为确定带宽的标准,其中AICc的计算公式如下：
式中,σ为样本标准差,n为样本含量,tr(S)为矩阵S的迹,矩阵S是模型的帽子矩阵。
在GWR模型中,确定后的最优有效带宽是所有自变量共用的,即在建模中所有自变量的有效带宽都是一样的,空间权重矩阵也是一致的。在GWR模型中未考虑不同环境协变量与因变量间关系不同的的空间尺度,而是预设所有环境协变量的空间非平稳性特征的空间尺度一致。
1.3.4 多重尺度地理加权回归克里金（MGWRK） MGWRK是多重尺度地理加权回归（multiscale geographically weighted regression,MGWR）方法与克里金方法的结合,也可看做是对于GWRK的改进。MGWR[27]是FOTHERINGHAM等提出的一种基于有效带宽优化从而使每个自变量都具有不同的空间带宽的地理加权回归方法。与GWR不同的是,GWR确定的模型带宽是所有自变量共用的,而实际情况中不同的自变量的空间尺度效应和对因变量的影响程度是不一样的,所以MGWR方法考虑到了这一点,MGWR方法使每个自变量都有各自的有效带宽,即为多重尺度。MGWR模型如下：
式中,βbwj是经过第j个自变量有效带宽校正后的回归系数。
在本研究中,MGWR与GWR模型的核函数和核类型均保持一致,核函数均采用高斯函数,核函数采用自适应核函数。两种模型最大的区别就是确定有效带宽的方法,有效带宽的本质即是空间尺度,也正是确定带宽方法的不同决定了MGWR多重尺度的特性。有效带宽的选择对于模型计算结果影响巨大,我们可以将有效带宽看作一个具有平滑性质的参数,当有效带宽太大有可能造成整个研究区域的参数相似,掩盖研究变量的局部特征;而有效带宽太小则会造成过多的局部变异,难以识别研究空间变量之间的规律[28]。选取一个最优带宽避免以上两种极端情况,提供良好的空间关系描述效果就显得尤为重要。
在MGWR模型中,在不同的自变量中有着不同的带宽,这也意味着在建模中不同自变量在同一位置将具有完全不同的空间权重矩阵,在GWR模型中使用的具有平滑作用的参数（有效带宽）将不再适用于MGWR模型。MGWR模型中采用向后拟合（Back-fitting）算法[27]进行模型校正。首先使用GWR模型计算的各位置自变量参数以及模拟结果（y）作为初始化,使用这些初始值（βbwjxj）以及求得的残差（ε=y-Σm j=0βbwjxij）,残差加当前的βbwjxj （βbwjxj+ε）,利用GWR模型将该值与x0（第一个自变量）进行回归,此时得到因变量与x0之间的参数βbw0的局部估计,即得到了因变量与x0之间的最优带宽bw0。接下来使用更新后的βbwjxj与下一个自变量x1进行同样的过程,得到直到所有的自变量（x0,x1,…,…, xm）都完成该过程（图2）。
图2
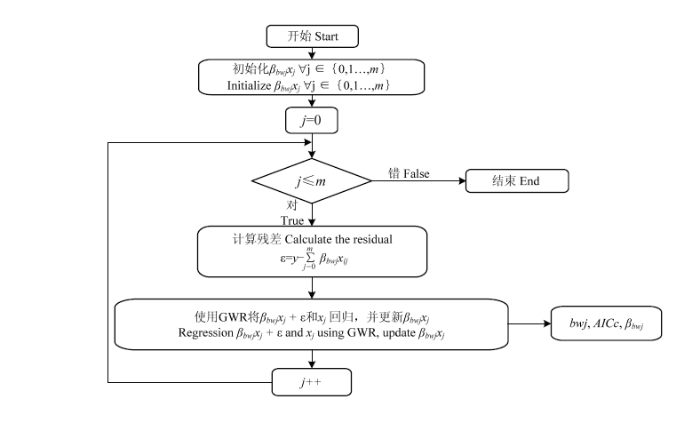新窗口打开|下载原图ZIP|生成PPT图2MGWR模型的向后拟合（Back-fitting）算法[27]
Fig. 2Back-fitting algorithm for multiscale geographically weighted regression model (MGWR)
1.4 模型评价
本研究使用平均误差（ME）、平均绝对误差（MAE）、均方根误差（RMSE）评价模型精度[29],这三项指数的公式如下：式中,n是用于验证的观测点数量,Z(xi)是实测值,Z*(xi)是模型预测值。理论上MAE和RMSE越接近于0模型预测效果越好。在一些研究中3个指标很难同时达到最佳水平,所以除上述指标外,引进YANG等[29]提出的Radius指数（式 10）,以便于结合3个指数确定最优模型。
式中,Radius即为Radius指数,MES、MAES、RMSES是使用Z得分法进行标准化后的ME、MAE、RMSE,该指数越小则说明模型效果越好。
2 结果
2.1 环境协变量选择及MLR建模
土壤有机质的影响因素众多,在多元线性回归建模选取变量的过程当中需要考虑如下因素[30,31]： （1）各环境协变量对于有机质的分布有显著影响,影响极其微弱的不予考虑;（2）各环境协变量在空间分布中具有一定的空间异质性;（3）各环境协变量之间不存在多重共线性,这也是多元线性回归建模的必要条件之一。本研究选取坡向、坡度、年均降水量、年平均温度、海拔、植被年总初级生产力、年蒸散量、地形湿度指数、平面曲率、汇流动力指数、地形指数、地形粗糙指数、年平均NDVI共13项指标（图3）作为建模的环境协变量,以有机质作为因变量。其中环境协变量之间的多重共线性诊断以容差和方差膨胀因子（VIF）作为依据,容差越小,表明该自变量作为因变量进行回归分析时被其他变量解释的程度越高,越可能存在严重的共线性,容差合理的范围是（0.1,+∞）;方差膨胀因子是容差的倒数,若其值≥10,说明自变量间可能存在严重的共线性现象[32],模型的共线性诊断结果见表2。其中VIF均未超过10,故认为在该模型中不存在严重的多重共线性现象。
图3
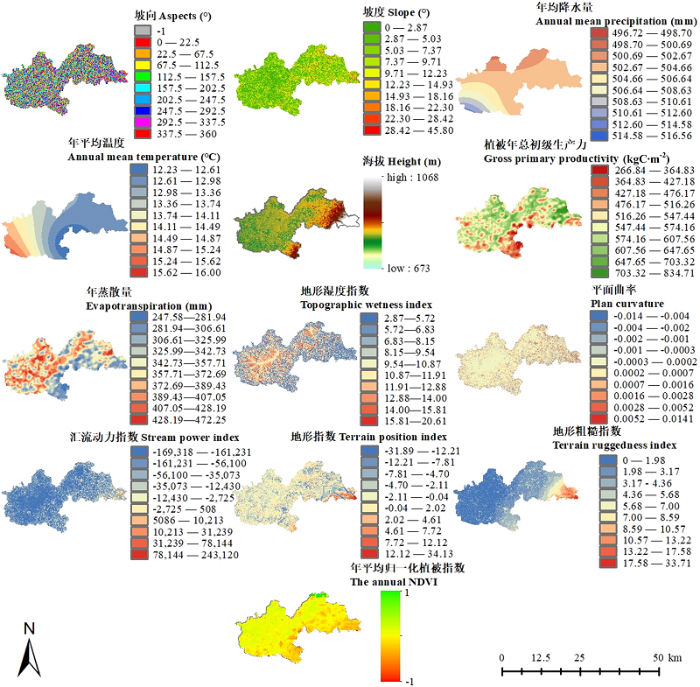新窗口打开|下载原图ZIP|生成PPT图3环境协变量空间分布坡向以正北为0°,顺时针计数,-1为平地 Aspect direction is defined as zero degrees due north, clockwise count, -1 is flat
Fig. 3Spatial distribution of environmental covariates
Table 2
表2
表2模型多重共线性检验
Table 2
| 指标Index | 容差 Tolerance | VIF |
|---|---|---|
| 坡向Aspects (°) | 0.993 | 1.007 |
| 坡度Slope (°) | 0.548 | 1.824 |
| 年均降水量Annual mean precipitation (mm) | 0.514 | 1.944 |
| 年平均温度Annual mean temperature (℃) | 0.417 | 2.400 |
| 海拔Height (m) | 0.670 | 1.493 |
| 植被年总初级生产力Gross primary productivity (kgC·m-2) | 0.216 | 4.636 |
| 年蒸散量Evapotranspiration (mm) | 0.194 | 5.168 |
| 地形湿度指数 Topographic wetness index | 0.652 | 1.534 |
| 平面曲率Plan curvature | 0.928 | 1.078 |
| 汇流动力指数 Stream power index | 0.980 | 1.021 |
| 地形指数 Terrain position index | 0.730 | 1.369 |
| 地形粗糙指数 Terrain ruggedness index | 0.548 | 1.824 |
| 年平均归一化植被指数 The annual NDVI | 0.893 | 1.120 |
新窗口打开|下载CSV
对土壤有机质以及各环境协变量进行描述性统计（表3）,可以看出,不同环境协变量的变异系数是不同的,其中地形指数的变异系数是最大的,年均降水量的变异系数是最小的。
Table 3
表3
表3土壤有机质及环境协变量描述性统计
Table 3
| 指标 Index | 最小值 Minimum | 最大值 Maximum | 平均值 Mean | 标准差 Standard deviation | 方差 Variance | 变异系数 Coefficient of variation (%) |
|---|---|---|---|---|---|---|
| 有机质Soil organic matter (g·kg-1) | 2.10 | 33.00 | 13.91 | 5.01 | 25.09 | 36.00 |
| 坡向Aspects (°) | -1.00 | 359.12 | 180.32 | 106.64 | 11373.13 | 59.14 |
| 坡度Slope (°) | 0.00 | 33.37 | 6.84 | 4.60 | 21.20 | 67.36 |
| 年均降水量 Annual mean precipitation (mm) | 499.01 | 511.01 | 503.72 | 2.00 | 3.98 | 0.40 |
| 年平均温度 Annual mean temperature (℃) | 12.25 | 15.20 | 13.37 | 0.73 | 0.53 | 5.45 |
| 海拔Height (m) | 690.00 | 927.00 | 744.04 | 22.77 | 518.46 | 3.06 |
| 植被年总初级生产力 Gross primary productivity (kgC·m-2) | 270.28 | 817.96 | 557.30 | 68.57 | 4702.51 | 12.30 |
| 年蒸散量Evapotranspiration (mm) | 248.43 | 461.20 | 358.95 | 37.47 | 1403.98 | 10.44 |
| 地形湿度指数 Topographic wetness index | 0.00 | 19.39 | 9.61 | 3.14 | 9.86 | 32.67 |
| 平面曲率 Plan curvature | -0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 1281.06 |
| 汇流动力指数 Stream power index | -167350.00 | 11730.90 | -3405.69 | 18999.56 | 360983218.24 | -557.88 |
| 地形指数 Terrain position index | -21.49 | 21.78 | -0.47 | 4.88 | 23.78 | -1040.39 |
| 地形粗糙指数 Terrain ruggedness index | 0.00 | 18.72 | 3.81 | 2.25 | 5.05 | 58.96 |
| 年平均归一化植被指数 The annual NDVI | 0.00 | 2.80 | 0.71 | 0.19 | 0.04 | 26.44 |
新窗口打开|下载CSV
多元线性回归（MLR）的最终拟合模型为：
SOM=-131.09-0.0016×Aspects-0.01×Slope+0.46×Pre-3.74×Tem-0.04×Height-0.009×GPP+0.01×ET-0.08×TWI-92.15×PC+0.000007×SPI+0.06×TPI+0.03×TRI-1.51×NDVI
式中,SOM为土壤有机质,Aspects为坡向,Slope为坡度,Pre为年均降水量,Tem为年平均温度,Height为海拔,GPP为植被年总初级生产力,ET为年蒸散量,TWI为地形湿度指数,PC为平面曲率,SPI为汇流动力指数,TPI为地形指数,TRI为地形粗糙指数,NDVI为年平均归一化植被指数。对模型进行方差检验,F统计量[33]为43.39,模型具有统计学显著意义,即回归方程有效。
同样,在GWRK与MGWRK模型中也采用同样的环境协变量作为模型自变量。
2.2 各模型预测结果空间变异
对不同模型的残差结果空间半变异函数拟合（图4）,模型参数及最优模型见表4。3种模型残差值半变异函数的最优拟合模型从指数模型、高斯模型和球状模型[34]中选取。GWR残差的半变异函数最优拟合模型为高斯模型,其他最优拟合模型均为指数模型。从块金系数[35]可以看出,各模型残差最优模型的块金系数均小于50%,这意味着模型预测过程的残差具有空间结构性,使用各自的半变异函数进行空间插值,结果见图5。图4
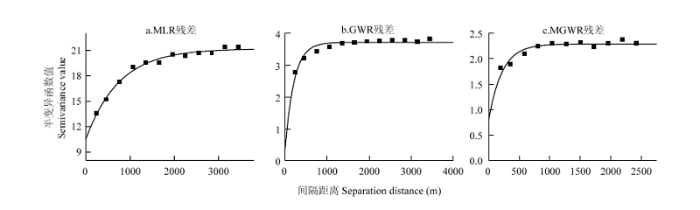新窗口打开|下载原图ZIP|生成PPT图4半变异函数图
Fig. 4Semivariogram
图5
新窗口打开|下载原图ZIP|生成PPT图5各模型残差图
Fig. 5Map of different Model residuals (MLR residuals, GWR residuals, MGWR residuals)
Table 4
表4
表4各模型结果空间变异
Table 4
| 拟合模型 Fitting model | 块金值 Nugget | 基台值 Sill | 变程 Range (m) | 块金系数 Nugget/Sill (%) | |
|---|---|---|---|---|---|
| MLR残差 MLR residuals | E | 10.59 | 21.20 | 2265 | 49.95 |
| GWR残差 GWR residuals | E | 0.38 | 3.72 | 636 | 10.22 |
| MGWR残差MGWR residuals | E | 0.81 | 2.29 | 657 | 35.37 |
新窗口打开|下载CSV
2.3 各模型评价
各模型评价指标见表5,从Radius指数来看,各模型模拟效果由好到差依次为：RK、OK、GWRK、MGWRK。MGWRK模型的空间预测精度相对于其他模型欠佳,而RK模型的空间预测精度则表现最优。Table 5
表5
表5各模型评价指标
Table 5
| 模型 Model | RMSE | MAE | ME | R2 | Radius |
|---|---|---|---|---|---|
| OK | 2.8553 | 2.1009 | 0.0009 | 0.6984 | 107.4383 |
| RK | 2.7613 | 2.0396 | -0.0001 | 0.7207 | 98.1195 |
| MGWRK | 3.5430 | 2.6292 | 0.0036 | 0.5010 | 172.8181 |
| GWRK | 3.0622 | 2.2402 | 0.0978 | 0.6492 | 133.6925 |
新窗口打开|下载CSV
2.4 各模型土壤制图结果
根据以上分析及模型参数,依照不同模型绘制土壤有机质分布图（图6）。可以看出4种不同的土壤制图方法,得到空间基本趋势是类似的。MGWRK与GWRK方法的效果相对其他两种方法更为平滑,这可能是由于两种方法考虑了各环境协变量的空间非平稳性特征导致的,OK和RK两种方法高低值交错明显,“牛眼”现象明显,与有机质空间实际分布情况不符。从制图效果来看,GWRK方法与MGWRK方法的效果相当。图6
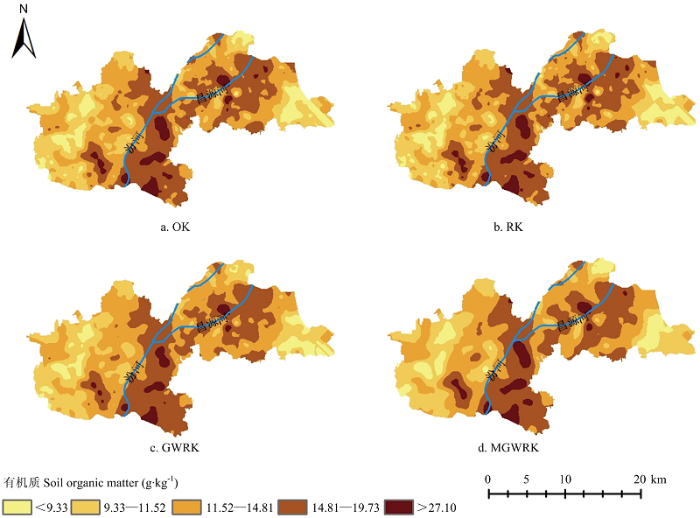新窗口打开|下载原图ZIP|生成PPT图6各模型土壤制图结果
该图制图的空间分辨率为30 m The mapping spatial resolution is 30 m
Fig. 6Soil mapping results of each model
土壤有机质在研究区呈现东西两侧偏低,中部偏高的空间格局。其中汾河以东、昌源河流经区域土壤有机质普遍偏高,沿河土壤的土壤水分受到河流影响,而土壤水分影响着土壤有机质的分解与转化过程,土壤微生物的活动与土壤水分密切相关,土壤水分过高时土壤中形成厌氧环境,从而改变土壤有机质的分解过程与产物,进而影响土壤有机质含量;土壤水分过低时则有可能影响土壤微生物的生存状况,降低土壤微生物的活性[36]。
2.5 有机质影响因子回归系数空间分布
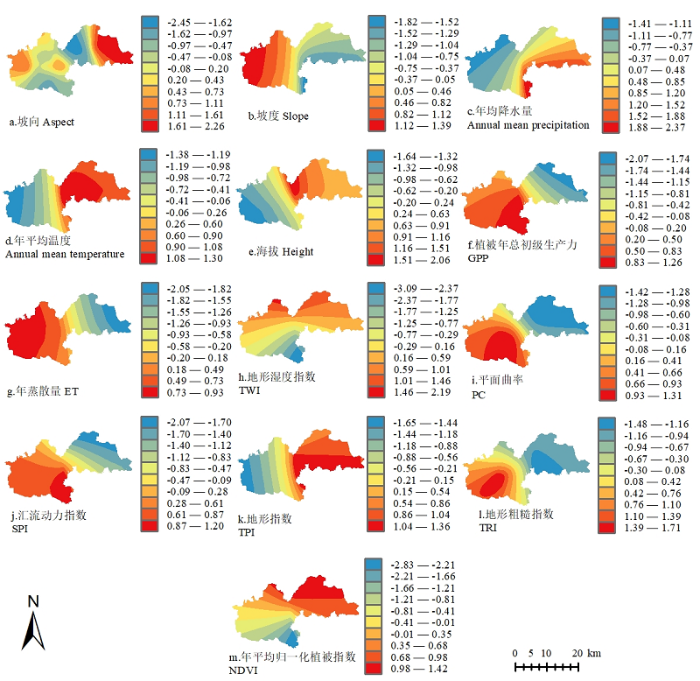
结合土壤有机质及回归参数的统计特征、多元线性回归方程可知,在全局尺度上土壤有机质与全氮、年均降水量呈现正相关关系,土壤有机质与其余指标均呈现负相关关系。但在实际情况中随着地理位置的变化因变量与自变量之间的关系也是变化的,即空间非平稳性,MGWR模型针对不同环境协变量使用不同的空间尺度,在进行空间预测的同时也对自变量在每个空间位置的回归参数局部估计[37]。为了避免建模过程当中不同变量的数量级对回归系数的相对大小造成影响,在对比影响因素随着位置变化影响程度的不同时使用经过z分数方法标准化后的局部回归系数进行空间非平稳性特征描述,即标准化回归系数。图7-a中,坡向的标准化回归系数范围在-2.45—2.26之间,整体呈现东高西低的空间格局,其中正值区域占绝大部分。在研究区东部区域为正相关影响,即坡向角度越大有机质增长幅度越大,在南政乡回归系数达到了最小值,在此处呈现负相关影响,即坡向角度越大有机质减少幅度越大。
图7
新窗口打开|下载原图ZIP|生成PPT图7土壤有机质影响因子标准化回归系数分布
Fig. 7Standardized regression coefficient distribution of soil organic matter influencing factors
图7-b中,坡度的标准化回归系数范围在-1.82—1.39之间,整体呈现东低西高的空间格局,正负值区域参半,正负值预取之间分界明显,大致表现为汾河以东为负相关影响,汾河以西为正相关影响。
图7-c中,年均降水量的标准化回归系数范围在-1.41—2.37之间,整体呈现东高西低的空间格局,在东部区域降水量偏少（低于500 mm）,此处表现为正相关影响,即在该部分区域内降水量越大有机质随之增加;而在西部区域降水量相对较大,表现为负相关影响,即在此区域内降水量越大有机质越小。
图7-d中,年平均温度的标准化回归系数范围在-1.38—1.30之间,整体呈现东高西低的空间格局,在年平均温度小于12℃的区域表现为正相关影响,在南政乡这种影响效应达到了最强,即随着年平均温度的增加有机质随之增加且增长幅度最大;年平均温度大于14℃的区域负相关影响达到最强,该区域内随着温度的增加有机质减少幅度达到最大。
图7-e中,海拔的标准化回归系数范围在-1.64—2.06之间,整体呈现东高西低的空间格局,正负值区域参半。在西南部区域,海拔是整个研究区最低的,海拔对于有机质的负相关影响效应达到最大,即海拔降低有机质随之减少的幅度达到最大。
图7-f中,植被年总初级生产力的标准化回归系数范围在-2.07—1.26之间,整体呈现东低西高的空间格局,正值区域占大部分。在东部区域GPP水平达到区域最高,而此处回归系数则达到最低水平,即随着GPP的增加有机质减少的幅度达到最大;而南部GPP水平为区域最低,回归系数却达到最高,即此处GPP越小有机质增长幅度越大。
图7-g中,年蒸散量的标准化回归系数范围在-2.05—0.93之间,整体呈现东低西高的空间格局,正值区域占大部分。研究区西部蒸散量达到最大,与此同时年蒸散量对有机质的正相关影响效应达到最大,东部蒸散量最小,相关系数也达到最小,负相关影响程度达到最强。
图7-h中,地形湿度指数的标准化回归系数范围在-3.09—2.19之间,整体呈现北高南低的空间格局,正负值区域参半。TIW在宁固乡北部影响程度最为微弱,此时TWI的范围大致为10.81—10.91,TWI反映土壤水分的干湿状况[38],从而间接地说明在一定土壤水分范围内对有机质的影响程度达到最弱。
图7-i中,平面曲率的标准化回归系数范围在-1.42—1.31之间,整体呈现东低西高的空间格局,正负值区域参半。结合图3,研究区的平面曲率在宁固乡最接近0,即地形更为平整[6],此处有机质也是增长幅度最大的,表现为正相关影响。东部地形变化较为剧烈的区域均表现为负相关影响。
图7-j中,汇流动力指数的标准化回归系数范围在-2.07—1.21之间,整体呈现东低西高的空间格局,正负值区域参半。与SPI的空间分布格局恰恰相反,SPI越大对有机质的负相关影响越强,反之SPI越小则正相关影响越强。
图7-k中,地形指数的标准化回归系数范围在-1.65—1.36之间,整体呈现东高西低的空间格局,正值区域占大部分。TPI在研究区东部达到最大,TPI的标准化回归系数也达到了最大水平,即在地形变化剧烈[38]的区域有机质变化也是剧烈的。
图7-l中,地形粗糙指数的标准化回归系数范围在-1.48—1.71之间,整体呈现东低西高的空间格局,正负值区域参半。TRI在研究区呈现东高西低的空间格局,恰恰与标准化回归系数相反,TRI<1.98时标准化回归系数达到最小,即地形异质性[39]越小有机质的增长幅度越大。当TRI>8.59时标准化回归系数达到最大,即地形异质性越大有机质的减少幅度越大。
图7-m中,年平均NDVI的标准化回归系数范围在-2.83—1.42之间,整体呈现北高南低的空间格局,正负值区域参半。结合图3,NDVI在研究区南部达到最小,北部达到最大,在北部有机质随着年平均NDVI的增加而增加,越往北增加幅度越大,反之越往南随着NDVI的减少有机质随之降低且降低幅度变大。
2.6 MGWR与GWR模型带宽对比
GWR模型及MGWR各协变量的最优带宽见图8,可以清楚地看出,两种模型在带宽方面有着截然不同的特性,在MGWR模型中各协变量均有着不同的带宽,而GWR模型仅有一种带宽,不同环境协变量的空间非平稳性特征有着不同的空间尺度,GWR模型中忽视了这种空间尺度效应,而MGWR模型对这种特性加以描述并参与建模,达到了可观的效果。图8
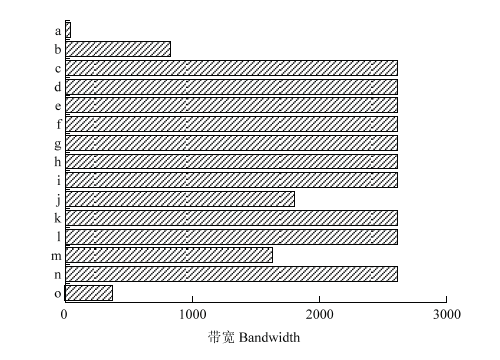新窗口打开|下载原图ZIP|生成PPT图8MGMR与GWR模型带宽对比
a：坡向;b：坡度;c：年均降水量;d：年平均温度;e：海拔;f：植被年总初级生产力;g：年蒸散量;h：TPI;i：平面曲率;j：SPI;k：TPI;l：TRI;m：NDVI;n：截距项;o：GWR模型
Fig. 8Bandwidth comparison of MGMR and GWR
a: Aspect of MGWR; b: Slope of MGWR; c: Annual mean precipitation of MGWR; d: Annual mean temperature of MGWR; e: Height of MGWR; f: Gross primary productivity of MGWR; g: Evapotranspiration of MGWR; h: TPI of MGWR; i: Plan curvature of MGWR; j: SPI of MGWR; k: TPI of MGWR; l: TRI of MGWR; m: NDVI; n: Intercept of MGWR; o: Geographically Weighted Regression (GWR)
3 讨论
为了更加全面地探究MGWRK方法精度比GWRK方法精度低的原因,对MLR、GWR和MGWR 3种方法的预测精度也进行评价（表6）,并结合文章2.3部分的模型评价绘制Radius指标的弧度图（图9）。由图表可以看出,MGWR模型的Radius指标比GWR模型降低了141.8024,GWRK的Radius指标相对于GWR降低了218.94,MGWRK相对于MGWR仅降低了38。MGWR模型的表现优于GWR模型,但MGWRK模型的表现却逊于GWRK模型。结合图5,对比不同模型的残差空间分布图,GWR的残差高低交错结构明显,这也是GWR模型中带宽固定的结果;而MGWR的残差空间分布图高低交错并没有GWR的残差明显,这是因为MGWR模型中不同自变量的带宽不同对残差的空间分布造成影响而导致MGWRK预测精度相对于GWRK模型有所降低。Table 6
表6
表6其他模型评价
Table 6
| 模型 Model | RMSE | MAE | ME | R2 | Radius |
|---|---|---|---|---|---|
| MLR | 4.5402 | 3.4510 | 0.0000 | 0.1782 | 727.4052 |
| GWR | 3.9863 | 2.9921 | 0.0375 | 0.3731 | 352.6252 |
| MGWR | 3.5959 | 2.6806 | -0.0005 | 0.4916 | 210.8228 |
新窗口打开|下载CSV
图9
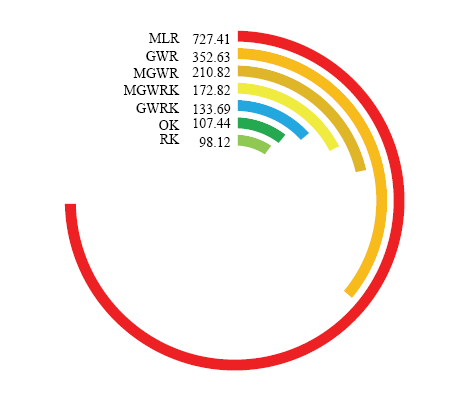新窗口打开|下载原图ZIP|生成PPT图9不同模型的Radius指数弧形图
Fig. 9Radius indices shown in an arc diagram for different models
GWR模型模拟结果的信息准则指数分别为：AICc（6705.059）、AIC（6665.335）,MGWR模型计算结果信息准则指数分别为AICc（6123.467）、AIC（6090.237）,MLR模型计算结果信息准则指数分别为AICc（6940.712）、AIC（6938.527）。信息准则指数越小模型效果越好,从信息准则指数看,MGWR、GWR模型的模拟效果均优于MLR模型。MLR、GWR、MGWR的拟合度分别为0.178、0.366、0.484,各自的调整后R2分别为0.174、0.309、0.442,从拟合度来看,与信息准则和Radius指标表现的结果一致。
由于MGWR模型多重尺度的特性,使得各种环境协变量对于因变量影响程度的空间尺度效应得以很好的描述,这种多重尺度特性提高了MGWR模型的预测能力,但是由于多重尺度对于MGWR残差的影响,这种特性反而降低了MGWRK的预测精度。MGWR模型针对不同环境协变量的空间影响能力给予了不同的空间带宽,切实地解释了不同环境协变量不同的尺度特性,而GWR模型由于统一带宽使得环境协变量的空间多重尺度效应被掩盖。
4 结论
研究区土壤有机质呈现东西两侧偏低、中部偏高的空间格局,其中汾河以东、昌源河流经区域土壤有机质普遍偏高。多重尺度地理加权回归克里金（MGWRK）能够良好的实现土壤有机质的空间预测,并且能够得到各环境协变量随着位置变化对有机质影响效应的变化,这种影响效应在不同环境协变量中有着不一样的空间尺度。MGWRK方法的空间预测精度分别达到了RK方法的69.52%、OK方法的71.74%、GWRK方法的71.17%。土壤有机质的影响因素众多,包括温度、水分状况、通气情况、植物残体特性、土壤特性等,本文仅选取了部分协变量参与建模,在后续研究中可以引入更加详尽综合的环境变量以提高预测精度,并且多重尺度地理加权回归克里金方法的特性与表现有待进一步研究。
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
URL [本文引用: 1]
针对中国西北干旱半干旱地区降水年际变率大、年内分配不均衡的气候特点，探究更为有效的农田集雨模式以实现农业的稳产高效和可持续发展。通过2 a田间试验，对比研究了不覆盖（CK）、垄覆白膜沟不覆盖（M1）、垄不覆盖沟覆秸秆（M2）、垄覆白膜沟覆秸秆（M3）和垄覆黑膜沟覆秸秆（M4）5种集雨模式对夏玉米生长、养分吸收利用及土壤有机质含量和硝态氮分布的影响。结果表明，夏玉米地上部生物量随生育进程的动态变化符合Logistic生长模型。处理M4地上部生物量理论最大值最高，快速生长持续时间最长，根系最发达；夏玉米根系主要分布在0～40 cm土层，且覆盖条件下，根长分布呈浅根化趋势。覆盖秸秆可有效提高土壤有机质含量；不同集雨模式下土壤硝态氮峰值所在土层深度存在差异，其中处理M3和M4硝态氮入渗较深，但其峰值仍保持在200 cm土层内，不会产生深层渗漏。夏玉米各器官中养分累积量表现为果＞叶＞茎＞根（其中K素累积量为茎略大于叶）。2 a中各覆盖处理夏玉米植株氮、磷和钾吸收效率及肥料偏生产力均显著（P＜0.05）高于对照。其中处理M4的平均肥料偏生产力分别较处理M1、M2和M3提高8.37%、14.93%和3.74%。综合分析，全程微型聚水覆盖（M3和M4）尤其是垄覆黑膜沟覆秸秆可较好的促进植株生长及养分吸收，同时能维持地力，具有较大的增效潜力。该研究可为干旱半干旱地区改善集雨种植模式、提高农业生产力提供参考。
URL [本文引用: 1]
针对中国西北干旱半干旱地区降水年际变率大、年内分配不均衡的气候特点，探究更为有效的农田集雨模式以实现农业的稳产高效和可持续发展。通过2 a田间试验，对比研究了不覆盖（CK）、垄覆白膜沟不覆盖（M1）、垄不覆盖沟覆秸秆（M2）、垄覆白膜沟覆秸秆（M3）和垄覆黑膜沟覆秸秆（M4）5种集雨模式对夏玉米生长、养分吸收利用及土壤有机质含量和硝态氮分布的影响。结果表明，夏玉米地上部生物量随生育进程的动态变化符合Logistic生长模型。处理M4地上部生物量理论最大值最高，快速生长持续时间最长，根系最发达；夏玉米根系主要分布在0～40 cm土层，且覆盖条件下，根长分布呈浅根化趋势。覆盖秸秆可有效提高土壤有机质含量；不同集雨模式下土壤硝态氮峰值所在土层深度存在差异，其中处理M3和M4硝态氮入渗较深，但其峰值仍保持在200 cm土层内，不会产生深层渗漏。夏玉米各器官中养分累积量表现为果＞叶＞茎＞根（其中K素累积量为茎略大于叶）。2 a中各覆盖处理夏玉米植株氮、磷和钾吸收效率及肥料偏生产力均显著（P＜0.05）高于对照。其中处理M4的平均肥料偏生产力分别较处理M1、M2和M3提高8.37%、14.93%和3.74%。综合分析，全程微型聚水覆盖（M3和M4）尤其是垄覆黑膜沟覆秸秆可较好的促进植株生长及养分吸收，同时能维持地力，具有较大的增效潜力。该研究可为干旱半干旱地区改善集雨种植模式、提高农业生产力提供参考。
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOI:10.18402/resci.2016.05.18URL [本文引用: 2]
Soil organic matter（SOM）is an important representation of soil quality or soil fertility,and its spatial distribution characteristic correlates with the ecological environment regionally. The Mongolia Plateau is in an arid and semi-arid climate zone and disturbed by wind erosion and other natural disasters perennially coupled with destruction of human activities,soil nutrient loss is serious and the local ecologic system is vulnerable. This study took the middle and northern area of the Mongolian Plateau as a study area. Elevation,mean annual temperatures,mean annual precipitation and NDVI were selected as environmental indicators,and correlated with SOM content of sample points to construct a geographically weighted regression model to gain the spatial distribution of SOM. Land cover types were also used in combination with interpolation results to analyze the spatial distribution characteristics of SOM and influence on SOM content. We found that the content of SOM in the study area had regional differences,content in the northern mountainous areas was generally higher than 40%,while in the southern desert area the content was close to zero. Landform and climate were the main factors affecting spatial distribution differences. In the north,there were more mountains covered by forest,bush and grass with plenty of moisture from the Arctic Ocean,beneficial for the accumulation of SOM. In the south it was always desertification area and the soil was barren with rare vegetation,bad for the accumulation of SOM.
DOI:10.18402/resci.2016.05.18URL [本文引用: 2]
Soil organic matter（SOM）is an important representation of soil quality or soil fertility,and its spatial distribution characteristic correlates with the ecological environment regionally. The Mongolia Plateau is in an arid and semi-arid climate zone and disturbed by wind erosion and other natural disasters perennially coupled with destruction of human activities,soil nutrient loss is serious and the local ecologic system is vulnerable. This study took the middle and northern area of the Mongolian Plateau as a study area. Elevation,mean annual temperatures,mean annual precipitation and NDVI were selected as environmental indicators,and correlated with SOM content of sample points to construct a geographically weighted regression model to gain the spatial distribution of SOM. Land cover types were also used in combination with interpolation results to analyze the spatial distribution characteristics of SOM and influence on SOM content. We found that the content of SOM in the study area had regional differences,content in the northern mountainous areas was generally higher than 40%,while in the southern desert area the content was close to zero. Landform and climate were the main factors affecting spatial distribution differences. In the north,there were more mountains covered by forest,bush and grass with plenty of moisture from the Arctic Ocean,beneficial for the accumulation of SOM. In the south it was always desertification area and the soil was barren with rare vegetation,bad for the accumulation of SOM.
[本文引用: 3]
[本文引用: 3]
DOI:10.1016/j.geoderma.2016.06.033URL [本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
URL [本文引用: 1]
The aim of this paper was to provide methodological support for understanding the response mechanism of soil properties to external factors and the related spatial distribution, which could also serve as a decision-making reference for farmers and agricultural management authorities. Using geostatistical theory, spatial analysis in GIS and geographically weighted regression (GWR) model, the study analyzed the response of soil organic matter to climatic and socio-economic factors in the central Heilongjiang Province in years of 2000 to 2005. For the period 2005, soil organic matter was spatially interpolated along with auxiliary soil type and pH datasets using Co-Kriging in GIS and the temporal variability analyzed. The result showed that in the western region of the study area, organic matter was higher in the east than in the west. Then in the eastern region of the study area, organic matter was higher in the central zone than in the northern and southern zones. Based on conventional regression model and variance inflation factor (VIF), the paper selected suitable variables for GWR model. Spatial autocorrelation analysis of soil organic matter content yielded global Moran's I index of 0.433 (P = 0.00), indicating that significant spatial autocorrelation in soil organic matter. Thus the GWR model was considered to be suitable for local parameter estimation and was used to determine the relationship between organic matter content and its driving factors. The CV method was used to determine the optimal bandwidth and to establish an adaptive kernel-type GWR model. Results showed that the GWR model accounted for over 57% of the total variance in soil organic matter content in the region. The spatial stability of the strength of the influence of each variable on organic matter content was analyzed. It showed that all variables had significant spatial instability. In addition, the minimum, maximum, upper quartile and lower quartile of the regression coefficients of the variables were largely different, and with both positive and negative correlations. This showed that the influence of each variable on soil organic matter content was spatially variable and was either positive or negative. Results from the GWR model showed that precipitation and annual average temperature negatively influenced organic matter content. Annual sunshine hours positively influenced organic matter content in most areas, except southwest Nenjiang Plain and south Songjiang Plain. The influence of mechanized farming level (as a socio-economic factor) on soil organic matter was positive in both north and west Nenjiang Plain and also in some parts of the Kebai Hills. Irrigation areas had relatively large positive effect on soil organic mat-ter in the study area. Fertilizer had negative effect on soil organic matter in areas of south Nenjiang Plain, northwest Songjiang Plain and northeast Sanjiang Plain, but positive effects in other areas. Mulch film consumption had a large positive effect on soil organic matter. The effect of pesticide consumption on soil organic matter was mainly positive in the west of the study area, while it was mainly negative in the east (all significant at the 0.01 level). It was concluded that the effects of climatic factors (which reflect dif-ferences in natural conditions) and socio-economic factors (which reflect agricultural inputs) on soil organic matter were largely het-erogeneous.
URL [本文引用: 1]
The aim of this paper was to provide methodological support for understanding the response mechanism of soil properties to external factors and the related spatial distribution, which could also serve as a decision-making reference for farmers and agricultural management authorities. Using geostatistical theory, spatial analysis in GIS and geographically weighted regression (GWR) model, the study analyzed the response of soil organic matter to climatic and socio-economic factors in the central Heilongjiang Province in years of 2000 to 2005. For the period 2005, soil organic matter was spatially interpolated along with auxiliary soil type and pH datasets using Co-Kriging in GIS and the temporal variability analyzed. The result showed that in the western region of the study area, organic matter was higher in the east than in the west. Then in the eastern region of the study area, organic matter was higher in the central zone than in the northern and southern zones. Based on conventional regression model and variance inflation factor (VIF), the paper selected suitable variables for GWR model. Spatial autocorrelation analysis of soil organic matter content yielded global Moran's I index of 0.433 (P = 0.00), indicating that significant spatial autocorrelation in soil organic matter. Thus the GWR model was considered to be suitable for local parameter estimation and was used to determine the relationship between organic matter content and its driving factors. The CV method was used to determine the optimal bandwidth and to establish an adaptive kernel-type GWR model. Results showed that the GWR model accounted for over 57% of the total variance in soil organic matter content in the region. The spatial stability of the strength of the influence of each variable on organic matter content was analyzed. It showed that all variables had significant spatial instability. In addition, the minimum, maximum, upper quartile and lower quartile of the regression coefficients of the variables were largely different, and with both positive and negative correlations. This showed that the influence of each variable on soil organic matter content was spatially variable and was either positive or negative. Results from the GWR model showed that precipitation and annual average temperature negatively influenced organic matter content. Annual sunshine hours positively influenced organic matter content in most areas, except southwest Nenjiang Plain and south Songjiang Plain. The influence of mechanized farming level (as a socio-economic factor) on soil organic matter was positive in both north and west Nenjiang Plain and also in some parts of the Kebai Hills. Irrigation areas had relatively large positive effect on soil organic mat-ter in the study area. Fertilizer had negative effect on soil organic matter in areas of south Nenjiang Plain, northwest Songjiang Plain and northeast Sanjiang Plain, but positive effects in other areas. Mulch film consumption had a large positive effect on soil organic matter. The effect of pesticide consumption on soil organic matter was mainly positive in the west of the study area, while it was mainly negative in the east (all significant at the 0.01 level). It was concluded that the effects of climatic factors (which reflect dif-ferences in natural conditions) and socio-economic factors (which reflect agricultural inputs) on soil organic matter were largely het-erogeneous.
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOI:10.1016/j.jclepro.2019.118084URL [本文引用: 1]
DOI:10.11821/dlxb201806007URL [本文引用: 1]
Research into urban expansion patterns and their driving forces is of great significance. Under the background of the integrated development of the Beijing-Tianjin-Hebei (Jing-Jin-Ji) urban agglomeration, it is important to study the temporal and spatial patterns of urban land expansion and the driving forces development. This paper uses land-use data of the Jing-Jin-Ji urban agglomeration from 1990 to 2015 and reveals the multi-dimensional characteristics of the urban land expansion patterns. We then combine the urban spatial interaction and the spatial and temporal nonstationarity of the urban land expansion process and build the center of gravity-geographically and temporally weighted regression (GTWR) model by coupling the center of gravity model with the GTWR model. Using the center of gravity-GTWR model, we analyze the driving forces of urban land expansion at the city scale, and summarize the dominant mode and core driving forces of the Jing-Jin-Ji urban agglomeration. The results show that: (1) Between 1990 and 2015, the expansion intensity of the Jing-Jin-Ji urban agglomeration showed a down-up-down trend, and the peak period of expansion was in 2005-2010. Before 2005, high-speed development was seen in Beijing, Tianjin, Baoding, and Langfang, which were then followed by rapid development in Xingtai and Handan. (2) Although the center of gravity of cities in the Jing-Jin-Ji urban agglomeration showed a divergent trend, the local interaction between cities was enhanced, and the driving forces of urban land expansion showed a characteristic of spatial spillover. (3) The spatial development mode of the Jing-Jin-Ji urban agglomeration changed from a dual-core development mode to a multi-core development mode, which was made up of three function cores: the transportation core in the northern part, the economic development core in the central part, and the investment core in the southern part. The integrated development between functional cores led to the multi-core development mode. (4) The center of gravity-GTWR model analyzes urban land expansion as a space-time dynamic system. The model proved to be feasible in the analysis of the driving forces of urban land expansion.
DOI:10.11821/dlxb201806007URL [本文引用: 1]
Research into urban expansion patterns and their driving forces is of great significance. Under the background of the integrated development of the Beijing-Tianjin-Hebei (Jing-Jin-Ji) urban agglomeration, it is important to study the temporal and spatial patterns of urban land expansion and the driving forces development. This paper uses land-use data of the Jing-Jin-Ji urban agglomeration from 1990 to 2015 and reveals the multi-dimensional characteristics of the urban land expansion patterns. We then combine the urban spatial interaction and the spatial and temporal nonstationarity of the urban land expansion process and build the center of gravity-geographically and temporally weighted regression (GTWR) model by coupling the center of gravity model with the GTWR model. Using the center of gravity-GTWR model, we analyze the driving forces of urban land expansion at the city scale, and summarize the dominant mode and core driving forces of the Jing-Jin-Ji urban agglomeration. The results show that: (1) Between 1990 and 2015, the expansion intensity of the Jing-Jin-Ji urban agglomeration showed a down-up-down trend, and the peak period of expansion was in 2005-2010. Before 2005, high-speed development was seen in Beijing, Tianjin, Baoding, and Langfang, which were then followed by rapid development in Xingtai and Handan. (2) Although the center of gravity of cities in the Jing-Jin-Ji urban agglomeration showed a divergent trend, the local interaction between cities was enhanced, and the driving forces of urban land expansion showed a characteristic of spatial spillover. (3) The spatial development mode of the Jing-Jin-Ji urban agglomeration changed from a dual-core development mode to a multi-core development mode, which was made up of three function cores: the transportation core in the northern part, the economic development core in the central part, and the investment core in the southern part. The integrated development between functional cores led to the multi-core development mode. (4) The center of gravity-GTWR model analyzes urban land expansion as a space-time dynamic system. The model proved to be feasible in the analysis of the driving forces of urban land expansion.
DOI:10.11821/dlxb201906012URL [本文引用: 1]
Villages in mountainous areas are under the risk of topography, geomorphology and frequent natural disasters in a long term. Rural transportation system is characterized by low network degree and weak capacity to resist disasters, and the problem of vulnerability of traffic environment is prominent. Taking Luonan county in the Qinling-Daba mountainous areas as an example and based on exposure, sensitivity and response capacity of human-environment system vulnerability, this paper constructed a basic framework of rural transportation environment vulnerability, which contained the key elements of risk events, geographical features, key travel path, road network structures, public and private vehicles, family capital etc., and established a targeted evaluation index system. With the aid of ArcGIS and GeoDa, this research examined the spatial structure and spatial autocorrelation of the transportation environment vulnerability in Luonan county at the village level. It also utilized a geographical weighted regression model to explore the factors of natural conditions, population, socio-economic development, which had influence on response capacity of traffic risk and its spatial difference. The results showed that the vulnerability of transportation environment took the county seat and the suburbs as the center increasing outward, which presents a circle structure featured by great difference in vertical direction. Simultaneously, the vulnerability of the transportation environment in village-level residential areas showed a significant positive spatial autocorrelation, but both exposure degree and sensitivity showed a significant spatial negative correlation with the response capacity. There were three patterns of local spatial correlation in transportation environment vulnerability: the vulnerability of the local "hot spots" areas was widely observed in the north- central mountainous area and fell into the dilemma of high exposure, high sensitivity and low response capacity, while the "cold spots" villages were founded in suburbs or areas adjacent to the towns with higher income, which had low sensitivity and high response capacity. There were a few "heterogeneity points", and these villages were adjacent to low-vulnerable villages, but they belonged to high-vulnerable areas. Moreover, topographical condition, industrial distribution, population structure, education level and family size had a significant impact on response capacity of transportation risk. In addition, the effect direction and intensity of the influencing factors had significant spatial differences.
DOI:10.11821/dlxb201906012URL [本文引用: 1]
Villages in mountainous areas are under the risk of topography, geomorphology and frequent natural disasters in a long term. Rural transportation system is characterized by low network degree and weak capacity to resist disasters, and the problem of vulnerability of traffic environment is prominent. Taking Luonan county in the Qinling-Daba mountainous areas as an example and based on exposure, sensitivity and response capacity of human-environment system vulnerability, this paper constructed a basic framework of rural transportation environment vulnerability, which contained the key elements of risk events, geographical features, key travel path, road network structures, public and private vehicles, family capital etc., and established a targeted evaluation index system. With the aid of ArcGIS and GeoDa, this research examined the spatial structure and spatial autocorrelation of the transportation environment vulnerability in Luonan county at the village level. It also utilized a geographical weighted regression model to explore the factors of natural conditions, population, socio-economic development, which had influence on response capacity of traffic risk and its spatial difference. The results showed that the vulnerability of transportation environment took the county seat and the suburbs as the center increasing outward, which presents a circle structure featured by great difference in vertical direction. Simultaneously, the vulnerability of the transportation environment in village-level residential areas showed a significant positive spatial autocorrelation, but both exposure degree and sensitivity showed a significant spatial negative correlation with the response capacity. There were three patterns of local spatial correlation in transportation environment vulnerability: the vulnerability of the local "hot spots" areas was widely observed in the north- central mountainous area and fell into the dilemma of high exposure, high sensitivity and low response capacity, while the "cold spots" villages were founded in suburbs or areas adjacent to the towns with higher income, which had low sensitivity and high response capacity. There were a few "heterogeneity points", and these villages were adjacent to low-vulnerable villages, but they belonged to high-vulnerable areas. Moreover, topographical condition, industrial distribution, population structure, education level and family size had a significant impact on response capacity of transportation risk. In addition, the effect direction and intensity of the influencing factors had significant spatial differences.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOI:10.1016/j.cageo.2007.05.001URL [本文引用: 1]
DOI:10.1016/j.catena.2018.10.052URL [本文引用: 1]
URLPMID:26572015 [本文引用: 1]
Relative elevation and stream power index were selected as auxiliary variables based on correlation analysis for mapping soil organic matter. Geographically weighted regression Kriging (GWRK) and regression Kriging (RK) were used for spatial interpolation of soil organic matter and compared with ordinary Kriging (OK), which acts as a control. The results indicated that soil organic matter was significantly positively correlated with relative elevation whilst it had a significantly negative correlation with stream power index. Semivariance analysis showed that both soil organic matter content and its residuals (including ordinary least square regression residual and GWR residual) had strong spatial autocorrelation. Interpolation accuracies by different methods were estimated based on a data set of 98 validation samples. Results showed that the mean error (ME), mean absolute error (MAE) and root mean square error (RMSE) of RK were respectively 39.2%, 17.7% and 20.6% lower than the corresponding values of OK, with a relative improvement (RI) of 20.63. GWRK showed a similar tendency, having its ME, MAE and RMSE to be respectively 60.6%, 23.7% and 27.6% lower than those of OK, with a RI of 59.79. Therefore, both RK and GWRK significantly improved the accuracy of OK interpolation of soil organic matter due to their incorporation of auxiliary variables. In addition, GWRK performed obviously better than RK did in this study, and its improved performance should be attributed to the consideration of sample spatial locations.
URLPMID:26572015 [本文引用: 1]
Relative elevation and stream power index were selected as auxiliary variables based on correlation analysis for mapping soil organic matter. Geographically weighted regression Kriging (GWRK) and regression Kriging (RK) were used for spatial interpolation of soil organic matter and compared with ordinary Kriging (OK), which acts as a control. The results indicated that soil organic matter was significantly positively correlated with relative elevation whilst it had a significantly negative correlation with stream power index. Semivariance analysis showed that both soil organic matter content and its residuals (including ordinary least square regression residual and GWR residual) had strong spatial autocorrelation. Interpolation accuracies by different methods were estimated based on a data set of 98 validation samples. Results showed that the mean error (ME), mean absolute error (MAE) and root mean square error (RMSE) of RK were respectively 39.2%, 17.7% and 20.6% lower than the corresponding values of OK, with a relative improvement (RI) of 20.63. GWRK showed a similar tendency, having its ME, MAE and RMSE to be respectively 60.6%, 23.7% and 27.6% lower than those of OK, with a RI of 59.79. Therefore, both RK and GWRK significantly improved the accuracy of OK interpolation of soil organic matter due to their incorporation of auxiliary variables. In addition, GWRK performed obviously better than RK did in this study, and its improved performance should be attributed to the consideration of sample spatial locations.
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
DOI:10.1080/24694452.2017.1352480URL [本文引用: 3]
URL [本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOI:10.11707/j.1001-7488.20160717URL [本文引用: 1]
[Objective] Taking foresters who are taking part in forest carbon sequestration project in Sichuan Province as research objects, this paper analyzed foresters'constant participation willingness and its affecting factors in order to provide countermeasures and suggestions for increasing foresters' enthusiasm to constantly participating forest carbon sequestration project, realizing the construction goal of project and speeding up sustainable development of forestry which is regarded carbon sequestration as the main objective in dealing with global climate change.[Method] Based on the survey data of 397 foresters in Novartis forestry carbon sequestration, community and biodiversity project construction zone in the southwest of Sichuan Province, the orderly Probit model was used to conduct an empirical analysis on foresters' constant participation willingness for forest carbon sequestration project and its affecting factors.[Result] The research results indicated that the willingness of foresters to constantly participate in forest carbon sequestration project was not high, and need to be further improved. The parameters such as land area of participation, family income level, satisfaction for early returns, the late earnings forecast, government support, the degree of difficulty in obtaining the forestry information and road traffic etc. haves significant positive influences on foresters' willingness of constant participation. While the age, multiple occupations level and project organization model showed significant negative effects.[Conclusion] We put forward some suggestions to promote the sustainable development of forest carbon sequestration projects from both business and government. For the forestry entity (enterprise), they should carry out multiple targets considering area, land and population, adjust measurements for local conditions to optimize the organization model of project, balance the early earns and late benefits. As for the government, they should intensify policy support, establish and perfect the forestry information release and disaster warning mechanism, introduce financial support policy to improve infrastructure construction of forest carbon sequestration project area. In this way, the sustainable development of forest carbon sequestration project would be promoted, and then realize the climate improvement, ecological prosperity and income increasing of foresters.
DOI:10.11707/j.1001-7488.20160717URL [本文引用: 1]
[Objective] Taking foresters who are taking part in forest carbon sequestration project in Sichuan Province as research objects, this paper analyzed foresters'constant participation willingness and its affecting factors in order to provide countermeasures and suggestions for increasing foresters' enthusiasm to constantly participating forest carbon sequestration project, realizing the construction goal of project and speeding up sustainable development of forestry which is regarded carbon sequestration as the main objective in dealing with global climate change.[Method] Based on the survey data of 397 foresters in Novartis forestry carbon sequestration, community and biodiversity project construction zone in the southwest of Sichuan Province, the orderly Probit model was used to conduct an empirical analysis on foresters' constant participation willingness for forest carbon sequestration project and its affecting factors.[Result] The research results indicated that the willingness of foresters to constantly participate in forest carbon sequestration project was not high, and need to be further improved. The parameters such as land area of participation, family income level, satisfaction for early returns, the late earnings forecast, government support, the degree of difficulty in obtaining the forestry information and road traffic etc. haves significant positive influences on foresters' willingness of constant participation. While the age, multiple occupations level and project organization model showed significant negative effects.[Conclusion] We put forward some suggestions to promote the sustainable development of forest carbon sequestration projects from both business and government. For the forestry entity (enterprise), they should carry out multiple targets considering area, land and population, adjust measurements for local conditions to optimize the organization model of project, balance the early earns and late benefits. As for the government, they should intensify policy support, establish and perfect the forestry information release and disaster warning mechanism, introduce financial support policy to improve infrastructure construction of forest carbon sequestration project area. In this way, the sustainable development of forest carbon sequestration project would be promoted, and then realize the climate improvement, ecological prosperity and income increasing of foresters.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[D].
[本文引用: 1]
[D].
[本文引用: 1]
DOI:10.13227/j.hjkx.201705122URLPMID:29964548 [本文引用: 1]
PM2.5 pollution in China has become an extreme environmental and social problem and has generated widespread public concern. We estimate ground-level PM2.5 from satellite-derived aerosol optical depth (AOD), topography data, meteorological data, and pollutant emissions using a new technique, Bayesian maximum entropy (BME) combined with geographically weighted regression (GWR), to evaluate the spatial and temporal characteristics of PM2.5 exposure in an eastern region of China in winter. The overall 10-fold cross-validation R2 is 0.92, and the root mean squared prediction error (RMSE) is 8.32 μg·m-3. The mean prediction error (MPE) of the predicted monthly PM2.5 is -0.042 μg·m-3, the mean absolute prediction error (MAE) is 4.60 μg·m-3. Compared with the results of the Geographically Weighted Regression model-GWR (R2=0.71, RMSE=15.68 μg·m-3, MPE=-0.095 μg·m-3, MAE=11.14 μg·m-3), the prediction by the BME were greatly improved. In this location, the high PM2.5concentration area is mainly concentrated in North China, the Yangtze River Delta, and Sichuan Basin. The low concentration area is mainly concentrated in the south of China, including the Pearl River Delta and southwest of Yunnan. Temporally, there is migration trend from the coastal areas inland, and PM2.5 pollution is most serious in December 2015 and January 2016. It is relatively low in November 2015 and February 2016.
DOI:10.13227/j.hjkx.201705122URLPMID:29964548 [本文引用: 1]
PM2.5 pollution in China has become an extreme environmental and social problem and has generated widespread public concern. We estimate ground-level PM2.5 from satellite-derived aerosol optical depth (AOD), topography data, meteorological data, and pollutant emissions using a new technique, Bayesian maximum entropy (BME) combined with geographically weighted regression (GWR), to evaluate the spatial and temporal characteristics of PM2.5 exposure in an eastern region of China in winter. The overall 10-fold cross-validation R2 is 0.92, and the root mean squared prediction error (RMSE) is 8.32 μg·m-3. The mean prediction error (MPE) of the predicted monthly PM2.5 is -0.042 μg·m-3, the mean absolute prediction error (MAE) is 4.60 μg·m-3. Compared with the results of the Geographically Weighted Regression model-GWR (R2=0.71, RMSE=15.68 μg·m-3, MPE=-0.095 μg·m-3, MAE=11.14 μg·m-3), the prediction by the BME were greatly improved. In this location, the high PM2.5concentration area is mainly concentrated in North China, the Yangtze River Delta, and Sichuan Basin. The low concentration area is mainly concentrated in the south of China, including the Pearl River Delta and southwest of Yunnan. Temporally, there is migration trend from the coastal areas inland, and PM2.5 pollution is most serious in December 2015 and January 2016. It is relatively low in November 2015 and February 2016.
DOI:10.11820/dlkxjz.2013.01.013URL [本文引用: 2]
In this paper, based on review of the studies on methods and techniques of terrain information description, topographic unit diversity index (TUDI), a new concept and quantification method, was proposed. The diversity index integrates several terrain parameters, e.g., elevation, slope, slope position, slope aspect, water confluences and distributions information. By combining the algorithms of the topographic position index and the topographic wetness index, using layer overlay analysis method and appropriate indicators for classification and grading, TUDI algorithm re-classifies the types of topographic units, and then calculate the TUDI using the neighborhood statistics and analysis method. The results of the experiment in Sichuan Province as a test region using DEM (100 m×100 m) and waters distribution data (1:250,000, 2005) show that TUDI is a comprehensive index, revealing the complexity and variations of the true surface. In the process of calculation, the topographic units were divided into 13 different types. The topographic unit diversity index was calculated with the statistics window radius set to 900m based on division results of the topographic units. The areas with diversity index value less than 0.5 cover around 11 percent of the whole region; the areas with the value more than 0.75 take up as much as 57 percent. Basically the results of the calculation agree with the topographic features of the study areas. In addition to the experiment to test the reliability of the algorithm, the advantages and disadvantages of it were also evaluated. This research provides a good basis for constructing a conceptual system of DEM-based topographic attributes, as well as for the spatial analysis of terrain information from micro to macro scales.
DOI:10.11820/dlkxjz.2013.01.013URL [本文引用: 2]
In this paper, based on review of the studies on methods and techniques of terrain information description, topographic unit diversity index (TUDI), a new concept and quantification method, was proposed. The diversity index integrates several terrain parameters, e.g., elevation, slope, slope position, slope aspect, water confluences and distributions information. By combining the algorithms of the topographic position index and the topographic wetness index, using layer overlay analysis method and appropriate indicators for classification and grading, TUDI algorithm re-classifies the types of topographic units, and then calculate the TUDI using the neighborhood statistics and analysis method. The results of the experiment in Sichuan Province as a test region using DEM (100 m×100 m) and waters distribution data (1:250,000, 2005) show that TUDI is a comprehensive index, revealing the complexity and variations of the true surface. In the process of calculation, the topographic units were divided into 13 different types. The topographic unit diversity index was calculated with the statistics window radius set to 900m based on division results of the topographic units. The areas with diversity index value less than 0.5 cover around 11 percent of the whole region; the areas with the value more than 0.75 take up as much as 57 percent. Basically the results of the calculation agree with the topographic features of the study areas. In addition to the experiment to test the reliability of the algorithm, the advantages and disadvantages of it were also evaluated. This research provides a good basis for constructing a conceptual system of DEM-based topographic attributes, as well as for the spatial analysis of terrain information from micro to macro scales.
[本文引用: 1]
