,1,*, 闫慧峰1, 褚继登1, 李彩斌2Statistical analysis of randomized complete block design with repeated measure data using Generalized Linear Mixed Models (GLIMMIX)
ZHANG Jiu-Quan,1,*, YAN Hui-Feng1, CHU Ji-Deng1, LI Cai-Bin2通讯作者:
收稿日期:2020-04-1接受日期:2020-07-2网络出版日期:2020-07-15
| 基金资助: |
Received:2020-04-1Accepted:2020-07-2Online:2020-07-15
| Fund supported: |
摘要
关键词：
Abstract
Keywords：
PDF (340KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张久权, 闫慧峰, 褚继登, 李彩斌. 运用广义线性混合模型分析随机区组重复测量的试验资料[J]. 作物学报, 2021, 47(2): 294-304. doi:10.3724/SP.J.1006.2021.04085
ZHANG Jiu-Quan, YAN Hui-Feng, CHU Ji-Deng, LI Cai-Bin.
农业科研常常需要进行长期定位试验和多点试验, 需要对同一对象(小区、某株作物等)进行重复测量, 例如, 为了探明烤烟移栽后的生长速度, 需要定点定株对烤烟的株高进行连续测量。这种对同一受试对象(subject)进行多次测量的试验即为重复测量试验[1,2,3]。在农业试验中, 主要包括3种类型的重复测量: (1)不同时间点对同一对象测量; (2)对同一对象不同部位的测量, 如烤烟上、中、下3个部位; (3)不同地点的测量, 如作物品种区试。时间、部位、地点均可以视为重复测量因子。由于个体间的差异, 观测值开始就高的个体, 后面也高, 反之一样, 例如, 定点测量烟株的高度, 第1次测量较高的烟株, 后面测量时也会高。因此, 同一对象不同观察值间往往存在时间或空间上的自相关性, 观测点间隔越近, 往往相关性越大[3,4,5,6], 自相关是重复测量数据最大的特点。由于存在自相关性, 数据间相互独立的基本要求不能满足, 不能采用常规的统计方法进行统计分析[4-5,7-8]。
重复测量试验在医学领域十分普遍, 在农业研究领域也越来越受到人们的重视, 特别是长期定位试验。过去, 主要采用裂区设计或多变量统计方法分析这类数据[2,6,9], 不仅忽视了分析的前提条件[10], 可能得出错误的结论, 也大大浪费了重复测量因素的时间或空间信息, 降低了统计分析的效能, 导致高层次、高效率的试验得出低质量、低水平的研究结论, 造成不必要的浪费与损失[4,11-12]。国外期刊从2004年开始就已经对重复测量数据的分析进行了严格要求[1]。目前, 我国农业领域, 有关对重复测量试验数据进行科学统计分析方法的报道鲜见。
近年来, SAS等统计软件进行了创新和发展。运用混合模型(mixed)和广义线性混合模型(Generalized Linear Mixed Models, GLIMMIX)能很好地进行重复测量的数据分析[13]。重复测量试验可以与许多试验设计结合, 如完全随机、随机区组、裂区、拉丁方等等。随机区组试验是农业试验中普通采用的试验设计, 尤其是田间试验。因此, 本文以两因素随机区组试验数据为例, 系统介绍应用GLIMMIX进行重复测量数据方差分析和均值比较的方法, 并阐明传统统计方法的不足, 供广大农业科研工作者参考。
1 材料与方法
1.1 试验设计
1.1.1 土柱试验 该试验为室内模拟试验二因子(降水强度、N肥水平)三重复全因子设计, 小区排列方式为随机区组。土壤为中国农业科学院西南试验基地(四川西昌市)收集的紫色土。降水强度分别为0.44、0.68、1.20 mm min-1, 降水量均为50 mm 次-1。设N1 (常规施肥, CK)、N2 (减量30%)、N3 (减量30%+生物炭)共3个氮肥水平。对土柱进行了12次模拟降雨, 第6次开始收集到下渗淋洗液, 一直到第12次降雨完成, 每个土柱收集到7次淋洗液, 时间间隔相等。采用碱性过硫酸钾消解紫外分光光度法测定淋洗液中的全氮[14]。7次淋洗被当作重复测量因素。采用SAS 9.4的GLIMMIX进行统计分析, 数据输入示例见表1。Table 1
表1
表1数据Microsoft Excel输入表示例
Table 1
| Rain | N | Block | Core | Times | Y |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 6 | 20.20 |
| 1 | 1 | 1 | 1 | 7 | 7.37 |
| 1 | 1 | 1 | 1 | 8 | 5.75 |
| 1 | 1 | 1 | 1 | 9 | 4.25 |
| 1 | 1 | 1 | 1 | 10 | 2.42 |
| 1 | 1 | 1 | 1 | 11 | 4.69 |
| 1 | 1 | 1 | 1 | 12 | 5.13 |
| 1 | 1 | 2 | 2 | 6 | 20.45 |
| 1 | 1 | 2 | 2 | 7 | 12.33 |
| … | … | … | … | … | |
| 3 | 3 | 3 | 27 | 12 | 6.16 |
新窗口打开|下载CSV
1.1.2 田间试验 2018年4月开始, 在贵州毕节威宁县黑石镇开展烟田生物炭长期定位试验, 采用单因子(生物炭用量)三水平(0、15、40 t hm-2)三重复随机区组设计, 小区面积67 m2, 供试作物为烤烟, 分别于2018年的6月13日、7月17日、9月20日, 2019年的6月11日、7月24日、9月26日采集0~20 cm耕层土壤测定土壤速效钾含量。为了进行说明, 设置2018年7月17日取样的处理15 t hm-2重复1数据缺失, 按缺区处理。
1.2 分析比较
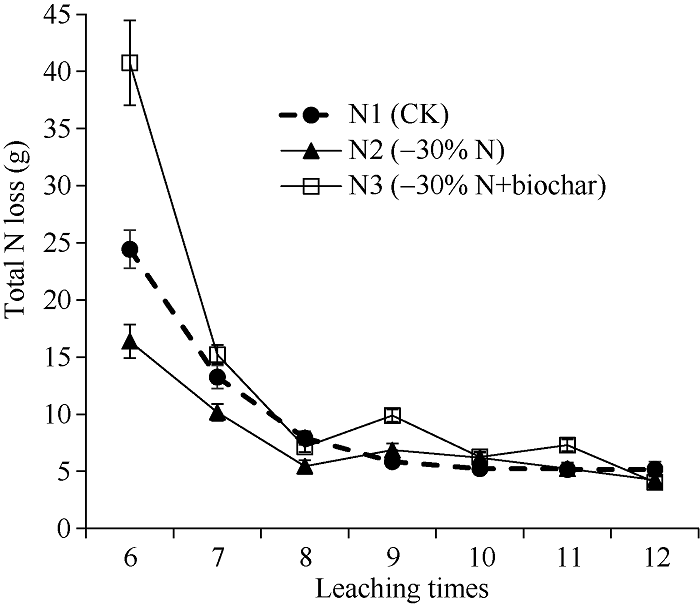
图1显示了土柱试验3种不同施肥方式下总N淋失量随淋次数的变化, 淋洗次数为重复测量的时间因素。我们可能需要确定如下处理组合间的差异是否显著: (1)特定时间两处理水平间的差异, 如第6次淋洗时, 全氮淋失量N1与N2处理的差异; (2)特定处理随时间的变化, 如N2处理, 全氮淋失量第6次与第8次淋洗的差异; (3)两处理水平在各特定时间点的差异, 以便确定最优处理组合, 如N1第7次淋洗与N2第9次淋洗全氮淋失量的差异显著性; (4)随时间的变化(所有处理平均), 如3种氮处理平均, 全氮淋失量第8次与第10次淋洗的差异; (5)处理间差异(所有时间点平均), 如N1与N2处理在所有时间点平均, 全氮淋失量的差异; (6)其他差异比较。图1
新窗口打开|下载原图ZIP|生成PPT图13种施肥处理总氮淋失量随淋洗次数的变化
误差线为标准误。
Fig. 1Total N loss varied with leaching times at three N fertilizer treatments
The error lines are standard errors (SEs).
田间试验与土柱试验类似, 我们可以比较2018年6月13日取样时, 不同生物炭用量间土壤速效钾含量的差异; 施用生物炭15 t hm-2后, 2018年6月与2019年6月土壤速效钾含量的差异等。
1.3 方差分析模型
对于三因素(2个处理因素和1个时间因素)随机区组设计(土柱试验), 其线性可加效应模型如下:式中, Yabij为某小区的观察值, 如全N淋失量; μ为总体均值; αa为因素A第a水平的效应; βb 为因素B第b水平的效应; (αβ)ab为因素A与因素B在ab水平上的交互作用效应; Bk为第k个区组效应; δi(ab)为第i个对象(小区)在ab水平上的效应, 即对象间误差, 满足i.i.d. N (0, σ2主间); rj为重复测量因素在时间点j的效应; (αr)aj、(βr)bj分别为因素A、B与时间点的交互作用; (αβr)abj为三因素交互作用; eabij为误差项, 满足i.i.d. N (0, σe2)。Bk、δi(ab)、eabij为随机效应, 其余各项为固定效应。δi(ab)、eabij相互独立。
对于一因素三水平随机区组设计(田间试验), 其线性可加效应模型如下:
式中, αa为处理因素A第a水平的效应; Bk为第k个区组效应; δia为对象间误差, 满足i.i.d. N (0, σ2主间); rj为重复测量因素在时间点j的效应; (αr)aj为因素A与时间点的交互作用; eaij为误差项, 满足i.i.d. N (0, σe2)。
1.4 协方差结构的筛选
在重复测量试验中, 某一测量时间点上测定值变异的大小构成方差, 2个不同时间点上测定值相互变异的大小用协方差来度量。如果时间点I上的取值不影响时间点II上的取值, 则协方差为0, 反之则大于0。运用GLIMMIX程序分析重复测量的数据主要分两步, 首先是挑选协方差结构, 其次是进行方差分析和均值比较。对于土柱试验, 土柱(core)为受试对象(subject)。运用GLIMMIX挑选最恰当的协方差结构的参考SAS程序如下。SAS程序I SAS program I
PROC IMPORT /*(1)*/
OUT= totalN
DATAFILE= "E:\数据\N.xls"
DBMS=EXCEL REPLACE;
SHEET="Sheet1$";
GETNAMES=YES;
SCANTEXT=YES;
RUN;
ODS RTF;
proc glimmix data=totalN; /*(2)*/
class Rain N Block Core Times;
model y=Rain|N|times /ddfm = kr;
random _residual_/type=VC sub=Core(Rain N);
ods output fitstatistics=fVC;
run;
proc glimmix data=totalN; /*(3)*/
class Rain N Block Core Times;
model y=Rain|N|times /ddfm = kr;
random _residual_/type=CS sub=Core(Rain N);
ods output fitstatistics=fCS;
run;
proc glimmix data=totalN; /*(4)*/
class Rain N Block Core Times;
model y=Rain|N|times /ddfm = kr;
random _residual_/type=UN sub=Core(Rain N);
ods output fitstatistics=fUN;
run;
proc glimmix data=totalN; /*(5)*/
class Rain N Block Core Times;
model y=Rain|N|times /ddfm = kr;
random _residual_/type=SP(POW)(Times) sub=Core(Rain N);
ods output fitstatistics=fSP;
run;
proc glimmix data=totalN; /*(6)*/
class Rain N Block Core Times;
model y=Block Rain|N|times /ddfm = kr;
random Block Core(Rain N);
random _residual_/type=AR(1) sub=Core(Rain N);
ods output fitstatistics=fAR;
run;
proc glimmix data=totalN; /*(7)*/
class Rain N Block Core Times;
model y=Block Rain|N|times /ddfm = kr;
random Block Core(Rain N);
random _residual_/type=TOEP sub=Core(Rain N);
ods output fitstatistics=fTOEP;
run;
proc glimmix data=totalN; /*(8)*/
class Rain N Block Core Times;
model y=Block Rain|N|times /ddfm = kr;
random Block Core(Rain N);
random _residual_/type=ANTE(1) sub=Core(Rain N);
ods output fitstatistics=fANTE;
run;
%macro rename(fit,a); /*(9)*/
data &fit;
set &fit;
rename value=&a;
run;
%mend rename;
%rename(fVC,VC)
%rename(fCS,CS)
%rename(fUN,UN)
%rename(fSP,SP)
%rename(fAR,AR1)
%rename(fTOEP,TOEP)
%rename(fANTE,ANTE1)
data merge_table; /*(10)*/
merge fVC fCS fUN fSP fAR fTOEP fANTE;
run;
proc print data=merge_table; /*(11)*/
format _numeric_ 5.1;
run;
ODS RTF close;
程序说明: 输入代码时注意分号为英文字符。数据存放在E:\数据\N.xls sheet1里, 格式见表1。程序(1)读取Excel文件的数据。程序(2)~(8)内容基本相同, 仅在“type =”后的协方差结构选项不同。对某些协方差结构, 包括一阶自回归[autoregressive(1), AR(1)]、循环相关(toeplitz, TOEP)、一阶前依赖[antedependence, ANTE(1)]等协方差结构, 需要考虑对象间误差, 因此需要增加random block core(Rain N)语句[15]。程序(2)~(8)调用GLIMMIX过程, 分别采用方差分量结构(variance components, VC)、复合对称结构(compound symmetry, CS)、不规则结构(unstructured, UN)、空间幂相关结构[space power, SP(POW)]、一阶自回归[AR(1)]、循环相关结构(TOEP)、一阶前依赖结构[ANTE(1)]模型进行方差分析。Class语句列出所有的分类变量。Model语句根据上文(1)式编写, Model语句后仅需要列出固定效应[4], 注意此与mixed的不同。Rain|N|times表示3个因素的主效应、2级和3级交互作用效应的线性组合。采用KR法对标准误和自由度进行修正[16]。random_residual_语句相当于mixed模型中的repeated语句[5]。选项type指定协方差结构类型。选项sub指定数据集中的受试对象(subject), 本例中为土柱(core), 即小区, 若为单因素试验, 直接指定对象名称; 若为多因素试验, 则在对象名称后加因素名称, 并加“()”。ods output语句输出模型拟合信息fitstatistics。程序(9)建立宏rename, 对数据集中已有变量名value更名, 否则原有数据列value的数据会被覆盖[17]。程序(10)对不同协方差结构拟合参数进行合并, 以便程序(11)输出拟合结果, 为挑选最佳协方差结构提供依据。
对于田间试验, SAS代码与上述类似, 现就VC结构的代码列出如右上:
proc glimmix data=bijie; /*(12)*/
class rate block plot time;
model y=rate|time /ddfm = kr;
random _residual_/type=VC sub=plot;
run;
这里, rate为生物炭用量, block为区组, plot为小区, 即试验对象, time为取样时间。由于本田间试验取样时间间隔不相等, 对于SP(POW)协方差结构, 需要计算时间间隔变量, 本列以天数days表示, 并增加语句 “random _residual_/type=SP(POW)(days) sub=plot;”。对于需要增加random语句的协方差结构, 包括SP(POW)、ANTE(1)、AR(1)+RE、TOEP, random语句写法为“random plot block block*time;”。
1.5 方差分析和均值比较
挑选出最恰当的协方差结构后, 就可以运用GLIMMIX进行方差分析和均值比较了。土柱试验以一阶前依赖结构ANTE(1)模型为例进行说明, 参考SAS程序如下。SAS程序II SAS program II
同SAS程序I(1) /* (1) */
ods RTF;
ods graphics on;
proc glimmix data=totalN; /* (2) */
class Rain N Block Core Times;
model y=Rain|N|times /ddfm = kr;
random Block Core(Rain N);
random _residual_/type=ANTE(1) sub=Core(Rain N);
lsmeans Rain N Times Rain*N Rain*Times N*times Rain*N*times/diff; /*(3) */
lsmestimate N*times "N1 vs N2 at times6" 1 0 0 0 0 0 0 -1; /* (4a) */
lsmestimate N*times "N1 vs N2 at times6" [1,1 1] [-1,2 1]; /* (4b) */
lsmestimate N*times "N2 in times6 vs times8" [1,2 1] [-1,2 3]; /* (5) */
lsmestimate N*times "N1 at times7 vs N2 at times9" [1,1 2] [-1,2 4]; /* (6) */
lsmestimate times "times8 vs times10" [1,3] [-1,5]; /* (7) */
lsmestimate N "N1 vs N2 " [1,1] [-1,2] ; /* (8) */
lsmeans N*times/plot=meanplot(sliceby=N join cl);/* (9) */
nloptions tech=nrridg;
run;
ods graphics off;
ods RTF close;
程序说明: 程序的开始部分读入数据, 代码同上文的程序I (1), 读者可拷贝粘贴。程序(2)以一阶前依赖协方差结构ANTE(1)模型进行F检验, 代码基本上同程序I (8)。输出结果主要包括拟合情况和F检验结果(表4)。语句(3)输出所有因子主效应及交互作用最小二乘均值及其差值的t检验结果, 由于输出内容庞大, 本例为83页文档, 许多内容我们不用关注。为了减少篇幅, 突出重点, 建议将该语句注释掉。利用特定的lsmestimate语句进行均值比较。用法可参阅文献[5]、文献[18]和查阅SAS帮助文档和文献[4]。
Table 4
表4
表4F检验结果(III型, ANTE1, 土柱试验)
Table 4
| 效应 Effect | 分子自由度 Numerator DF | 分母自由度 Denominator DF | F值 F-value | P值 P-value |
|---|---|---|---|---|
| Rain | 2 | 28.62 | 30.49 | <0.0001 |
| N | 2 | 28.62 | 22.89 | <0.0001 |
| Rain*N | 4 | 28.62 | 1.34 | 0.2806 |
| Times | 6 | 29.40 | 36.54 | <0.0001 |
| Rain*Times | 12 | 39.27 | 0.90 | 0.5509 |
| N*Times | 12 | 39.27 | 4.21 | 0.0003 |
| Rain*N*Times | 24 | 47.73 | 0.48 | 0.9725 |
新窗口打开|下载CSV
语句(4)检验第6次淋洗N1与N2处理全N淋失量差异显著性, 即进行特定时间两处理水平间的比较。语句(4a)和(4b)作用完全相同, 前者采用传统的定位式(positional)写法, 较为复杂; 后者采用新式的非定位式(non-positional)写法[18], 更为简单, 读者可以任选其一。语句(5)检验N2处理第6次淋洗与第8次淋洗全N淋失量差异显著性, 即特定处理随时间的变化差异; 语句(6)检验N1处理第7次淋洗与N2处理第9次淋洗全氮淋失量差异显著性, 即两处理水平在各特定时间点的差异, 由此可以找出最优处理组合; 语句(7)检验3种氮水平处理平均全氮淋失量, 第8次淋洗与第10次淋洗的差异显著性, 即所有处理平均随时间的变化差异是否显著; 语句(8)检验N1与N2在所有时间点平均, 全氮淋失量的差异显著性, 即两处理水平在所有时间点平均的差异, 输出结果见表5。读者可以根据需要, 进行其他处理组合间的差异显著性检验。
Table 5
表5
表5处理均值两两比较示例
Table 5
| 语句# Code # | 处理组合¶ Treatment ¶ | 差值 Difference | 标准误 SE | 自由度 DF | t值 t-value | Pr > |t| |
|---|---|---|---|---|---|---|
| (4a) | (1)定位法Positional | 8.05 | 4.32 | 17.85 | 1.87 | 0.0786 |
| (4b) | (1)非定位法Non-positional | 8.05 | 4.32 | 17.85 | 1.87 | 0.0786 |
| (5) | (2) | 10.94 | 3.19 | 20.36 | 3.43 | 0.0026 |
| (6) | (3) | 6.38 | 1.73 | 33.37 | 3.70 | 0.0008 |
| (7) | (4) | 0.94 | 0.60 | 31.51 | 1.58 | 0.1248 |
| (8) | (5) | 1.78 | 0.77 | 28.62 | 2.31 | 0.0285 |
新窗口打开|下载CSV
语句(9)以淋洗次数times为横坐标, 总氮淋失量为纵坐标, 输出类似图1的折线图。“sliceby=N”表示按N水平进行分类。Join将各点连成线。cl表示输出95%的置信区间(confident interval)。图1中误差线为标准误, 该语句输出的误差线为95%置信区间。NLOPTIONS语句是为了将 PROC GLIMMIX 的优化技术设置为与mixed 程序(Newton-Raphson算法)相同的技术[5]。
田间试验由于处理组合较少, 我们可以所有处理组合均值的差异输出, 不需要lsmestimate, 以VC结构为例, 仅需要在代码(12)的run之前增加如下语句:
lsmeans rate Time rate*Time/diff;
lsmeans rate*time/plot=meanplot(sliceby=rate join);
nloptions tech=nrridg;
由于采用极大似然分析, 缺区时自动按不等重复进行, 如本例中的缺区处理按2个重复进行计算, 代码不需要改动。
2 结果与分析
2.1 不同协方差结构模型引起的F检验结果差异
SAS程序I输出了F检验结果, 表2是对土柱试验数据7种协方差结构模型F检验结果的汇总。可以看出, 协方差结构模型对F检验的结果影响较大。降雨强度与施肥方式之间的交互作用(Rain*N)虽然P值都大于0.05, 但差异较大, 最低的为0.2375, 最高的为0.3161, 相差33.09%。降雨强度与淋洗次数之间的交互作用效应(Rain*Times) UN和ANTE(1)不显著, 而其余4种模型显示极显著。因此, 选用恰当的协方差结构模型进行F检验很关键, 否则有可能得出错误的结论。Table 2
表2
表2采用不同协方差结构模型时F检验P值(III型检验)
Table 2
| 效应 Effect | 方差分量 VC | 复合对称 CS | 不规则 UN | 空间幂相关 SP | 一阶自回归AR(1) | 循环相关 TOEP | 一阶前依赖ANTE(1) |
|---|---|---|---|---|---|---|---|
| Rain | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| N | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | 0.0001 | <0.0001 |
| Rain*N | 0.2375 | 0.2609 | 0.2809 | 0.3023 | 0.3023 | 0.3161 | 0.2822 |
| Times | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| Rain*Times | 0.0033 | 0.0038 | 0.6167 | 0.0059 | 0.0059 | 0.0172 | 0.5533 |
| N*Times | <0.0001 | <0.0001 | 0.0017 | <0.0001 | <0.0001 | <0.0001 | 0.0003 |
| Rain*N*Times | 0.8526 | 0.8537 | 0.9457 | 0.8584 | 0.8584 | 0.9225 | 0.9727 |
新窗口打开|下载CSV
2.2 协方差结构模型的优选
根据统计学理论, 选用协方差结构模型时, 可参考赤池信息准则(akaike information criterion, AIC)、为小样本修正的赤池信息准则(akaike information corrected criterion, AICC)、修正的赤池信息准则(corrected akaike information criterion, CAIC)、贝叶斯信息准则(bayesian information criterion, BIC)、汉南-奎因信息准则(hannan-quinn information criterion, HQIC)、-2残差对数似然值准则(-2 res log likelihood, -2logL)[1,4-5,15,17]等, 值越小表示拟合性越好, 如果相近, 可通过χ2检验[17]并结合试验本身的特点进行判断。另外, 协方差结构模型需要估算的参数个数越少越好。从表3可以看出, 土柱试验UN和ANTE(1)模型各准则值明显低于其余5种协方差模型的值, 应优先考虑。UN模型协方差矩阵中需要估算的参数个数在所有模型中最多, 为n(n-1)/2, n为重复测量次数, 计算时可能无法收敛, 估算无法完成[5]。本例中n=7, 参数个数为21个; ANTE(1)模型需要估算的参数为2n-1, 本例中为15。综合考虑, 选用ANTE(1)模型进行F检验和均值比较。Table 3
表3
表3不同协方差结构模型拟合性(土柱试验)
Table 3
| 准则 Criteria | 方差分量 VC | 复合对称 CS | 不规则 UN | 空间幂相关 SP | 一阶自回归AR(1) | 循环相关 TOEP | 一阶前依赖ANTE(1) |
|---|---|---|---|---|---|---|---|
| -2logL | 790.7 | 790.7 | 638.5 | 790.4 | 790.4 | 677.0 | 790.7 |
| AIC | 792.7 | 794.7 | 694.5 | 794.4 | 794.4 | 703.0 | 792.7 |
| AICC | 792.7 | 794.8 | 711.3 | 794.5 | 794.5 | 706.3 | 792.7 |
| BIC | 794.0 | 797.2 | 730.8 | 797.0 | 792.6 | 691.3 | 794.0 |
| CAIC | 795.0 | 799.2 | 758.8 | 799.0 | 794.6 | 704.3 | 795.0 |
| HQIC | 793.0 | 795.4 | 705.3 | 795.2 | 790.8 | 679.5 | 793.0 |
新窗口打开|下载CSV
田间试验结果显示, UN结构无法收敛, 无法计算拟合参数, 其余6种协方差结构模型均收敛。综合比较, VC结构模型最合适。
2.3 F检验结果
选用ANTE(1)模型并运用GLIMMIX对土柱试验数据进行F检验(SAS程序II), 结果见表4。可以看出, 区组间无显著差异。降雨强度(Rain)、施肥方式(N)和淋洗次数(Times) 3级交互作用(Rain*N* Times)效果不显著。二级交互作用效果降雨强度与施肥方式、降雨强度与淋洗次数不显著。施肥方式与淋洗次数之间的交互作用效果极显著(P<0.001), 主效应降雨强度、施肥方式、淋洗次数不同水平间差异达极显著水平(P<0.001), 因此有必须进一步分析。田间试验的F检验结果显示, 生物炭用量、取样时间以及他们的交互作用均达到极其显著水准(P<0.01)。
2.4 处理组合均值比较结果
根据F检验结果, 土柱试验数据仅仅需要对效应显著的均值进行显著性检验, 但为了让读者全面掌握重复测量数据均值比较的方法, 下面针对“1.2 分析比较”所提出的5种情况进行说明。表5是SAS程序II输出的结果汇总。可以看出, 5种比较都能进行。语句(4a)和(4b)所得结果完全一致, 说明采用传统的定位句法和新式的非定位句法[18]能达到同样的效果, 但后者不需要用“0”占位, 更直观简洁, 书写更方便, 尤其是一些比较复杂的比较[18], 因此建议使用新式的非定位句法。从表2可以看出, 第6次淋洗时, N2比N1的总氮淋失量低8.05 g (图1), 接近5%差异显著水准(P = 0.078), 此为特定时间(第6次淋洗)两处理水平(N1 vs. N2)间的比较; 语句(5)输出的结果表明, N2处理总N淋失量第6次比第8次淋洗高10.94 g, 差异达1%极显著水平(P = 0.0025), 我们还可以检验第6次与第8、9、10、11、12次淋洗的差异显著性, 也可以对其他时间进行差异显著性比较, 确定总N淋失量随时间的变化规律。语句(6)输出的结果表明, N1第7次淋洗比N2处理第9次淋洗全氮淋失量多6.38 g氮(表5和图1), 差异极显著(P = 0.0008)。可以继续进行两处理水平在各特定时间点的差异比较, 找出最优处理组合。
语句(7)输出结果表明, 3种氮水平平均全氮淋失量第8次与第10次淋洗相差0.94 g, 未达到5%差异显著水平。由于N*Times交互作用效果显著, 这种比较并不合适, 此处仅仅用来说明方法。语句(8)输出的结果表明, 所有淋洗平均全氮淋失量N2比N1处理低1.78 g, 差异达5%显著水平。同样原因, 这种比较在此例中不合适, 仅用于方法说明。田间试验均值间比较思路类似, 不再赘述。
3 讨论
3.1 混合效应模型
固定效应是研究几个样本是否来自于同一个总体的推断。随机效应是由2个或多个总体分别抽出的几个样本, 用这些样本去研究总体是不是相同的推断。如果一个模型中既包括固定效应, 又包括随机效应, 为混合效应模型[5]。本研究中, 3种降雨强度、3种施肥处理、不同测定时间以及它们的交互作用均为固定效应。区组为随机效应。重复测量中的受试对象(小区)是总体中的样本, 拟通过比较这些样本经过不同处理后重复测量的效应, 以便推论到其所代表的总体中去, 因此重复测量中受试对象效应为随机效应。对象变异包括对象内变异和对象间变异, 重复测量试验不同对象间一般是相互独立的, 但对同一对象不同时间点的测定几乎总存在相关性, 间隔越近相关性越强, 因此, 重复测量不满足一般线性模型方差分析对变量独立性的要求。混合模型既考虑了固定效应, 也考虑了随机效应, 对于重复测量数据, 通过预先指定协方差结构模型, 能够很好地进行重复测量数据的统计分析[3-5,15], 此在本例中也得到了验证。
除了用GLIMMIX进行重复测量的数据分析外, 也可以用mixed程序进行。前者是SAS公司后来开发的程序, 比mixed功能更强大, 例如, 能直接输出类似图1的图; 进行均值比较时, 编写代码更简单[5]。
3.2 用于重复测量方差分析的协方差结构模型
选用适当的协方差结构模型对于重复测量数据的统计分析至关重要。忽视重复测量数据间的相关性而采用过于简单的协方差模型, 会导致标准误偏低, 处理效应会犯I型错误; 而模型过于复杂, 检验效能会受到严重影响[1,3,19]。早已有研究表明, 重复测量分析结果会因协方差模型选择不当而严重受损[19]。尽管特定数据集的真实协方差结构鲜为人知, 但必须指定接近的协方差模型才能获得可靠的结果。Guerin等[20]的研究表明, 只要选择合适的协方差结构, 采用混合模型进行重复测量的统计分析总能得到正确的结果。SAS软件提供了30多种协方差结构模型[4], 读者可以根据需要选用。本例通过方差分量结构(VC)等7种结构进行模拟。VC又称简单方差结构, 他假定同一对象各时间点重复测量值相互独立, 在协方差矩阵中主对角线元素均为σ2, 其他为0 (图2), 该结构仅有一个参数σ需要估算[5]。然而, 这种情况在重复测量试验中极少出现。
图2
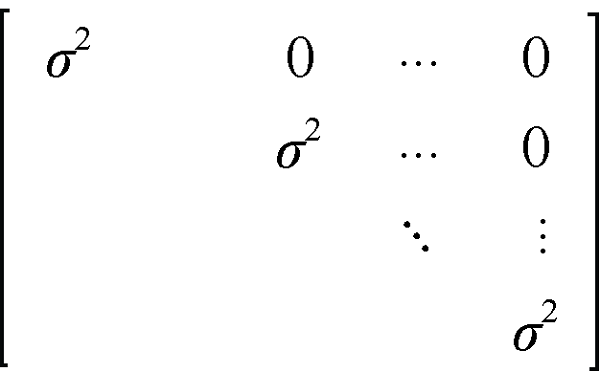新窗口打开|下载原图ZIP|生成PPT图2方差分量结构
Fig. 2Variance components
复合对称结构(compound symmetry, CS)主对角线元素为σd2+σe2, 其他为σd, 这里σd为对象间方差, σe为对象内方差, 需要对这2个参数进行估计。对于重复测量数据, 这是最简单的方差结构。它假定不同重复测量点数据之间具有恒定的相关性, 与重复测量点之间的距离无关。过去, 我们对重复测量试验数据进行球型检验(H-F检验), 如果满足就可以把重复测量因素当成裂区设计来进行方差分析[9,21-22], 实际上就是检验协方差是否与测量距离有关。如果检验未通过, 为了减少犯I类错误的几率, 常常采用校正的方法, 但这些方法的可靠性仍然不高, 更可靠的办法是采用恰当的协方差结构, 按照一般线性混合模型的方法进行分析。在重复测量农业试验中, 能满足复合对称结构条件的情况不多, 除非重复测量之间的时间距离特别长, 影响可以忽略不计。
一阶前依赖结构[ANTE(1)]允许不同重复测量点间的方差不同, 以及不同测量点对之间相关性和协方差不等。此很符合本研究的实际情况, 在所有协方差结构模型中, 该模型最优(表3), 进一步证实了该模型的实用性。使用ANTE(1)时, 测量点必需要按先后顺序正确排列, 但各测量点之间时间间隔不必相等。这也很符合一般作物类试验的实际情况。本研究中对不规则(UN)、空间幂相关[SP(POW)]、一阶自回归[AR(1)]、循环相关(TOEP)等协方差结构模型进行了尝试, 限于篇幅, 此处不进行深入讨论。有兴趣的读者请参阅文献[1]、[5]、[15]和[19]。
选择协方差结构模型时, 首先应排除明显无意义的协方差结构。如田间试验中, 同一小区不同时间重复测量数据一般具有相关性, VC模型不合适, 应排除。对于时间间隔不等的情况, AR(1)结构肯定不合适[1]。下一步, 可以以时间间隔为横坐标, 以对象内协方差为纵坐标作图, 考察协方差的变化规律, 初步判定合适的协方差结构。最后, 查看如表3所示的拟合性信息, 必要时进行卡方检验, 确定最合适的协方差结构。
3.3 与裂区设计方差分析或多变量方差分析的比较
在进行重复测量数据的统计分析时, 许多教材和学术论文中主要采用以下4种方法。(1)在各时间点分别进行F检验和均值比较, 该方法孤立地看待各时点的数据, 完全忽视了时间因素, 没有充分利用观察对象在不同观察时点间的内在联系, 无法发现随时间变化的趋势。在农业类等已发表的论文中非常普遍[11,23-25], 是对信息资源的极大浪费[26]。(2)裂区设计分析法, 把重复测量因子作为副区因子, 把不同时间点视为副处理水平进行分析[3,9,12], 该方法需要满足球对称条件[21,22], 即满足复合对称协方差结构的条件。在农业试验中, 协方差会随时间间隔的大小发生变化, 条件很难满足, 采用此方法会增大犯 I 类错误的概率[1,4-5,12,27]。虽然可以进行校正, 但结果往往不理想, 甚至会得出错误的结论[13], 且该方法没有触及协方差不等的实质, 而是对问题进行了回避, 没有从根本上解决问题[3,15]。(3)多变量统计分析法, 该方法对重复测定各时间点的相关性要求不高, 仅要求每对时点间的相关性唯一, 但采用该方法分析重复测量数据会浪费大量信息, 损失统计功效。另外, 如果受试对象即使只有一个时间点的数据缺失(此在农学类试验中常常出现), 也必须删除该对象的全部数据, 造成信息的不完整[8,15], 该方法也是回避了不同时间点数据有相关性的问题, 不是一个理想的方法[13]。(4)混合模型(mixed)分析法, 该方法直接处理重复测量中数据的相关性问题[5], 允许不同时间点数据存在相关性, 不必对自由度进行校正, 可以处理缺值问题, 允许时间点不等距[4,11,28], 完全符合重复测量试验的特点, 是一种理想的方法。通过事先指定一个恰当的协方差结构, 根据此结构计算各处理水平的最小二乘均值及其差值。协方差结构不同, 均值和标准误计算结果也不同, 尤其是对非平衡设计[29]。广义线性混合模型(GLIMMIX)是近年来SAS在mixed模型的基础上开发的程序模块, 是对mixed的扩展和改善, 均值间比较的句法更简单, 能很方便的输出图形等[5], 正如本例所示, 是目前进行重复测量数据统计分析的有力工具, 为重复测量数据分析提供了极大方便。
4 结论
重复测量试验对同一对象进行多次观测, 各数据点之间存在自相关性。用传统的裂区设计、多变量方差分析会造成数据的信息浪费、统计功效降低、缺区无法处理等问题, 甚至会导致错误的结论。广义线性混合模型GLIMMIX能很好地处理相关性问题, 功能强大, 结构可靠性高, 使用简单, 允许缺区, 是进行重复测量试验数据方差分析和均值比较理想的方法, 值得推广运用。参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 7]
[本文引用: 2]
[本文引用: 6]
URL [本文引用: 9]
[本文引用: 15]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[J]
[本文引用: 2]
[本文引用: 3]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 3]
[本文引用: 3]
[本文引用: 3]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 6]
[本文引用: 1]
[本文引用: 3]
[本文引用: 3]
[本文引用: 4]
[本文引用: 3]
In: Stroup W W eds. Proceedings of the 12th Annual Conference on Applied Statistics in Agriculture.
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
