直接瞬时转矩控制(DITC)是近年来提出的一种新的SRM转矩控制方法[10]。该方法主要是针对被控SRM,预先测得“电流-转子位置-转矩”的非线性映射关系,通过实时电流和转子位置信号确定瞬时转矩进行反馈控制,从而使总输出转矩维持恒定。文献[11]针对SRM调速系统存在的外部负载扰动和未知参数波动问题,提出了基于最小学习参数的直接自适应神经网络控制算法的DITC方法,实现SRM高品质调速控制。文献[12]针对无轴承SRM具有双凸极结构、转矩脉动大的问题,采用DITC和直接悬浮力控制(DFC)方法有效抑制其转矩脉动。文献[13]针对SRM DITC系统速度外环控制器中存在非线性饱和、控制器的积分控制环节会对误差进行积累并逐渐使误差增大的问题,提出一种抗饱和自适应PID控制器,提高了电机速度响应,降低转速脉动,系统稳定性和鲁棒性较好。文献[14]针对SRM在换相阶段由于转矩特性、电压限制、转速升高等因素而引起的转矩脉动问题,研究一种基于转矩分配函数(TSF)在线修正的DITC方案,实现电机在换相阶段总转矩脉动的抑制。可知,DITC不但能抑制电机的转矩脉动,而且实际控制系统的设计更为简单直接,但实践表明,常规的DITC还存在一些不足,如换相区转矩脉动过大,起动阶段电流过大。
本文对传统的DITC进行改进,提出了一种基于最优角度自适应TSF的SRM DITC方法,改进思路如下:针对换相区转矩脉动大,引入余弦型TSF,由于TSF与开关角和转子位置相关,基于BP神经网络强大的学习能力,设计了最优角度模块,以此获得任意转速下的最优开关角,将最优开关角导入TSF中,实现根据转速动态调整函数形状的自适应TSF,从而得到各相最优的参考转矩,实现对相转矩的精确控制,以此达到抑制转矩脉动的效果。同时TSF将转矩分配到各相,可以避免为了跟踪给定转矩而造成的相电流过大的问题,有效提升了系统的运行效率。
1 改进型DITC系统设计 1.1 控制系统总体设计 如图 1所示,改进型DITC系统由转速环、转矩计算模块、滞环控制器、功率变换器、自适应余弦型TSF、最优角度模块和SRM本体组成。图 1中,ωref为给定转速,ω为实时转速,T*为参考转矩,TA*、TB*、TC*分别为相参考转矩,θon、θoff分别为最优开通、关断角,θ为转子位置,TA、TB、TC分别为相瞬时转矩,SA、SB、SC分别为各相控制信号,i为定子电流。
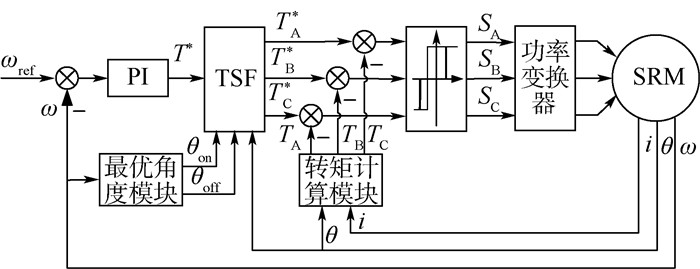 |
| 图 1 基于最优角度TSF的SRM DITC系统框图 Fig. 1 Block diagram of SRM DITC system based onoptimal angle TSF |
| 图选项 |
该系统增加了TSF,以转矩脉动最小化为目标,分别对不同转速情况进行仿真,得到不同转速下转矩脉动最小时对应的最优开关角。将得到的最优开关角输入到自适应TSF中,可以使得各相电流变化更加平稳,降低换相区转矩脉动。
1.2 自适应余弦型TSF设计 常规的DITC是以合成转矩为反馈量,通过与总参考转矩作差产生控制信号,实现对电机的控制。由于总参考转矩比相参考转矩大,为了有效跟踪总参考转矩,通常需要给相绕组输入较大的有效电流,这不仅会在一定程度上降低系统运行效率,同时会造成换相时转矩脉动变大。针对此问题,本文在传统的DITC系统基础上引入自适应余弦型TSF,在电机运行过程中,将总参考转矩分配到各相,与各相的实时反馈转矩作差产生控制信号,各相协同输出转矩,维持电机运行。
自适应余弦型TSF是在余弦型TSF的基础上进行改进,余弦型TSF曲线如图 2所示。图 2中:θ1为当前相导通并且前一相完全关断的转子位置角,θ2为当前相完全关断并且后一相独立导通的转子位置角。可以看出,余弦型TSF严格遵循同一时刻各相TSF具体数值总和等于1的要求。余弦型TSF主要分为3个部分:第1部分是θon≤θ≤θ1,此时当前相按fk(θ)分段函数从0增加到1,而前一相则按fk(θ)逐渐减小至0。第2部分是θ1≤θ≤θoff,此时只有当前相进行导通,前一相和后一相均属于关断状态。第3部分是θoff≤θ≤θ2,此时当前相按fk(θ)分段函数逐渐减小至0,后一相按照逐渐从0增加至1。可以看出,余弦型TSF比较接近SRM各相转矩的实际变化情况。为使换相区的转矩变化更加平滑,本文设计了自适应余弦型TSF,如下:
 | (1) |
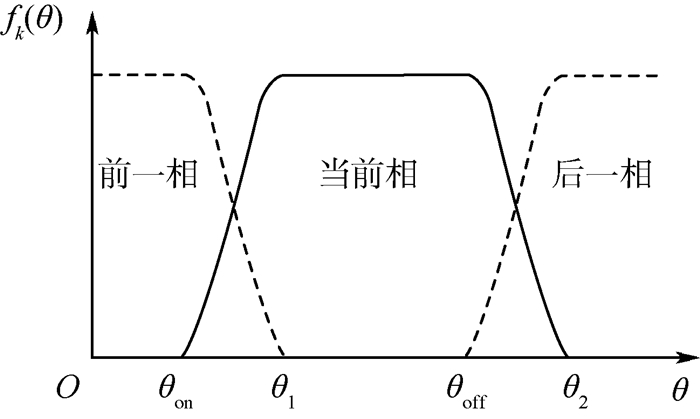 |
| 图 2 余弦型TSF曲线示意图 Fig. 2 Schematic diagram of cosine-type TSF curve |
| 图选项 |
式中:θon和θoff分别为最优开通角和关断角,随着转速变化而变化。求解转矩脉动取最小值时不同转速对应的开通角和关断角,并输入到自适应余弦型TSF中,不同转速下对TSF曲线形状进行调整,从而实现降低换相区转矩脉动的目的。
1.3 最优开通关断角模块设计 DITC是根据参考转矩与实际转矩的转矩差并结合开关角按照一定的规则对空间电压矢量进行控制,从而实现对功率变换器IGBT的控制,因此,设计合理的开关角非常重要。
以转矩脉动最小化为目标,通过离线开关角寻优方式,在0~1 000 r/min范围内,每隔100 r/min共选取10个转速。考虑到在改变开通角θon时,会对电流波形的峰值和有效值产生影响,并会改变电流波形和电感波形的相对位置。而改变关断角θoff会影响电流波形的宽度及其与电感曲线的相对位置。如果不考虑开通角关断角的变化,一般取θon=0°,θoff=30°,为了能在最大范围内选取最优的开关角,其取值范围应该包括整个角度周期,因此设置θon的取值范围为-15°~15°,θoff的取值范围为15°~45°。每隔1°进行仿真以获得最优开关角,进而得到在各转速下转矩脉动最小时对应的最优开关角,如表 1所示。
表 1 不同转速下开关角寻优结果 Table 1 Switching angle optimization results at different rotation speeds
| 转速/(r·min-1) | θon/(°) | θoff/(°) | 转矩脉动 |
| 100 | -3.0 | 40 | 0.117 |
| 200 | -2.9 | 36.8 | 0.112 |
| 300 | -2.8 | 36 | 0.117 |
| 400 | -2.8 | 35 | 0.114 |
| 500 | -2.8 | 34 | 0.109 |
| 600 | -3.9 | 33 | 0.107 |
| 700 | -5.7 | 31.5 | 0.109 |
| 800 | -6.8 | 31 | 0.105 |
| 900 | -7.2 | 30.6 | 0.100 |
| 1 000 | -7.9 | 28.4 | 0.097 |
表选项
表 1中的最优开关角只是离散的数据,不能覆盖整个转速范围。为了获得全速范围内的最优开关角,采用BP神经网络对离散的最优开关角进行学习。因为BP神经网络[15]存在易陷入局部最小值和收敛速度慢的缺点,因此在传统的BP神经网络上增加了附加动量和自适应学习率[16],其学习过程如图 3所示。
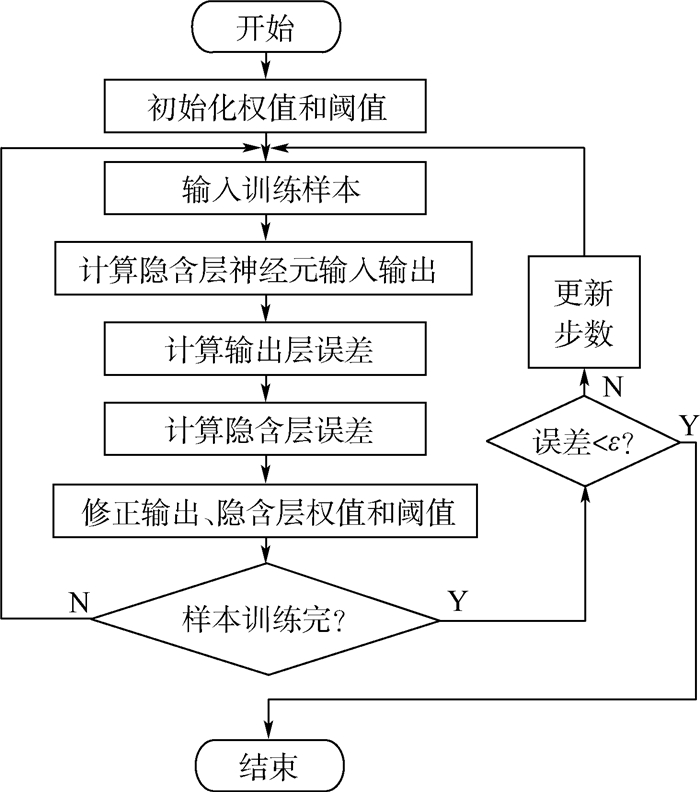 |
| 图 3 BP神经网络学习流程 Fig. 3 Flowchart of BP neural network learning |
| 图选项 |
在误差逆传播过程中,仅仅考虑在误差负梯度方向修改权值则容易陷入局部极值。因此增加了附加动量,增加前一项权值对本次权值的影响,如下:
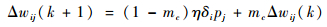 | (2) |
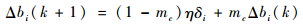 | (3) |
式中:δi为残差;pj为输出层第j个节点的输出误差;k为训练次数;Δwij为隐含层第i个节点到输入层第j个节点之间的权值修正量;Δbi为隐含层第i个节点的阈值修正量;η为学习速率;mc为动量系数,mc限制条件如下:
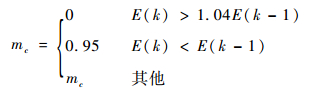 | (4) |
其中:E(k)为第k步误差平方和。
固定的BP神经网络学习速率并不适用于训练的全部阶段,在训练的前期、中期和后期都需要设置不同的学习速率,从而提高训练速度。因此采用自适应学习速率,若修正后的权值使得误差增大,说明学习速率η较大,应降低η,反之则增大此值。具体调整如下:
 | (5) |
由式(5)可知,在一定范围内进行调整,与固定学习速率相比,初始学习速率η(0)的选取对结果影响较小。
通过上述方法对传统的BP神经网络进行改进,将其应用于SRM以转矩脉动最小化为目标的最优开关角训练,训练效果如图 4所示。将训练完成的映射关系导入到Simulink之中,建立最优角度模块。
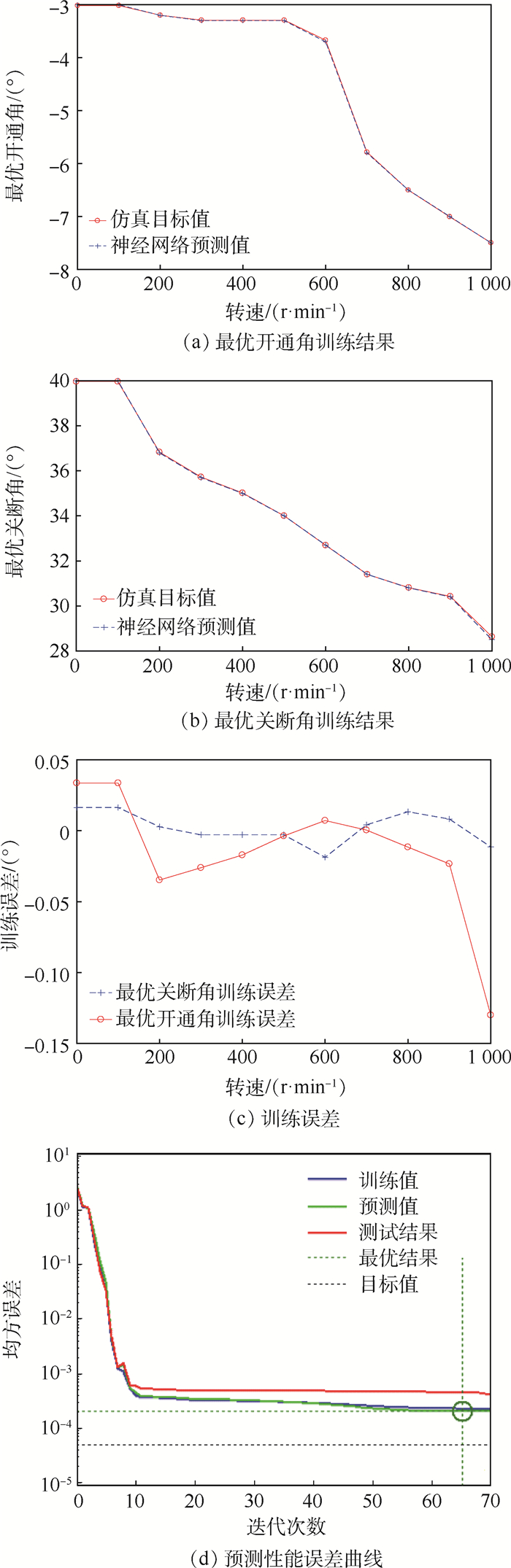 |
| 图 4 BP神经网络最优开通角和关断角训练结果 Fig. 4 Training results of BP neural network on optimal turn-on angle and turn-off angle |
| 图选项 |
1.4 转矩解算模块设计 SRM的转矩与转子位置角、相电流有关,即T(i,θ)。在基于TSF的DITC控制系统中,需要将各相实时转矩作为反馈量与经TSF分配之后的各相参考转矩进行比较,产生控制信号,而相转矩在实际工程中很难直接测得,因此本文通过有限元仿真,获得SRM静态转矩特性数据,将该数据导入到MATLAB中建立转矩特性表格,通过查表法根据实测电流和转子位置获得电机的实时相转矩。SRM的转矩特性如图 5所示。
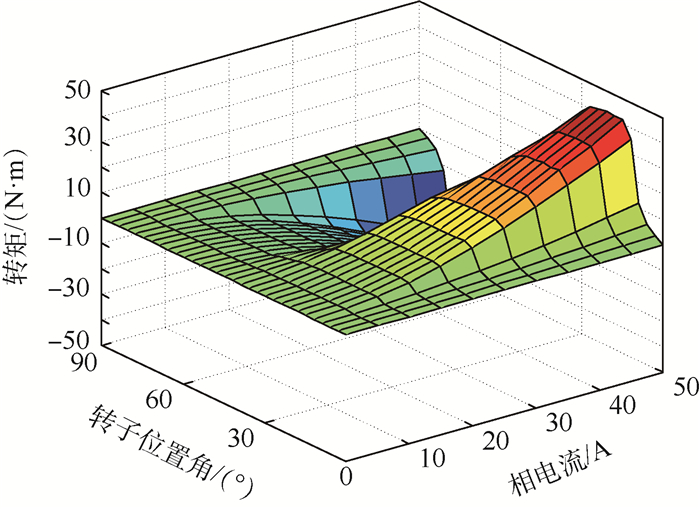 |
| 图 5 SRM的转矩特性曲线 Fig. 5 Torque characteristic curves in SRM |
| 图选项 |
2 仿真分析 基于MATLAB/Similink建立SRM调速系统仿真模型,电机本体模型利用查表法建立,将有限元软件Ansoft计算得到的磁链ψ(θ,i)和转矩T(θ,i)数据导入Lookup Table (2D)模块,完成电机非线性建模[17]。DITC系统结构如图 1所示。SRM本体结构参数如表 2所示。
表 2 SRM模型参数 Table 2 Parameters of SRM model
| 参数 | 数值 |
| 定子/转子极 | 6/4 |
| 额定功率/kW | 3 |
| 额定转速/(r·min-1) | 1 000 |
| 定子外径/mm | 135 |
| 定子内径/mm | 75 |
| 铁芯长度/mm | 123.5 |
| 转子外径/mm | 74.5 |
| 转子内径/mm | 30.5 |
表选项
为了对改进型DITC方法的性能进行验证,选择常规DITC控制系统作为比较对象进行仿真。设定电机转速为1 000 r/min,负载转矩为10 N·m,分别采用2种不同的控制方法对电机进行控制,当电机稳定运行时,其仿真结果如图 6和图 7所示。
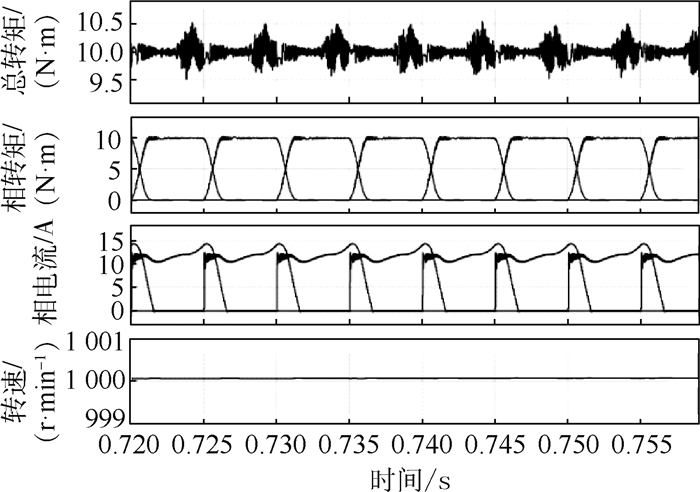 |
| 图 6 稳定运行时改进型DITC仿真图 Fig. 6 Parameters of SRM model |
| 图选项 |
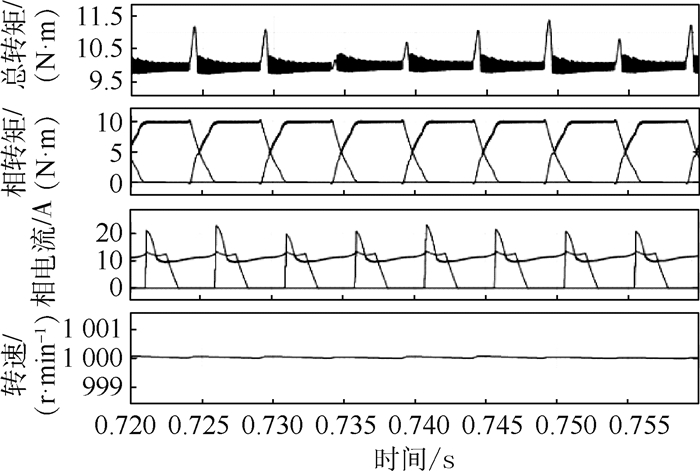 |
| 图 7 稳定运行时常规DITC仿真图 Fig. 7 Conventional DITC simulation diagram for stable operation |
| 图选项 |
通过仿真结果可知,改进型DITC相比常规DITC,对于换相过程中电机的转矩脉动具有很好的抑制作用。同时在换相过程中,相电流尖峰明显下降,各项电流分布更加平缓,使相电流有效值降低,从而有效提升了电机运行效率。通过对仿真结果的计算分析,表 3中给出了不同控制方式下SRM的相关性能数据。
表 3 不同控制方式性能对比 Table 3 Performance comparison of different control methods
| 控制方式 | 转矩脉动 | 相电流均方值/A |
| 常规DITC | 0.17 | 8.463 |
| 改进型DITC | 0.10 | 7.564 |
表选项
由表 3可知,改进型DITC控制方式在抑制转矩脉动和提高系统效率方面都表现出更优异的性能,相比常规DITC方式,转矩脉动减少41.2%,相电流均方值减少10.6%。电机的效率计算公式为
 | (6) |
式中:U为绕组端电压;I为绕组电流;R为绕组电阻;Pmech为电机的输出功率;Pe为输入功率;Tav为输出平均转矩;ω为角速度;E=dψ/dt。经过计算,在改进型DITC和常规DITC方式下,Tav分别等于10 N·m和9.996 N·m,两者基本相等,又因为在电机稳定运行时,在2种控制方式下电机转速都为1 000 r/min,所以角速度ω相同,因此电机输出功率基本相同。由式(6)可知,输入功率和相电流有效值呈反比关系,相电流有效值越大,输入功率越大,电机效率越低。由表 3可知,改进型DITC相比常规DITC,电流有效值减小10.6%,因此电机效率至少提高10.6%。综上证明,本文设计的基于TSF的SRM DITC系统有效。
3 实验结果与分析 为验证改进型DITC方法的可行性,依托实验已有三相6/4极SRM,搭建了改进型DITC实验平台。平台主要包括SRM样机、控制电路、检测电路和负载电机。样机参数和仿真实验一致,如表 1所示。控制器采用TMS320F2812型DSP芯片,载波频率为9.6 kHz,转子位置检测由线光电位置传感器测得,合成转矩测量采用动态旋转扭矩传感器测得,最大可测转矩为20 N·m,误差≤0.5%,负载采用磁粉制动器。实验平台如图 8所示。
 |
| 1—仿真器;2—DSP控制板;3—显示按键板;4—DC电源;5—驱动板;6—霍尔电流传感器;7—TDS2012C示波器;8—SRM。 图 8 实验平台 Fig. 8 Experimental platform |
| 图选项 |
图 9给出了电机空载稳定运行时的相电压波形。由于TDS2012C示波器是双通道的,受实验设备限制,只能同时测量两相电压波形。从实验结果可以看出,该电压波形包括正电压、负电压和零电压3种状态,符合DITC控制的实际情况。
 |
| 图 9 两相电压波形 Fig. 9 Two-phase voltage waveform |
| 图选项 |
图 10给出了电机空载稳定运行时,单相绕组的电压和电流波形。可以看出,当相绕组开通时,其承受正向电压,此时绕组电流开始上升。当绕组关断时,电机承受反向电压直至续流结束至电压为零,此时绕组电流逐渐减小,并最终为零。相电流波形和仿真波形形状基本相同。
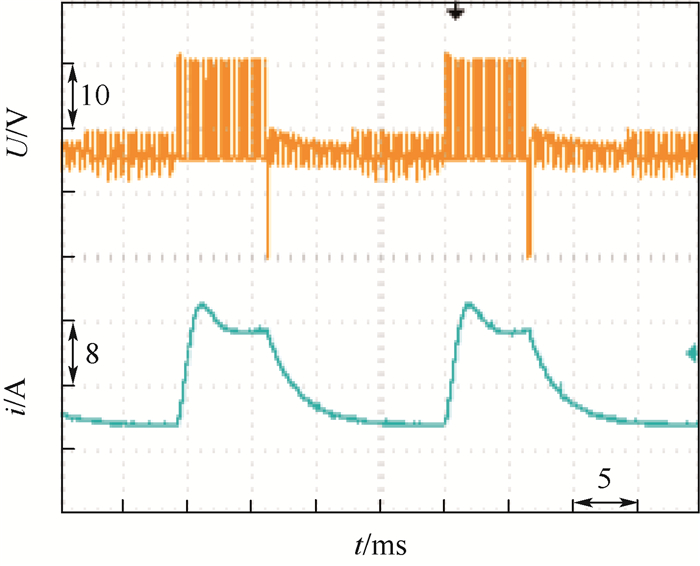 |
| 图 10 单相电压和电流波形 Fig. 10 Single-phase voltage and current waveforms |
| 图选项 |
图 11给出了电机空载稳定运行时,单相电流、电压和驱动信号的波形。可以看出,驱动信号和电压、电流协调一致的变化。通过以上对电压、电流和驱动信号的测量,充分验证了平台的有效性和本文所提控制方法的可行性。
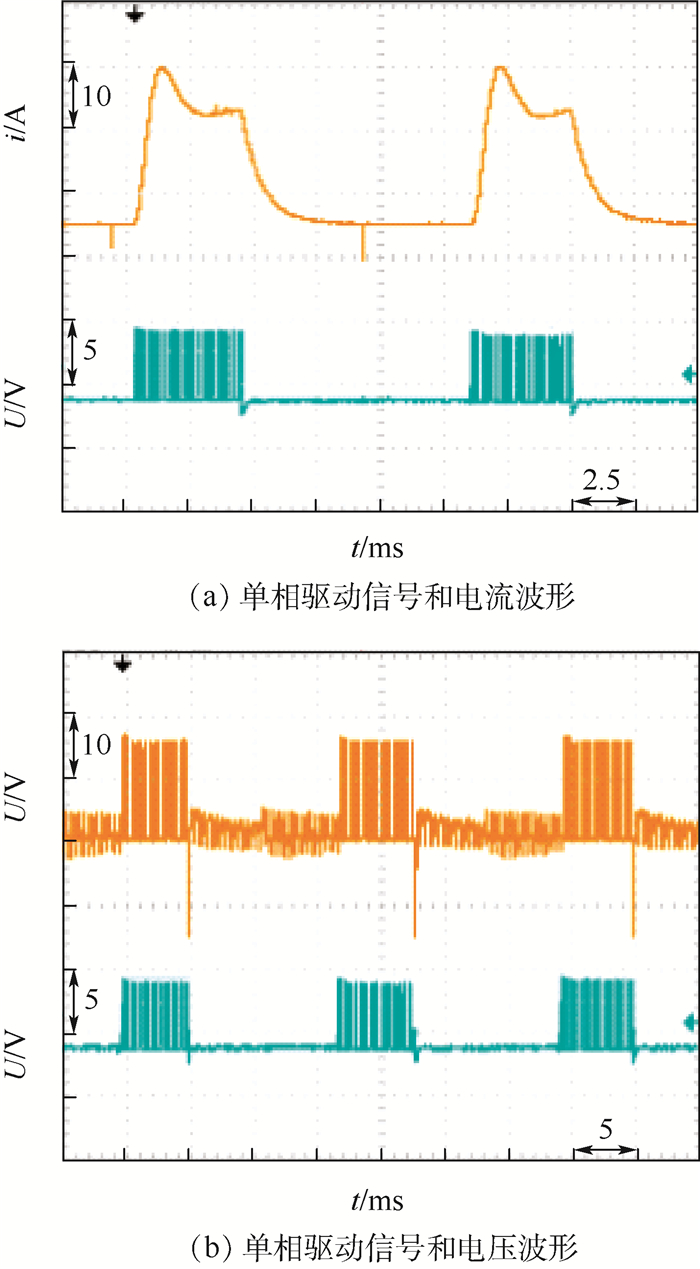 |
| 图 11 单相驱动信号和电压电流波形 Fig. 11 Single-phase driving signal and voltage and current waveforms |
| 图选项 |
由于改进型DITC和常规DITC的差别主要体现在TSF上,而TSF主要是通过算法编程来实现,硬件电路并无差别。因此本文在已搭建的实验平台基础上,分别编写了不同的控制算法,以此对比验证2种控制方法对电机转矩脉动的控制效果。由于电机转矩不能直接通过示波器进行测量,因此本文通过数据采集卡采集转矩数据,利用虚拟仪器绘制转矩波形图,如图 12所示。
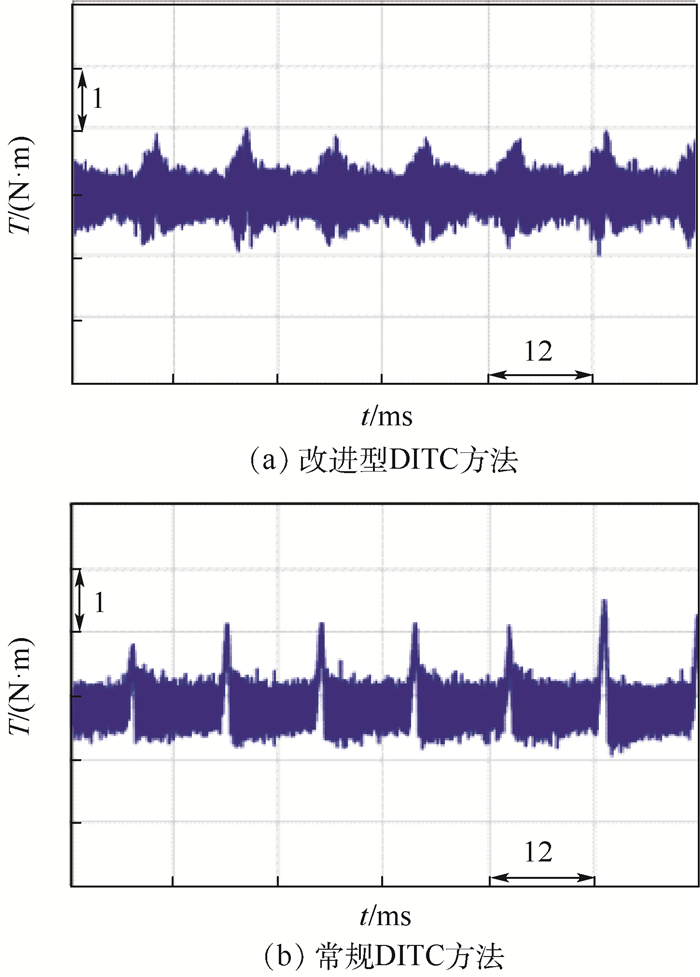 |
| 图 12 不同控制方法的转矩波形 Fig. 12 Torque waveform corresponding to different control methods |
| 图选项 |
从实验结果可以看出,在采用改进型DITC方法时,电机输出转矩在9.1~10.8 N·m之间波动,小于采用常规DITC方法的9.2~11.6 N·m,使转矩脉动减小了29.2%,对于电机的转矩脉动起到很好的抑制作用,验证了本文所提方法的有效性。
4 结论 本文针对常规DITC方法存在的换相区转矩脉动过大的问题,设计了基于最优角度的自适应TSF,建立了改进型DITC控制系统,通过建模仿真和实验分析,得出以下结论:
1) 本文所设计的改进型DITC控制系统,在电机换相区间,减小了相电流有效值,提升了系统运行效率,同时对电机换相区间的转矩脉动具有很好抑制效果。
2) 增加附加动量和自适应学习率后,BP神经网络的数据预测误差更小。训练完成的BP神经网络能够对以转矩脉动最小化为目标的不同转速下的最优开关角进行有效预测。
3) 本文提出的基于最优角度TSF的SRM DITC方法,对于SRM系统的转矩控制具有很好效果。
参考文献
| [1] | 杨晴晴, 张兴, 马铭遥, 等. 提高开关磁阻电机数字电流控制性能的方法[J]. 中国电机工程学报, 2018, 38(14): 4252-4261. YANG Q Q, ZHANG X, MA M Y, et al. Improving digital current control performance of switched reluctance motor drive[J]. Proceedings of the CSEE, 2018, 38(14): 4252-4261. (in Chinese) |
| [2] | LABIOD C, SRAIRI K, MAHDAD B, et al. A novel control technique for torque ripple minimization in switched reluctance motor through destructive interference[J]. Electrical Engineering, 2017, 100(9): 1-10. |
| [3] | MARCSA D, KUCZMANN M. Design and control for torque ripple reduction of a 3-phase switched reluctance motor[J]. Computers & Mathematics with Applications, 2017, 74(1): 89-95. |
| [4] | 朱叶盛, 章国宝, 黄永明. 基于PWM的开关磁阻电机直接瞬时转矩控制[J]. 电工技术学报, 2017, 32(7): 31-39. ZHU Y S, ZHANG G B, HUANG Y M. PWM-based direct instantaneous torque control of switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 31-39. (in Chinese) |
| [5] | 刘勇智, 鄯成龙, 林博闻, 等. 基于自适应二阶终端滑模的SRM直接转矩控制[J]. 北京航空航天大学学报, 2018, 44(10): 2043-2051. LIU Y Z, SHAN C L, LIN B W, et al. Direct torque control of switched motor based on adaptive second-order terminal sliding mode[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(10): 2043-2051. (in Chinese) |
| [6] | 王喜莲, 许振亮. 基于PI参数自适应的开关磁阻电机调速控制研究[J]. 中国电机工程学报, 2015, 35(16): 4215-4223. WANG X L, XU Z L. Speed regulation control of switched reluctance motors based on PI parameter self-adaptation[J]. Proceedings of the CSEE, 2015, 35(16): 4215-4223. (in Chinese) |
| [7] | 花为, 华浩, 赵桂书, 等. 一种用于电动自行车的高性能开关磁阻电机系统[J]. 南京航空航天大学学报, 2014, 46(1): 37-43. HUA W, HUA H, ZHAO G S, et al. High-performance switched reluctance machine for electric bicycle[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2014, 46(1): 37-43. DOI:10.3969/j.issn.1005-2615.2014.01.005 (in Chinese) |
| [8] | 王旭东, 王喜莲, 王炎, 等. 开关磁阻电动机电流双幅值斩波控制[J]. 中国电机工程学报, 2000, 20(4): 83-86. WANG X D, WANG X L, WANG Y, et al. Double amplitude chopping control of switched reluctance motor[J]. Proceedings of the CSEE, 2000, 20(4): 83-86. DOI:10.3321/j.issn:0258-8013.2000.04.018 (in Chinese) |
| [9] | HAN S, LIU C, LEI Z, et al.Mutual coupling and its effect on current and torque of six phases switched reluctance motor[C]// Eleventh International Conference on Ecological Vehicles & Renewable Energies.Piscataway, NJ: IEEE Press, 2016: 16005657. http://www.researchgate.net/publication/303513570_Mutual_coupling_and_its_effect_on_current_and_torque_of_six_phases_Switched_Reluctance_Motor |
| [10] | YAO S, WEI Z. A simple strategy for parameters identification of SRM direct instantaneous torque control[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3622-3630. DOI:10.1109/TPEL.2017.2710137 |
| [11] | 李存贺, 王国峰, 李岩, 等. 开关磁阻电机直接自适应神经网络控制[J]. 电机与控制学报, 2018, 22(1): 29-36. LI C H, WANG G F, LI Y, et al. Direct adaptive neural network control of switched reluctance[J]. Electric Machines and Control, 2018, 22(1): 29-36. (in Chinese) |
| [12] | 张蕾, 曹鑫, 邓智泉, 等. 一种单绕组无轴承开关磁阻电机绕组开路故障容错控制策略[J]. 电工技术学报, 2018, 33(15): 3564-3571. ZHANG L, CAO X, DENG Z Q, et al. A fault-tolerant control strategy for open circuit in single-winding bearingless switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3564-3571. (in Chinese) |
| [13] | 秦晓飞, 刘杰, 李峰. SRM直接瞬时转矩系统抗饱和控制器设计[J]. 系统仿真学报, 2017, 29(12): 3160-3167. QIN X F, LIU J, LI F. Design of anti-windup controller for SRM direct instantaneous torque system[J]. Journal of System Simulation, 2017, 29(12): 3160-3167. (in Chinese) |
| [14] | WU J H, SUN Q G. Torque ripple minimization for switched reluctance motorsby online modification of torque sharing function[J]. Electric Machines and Control, 2017, 21(12): 1-8. |
| [15] | REN T, SHI L, YAN G, et al. Temperature prediction of the molten salt collector tube using BP neural network[J]. IET Renewable Power Generation, 2016, 10(2): 212-220. DOI:10.1049/iet-rpg.2015.0065 |
| [16] | JIANG L, ZHANG J, XUAN P, et al. BP neural network could help improve pre-miRNA identification in various species[J]. Biomed Research International, 2016, 2016: 1-11. |
| [17] | 丁文, 梁得亮, 鱼振民, 等. 基于磁链与转矩特性的开关磁阻电机建模研究[J]. 西安交通大学学报, 2007, 41(2): 214-218. DING W, LIANG D L, YU Z M, et al. Modeling for switched reluctance motor based on flux linkage and torque characteristics[J]. Journal of Xi'an Jiaotong University, 2007, 41(2): 214-218. DOI:10.3321/j.issn:0253-987X.2007.02.019 (in Chinese) |
