为保证航班准点率,航空公司多采用正点推出策略。但随着航班数量的增加,大型枢纽机场在高峰时段易产生拥堵,滑行和排队时间大大增加。为此,****们提出了机位等待策略。Carr基于机场观测数据采用N-control理论,在场面拥挤时,令超出给定控制阈值的航班在停机位等待,当场面拥挤状态下降到阈值以下时,立即给机位等待的航班发出推出指令[1]。Atkin等研究了离港航空器跑道端等待的虚拟队长,分析了在拥堵机场采用机位等待策略的经济效益[2]。Ravizza等提出了一种更贴近实际运行的滑行时间预测方法,采用机位等待策略对欧洲典型枢纽机场瑞士苏黎世机场进行实例仿真,研究结果表明机位等待策略可最多减少约30.3%的总滑行时间,有效减少了滑行阶段的油耗和污染物排放[3]。赵向领等将机位等待策略和虚拟队列相结合,通过构造虚拟队列以控制航班推出率,进而缓解场面拥堵并减少油耗和排放[4]。航空器滑行策略优化也是扩大滑行道系统容量和缓解拥堵的重要途径之一。传统的航空器滑行策略优化模型多以最小总滑行时间、最小延误时间等为优化目标,但少有****考虑环境影响如污染物排放,并对滑行带来的环境影响作定量分析研究。且在研究中,****们多假设航空器滑行速度恒定以简化计算,如假设整个滑行阶段匀速滑行或是直线和转弯段分别以固定值匀速滑行。但若仅考虑匀速滑行会忽视航空器实际运行过程中速度的变化情况,研究结果与实际情况存在较大偏差[5]。因此,近年来,若干****对航空器滑行阶段进行了更加细致的研究,根据速度变化将滑行过程划分为多个阶段,更加贴近航空器滑行的实际情况[6-8]。
综合现有研究文献,关于机位等待策略和航空器滑行策略问题的研究,国内外研究成果丰富,但仍有如下问题值得进一步深入:①滑行策略优化中较少考虑污染物排放,关于污染物排放影响的定量分析研究较少;②较少细致考虑滑行速度优化对拥堵缓解和减排的影响,关于将机位等待策略与航空器滑行速度优化问题相结合的研究较少。因而,针对以上不足,开展高峰时段下考虑污染物排放的航空器绿色滑行路径问题研究具有重要的现实意义。航空器的滑行策略优化可分为进港和离港两方面,考虑到相对于进港,离港航空器策略优化对提升场面运行效率、提高航班运行正常性更具有意义,故本文主要研究离港航空器的滑行策略优化问题。
1 滑行策略设计 1.1 滑行成本计算模型 离港航空器的滑行成本主要包含滑行时间成本、油耗成本以及环境成本(污染物排放成本),其中滑行时间成本包含除油耗以外的航空公司成本及因延误而产生的旅客延误成本[9]。除正常滑行阶段外,离港航空器还可能因在机位等待推出或在跑道端停止等待而产生各项成本。因此,综合考虑上述因素,某时段内全部离港航空器的各项成本通用计算模型如下。
滑行时间成本T0的计算模型为
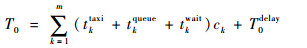 | (1) |
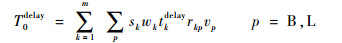 | (2) |
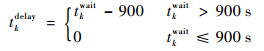 | (3) |
式中:k为离港航班编号;m为航班数目;tktaxi为航班k的滑行时间;tkqueue为k的排队时间;tkwait为k的机位等待时间;ck为不考虑燃油和污染物排放成本的航班k的单位时间成本;Tdelay0为旅客延误成本,下文旅客延误成本计算方法相同;sk为k的座位数;wk为k的客座率;rkp为k的商务/休闲旅客比例,p=B, L,B表示商务旅客,L表示休闲旅客;vp为商务/休闲旅客的时间价值;tkdelay为k的延误时间,根据民航局关于航班正常性管理规定,若机位等待时间超过15min即900s,则延误时间为超出的部分,若机位等待时间不超过15min,则无延误。
因航班机位等待阶段无油耗和排放,所以计算油耗及污染物排放成本时无需考虑机位等待阶段的影响。油耗成本F0的计算模型为
 | (4) |
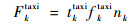 | (5) |
 | (6) |
式中:Fktaxi为k在滑行阶段的油耗;Fkqueue为k在排队阶段的油耗;cfuel为燃油价格;fktaxi为k滑行阶段的燃油流量;fkidle为k排队阶段的燃油流量;nk为k的发动机台数。
污染物排放成本E0的计算模型为
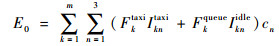 | (7) |
式中:Ikntaxi为航班k排放的第n种污染物在滑行阶段的排放指数,本文主要考虑HC、NOx与CO这3种污染物,故n=1, 2, 3;cn为第n种污染物的单位排放成本;Iknidle为k排放的第n种污染物在排队等待阶段的排放指数。
1.2 正点推出策略 航空公司多采用正点推出策略以保证离港航班的准点率。但在实际运行中,受空管流控等因素的影响,特别是高峰时段,部分离港航班无法按时起飞,需要在跑道端排队等待,因此其滑行时间成本主要包括滑行和跑道端排队的时间成本。采用传统的滑行速度约束,假设离港航空器在滑行路径的直线段和转弯段上分别匀速滑行,则高峰时段正点推出下基于最小总滑行成本的离港航空器滑行策略为
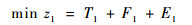 | (8) |
 | (9) |
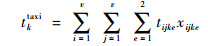 | (10) |
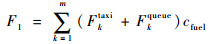 | (11) |
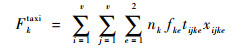 | (12) |
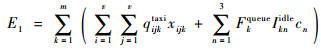 | (13) |
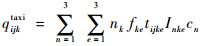 | (14) |
式中:i和j为网络节点;v为节点个数,V为网络节点的集合;xijke=1为k从节点i滑行至节点j,否则xijke=0;e为第e个滑行阶段;yijk为节点i在yijk=0的滑行路径上,否则,yijk=0;tijke为k在第e个滑行阶段从点i到点j的时间,滑行阶段分别有直线段和转弯段;fke为k在第e个滑行阶段时每台发动机的燃油流量;qijktaxi为k从点i到点j的污染物排放成本;Inke为k第n种污染物在第e个滑行阶段的排放指数,n=1, 2, 3;ck为不考虑燃油和排放成本的航班k的单位时间成本。
模型约束条件为
 | (15) |
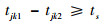 | (16) |
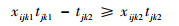 | (17) |
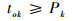 | (18) |
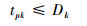 | (19) |
式中:ts为安全滑行间隔。
式(15)避免交叉冲突,表示在ij段滑行区间只有一架航空器滑行,两航空器在经过交叉节点j处满足一定的时间间隔;式(16)确保航空器之间保持一定安全距离;式(17)避免超越冲突,即在航空器滑行过程中不会出现一架航空器超越另一架航空器的情形;式(18)确保k开始在停机位滑行时刻不小于预计推出时刻Pk;式(19)确保k在其预计起飞时刻Dk之前结束滑行,抵达起飞跑道入口。
1.3 机位等待策略 机位等待策略是指航班被控制在机位,不撤轮挡且不启动发动机直至航班可以无障碍滑行至跑道端部,从而避免场面滑行等待以缓解拥堵、减少油耗及排放。本文选取离港地面航班数表征场面拥堵程度,即在单位时间内已推出尚未起飞的航班数[10-11],当离港地面航班数超过规定阈值时则需控制推出率,使部分航班在机位等待。
假设m架离港航空器在[0, T]时间内从停机位推出,滑行速度约束同1.2节。将时间间隔[0, T]等分成个t时间片T1, T2, …, Tt。若k预计将在第qk(qk=1, 2, …, t)个时间片内起飞,采用机位等待策略后,k在预计推出时刻无法按时推出,需在停机位等待一定时间后推出,因此k到达跑道端部的时间也被相应地延迟[4],并可能产生地面等待成本和旅客延误成本。因此,高峰时段机位等待下基于最小总滑行成本的离港航空器滑行策略为
 | (20) |
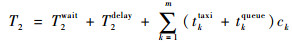 | (21) |
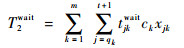 | (22) |
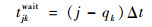 | (23) |
 | (24) |
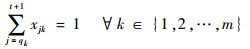 | (25) |
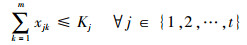 | (26) |
式中:xjk(j=1, 2, …, t且k=1, 2, …, m)为航班状态变量;如果k在时间片Tj内抵达跑道端部准备起飞,则xjk=0,否则xjk=1,只有当pk≥qk时xjk才有意义;tjkwait为k在时间片Tj内抵达跑道端部后的机位等待时间;Δt为单个时间片长度;Kj(j=1, 2, …, t)为机场在时间Tj(j=1, 2, …, t)内最大服务航班数。
式(24)~式(26)为约束条件,式(24)为k在预计起飞时间qk不会抵达跑道端部准备起飞;式(25)为k必须在预计到达时间qk或之后一个时间片内抵达跑道端部准备起飞;式(26)为在任意一个时间片Tj内推出的航班数不能超过机场的最大服务航班数。
航班机位等待时无燃油消耗和污染物排放,因此高峰时段内全部离港航班的燃油成本模型和污染物排放成本模型同1.2节类似。
1.4 速度优化策略 速度优化策略是指在机位等待策略的基础上,进一步考虑滑行速度优化以达到缓解拥堵和减少污染物的目的。航空器的滑行速度直接影响滑行时间,且与燃油消耗和污染物排放之间存在关联。当滑行速度较快时,滑行时间较少,但油耗量较大,污染物排放情况与具体机型相关;当滑行速度较慢时,滑行时间较长,但油耗量较小[5]。1.2和1.3节中均假设航空器在直线段和转弯段上分别匀速滑行,而本节则根据航空器的滑行速度变化将航空器的滑行轨迹划分为5个阶段(加速、匀速、减速、停止等待和转弯),图 1给出了滑行过程中速度变化的一个示例。
 |
| 图 1 离港航空器滑行速度变化示意图 Fig. 1 Schematic diagram of taxiing speed variation of a departure aircraft |
| 图选项 |
速度优化策略下的离港航空器在滑行路径的单个组成路段上可能会经历加速、匀速和减速等多个阶段,而不是仅仅匀速滑行。离港航空器的滑行时间、燃油、排放均为这5个阶段的数值之和。因此,基于最小总滑行成本的速度优化策略为
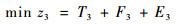 | (27) |
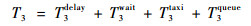 | (28) |
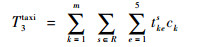 | (29) |
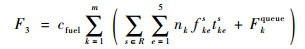 | (30) |
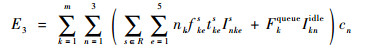 | (31) |
式中:T3delay、T3wait和T3queue的计算方法同上;tkes为k在单个路段s上第e个阶段所用的时间;fkes为k在单个路段s上第e个阶段时的燃油流量;Inkes为k在单个路段s上第e个阶段时的排放指数。该模型约束条件与1.3节中相同。
2 滑行策略评价 2.1 算法简介 考虑到遗传算法在求解效率上较常规精确算法有巨大的优势,且****们对遗传算法在滑行相关问题上的应用作了改进和优化[12],因此采用优化后的遗传算法对3个模型进行求解。以速度优化策略仿真为例,具体算法设计思路如下:首先,根据每个离港航班的路径集和该航空器在路径上的3种滑行速度方式(即分别对应最小时间成本、最小燃油成本以及最小污染物排放成本),依次形成了所有离港航班的滑行方案集合。其次,采用实数编码,不同于传统编码将网络节点当作染色体的基因,文中染色体基因表示一个航班所对应的滑行方案编号,染色体则表示高峰时段内所有离港航班的滑行方案选择结果。再次,采用随机初始化产生了多种滑行方案,初始群体中的每一个值代表一个航班所对应的滑行方案编号。之后,形成了以最小总滑行成本为目标的适应度函数。最后,通过选择、交叉、变异、重插入等操作进行迭代生成符合优化目标的染色体。
2.2 数据准备 1) 场面建模及仿真数据
以上海虹桥国际机场为例,以滑行道和跑道的部分飞行区网络图为研究对象,其中包含22个节点和29条边,1条用于起飞离港的跑道,3个集中停机区A1、A2、A3,机场的离港滑行道系统网络如图 2所示。选用2018年1月15日高峰时段8:00—9:00离港航班数据,见表 1。
 |
| 图 2 离港滑行道系统网络示意图 Fig. 2 Schematic diagram of departure taxiway system network |
| 图选项 |
表 1 离港航班信息汇总 Table 1 Summary of departure flight information
| 航班号 | 预计推出时刻 | 停机区 | 机型 |
| CSH9217 | 8:00 | 3 | B738 |
| CHH7604 | 8:03 | 2 | B738 |
| CSH9515 | 8:04 | 3 | B738 |
| DKH1119 | 8:05 | 1 | A320 |
| DKH1005 | 8:06 | 1 | A320 |
| CSH9331 | 8:06 | 3 | B763 |
| CSH9213 | 8:10 | 3 | B738 |
| CSH9301 | 8:13 | 3 | A333 |
| CES5151 | 8:14 | 1 | A333 |
| CES511 | 8:15 | 1 | A333 |
| CSH9395 | 8:18 | 3 | B738 |
| CSH9239 | 8:21 | 3 | B738 |
| CSH9463 | 8:23 | 3 | B738 |
| CES2994 | 8:25 | 2 | A321 |
| CSN6998 | 8:26 | 2 | B73G |
| CSH9513 | 8:28 | 3 | B738 |
| CCA1590 | 8:33 | 1 | B747 |
| CSN3596 | 8:42 | 2 | B77W |
| CES5103 | 8:42 | 1 | A333 |
| CES5333 | 8:44 | 2 | A321 |
| CSH9451 | 8:47 | 3 | B763 |
| CQH8887 | 8:48 | 1 | A320 |
| CHH7851 | 8:49 | 2 | B738 |
| CES5529 | 8:51 | 1 | A320 |
| CSH815 | 8:51 | 3 | A333 |
| CSH9131 | 8:54 | 3 | B738 |
| CES5663 | 8:55 | 1 | A320 |
| CSH9201 | 8:58 | 3 | B738 |
表选项
2) 离港航班参数
为获取机场场面拥堵临界值Nsat和推出率控制阈值Nc,选用虹桥机场2018年1~6月共计66387个离港航班数据进行拟合。以每15 min为时间片,确定离港地面航班数和下一时间片航班起飞量的对应关系(图 3)[10-11]。由图 3可知,单个时间片内离港航班饱和量Nsat取值为5,最大离港航班量Nc取值为7,当航班数量大于7时则需进行推出率控制。
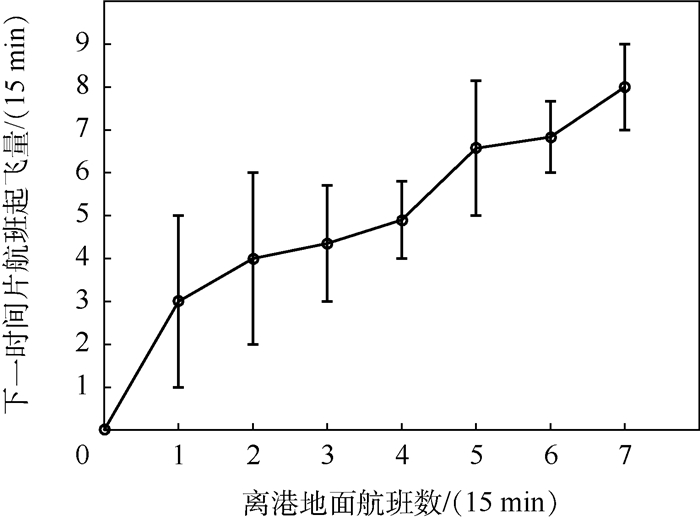 |
| 图 3 离港地面航班数和航班起飞量关系 Fig. 3 Relationship between departure ground throughput and number of aircraft taxiing out |
| 图选项 |
3) 航班滑行成本数据
根据Cherie等的研究成果[13-14]、当期中国航油价格与历年价格指数,可计算获得2018年典型机型的单位滑行时间成本、污染物单位环境外部成本以及旅客单位时间价值,见表 2。
表 2 航班滑行成本数据汇总 Table 2 Summary of flight taxiing cost data
| 成本类型 | 类别 | 成本值 |
| 单位滑行时间成本/(元·min-1) | B73G | 131.07 |
| A320 | 133.76 | |
| A321 | 126.58 | |
| B738 | 135.37 | |
| B763 | 195.12 | |
| A333 | 276.12 | |
| B77W | 256.71 | |
| B747 | 320.89 | |
| 单位污染物排放成本/(元·kg-1) | HC | 50.50 |
| CO | 1.12 | |
| NOx | 113.46 | |
| 旅客时间价值/(元·min-1) | 国内休闲旅客 | 1.057 |
| 国内商务旅客 | 2.961 | |
| 国际休闲旅客 | 1.762 | |
| 国际商务旅客 | 4.935 |
表选项
2.3 仿真结果
2.3.1 缓解拥堵的有效性评价 根据虹桥机场2018年1月15日8:00—9:00离港航班信息,分别统计出4个时间片的航班分布情况,见表 3。
表 3 离港航班分布统计结果 Table 3 Statistic result of departure flight distribution
| 参数 | 时段 | |||
| 8:00—8:14 | 8:15—8:29 | 8:30—8:44 | 8:44—8:59 | |
| 该时段内推出的航班数 | 9 | 6 | 5 | 8 |
| 该时段内起飞的航班数 | 6 | 7 | 8 | 3 |
| 该时段内的航班增量 | 3 | -1 | -3 | 5 |
| 该时段末的地面航班数 | 9 | 8 | 5 | 10 |
表选项
由表 3可知,8:00—8:14、8:15—8:29和8:44—8:59这3个时段末的地面航班数均超过最大离港航班量Nc=7,已经产生明显的场面拥堵,可基于推出率控制实施机位等待策略,减少航空器在滑行道或跑道端的拥堵等待时间。表 4给出了航班调整前后的推出时刻。
表 4 基于机位等待策略的航班调整方案 Table 4 Flight adjustment plan based on stand holding strategy
| 航班号 | 原推出时刻 | 新推出时刻 |
| DKH1005 | 8:06 | 8:17 |
| CSH9301 | 8:13 | 8:26 |
| CSH9463 | 8:23 | 8:34 |
| CQH8887 | 8:48 | 8:36 |
表选项
通过仿真计算,可分别获得3种策略下8:00—9:00所有推出航班的仿真结果,见表 5。
表 5 3种策略的滑行时间与成本汇总 Table 5 Summary of taxiing time and cost for three strategies
| 参数 | 滑行策略 | ||
| 正点推出 | 机位等待 | 速度优化 | |
| 总排队时间/s | 1413 | 842 | 508 |
| 总滑行时间/s | 9684 | 9113 | 7506 |
| 总滑行时间成本/元 | 27272.24 | 25663.46 | 21773.79 |
| 总滑行成本/元 | 34296.68 | 32348.62 | 29991.66 |
表选项
由表 5结果可知,相较于正点推出策略,机位等待的总滑行时间和成本分别减少了571s和1948.06元,可见机位等待策略在高峰时段可有效缓解拥堵,降低成本;而相较于机位等待策略,速度优化策略总滑行时间与总排队时间又分别减少了1607s和334s,可见滑行速度优化策略的缓解拥堵更加有效。
2.3.2 减少排放的有效性评价 表 6给出了3种不同策略下所有航班的油耗与排放结果。
表 6 3种策略的燃油与排放结果汇总 Table 6 Summary of fuel and emission result for three strategies
| 参数 | 滑行策略 | ||
| 正点推出 | 机位等待 | 速度优化 | |
| 总燃油消耗/kg | 1191.91 | 1138.66 | 1369.75 |
| 总污染物排放/kg | 56.41 | 50.98 | 47.52 |
| 总污染物排放成本/元 | 1064.89 | 991.85 | 1369.11 |
表选项
由表 6数据可得,相较于正点推出策略,机位等待与速度优化策略的总污染物排放分别减少了5.43kg和8.89kg,减排比例达到9.63%和15.76%,可见此2种滑行策略均具有较高的环保性。此外,速度优化策略的总燃油消耗、总排放成本均较高,这是因为该策略下滑行速度快,推力等级高导致燃油流量大、油耗增多。同时考虑到污染物排放因子与推力等级设置的关系,致使NOx排放增多;尽管污染物总量减少了,但因NOx的单位成本远高于其他污染物[7],因而总污染物排放成本增大。
通过上述不同滑行策略的评估与对比,开展高峰时期离港滑行策略设计与路径优化时需特别关注如下2个问题:
1) 正点推出与机位等待的平衡。在高峰时刻,航空器正点推出会增加场面航空器数量、加剧场面拥堵,且增加了滑行时间、燃油消耗及污染物排放,但有效地保证了航班正常性;而机位等待可有效缩短滑行时间、缓解场面拥堵及减少油耗与排放,但较长时间的机位等待又会造成航班延误,影响航班正常性、带来额外的延误成本。因此,需合理确定机位等待时机及时长,实现航班正常与运行成本的最优平衡。
2) 滑行速度与滑行时间的平衡。较快的滑行速度可减少场面滑行时间、提高场面运行效率、缓解场面拥堵;但同时,较快的滑行速度需要较大的推力设置及燃油流量,增加了燃油消耗与污染物排放。因而,需根据机场场面运行状态,合理优化滑行速度,实现拥堵缓解与成本减少的最佳平衡。
3 结论 本文研究了高峰时段离港航空器滑行策略优化问题,提出了正点推出、机位等待及速度优化3种绿色滑行策略,并开展仿真与对比分析。研究结果表明:
1) 机位等待和滑行速度优化策略可减少离港航班总滑行时间以及总滑行成本,具有缓解场面拥堵和降低滑行成本的优势。
2) 速度优化滑行策略可有效减少污染物排放总量从而实现绿色滑行,具有一定的环保性。
3) 滑行策略设计与优化需综合考虑推出时刻、滑行速度、滑行路径等因素。
未来可综合考虑进离港航班及机位等待策略的公平性问题,进一步深入研究高峰时段航空器滑行策略优化问题。
参考文献
| [1] | CARR F R.Stochastic modeling and control of airport surface traffic[D]. Cambridge: Massachusetts Institute of Technology, 2001. |
| [2] | ATKIN J A, BURKE E K, GREENWOOD J S. A comparison of two methods for reducing take-off delay at London Heathrow airport[J]. Journal of Scheduling, 2011, 14(5): 409-421. DOI:10.1007/s10951-011-0228-y |
| [3] | RAVIZZA S, ATKIN J A D, BURKE E K. A more realistic approach for airport ground movement optimization with stand holding[J]. Journal of Scheduling, 2014, 17(5): 507-520. DOI:10.1007/s10951-013-0323-3 |
| [4] | 赵向领, 唐建勋, 卢飞. 航班延迟推出策略及虚拟队列长度灵敏度分析[J]. 四川大学学报(工程科学版), 2016, 48(3): 115-123. ZHAO X L, TANG J X, LU F. Strategy analysis for delayed fights pushback and sensitivity analysis of the length of virtual queue[J]. Journal of Sichuan University(Engineering Science Edition), 2016, 48(3): 115-123. (in Chinese) |
| [5] | CHEN J, WEISZER M, STEWART P.Optimal speed profile generation for airport ground movement with consideration of emissions[C]//18th IEEE International Conference on Intelligent Transportation Systems.Piscataway, NJ: IEEE Press, 2015: 1797-1802. |
| [6] | NIKOLERIS T, GUPTA G, KISTLER M. Detailed estimation of fuel consumption and emissions during aircraft taxi operations at Dallas/Fort Worth International Airport[J]. Transport Research Part D:Transport & Environment, 2011, 16(4): 302-308. |
| [7] | EVERTSE C. A low emissions taxi movement planning tool[D]. Delft: Delft University of Technology, 2014. |
| [8] | CHEN J, WEISZER M, STEWART P, et al. Toward a more realistic, cost-effective and greener ground movement through active routing-part Ⅰ:Optimal speed profile generation[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(5): 1196-1209. DOI:10.1109/TITS.2015.2477350 |
| [9] | 陈琳, 胡荣, 郑丽君, 等. 考虑环境成本的航班滑行等待成本研究[J]. 中国民航大学学报, 2018, 36(2): 28-32. CHEN L, HU R, ZHENG L J, et al. Study on the cost of flight delays during the taxi-out and waiting period with the consideration of environmental cost[J]. Journal of Civil Aviation University of China, 2018, 36(2): 28-32. DOI:10.3969/j.issn.1674-5590.2018.02.007 (in Chinese) |
| [10] | SIMAIAKIS I, BALAKRISHNAN H, KHADILKAR H, et al. Demonstration of reduced airport congestion through pushback rate control[J]. Transportation Research Part A:Policy and Practice, 2014, 66(1): 251-267. |
| [11] | SIMAIAKIS I, SANDBERG M, BALAKRISHNAN H. Dynamic control of airport departures:Algorithm development and field evaluation[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 285-295. |
| [12] | 孙广义, 刘长有. 基于蜂群算法的飞机滑行路径优化[J]. 航空计算技术, 2016, 46(1): 56-59. SUN G Y, LIU C Y. Optimization of aircraft taxiing path based on artificial bees colony[J]. Aeronautical Computing Technique, 2016, 46(1): 56-59. DOI:10.3969/j.issn.1671-654X.2016.01.014 (in Chinese) |
| [13] | CHERIE L. The economic benefits and environmental costs of airport operations:Taiwan Taoyuan International Airport[J]. Journal of Air Transport Management, 2011, 17(6): 360-363. DOI:10.1016/j.jairtraman.2011.02.006 |
| [14] | 李雄, 刘光才, 颜明池. 航班延误引发的航空公司及旅客经济损失[J]. 系统工程, 2007, 25(12): 20-23. LI X, LIU G C, YAN M C. The economic loss of airlines and passengers caused by flight delays[J]. Systems Engineering, 2007, 25(12): 20-23. DOI:10.3969/j.issn.1001-4098.2007.12.004 (in Chinese) |
