对卫星而言,其运行轨道根据任务需求提前确定;对导弹和无人机等飞行器而言,随着相关技术的发展,飞行中段往往过程复杂,不确定因素多[1-2],需要考虑路径约束、状态约束、必经点、禁飞区等诸多约束条件[3-4],将制约机动发射水平。目前,针对传统弹道导弹机动发射问题的研究相对成熟,而对于飞行中段复杂的空间飞行器机动发射研究较少[5]。文献[1]研究了基于Gauss伪谱法的滑翔段弹道快速规划方法,但是采用的弹道规划模型有所简化,并且未考虑对制导控制系统的影响;文献[5]对全程弹道诸元的快速解算问题进行了研究,能够做到全程弹道的快速生成,但是该方法得到的入轨点高度、速度有一定的不确定性,对制导控制系统而言存在一定隐患;在机动发射背景下,文献[6]联合BP神经网络和L-M算法研究了上升段弹道快速计算方法,可以实现上升段弹道的快速设计,但是没有将入轨点位置和速度方位角作为终端约束,仍需研究飞行中段弹道快速规划方法。
本文从另外一个思路出发,在机动发射条件下,不改变飞行中段弹道,创新性地将研究方向转为对上升段弹道进行设计,并实现与飞行中段的高精度交班。目前,对上升段弹道的研究较为广泛,如文献[7-8]对空间飞行器入轨问题进行了研究,但是未对入轨点位置和速度方位角进行约束。在轨迹优化方面,文献[9]采用改进的粒子群算法对上升段轨迹进行优化,在收敛速度及精度上有很大提高;文献[10]采用梯度粒子群算法对上升段交会弹道进行优化,显著提高了全局寻优能力和收敛速度。本文在此基础上,参考文献[11-13],加入混合扰动算子(BDO),减小搜索后期陷入局部最优解的概率。
机动发射条件下,传统的射面内飞行弹道将无法满足空间飞行器苛刻的入轨点交班精度要求,因此引入变射面横向机动模型。文献[14-16]对变射面横向机动弹道进行了深入研究,为本文研究提供了理论基础。
基于上述分析,本文以三级固体火箭为研究对象,通过设计二级和三级能量管理模型对入轨点速度大小进行调整,设计变射面横向机动模型来满足入轨点位置、高度、速度、速度方位角、弹道倾角等约束。通过仿真实验,对机动发射上升段弹道设计方法的有效性进行了验证。
1 机动发射 按照预定发射任务,根据发射点大地坐标(B0, L0, H0)和目标点大地坐标(Bm, Lm, Hm)设计上升段及飞行中段弹道,将其称为基准弹道。其中,B为纬度,L为经度,H为高度。为增强空间飞行器机动发射能力,允许其在以(B0, L0, H0)为中心、半径为R的发射区域内机动。当机动到(B1, L1, H1)后,保持基准弹道中的飞行中段弹道及入轨点状态不变,通过合理设计上升段弹道,使其同样满足入轨要求,完成与飞行中段的交班。文献[1]指出,飞行中段可通行区域小,并且综合考虑飞行中段各种约束条件,容易得到高精度交班对后续飞行十分重要,因此可将入轨点位置(经纬度)、高度、速度、速度方位角、弹道倾角作为入轨状态指标。
当空间飞行器机动至偏离基准弹道射面位置时,传统的射面内弹道设计方法将难以满足速度方位角要求,无法与基准弹道飞行中段实现交班,并最终导致严重偏离目标点。通过上升段横向机动可以完成对速度方位角的调整,并优化设计相关参数,形成变射面横向机动上升段弹道,实现与飞行中段高精度交班。变射面横向机动相关概念可以参考文献[14-16]。
为方便表述发射车机动后的位置,使用(r, Ad)表示与基准弹道发射点的相对位置关系,r为两者之间的距离,取值范围为(0, R),Ad为两者连线偏离基准弹道射击方位角的角度,取值范围为(0°, 360°),顺时针方向为正。
机动发射条件下,空间飞行器横向机动上升段弹道示意图如图 1所示。可知,空间飞行器机动位置可以分为3种情况:①机动后发射车仍在原瞄准方向;②机动后发射车在原瞄准方向偏北;③机动后发射车在原瞄准方向偏南。图 1中,虚线为基准弹道与横向机动上升段弹道在地面投影,OF为基准弹道上升段,AF为横向机动弹道上升段,F为空间飞行器入轨点,A为发射点,B为一级关机点,C为二级关机点,D为三级关机点。
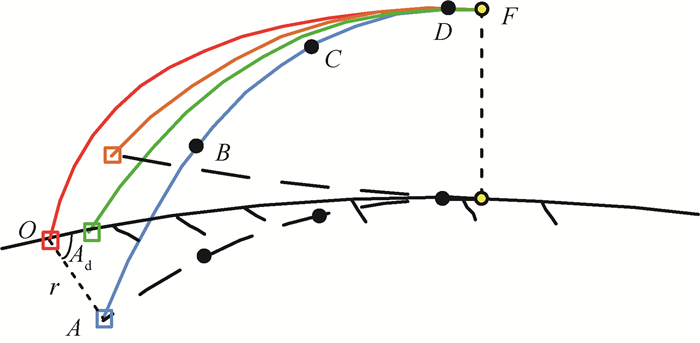 |
| 图 1 空间飞行器机动发射示意图 Fig. 1 Schematic diagram of mobile launch of space vehicle |
| 图选项 |
2 弹道设计 本文以三级固体火箭为例,主要由一、二、三级固体火箭及分导级组成。先需对基准弹道进行设计,实现空间飞行器入轨,由于本文主要研究对象为上升段,因此不对飞行中段进行建模;再以基准弹道入轨点状态作为发射车机动后空间飞行器入轨需要达到的状态,进行建模分析。传统弹道设计方法已经较为成熟,具体可参考文献[17],本文不再赘述。
2.1 基准弹道飞行程序角设计
2.1.1 一级飞行程序角设计 为提高一级飞行程序对不同终端约束的适应性,在跨声速前后分别进行2次指数形式攻角转弯,具体形式可参考文献[18]。
2.1.2 二级飞行程序角设计 火箭二级飞行环境影响因素相对较少,按照等斜率转弯方式设计二级飞行程序角,其表达式为
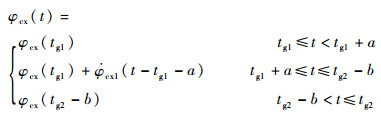 | (1) |
式中:tg1为一级分离时刻;tg2为二级分离时刻;
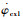
2.1.3 三级飞行程序角设计 三级飞行程序与二级类似,表达式为
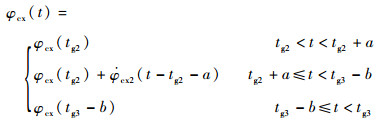 | (2) |
式中:tg3为三级分离时刻;

2.1.4 分导级飞行程序角设计 在基准弹道设计中,分导级姿态保持不变,按照最大工作时间进行飞行,即
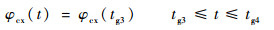 | (3) |
式中:tg4为分导级关机时刻。
2.2 横向机动上升段弹道设计 火箭一级飞行高度低、空气稠密,为了减小控制系统压力,不适合做大幅度机动。因此,横向机动上升段弹道的一级飞行程序模型与基准弹道相同,对二、三级和分导级飞行程序模型进行优化。在基准弹道设计中,仅对入轨点高度、速度和弹道倾角进行约束,较为简单,而当发射车机动后,需要同时满足入轨点位置要求,约束更强。针对固体火箭通常采用耗尽关机方式,为能够对入轨点速度大小进行有效调整,本文设计了二、三级能量管理模型。
2.2.1 能量管理模型 入轨点能量是推力、引力和空气动力等共同做功的结果,而入轨点能量包括势能与动能。当入轨点高度一定时,引力做功为定值,因此,在火箭性能一定的情况下,必须调节推力对火箭做功大小,才能满足终端速度大小要求。本文通过控制火箭产生多余路径,从而对火箭能量进行消耗[19-20]。
以二级能量管理模型为例,给出俯仰程序角交变模型(见图 2)。为了增大上升段能量管理可调整范围,同样对三级进行能量管理,其模型与二级类似。
 |
| 图 2 俯仰程序角交变模型示意图 Fig. 2 Schematic diagram of alternating model of pitching program angle |
| 图选项 |
横向机动同样会产生多余的能量消耗,因此,最终的能量管理是纵横向飞行程序综合设计的结果。
2.2.2 横向机动上升段弹道飞行程序角模型 1) 纵向飞行程序角设计
横向机动上升段弹道二、三级采用能量管理思想,一方面可以消耗能量,另一方面增加程序可调整范围,满足苛刻的多约束终端状态。纵向飞行程序设计如下:
二级飞行程序角为
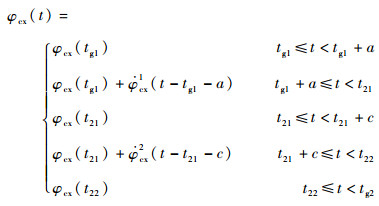 | (4) |
式中:
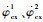
三级飞行程序角为
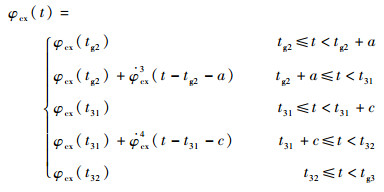 | (5) |
式中:
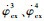
分导级飞行程序角为
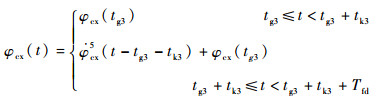 | (6) |
式中:
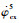
2)横向飞行程序角设计
通过改变三级偏航程序角,实现横向机动,为防止偏航角出现突变,在按照反正切函数转弯前5 s,先按照线性函数转弯至需要角度[16],偏航程序角ψcx(t)为
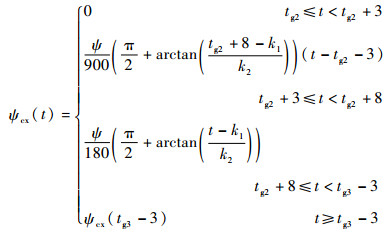 | (7) |
式中:ψ为最大偏航角,控制转弯幅度;k1为转弯时刻控制参数;k2为转弯快慢控制参数。
3 优化模型设计 3.1 转换入轨点状态 为了更方便描述入轨点状态与基准弹道入轨点状态的差别,以基准弹道入轨点在地面投影m为原点,建立北东坐标系mxnynzn,具体定义见文献[17]。通常,入轨点位置速度是在地心大地直角坐标系下给出的,位置坐标可根据式(8)、式(9)将其转换到北东坐标系,速度坐标转换方法类似。
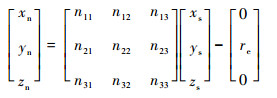 | (8) |
式中:xn、yn、zn为北东坐标系下的坐标;xs、ys、zs为地心大地直角坐标系下的坐标;re为φsm下的地球半径,φsm为入轨点的地心纬度。
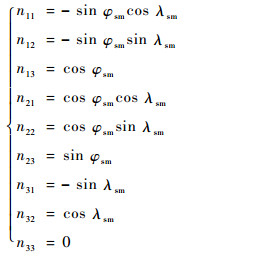 | (9) |
其中:λsm为入轨点的地心经度。
为方便优化时加权处理,以myn为轴,逆时针旋转
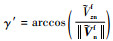
3.2 横向机动上升段弹道约束条件 为保证上升段固体火箭结构稳定,仪器工作正常并减小控制系统控制难度,需要对上升段飞行加入一定的约束,主要包括过程约束、控制量约束及终端约束。
1) 过程约束
为保证弹体结构不受损且弹载仪器工作正常,在火箭飞行过程中必须考虑动压及法向过载等过程约束。
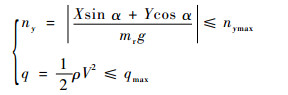 | (10) |
式中:ny为法向过载;nymax为弹体可承受最大法向过载;X和Y分别为火箭所受阻力和升力;α为攻角;mr为火箭质量;g为重力加速度;q为动压;ρ为大气密度;V为速度大小;qmax为最大动压值。本文中,nymax=3g,qmax=90 kPa。
2) 控制量约束
控制量约束包括攻角约束、纵横向转弯角速率约束,防止超出控制系统控制能力。
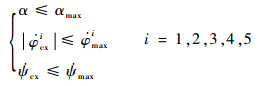 | (11) |
式中:αmax为最大攻角;
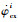
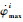
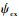
3) 终端约束
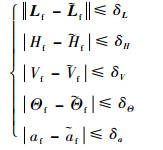 | (12) |
式中:
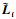
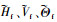
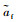
3.3 建立优化模型
3.3.1 优化变量及目标函数 1) 优化变量的确定
根据第2节分析,本文确定优化变量如下:
 | (13) |
式中:θ0为初始离面角;Tcz为垂直起飞时间;
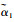

2) 目标函数
在弹道优化方面,通常将不等式约束处理成罚函数形式。
 | (14) |
式中:M为惩罚量,取很大的一个正数。
将终端状态表示在mx′nynz′n坐标系下,按照线性加权方式将终端约束处理成如下目标函数:
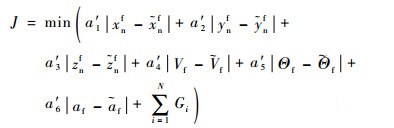 | (15) |
式中:
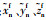

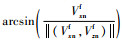
本文借鉴文献[3, 5-6]给出的终端状态,以式(16)为例,作为本文的终端约束。
 | (16) |
3.3.2 优化算法 文献[10]采用梯度粒子群算法,已经很好地解决了弹道优化问题,本文借鉴该算法,将其用于横向机动上升段弹道相关参数的优化,并进行了相应改进。
文献[12]提到粒子速度趋于0时,粒子群算法趋于收敛,若未达到全局最优解,将陷入局部最优解。因此,本文在梯度粒子群算法后期,引入混合扰动算子[11]对粒子速度进行扰动,减小算法早熟概率。
1) 混合扰动算子
文献[11]在优化算法中采用扰动操作,增大跳出局部最优的概率,并给出了混合扰动算子表达式。混合扰动算子能够综合Gauss分布及柯西分布特点,产生范围更广的随机数,其表达式为
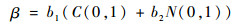 | (17) |
式中:C(0, 1)服从标准柯西分布;N(0, 1)服从标准Gauss分布;b1、b2为很小的正数。
2) 改进速度更新公式
首先,随机选取第i个粒子的第j个变量作为增加采取扰动操作的对象。然后,按照式(18)对粒子速度进行更新。
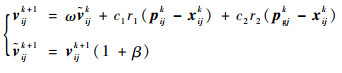 | (18) |
式中:k为代数;?ijk和?ijk+1分别为扰动后的第k和k+1代粒子速度;xijk为第k代粒子位置;pijk和pgjk分别为第k代个体最优解和全局最优解;r1、r2为服从标准Gauss分布的随机数;ω为惯性权重;c1、c2为学习因子。
4 仿真计算与结果分析 本文借鉴文献[21]中固体火箭参数,并做适当改进,以适应本文对运载火箭的要求。假定(N38°10′, E117°37′, 1 km)为基准发射点,根据基准弹道模型得到其入轨点位置为(N44°15′35″, E119°24′18″, 90 km),在地心大地直角坐标系下的速度矢量为(669.982 8, -4 423.480 6, 4 292.425 1) m/s。以发射点(270°, 25 km)为例进行横向机动上升段弹道优化,其优化变量取值范围及优化结果如表 1所示。同时以25 km发射范围为例,对本文模型进行检验。
表 1 优化变量取值范围及优化结果 Table 1 Range of value for variable optimization and results
| 变量 | 下限 | 上限 | 优化结果 |
| θ0/(°) | -2.0 | 2.0 | 0.877 1 |
| Tcz/s | 3.0 | 9.0 | 3.872 8 |
| Tfd/s | 3.0 | 16.0 | 12.127 5 |
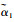 /(°) /(°) | 3.9 | 8.0 | 5.467 1 |
| a1 | 0.5 | 0.6 | 0.570 0 |
 /(°) /(°) | 3.0 | 12.0 | 8.752 0 |
| a2 | 0.05 | 0.29 | 0.281 0 |
 /((°)·s-1) /((°)·s-1) | -3.0 | 0 | -3.000 0 |
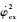 /((°)·s-1) /((°)·s-1) | -3.0 | 2.0 | 0.151 3 |
 /((°)·s-1) /((°)·s-1) | -2.0 | 4.0 | 0.983 6 |
 /((°)·s-1) /((°)·s-1) | -3.0 | 3.0 | 1.151 3 |
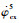 /((°)·s-1) /((°)·s-1) | -4.0 | 4.0 | -2.497 0 |
| ψ/(°) | -25.0 | 25.0 | 24.205 7 |
| k1 | 143.0 | 183.0 | 182.113 3 |
| k2 | 3.0 | 12.0 | 4.602 8 |
表选项
对发射坐标为(270°, 25 km)的点位进行仿真,得到空间飞行器横向机动上升段弹道参数仿真结果,如图 3~图 8所示。图 3~图 8分别给出了横向机动上升段弹道高度、横向机动距离、速度、横向速度、绝对俯仰角、绝对偏航角、攻角和当地弹道倾角随时间的变化曲线。发射点(270°, 25 km)是偏离基准弹道最远的位置,其所需横向机动距离将是最大的位置之一,横向机动距离越大,消耗能量越多,受火箭能量限制,将会制约可机动范围。仿真结果表明,在(270°, 25 km)处入轨精度仍然较高,如表 2所示,这也间接验证了25 km范围任意位置高精度入轨的可行性。
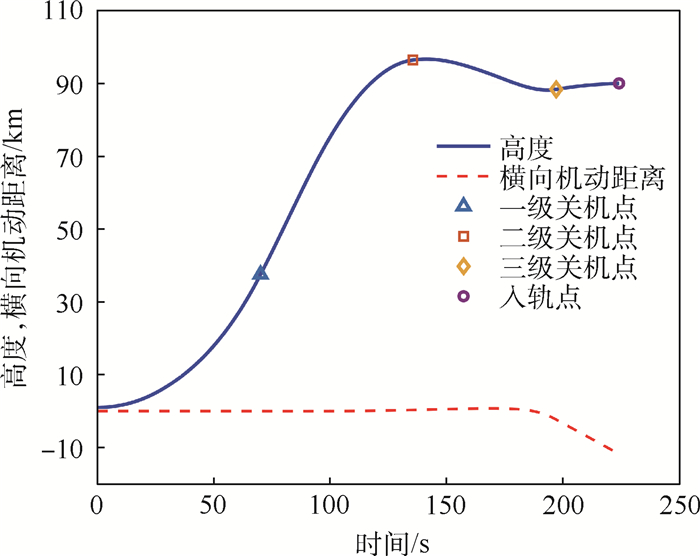 |
| 图 3 高度、横向机动距离随时间变化曲线 Fig. 3 Variation curves of height and transverse maneuvering distance with time |
| 图选项 |
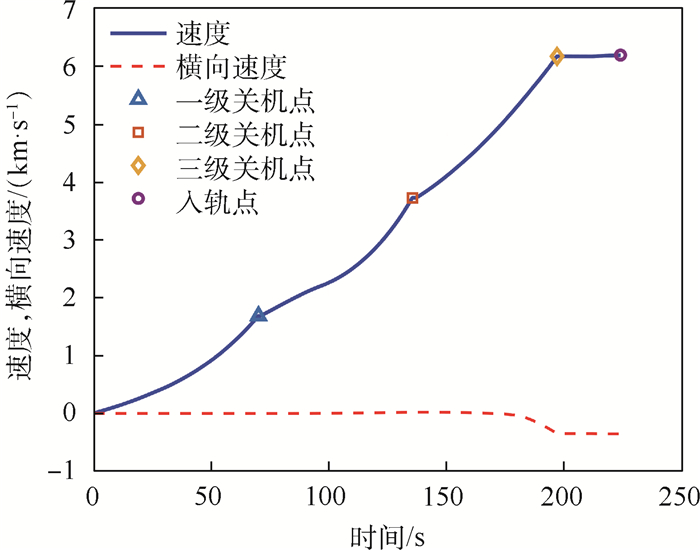 |
| 图 4 速度、横向速度随时间变化曲线 Fig. 4 Variation curves of velocity and transverse velocity with time |
| 图选项 |
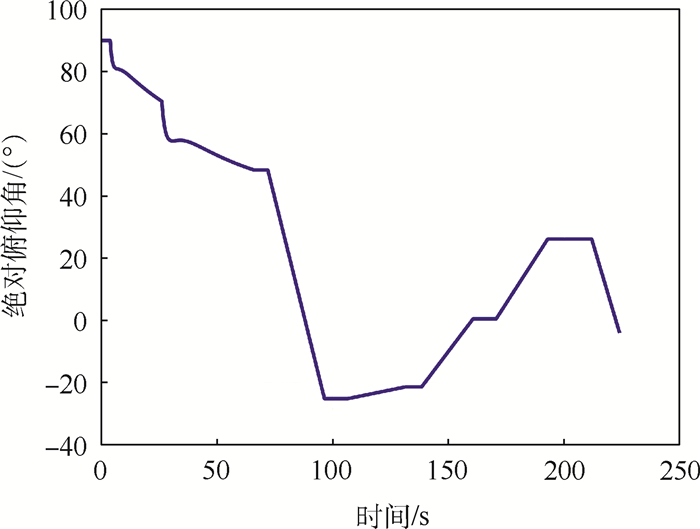 |
| 图 5 绝对俯仰角随时间变化曲线 Fig. 5 Variation curve of absolute pitch angle with time |
| 图选项 |
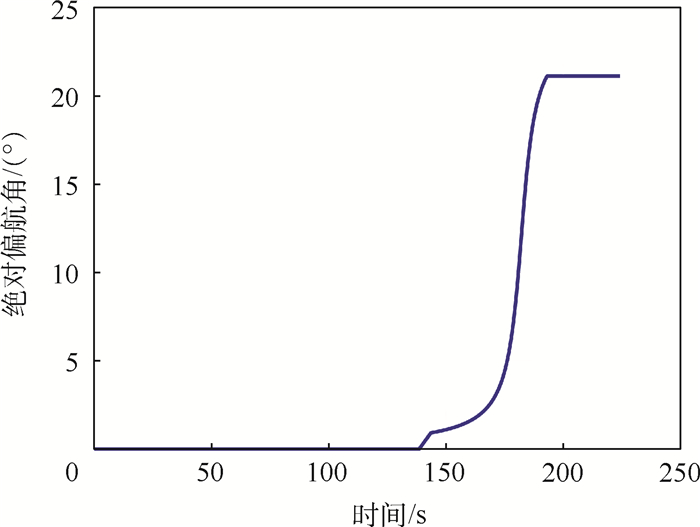 |
| 图 6 绝对偏航角随时间变化曲线 Fig. 6 Variation curve of absolute yaw angle with time |
| 图选项 |
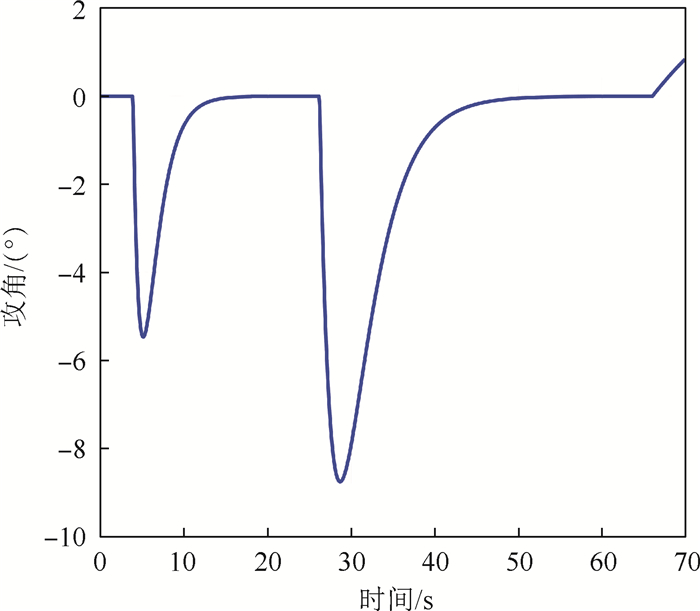 |
| 图 7 前70 s攻角随时间变化曲线 Fig. 7 Variation curve of first 70 s' attack angle with time |
| 图选项 |
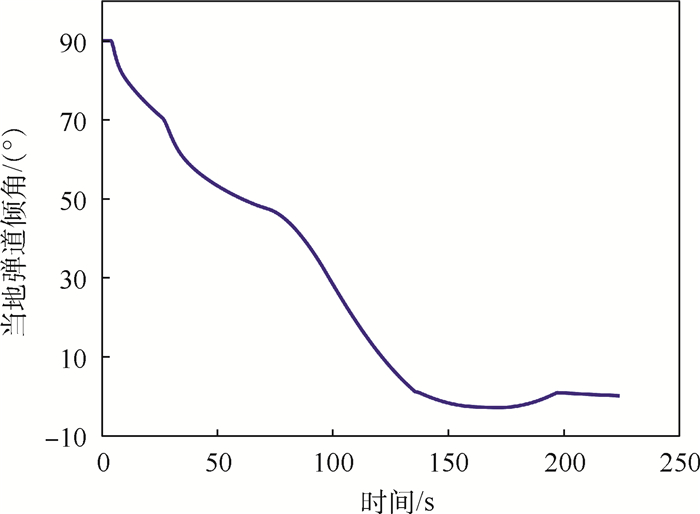 |
| 图 8 当地弹道倾角随时间变化曲线 Fig. 8 Variation curve of local ballistic inclination with time |
| 图选项 |
表 2 横向机动上升段弹道入轨点参数偏差 Table 2 Parameter deviation of injection point of transverse maneuvering ascent trajectory
| 入轨点参数 | 与基准弹道入轨点偏差 |
| 位置/m | 18.737 5 |
| 高度/m | 0.516 4 |
| 速度/(m·s-1) | 0.775 6 |
| 速度方位角/(°) | 0.028 8 |
| 弹道倾角/(°) | 0.009 1 |
表选项
在不加入变射面横向机动模型的情况下,本文采用相同的弹道设计方法,对发射坐标为(270°, 25 km)的点位进行仿真,验证采用变射面横向机动模型的必要性。仿真结果表明,该情况下能够在入轨点位置、高度、速度、弹道倾角方面实现高精度入轨,如表 3所示,但是速度方位角偏差高达2.320 1°,而加入变射面横向机动模型后,速度方位角偏差仅为0.028 8°,极大地降低了空间飞行器在飞行中段的修正难度。
表 3 无变射面横向机动的上升段弹道入轨点参数偏差 Table 3 Parameter deviation of injection point of ascent trajectory without changeable-launching-plane transverse maneuvering
| 入轨点参数 | 与基准弹道入轨点偏差 |
| 位置/m | 1.547 4 |
| 高度/m | 0.181 3 |
| 速度/(m·s-1) | 0.271 0 |
| 速度方位角/(°) | 2.320 1 |
| 弹道倾角/(°) | 0.005 5 |
表选项
本文在此基础上,在25 km范围内随机产生100个发射点,如图 9所示,以及(0°, 25 km)、(90°, 25 km)、(180°, 25 km)、(270°, 25 km)4个点,共仿真104个发射车机动后的位置,采用上述模型实现入轨,得到图 10~图 13所示结果。
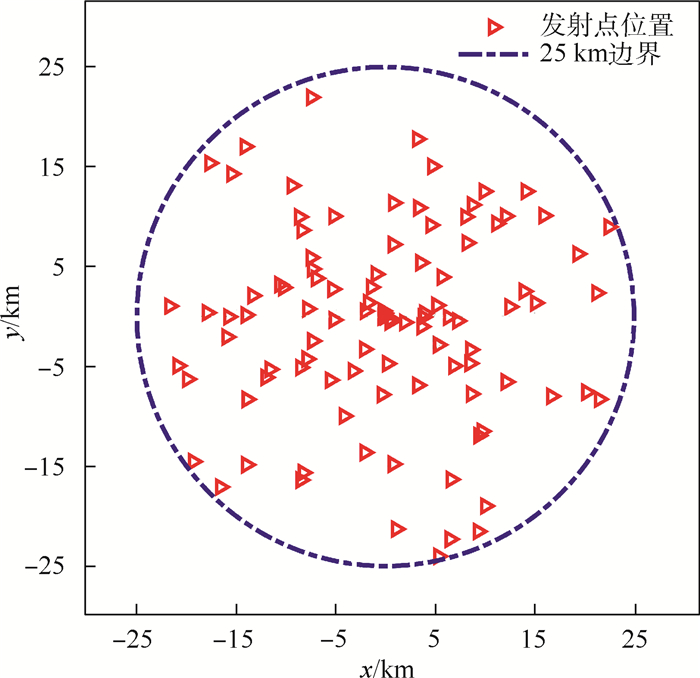 |
| 图 9 100个随机发射点位置 Fig. 9 Position of 100 stochastic launch sites |
| 图选项 |
 |
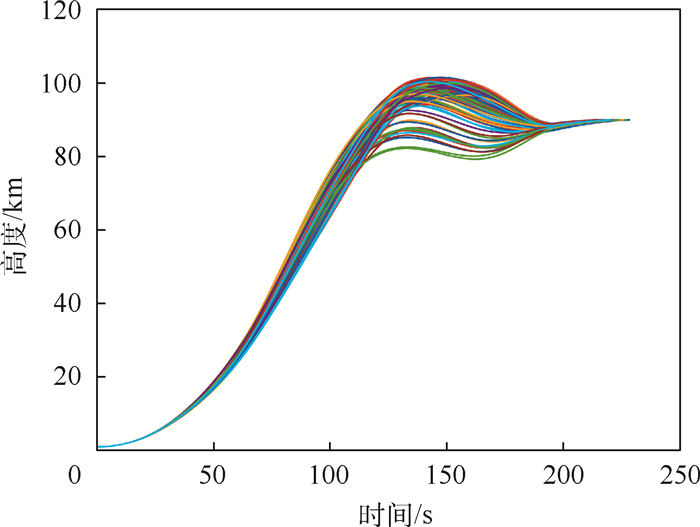
| 图 10 高度随时间变化仿真 Fig. 10 Variation simulation of height with time |
| 图选项 |
 |
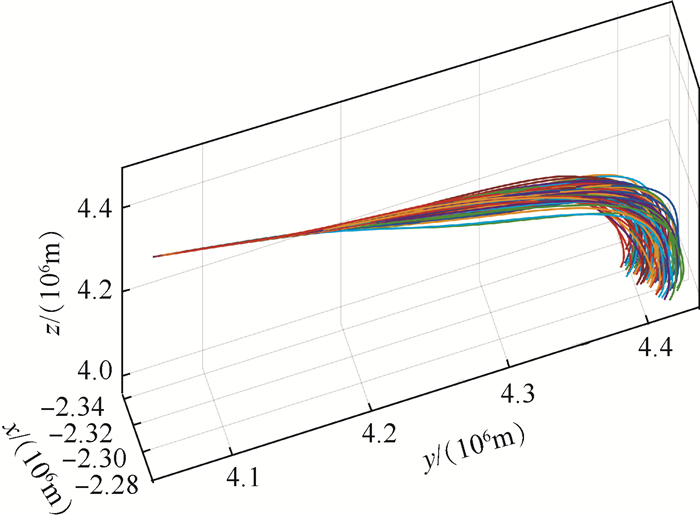
| 图 11 弹道三维仿真 Fig. 11 Three-dimensional simulation of ballistic |
| 图选项 |
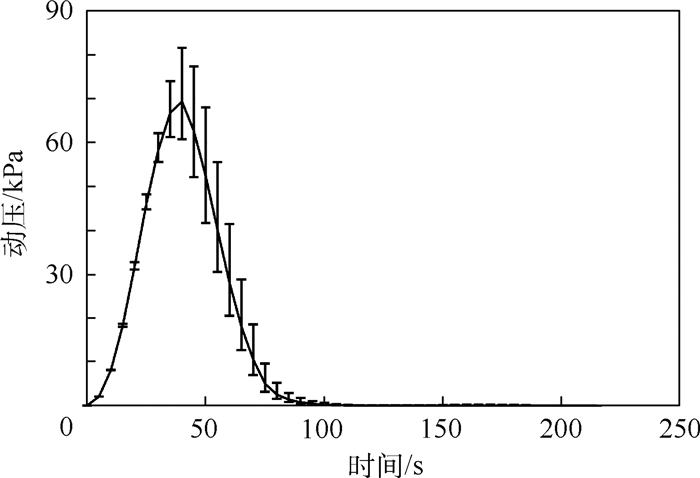 |
| 图 12 动压随时间变化仿真 Fig. 12 Variation simulation of dynamic pressure with time |
| 图选项 |
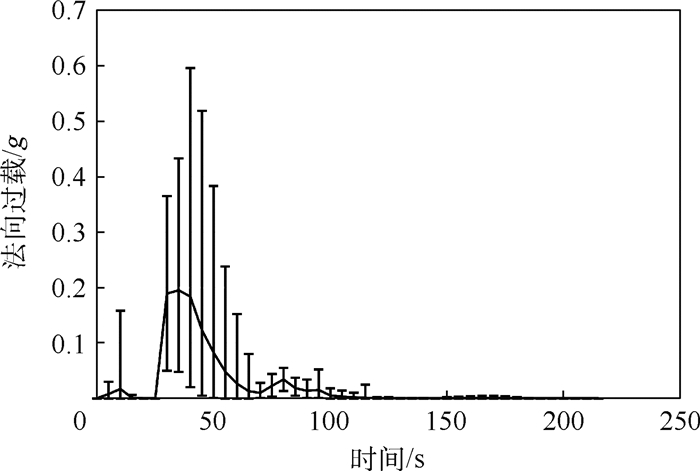 |
| 图 13 法向过载随时间变化仿真 Fig. 13 Variation simulation of normal overload with time |
| 图选项 |
图 10、图 11分别给出了104个横向机动上升段弹道的高度随时间变化曲线及三维轨迹。
在前220 s内,每隔5 s记录一次该时刻对应的动压值,并统计104次仿真过程中t时刻的平均动压、最大动压和最小动压,得到图 12,可以看出,最大动压值小于90 kPa,能够满足火箭飞行中的过程约束。
采用与图 12类似的方法,图 13给了法向过载随时间的变化曲线,最大法向过载值小于0.6g。本文中一级火箭的工作时间为70 s,从图 12、图 13中可以看出,70 s以后,法向过载和动压都很小,最大值分别不超过0.1g和20 kPa,平均值分别不超过0.1g和11 kPa,说明本文设计的二、三级能量管理模型并不会对弹体造成太大影响,具有一定的工程可行性。
表 4给出了104条横向机动上升段弹道在入轨点的位置、高度、速度、速度方位角、弹道倾角与基准弹道对应状态量的平均偏差值及最大偏差值。可以看出,所有状态量的最大偏差值都在指标要求范围内。
表 4 104条弹道入轨点参数偏差统计 Table 4 Statistics of parameter deviation of 104 ballistic injection points
| 入轨点参数 | 平均偏差 | 最大偏差 |
| 位置/m | 27.506 2 | 70.431 9 |
| 高度/m | 2.125 4 | 7.003 6 |
| 速度/(m·s-1) | 1.652 2 | 4.769 1 |
| 速度方位角/(°) | 0.072 8 | 0.289 6 |
| 弹道倾角/(°) | 0.029 0 | 0.124 6 |
表选项
5 结论 本文针对空间飞行器机动发射上升段弹道设计问题进行了研究,总结如下:
1) 针对机动发射条件下上升段弹道规划难题,提出横向机动上升段弹道解决方案。以基准弹道入轨点状态为终端约束,合理设计上升段弹道,完成与基准弹道飞行中段的高精度交班,仿真结果表明,能够实现发射车在25 km范围内机动。
2) 对横向机动上升段弹道模型进行设计。以入轨点位置、高度、速度、速度方位角、弹道倾角等作为终端约束指标,通过设计二、三级能量管理模型及改变三级偏航角的变射面横向机动模型,满足了苛刻的多约束终端状态。
3) 针对横向机动上升段弹道非线性、强耦合、终端状态多约束问题,采用梯度粒子群算法对参数进行优化,并引入混合扰动算子,降低陷入局部最优解概率。仿真结果表明,能够解决本文面临的15个优化变量问题,精度较高。
本文建立的横向机动上升段弹道模型能够较好地解决空间飞行器机动发射问题,并且由于火箭的性能将会影响入轨精度,本文模型也可以为火箭设计提供一定参考。同时,需要指出的是,本文尚未考虑弹道参数的快速计算问题,而要做到真正的机动发射,必须缩短诸元准备时间,这是后续需要进一步研究的方向。
参考文献
| [1] | 陈法龙.高超声速滑翔飞行器弹道快速规划研究[D].长沙: 国防科学技术大学, 2012. CHEN F L.Research of rapid trajectory planning for hypersonic glide vehicle[D].Changsha: National University of Defense Technology, 2012(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-90002-1014047580.htm |
| [2] | 谢愈, 潘亮, 谷学强, 等. 高超声速飞行器多目标复杂约束滑翔弹道优化[J]. 国防科技大学学报, 2017, 39(2): 9-17. XIE Y, PAN L, GU X Q, et al. Gliding trajectory optimization with multiple objectives and complicated constraints for hypersonic vehicles[J]. Journal of National University of Defense Technology, 2017, 39(2): 9-17. (in Chinese) |
| [3] | 陈铁彪, 龚旻, 王洪波, 等. 临近空间可变形滑翔飞行器轨迹优化与性能分析[J]. 宇航学报, 2018, 39(9): 944-952. CHEN T B, GONG M, WANG H B, et al. Trajectory optimization and performance analysis of the near-space morphing glide vehicles[J]. Journal of Astronautics, 2018, 39(9): 944-952. (in Chinese) |
| [4] | 王青, 莫华东, 吴振东, 等. 基于能量的高超声速飞行器再入混合制导方法[J]. 北京航空航天大学学报, 2014, 40(5): 579-584. WANG Q, MO H D, WU Z D, et al. Energy-based hybrid reentry guidance for hypersonic vehicles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(5): 579-584. (in Chinese) |
| [5] | 何睿智, 刘鲁华, 汤国建, 等. 机动发射条件下助推滑翔导弹射击诸元快速解算[J]. 国防科技大学学报, 2017, 39(4): 56-61. HE R Z, LIU L H, TANG G J, et al. Efficient method for firing data calculation of boost-glide missile in mobile condition[J]. Journal of National University of Defense Technology, 2017, 39(4): 56-61. (in Chinese) |
| [6] | 郭玮林, 鲜勇, 张大巧, 等. 高超声速飞行器助推段弹道快速计算方法[J]. 中国惯性技术学报, 2018, 26(1): 109-114. GUO W L, XIAN Y, ZHANG D Q, et al. Fast calculation method of booster trajectory for hypersonic vehicle[J]. Journal of Chinese Inertial Technology, 2018, 26(1): 109-114. (in Chinese) |
| [7] | 鲜勇, 郭玮林, 张大巧, 等. 高超声速飞行器非连续点火助推增程弹道设计[J]. 固体火箭技术, 2017, 40(3): 397-402. XIAN Y, GUO W L, ZHANG D Q, et al. Trajectory design of improving range for hypersonic vehicle based on discontinuous booster[J]. Journal of Solid Rocket Technology, 2017, 40(3): 397-402. (in Chinese) |
| [8] | 任京涛.助推滑导弹上升段多终端约束弹道设计及制导方法研究[D].哈尔滨: 哈尔滨工业大学, 2013. REN J T.Study on the multi-terminal constraint ballistic design and guidance method of the ascent segment of the boost-glidemissile[D].Harbin: Harbin Institute of Technology, 2013(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1014002544.htm |
| [9] | WU G, LIU L, WANG Y, et al.Ascent trajectory optimization of hypersonic vehicle based on improved particle swarm algorithm[C]//Chinese Automation Congress.Piscataway, NJ: IEEE Press, 2015: 115-120. |
| [10] | 李振华, 鲜勇, 雷刚, 等. 基于混合粒子群算法的上升段交会弹道快速优化设计[J]. 航空动力学报, 2015, 30(12): 3029-3034. LI Z H, XIAN Y, LEI G, et al. Rapid optimum design of ascent rendezvous trajectory for launch vehicles based on hybrid particle swarm algorithm[J]. Journal of Aerospace Power, 2015, 30(12): 3029-3034. (in Chinese) |
| [11] | 陈道君, 龚庆武, 金朝意, 等. 基于自适应扰动量子粒子群算法参数优化的支持向量回归机短期风电功率预测[J]. 电网技术, 2013, 37(4): 974-980. CHEN D J, GONG Q W, JIN Z Y, et al. Short-term wind power prediction based on support vector regression machine optimized by adaptive disturbance quantum-behaved particle swarm optimization[J]. Power System Technology, 2013, 37(4): 974-980. (in Chinese) |
| [12] | 王敏, 唐俊. 基于自适应扰动的粒子群优化算法[J]. 计算机工程与应用, 2014, 50(9): 111-115. WANG M, TANG J. Particle swarm optimization based on adaptive disturbance[J]. Computer Engineering and Applications, 2014, 50(9): 111-115. DOI:10.3778/j.issn.1002-8331.1206-0460 (in Chinese) |
| [13] | BERGH F V D, ENGELBRECHT A P. A study of particle swarm optimization particle trajectories[J]. Information Sciences, 2006, 176(8): 937-971. DOI:10.1016/j.ins.2005.02.003 |
| [14] | 鲜勇, 刘炳琪, 李振华, 等. 一种横向机动弹道能量管理方法[J]. 弹道学报, 2014, 26(2): 43-47. XIAN Y, LIU B Q, LI Z H, et al. An energy management method of trajectory of transversely maneuvering missile[J]. Journal of Ballistics, 2014, 26(2): 43-47. DOI:10.3969/j.issn.1004-499X.2014.02.009 (in Chinese) |
| [15] | 鲜勇, 刘炳琪, 王安民, 等. 变射面弹道横向转弯飞行程序的设计与优化[J]. 弹道学报, 2014, 26(4): 30-35. XIAN Y, LIU B Q, WANG A M, et al. Design and optimization of lateral turning flight program on changeable launching plane trajectory[J]. Journal of Ballistics, 2014, 26(4): 30-35. DOI:10.3969/j.issn.1004-499X.2014.04.006 (in Chinese) |
| [16] | 鲜勇, 李少朋, 李振华, 等. 基于梯度粒子群算法的纵横向机动跳跃弹道设计及优化[J]. 弹道学报, 2015, 27(3): 1-6. XIAN Y, LI S P, LI Z H, et al. Design and optimization of vertical wavy and crosswise maneuvering trajectory based on grads particle swarm algorithm[J]. Journal of Ballistics, 2015, 27(3): 1-6. DOI:10.3969/j.issn.1004-499X.2015.03.001 (in Chinese) |
| [17] | 张毅, 肖龙旭, 王顺宏. 弹道导弹弹道学[M]. 长沙: 国防科技大学出版社, 1999. ZHANG Y, XIAO L X, WANG S H. Missile ballistics[M]. Changsha: National University of Defense Technology Press, 1999. (in Chinese) |
| [18] | 鲜勇, 刘凯, 凌王辉, 等. 基于二次点火的飞行器横向转移入轨弹道设计[J]. 航空动力学报, 2018, 33(2): 320-326. XIAN Y, LIU K, LING W H, et al. Trajectory design of launching-plane transforming orbit-injection of spacecraft based on engine twice ignition[J]. Journal of Aerospace Power, 2018, 33(2): 320-326. (in Chinese) |
| [19] | 陈喆, 唐胜景, 郭杰. 固体火箭主动段终端多约束能量管理制导方法[J]. 系统工程与电子技术, 2014, 36(12): 2484-2489. CHEN Z, TANG S J, GUO J. Energy management based guidance of solid rocket with multi-constraints[J]. Systems Engineering and Electronics, 2014, 36(12): 2484-2489. (in Chinese) |
| [20] | 陈克俊. 耗尽关机制导方法研究[J]. 国防科技大学学报, 1996, 18(3): 35-39. CHEN K J. An approach to depleted shutdown guidance[J]. Journal of National University of Defense Technology, 1996, 18(3): 35-39. (in Chinese) |
| [21] | 杨希祥, 江振宇, 张为华. 基于粒子群算法的固体运载火箭上升段弹道优化设计研究[J]. 宇航学报, 2010, 31(5): 1304-1309. YANG X X, JIANG Z Y, ZHANG W H. A particle swarm optimization algorithm-based solid launch vehicle ascent trajectory optimum design[J]. Journal of Astronautics, 2010, 31(5): 1304-1309. DOI:10.3873/j.issn.1000-1328.2010.05.008 (in Chinese) |
