针对这一问题,****提出了预处理矩阵技术[3],以改变原控制方程的数学性质,再用现有通量格式进行计算。数值实验表明,该方法一定程度上改善了低速流动的求解精度。但该方法通常需要设置经验参数,参数的选择对计算效率及精度影响较大,尤其在流场中流速跨度较大的情况下难以保证鲁棒性。另一部分****则提出了对现有通量格式(如Roe格式、AUSM系列格式)的修正技术,较为常见的有:修正了AUSM+格式中压力通量的AUSM+up格式[4],无需调节人工参数的SLAU、SLAU2格式[5],以及通过对Roe格式理论分析获得的LMRoe格式[6]、F-Roe格式[7]、Roe-m格式[8]等。这些研究对不同马赫数下普通通量格式和全速域格式的计算结果进行了深入对比和分析,马赫数的模拟范围可低至10-3[6]。
值得注意的是,在研究低速问题计算时,为了简化模型,****们大多围绕Euler方程开展研究,并使用阶次较低的计算精度以突显低速修正对计算精度的影响。但在开展湍流模拟时,使用的计算方法精度较高,网格量较大,这些因素将与求解器低速修正耦合,对湍流模拟产生综合影响。
因此,本文重点研究有无低速修正的可压缩求解器对湍流模拟的影响,旨在定量分析不同精度、网格量下,低速修正对模拟精度的改进效果,评估低速修正的可压缩求解器的使用范围,为今后计算格式的构造和应用提供参考。
1 控制方程及计算方法 1.1 三维可压缩Navier-Stokes方程及离散方法 本文的控制方程为三维可压缩Navier-Stokes方程组[9],即
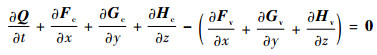 | (1) |
式中:Q为守恒变量;F、G、H分别代表x、y和z三方向的通量,下标c表示对流通量,下标v表示黏性通量。
将式(1)写成半离散形式为
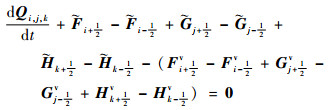 | (2) |
式中:下标i、j、k分别代表x、y和z三方向的离散节点,i±1/2、j±1/2、k±1/2分别表示对应节点左右半节点;上标“~”表示半节点处x、y和z三方向的无黏通量,通常使用重构格式和通量格式联合计算获得;上标v表示半节点处x、y和z三方向的黏性通量,使用中心差分格式求解。
空间离散变量求解完成后,方程[9]变成常微分方程,使用三阶TVD型Runge-Kutta方法[10]进行时间推进,获得下一时刻流场变量Q的分布。
通过对上述流场计算过程的分析可知,方程中空间项的模拟精度主要受通量格式和重构格式的双重影响。在低速问题中,2类格式共同影响计算结果。
1.2 通量格式 Roe格式[11]是Godunov类方法,是目前经典的通量格式,通过求解线化Riemann问题获得全场的数值近似解, 其具有间断分辨率高、稳定性强、计算效率高等优点,广泛使用于可压缩流动求解中。以x方向为例,Roe格式可以写成
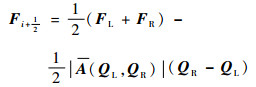 | (3) |
式中:A为Roe格式平均雅可比矩阵;下标L和R分别表示网格界面两侧的变量值。
低速情况下,原始Roe格式压强与马赫数的变化关系和控制方程不同,这将导致求解精度降低、收敛速度变慢等问题。针对这一问题,可引入当地马赫数[6],即
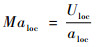 | (4) |
式中:Uloc为当地流速;aloc为当地声速。
利用当地马赫数修正原始Roe格式左右界面的速度差ΔU,将其替换成min(Maloc, 1)ΔU。通过这一修正,在马赫数趋近于0时,格式的压强与马赫数的关系和原控制方程相同。修正后的格式即为LMRoe格式[6]。
1.3 重构格式 为了全面分析通量格式与不同阶次、分辨率的重构格式组合后的模拟效果,本文使用的重构格式包括三/五/七阶WENO格式和五阶线性紧致格式。其中,WENO格式通过低阶模板的加权组合达到高阶精度,同时在间断区域降低相应模板的权重,从而稳定捕捉激波,常用于对计算精度要求较高的高速流动模拟;五阶线性紧致格式能够在相同阶数的情况下获得更高的分辨率。
2m-1阶WENO格式的表达式可写为
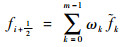 | (5) |
式中
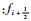
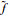
以五阶WENO格式为例,
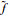
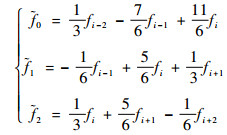 | (6) |
非线性权系数ω的表达式为
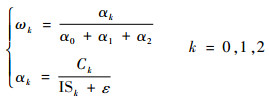 | (7) |
式中:Ck为理想权系数,对于五阶WENO格式,其值为C0=0.1,C1=0.6,C2=0.3;ISk为衡量当地模板光滑性的光滑因子,详细表达式见文献[12]。
其他阶数的WENO格式可以通过类似方法获得。
五阶线性紧致格式的表达式为
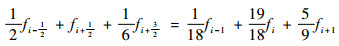 | (8) |
从式(8)可见,五阶线性紧致格式不需要计算非线性系数,计算量较小。但线性格式对数据光滑性的要求非常高,在流场具有间断的可压缩流动数值模拟中容易产生非物理振荡,甚至发散。因此,单纯的线性格式难以在可压缩复杂流动数值模拟中直接应用。
为了表述方便,称三/五/七阶WENO格式为WENO3、WENO5和WENO7,称五阶线性紧致格式为compact5。
傅里叶分析可以衡量格式的分辨率[13-14],即表征在网格量不足情况下格式的计算精度(见图 1)。图中:k为波数,Re(k′)和Im(k′)分别为色散和耗散特性,横、纵轴均使用π归一化。可见,随着阶数升高,WENO格式的分辨率提高。而五阶紧致格式的分辨率远优于七阶WENO格式,表明了紧致格式在分辨率具有优势。
 |
| 图 1 不同重构格式的分辨率特性曲线 Fig. 1 Resolution properties of different reconstruction schemes |
| 图选项 |
2 泰勒-格林涡算例 2.1 算例设置 为了定量分析不同格式的计算性能,本文选择了经典的泰勒-格林涡算例。算例的流动演化包括了“层流—转捩—湍流—衰减”这几个湍流发展的典型阶段[15],能够反映数值方法对湍流不同发展阶段的模拟能力。同时,该算例的初始流场有解析表达式,可以避免“启动问题”(set-up problem)。此外,该算例本质上是不可压缩流动,实际模拟时马赫数非常小,低速通量格式在模拟中能够体现其作用。
算例的初始流场为
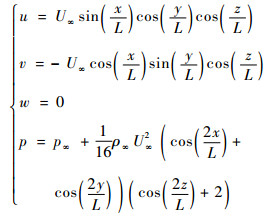 | (9) |
式中:u、v、w分别为三方向速度;p为压强;ρ为密度;下标“∞”表示自由来流;U∞=1;L=1。雷诺数Re=ρ∞U∞L/μ=1 600,μ为黏性系数;马赫数Ma=U∞/a∞=0.1,a∞为声速,由a∞2=γp∞/ρ∞获得,γ为比热比。流动区域为一边长为2πL的立方体,采用周期边界条件。计算时间截止至t=20。计算结果以U∞、ρ∞和p∞为参考量进行无量纲化。
下文的分析中主要用到了体平均动能Ek及其耗散率εEk这2个平均量。体平均动能的计算式为
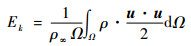 | (10) |
式中:u为速度矢量;Ω表示积分域。其对应的动能耗散率的计算式为
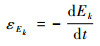 | (11) |
Ek和εEk能够反映流动发展过程中流场动能变化的情况,从而衡量模拟结果的精度。
2.2 计算结果与讨论 在网格间距为2π/64、2π/128和2π/256的3套网格下开展算例计算,以分析不同网格量下不同格式对计算结果的影响。在间距为2π/256的密网格上使用compact5获得的结果与文献[16]使用DRP方法在5123自由度上的DNS结果精度相当,作为参考解进行计算结果误差的定性和定量分析。在粗网格(间距2π/64)上使用3种阶数WENO格式和compact5与Roe和LMRoe 2种通量格式分别组合,重点考察粗网格量下重构格式精度不同时,低速修正通量格式的使用对计算精度的影响程度。在中等网格(间距2π/128)上使用WENO5、compact5与Roe和LMRoe 2种通量格式两两组合,进一步研究网格量变化后通量格式的低速修正对计算结果的影响。
图 2和图 3为粗网格上不同重构格式下获得的体平均动能及其耗散率随时间变化曲线,其中文献[16]的DNS结果(图中“reference-DRP5123”)和compact5在密网格的结果(图中“256-Roe-compact5”)为参考解。总体上看,在网格量相同的情况下,重构格式的精度越高,分辨率越高,计算结果越接近参考解。相同重构格式下,LMRoe格式的计算结果更接近参考解,可见在粗网格下,低速修正起到了提高计算精度的作用。
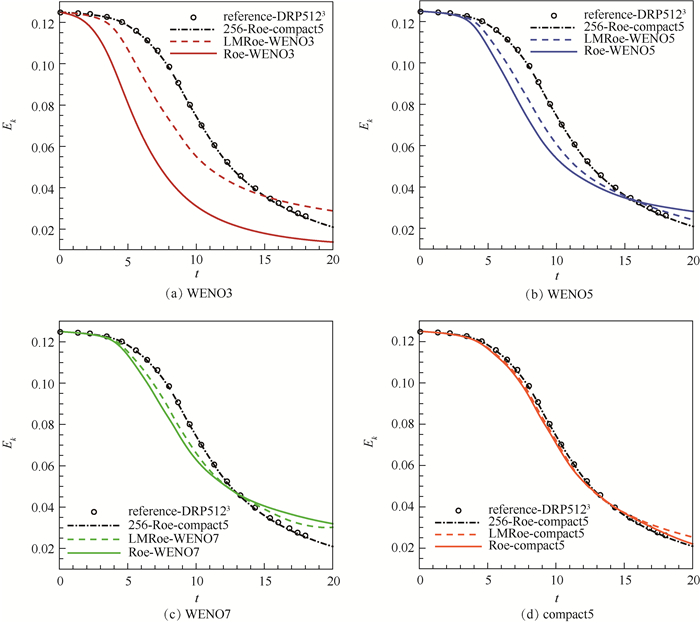 |
| 图 2 体平均动能随时间变化曲线(网格间距2π/64) Fig. 2 Variation of volume-averaged kinetic energy with time under grid space 2π/64 |
| 图选项 |
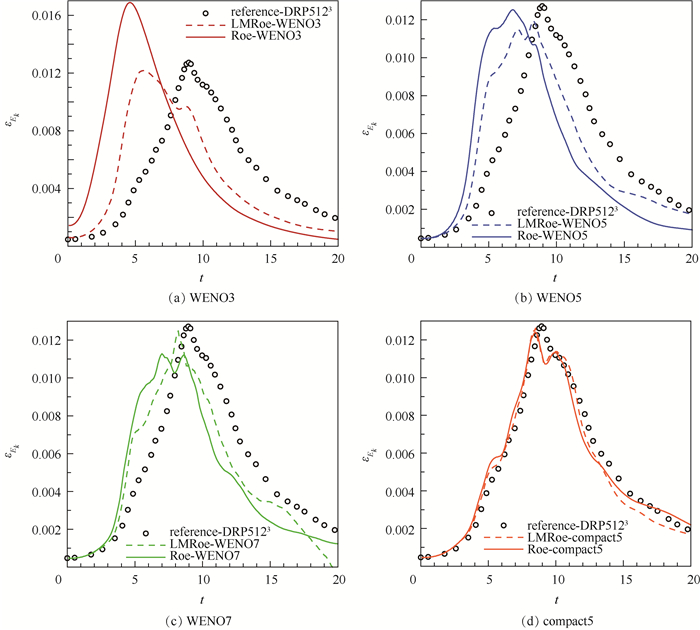 |
| 图 3 动能耗散率随时间变化曲线(网格间距2π/64) Fig. 3 Variation of energy dissipation rate with time under grid space 2π/64 |
| 图选项 |
图 4和图 5为中等网格下WENO5和compact5两种重构格式、Roe和LMRoe两种通量格式两两组合的计算结果。与粗网格结果相比,密网格下的计算结果精度更高,且2种通量格式计算结果间的差别变小。
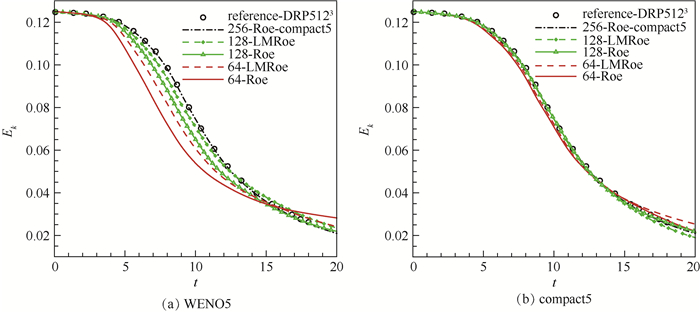 |
| 图 4 体平均动能随时间变化曲线(网格间距2π/64和2π/128) Fig. 4 Variation of volume-averaged kinetic energy with time (grid space 2π/64 and 2π/128) |
| 图选项 |
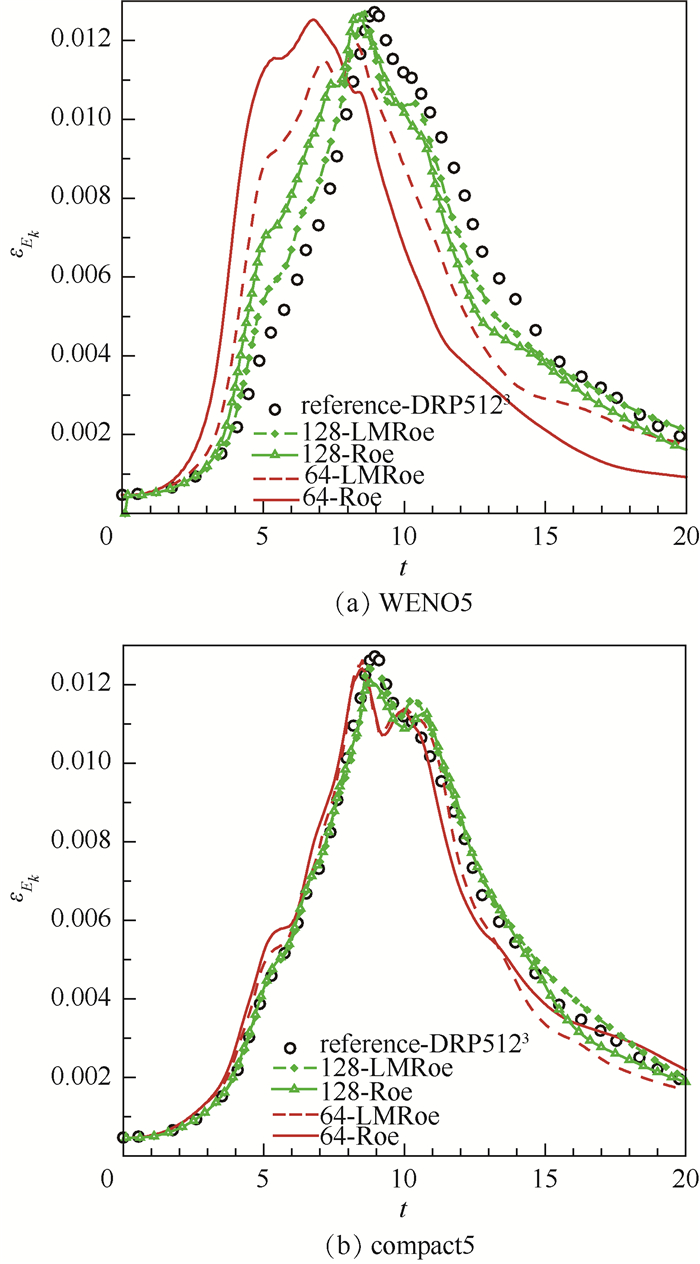 |
| 图 5 动能耗散率随时间变化曲线(网格间距2π/64和2π/128) Fig. 5 Variation of energy dissipation rate with time (grid space 2π/64 and 2π/128) |
| 图选项 |
为了定量比较不同格式的计算结果差异,以网格间距2π/256的密网格compact5计算获得的参考解为基准,得到不同计算结果与基准解间的相对误差,公式为
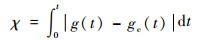 | (12) |
式中:g(t)表示某格式计算结果中某个变量随时间的变化;gc(t)表示密网格compact5计算结果中对应变量随时间的变化。
由此获得2套网格下格式的误差并制成柱状图,如图 6和图 7所示。表 1和表 2则给出2种通量格式误差的相对量,即
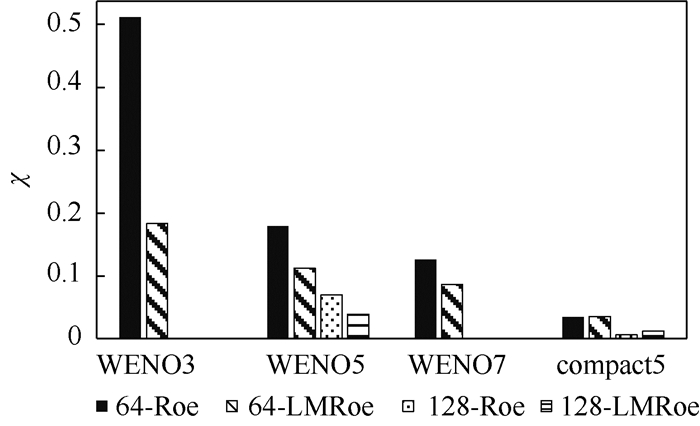 |
| 图 6 不同格式和网格量下体平均动能误差柱状图 Fig. 6 Histogram of volume-averaged kinetic energy error for different schemes with different grids |
| 图选项 |
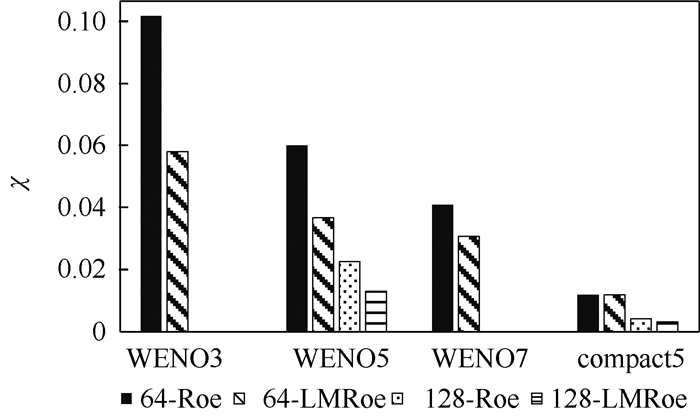 |
| 图 7 不同格式和网格量下动能耗散率误差柱状图 Fig. 7 Histogram of energy dissipation rate error for different schemes with different grids |
| 图选项 |
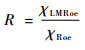 | (13) |
可以看出,对于WENO系列格式,随着格式阶数的提高,计算精度提高明显;使用LMRoe格式的精度略高于相同网格量时的Roe格式;加密网格后计算精度显著提高。而当使用compact5作为重构格式时,相同网格量下2种通量格式的计算差异不明显,尤其是体平均动能,LMRoe格式的计算误差甚至大于Roe格式。Compact5和WENO格式的计算结果比较则可看出,compact5 格式的计算精度高于所有WENO格式;特别是相同精度阶数情况下,compact5在粗网格(2π/64)上的计算结果与WENO5在密网格(2π/128)上的最佳结果(LMRoe的计算结果)精度相当。
利用如下公式:
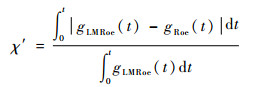 | (14) |
可以更加清晰地衡量2个通量格式的计算差别(下标Roe和LMRoe表示计算使用的是原始Roe格式或LMRoe格式)。
图 8和图 9为2套网格下原始Roe格式和LMRoe格式的计算差别χ′柱状图。可以看出,随着网格加密,2种通量格式的计算结果间差别变小,表现出向精确解收敛的特征。
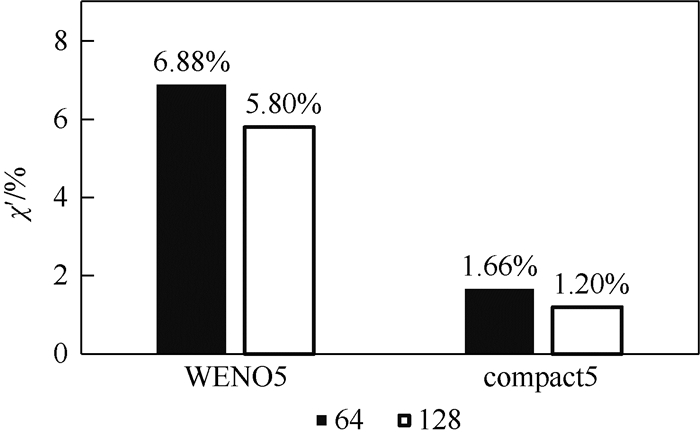 |
| 图 8 不同网格量下Roe和LMRoe通量格式的计算差异(体平均动能) Fig. 8 Calculation difference of Roe and LMRoe flux schemes with different amounts of grid (volume-averaged kinetic energy) |
| 图选项 |
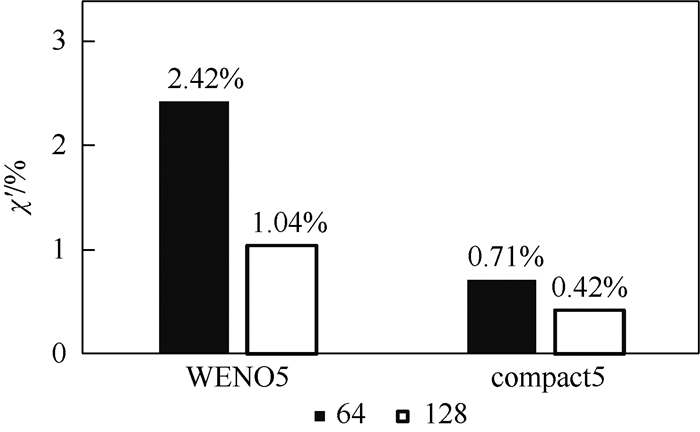 |
| 图 9 不同网格量下Roe和LMRoe通量格式的计算差异(动能耗散率) Fig. 9 Calculation difference of Roe and LMRoe flux schemes with different amounts of grid (energy dissipation rate) |
| 图选项 |
上述分析表明,通量格式、重构格式对计算精度的影响是耦合的,通量格式、重构格式、网格量等各部分数值误差的总和构成了最终的计算误差。在网格较粗且重构格式精度较低的情况下,LMRoe格式能够显著提高计算精度。结合LMRoe格式修正原理,这是由于在较粗网格下,低马赫数下LMRoe格式求解的压强与马赫数的对应关系与Navier-Stokes方程一致,导致求解误差明显降低,整体计算结果显著改善;而原始Roe格式低速时,压强与马赫数对应关系与Navier-Stokes方程不一致的问题在粗网格下凸显,对整体计算结果的影响较大。但网格加密、重构格式精度提高后,这两部分误差的减小一定程度上弥补了原始Roe格式带来的误差,使得总体的计算精度有所提升。且对于网格收敛的格式,当网格足够密时,能够给获得收敛的结果,也就是当网格足够密时,原始Roe格式也能够得到精度足够高的结果。因此,当使用密网格、高分辨率重构格式时,原始Roe格式和LMRoe格式的计算差异很小。
表 1 网格间距2π/64时不同通量格式结果的误差比值 Table 1 Ratio of two flux schemes' result errors with grid space being 2π/64
| 重构格式 | 体平均动能 | 动能耗散率 |
| WENO3 | 0.36 | 0.57 |
| WENO5 | 0.63 | 0.61 |
| WENO7 | 0.69 | 0.75 |
| compact5 | 1.04 | 1.00 |
表选项
表 2 网格间距2π/128时不同通量格式结果的误差比值 Table 2 Ratio of two flux schemes' result errors with grid space being 2π/128
| 重构格式 | 体平均动能 | 动能耗散率 |
| WENO5 | 0.56 | 0.57 |
| compact5 | 1.85 | 0.76 |
表选项
3 结论 通量格式和重构格式的精度均会影响湍流流动的模拟结果。本文利用泰勒-格林涡算例,研究了有无低速修正的通量格式对模拟结果的影响,结论如下:
1) 当流场中存在低速流动时,使用低速修正的通量格式能够一定程度上改进计算结果。
2) 通量格式对模拟结果的影响是与重构格式耦合的。当重构格式的精度较低时,通量格式对结果的影响显著,但当重构格式的精度足够高后,通量格式对结果的影响不明显。
3) 随着网格加密,有无低速修正的通量格式计算结果都呈现出向精确解收敛的特征。使用较粗网格时,低速修正的通量格式对计算结果的改进更明显。
考虑到在实际工程应用时,由于研究对象外形通常较复杂,需要使用鲁棒性较高、耗散较大的重构格式以保证计算稳定性,且受到研究周期和计算条件的限制,网格量通常相对较小,使用低速修正的通量格式能够提高计算精度。在开展湍流流动机理研究时,对计算精度要求较高,通常使用高精度高分辨率重构格式及较密的网格开展模拟,此时低速修正的通量格式对计算结果改进有限,未经过低速修正的原始通量格式也能够获得较好的计算结果。
参考文献
| [1] | 傅德薰, 马延文, 李新亮, 等. 可压缩湍流直接数值模拟[M]. 北京: 科学出版社, 2010. FU D X, MA Y W, LI X L, et al. Direct numerical simulations for compressible turbulence[M]. Beijing: Science Press, 2010. (in Chinese) |
| [2] | 屈峰.高分辨率格式的研究及其应用[D].北京: 北京航空航天大学, 2015. QU F.Research and application of high resolution schemes[D].Beijing: Beihang University, 2015(in Chinese). |
| [3] | WEISS J M, SMITH W A. Preconditioning applied to variable and constant density flows[J]. AIAA Journal, 1995, 33(11): 2050-2057. DOI:10.2514/3.12946 |
| [4] | LIOU M S. A sequel to AUSM.Part Ⅱ:AUSM+-up for all speeds[J]. Journal of Computational Physics, 2006, 314(1): 137-170. |
| [5] | KITAMURA K, SHIMA E. Towards shock-stable and accurate hypersonic heating computations:A new pressure flux for AUSM-family schemes[J]. Journal of Computational Physics, 2013, 245: 62-83. DOI:10.1016/j.jcp.2013.02.046 |
| [6] | RIEPER F. A low-Mach number fix for Roe's approximate Riemann solver[J]. Journal of Computational Physics, 2011, 230(13): 5263-5287. DOI:10.1016/j.jcp.2011.03.025 |
| [7] | FILLION P, CHANOINE A, DELLACHERIE S, et al. FLICA-OVAP:A new platform for core thermal-hydraulic studies[J]. Nuclear Engineering and Design, 2011, 241(11): 4348-4358. DOI:10.1016/j.nucengdes.2011.04.048 |
| [8] | LI X, GU C. An all-speed roe-type scheme and its asymptotic analysis of low Mach number behaviour[J]. Journal of Computational Physics, 2008, 227(10): 5144-5159. DOI:10.1016/j.jcp.2008.01.037 |
| [9] | 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006. YAN C. Method and application of computational fluid dynamics[M]. Beijing: Beihang University Press, 2006. (in Chinese) |
| [10] | GOTTLIEB S, SHU C W. Total variation diminishing Runge-Kutta schemes[J]. Mathematics of computation of the American Mathematical Society, 1998, 67(221): 73-85. DOI:10.1090/S0025-5718-98-00913-2 |
| [11] | ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1997, 135(2): 250-258. DOI:10.1006/jcph.1997.5705 |
| [12] | JIANG G, SHU C. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [13] | PIROZZOLI S. On the spectral properties of shock-capturing schemes[J]. Journal of Computational Physics, 2006, 219(2): 489-497. DOI:10.1016/j.jcp.2006.07.009 |
| [14] | FAUCONNIER D, DICK E. On the spectral and conservation properties of nonlinear discretization operators[J]. Journal of Computational Physics, 2011, 230(12): 4488-4518. DOI:10.1016/j.jcp.2011.02.025 |
| [15] | BRACHET M E, MEIRON D I, ORSZAG S A, et al. Small-scale structure of the Taylor-Green vortex[J]. Journal of Fluid Mechanics, 1983, 130: 411-452. DOI:10.1017/S0022112083001159 |
| [16] | DEBONIS J.Solutions of the Taylor-Green vortex problem using high-resolution explicit finite difference methods: AIAA-2013-0382[R].Reston: AIAA, 2013. |
