理论上,结构重叠网格技术同样适用于非结构重叠网格。但非结构网格分布的随意性以及隐式装配方法过程的相对简单性,使得非结构重叠网格技术的研究大都基于Nakahashi所提出的隐式装配算法。近年来,该方法已被成功应用于多体相对运动[8]、高超声速边界层转捩[9]、旋翼翼型[10]、桨-涡干扰[11]等研究。Lohner等[12]和Luo[13]在Nakahashi方法的基础上将网格的尺度与物面距的乘积量作为网格类别的判断标准,提高了插值稳定性。Landmann和Montagnac[14]、Xu等[15]分别通过几种不同方法提高了隐式装配算法的鲁棒性,其中Xu等[15]更是成功地将该种方法应用于飞行器的抖振研究。田书玲[16]发展了一种基于阵面的相邻单元搜索法,提高了隐式装配效率。
贡献单元的搜索占据了非结构重叠网格过程的大部分时间,且非结构重叠网格隐式算法需要针对所有网格点搜索贡献单元。然而,在结构重叠网格技术中,首先通过显式的挖洞过程识别出所有位于物面内部的单元,然后可通过割补法[17]等阵面推进方法[18]对网格重叠区域进行优化,并且只需在网格割补的同时搜索重叠区域网格的贡献单元,而非所有网格点的贡献单元。显然,相较于结构重叠网格的显式装配算法,传统非结构重叠网格隐式装配算法针对所有网格点进行贡献单元搜索的过程是低效的。
作为显式重叠网格装配算法的首要步骤,挖洞过程可以由多种方法实现,如洞映射法[19]、射线求交法[20]、矢量判别法[21]、直接法[22]和目标X射线法[23]等。其中,洞映射法采用辅助笛卡儿网格近似挖洞曲面,进而将点与曲面的关系转化为点与洞映射单元的简单关系。由于效率高、算法实现简单等,洞映射法已被广泛应用于旋翼流场计算[24]、叶轮机流场分析[25]、飞行器外挂物分离[26]和网格生成[27]等领域。但是,洞映射法要求物面必须封闭,且当笛卡儿网格具有一定精度时所消耗的物理内存也急剧升高。淮洋等[28]发展了一种改进型洞映射法,解决了物面必须封闭的问题。袁武[29]、王文[30]等提出了一种“最小洞映射”的概念,节约了内存的开销。
本文首先针对洞映射法内存占用过大的问题进行了研究,发展了一种改进型洞映射法,降低了内存的占用率;其次,通过将割补法与非结构重叠网格中隐式切割技术相结合提出了一种非结构重叠网格显式装配算法;然后,为进一步优化贡献单元搜索效率,对相邻单元搜索法进行了改进,发展了一种基于相邻阵面的贡献单元搜索法;最后,将该显式网格装配算法应用于2个典型流动算例,验证了本文算法的有效性。
1 洞映射法及其改进 1.1 传统洞映射法 传统洞映射法一般首先根据洞曲面的坐标范围建立包围盒,以洞曲面单元的平均尺寸对包围盒进行划分从而形成笛卡儿网格。然后,查找与洞曲面接触的网格单元并标记为边界单元。接着,由笛卡儿网格各个角点开始向内推进并标记洞外单元,最后剩余单元则为洞内单元。映射完成后,对于任一点P(X, Y, Z),其对应笛卡儿网格编号的计算式为
 | (1) |
式中:I、J和K分别为点P在X、Y和Z 3个方向上的编号;INT()表示取整运算;X0、Y0和Z0为笛卡儿网格起点坐标;ΔX、ΔY和ΔZ分别为笛卡儿网格在X、Y和Z 3个方向上的分辨率。
1.2 改进型洞映射法 传统洞映射法需要针对所有笛卡儿网格进行遍历并计算其属性(洞内单元、边界单元或洞外单元);另外,对于物面特征复杂或存在狭小缝隙的模型,笛卡儿网格分辨率必须提高很多倍才能满足挖洞需求。因此,为存储所有笛卡儿网格单元是否洞内单元的属性而所消耗的内存空间通常是庞大的。
实际上,针对一个封闭洞面,在查找出所有与洞曲面接触的边界单元之后,若点Q(XQ, YQ, ZQ)位于2个或多个边界单元之间,则其必是洞内单元;反之,则为洞外单元。即是说,仅存储笛卡儿网格中边界单元的属性即可,而针对所有笛卡儿网格单元属性的存储不是必须的。由此,便可大大地节约洞映射法对物理内存的消耗。本文对传统洞映射法做出如下改进。
首先,查找出所有与洞面相交的边界单元,并根据其编号N(I, J, K)顺序存储边界单元。对于任一点Q(XQ, YQ, ZQ),首先根据其编号NQ(IQ, JQ, KQ)判断是否位于某个边界单元内;若不是,则从所存储边界单元信息中查找IQ行所包含的不同边界单元编号,若同时存在编号大于NQ和小于NQ的不同边界单元,则点Q为洞内单元,反之则为洞外单元。图 1所示为改进型洞映射法产生的笛卡儿网格示意图,图中黑色单元表示边界单元。对于洞内任一点O,编号记为NO(IO, JO, KO),在IO行必然存在编号小于NO的边界单元BO1和大于NO的边界单元BO2。而对于点P,由于其编号小于其所在行编号最小的边界单元BP,故点P为洞外点;对于点Q,由于其编号大于其所在行编号最大的边界单元BQ,故点Q也为洞外点。
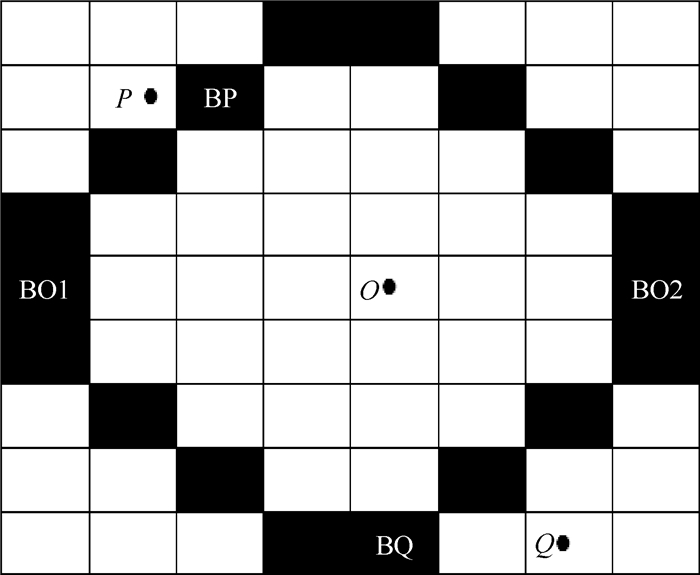 |
| 图 1 改进型洞映射法产生的笛卡儿网格示意图 Fig. 1 Cartesian grids of improved hole mapping method |
| 图选项 |
可见,相较于传统洞映射过程中需要存储所有笛卡儿网格是否位于物面内的信息,本文改进型洞映射法仅需按一定顺序存储边界单元的信息即可,因此降低了内存空间的占用率。
2 显式网格装配算法 2.1 割补法 割补法是在初始挖洞的基础上经“切割”和“填补”2个阶段使得各子网格间的洞边界最优化的过程,贡献单元的搜索也在该过程中完成。
在切割阶段,所有洞边界点依次寻找贡献单元,若贡献单元的所有节点都为正常点,则该洞边界点转变为洞内点,与其相邻的正常点转变为洞边界点,由此将洞边界推离物面;若贡献单元的节点不全为正常点,则停止该过程。
经切割之后,没有网格单元重叠,而填补阶段本质上是切割阶段的逆过程,其目的是将洞边界逐步收缩从而实现网格单元的重叠。在填补阶段,所有洞边界点依次寻找贡献单元,若贡献单元的节点不全为正常点,则该洞边界点转变为正常点,与其相邻的洞内点转变为洞边界点,由此收缩洞边界,直至再无洞内点转变为洞边界。
2.2 基于相邻阵面的贡献单元搜索技术 在割补过程中,ADT(Alternating Data Tree)寻点技术[31]是常用的贡献单元搜索方法。但是,考虑到割补法本质上是一种阵面推进技术;在阵面推进过程中,对于当前阵面中的网格点,若将上一阵面中与其相邻的点的贡献单元作为其贡献单元搜索的起始单元,便可采用相邻单元搜索法[32]通过很少的几步迭代快速找到当前阵面中点的贡献单元。
相较于ADT寻点技术,田书玲等[33]提出的基于阵面推进的相邻单元搜索法是一种更高效的贡献单元搜索方法,其结合了阵面推进技术与相邻单元搜索法的特点,核心步骤与上述思想类似:首先确定任一网格点的贡献单元,同时以该节点为首节点建立一个链表;然后循环搜索该点周围邻居节点的贡献单元,并将所有邻居节点推入链表,在搜索完所有邻居节点的贡献单元后删除首节点,接着搜索新的首节点的邻居节点;如此循环维护该链表中节点的增减,直至链表为空,贡献单元搜索结束。
图 2所示为由红蓝两套网格组成的重叠网格系统。可看出蓝色网格点P0的贡献单元为红色网格单元C、D、I。在搜索P0点的相邻节点q1~q5的贡献单元时,将单元C、D、I作为搜索的起始单元,采用相邻单元搜索法通过很少的几步迭代便可确定出点q1~q5的贡献单元。如:在单元C、D、I的相邻单元中,D、E、I是距离点q4最近的单元,再由D、E、I查找到其相邻单元I、E、F即是点q4的贡献单元;再如:从C、D、I出发通过一步迭代便可查找到其相邻单元D、E、I即是点q3的贡献单元。
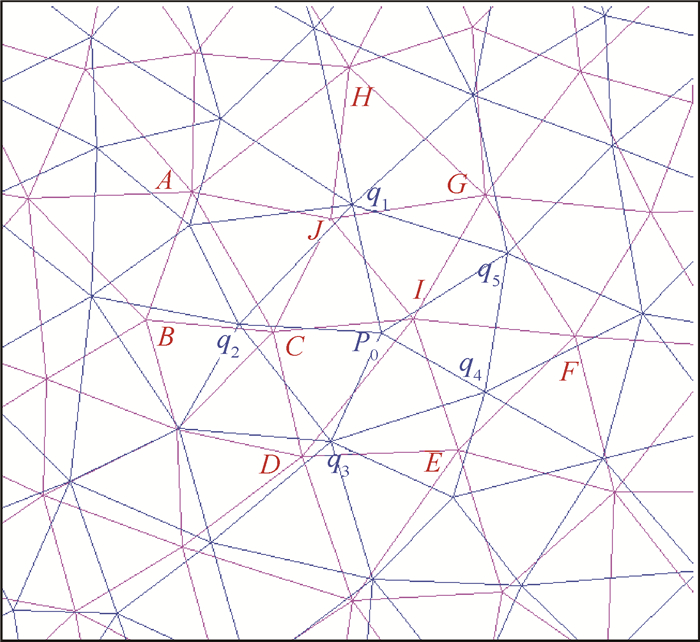 |
| 图 2 基于阵面推进的相邻单元搜索法 Fig. 2 Neighbor-to-neighbor search algorithm based on advancing front |
| 图选项 |
基于阵面推进的相邻单元搜索法会搜索所有网格点的贡献单元。但在割补法过程中仅须在切割过程中搜索当前洞边界点的贡献单元,因此本文在该方法基础上发展了一种基于相邻阵面的贡献单元搜索法以适配割补法。具体步骤如下:
1) 在初始挖洞结束之后,建立2个空链表LI和LJ,将所有当前洞边界点(I0,I1,…,In)推入链表LI。
2) 查找链表LI中首节点I0的贡献单元D0。
3) 以D0为起始单元通过相邻单元搜索法查找I1的贡献单元D1,再以D1为起始单元搜索I2的贡献单元D2,如此推进直至遍历链表LI中所有节点并对所有已搜索过贡献单元的节点进行标记。
4) 清空链表LJ,遍历链表LI,查询每个节点Ii的相邻节点Ji,若Ji未被标记则以Ii的贡献单元Di为起始单元通过相邻单元搜索法搜索节点Ji的贡献单元,然后将其推入链表LJ。
5) 清空LI,将LJ中所有节点推入LI,重复步骤4),如此通过2个链表互相迭代推进洞边界位置。
2.3 网格装配算法 贡献单元的搜索是传统非结构重叠网格隐式挖洞技术的核心,同时也是耗时最多的环节。隐式挖洞方法仅仅通过比较网格质量(如体积、物面距离等)区分插值单元与计算单元,不会挖去落在物体内部的非计算单元。虽然不影响计算结果的准确性,但这些洞内单元却参与到了贡献单元的搜索过程中,降低了装配效率。本文基于结构重叠网格理论,首先通过改进型洞映射法排除洞内单元,其次通过将割补法与隐式切割技术相结合进一步优化非结构重叠网格中贡献单元的搜索过程,提高网格装配效率。具体过程如下:
1) 循环所有网格,计算各网格单元到物面的距离并将所有单元标记为正常单元。
2) 采用本文改进型洞映射法挖去所有洞内单元,将位于物面内部的网格单元标记为洞内单元,与洞内单元相邻的正常单元标记为洞边界单元。
3) 以上述洞边界单元为初始阵面推进,并以本文所发展的基于相邻阵面的贡献单元搜索法搜索并保存其贡献单元信息。在阵面推进过程中,比较该洞边界单元与其贡献单元的物面距大小。若前者大于后者,则将该洞边界单元标记为洞内单元,而与其相邻的正常单元标记为洞边界单元。当洞边界单元的物面距小于或等于其贡献单元的物面距时结束该过程。
4) 为保证二阶计算精度,将与洞边界单元相邻的2个洞内单元标记为插值单元,同时将该洞边界单元标记为正常单元。
图 3所示为本文算法过程,该套非结构重叠网格系统由3块二维NACA0012翼型子网格和一块矩形背景网格组成。每块子网格包含11 930个三角形单元,背景网格包含3 025个四边形单元,共计38 815个单元。图 3(a)所示为以物面边界为初始挖洞边界的结果示意图,从图中可以看出,位于物面内部的网格均已被挖去,将已挖去网格单元标记为洞内单元。接着,将与洞内单元相邻的正常单元标记为洞边界单元。以所有洞边界单元为初始阵面开始推进,并使用基于相邻阵面的贡献单元搜索法搜索所有洞边界单元的贡献单元,比较洞边界点与其贡献单元的物面距大小,迭代更新洞边界,图 3(b)和图 3(c)分别表示迭代推进25步和35步时的效果图。可以看出,重叠区域逐渐减小。当所有洞边界点的物面距小于或等于其贡献单元的物面距时,停止迭代。最终的洞边界位置如图 3(d)所示。图 3(e)所示为3个翼型之间近壁面处的局部放大图。可以看出,洞边界位于不同物面的中间位置,重叠效果理想。为保证二阶计算精度,将与洞边界点相邻的2个洞内点标记为插值点。
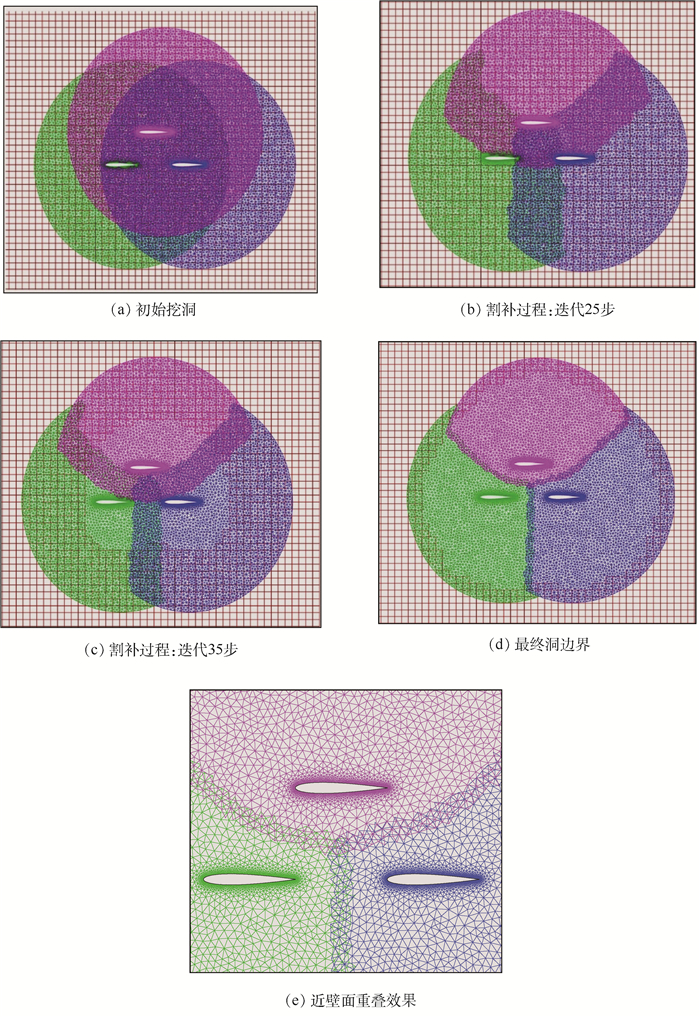 |
| 图 3 非结构重叠网格显式装配技术 Fig. 3 Explicit assembly technique of unstructured overset grid |
| 图选项 |
使用传统隐式算法对该套网格系统进行了装配,其与本文算法的效率对比情况如表 1所示。可以看出,本文算法所需进行的贡献单元搜索次数明显少于传统隐式算法,因而也具有更高的效率。本文所有计算基于Intel Xeon CPU E5-2650平台,主频为2.00 GHz。
表 1 不同算法的效率比较 Table 1 Comparison of efficiency between different algorithms
| 算法 | 贡献单元搜索次数 | 时间/s |
| 本文算法 | 4 134 | 1.25 |
| 传统隐式算法 | 38 815 | 5.12 |
表选项
3 算例 3.1 计算方法 本文采用有限体积法对Navier-Stokes控制方程进行离散求解,空间离散采用Roe-FDS(Flux Difference Splitting)格式、Piecewise Linear插值方法,提供二阶空间离散精度;湍流模型采用Menter SST(Shear Stress Transport)模型;时间离散采用LUSGS(Lower-Upper Symmetric Gauss-Seidel)隐式计算方法。
3.2 30P30N三段式机翼 对经典的二维三段式机翼30P30N[34]进行了数值模拟。来流马赫数Ma=0.2,雷诺数Re=8.7×106,迎角α=8°。流场网格由4部分组成,前缘缝翼网格包含9 996个三角形单元、主翼面网格包含48 361个三角形单元,后缘襟翼网格包含25 203个三角形单元,背景网格为348 401个四边形单元。采用本文算法后的重叠效果如图 4(a)所示。图 4(b)和图 4(c)分别为前缘和后缘的局部放大图。可以看出,重叠网格的洞边界清晰整洁,位于不同翼面的中间位置。图 5所示为该三段翼型马赫数云图,从图中可看出,流场分布合理,重叠边界处等马赫线过渡光滑。图 6为翼面压力系数Cp的数值与试验结果对比,可以看出计算结果与试验值吻合良好,表明本文算法准确可靠。
 |
| 图 4 30P30N机翼重叠网格图 Fig. 4 Overset mesh of 30P30N wing |
| 图选项 |
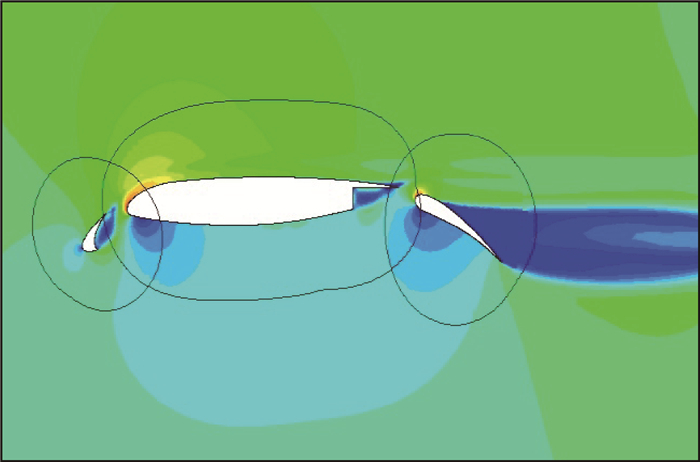 |
| 图 5 30P30N翼面马赫数云图 Fig. 5 Mach number contour of 30P30N wing surface |
| 图选项 |
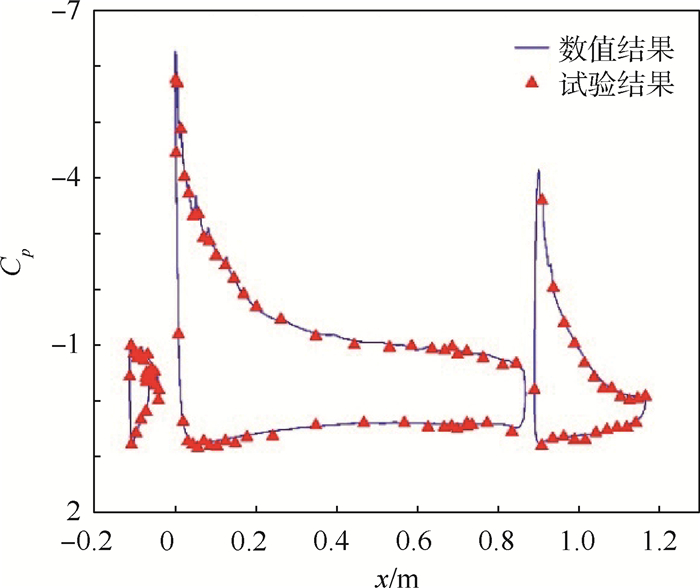 |
| 图 6 30P30N翼面压力系数的数值与试验结果对比 Fig. 6 Comparison of pressure coefficient of 30P30N wing surface between numerical and experimental results |
| 图选项 |
3.3 Titan Ⅳ运载火箭 为进一步验证本文算法在三维复杂流场中的适用性,对美国大力神Titan Ⅳ运载火箭[35]超声速外流场进行了数值仿真。计算条件为:马赫数Ma=1.6, 迎角α=0°,雷诺数Re=1.15×107。图 7所示为Titan Ⅳ火箭非结构重叠网格系统,由3部分组成:一个芯级网格以及2个助推器网格,共4 532 680个四面体单元。采用本文算法进行挖洞后的对称面网格重叠效果如图 8(a)所示,图 8(b)为助推器局部放大视图。对称面流场压力分布如图 9所示。可以看出,网格重叠区域流场分布合理、光滑。图 10给出了芯级中心线压力数值结果与试验值的比较,其中p为芯级中心线压强,pref为来流远场压强,x为沿芯级中心线位置,r为芯级半径。计算结果与试验值吻合良好。芯级与助推级之间存在连接机构, 导致试验的峰值点略高,且在连接机构附近数值结果与实验值之间的偏差稍大(图中x/r在25~35之间的区域)。
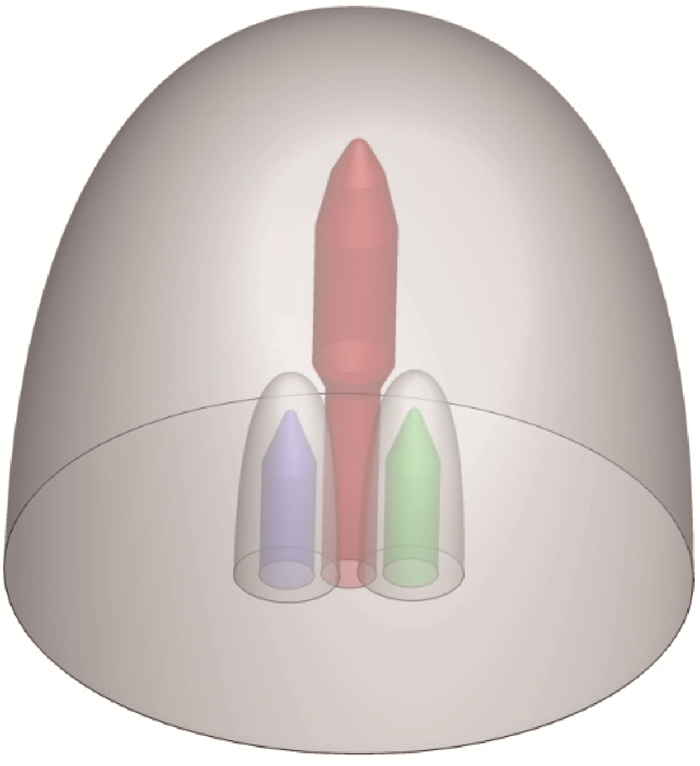 |
| 图 7 Titan Ⅳ非结构重叠网格系统 Fig. 7 Unstructured overset mesh system for Titan Ⅳ |
| 图选项 |
 |
| 图 8 Titan Ⅳ对称面重叠网格 Fig. 8 Overset mesh of Titan Ⅳ's symmetry plane |
| 图选项 |
 |
| 图 9 Titan Ⅳ对称面压力云图 Fig. 9 Pressure contour of Titan Ⅳ symmetry plane |
| 图选项 |
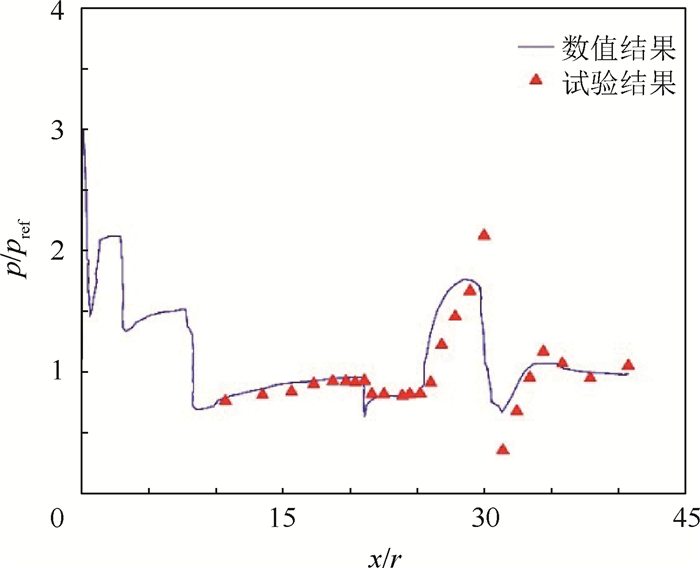 |
| 图 10 芯级中心线压力分布 Fig. 10 Pressure distribution along rocket center line |
| 图选项 |
针对上述2种模型,分别采用本文算法与传统隐式算法进行了重叠网格装配,效率对比情况如表 2所示。从表中可以看出,本文所发展的改进型洞映射法的内存占用率更低;同时相较于传统隐式装配算法,本文算法具有更好的效率。
表 2 不同算法的性能比较 Table 2 Comparison of performance among different algorithms
| 性能指标 | 算法 | 30P30N | Titan Ⅳ |
| 内存占用/MB | 本文算法 | 77.66 | 1 023.77 |
| 传统洞映射 | 151.23 | 1 903.58 | |
| 贡献单元搜索时间/s | 本文算法 | 2.12 | 29.50 |
| 传统隐式算法 | 10.35 | 126.43 |
表选项
4 结论 本文通过对传统非结构重叠网格装配过程进行优化,提出了一种显式非结构重叠网格装配算法,并得出以下几点结论:
1) 通过对传统洞映射过程进行优化,发展了一种改进型洞映射法,并大大减少了洞映射过程中对计算机内存空间的占用。
2) 结合割补法与相邻单元搜索法的特点,发展了一种基于相邻阵面的贡献单元搜索法,优化了贡献单元搜索过程,提高了搜索效率。
3) 与传统非结构重叠网格隐式装配过程相比,本文所提显式装配过程具有更高的效率。
4) 通过30P30N三段式机翼和Titan Ⅳ运载火箭2个经典算例验证了本文算法的准确性与可靠性。
参考文献
| [1] | BENEK J A, STEGER J L, DOUGHERTY F C.A flexible grid embedding technique with applications to the Euler equations: AIAA-1983-1944[R].Reston, VA: AIAA, 1983. |
| [2] | NAKAHASHI K, GUMIYA T.An intergrid boundary definition method for overset unstructured grid approach: AIAA-1999-3304[R].Reston, VA: AIAA, 1999. |
| [3] | TOGASHI F, NAKAHASHI K, ITO Y, et al.Flow simulation of NAL experimental supersonic airplane/booster separation using overset unstructured grids: AIAA-2000-1007[R].Reston, VA: AIAA, 2000. |
| [4] | TOGASHI F, ITO Y, MURAYAMA M, et al.Flow simulation of flapping wings of an insect using overset unstructured grid: AIAA-2001-2619[R].Reston, VA: AIAA, 2001. |
| [5] | TOGASHI F, ITO Y.Extensions of overset unstructured grids to multiple bodies in contact: AIAA-2002-2809[R].Reston, VA: AIAA, 2002. |
| [6] | TOGASHI F, ITO Y.Overset unstructured grids method for viscous flow computations: AIAA-2003-3405[R].Reston, VA: AIAA, 2003. |
| [7] | LEE Y L, BAEDER J D.Implicit hole cutting-a new approach for overset grid connectivity: AIAA-2003-4128[R].Reston, VA: AIAA, 2003. |
| [8] | XIAO T, QIN N, LUO D, et al. Deformable overset grid for multibody unsteady flow simulation[J]. AIAA Journal, 2016, 54(8): 2392-2406. DOI:10.2514/1.J054861 |
| [9] | XU X, WANG X D, ZHANG M, et al. A parallelized hybrid N-S/DSMC-IP approach based on adaptive structured/unstructured overlapping grids for hypersonic transitional flows[J]. Journal of Computational Physics, 2018, 371(15): 409-433. |
| [10] | MISHRA A, BAEDER J D. Coupled aeroelastic prediction of the effects of leading-edge slat on rotor performance[J]. Journal of Aircraft, 2012, 53(1): 141-157. |
| [11] | LEE Y, BAEDER J.High-order overset method for blade vortex interaction[C]//AIAA Aerospace Sciences Meeting & Exhibit.Reston, VA: AIAA, 2013: 1-10. |
| [12] | LOHNER R, SHAROV D, LUO H.Overlapping unstructured grids: AIAA-2001-0439[R].Reston, VA: AIAA, 2001. |
| [13] | LUO H.An overlapping unstructured grid method for viscous flows: AIAA-2001-2603[R].Reston, VA: AIAA, 2001. |
| [14] | LANDMANN B, MONTAGNAC M. A highly automated parallel Chimera method for overset grids based on the implicit hole cutting technique[J]. International Journal for Numerical Methods in Fluids, 2011, 66(6): 778-804. DOI:10.1002/fld.2292 |
| [15] | XU J, CAI J, LIU Q, et al. Flow simulations by enhanced implicit-hole-cutting method on overset grids[J]. Journal of Aircraft, 2014, 51(5): 1401-1409. DOI:10.2514/1.C032283 |
| [16] | 田书玲.基于非结构网格方法的重叠网格算法研究[D].南京: 南京航空航天大学, 2008. TIAN S L.Investigation of overset unstructured grids algorithm[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2008(in Chinese). |
| [17] | CHO K W, KWON J H, LEE S. Development of a fully systemized Chimera methodology for steady/unsteady problems[J]. Journal of Aircraft, 1999, 36(6): 973-980. DOI:10.2514/2.2538 |
| [18] | WEY T C.Development of a mesh interface generator for overlapped structured grids: AIAA-1994-1924[R].Reston, VA: AIAA, 1994. |
| [19] | BENEK J A, STEGER J L, DOUGHERTY F A.A flexible grid embedding technique with application to the Euler equations: AIAA-1983-1944[R].Reston, VA: AIAA, 1983. |
| [20] | LABOZZETTA W F, GATZKE T D.MACGS-towards the complete grid generation system: AIAA-1994-1923[R].Reston, VA: AIAA, 1994. |
| [21] | CHIU I T, MEAKIN R.On automating domain connectivity for overset grids: AIAA-1995-0854[R].Reston, VA: AIAA, 1995. |
| [22] | CRABILL J A, WITHERDEN F D, JAMESON A. A parallel direct cut algorithm for high-order overset methods with application to a spinning golf ball[J]. Journal of Computational Physics, 2018, 374: 692-723. DOI:10.1016/j.jcp.2018.05.036 |
| [23] | MEAKIN R L.Object X-rays for cutting holes in composite overset structured grid: AIAA-2001-2537[R].Reston, VA: AIAA, 2001. |
| [24] | YANG X, YANG A, SI J. Efficient numerical techniques for simulating a rotorcraft flow field with overlapping grids[J]. AIAA Journal, 2015, 53(5): 1372-1383. DOI:10.2514/1.J053426 |
| [25] | NINI M, MOTTA V, BINDOLINO G, et al. Three-dimensional simulation of a complete vertical axis wind turbine using overlapping grids[J]. Journal of Computational & Applied Mathematics, 2014, 270: 78-87. |
| [26] | DI Y C, GAO G, XU J L, et al. Time-accurate simulation of the aircraft external store separation[J]. Applied Mechanics and Materials, 2013, 444-445: 854-859. DOI:10.4028/www.scientific.net/AMM.444-445.854 |
| [27] | ZHAO Y, YU B, YU G. A new two-dimensional hybrid grid generation method based on improved hole cutting[J]. International Communications in Heat and Mass Transfer, 2014, 54: 103-114. DOI:10.1016/j.icheatmasstransfer.2014.03.015 |
| [28] | 淮洋, 郝海兵, 姚冰, 等. 一种改进型洞映射法[J]. 航空计算技术, 2015, 45(2): 31-34. HUAI Y, HAO H B, YAO B, et al. An improved method of hole-map[J]. Aeronautical Computing Technique, 2015, 45(2): 31-34. DOI:10.3969/j.issn.1671-654X.2015.02.008 (in Chinese) |
| [29] | 袁武, 阎超, 席柯. 洞映射方法的研究和改进[J]. 北京航空航天大学学报, 2012, 38(4): 563-568. YUAN W, YAN C, XI K. Investigation and enhancement of hole mapping method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 563-568. (in Chinese) |
| [30] | 王文, 阎超, 袁武, 等. 鲁棒的结构网格自动化重叠方法[J]. 航空学报, 2016, 37(10): 2980-2991. WANG W, YAN C, YUAN W, et al. A robust and automatic structured overlapping grid approach[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 2980-2991. (in Chinese) |
| [31] | BONET J, PERAIRE J. An alternating digital tree(ADT) algorithm for 3D geometric searching and intersection problems[J]. International Journal for Numerical Methods in Engineering, 1991, 31: 1-17. DOI:10.1002/nme.1620310102 |
| [32] | 董国国, 王立强. 基于动态结构重叠网格的三维外挂物分离的数值模拟[J]. 航空兵器, 2011(2): 21-25. DONG G G, WANG L Q. Three-dimensional store separation simulation using moving structured overlapping grid technique[J]. Aero Weaponry, 2011(2): 21-25. DOI:10.3969/j.issn.1673-5048.2011.02.005 (in Chinese) |
| [33] | 田书玲, 伍贻兆, 夏健. 用动态非结构重叠网格法模拟三维多体相对运动绕流[J]. 航空学报, 2007, 28(1): 46-51. TIAN S L, WU Y Z, XIA J. Simnlation of flows past multi-body in relative motion with dynamic unstructured overset grid method[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 46-51. DOI:10.3321/j.issn:1000-6893.2007.01.008 (in Chinese) |
| [34] | CHIN V D, PETER D W, SPAID F W.Flow field measurements about a multi-element airfoil at high Reynolds numbers: AIAA-1993-3137[R].Reston, VA: AIAA, 1993. |
| [35] | BIEDRON S, JOHNSON C T, WANG L V.Simulations using a concurrent implicit Navier-Stokes solver: AIAA-1995-223[R].Reston, VA: AIAA, 1995. |
