参考大气模型在空天试验中有着重要的应用^[1-3]。它表征了大气的理想气体性质，包括压力、密度、温度、各元素分子量等随时间、空间的变化情况。模型的输入可以是高度、纬度、或者在一年中所处的天数。不同的参考大气模型有不同的输入和输出。例如美国标准大气模型(USSA—1962)以及其后续型号(USSA—1976)，其输入为海拔高度，输出内容包括大气温度、压力和密度。不考虑时间因素的一类参考大气模型被称为静态大气模型，例如中国的参考大气模型GJB 365.1—87^[4]。在静态模型的基础上，如果考虑了随时间的变化，如中国的参考大气模型GJB 5601—2006^[5], 则模型可以同时反映大气参数随时间和空间变化。
真实大气环境中还存在着大小尺度的扰动，传统的大气参考模型中缺乏对扰动量的表征。大气环境中的大尺度扰动是大气环境中扰动尺度与时间尺度较长的扰动现象，主要包括时间尺度为数天至一个月，扰动尺度与地球纬度长度相当行星波以及24 h周期及其高次谐波的潮汐波等。中小尺度扰动的扰动尺度与时间尺度相对较短，如几分钟至十几个小时周期的重力波与时间尺度更短的大气湍流扰动等^[6-7]。大气环境中的扰动对于空天试验有着重要的影响，例如密度的扰动会影响飞行器的热流，风场的扰动会影响到弹体的落点精度。对大气扰动进行研究并构建合适的仿真模型对于提升空天试验仿真精度具有最重要意义。早在20世纪70年代，国外****Justus在文献[8]中对重力波上层大气的混合作用进行了研究，并在文献[9]中利用蒙特卡罗仿真对大气密度扰动进行了研究。国内****肖存英等在文献[7]中对临近空间的大气扰动量变化特性进行了定量研究，并在文献[10]中对临近空间大气密度建模进行了研究，但由于2篇文献所使用的数据来源为SABER探测器，该探测器只可探测到水平尺度大于100~200 km的波动，数据无法反映小尺度扰动的影响^[10]。
空天试验的跨度极广，航程上常常超过数千公里，航线跨越多个气候带甚至南北半球，在导航、制导与控制的设计过程中需要考虑大气环境随时空大幅度改变。传统工程应用中仅仅对起飞点或者降落点的大气环境测量与建模不能完全地满足空天试验需求。为此美国、俄罗斯等国都构建了具有全球覆盖尺度的大气参考模型。例如美国宇航局马歇尔太空飞行中心，利用美国国家环境预测中心(National Centers for Environmental Prediction, NCEP)全球再分析数据库, 全球上层大气气候图集(Global Upper Air Climatic Atlas, GUACA)等气候数据，研发了一种涵盖有完整的地面到轨道高度的、且体现完整的全球地理差异变化以及完整的热力学变量随季节以及月度差异变化的全球参考大气模型(Global Reference Atmospheric Model, GRAM), 并对其不断进行着更新升级^[11-14]。GRAM提供了温度、密度、压强、风场、各分子量浓度等大气参数的气候期望值及其扰动量随时空的变化的输出。但客观上来自气象卫星、火箭、遥感器、探空器等的观测数据并不足以覆盖全部时空，在参考大气模型构建过程中必须使用插值技术进行补充，例如在GRAM构建的过程中，使用到了垂直插值、二维插值、过极点插值、数据集合间的过渡插值、季节与月份数据插值等过渡等插值技术^[11-14]。因此对于特定的空域，全球参考大气模型可能不如该地区长时间实际测量所得的结果精度高。一种将基于实测数据的局部参考大气与高覆盖性的大气参考模型相结合的建模方法，对于提高模型的局部精度，更好地满足空天试验对大气模型的需求具有重要意义。
酒泉地区是中国的重要空天试验基地，中国****对该地区的大气环境特性进行过多方面的研究。杨钧烽等基于MERRA(the Modern Era Retrospective-analysis for Research and Applications)再分析资料的风场数据，对酒泉地区上空的风切变特性进行了分析^[15]。高振荣等基于酒泉等6个地面气象站的数据对河西走廊地区近58年的气温变化与突变分析进行了研究^[16]。刘晓云等基于酒泉测站数据，对酒泉地区的气温和降水特征进行了分析^[17]。
本文利用酒泉地区(98.5°E, 39.5°N)的典型气象站2010—2011年2年的逐日探空试验密度数据，对该地区海拔1~23.5 km的大气密度均值与扰动的冬夏季节性差异进行了分析。通过将实测数据与GRAM进行对比分析，提出了基于实测数据的均值与扰动量参数的模型定量修正方法，从而构建起了区域参考大气模型。在此基础上通过蒙特卡罗仿真与实测数据的对比，说明了该种建模方式的可行性与实用性。最后将局部大气密度模型与GRAM相结合，提出了一种由基于实测数据的局部参考大气向高覆盖范围的全球动态参考大气环境过渡的方法，使参考大气模型既具有全球尺度的覆盖性，又具有很高的局部精度，可以更好地满足空天试验需求。
1 大气密度特性冬夏季节差异分析 1.1 数据来源与处理 本文中所使用的实测数据来自于酒泉地区(98.5°E, 39.5°N)典型气象站2010—2011年的逐日探空试验(部分日期单日内进行了若干次探空试验)，探测信息包括温度、密度、压强、经纬向风风速，探测空间包括对流层至平流层下部的部分空域。相较于卫星探测器，探空气球所搭载的探测设备是对密度的直接测量，因此数据中包含了中小尺度扰动的影响。实际测量过程中，受恶劣自然环境影响，部分日期探空气球在进入平流层之前信号丢失，本文在数据处理过程中舍弃了这部分数据。对于顺利进入平流层的试验所测得的各组数据，选取海拔高度范围1~23.5 km，将逐日数据中超出3倍标准差的异常值剔除，并对逐日数据按月份归类处理，方便分析大气参数随季节变化。经过上述处理后，最终1月剩余数据组数为49组，7月为59组。
在本文的研究中所应用的另一个研究对象是GRAM, 其数据来源随海拔高度不同而不同^[11-14]：从0~27 km，热力学和风的数据来源于全球上层大气气候图集(GUACA)；20~120 km之间的数据来自中层大气计划(Middle Atmosphere Program, MAP)；120 km以上的热层大气，数据来源可以由用户在马歇尔工程热层模型(the Marshall Engineering Thermosphere model Met-2007，MET-2007)、雅里奇·鲍曼热层模型(Jacchia-Bowman 2006 thermosphere model, JB2006)、海军研究实验室质谱仪非相干散射雷达扩展模型(Naval Research Labs Mass Spectrometer, Incoherent Scatter Radar Extended Model, NRLMSISE-00)以及相关的谐波风模型(Harmonic Wind Model, HWM-93)等数个模型中进行选择。在全球参考大气模型的最新版本Earth-GRAM2010中，来自GUACA的数据已被NCEP全球再分析数据库的数据所取代^[14]。
1.2 大气密度特性冬夏季节差异 本文选取1月作为冬季的典型月份，7月作为夏季典型月份。同时为了更直观地表征密度扰动量，将扰动量无量纲化表示，定义密度扰动为实际值偏离统计月均值地百分比。对实测数据地统计分析表明，冬夏两季酒泉地区海拔1~23.5 km的大气密度特性，具体包括大气密度均值与扰动量均有明显差异。实测大气密度数据的均值与扰动量如图 1~图 3所示。图 2、图 3中的粗实线表示实测数据的3倍标准差范围。

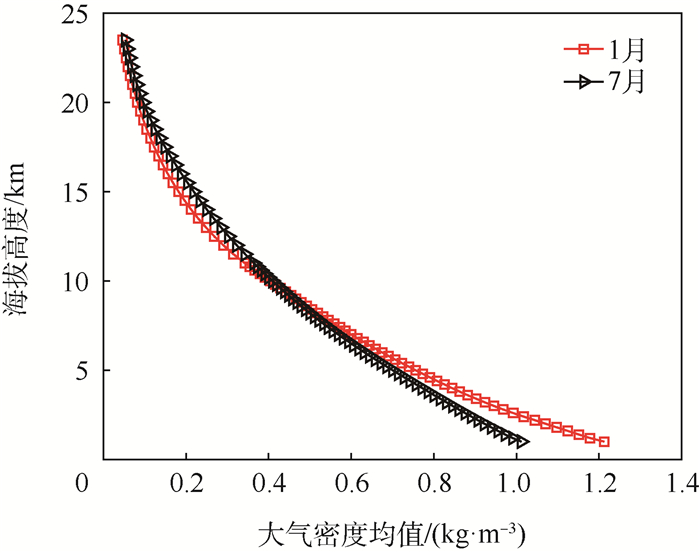图 1 1月与7月大气密度均值随海拔高度变化 Fig. 1 Variation of mean atmospheric density with altitude in January and July

图选项

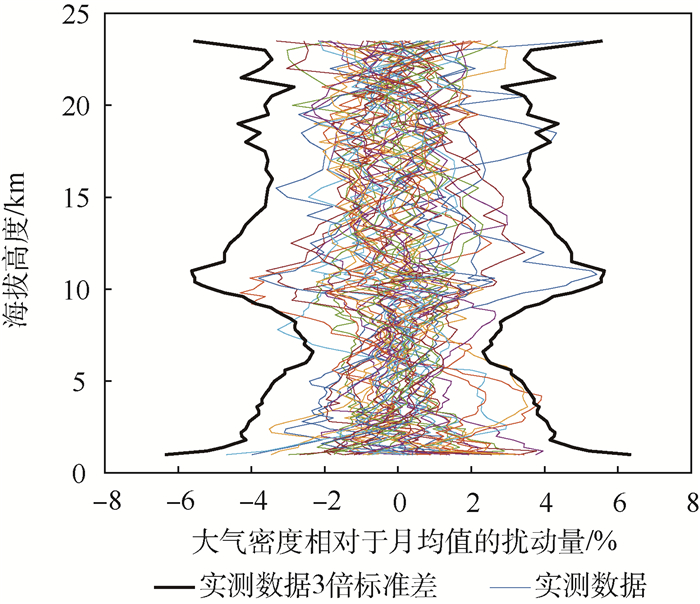图 2 1月大气密度扰动量随海拔高度变化 Fig. 2 Variation of atmospheric density perturbation with altitude in January

图选项

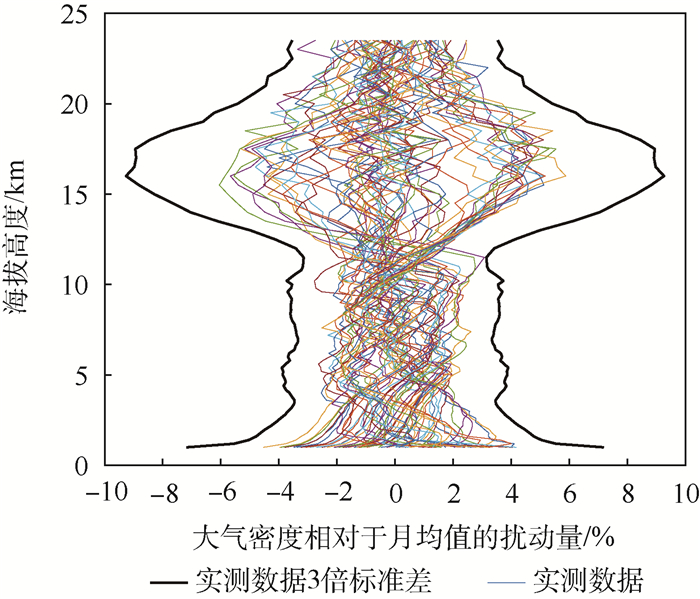图 3 7月大气密度扰动量随海拔高度变化 Fig. 3 Variation of atmospheric density perturbation with altitude in July

图选项

密度均值方面，海拔9.6 km是一个分界点。在海拔1~9.6 km范围内，冬季密度均值小于夏季，该范围内在海拔1 km处两者差值达到最大值16.56%(相对于冬季均值)，差值随海拔增加呈减小趋势。在海拔9.6~23.5 km范围内，冬季密度均值大于夏季，两者差值在16.5 km处达到最大值-21.67%(相对于1月均值)，在这一范围内两者差值随海拔高度增加呈先增加后减小的趋势。
扰动量方面，1月与7月的数据整体上均呈现随海拔高度增加，扰动量先减小再增大之后继续减小的趋势。为了可以更加直观地分析扰动量的变化并进行对比，对扰动量数据进一步处理。当实测样本足够多时，相对统计月期望值的随机偏差量基本满足具有统计月标准差的高斯分布^[10]：

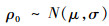(1)

式中：ρ₀为大气密度；μ为大气参数月均值；σ为大气参数标准差。
相对于统计月均值的扰动量ρ_pm0自身的分布，应当是一种期望值为零的高斯分布：

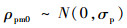(2)

式中：σ_p为相对于统计月均值的扰动量的标准差。
因此可以将σ_p作为扰动量的一个特征参数来进行定量分析。1月与7月的大气密度相对于统计月均值的扰动量标准差σ_p随海拔高度的变化及两者的对比情况如图 4所示。

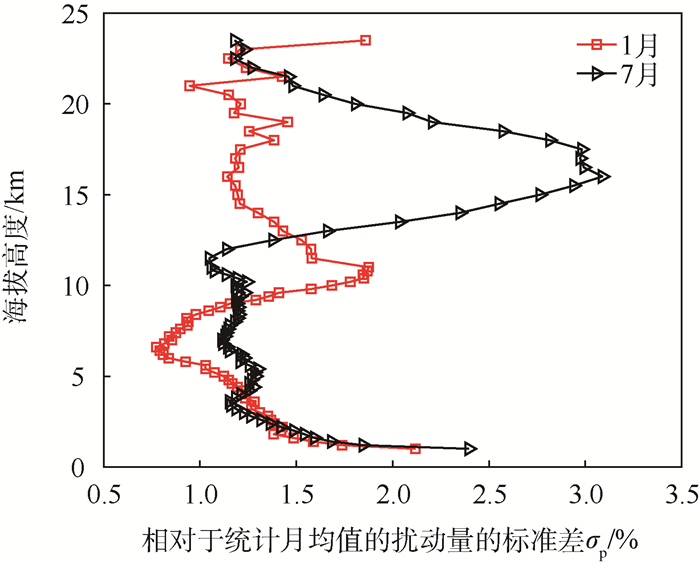图 4 1月与7月大气密度相对月均值的扰动量的标准差随海拔高度变化 Fig. 4 Variation of standard deviation of perturbation compared with mean atmospheric density of statistical month with altitude in January and July

图选项

随海拔高度变化的趋势方面，1月与7月的大气密度扰动量的标准差σ_p在海拔高度1~23.5 km范围内整体上均呈现先减小再增大之后继续减小的趋势，2个月份的数据在对流层内有2个明显的拐点。其中1月份σ_p数据的这2个拐点对应的海拔高度分别为6.6 km与11 km，7月份σ_p数据的这2个拐点对应的海拔高度分别为11.5 km，16 km。1月份σ_p数据在1~17.5 km范围内随海拔高度升高的单调性有着较为明显的趋势，但在17.5 ~23.5 km范围内的随海拔高度升高出现了增减的反复。7月份σ_p数据在海拔高度11.5 km以下随海拔高度升高存在增减的反复，但在11.5 ~23.5 km范围内，随海拔高度升高σ_p有着明显而平稳的单调性趋势。
数值变化方面，1月的大气密度扰动量的标准差σ_p在海拔高度1 km(接近酒泉地区地面)处达到最大值2.118%，在海拔高度6.6 km处达到最小值0.773%，此外11 km处σ_p为1.876%，在海拔高度23 km以上出现了突增，在23.5 km处达到了1.859%；7月的大气密度扰动量的标准差σ_p在海拔高度16 km处达到了最大值3.088%，在海拔高度11.5 km处达到最小值1.049%。
通过变化趋势与数值2个方面的分析可知，7月大气密度的扰动量的标准差σ_p随海拔高度的变化幅度整体上大于1月，数值上整体偏大，这意味着酒泉地区海拔高度1~23.5 km范围内的7月份大气密度扰动整体上更为剧烈。
2 区域参考大气密度建模 20世纪80年代Justus提出了将大气参数表示为均值与密度扰动之和的建模方式^[8]，在后续数十年的空天试验当中也依旧采用了这种建模方式^[11-14]。本文中的大气密度建模同样采用均值与随机扰动叠加构成大气参数的方式进行建模，即每一个蒙特卡罗仿真值是按照式(3)产生的：

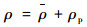(3)

式中：ρ为大气密度的仿真值；ρ为大气密度的统计月均值的仿真值；ρ_p为大气密度的扰动值的仿真值。
本文所述扰动量ρ_pm是一个无量纲化的概念，它是在扰动值的基础上提出的，表示扰动值相对于月均值的比例：

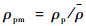(4)

区域参考大气密度的建模基于实测数据，通过对GRAM均值与扰动量2个方面的修正来实现。通过GRAM与实测数据的对比分析可以说明进行修正的必要性。将酒泉地区的经纬度坐标及对应统计月份输入GRAM后，可得1月与7月的均值输出与扰动输出。
2.1 基于实测数据的均值修正 由于均值是高斯分布的位置尺度参数，对均值的修正可以提升蒙特卡罗仿真对大气环境的模拟效果。通过对比实测数据与GRAM输出的酒泉地区1月与7月数据密度均值，可以发现1月数据海拔高度6 km以下GRAM数据的均值相较实测数据偏小，6~23.5 km范围GRAM数据的均值相较实测数据偏大，且在海拔高度16~23.5 km范围内两者误差超过了5%；7月全球参考大气模型的数据与实测数据的差距相较于1月更大，在海拔高度10.6 km以下模型的仿真均值输出小于实测数据，而在10.6~23 km范围内则大于实测数据，并且两者误差也超过了5%。实测数据与GRAM输出的相应月份的大气密度均值具体对比如图 5和图 6所示。

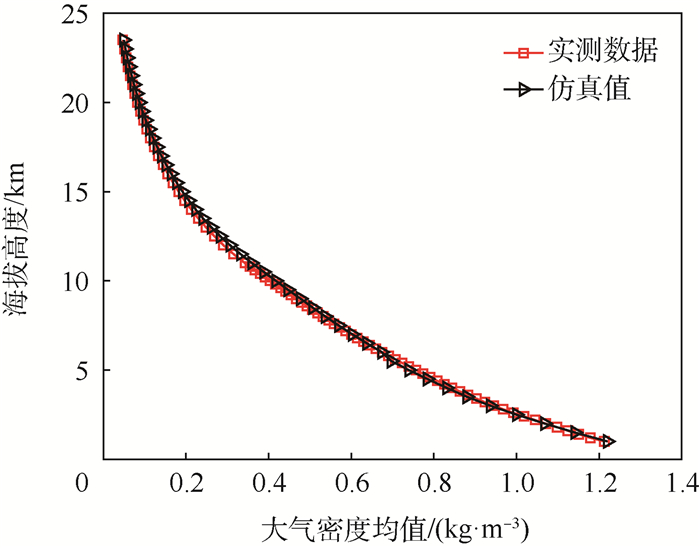图 5 实测数据与GRAM输出的1月大气密度均值对比 Fig. 5 Contrast of mean atmospheric density of measured data to that of output of GRAM in January

图选项

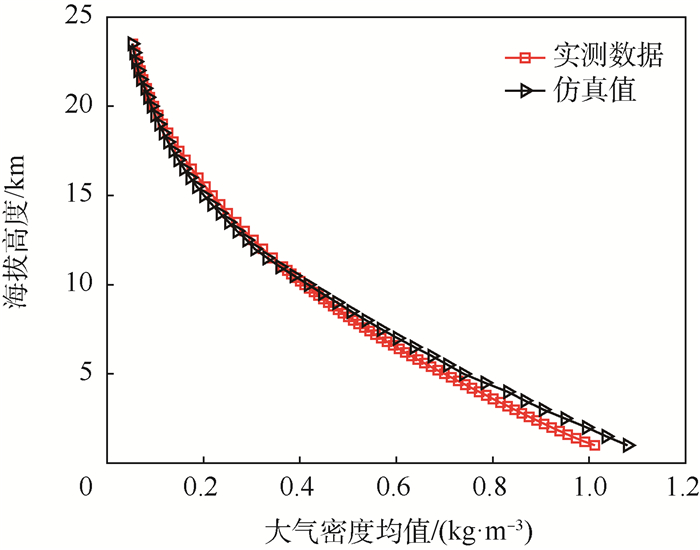图 6 实测数据与GRAM输出的7月大气密度均值对比 Fig. 6 Contrast of mean atmospheric density of measured data to that of output of GRAM in July

图选项

通过对比分析可以说明进行基于实测数据的均值修正是十分必要的。通过使用实测数据的均值替代原大气模型中的均值数据来实现对均值的修正，本文中使用修正量占相对原大气模型输出的百分比来定量描述修正，1月与7月的修正结果分别如表 1和表 2所示。
表 1 1月大气密度均值相对GRAM原输出的修正 Table 1 Correction of mean atmospheric density compared to GRAM primary output in January

海拔高度/km	均值相对原输出的修正量y/%
1	-0.60
2	0.22
3	0.91
4	1.57
5	2.26
6	0.10
7	-0.43
8	-1.03
9	-2.20
10	-3.37
11	-4.61
12	-5.20
13	-4.87
14	-4.85
15	-4.83
16	-4.91
17	-5.13
18	-5.28
19	-5.56
20	-5.57
21	-5.62
22	-5.57
23	-5.43
23.5	-5.57

表选项






表 2 7月大气密度均值相对GRAM原输出的修正 Table 2 Correction of mean atmospheric density compared to GRAM primary output in July

海拔高度/km	均值相对原输出的修正量y/%
1	6.69
2	7.84
3	7.05
4	7.66
5	5.69
6	6.67
7	6.00
8	5.21
9	4.06
10	1.81
11	-1.58
12	-5.07
13	-5.33
14	-6.35
15	-8.18
16	-9.02
17	-8.95
18	-7.97
19	-6.72
20	-5.16
21	-3.87
22	-6.59
23	-4.46
23.5	-3.43

表选项






2.2 基于实测数据的扰动修正 全球参考大气模型中对密度大小尺度的扰动均有建模^[11-14]。其中大尺度扰动使用了随机的变幅值、变波长、变相位的大尺度扰动建模方法。假设为变幅值的余弦函数，扰动为在一定数值区间内的随机数，构建无量纲化的大尺度扰动函数如下:

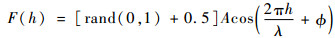(5)

式中：h为海拔高度；rand(0, 1)表示在0至1区间内产生的随机数；A为幅值；λ为波长；?为相位。A与λ为高度的函数，?与初始位置选取有关。
小尺度扰动则使用了一阶自回归模型来表示，通过连续的扰动值之间的必要相关性来计算在新位置处的扰动。该建模方式的主要思路是假设已知x方向上某位置x₁处的归一化变量α(x₁)(α为x₁方向上相对均值的偏差值与标准差之比), 则下一位置x₂的变量α(x₂)表达式为

(6)

式中：q(x)为期望值为0以及标准差为1的标准高斯分布；r为一系列归一化变量之间的自相关系数。
但通过实际仿真检验，全球参考大气模型中酒泉地区1月与7月扰动量的输出与实测数据存在一定差异，对扰动量的修正也是十分必要的。标准差是高斯分布的尺度参数，大气扰动对于大气参数的影响体现在数据标准差上，基于前文对于扰动量自身分布的分析，本文中使用相对于统计月均值的扰动量的标准差σ_p来作为修正的依据。由于扰动量修正是在均值修正的基础上进行的，所以计算σ_p时所用到的统计月密度均值实际为实测数据的均值。
首先以1月数据的修正为例，统计处理全球参考大气模型酒泉地区1月大气密度250次蒙特卡罗的仿真结果，得到相对于统计月均值的扰动量的标准差σ_p扰动量仿真值与实测数据的扰动量的对比如图 7所示。

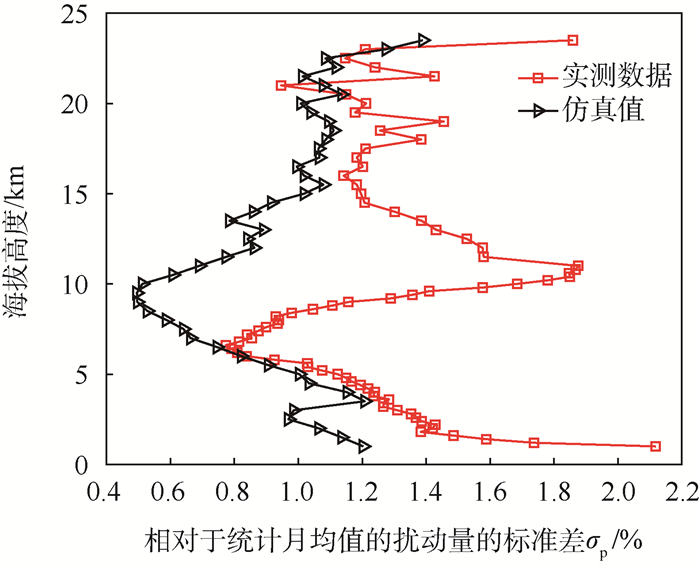图 7 1月实测数据与GRAM输出的大气密度相对月均值的扰动量的标准差的对比 Fig. 7 Contrast of standard deviation of measured data to that of output of GRAM in terms of perturbation compared with monthly mean atmospheric density in January

图选项

与实测数据对比可知，海拔高度1~3 km以及7~20 km范围，全球参考大气模型仿真输出的扰动量相较实际情况偏小，3.5~6.5 km以及20.5~23.5 km范围模拟效果相对较好。为了定量说明针对相对于统计月均值的扰动量的标准差σ_p的修正，按照式(7)定义修正因子k：

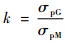(7)

式中：σ_pG为对全球参考大气模型输出统计计算后得到的相对于统计月均值的扰动量的标准差；σ_pM为实测数据相对于统计月均值的扰动量的标准差。
通过调整修正因子使得σ_pG接近σ_pM，从而使得蒙特卡罗仿真的扰动输出更加接近实测数据，对于7月的扰动量修正过程与此相同。最终1月与7月的定量修正结果如表 3和表 4所示。
表 3 1月大气密度相对月均值的扰动量的标准差相对GRAM原输出的修正 Table 3 Correction of standard deviation of atmospheric density perturbation compared to GRAM primary output in January

海拔高度/km	修正因子k
1	1.76
2	1.33
3	1.31
4	1.06
5	1.12
6	1.02
7	1.29
8	1.60
9	2.85
10	3.28
11	2.70
12	1.82
13	1.61
14	1.51
15	1.17
16	1.12
17	1.11
18	1.27
19	1.33
20	1.20
21	1.07
22	1.11
23	0.95
23.5	1.34

表选项






表 4 7月大气密度相对月均值的扰动量的标准差相对GRAM原输出的修正 Table 4 Correction of standard deviation of atmospheric density perturbation compared to GRAM primary output in July

海拔高度/km	修正因子k
1	1.99
2	1.40
3	1.25
4	1.05
5	1.28
6	1.50
7	1.68
8	2.01
9	2.40
10	2.31
11	1.53
12	1.32
13	1.87
14	2.73
15	2.72
16	3.03
17	2.79
18	2.59
19	2.02
20	1.79
21	1.42
22	1.28
23	1.24
23.5	1.17

表选项






2.3 修正的仿真校验 经过2.1节中的均值修正与2.2节中扰动量的修正，可以通过蒙特卡罗仿真对修正后整体输出结果进行检验，每一个蒙特卡罗的输出值产生过程为

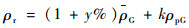(8)

式中：ρ_r表示修正后的仿真值；ρ_G表示GRAM原输出的均值；y为2.1节表 1与表 2中所述修正量；ρ_pG为GRAM原输出的扰动值；k为2.2节所述修正因子。
通过大量蒙特卡罗仿真与实测数据的对比可以说明这种建模方式的可行性与实用性。1月与7月各250次仿真结果如图 8与图 9所示。

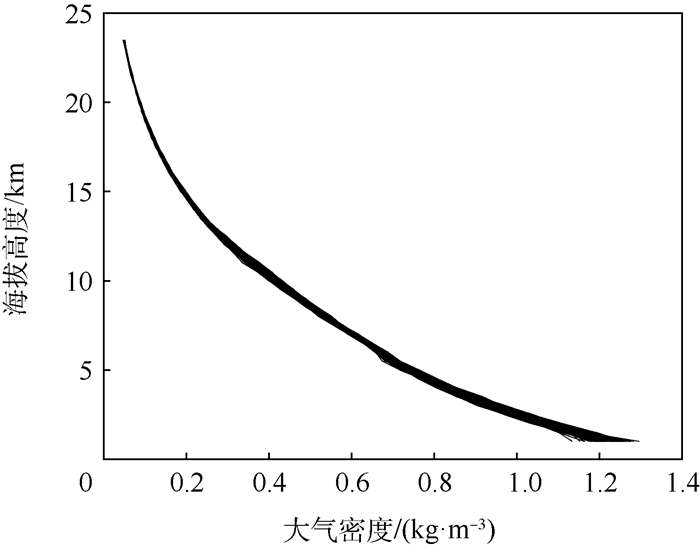图 8 区域参考大气密度模型1月的蒙特卡罗仿真结果 Fig. 8 Monte Carlo simulation results of range reference atmospheric density model in January

图选项

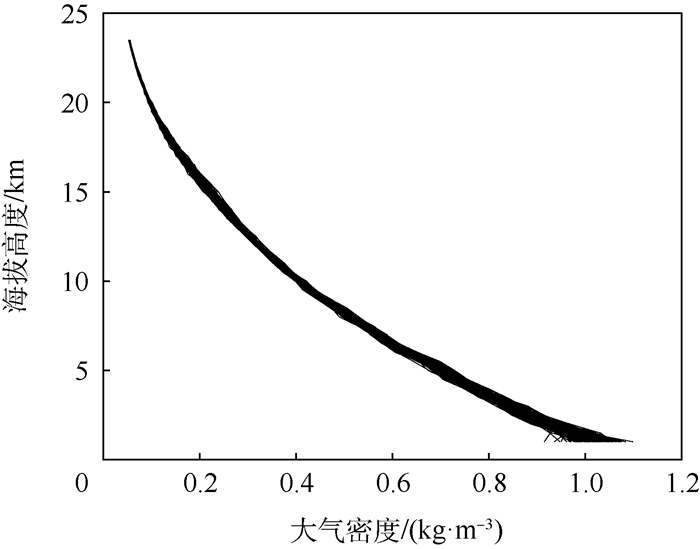图 9 区域参考大气密度模型7月的蒙特卡罗仿真结果 Fig. 9 Monte Carlo simulation results of range reference atmospheric density model in July

图选项

由于仿真过程中每一个仿真值是按照均值与扰动值叠加的方法产生的，其中均值本身就是实测数据的统计月均值，所以可以通过检验仿真对实测数据的扰动量的模拟效果来进一步校验区域参考大气模型。统计计算1月与7月250次蒙特卡罗仿真的扰动量，并与1月49组实测数据和7月59组实测数据的扰动量进行对比。结果如图 10~图 13所示，各图中粗实线为实测数据的大气密度扰动量的3倍标准差。

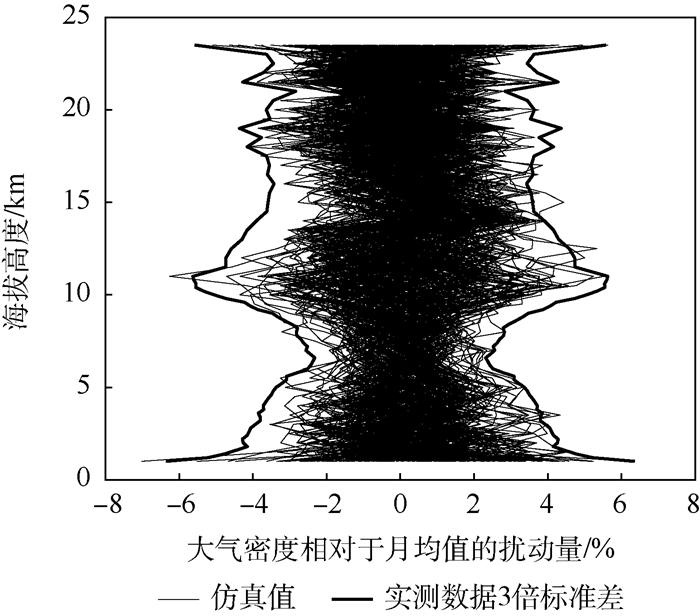图 10 区域参考大气密度模型1月密度扰动量的蒙特卡罗仿真结果 Fig. 10 Monte Carlo simulation results of density perturbation of range reference atmospheric density model in January

图选项

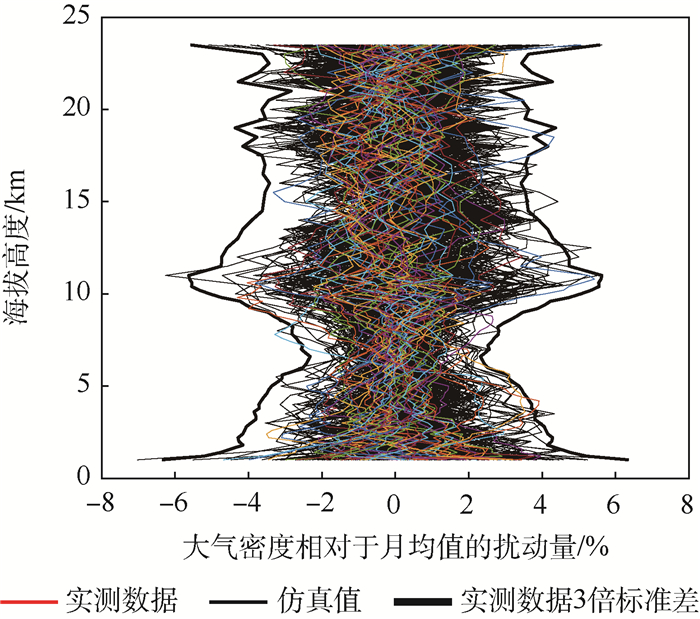图 11 区域参考大气密度模型1月密度扰动量的蒙特卡罗仿真结果与实测数据对比 Fig. 11 Contrast of Monte Carlo simulation results of density perturbation of range reference atmospheric density model to that of measured data in January

图选项

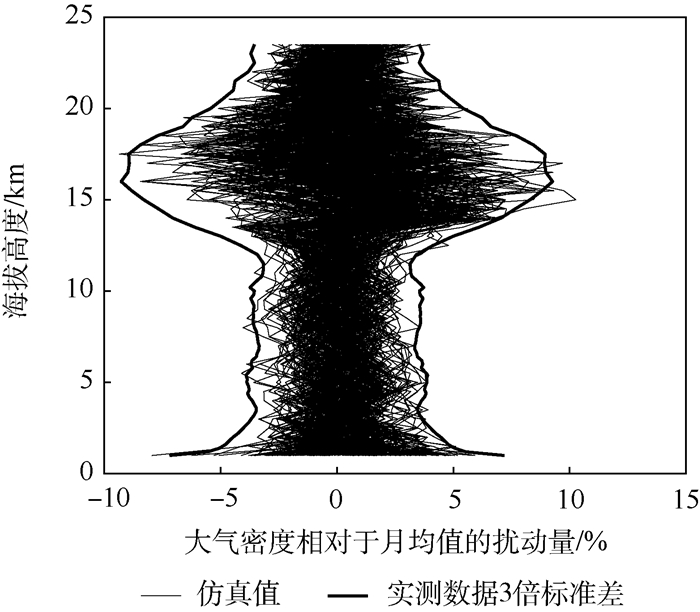图 12 区域参考大气密度模型7月密度扰动量的蒙特卡罗仿真结果 Fig. 12 Monte Carlo simulation results of density perturbation of range reference atmospheric density model in July

图选项

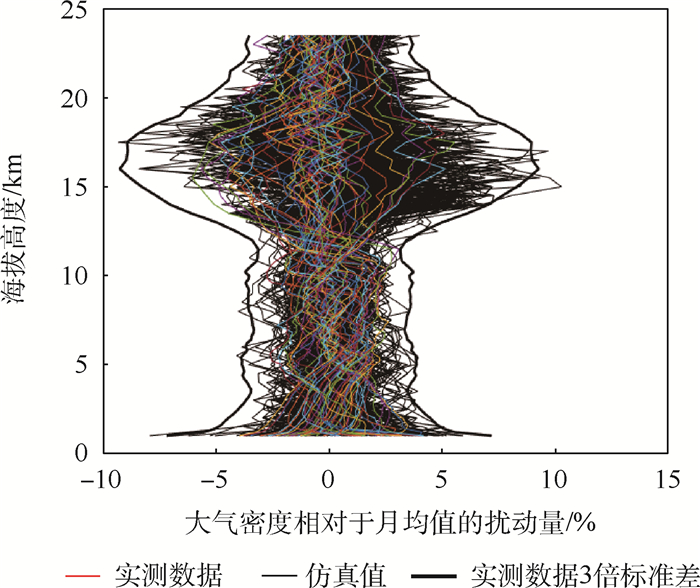图 13 区域参考大气密度模型7月密度扰动量的蒙特卡罗仿真结果与实测数据对比 Fig. 13 Contrast of Monte Carlo simulation results of density perturbation of range reference atmospheric density model to that of measured data in July

图选项

通过扰动量的对比，可以更加直观地看出实测数据落在了仿真值的包络范围内，且仿真值基本都在实测数据的3倍标准差范围内。通过相对统计月均值的扰动量的标准差这一特征参数的对比，可以进一步说明区域参考大气对于实测数据的扰动量也有很好的模拟效果。扰动量的标准差的蒙特卡罗仿真结果与实测数据的对比如图 14和图 15所示。

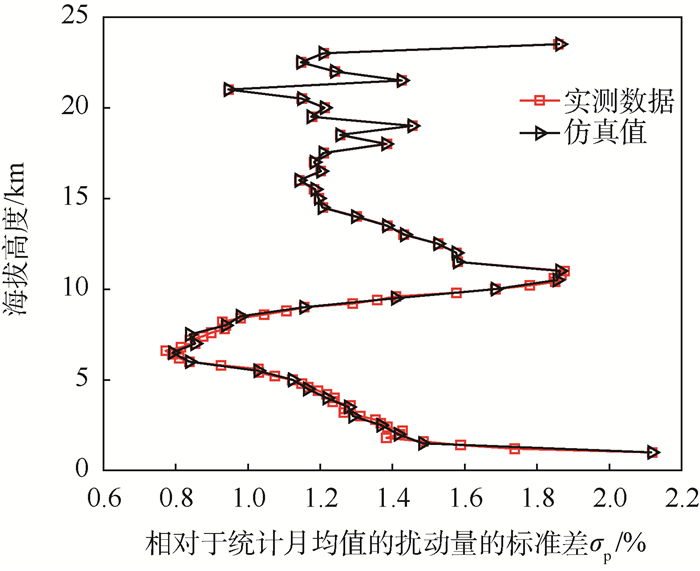图 14 定量修正后1月实测数据与GRAM输出的大气密度相对月均值的扰动量的标准差的对比 Fig. 14 Contrast of standard deviation of measured data to that of output of GRAM in terms of perturbation compared with monthly mean atmospheric density after quantitative correction in January

图选项

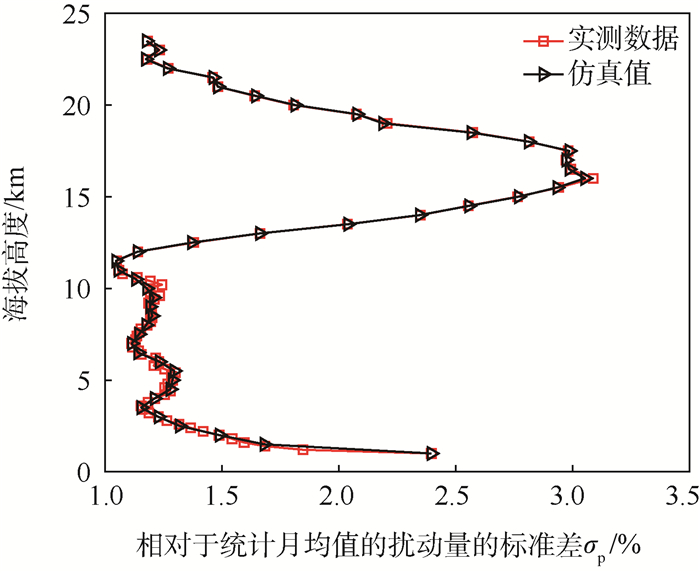图 15 定量修正后7月实测数据与GRAM输出的大气密度相对月均值的扰动量的标准差的对比 Fig. 15 Contrast of standard deviation of measured data to that of output of GRAM in terms of perturbation compared with monthly mean atmospheric density after quantitative correction in July

图选项

3 区域参考模型向GRAM的过渡与应用方法 为了适应跨越时空范围极为广阔的空天试验需求，还需要将修正后的局部大气模型与全球参考大气模型进行过渡。本文中采用一种相对简单的过渡算法处理局部参考大气向全球参考大气过渡的问题。
首先以实测数据的经纬坐标作为中心点，规定经纬度半径值为R, 当R=2°时的半径值为R_t；当R=5°时的半径值为R_l。对于半径范围在2°之内的大气参数，模型输出经过修正的局部参考大气模型的数据；对于半径范围大于5°的大气参数，输出全球参考大气模型的数据；对于半径范围在2°~5°之间的大气参数，输出2种大气模型的过渡数据。即数据输出按照式(9)过渡算法执行：

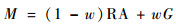(9)

式中：M为参考大气模型最终输出；RA为区域参考大气模型的输出；G为GRAM输出；w为过渡权重数值。w具体计算方法如下：

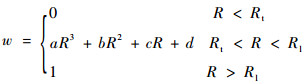(10)

为了使过渡平滑光顺，各项参数如下:

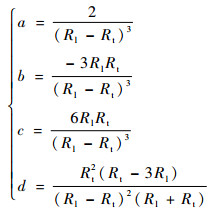(11)

以东经86°~94°，北纬36°~42°范围为例，通过海拔高度21 km处的大气密度输出情况来表示局部参考大气模型向全球参考大气模型过渡方法，如图 16所示。

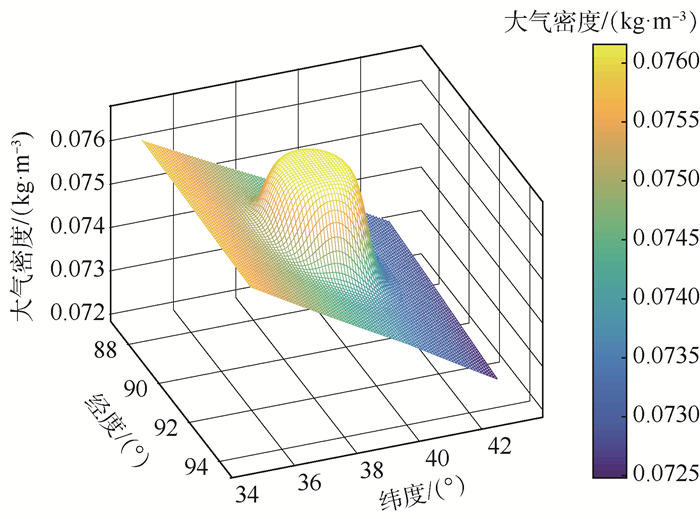图 16 区域参考大气密度模型向GRAM的过渡方法示意 Fig. 16 Illustration of transition method for range reference atmospheric density model to GRAM

图选项

以海拔高度21 km为例，区域参考大气向全球参考大气过渡的建模技术的应用方法如图 17所示。图中黄色实线为假设的飞行器航迹，例如发射点为酒泉地区，降落点为西部某地，红色与蓝色圆环分别表示发射点与降落点的区域参考大气模型范围。在进行飞行仿真的过程中，航迹处于小圆以内的部分使用区域参考大气数据，大圆以外的部分使用全球参考大气模型的数据，内外圆之间属于过渡范围，按照前文所述的过渡方法使用过渡数据。这样既可以保证关键航迹点的模型精度，同时还使模型具有了全球尺度的覆盖性，并且可以在2种模型间平滑过渡。

图 17 与GRAM过渡结合的区域参考大气密度模型的应用方法示意 Fig. 17 Illustration of application method for range reference atmospheric density model combined with GRAM transition

图选项

4 结论 为满足空天试验对参考大气模型对跨时空的全球覆盖性与局部高精度性的要求，本文探空实测大气密度冬夏典型代表月份的数据分析了探测地区的大气密度特性冬夏季节性差异，通过定量修正GRAM，构建了区域参考大气密度模型，模型的蒙特卡罗仿真结果可以有效模拟实测数据。最后通过本文所提出的区域参考大气向GRAM的过渡与应用方法，使参考大气模型即具有全球尺度的覆盖性，又具有很高的局部精度。受气球探空的试验条件限制，本文仅对海拔高度1~23.5 km空域范围进行了研究，而临近空间范围的大气探测需要探空火箭与遥感技术来实现。但本文所提出的区域参考大气密度的建模与应用方法在包括临近空间在内的更广阔的空域也同样适用。

参考文献

[1]	DALE J, BARRY R, WILLIAM V, et al.Atmospheric models for engineering applications: AIAA-2003-0894[R].Reston, VA: AIAA, 2003.
[2]	DALE J, WILLIAM V.How atmospheric thermodynamic parameters and model atmospheres have been used to help engineering in aerospace launch vehicle design & development[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition.Reston, VA: AIAA, 2012.
[3]	ALETA D, JUSTUS C G, VERNON K.Global reference atmospheric model (GRAM) series for aeroassist applications[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit.Reston, VA: AIAA, 2005.
[4]	陈昭.北半球标准大气(-2~80公里): GJB 365.1-87[S].北京: 国防工业技术科技委员会, 1987. CHEN Z.Standard atmosphere in northern hemisphere (-2-80 km): GJB 365.1-87[S].Beijing: Commission of Science Technology and Industry for National Defense, 1987(in Chinese).
[5]	李群, 谢志辉, 阎书源, 等.中国参考大气(地面~80 km): GJB 5601-2006[S].北京: 中国人民解放军总装备部, 2006. LI Q, XIE Z H, YAN S Y, et al.China reference atmosphere(ground~80 km): GJB 5601-2006[S].Beijing: The PLA General Armament Department, 2006(in Chinese).
[6]	姚志刚, 孙睿, 赵增亮, 等. 风云三号卫星微波观测的临近空间大气扰动特征[J]. 地球物理学报, 2019, 62(2): 473-488. YAO Z G, SUN R, ZHAO Z L, et al. Gravity waves in the near space observed by the microwave temperature sounder of the FY 3C meteorology satellite[J]. Chinese Journal of Geophysics, 2019, 62(2): 473-488. (in Chinese)
[7]	肖存英, 胡雄, 王博, 等. 临近空间大气扰动变化特性的定量研究[J]. 地球物理学报, 2016, 59(4): 1211-1221. XIAO C Y, HU X, WANG B, et al. Quantitative studies on the variations of near space atmospheric fluctuation[J]. Chinese Journal of Geophysics, 2016, 59(4): 1211-1221. (in Chinese)
[8]	JUSTUS C G.Upper atmospheric mixing by gravity waves[C]//International Conference on the Environmental Impact of Aerospace Operations in the High Atmosphere.Reston, VA: AIAA, 1973: 1-4.
[9]	JUSTUS C G.Density perturbation simulation with the global reference atmospheric model[C]//26th Aerospace Sciences Meeting.Reston, VA: AIAA, 1988: 1-8.
[10]	肖存英, 胡雄, 杨钧烽, 等. 临近空间38°N大气密度特性及建模技术[J]. 北京航空航天大学学报, 2017, 43(9): 1757-1765. XIAO C Y, HU X, YANG J F, et al. Characteristics of atmospheric density at 38°N in near space and its modeling technique[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(9): 1757-1765. (in Chinese)
[11]	JUSTUS C G, JOHNSON D L. The GRAM model:Status of development and future aspects[J]. Advances in Space Research, 1997, 19(4): 549-558. DOI:10.1016/S0273-1177(97)00170-1
[12]	JUSTUS C G, DUVALL A, JOHNSON D L. Earth global reference atmospheric model (GRAM-99) and trace constituents[J]. Advances in Space Research, 2004, 34(8): 1731-1735. DOI:10.1016/j.asr.2003.04.057
[13]	LESLIE F.Earth global reference atmospheric model 2007(Earth-GRAM07)[C]//37th COSPAR Scientific Assembly.Washington, D.C.: NASA, 2008.
[14]	LESLIE F W, JUSTUS C G.The NASA marshall space flight center earth global reference atmospheric model-2010 Version: NASA/TM-2011-216467[R].Washington, D.C.: NASA Marshall Space Flight Center, 2019.
[15]	杨钧烽, 肖存英, 胡雄, 等. 临近空间风切变特性及其对飞行器的影响[J]. 北京航空航天大学学报, 2019, 45(1): 57-65. YANG J F, XIAO C Y, HU X, et al. Wind shear characteristics in near space and their impacts on air vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(1): 57-65. DOI:10.3969/j.issn.1005-4561.2019.01.019 (in Chinese)
[16]	高振荣, 田庆明, 刘晓云, 等. 近58年河西走廊地区气温变化及突变分析[J]. 干旱区研究, 2010, 27(2): 194-203. GAO Z R, TIAN Q M, LIU X Y, et al. Analysis of temperature change and abrupt change in Hexi Corridor in recent 58 years[J]. Research in the Arid Areas, 2010, 27(2): 194-203. (in Chinese)
[17]	刘晓云, 岳平, 徐殿祥. 酒泉市最近54a气温和降水特征分析[J]. 干旱区研究, 2006, 23(3): 495-499. LIU X Y, YUE P, XU D X. Analysis of temperature and precipitation characteristics in Jiuquan City in recent 54 years[J]. Research in the Arid Areas, 2006, 23(3): 495-499. (in Chinese)