为使获取的LDCT图像满足临床诊断需求,有效提高LDCT图像的质量成为当前的研究热点[9-13]。****们探索了许多策略[14-16]来提高LDCT图像的质量,目前直接对重建的LDCT图像实现消除噪声和抑制条形伪影的后处理方法是不依赖投影数据的,易于集成到大多数CT系统中,为LDCT成像技术的临床应用发展注入新的活力。鉴于难以对LDCT图像中分布不均匀的噪声和条形伪影进行统计建模,目前大多数后处理技术往往依赖于更多的启发式(heuristic)方法。近20年来,变分法在图像去噪领域独树一帜,具有良好的保边去噪性能[17-19]。基于此,研究者们将变分法应用到医学成像领域并取得新成效。受文献[17]启发,本文提出了一种基于可变阶变分模型的后处理技术,用于改善LDCT图像的质量,该模型根据图像的局部特征自适应地选择正则化算子的阶数,在抑制斑点噪声和条形伪影的同时可以保留具有临床诊断意义的结构特征。
1 可变阶变分模型 基于变分法的图像降噪是求解关于图像的能量泛函最优解的问题,而图像降噪是一个不适定的反问题,所以常常运用正则化理论将不适定问题转变为适定性问题来求最优解。
首先提出如下凸结合变分正则化模型:
 | (1) |
式中:Ω为图像的定义域;u为降噪后的低剂量图像;u0为带噪声和伪条纹的低剂量图像;▽为梯度算子;λ为正则化参数;θ∈[0, 1]为变分阶数控制参数;等式右边第1项为保真项,第2项为对图像具有平滑作用的正则项。此外,本文模型中Hessian矩阵(即
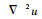
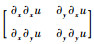
1) 当θ=1时,本文模型可以改写为
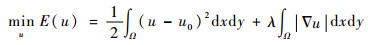 | (2) |
此时模型退化为正则化算子为一阶变分的总变分(TV)模型,该模型具有良好的保边性能,但会产生阶梯效应。
2) 当θ=0时,本文模型可以改写为
 | (3) |
此时模型退化为正则化算子为二阶变分的有界Hessian(BH)模型,该模型具有良好的平滑性能,但是保边能力欠佳。
3) 当θ∈(0, 1)时,本文模型类似于TVBH模型,兼顾了一阶变分和二阶变分,是对TV模型和BH模型的融合。
综上所述,参数θ的选择决定着本文模型的滤波形式与滤波性能。由于参数常量θ通常通过大量实验来试凑或凭经验取得最佳值,是对全局内容的粗略评估,忽略了图像的局部特征。
接下来考量图像的局部特征, 用边缘扩散函数θ(z)来代替常量θ改善本文模型的自适应性,提出了可变阶变分模型,优化的模型形式为
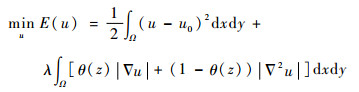 | (4) |
 | (5) |
式中:k为边缘阈值参数。
为了更好地保持医学图像中所包含的边缘细节信息,关于边缘扩散函数θ(z)的特征检测因子z的构造,融合了梯度和局部熵2种特征检测算子。
1) 图像的梯度
梯度表征了图像灰度值的变化大小和方向,因此常用梯度模值来区分图像的边缘区域和非边缘区域。边缘区域梯度较大,平坦区域梯度较小,但是有些细节信息的梯度与平坦区域相差不大,噪声点处的梯度甚至比边缘的梯度还要大,这样梯度边缘检测算子可能会对图像中细节丰富的弱边缘区域和强噪声点造成误判,导致处理后的图像细节信息损失或者去噪不彻底。
2) 图像的局部熵
局部熵表征了图像中局部区域的像素灰度值变化的剧烈程度,从而可以反映图像中所包含信息的丰富程度。一副大小为M×N的灰度图像f的熵值定义为
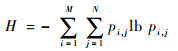 | (6) |
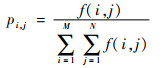 | (7) |
式中:f(i, j)为位于图像(i, j)点处像素的灰度值;pi, j表示(i, j)点处像素的灰度值在大小为M×N的局部邻域中的分布概率;H为图像的局部熵。
根据局部熵可以有效地判定图像的局部特性,在灰度分布复杂的边缘细节区域,局部熵值较大;在灰度分布均匀的平坦区域,局部熵值较小。此外,局部熵具有较强的抗噪能力,独立噪声点对其影响很小。因此,局部熵可被广泛应用于图像处理中。
根据梯度和局部熵的特性,新的特征检测因子z设计为

2 可变阶变分模型的数值解法 2.1 离散化 为了提高本文提出的可变阶变分模型的运算速率,类似文献[17]采用基于快速傅里叶变换(FFT)的分裂Bregman算法求解。
首先对连续的一阶、二阶和四阶微分算子及散度算子进行离散化。此外,为了进一步提高分裂Bregman算法计算的速度,采用周期性边界条件使FFT适用于分裂Bregman算法。设Ω为尺寸大小为M×N的二维灰度图像区域,图像列和行方向的坐标分别用x和y表示。在像素点(i, j)处沿着坐标x和y方向的一阶向前差分记为
 | (8) |
 | (9) |
一阶向后差分记为
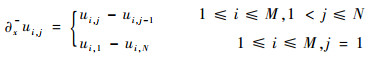 | (10) |
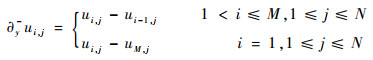 | (11) |
离散的二阶差分记为
 | (12) |
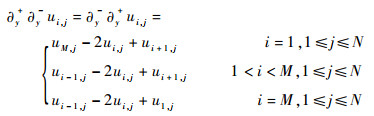 | (13) |
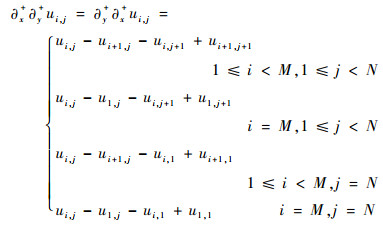 | (14) |
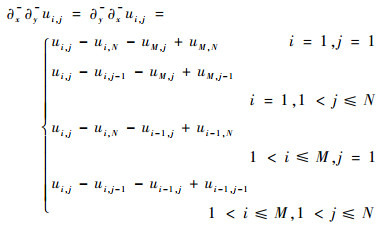 | (15) |
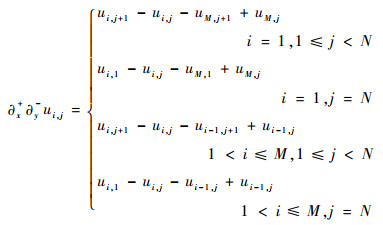 | (16) |
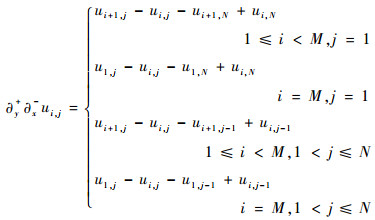 | (17) |
离散的四阶差分形式如式(18)~式(20)所示,其中关于边界的有限差分的离散形式可参考式(12)~式(15)。
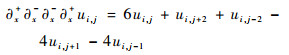 | (18) |
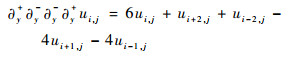 | (19) |
 | (20) |
离散化的梯度、Hessian矩阵为
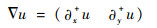 | (21) |
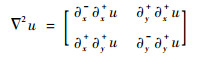 | (22) |
最后对于任意p=(p1 p2)的一阶散度div,任意
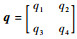
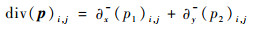 | (23) |
 | (24) |
2.2 本文模型的分裂Bregman算法 为了求得本文提出的可变阶变分模型的能量泛函的最优值,首先引入辅助变量w、v,Bregman迭代参数b、d和惩罚参数θ1、θ2。将本文提出模型的能量泛函转换为以下形式:
 | (25) |
式中:w=(w1 w2)为一个与函数u的梯度相关的二维函数且
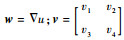
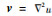
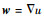
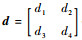
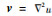
接下来固定变量(w, v; b, d),得到关于u的欧拉方程为
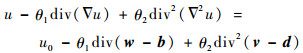 | (26) |
根据式(21)~式(24)可得式(26)的离散形式为
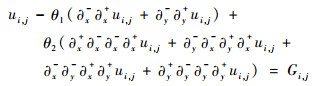 | (27) |
式中:Gi, j为式(26)等号右侧部分,离散形式为
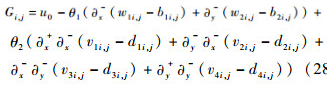 | (28) |
在周期边界的条件下,对等式(27)两端分别进行离散傅里叶变换,变换形式为
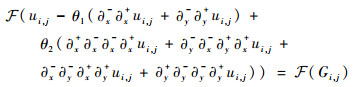 | (29) |
式中:
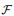
式(29)关于离散频率r和s的等价形式为
 | (30) |
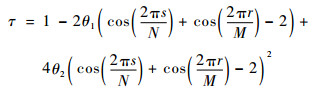 | (31) |
通过对式(29)进行傅里叶逆变换,求得u的解析解:
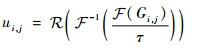 | (32) |
式中:
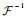
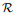
此外,关于变量w的更新,通过固定(u, w; b, d),获得与w相关的欧拉方程:
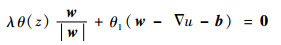 | (33) |
式(33)关于w的解析解可以用如下二维广义软阈值公式求得:
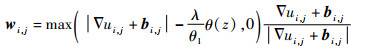 | (34) |
采用同样的方法更新变量v,其解析解为
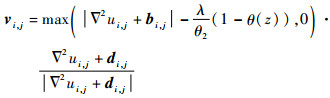 | (35) |
最后更新Bregman迭代参数b、d。
综上所述, 本文提出的可变阶变分模型的基于FFT的分裂Bregman算法的求解流程可以归结如下:
步骤1 ????初始化:u0(u0设定为待改善的LDCT图像)。
步骤2????初始化:(w, v; b, d)=0。
步骤3????设定参数λ、θ1及θ2。
步骤4????由
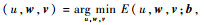
步骤5????更新Bregman迭代参数

步骤6????更新Bregman迭代参数
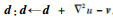
步骤7????若满足迭代终止条件:
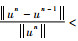
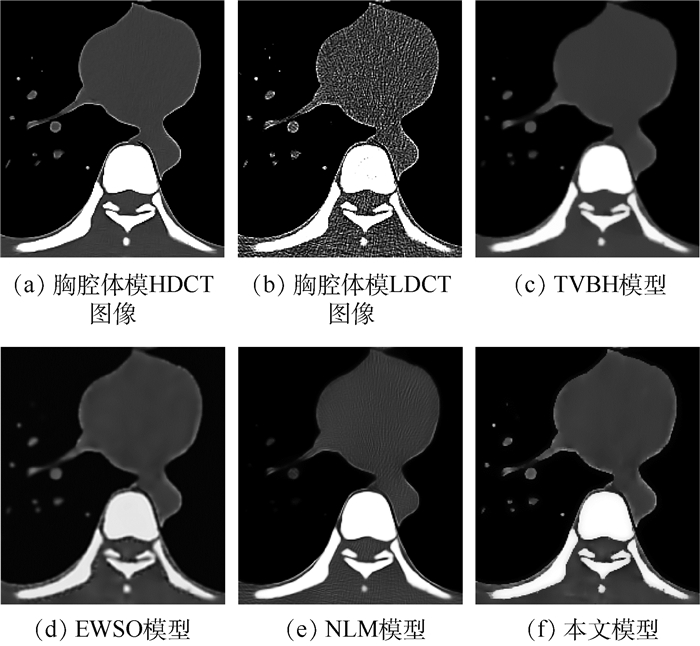
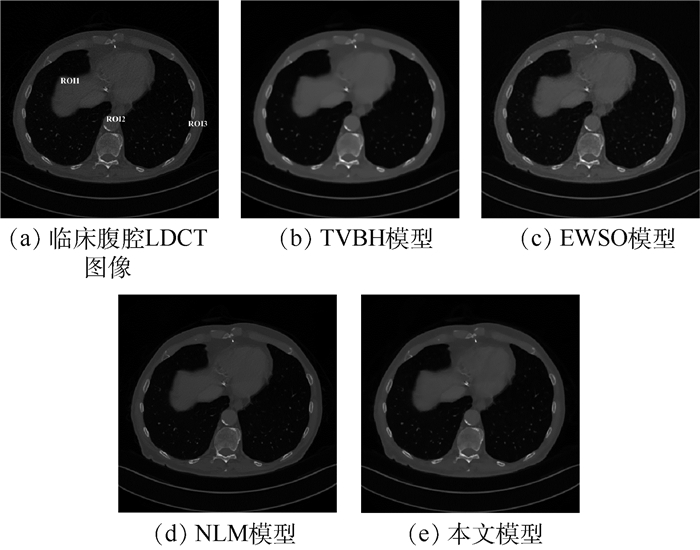
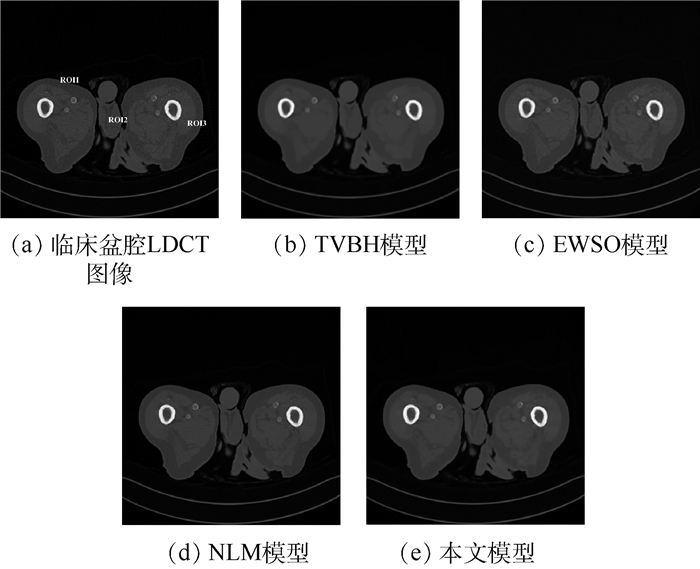
3 实验结果与分析 为了验证本文提出的可变阶变分模型对医用LDCT图像的去噪性能及在临床应用上的价值,选择实际CT扫描的胸腔体模、临床数据作为实验对象,其尺寸均为512 mm×512 mm。图 1(a)为胸腔体模HDCT图像,其通过一台多排探测器西门子16 CT扫描仪在管电流为240 mAs、管电压为120 kVp(千伏峰值)的高剂量扫描协议下实际扫描一个人体胸腔的仿真体模,获得经反投影重建(Filtered Back Projection,FBP)算法重建后的图像,再利用大尺度邻域非局部伪影抑制(AS-LNLM)算法对重建后的图像质量进行进一步的改善而获得[20]。图 1(b)为胸腔体模LDCT图像,其是通过将管电流降为30 mAs,在此低剂量的条件下扫描胸腔仿真体模的同一部位,经FBP重建后获得。图 2(a)为胸腔体模HDCT图像的局部放大部分, 图 2(b)为胸腔体模LDCT图像的局部放大部分。图 3(a)为临床胸腔LDCT数据,该数据是在管电流为60 mAs、管电压为120 kVp的低剂量扫描协议下得到的FBP重建后的DICOM格式的低剂量图像。图 4(a)和图 5(a)分别为临床腹腔和盆腔LDCT数据,这2个数据是将辐射剂量降为标准剂量的25%的低剂量扫描协议下得到的FBP重建后的DICOM格式的低剂量图像。
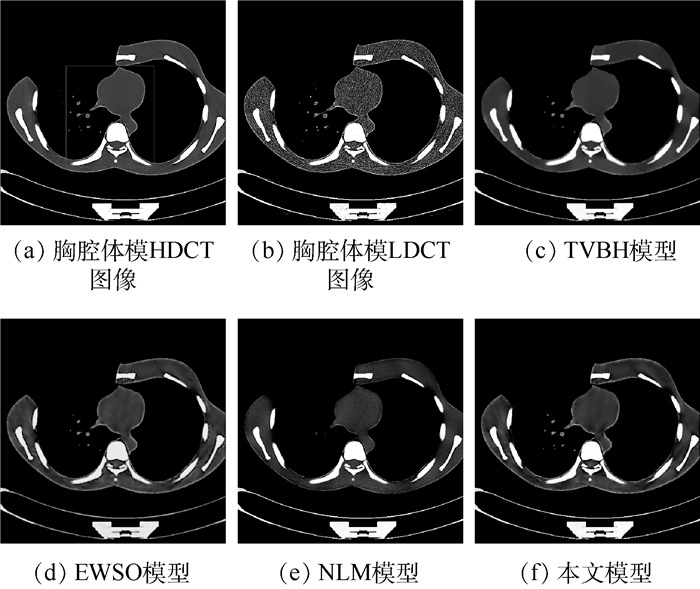 |
| 图 1 真实胸腔体模LDCT图像降噪结果的视觉比较 Fig. 1 Visual comparison of denoising results on LDCT image of actual thoracic phantom |
| 图选项 |
 |
| 图 2 真实胸腔体模局部放大图的视觉比较 Fig. 2 Visual comparison of denoising results on the local enlarged drawing by the squares in Fig. 1(a). |
| 图选项 |
 |
| 图 3 临床胸腔LDCT图像降噪结果的视觉比较 Fig. 3 Visual comparison of denoising results on LDCT image of clinical thoracic |
| 图选项 |
 |
| 图 4 临床腹腔LDCT图像降噪结果的视觉比较 Fig. 4 Visual comparison of denoising results on LDCT image of clinical abdominal |
| 图选项 |
 |
| 图 5 临床盆腔LDCT图像降噪结果的视觉比较 Fig. 5 Visual comparison of denoising results on LDCT image of clinical pelvic |
| 图选项 |
实验中,分别采用TVBH模型[17]、EWSO模型[18]、NLM模型[21]和本文模型对胸腔体模LDCT图像和临床LDCT图像进行处理。本文模型的边缘扩散函数θ(z)中,k是一个重要参数,其决定着要保持边缘的对比度并影响扩散过程。更具体地说,如果k值过大,图像的边缘被过度平滑;如果k值过小,图像中的一些噪声和伪影难以滤除。经大量实验验证,当k=10时,本文模型降噪效果最佳。对于胸腔体模,本文模型的参数设定为:λ=30,θ1=θ2=5。对于临床胸腔数据,本文模型的参数设定为:λ=80,θ1=θ2=10。对于临床腹腔和盆腔数据,本文模型的参数设定为:λ=50,θ1=θ2=10。为了客观说明本文模型的性能,其他对比模型的参数均按取得最优降噪效果设定。图 1~图 5展示了各模型的降噪结果。
观察图 1可知,本文模型对胸腔体模LDCT图像降噪效果在视觉上整体优于其他3种模型。为了更清晰地展示各模型的降噪效果,对图 1进行了局部放大(见图 2)。图 2(c)为TVBH模型的降噪效果,该模型有效去除了噪声和条形伪影,但是过度平滑LDCT图像的一些细节信息会造成临床诊断的误诊。图 2(d)为EWSO模型的处理结果,该模型虽然可以抑制大部分噪声和条形伪影,但是把LDCT图像的组织结构附近的伪影误判为结构信息保留了下来,不能满足临床诊断需求。图 2(e)所示NLM模型的结果较好地保留了边缘信息,但是丢失了一些细小结构,同时也引入了一些新的细小伪影,亦不能满足临床诊断需求。图 2(f)为本文模型的去噪结果,相对于其他3种对比模型,本文模型在抑制LDCT图像的条形伪影和边缘保持方面具有明显优势,其处理结果与HDCT图像最为相似,具有更加理想的视觉效果,为临床诊断带来便利。临床医学图像含有大量的弱边缘信息,相对仿真体模而言,临床医学LDCT图像的伪影去除难度更大。为了进一步验证本文模型在临床上的有效性,图 3~图 5给出了各模型对临床数据LDCT图像的处理结果。根据对比结果可知,TVBH模型很好地滤除了条形伪影,但是严重破坏了LDCT图像中组织结构;EWSO模型和NLM模型的处理结果均含有部分伪影,视觉效果较差;本文模型可以有效滤除LDCT图像中的条形伪影,而且较好地保留了LDCT图像中的边缘组织结构信息,比其他3种模型具有更佳的视觉效果。
此外,为了验证上述实验的有效性和合理性,针对图 1(a)所示的实际胸腔体模采用峰值信噪比(Peak Signal to Noise Ratio, PSNR)、平均结构相似度(Mean Structural Similarity Index Measure, MSSIM)和降噪时间作为衡量各模型去噪性能的客观性能评价指标,如表 1所示。显然,本文模型相比于其他3种模型取得了较高的PSNR值和MSSIM值,这与上述实验的视觉效果对比图是吻合的,说明本文模型处理结果的降噪效果最优,且与对应的HDCT图像的相似度最高。另外,本文模型的降噪时间略高于TVBH模型和EWSO模型,明显低于NLM模型,总的来说耗时较短,便于应用于临床中。针对图 3~图 5中的(a)图所示的临床数据缺乏高质量的参考图像,采用信噪比[22](Signal to Noise Ratio, SNR)对局部感兴趣区域(ROI)进行质量评价,如表 2所示。可以看出,本文模型对临床LDCT图像处理结果的定量评价均优于其他模型,进一步说明了本文模型处理临床数据的有效性。综上所述,本文模型是一个综合性能较优的去噪模型。
表 1 实际胸腔体模的定量比较 Table 1 Quantified comparison of actual thoracic phantom
| 降噪模型 |  | ||
| PSNR/dB | MSSIM | 除噪时间/s | |
| TVBH模型 | 25.259 3 | 0.886 4 | 19.45 |
| EWSO模型 | 24.213 9 | 0.914 9 | 10.83 |
| NLM模型 | 26.664 1 | 0.908 8 | 379.78 |
| 本文模型 | 27.205 1 | 0.926 6 | 27.88 |
表选项
表 2 临床数据的SNR值比较 Table 2 Comparison of SNR values of clinical data
| LDCT图像及降噪模型 |  |  |  | ||||||||
| ROI1 | ROI2 | ROI3 | ROI1 | ROI2 | ROI3 | ROI1 | ROI2 | ROI3 | |||
| LDCT图像 | 0.529 0 | 0.049 7 | 0.093 7 | 0.073 3 | 0.275 6 | 0.120 0 | 0.067 0 | 1.201 4 | 0.069 9 | ||
| TVBH模型 | 9.306 3 | 0.054 7 | 0.098 3 | 0.165 0 | 0.697 8 | 0.209 4 | 0.341 7 | 2.421 4 | 0.078 0 | ||
| EWSO模型 | 14.386 6 | 0.054 6 | 0.099 2 | 0.093 5 | 0.485 6 | 0.162 4 | 0.108 5 | 1.320 2 | 0.072 2 | ||
| NLM模型 | 1.301 1 | 0.058 0 | 0.094 6 | 0.173 1 | 0.890 9 | 0.159 4 | 0.110 5 | 1.446 7 | 0.069 7 | ||
| 本文模型 | 26.270 6 | 0.360 8 | 2.099 4 | 0.875 0 | 1.288 4 | 1.129 7 | 0.641 6 | 3.049 5 | 0.093 1 | ||
表选项
4 结论 本文针对LDCT图像存在严重的斑点噪声和条纹伪影问题,提出了一种可变阶变分模型降噪模型。该模型兼顾了一阶变分模型和二阶变分模型的优点,根据图像的梯度模值和局部熵融合的特征检测因子将图像划分为平坦区域和细节区域,在不同的区域自适应地选择变分阶数,从而实现不同的扩散模式。同时采用基于FFT的分裂Bregman算法求解所提出的变分模型,提高了运算速度。仿真实验表明,本文所提出的可变阶变分模型不但有效地去除了LDCT图像中存在的噪声和条纹伪影,而且很好地保留了图像的边缘细节,明显改善了LDCT图像的质量,获得了与HDCT图相近的视觉效果,适用于临床诊断,具有实际应用价值。
参考文献
| [1] | ZHU Y, ZHAO M, ZHAO Y, et al. Noise reduction with low dose CT data based on a modified ROF model[J]. Optics Express, 2012, 20(16): 17987-18004. DOI:10.1364/OE.20.017987 |
| [2] | CHEN Y, YIN X, SHI L, et al. Improving abdomen tumor low-dose CT images using a fast dictionary learning based processing[J]. Physics in Medicine and Biology, 2013, 58(16): 5803-5820. DOI:10.1088/0031-9155/58/16/5803 |
| [3] | ZHANG C, ZHANG T, LI M, et al. Low-dose CT reconstruction via L1 dictionary learning regularization using iteratively reweighted least-squares[J]. BioMedical Engineering OnLine, 2016, 15(1): 66. DOI:10.1186/s12938-016-0193-y |
| [4] | LEE D, LEE J, KIM H, et al. A feasibility study of low-dose single-scan dual-energy cone-beam CT in many-view under-sampling framework[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2578-2587. DOI:10.1109/TMI.2017.2765760 |
| [5] | CHEN Y, LIU J, HU Y, et al. Discriminative feature representation:An effective postprocessing solution to low dose CT imaging[J]. Physics in Medicine and Biology, 2017, 62(6): 2103-2131. DOI:10.1088/1361-6560/aa5c24 |
| [6] | CHEN Y, LIU J, XIE L, et al. Discriminative prior-prior image constrained compressed sensing reconstruction for low-dose CT imaging[J]. Scientific Reports, 2017, 7(1): 13868. DOI:10.1038/s41598-017-13520-y |
| [7] | FRUSH D P, DONNELLY L F, ROSEN N S. Computed tomography and radiation risks:What pediatric health care providers should know[J]. Pediatrics, 2003, 112(4): 951-957. DOI:10.1542/peds.112.4.951 |
| [8] | BRENNER D J, HALL E J. Computed tomography-An increasing source of radiation exposure[J]. New England Journal of Medicine, 2007, 357(22): 2277-2284. DOI:10.1056/NEJMra072149 |
| [9] | CHEN Y, SHI L, YANG J, et al. Radiation dose reduction with dictionary learning based processing for head CT[J]. Australasian Physical and Engineering Sciences in Medicine, 2014, 37(3): 483-493. DOI:10.1007/s13246-014-0276-7 |
| [10] | YANG Q, YAN P, ZHANG Y, et al. Low dose CT image denoising using a generative adversarial network with wasserstein distance and perceptual loss[J]. IEEE Transactions on Medical Imaging, 2018, 37(6): 1348-1357. DOI:10.1109/TMI.2018.2827462 |
| [11] | LIU J, MA J, ZHANG Y, et al. Discriminative feature representation to improve projection data inconsistency for low dose CT imaging[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2499-2509. DOI:10.1109/TMI.2017.2739841 |
| [12] | HASAN A M, MELLI A, WAHID K A, et al. Denoising low-dose CT images using multi-frame blind source separation and block matching filter[J]. IEEE Transactions on Radiation and Plasma Medical Sciences, 2018, 2(4): 279-287. DOI:10.1109/TRPMS.2018.2810221 |
| [13] | DIWAKAR M, KUMAR M. CT image denoising using NLM and correlation-based wavelet packet thresholding[J]. IET Image Processing, 2018, 12(5): 708-715. DOI:10.1049/iet-ipr.2017.0639 |
| [14] | YOU C, YANG Q, SHAN H, et al. Structure-sensitive multi-scale deep neural network for low-dose CT denoising[J]. IEEE Access, 2018, 6: 41839-41855. DOI:10.1109/Access.6287639 |
| [15] | LIU Y, ZHANG Y. Low-dose CT restoration via stacked sparse denoising autoencoders[J]. Neurocomputing, 2018, 284: 80-89. DOI:10.1016/j.neucom.2018.01.015 |
| [16] | 罗立民, 胡轶宁, 陈阳. 低剂量CT成像的研究现状与展望[J]. 数据采集与处理, 2015, 30(1): 24-34. LUO L M, HU Y N, CHEN Y. Research status and prospect for low-dose CT imaging[J]. Data Acquisition and Processing, 2015, 30(1): 24-34. (in Chinese) |
| [17] | LU W, DUAN J, QIU Z, et al. Implementation of high-order variational models made easy for image processing[J]. Mathematical Methods in the Applied Sciences, 2016, 39(14): 4208-4233. DOI:10.1002/mma.v39.14 |
| [18] | DUAN J, QIU Z, LU W, et al. An edge-weighted second order variational model for image decomposition[J]. Digital Signal Processing, 2016, 49: 162-181. DOI:10.1016/j.dsp.2015.10.010 |
| [19] | DUAN J, WARD W O C, SIBBETT L, et al. Introducing anisotropic tensor to high order variational model for image restoration[J]. Digital Signal Processing, 2017, 69: 323-336. DOI:10.1016/j.dsp.2017.07.001 |
| [20] | CHEN Y, YANG Z, HU Y, et al. Thoracic low-dose CT image processing using an artifact suppressed large-scale nonlocal means[J]. Physics in Medicine and Biology, 2012, 57(9): 2667-2688. DOI:10.1088/0031-9155/57/9/2667 |
| [21] | BUADES A, COLL B, MOREL J M.A non-local algorithm for image denoising[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2005, 2: 60-65. |
| [22] | WANG J, LU H, WEN J, et al. Multiscale penalized weighted least-squares sinogram restoration for low-dose X-ray computed tomography[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(3): 1022-1031. DOI:10.1109/TBME.2007.909531 |
