目前,针对传统图像的全聚焦融合主要分为空间域[6-7]和变换域[8-11]。空间域基于像素或块进行清晰度评价,从不同图像中提取质量好的像素来构成全聚焦图像,计算时间快但存在块效应问题[6]。变换域将图像分解为不同分辨率层或不同频带的子图像,通过评价重建分辨层或子图像构建重聚焦图像,可有效避免块效应[9]。作为变换域的一种普遍方法,小波变换将待融合图像分解到一系列频率信道中,利用其分解后的塔形结构构建高、低频子图像,分别对高、低频子图像进行融合后经小波反变换得到全聚焦图像。小波变换融合图像的质量决定于高、低频子图像的融合规则选择:对于低频子图像,一般采用均值计算法实现融合;对于高频子图像,常采用Sobel算子、Prewitt算子及拉普拉斯算子等进行评价建立融合规则[12-14]。
为了有效避免传统空域图像融合算法的块效应,获得较高质量的光场全聚焦图像,本文采用小波变换的方法来进行图像的融合。首先解码4D光场并采用数字重聚焦算法得到不同深度的重聚焦图像;然后通过对各重聚焦图像集进行小波分解及塔型重构构建高、低频子图像集;最后提出区域均衡拉普拉斯算子、像素可见度函数分别构建融合图像的高、低频小波系数实现图像融合。该算法有效实现了光场原始数据到全聚焦图像的转化,且图像融合质量较传统算法有所提高。
1 不同空间深度的重聚焦图像计算 图 1为光场的双平面参数化模型。空间任一光线均可用其与两平面的交点确定,设光场相机的主透镜平面为(u, v)面,传感器平面为(x, y)面,光场相机记录的4D光场为LF(x, y, u, v),由经典光辐射公式可得到全光相机焦平面的积分图像[1]:
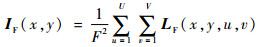 | (1) |
 |
| 图 1 双平面参数化模型 Fig. 1 Two-plane parametric model |
| 图选项 |
式中:F为主透镜平面和传感器平面间的距离;用X×Y×U×V表示4D光场矩阵LF(x, y, u, v)的大小。如果将像平面(传感器平面)与主透镜平面的距离由F变为F′,新的4D光场矩阵用LF′(x′, y′, u′, v′)表示,此时相机焦平面重聚焦图像表示为
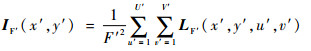 | (2) |
令F′=αnF,其中αn为调焦系数,为了方便图形表示,取4D空间的一个切面来得到坐标间的几何关系,如图 2所示。
 |
| 图 2 光场相机数字重聚焦原理 Fig. 2 Digital refocusing principle of light field camera |
| 图选项 |
根据相似三角形原理,可得到新光场与原始光场的坐标满足[1]:
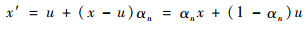 | (3) |
 | (4) |
同理可得到:
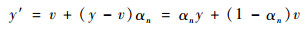 | (5) |
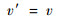 | (6) |
式(3)~式(6)可表示为矩阵形式:
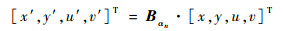 | (7) |
式中:Bαn为坐标变换矩阵,具体形式为
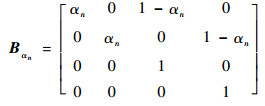 | (8) |
式(7)也等价于:
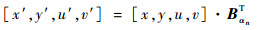 | (9) |
根据式(9),式(2)可改写为
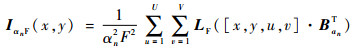 | (10) |
改变αn的取值,即可达到改变像平面的位置的目的,继而得到不同空间深度重聚焦图像。
2 小波域光场高、低频子图像融合 根据小波变换图像融合理论,通过小波变换将待融合图像分解到一系列频率信道中,利用其分解后的塔型结构构建高、低频子图像,该过程可描述为
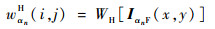 | (11) |
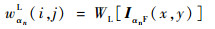 | (12) |
式中:(x, y)表示图像坐标;(i, j)表示小波域坐标;W[·]表示小波塔型分解操作符;WH[·]表示小波塔型分解后提取高频系数(高频子图像);WL[·]表示小波塔型分解后提取低频系数(低频子图像)。根据各重聚焦图像的高、低频子图像矩阵,运用清晰度评价函数计算融合后的高、低频子图像的系数,最后进行小波逆变换可得到全聚焦图像。
小波变换图像融合方法的核心在于建立有效的高、低频子图像清晰度评价函数[9, 14],本文针对现有民用级光场相机拍摄图像对比度不高、经数字重聚焦技术获得的重聚焦图像集分辨率有限、且存在由标定误差造成的局部噪声等特点,建立高频系数区域均衡拉普拉斯(Balanced Laplace based on local area,BL)算子、低频系数像素可见度(Pixel Visibility,PV)函数的清晰度评价函数实现光场全聚焦图像生成,具体算法流程如图 3所示。
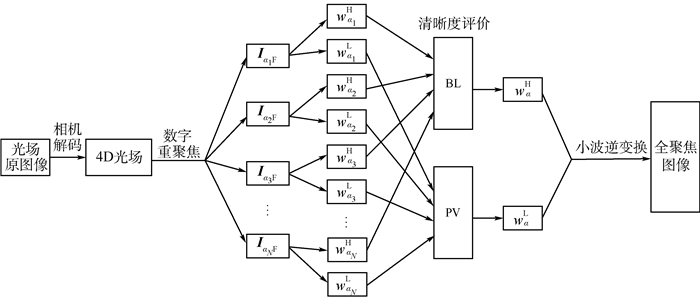 |
| 图 3 光场全聚焦图像融合流程 Fig. 3 Procedure of light field all-in-focus image fusion |
| 图选项 |
光场原图像经相机解码后得到4D光场,选择不同的αn(n=1, 2, …),利用数字重聚焦技术得到不同空间深度的重聚焦图像IαnF;计算每一帧重聚焦图像的小波高、低频子图像wαnFH、wαnFL,高、低频子图像分别采用BL算子和PV函数作为图像融合清晰度评价指标,实现高低频系数的融合;最后经小波逆变换得到融合后的全聚焦图像。
2.1 基于区域均衡拉普拉斯算子的高频系数融合 小波变换的高频子图像反映图像的亮度突变特性,即边界特性,拉普拉斯算子能对任何走向的边界和线条进行锐化,且保持各向同性特性,在对高频子图像进行清晰度评价时被广泛使用。针对拉普拉斯算子在x方向和y方向的二阶导数极可能出现符号相反的情况,如图 4(a)所示,Nayar和Nakagawa[11]提出改进的拉普拉斯能量和(Sum of Modified Laplace,SML),可有效避免了两方向的能量抵消,同时引入窗口的思想来计算区域拉普拉斯能量和,可有效提高算法的抗噪能力。之后,SML又充分考虑了周边点对当前位置清晰度评价函数的影响,改进为水平、垂直以及斜对角线(45°、135°方向)共8个方向的梯度能量和。区域拉普拉斯能量求和的方法可提高图像融合质量,同时也增加了计算所需时间。基于此,本文提出区域均衡拉普拉斯算子,通过增加二阶导的数量和方向来实现能量均衡,该算法的表达式为
 | (13) |
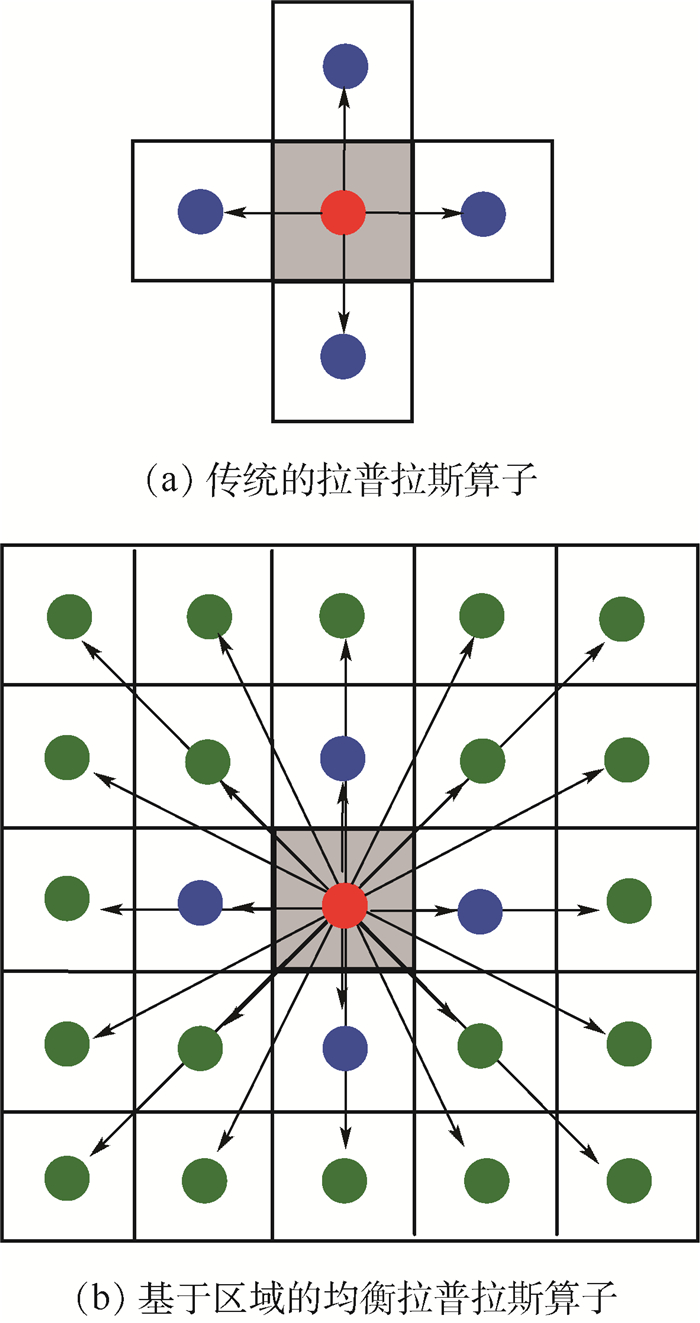 |
| 图 4 基于拉普拉斯算子的高频子图像清晰度评价 Fig. 4 High-frequency sub-image sharpness evaluation based on Laplace operator |
| 图选项 |
式中:wanH表示不同空间深度各重聚焦图像经小波分解后各自的高频子图像,n=1, 2, …, N,N为参与全聚焦图像融合的重聚焦图像帧数;S×T表示均衡区域大小,且S、T只能取奇数;s、t分别为水平、垂直方向二阶导步长;
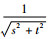
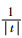
考虑到微透镜标定误差会引起重聚焦图像产生局部噪声,拉普拉斯算子对噪声敏感的缺点,在对高频子图像进行融合前先进行双边滤波预处理,本文基于区域均衡拉普拉斯算子的高频系数融合规则可表述为:根据式(13)计算N帧待融合图像中任意2幅图像对应拉普拉斯算子的差值,记为D,D=(BLαA(i, j)-BLαB(i, j)),当所有差值D的最小值大于某一门限阈值时,取均衡拉普拉斯:能量最大者对应的高频系数wαpH作为融合系数,当差值小于门限阈值时,由多帧图像高频系数乘以权重因子来决定最后的融合系数。具体公式为
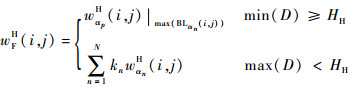 | (14) |
式中:max(·)、min(·)分别为取最大值、最小值操作;HH为自定义门限阈值(本文HH取0.1);权重因子kn计算式为
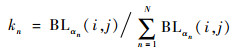 | (15) |
2.2 基于像素可见度函数的低频系数融合 小波塔型分解得到的低频系数,主要反映了原图像的平均灰度特征。计算低频融合系数的最简单方法是加权平均法[14],但加权平均法会降低融合图像的对比度并丢失原图像中一些有用信息。此外,空间频率法、点锐度算子等一些计算梯度的方法也被应用到低频融合系数的计算中[14-15]。在本文的光场图像低频系数融合中,借鉴了基于人类视觉特性的图像可见度(Image Visibility,Ⅳ)的概念[8-9],其定义如下:
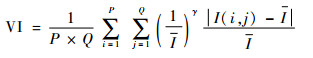 | (16) |
式中:P×Q表示图像I(i, j)的大小;I为图像I(i, j)的平均值;γ为视觉常量,其取值范围为0.6~0.7。Ⅳ的值越大,代表图像可见度越高。
在低频子图像的融合过程中,如果直接采用式(16)计算,只能得到整幅图像的Ⅳ值,无法用于多幅图像的区域级或像素级融合。为了合理建立有效的低频系数评价指标,对式(16)进行改进,建立基于像素的图像可见度函数,具体表达式为
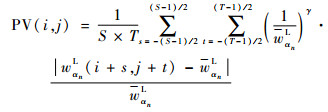 | (17) |
式中:S×T表示以当前像素点为中心的矩形邻域,且S、T只能取奇数;s、t分别为在矩形邻域内水平、垂直方向的扫描步长;wαnL为S×T区域像素的平均灰度值。在低频系数融合过程中,采用与高频系数相同的融合规则。
3 实验结果与分析 为验证本文算法的有效性,采用Lytro光场相机拍摄的原图像进行了实验(实验测试数据来源于文献[3])。图 5(a)为光场原图像,图 5(b)、(c)、(d)分别为α=0.52,0.78,0.98时根据式(10)计算得到的3幅不同空间深度的重聚焦图像,聚焦深度从前景逐渐变化到背景。图 5(e)为采用本文算法计算得到的全聚焦图像,红色虚线所框区域清晰度明显高于图 5(b)对应区域,黄色虚线所框区域清晰度明显高于图 5(c)对应区域,白色虚线所框区域清晰度明显高于图 5(d)对应区域,可见本文算法可有效利用光场原图像得到全聚焦图像。
 |
| 图 5 基于本文算法的Leaves样本图像融合 Fig. 5 Image Leaves fusion based on proposed algorithm |
| 图选项 |
为了从视觉上评价本文算法的优势,选取3种经典的小波变换图像融合算法与本文算法进行对比,这3种融合算法高频系数分别采用Sobel算子、Prewitt算子、传统拉普拉斯算子作为清晰度评价函数,低频系数均采用点锐度算子作为清晰度评价函数,由于低频系数选用同一清晰度评价函数,故在下文的表述中该3种算法分别简称为Sobel算法、Prewitt算法、Laplace算法。实验数据采用文献[3]的另外3组光场原图像(Flower、Forest、Zither)。图 6~图 8为对应实验结果:图 6~图 8的(a)、(b)分别为3幅光场原图像对应α=1,2时得到的2幅重聚焦图像,聚焦深度从前景变换到背景;图 6~图 8的(c)、(d)、(e)、(f)分别为采用Sobel算法、Prewitt算法、Laplace算法及本文算法对(a)、(b)两幅图像融合后得到的结果。
 |
| 图 6 Flower样本图像不同融合算法对比 Fig. 6 Comparison of different fusion algorithms based on image Flower |
| 图选项 |
 |
| 图 7 Forest样本图像不同融合算法对比 Fig. 7 Comparison of different fusion algorithms based on image Forest |
| 图选项 |
 |
| 图 8 Zither样本图像不同融合算法对比 Fig. 8 Comparison of different fusion algorithms based on image Zither |
| 图选项 |
从视觉效果看,图 6中Sobel算法、Prewitt算法得到的融合图像在虚线所框矩形区域的清晰度明显不如本文算法;图 7虚线所框区域Sobel算法、Prewitt算法得到的清晰度也明显不如本文算法;图 8采用Prewitt算法融合的植物叶子对应的清晰度也明显不如本文算法;说明本文算法在视觉效果上具有一定优势。
另外,考虑到人眼视觉限制,本文进一步选取了一些客观评价指标对图像质量进行评价,验证所提算法的优越性。本文分别选取信息熵E、平均梯度AG、图像清晰度FD和图像边缘强度EI作为评价指标,对图 6~图 8中多种方法得到的全聚焦图像的质量进行评价。其中E是度量信息大小的一个物理量,其值越大表示图像信息量越大。AG可以敏感地反映图像对微小细节反差能力,其值越高,代表它的能力越强。FD代表图像清晰程度,其值越高,代表其清晰程度越好。EI反映了图像的边缘强度,其值越高,代表图像边缘越清晰,具体评价指标对应结果如表 1~表 3所示。对比表中数据可知,本文算法在图像的4种客观评价指标上,均优于其他3种传统的小波变换方法,体现了本文算法的可行性和有效性。
表 1 Flower样本图像不同融合算法性能指标比较 Table 1 Comparison of performance indices of different fusion algorithms based on image Flower
| 算法 | E | AG | FD | EI |
| Sobel算法 | 6.867 6 | 6.247 0 | 6.899 1 | 66.534 0 |
| Prewitt算法 | 6.863 4 | 5.832 6 | 6.327 0 | 62.642 0 |
| Laplace算法 | 6.883 0 | 6.866 8 | 7.683 7 | 72.307 3 |
| 本文算法 | 6.889 6 | 7.005 5 | 7.849 8 | 73.720 3 |
表选项
表 2 Forest样本图像不同融合算法性能指标比较 Table 2 Comparison of performance indices of different fusion algorithms based on image Forest
| 算法 | E | AG | FD | EI |
| Sobel算法 | 5.754 4 | 2.532 8 | 2.913 6 | 26.515 7 |
| Prewitt算法 | 5.749 2 | 2.290 5 | 2.576 6 | 24.273 5 |
| Laplace算法 | 5.801 1 | 3.001 8 | 3.523 5 | 31.013 4 |
| 本文算法 | 5.809 9 | 3.087 5 | 3.630 5 | 31.903 3 |
表选项
表 3 Zither样本图像不同融合算法性能指标比较 Table 3 Comparison of performance indices of different fusion algorithms based on image Zither
| 算法 | E | AG | FD | EI |
| Sobel算法 | 6.293 5 | 4.467 5 | 5.186 5 | 48.385 4 |
| Prewitt算法 | 6.269 5 | 4.018 4 | 4.518 2 | 43.756 6 |
| Laplace算法 | 6.271 6 | 4.864 9 | 5.677 3 | 52.447 4 |
| 本文算法 | 6.298 7 | 4.942 5 | 5.794 0 | 53.150 1 |
表选项
4 结论 1) 基于光场原图像,完成了光场解码、数字重聚焦和全聚焦图像融合的全过程计算,利用小波变换实现多帧重聚焦图像融合,避免了传统空域图像融合算法造成的块效应。
2) 在小波高频子图像的融合中,提出了基于区域均衡拉普拉斯算子的清晰度评价函数;在小波低频子图像融合中,提出了基于像素可见度的清晰度评价函数,来提高全聚焦图像的融合质量。
3) 实验结果表明,与传统的基于小波变换的图像融合算法相比,利用本文算法得到的融合图像的视觉效果更好,图像评价指标更高:与Laplace算法相比,图像清晰度平均提高0.129 9,图像边缘强度平均提高1.001 9。
参考文献
| [1] | NG R.Light field photography with a hand-held plenoptic camera: CSTR 2005-02[R].Stanford: Stanford University, 2005. |
| [2] | NG R. Fourier slice photography[J]. ACM Transactions on Graphics, 2005, 24(3): 735-744. DOI:10.1145/1073204 |
| [3] | TAO M W, HADAP S, MALIK J, et al.Depth from combining defocus and correspondence using light-field cameras[C]//IEEE International Conference on Computer Vision.Piscataway, NJ: IEEE Press, 2013: 673-680. |
| [4] | BOK Y, JEON H G, KWEON I S.Geometric calibration of microlens-based light-field cameras using line features[C]//European Conference on Computer Vision.Berlin: Springer, 2014: 47-61. |
| [5] | YOON Y, JEON H G, YOO D, et al. Light-field image super-resolution using convolutional neural network[J]. IEEE Signal Processing Letters, 2017, 24(6): 848-852. DOI:10.1109/LSP.2017.2669333 |
| [6] | LIU J G. Smoothing filter-based intensity modulation:A spectral preserve image fusion technique for improving spatial details[J]. International Journal of Remote Sensing, 2000, 21(18): 3461-3472. DOI:10.1080/014311600750037499 |
| [7] | Li S T, KANG X D, HU J W. Image fusion with guided filtering[J]. IEEE Transactions on Image Processing, 2013, 22(7): 2864-2875. DOI:10.1109/TIP.2013.2244222 |
| [8] | FEICHTENHOFER C, FASSOLD H, SCHALLAUER P. A perceptual image sharpness metric based on local edge gradient analysis[J]. IEEE Signal Processing Letters, 2013, 20(4): 379-382. DOI:10.1109/LSP.2013.2248711 |
| [9] | QIN X, ZHENG J, HU G, et al. Multi-focus image fusion based on window empirical mode decomposition[J]. Infrared Physics & Technology, 2017, 85: 251-260. |
| [10] | FAKHARI F, MOSAVI M R, LAJVARDI M M. Image fusion based on multi-scale transform and sparse representation:Image energy approach[J]. IET Image Processing, 2017, 11(11): 1041-1049. DOI:10.1049/iet-ipr.2017.0104 |
| [11] | NAYAR S K, NAKAGAWA Y. Shape from focus[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(8): 824-831. DOI:10.1109/34.308479 |
| [12] | DENG C, MA W, YIN Y.An edge detection approach of image fusion based on improved Sobel operator[C]//IEEE International Congress on Image and Signal Processing.Piscataway, NJ: IEEE Press, 2011, 3: 1189-1193. |
| [13] | SHRIVAKSHAN G T, CHANDRASEKAR C. A comparison of various edge detection techniques used in image processing[J]. International Journal of Computer Science Issues, 2012, 9(5): 268-276. |
| [14] | YANG Y, PARK D S, HUANG S, et al. Fusion of MT and MR images using an improved wavelet based method[J]. Journal of X-ray Science and Technology, 2010, 18(2): 157-170. |
| [15] | HUANG W, JING Z. Evaluation of focus measures in multi-focus image fusion[J]. Pattern Recognition Letters, 2007, 28(4): 493-500. DOI:10.1016/j.patrec.2006.09.005 |
