两相流动过程是现代能源与环境领域中多相流与工程热物理研究的常见对象，经常出现于航空航天、石油、能源及化工等现代工程过程与设备中。20世纪以来, 流体力学的发展动力以航空航天发展的需要最为突出, 其中涉及到的技术挑战包括多相流、流场精细测量等问题^[1]。航空航天领域液液传输问题中通常会遇到两相流混合流动现象^[2]，由于航空航天技术对安全系数和设计精度都有较高要求，流场流动特性和建模成为研究重点，而该问题的基础是对流动状态和过程参数的测量和研究，其中流速的准确测量是两相流研究的重点问题^[3]，为计算流体动力学数值模拟验证、流变特性的检测等提供有力工具，也对提高工业过程整体效率、降低故障率起到重要的作用。不同于单相流，两相流流动结构复杂、状态多变、待测参数较多，因此给流速测量带来了诸多困难。如油水两相流，由于在流动过程中油水两相同时受到湍动力和界面张力的共同作用，导致流体中出现离散相和连续相，而根据连续相的不同，油水两相流又可以分为油连续和水连续状态，流体在流动过程中存在“反相”现象，且其流动结构具有瞬时性和随机性等不确定特性^[4]，加大了对流速准确测量的难度。
目前，已有的两相流流速测量方法有若干种，可分为侵入式和非侵入式。其中，比较典型的侵入式测量方法为使用单相流仪表进行油水两相流的测量。如使用涡轮流量计对油水两相流进行测量，但流型和混合流体黏度的变化给测量结果带来了较大误差^[5]。在管道中放置节流装置并结合单相流测量原理，如差压法，可对油水两相流流量进行测量^[6]。但侵入式测量方法会影响两相流原有的流动形态，并造成额外的压损。因此，非侵入式测量方法受到更多关注和应用。如互相关方法，基于“凝固”流动假设，利用不同敏感原理(光学、电学、声学等)获取油水两相流流速信息，但互相关流速的真实物理含义缺乏明确的解释^[7]，此外，当被测流体在流动过程中较为平稳，不存在明显的波动时，互相关流速的计算精度明显降低^[8]。
近几十年以来，随着超声技术的不断发展，超声多普勒方法由于其结构简单、成本低、非侵入等优点，开始逐渐用于多相流流速研究。其测量原理为多普勒效应，超声波在流体的相界面发生反射和散射，多普勒频移能够表征离散液滴的真实流速。该技术最初用于医学检测，如血液流速或疾病诊断等。Brody和Meindl^[9]以血流为基础，研究了多普勒频移的物理意义，即测量空间内离散相的真实平均流速。Takeda^[10]利用基于脉冲波多普勒方法的流速剖面测速技术(UVP)检测加有示踪粒子的单相流流速剖面。Murakawa等^[11]针对低含气率垂直气水泡状流，采用双频超声换能器同时获取气泡流速信息和连续相流速信息。Nguyen等^[12]利用双频方法实现垂直气水两相流的气泡上升速度和压缩率检测。Abbagoni和Yeung^[13]在水平气水两相流中使用连续波多普勒进行流速检测与流型识别。Dong等^[14]采用同侧双晶连续波多普勒传感器，建立双流体模型和弹状流封闭模型检测水平气水泡状流、塞状流和弹状流流速。由于气液两相介质的声阻抗差异大，超声波在两相界面处几乎能够发射全反射，大部分研究都侧重于单相流或低含气率的气水泡状流，而对于其他流型或其他多相流(如油水两相流)流速测量研究很少。Morriss和Hill^[15]将商用多普勒系统用于大管径垂直油水两相流的测量，发现相含率变化导致的流体声速改变会给测量结果带来误差。Dong等^[16]利用连续波多普勒系统结合漂移模型测得了油水两相流流速。Tan等^[17]基于边界层理论，结合连续波多普勒和电学传感器测量油水两相流流速。此外，Kouame等^[18]曾指出连续波多普勒因其测量空间固定，比脉冲波更适合进行流速检测，前者对流体的流速检测范围没有限制，而后者距离分辨率与最大可测流速互相制约，限制了该方法在流速检测中的应用。但目前连续波超声多普勒(CWUD)用于油水两相流检测的研究仍然较少。
对于水平油水两相流流速测量问题，本文提出了一种同侧双晶连续波超声多普勒的测量方法。利用油水两相在流动过程中会形成分散液滴的现象，采用连续波超声多普勒方法获取流速信息。超声传感器为双晶超声换能器，测量区间覆盖管道横截面整个径向范围。通过多普勒频移响应特性分析，分别得到水连续和油连续状态下总表观流速与测量空间内离散相平均真实流速之间的线性关系。据此，采用电导环传感器所测电压数据来判断流体的连续相，进而根据不同连续相下的测量模型计算流体总表观流速。
1 基本原理 同侧双晶连续波超声多普勒测量方法通过同侧双晶超声多普勒传感器完成超声波的发射和接收。传感器结构示意图如图 1(a)所示，包含接收和发射压电陶瓷晶片，晶片形状为圆形，中心频率f₀为1MHz，直径d为9mm，均附着在聚烯亚胺固体声耦合材料上，且与被测流体直接接触。耦合材料被切削成一定形状以保证2个晶片的法线方向与来流方向夹角θ₀为53°。此外，为防止声波通过声耦合材料的传播造成发射和接收声波的互相干扰，在2个晶片及耦合材料之间加入隔声材料。双晶超声换能器最外层为金属保护外壳，与地相连，保证高频信号不受干扰。

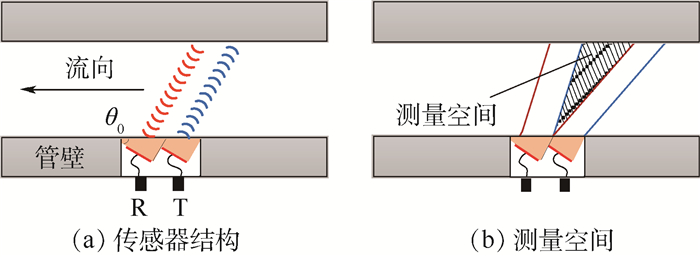图 1 同侧双晶超声多普勒传感器 Fig. 1 One-side two-chip ultrasonic Doppler sensor

图选项

综合考虑近场距离L和扩散角β对声场分布的影响，图 1(b)为超声测量场分布示意图，表示发射和接收超声波声束的有效边界，其重叠区域即为超声测量空间，可以看出覆盖管道横截面的整个径向范围。该超声换能器的L和β的表达式为

(1)

式中：λ为超声波在被测流体中的波长。
超声波经发射晶片连续地射入流体，同时另一个接收晶片接收遇到离散液滴后带有多普勒频移信息的超声散射信号，由于液滴具有一定的流动速度，因此接收到的回波信号会发生频移。根据多普勒原理和折射定律，测试空间内散射液滴产生的平均多普勒频移和平均真实流速(多普勒速度)分别为^[9]

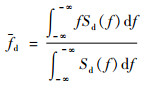(2)

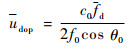(3)

式中：f为多普勒信号功率谱的频率成分；c₀为耦合材料声速，取值为2350m/s；f₀为超声发射频率；通过对多普勒信号的功率谱加权平均得到；S_d(f)为多普勒信号的功率谱。测量空间内，平均多普勒频移与离散液滴的平均真实流速呈正比关系。此外，超声换能器利用耦合材料，可以消除由油水两相流含率的变化对多普勒流速计算结果带来的影响；且固体材料中声速受温度变化的影响小，相比于液体更加稳定，因此使用耦合材料可以减小测量误差^[19]。
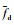
2 实验装置 油水两相流流速测量实验于天津大学多相流实验室完成，其实验装置结构如图 2所示。水平管道由内径50mm的不锈钢管组成，总长约为16.6m。实验用水为自来水(密度为998kg/m³，动力黏度为0.001Pa·s)，油为工业白油(密度为800kg/m³，动力黏度为0.017Pa·s)。在水相与油相入口分别设置精度为±0.5%的单相流量计，获得管道入口处的分相流量值。超声多普勒和电导环测量系统安装于入口下游以便流型充分发展，并在其下游安装快关阀装置用以相含率测量。实验过程中，水和油的压力均稳定在0.2MPa，平均气温约25℃。通过固定入口处的水流量、由低至高调节油流量的方式产生不同流型，同时使用高速摄像机记录流型照片，由于多普勒方法仅适用于含有离散相液滴的油水两相流，实验包含除层流外的水平油水两相流典型流型，分别为层流夹带液滴(ST&MI)、油包水和水包油(Dw/o&Do/w)、水和水包油(Do/w&w)、水包油(o/w)和油包水(w/o)5种流动状态。实验中，混合流体的总表观流速范围为0.25~3.17m/s，含水率变化范围为4%~96%。

图 2 实验装置示意图 Fig. 2 Schematic of experimental facility

图选项

测量系统结构如图 3所示，包括超声多普勒和电导环传感器。超声多普勒传感器利用FPGA产生1MHz连续方波逻辑信号控制MOSFET管输出峰峰值100V高压方波激励探头发射超声波，回波信号经接收探头进入信号调理电路，通过乘法解调和低通滤波最终输出仅含低频成分的多普勒频移信号^[20]。

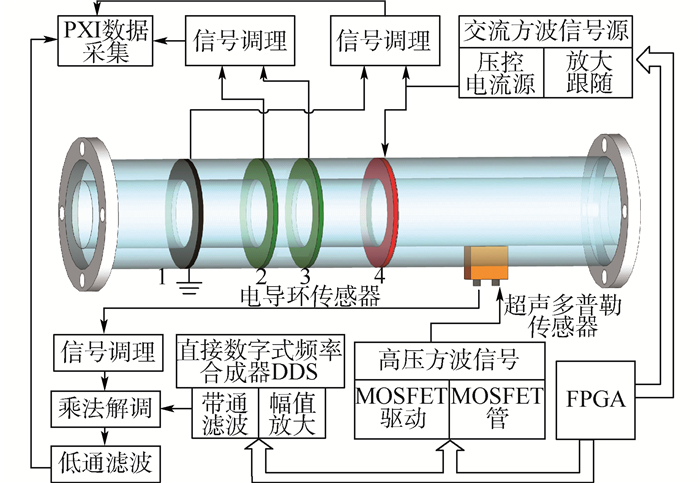图 3 超声多普勒和电导环测量系统 Fig. 3 Ultrasonic Doppler and conductance ring measurement system

图选项

对于电导环传感器，在流体连续相导电条件下，传感器能够正常工作获得含水率信息，如图 3所示，采用四环形电极结构^[20]，电极1与电极4作为激励电极对，电极2和电极3为测量电极对。为减少电极的腐蚀，由FPGA控制的压控电流源产生频率为20kHz、峰峰值为2mA交流方波电流信号注入到激励电极4，同时电极1接地，由此在电极1和电极4之间形成电学敏感场。采集测量电极2和电极3之间的电势差，该电势差即可反映连续相为导电相条件下的含水率信息，当连续相为油相时(含水率低于25%)^[4]，测量电极之间无法形成有效电场，因此不能获得有效含水率信息。
传感器的采集系统由基于PXI总线协议的采集板卡和图形化编程软件LabVIEW搭建完成，可实现对采样过程的控制。每个实验点采集10 s，超声多普勒频移信号的采样频率设置为50kHz，电导环传感器采样频率为200kHz。由式(3)可知，连续波超声多普勒传感器的速度分辨率受最小可测频移Δf_d影响, Δf_d=f_s/N_s, f_s为系统采样频率, N_s为采样点数，因此，超声多普勒系统的Δf_d为0.1Hz，相应的速度分辨率为0.20mm/s。
3 油水两相流多普勒频移特性 将采集到的多普勒信号进行频谱分析，并由式(2)计算得到相应的超声测量空间内离散液滴的平均多普勒频移。根据油水两相实验研究^[4]，连续相从油相向水相转变的含水率临界值范围为15%~30%。含水率较低时，油相是主导相，从而形成油连续流体，含水率较高时，形成水连续流体，中间范围为过渡状态。图 4给出了各实验点中平均多普勒频移与参考总表观流速J_r之间的关系。可以看出，测量空间内的随J_r的提高而增大，但是呈现出2个斜率不同的线性关系，即Line A和Line B。结合快关阀所测含水率信息发现，分布在Line A周围的实验点的含水率基本小于20%，Line B周围实验点的含水率基本大于30%，有一部分过渡流态的实验点位于Line A和Line B之间。因此，Line A和Line B分别代表了流体不同流动状态(即油连续和水连续状态)下与J_r的线性关系。此外，为方便流速计算，根据电导环传感器所测结果将过渡流态归为油或水连续状态。

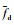
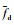
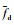
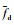
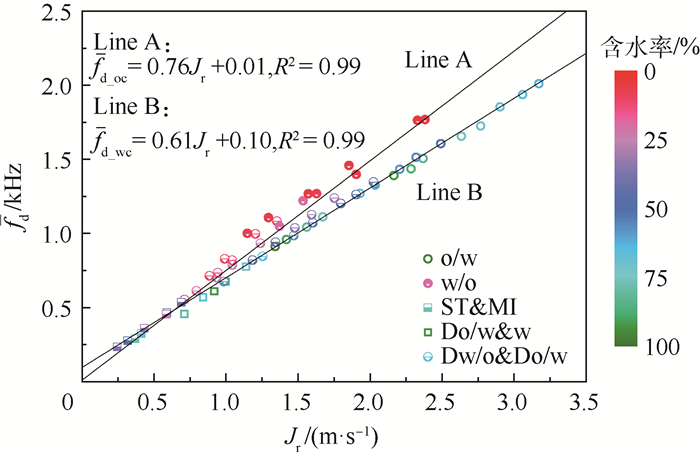图 4 油水两相流多普勒频移响应特性 Fig. 4 Doppler shift response characteristics in oil-water two-phase flow

图选项

由图 4可知，当总表观流速相同时，油连续状态时的比水连续状态下的结果要高，说明该测量空间内离散相的会受到不同连续相的影响。是测量空间内每个运动散射体产生频移的累积结果，即其表示的是这些液滴运动的一个综合频移响应。当相含率发生变化时，流体的混合雷诺数会随之改变，连续相也将在反相点附近发生改变，所以流体在湍流/层流或者水连续/油连续状态下的速度分布将不同^[16]。传感器测量空间的结构覆盖管道横截面的整个径向范围，离散相沿管道径向方向的完整速度剖面均包含在测量空间内，理想情况下能消除流速分布变化的影响，但是除速度分布外，测量空间内的还受液滴浓度分布对速度分布加权作用的影响。此外，两相间的密度和动力黏度的差异，使得在流体流动过程中离散相和连续相存在相间滑差，而且油连续和水连续下的相间滑差有所差别。因此，测量空间内的u_dop与各相的含率、传感器测量空间结构、流体属性均相关，以上因素产生的综合影响就是在总表观流速相同时，不同连续相条件下与J_r的关系出现2种线性趋势，且油连续时测得的或u_dop要高于水连续时的结果。
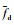
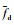
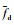
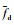
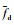
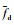
采用最小二乘拟合方法，得到水连续和油连续时测量空间内离散相的平均多普勒频移与参考总表观流速J_r间的线性关系分别为

(4)

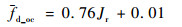(5)

式中：和分别为水连续和油连续条件下的平均多普勒频移。
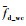
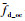
根据式(3)及超声换能器参数f₀、c₀、θ₀，可以得知该超声多普勒传感器测得的平均多普勒速度和频移之间满足：

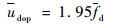(6)

将式(6)代入到式(4)和式(5)中，从而得到水连续和油连续条件下的流体总表观流速J与测量空间内离散液滴平均多普勒速度的线性关系分别为

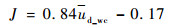(7)

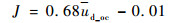(8)

式中：和分别为水连续和油连续条件下的平均多普勒速度。
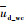
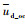
4 油水两相流的连续相识别 通过第3节对油水两相流多普勒频移响应特性分析，在不同连续相时测量区间内的平均多普勒速度与总表观流速分别遵循测量模型式(7)和式(8)。为获得油水两相流各实验点的总表观流速，首先需要流体的连续相进行判断，进而选取相应流动状态下的测量模型。本文利用电导环传感器的工作特性，根据所测数据来判断两相流的连续相。
电导环传感器对导电相流体敏感，可获得连续相为导电相条件下的相含率信息，本文即水连续油水两相流。由于两相介质电导率不同，当电学敏感场内的分相含率发生变化时，其混合电导率发生变化，进而敏感场的阻抗特性随之改变，导致测量电极对间的电势差V_m变化，因此V_m能够有效反映出流体相含率变化情况。通常定义一个无量纲电压参数V(即归一化电压)来表征相对电压变化量：

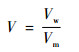(9)

式中：V_w为管道内充满水时的测量电压；V_m为管道内为油水两相流时的测量电压。
将所有实验点下得到的无量纲电压参数V与快关阀获得的含水率值H对比，如图 5所示。可以看出，当分散流含水率低于25%时，即在油连续状态下，V>1，相反，在水连续状态下，V < 1。这种现象是由于流体连续相不导电时，电导环传感器无法形成有效电场，实际测量的是电路自身阻抗，导致出现V>1的结果^[21]。

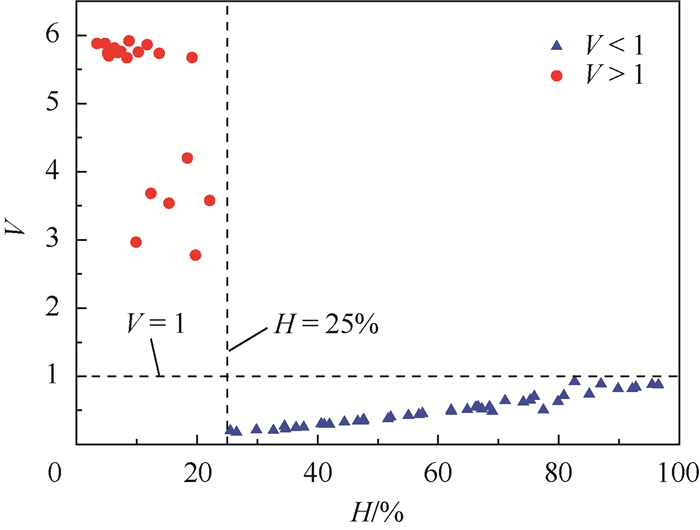图 5 无量纲电压参数V分布 Fig. 5 Distribution of dimensionless voltage parameter V

图选项

综上，通过无量纲电压参数V可判断各个实验点中流体的连续相，由此再选取相应流动状态下的测量模型计算两相流的总表观流速，整个计算过程如图 6所示。

图 6 总表观流速计算流程 Fig. 6 Calculation flowchart of overall superficial flow velocity

图选项

5 实验结果 根据第4节内容，对于不同流型的实验点，在判断流体连续相后，分别根据式(6)~式(8)计算出水连续和油连续条件下的总表观流速。使用相对误差ε作为测量误差评价指标：

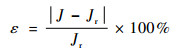(10)

如图 7所示，结果均与流速参考值呈较好的线性关系，其中水连续状态下的总表观流速估计值相对误差为2.75%，油连续状态下的总表观流速估计值相对误差为3.87%。

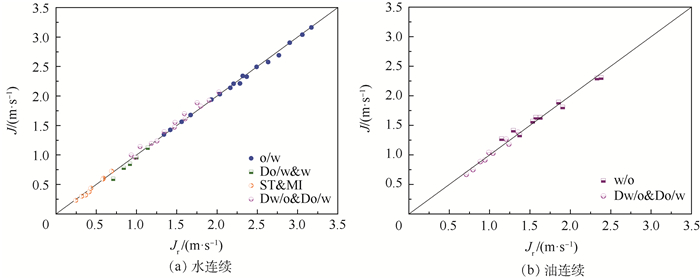图 7 流速测量结果 Fig. 7 Flow velocity measurement results

图选项

油水两相流实验的总表观流速估计结果和相对误差分布如图 8所示。可以看出，估计结果J与两相流总表观流速参考值J_r能够较好吻合，总表观流速估计值的均方根误差为0.01m/s，平均相对误差为3.09%，最大相对误差为10.84%，其中相对误差在5%以内的置信概率为70%。

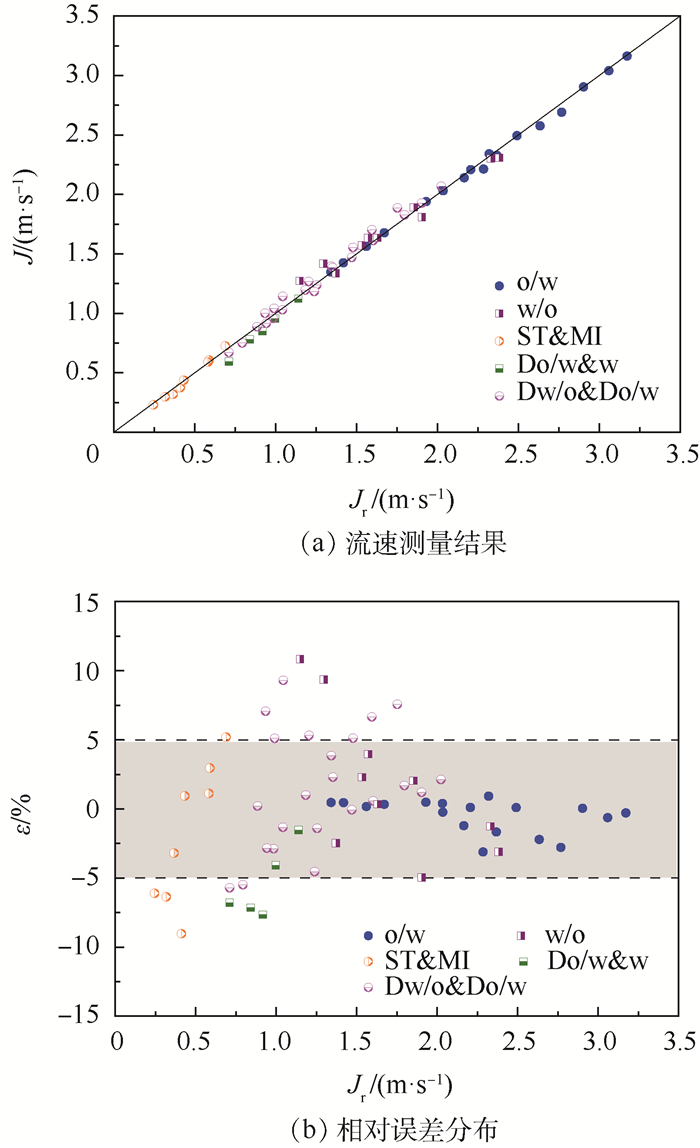图 8 总表观流速测量结果和相对误差分布 Fig. 8 Overall superficial flow velocity measurement results and relative error distribution

图选项

6 结论 1) 针对水平油水两相流流速测量问题，本文提出一种非侵入式的同侧双晶连续波超声多普勒的测量方法，超声测量空间能够覆盖管道横截面的整个径向范围，其内部的运动液滴平均真实流速可直接通过采集到的多普勒信号获得。
2) 通过油水两相流多普勒频移响应特性分析，发现测量空间内的平均多普勒频移与相含率、传感器测量空间结构、流体属性均相关，最终体现在水连续和油连续状态下，所测平均多普勒频移与流体总表观流速间呈现2种线性关系。
3) 根据电导环传感器的敏感原理和工作特性，其无量纲化电压参数V能够用于流体连续相的判别，继而选取相应流动状态下的测量模型计算两相流的总表观流速。
4) 实验结果表明，油水两相流的总表观流速估计值具有较好的结果，均方根误差为0.01m/s，平均相对误差为3.09 %，其中相对误差在5%以内的置信概率为70%。

参考文献

[1]	周恒. 新世纪对流体力学提出的要求[J]. 自然科学进展, 2000, 10(6): 491-494. ZHOU H. Requirements of fluid mechanics in the new century[J]. Advances in Natural Science, 2000, 10(6): 491-494. DOI:10.3321/j.issn:1002-008X.2000.06.002 (in Chinese)
[2]	陈云霞, 刘王佳. 考虑喷油润滑的附件机匣温度场分析[J]. 北京航空航天大学学报, 2015, 41(7): 1171-1176. CHEN Y X, LIU W J. Temperature field analysis of attachment case considering injection lubrication[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(7): 1171-1176. (in Chinese)
[3]	谭超, 董峰. 多相流过程参数检测技术综述[J]. 自动化学报, 2013, 39(11): 1923-1932. TAN C, DONG F. Parameters measurement for multiphase flow process[J]. Acta Automatica Sinica, 2013, 39(11): 1923-1932. (in Chinese)
[4]	BRAUNER N, ULLMANN A. Modeling of phase inversion phenomenon in two-phase pipe flows[J]. International Journal of Multiphase Flow, 2002, 28(7): 1177-1204. DOI:10.1016/S0301-9322(02)00017-4
[5]	LI D H, FENG F F, WU Y X, et al. Investigation of the mixture flow rates of oil-water two-phase flow using the turbine flow meter[J]. Journal of Physics:Conference Series, 2009, 147(1): 12062.
[6]	TAN C, WU H, DONG F. Horizontal oil-water two-phase flow measurement with information fusion of conductance ring sensor and cone meter[J]. Flow Measurement and Instrumentation, 2013, 34: 83-90. DOI:10.1016/j.flowmeasinst.2013.08.006
[7]	LUCAS G P, JIN N D. Measurement of the homogeneous velocity of inclined oil-in-water flows using a resistance cross correlation flow meter[J]. Measurement Science and Technology, 2001, 12(9): 1529. DOI:10.1088/0957-0233/12/9/320
[8]	NGUYEN T T, KIKURA H, DUONG N H, et al. Measurements of single-phase and two-phase flows in a vertical pipe using ultrasonic pulse Doppler method and ultrasonic time-domain cross-correlation method[J]. Vietnam Journal of Mechanics, 2013, 35(3): 239-256.
[9]	BRODY W R, MEINDL J D. Theoretical analysis of the CW Doppler ultrasonic flowmeter[J]. IEEE Transactions on Biomedical Engineering, 1974, 21(3): 183-192.
[10]	TAKEDA Y. Velocity profile measurement by ultrasound Doppler shift method[J]. International Journal of Heat and Fluid Flow, 1986, 7(4): 313-318. DOI:10.1016/0142-727X(86)90011-1
[11]	MURAKAWA H, KIKURA H, ARITOMI M. Application of ultrasonic Doppler method for bubbly flow measurement using two ultrasonic frequencies[J]. Experimental Thermal and Fluid Science, 2005, 29(7): 843-850. DOI:10.1016/j.expthermflusci.2005.03.002
[12]	NGUYEN T T, KIKURA H, MURAKAWA H, et al. Measurement of bubbly two-phase flow in vertical pipe using multiwave ultrasonic pulsed Doppler method and wire mesh tomography[J]. Energy Procedia, 2015, 71: 337-351. DOI:10.1016/j.egypro.2014.11.887
[13]	ABBAGONI B M, YEUNG H. Non-invasive classification of gas-liquid two-phase horizontal flow regimes using an ultrasonic Doppler sensor and a neural network[J]. Measurement Science and Technology, 2016, 27(8): 84002. DOI:10.1088/0957-0233/27/8/084002
[14]	DONG X, TAN C, DONG F. Gas-liquid two-phase flow velocity measurement with continuous wave ultrasonic Doppler and conductance sensor[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(11): 3064-3076. DOI:10.1109/TIM.2017.2717218
[15]	MORRISS S L, HILL A D.Measurement of velocity profiles in upwards oil/water flow using ultrasonic Doppler velocimetry[C]//SPE Annual Technical Conference and Exhibition.Richardson: SPE, 1991: 65-79.
[16]	DONG X, TAN C, YUAN Y, et al. Oil-water two-phase flow velocity measurement with continuous wave ultrasound Doppler[J]. Chemical Engineering Science, 2015, 135: 155-165. DOI:10.1016/j.ces.2015.05.011
[17]	TAN C, YUAN Y, DONG X, et al. Oil-water two-phase flow measurement with combined ultrasonic transducer and electrical sensors[J]. Measurement Science and Technology, 2016, 27(12): 125307. DOI:10.1088/0957-0233/27/12/125307
[18]	KOUAME D, GIRAULT J, PATAT F E D E. High resolution processing techniques for ultrasound Doppler velocimetry in the presence of colored noise.Ⅰ.Nonstationary methods[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2003, 50(3): 257-266. DOI:10.1109/TUFFC.2003.1193619
[19]	LIU W, TAN C, DONG X, et al. Dispersed oil-water two-phase flow measurement based on pulse-wave ultrasonic Doppler coupled with electrical sensors[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(9): 2129-2142. DOI:10.1109/TIM.2018.2814069
[20]	WU H, TAN C, DONG X, et al. Design of a conductance and capacitance combination sensor for water holdup measurement in oil-water two-phase flow[J]. Flow Measurement and Instrumentation, 2005, 46: 218-229.
[21]	董虓霄, 谭超, 董峰. 油水两相流含水率测量组合传感器[J]. 工程热物理学报, 2015, 36(7): 1487-1491. DONG X X, TAN C, DONG F. Combined sensor for water holdup measurement in oil-water two-phase flow[J]. Journal of Engineering Thermophysics, 2015, 36(7): 1487-1491. (in Chinese)