在矩张量反演中,噪声是一个不可忽视的问题。由于地质结构存在显著的不均匀性和各向异性[16-17],弹性波在介质中传播时会发生明显的散射、反射等现象[18-19]。另外,矩张量反演中的点震源假设和远场假设将弹性波信号理想化,导致反演过程不考虑裂纹开裂产生的高频波和中近场成分的影响。对于矩张量反演,这部分弹性波成分也可以看作特殊的噪声信号。由于噪声信号成分大多具有不确定性,因此矩张量反演结果会出现无法预料的偏差甚至错误[20-21]。针对噪声问题,目前常用的手段是在开始反演前,使用数字信号处理方法对声发射信号进行处理[22],然而,裂纹动力学特性无法预先了解,地质结构也是复杂且未知的,导致噪声信号的特征很难评估,由此可见对噪声信号的筛选和处理是一件非常困难的事情。
裂纹矩张量反演方法的本质,是通过传感器捕捉裂纹开裂产生的声发射信号幅值在空间中的分布规律,进而识别特定的裂纹。合理的传感器空间排布形式能够降低噪声对反演结果的影响,提高反演结果的精度。目前,对矩张量反演中传感器位置的研究还比较少。对于地震的矩张量反演[20, 23-24],由于地震台站多为永久性建筑,工程中一般根据震源定位选择临近的地震台站所得地震波形进行反演。对于实验室条件下的岩石压裂声发射实验[25-27],虽然试件尺寸较小且传感器布置的自由度很高,研究中传感器位置的选取仅仅根据均匀排布、尽可能扩大覆盖面等依据来确定。总体来看,矩张量反演中对于传感器(台站)位置选择的研究还不够深入。因此,本文从传感器空间排布形式入手,以相应的理论分析为基础,研究在声发射信号包含一定噪声的情况下,不同的传感器排布方案取得的矩张量反演精度,为工程应用提供相关的意见和指导,即如何选择合适的传感器排布形式来提高裂纹矩张量反演精度。
1 理论分析 1.1 裂纹矩张量反演理论 根据矩张量理论的裂纹载荷等效原理[10],任何一个裂纹都可以通过唯一的矩张量来描述。在均匀各向同性介质中,对于一个裂纹,假设裂纹面的法向向量为n,裂纹面开裂的位移向量为l,则其对应的矩张量形式为
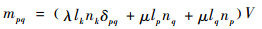 | (1) |
式中:mpq为矩张量元素;λ和μ为拉梅常数;当p=q时,δpq取1,否则取0;lk和lp为裂纹面位移单位向量的分量;nk和nq为裂纹面法向单位向量的分量;V为裂纹开裂体积。
由矩张量表述的裂纹开裂弹性波位移场的表达式为[10]
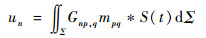 | (2) |
式中:un为弹性体中某处沿方向n的位移,n=1, 2, 3,分别代表x、y、z 3个坐标方向; Σ代表裂纹面; Gnp, q为第2类格林函数; S(t)为震源函数。由于式(2)展开后的形式过于复杂,不利于工程应用,因此引入远场假设和点震源假设来对其进行简化,其中远场假设认为传感器与震源的距离足够远,此时声发射信号中只包含远场成分;点震源假设认为震源尺寸远小于弹性波波长,因此裂纹面上每个点发出的弹性波的相位都相同,且每个点到任意一个传感器的距离也相同,此时裂纹的真实几何形状可以忽略。则由矩张量表述的裂纹弹性波表达式可简化为[10]
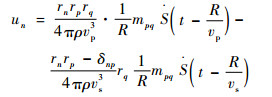 | (3) |
式中:rn、rp和rq为震源-传感器连线方向余弦的分量,n, p, q=1, 2, 3,分别代表x、y、z 3个坐标方向;ρ为介质材料密度;R为传感器与震源的距离;vp和vs分别为纵波波速和横波波速。进一步,可认为震源函数具有单位阶跃形式[28],且考虑到压缩波(P波)成分的波速最快,工程中使用式(4)来反演矩张量[29]:
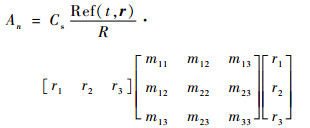 | (4) |
式中:An为传感器接收到的沿n方向位移信号的初动极大值;Cs为传感器灵敏度参数,工程中该参数一般通过试验测定,数值试验中取1;Ref(t, r)表示反射系数,用于修正地面反射对弹性波幅值的影响,数值试验中取rn;mpq表示矩张量元素,一个完整的矩张量包含9个元素,其中独立元素有6个。也就是说,通过6个不同位置的传感器可以得到6个与式(4)形式相同的代数方程,方程联立可以求解得到完整的矩张量。
1.2 传感器位置选择理论 矩张量反演方法的核心是求解一组方程组,即由6个传感器得到的形如式(4)的方程所组成的方程组,当考虑噪声信号时,方程组可以写成的矩阵形式为
 | (5) |
进而式(5)可写成
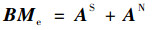 |
其中:B为方程组的系数矩阵;Me为矩张量元素组成的列向量;AS为真实信号幅值;AN为噪声信号幅值。本文希望在AN取值出现小幅度变化时,解向量Me的求解结果能够保持稳定。为了降低列向量Me对噪声信号的敏感度,根据数值分析理论,需要降低系数矩阵B的条件数,条件数的定义为
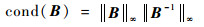 | (6) |
适中:范数取无穷范数形式。
选择合理传感器的依据是使得系数矩阵的条件数尽可能的取小值。对比式(4)和式(5)可知,影响系数矩阵B取值的因素包括传感器之间的相对位置和传感器与震源的相对位置。一般情况下,传感器的位置选定与地震发生之前,研究传感器与震源的相对位置意义较小且会大幅度增加研究复杂性。因此研究只考虑传感器之间的相对位置。由于矩张量反演至少涉及6个传感器,即6个空间位置,18个自由度。通过理论推导传感器最佳位置非常困难,因此本文通过枚举的方法,通过大量的随机分布实验寻找传感器布局的一般规律。
2 随机分布实验 2.1 传感器位置选取及坐标变换 为了寻找传感器布局的一般规律,研究使用枚举法随机选择不同的传感器布局,通过对比不同传感器布局下的矩张量反演误差来寻求最优的分布模式。首先在x-y面上一个半径为1 m的圆内(记作C0圆)随机选择6个初始传感器坐标点,记作L0,其中L0是6×3阶矩阵,每一行存储一个传感器的坐标。然后将传感器坐标进行坐标变换:
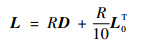 | (7) |
式中:D为平移矩阵,每一行都相同且等于方向向量
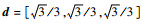
2.2 声发射信号构造 为了探究合理的传感器排布形式,研究需要合适的声发射数据用于矩张量反演。为了简化研究,排除其他因素的影响。本文使用人工合成的声发射信号,在基础信号中叠加一定比例的噪声信号,考察不同传感器排布形式对噪声信号的敏感程度。针对特定的裂纹类型,基础信号使用式(3)计算,震源函数取类单位阶跃形式[11]。噪声信号的幅值根据基础信号的均方根计算:
 | (8) |
式中:F为基础信号的整体幅值水平;f0(ti)为ti时刻基础信号的数值;N为位移序列中元素的个数。在基础信号f0(ti)的基础上,叠加白噪声信号,即
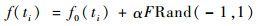 | (9) |
其中:f(ti)为叠加上噪声信号之后的声发射信号,称之为真实信号;α为噪声信号占基础信号的比例;Rand(-1, 1)表示区间[-1, 1]上的一个均布随机数。
2.3 反演误差计算 为了定量研究传感器排布形式对裂纹矩张量反演精度的影响,本文提出了一种矩张量反演误差计算方法。传统的矩张量分解处理方法计算过程复杂,且处理结果重点反映了裂纹的物理特性,对矩张量数学特征的反映则不够直接和明显。因此,参照线性代数中范数的概念,将矩张量看作一个3×3的矩阵,通过构造特定形式的范数来定量表征矩张量反演误差。
裂纹矩张量反演结果的误差计算方法应综合考虑2个方面:一方面,最终的误差结果应考虑所有矩张量元素的误差情况;另一方面,根据各个矩张量元素取值的大小,不同矩张量元素误差对最终误差结果影响的权重应具有区分度。综合以上两方面的考虑,误差计算方式为
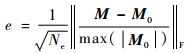 | (10) |
式中:e为矩张量的反演误差;M为矩张量反演结果;M0为矩张量真实结果;Ne为矩张量元素的个数;max(M0)为矩阵中所有元素绝对值中的最大值;||·||F表示矩阵Frobenius范数,相应的表达式为
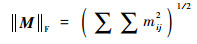 | (11) |
3 数值实验结果 根据式(7)产生100组传感器随机分布形式,进而根据式(3)求解相应位置处的声发射信号,根据式(4)反演矩张量,最后通过式(10)求解反演误差。文献[10]表明,地震裂纹主要以剪切裂纹为主,因此实验选择剪切裂纹作为震源。在岩石介质中,存在同一个区域内包含多个裂纹源的情况,多个裂纹的识别主要依赖于声发射信号初至波到时的拾取精度。另外,声发射事件的强度也是一个重要指标,但声发射事件强度的识别依赖于声发射信号初至波幅值的识别精度。总体来看,声发射事件的发生数和强度的识别主要依赖于信号处理精度,与传感器排布形式的关系相对较小。因此,为了简化研究过程,数值实验中只考虑单一震源具有相同震源强度的情况。
当噪声水平α=2%时,相应的误差统计结果如图 1所示。图中每一个点代表一种随机传感器分布模式,极坐标图径向坐标代表反演误差,周向坐标随机选取,没有实际物理意义,其作用是区分每次反演结果。
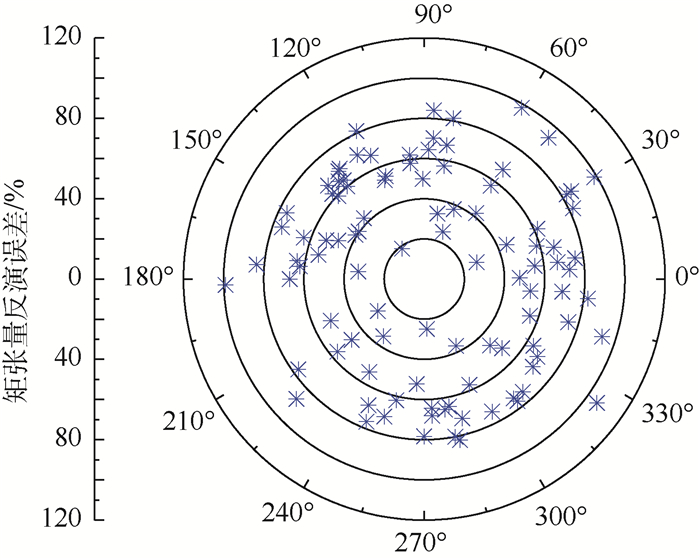 |
| 图 1 100种传感器随机排布形式反演得到的矩张量反演误差对比 Fig. 1 Comparison of moment-tensor inversion errors calculated with 100 sensor stochastic arrangements |
| 图选项 |
从图 1中找出最靠近中心,即误差最小的3个结果,画出对应的传感器排布形式,如图 2所示,图中星号代表传感器位置。由图 2可以看出,3种传感器排布形式存在一定的相似性,即一个传感器接近圆形区域的圆心,其他5个传感器则靠近圆形边界,且传感器之间的方位差别相对比较均衡。由此可以猜想,性能最好的传感器排布形式是正五边形的形式:第1个传感器布置在圆形,其他5个传感器分别布置在圆形内接正五边形的5个角点上,如图 3所示,图中黑色原点代表传感器位置。
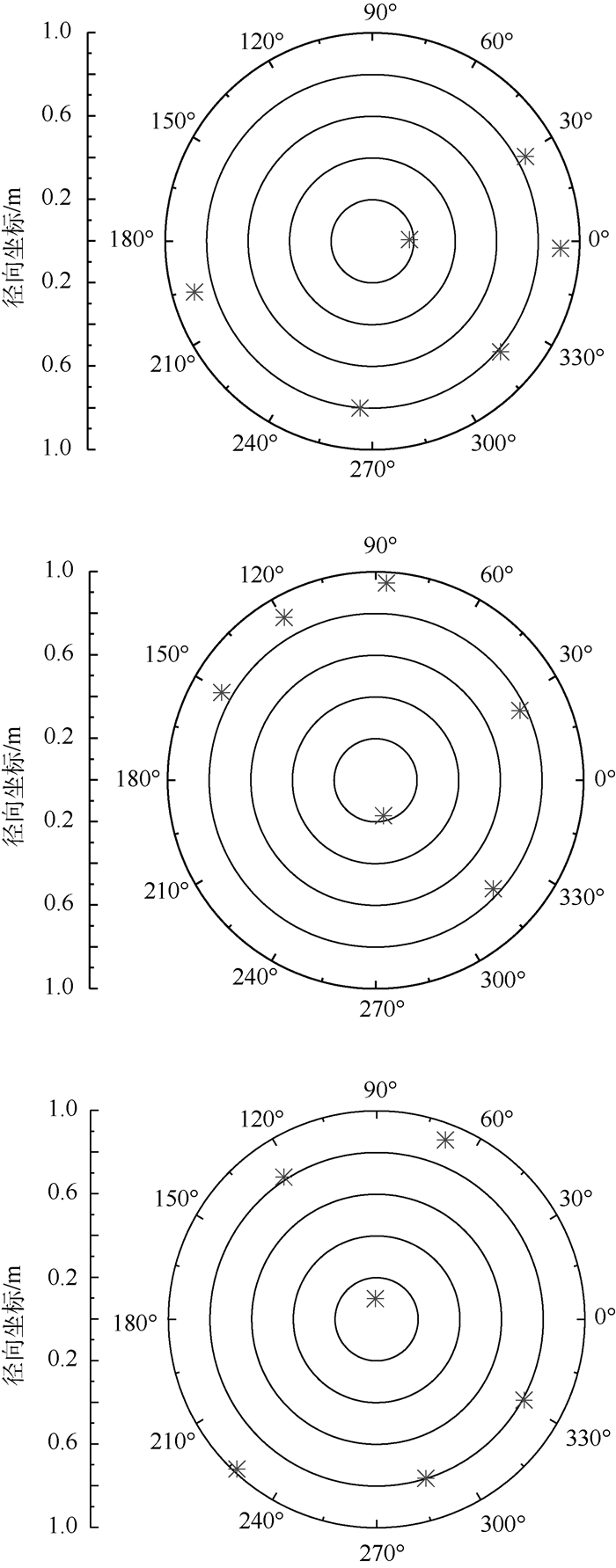 |
| 图 2 图 1中矩张量反演误差最小的3个结果对应的传感器排布形式示意图 Fig. 2 Schematic of sensor arrangements corresponding to three moment-tensor inversion errors with minimum values in Fig. 1 |
| 图选项 |
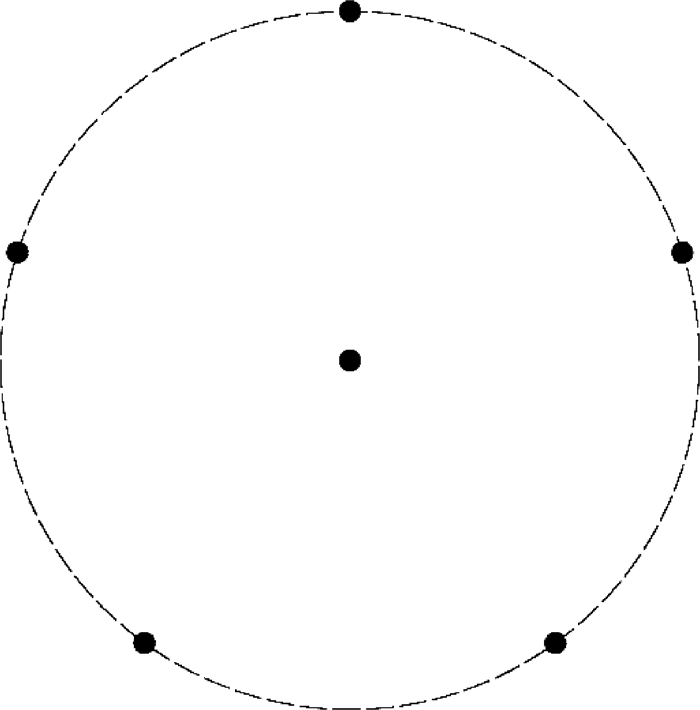 |
| 图 3 传感器正五边形排布形式示意图 Fig. 3 Schematic of sensors with an arrangement of regular pentagon |
| 图选项 |
为了探究正五边形传感器排布形式下的矩张量反演表现,将正五边形传感器排布形式应用于矩张量反演中,并将计算结果与随机传感器排布形式所得结果进行对比。根据式(7)计算出正五边形形式中6个传感器的空间最终位置为
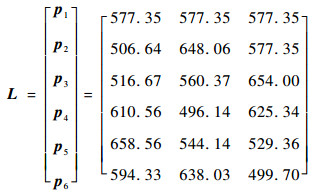 | (12) |
为使结果具有可比性,正五边形传感器(见式(12))分布在一个半径为100 m的圆形区域内,与随机传感器的分布范围相同。将不同传感器排布形式计算得到的矩张量反演误差画图,如图 4所示。其中,十字符号(10个)代表正五边形传感器排布形式得到的矩张量反演误差,米字符号(100个)代表随机传感器排布形式得到的反演误差。噪声水平α取1%,2%和3%。
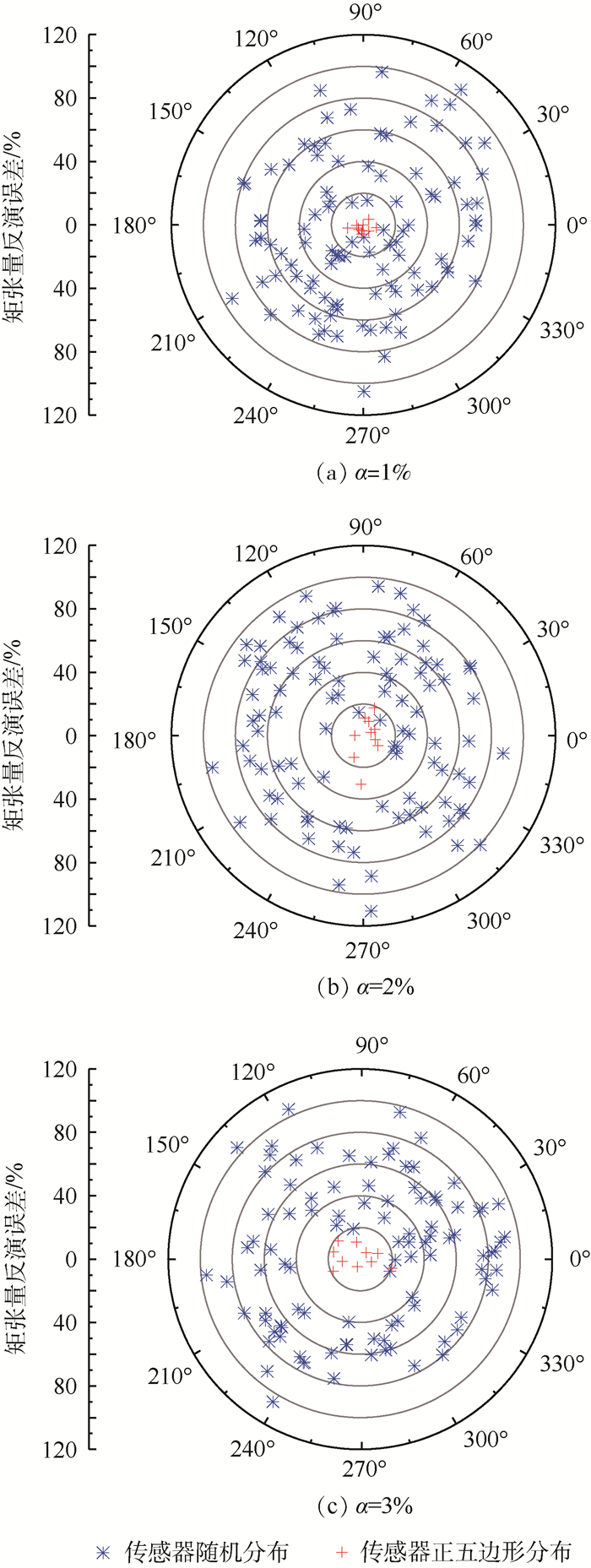 |
| 图 4 不同噪声水平下多种传感器排布形式反演得到的矩张量反演误差对比 Fig. 4 Comparison of moment-tensor inversion errors inverted with different sensor arrangements under different noise levels |
| 图选项 |
由图 4可以看出,在不同的噪声水平下,误差分布规律具有一致性。根据正五边形传感器排布形式计算得到的误差(符号)均集中于坐标图的中央,而随机传感器排布形式计算得到的误差则分布在周围很大的范围内。以上结果表明正五边形传感器排布形式在矩张量反演中具有非常优秀的精度表现,虽然随机噪声信号导致正五边形传感器分布形式的反演结果出现波动,但是波动的幅度很小,多次反演的结果非常接近并且集中,由此可知在正五边形传感器排布形式的条件下,矩张量反演结果非常稳定。相对于其他传感器排布形式,此时的矩张量反演结果对噪声的敏感程度很低。
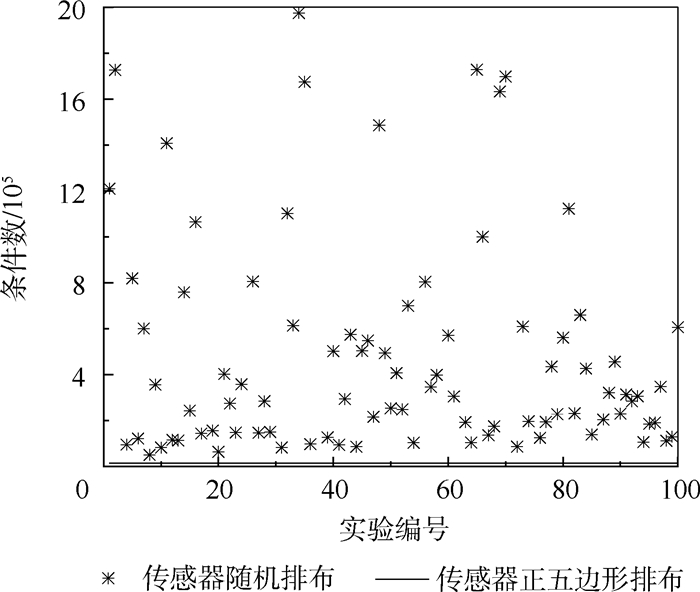
4 原理分析 由第3节可知,正五边形传感器排布形式在矩张量反演中具有较好的精度表现。这一结论可以通过方程组的条件数来验证和解释。根据式(6),可以计算出传感器正五边形排布以及每种随机排布形式得到的线性方程组的条件数,所有条件数如图 5所示。图中底部横线为传感器正五边形排布形式对应的条件数,星号表示每一次随机排布形式对应的条件数。图中横坐标表示每一次传感器随机排布的实验编号,纵坐标表示条件数。
 |
| 图 5 矩张量反演中不同传感器排布形式对应的方程组条件数对比 Fig. 5 Comparison of condition numbers of equation set corresponding to different sensor arrangements in moment-tensor inversion |
| 图选项 |
由图 5可知,数值试验涉及的传感器随机排布形式对应的条件数均大于正五边形排布形式对应的条件数,也就是说传感器正五边形排布形式的条件数是目前计算考虑的所有传感器排布形式的下界。当传感器排布形式取正五边形形式时,方程组中方程之间的线性度最低,良性度最高。此时,计算结果对噪声的敏感度最低。在相同的噪声水平下,反演结果最接近理论值,反演精度最高。
5 结论 1) 裂纹矩张量反演中,传感器接收到的声发射信号总包含一定比例的噪声信号,这些噪声信号会影响矩张量的反演精度,甚至导致反演结果完全错误。优化传感器排布形式能够有效降低反演结果对噪声的敏感程度,提高矩张量的求解精度和稳定性。
2) 数值实验结果表明,对于单震源的情况,将传感器按照正五边形布置的方案性能最好。该方案中,5个传感器布置在一个圆环上,且相邻传感器方位角间隔(传感器-圆心连线的夹角)为72°,第6个传感器布置在圆心。这种排布形式可以明显降低信号噪声对矩张量精度的影响,相比于相同分布范围内其他的排布形式,此时的矩张量反演结果更接近真实值,稳定性更好。需要指出的是,当传感器以正五边形形式排布时,根据工程应用条件,尽可能增大传感器的分布范围(即圆环半径)可进一步提高矩张量的反演精度。
3) 裂纹矩张量反演的核心是求解一组线性方程组。当传感器以正五边形形式排布时,方程组系数矩阵的条件数较小,此时虽然位移列向量由于噪声发生小幅度变化,求解结果依然非常接近真实值,且波动较小。
参考文献
| [1] | BAIG A, URBANCIC T. Microseismic moment tensors:A path to understanding FRAC growth[J]. The Leading Edge, 2010, 29(3): 320-324. DOI:10.1190/1.3353729 |
| [2] | BAIG A, URBANCIC T, PRINCE M.Microseismic moment tensors: A path to understanding growth of hydraulic fractures[C]//Canadian Unconventional Resources and International Petroleum Conference.Richardson, Texas: Society of Petroleum Engineers, 2010. |
| [3] | BURRIDGE R, KNOPOFF L. Body force equivalents for seismic dislocations[J]. Bulletin of the Seismological Society of America, 1964, 54(6A): 1875-1888. |
| [4] | KNOPOFF L, RANDALL M J. The compensated linear-vector dipole:A possible mechanism for deep earthquakes[J]. Journal of Geophysical Research, 1970, 75(26): 4957-4963. DOI:10.1029/JB075i026p04957 |
| [5] | AKI K, PATTON H. Determination of seismic moment tensor using surface waves[J]. Tectonophysics, 1978, 49(3-4): 213-222. DOI:10.1016/0040-1951(78)90180-4 |
| [6] | KANAMORI H, GIVEN J W. Use of long-period surface waves for rapid determination of earthquake-source parameters[J]. Physics of the Earth and Planetary Interiors, 1981, 27(1): 8-31. DOI:10.1016/0031-9201(81)90083-2 |
| [7] | KANAMORI H, GIVEN J W. Use of long-period surface waves for rapid determination of earthquake source parameters 2.Preliminary determination of source mechanisms of large earthquakes(MS ≥ 6.5)in 1980[J]. Physics of the Earth and Planetary Interiors, 1982, 30(2-3): 260-268. DOI:10.1016/0031-9201(82)90112-1 |
| [8] | SIPKIN S A. Interpretation of non-double-couple earthquake mechanisms derived from moment tensor inversion[J]. Journal of Geophysical Research, 1986, 91(B1): 531-547. DOI:10.1029/JB091iB01p00531 |
| [9] | JULIAN B R, MILLER A D, FOULGER G R.Non-double-couple earthquakes 1.Theory[J].Reviews of Geophysics, 1998, 36(4): 525-549. |
| [10] | AKI K, RICHARDS P G.Quantitative seismology[M].San Francisco, CA: W.H.Freeman & Co., 1980. |
| [11] | OHTSU M. Source inversion of acoustic emission waveform[J]. Doboku Gakkai Ronbunshu, 1988, 1988(398): 71-79. |
| [12] | HUDSON J A, PEARCE R G, ROGERS R M. Source type plot for inversion of the moment tensor[J]. Journal of Geophysical Research, 1989, 94(B1): 765-774. DOI:10.1029/JB094iB01p00765 |
| [13] | DAHM T. Relative moment tensor inversion based on ray theory:Theory and synthetic tests[J]. Geophysical Journal International, 1996, 124(1): 245-257. DOI:10.1111/gji.1996.124.issue-1 |
| [14] | CHAPMAN C H, LEANEY W S. A new moment-tensor decomposition for seismic events in anisotropic media[J]. Geophysical Journal International, 2012, 188(1): 343-370. DOI:10.1111/gji.2012.188.issue-1 |
| [15] | GU C, MARZOUK Y M, TOKS?KZ M.Bayesian moment tensor inversion and uncertainty quantification for induced seismicity:Uncertainties from both the location and velocity model[M]//SEG Technical Program Expanded Abstracts 2017.Tulsa, OK:Society of Exploration Geophysicists, 2017:2784-2790. |
| [16] | STANCHITS S, VINCIGUERRA S, DRESEN G. Ultrasonic velocities, acoustic emission characteristics and crack damage of basalt and granite[J]. Pure and Applied Geophysics, 2006, 163(5): 975-994. |
| [17] | HAMIEL Y, LYAKHOVSKY V, STANCHITS S, et al. Brittle deformation and damage-induced seismic wave anisotropy in rocks[J]. Geophysical Journal International, 2009, 178(2): 901-909. DOI:10.1111/gji.2009.178.issue-2 |
| [18] | HUDSON J A. Overall properties of a cracked solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 2008, 88(2): 371. |
| [19] | 刘宁, 李敏, 陈伟民. 基于EMT采用FEM研究含裂纹介质中弹性波传播机制[J]. 北京航空航天大学学报, 2015, 41(9): 1686-1692. LIU N, LI M, CHEN W M. Wave propagation in cracked elastic media based on EMT using FEM[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(9): 1689-1692. (in Chinese) |
| [20] | FORD S R, DREGER D S, WALTER W R. Identifying isotropic events using a regional moment tensor inversion[J]. Journal of Geophysical Research:Solid Earth, 2009, 114(B1): 593-602. |
| [21] | MUSTAC M, TKALCIC H. On the use of data noise as a site-specific weight parameter in a hierarchical bayesian moment tensor inversion:The case study of the geysers and long valley caldera earthquakes[J]. Bulletin of the Seismological Society of America, 2017, 107(4): 1914-1922. |
| [22] | 傅一钦.页岩气水力压裂微地震波的时域-频域二维瞬时谱全波形分析[D].北京: 中国科学院大学, 2017. FU Y Q.Full-waveform analysis in time-frequency domain of micro-seismic wave during shale hydraulic fracturing[D].Beijing: University of Chinese Academy of Sciences, 2017(in Chinese). |
| [23] | ABDEL-AAL A A K, YAGI Y. Earthquake source characterization, moment tensor solutions, and stress field of small-moderate earthquakes occurred in the northern Red Sea Triple Junction[J]. Geosciences Journal, 2017, 21(2): 235-251. |
| [24] | CESCA S, HEIMANN S, KRIEGEROWSKI M, et al. Moment tensor inversion for nuclear explosions:What can we learn from the 6 January and 9 September 2016 nuclear tests, North Korea[J]. Seismological Research Letters, 2017, 88(2): 300-310. |
| [25] | DAVI R, VAVRY?UK V, CHARALAMPIDOU E-M, et al. Network sensor calibration for retrieving accurate moment tensors of acoustic emissions[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 62: 59-67. DOI:10.1016/j.ijrmms.2013.04.004 |
| [26] | KWIATEK G, CHARALAMPIDOU E-M, DRESEN G, et al. An improved method for seismic moment tensor inversion of acoustic emissions through assessment of sensor coupling and sensitivity to incidence angle[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 65: 153-161. DOI:10.1016/j.ijrmms.2013.11.005 |
| [27] | STIERLE E, VAVRYCUK V, KWIATEK G, et al. Seismic moment tensors of acoustic emissions recorded during laboratory rock deformation experiments:Sensitivity to attenuation and anisotropy[J]. Geophysical Journal International, 2016, 205(1): 38-50. DOI:10.1093/gji/ggw009 |
| [28] | 刘培洵, 陈顺云, 郭彦双, 等. 声发射矩张量反演[J]. 地球物理学报, 2014, 57(3): 858-866. LIU P X, CHEN S Y, GUO Y S, et al. Moment tensor inversion of acoustic emission[J]. Chinese Journal of Geophysics, 2014, 57(3): 858-866. (in Chinese) |
| [29] | OHTSU M. Acoustic emission theory for moment tensor analysis[J]. Research in Nondestructive Evaluation, 1995, 6(3): 169-184. DOI:10.1080/09349849509409555 |
