在目标探测过程中，如何寻找一种有效的传感器管理方法使传感器网络发挥最大效用，一直是军事方面研究的热点和难点问题。目前，主要存在3类基于贝叶斯理论的传感器管理方法，即：基于任务的传感器管理方法^[1-3]、基于信息论的传感器管理方法^[4-6]、基于风险理论的传感器管理方法^[7-9]。
在以往对传感器管理问题研究中，并不区分目标种类，而在对目标拦截的作战背景下，探明目标类型至关重要，因为针对不同的目标后应对措施也应不同，例如当目标为侦察机时，即可采取干扰措施也可发射导弹拦截，甚至在威胁不大的情况下保持一定预警即可，而当目标为导弹时，应发射导弹拦截。由此，针对不同目标探测情况下的代价函数^[10]不同，传感器管理模型也应有所区别。此外，在目标来袭过程中，敌方会采取电子干扰等措施，探测到的目标中通常掺杂着虚假目标，在传感器资源十分珍贵有限的情况下，对这些目标探测必定造成资源浪费；此外，在判定来袭目标为导弹之后，应当通过武器系统对目标拦截，若对虚假目标拦截必定同时造成武器资源浪费。
本文主要研究传感器同时对目标识别跟踪背景下的传感器管理方法。首先建立风险理论、贝叶斯理论和证据理论的目标识别模型；随后考虑边跟踪边识别的情况，建立跟踪情况下的目标识别模型，并对模型进行理论分析，在模型求解过程中提出一种基于多Agent分布计算理论的分布式算法；最后通过仿真，验证了本文方法、模型和算法的有效性、可行性。
1 模型建立 目标t^j的状态由类别和运动状态组成，为E_k^j={C^j, X_k^j}，其中，C^j为目标类型，为目标t^j在k时刻运动状态。
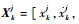
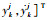
1.1 目标识别模型 本文将风险定义为不确定性事件发生后带来的损失与该事件发生的概率乘积。将来袭目标分为两类，一类是具有攻击性的真实导弹目标C(1)，另一类是虚假目标C(2)。当判定目标为C(1)时，我方将发射导弹拦截，则存在的风险为R(1)=c(1)p(2)，其中，c(1)为发射导弹产生的消耗，p(2)为k时刻目标类型为C(2)的概率。当判定目标为C(2)时，存在的风险为R(2)=c(2)p(1)，其中，c(2)为敌方导弹击中我方设施后带来的损失，p(1)为k时刻目标类型为C(1)的概率。
我方在作决策过程中，遵循风险最低原则，将风险定义为

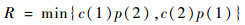(1)

对目标类型的判断为C=arg R。
设传感器sⁱ对目标t^j探测过程中，k+1时刻传感器sⁱ的识别观测值为O_k+1^{i, j}∈{C(1), C(2)}，p(O_k+1^{i, j}C(i))为真实值为C(i)而观测值为O_k+1^{i, j}的概率, i=1, 2，其中，p(O_k+1^{i, j}(1)C(1))=p_d为检测概率，p(O_k+1^{i, j}(1)C(0))=p_d为虚警概率。
传感器sⁱ在k+1时刻对目标t^j观测，观测值O_k+1^{i, j}=w, w∈{1, 2}出现的概率为

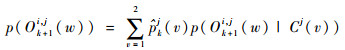(2)

在传感器sⁱ获得观测值后，sⁱ获得的关于k+1时刻目标t^j类型的后验概率为

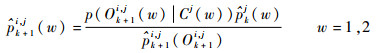(3)

若k+1时刻，同时有n_k+1^j个传感器对目标t^j探测，基于证据理论^[11]，及分布式融合检测原则，有

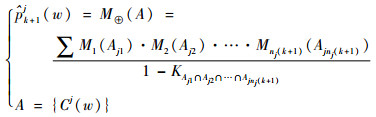(4)

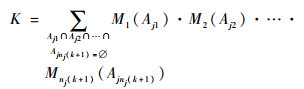(5)

式中：K为证据之间的冲突概率。
此时，在k+1时刻获得观测值后，风险为，对目标t^j类型的判断为。
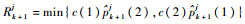
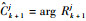
1.2 目标跟踪模型 目标t^j的运动状态X_k^j状态转移矩阵为

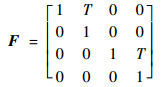(6)

式中：T为采样时间，本文取T=1 s。
在k+1时刻，目标t^j的状态为

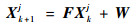(7)

式中：W为过程演化噪声，为均值为0的高斯白噪声。
协方差矩阵为

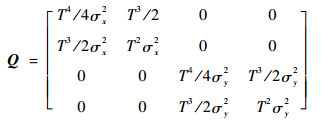(8)

式中：σ_x、σ_y为噪声的功率谱密度。
在k时刻传感器sⁱ对目标t^j的观测为

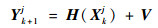(9)

式中：V为观测噪声，为均值为0的高斯白噪声，R=diag(σ_d², σ_α²)为其协方差矩阵。
状态观测矩阵为

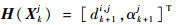(10)

式中：为传感器与目标之间的距离；为目标的方位角; (xⁱ, yⁱ)为传感器sⁱ坐标。
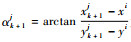
将上述极坐标转化为Cartesian坐标系坐标，有

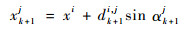(11)

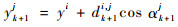(12)

对模型进行线性近似，观测矩阵为

(13)

此时，目标坐标协方差在Cartesian坐标系坐标中的协方差矩阵为

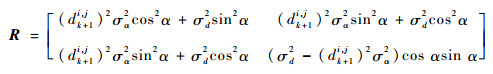(14)

给定k=0时刻目标t^j的初始状态X₀^j，及其均值E(X₀^j)=u₀, 协方差矩阵P₀=E[(X₀^j－u₀)·(X₀^j－u₀)^T]。
若k+1时刻，同时有n_k+1^j个传感器对目标t^j跟踪，目标t^j状态可以通过卡尔曼滤波进行估计，有

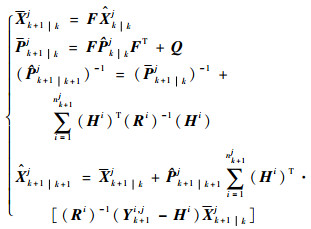(15)

式中：Hⁱ、Rⁱ分别为传感器sⁱ观测矩阵、观测噪声矩阵。
1.3 传感器管理模型 目标识别的过程是在目标跟踪的过程中进行的，在目标跟踪过程中，存在目标丢失的风险，同时考虑目标跟踪与目标识别，建立风险函数，有

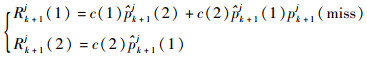(16)

式中：p_k+1^j(miss)为在k+1时刻目标t^j丢失的概率。
此时，有

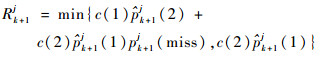(17)

给定c(1)=5、c(2)=10，R_k+1^j(1)、R_k+1^j(2)与关系如图 1所示。

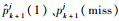
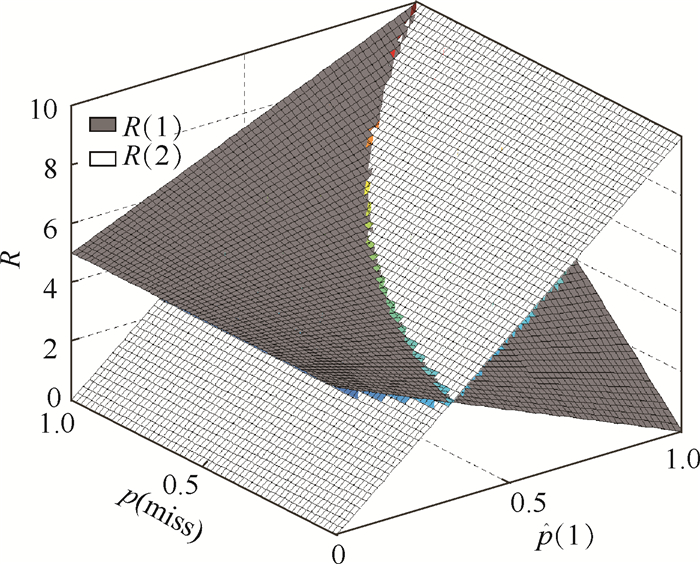图 1 风险值分析 Fig. 1 Analysis of value-at-risk

图选项

由图 1可知，当目标为虚假目标时，即p(1)=0，无论目标丢失概率为何值，风险值均为0；当目标为导弹时，即p(1)=1，目标丢失概率越低，风险值越低; 目标丢失概率越高，风险值越高，模型与实际情况相符。由式(16)和图 1可知，当目标为真目标C(1)的概率较低(p(1)→0)时，风险主要来自目标识别，一旦将真目标判定为假目标，真目标击毁我方军事设施，将会为我方带来损失；当目标为真目标C(1)的概率较高(p(1)→1)时，风险主要来自于目标跟踪，此时将发射导弹对目标实施拦截，在跟踪精度较低，目标丢失概率较高的情况下，一旦拦截失败，依然会给我方带来损失；若目标丢失概率较高(p(miss)→1)，则R(1)>R(2)恒成立，此时，不再发射导弹，由于目标跟踪精度较低，丢失概率较高，导弹命中率较低，使武器资源浪费。
目标丢失概率p_k+1^j(miss)与传感器辐射范围(Field of View，FOV)、目标位置估计值和协方差矩阵有关^[12]。如图 2所示，通过卡尔曼滤波得到的目标t^j状态服从分布。

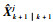
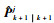
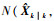
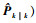
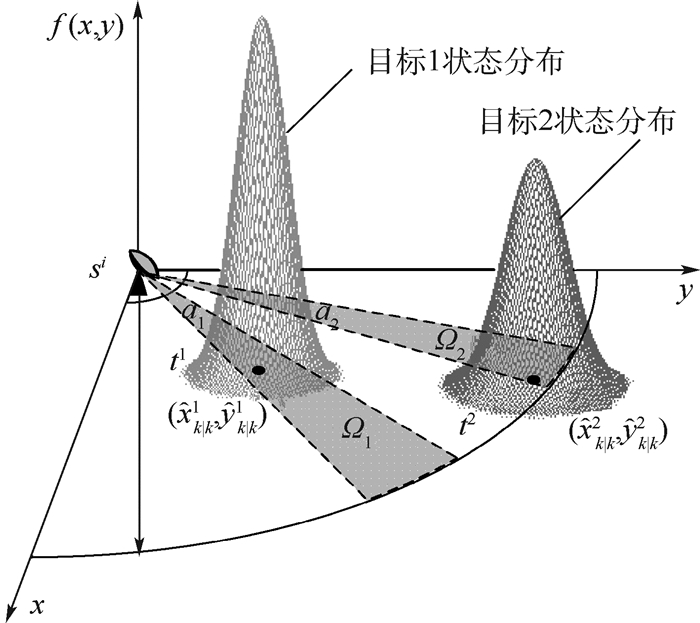图 2 目标丢失概率示意图 Fig. 2 Sketch map of target losing probability

图选项

假定雷达在跟踪目标过程中，波束a的中心对准，雷达的探测半径为R₀，在雷达探测区域内，有

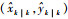
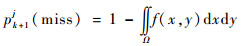(18)

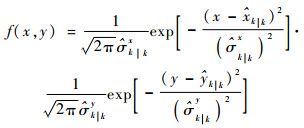(19)

式中：Ω为波束a照射区域，本文给定波束宽度θ=0.1°。
当用m个跟踪雷达对n个目标(m>n)进行跟踪时，在k时刻确定传感器管理方案为U_k+1，U_k+1为m×n矩阵，u_k+1^i.j为其中的第i行第j列元素。当u_k+1^{i, j}=1时，表示传感器sⁱ在k+1时刻对目标t^j进行跟踪; 当u_k+1^{i, j}=0时，表示传感器sⁱ在k+1时刻不对目标t^j进行跟踪。有目标函数为

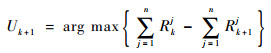(20)

限制条件：①每个传感器同时时刻跟踪的目标数目不超过其能够同时跟踪的最大目标数，本文规定1个传感器只能同时跟踪1个目标。②在k时刻，若目标t^j的时(Δ为阈值)，本文取Δ=0.9，则传感器在k+1时刻以及以后时刻将不会再对该目标跟踪，否则，至少存在一个传感器跟踪该目标。
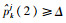
2 模型求解及算法设计 由于在k时刻尚未得到k+1时刻的观测值，R_k+1^j不能够通过计算得到，故不能根据式(20)求解传感器管理方案。本文通过用预测值R_k+1^j代替观测值的方法近似求解传感器管理方案。
用于求解传感器管理方案的算法主要有集中式算法和分布式算法两种^[13-15]，前者计算时间长、通信压力大，但求解质量高，后者计算时间短、通信压力小，但求解质量不如前者。由于传感器管理过程中作战态势变化较快，使用求解速度较快的分布式算法求解传感器管理方案，同时提高求解质量，成为研究的热点和难点。
本文采用分布计算的思想，其优化思路为将整体效能函数转化为单目标的局部效能函数，将每个传感器看作一个具有自主计算功能的Agent，每个目标通过分别优化自身局部效能，使局部效能最优的同时达到全局最优。
传感器sⁱ在选择跟踪对象时应使总风险值下降最大，则局部最优函数为max{R_k^v－ R_k+1^{i, v}}，其中，R_k+1^{i, v}为当且仅当sⁱ在k+1时刻对目标t^v跟踪时的风险值，令j=arg max{R_k^v－ R_k+1^{i, v}}，若同时存在多个传感器选择目标t^j跟踪，则经过融合后的风险值R_k+1^v < R_k+1^{i, v}，有(R_k^v－R_k+1^{i, v})>(R_k^v－R_k+1^v)，此时，依然能够保证t^j为传感器sⁱ的最佳选择。根据以上分析，在k时刻传感器确定U_k+1的步骤如下:
1) 在k时刻依次检查目标为虚假目标的概率，对于t^j，若，则在k+1时不再对该目标跟踪，否则，t^j∈A_T，A_T为应该被跟踪的目标集合。
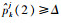
2) 传感器sⁱ在k时刻选择t^j(j=arg max{R_k^v－R_k+1^{i, v}})为k+1时刻的跟踪对象，令u_k+1^{i, j}=1，每个传感器选择目标后，生成方案U_k+1。
3) 依次检查每个应该被跟踪的目标是否分配传感器在k+1时刻对其跟踪，若任意t^j∈A_T，均有，则U_k+1=U_k+1，算法结束。
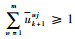
4) 对于t^j，若t^j∈A_T且，当满足时，其中R_k+1^{w, h}为当且仅当传感器s^w在k+1时刻对目标t^h跟踪时的风险值，u_k+1^{w, h}=1(u_k+1^{w, h}∈U_k+1)，传感器sⁱ放弃原来的跟踪对象，在k+1时刻转为对目标t^j跟踪，此时的传感器管理方案即为U_k+1，算法结束。
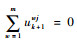
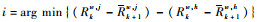
基于以上叙述，传感器管理流程如图 3所示。

图 3 传感器管理流程图 Fig. 3 Flowchart of sensor management

图选项

3 仿真实验 传感器的探测性能和目标参数如表 1、表 2所示, p_f为传感器的误警率。我方用于目标跟踪的传感器为4个，在k=0时刻，同时探测到4个目标，假定目标飞行过程中均在所有传感器的探测范围内，作战态势如图 4所示。
表 1 传感器信息 Table 1 Information of sensors

传感器	pd	pf	σd2	σα2	Ω/m2
s1	0.8	0.1	10	0.010	30×30
s2	0.9	0.2	20	0.020	30×30
s3	0.8	0.2	15	0.015	30×30
s4	0.7	0.1	30	0.030	20×20

表选项






表 2 目标信息 Table 2 Information of targets

目标	C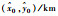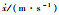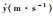
t1	C(1)	(500, 0)	0.5	-300	0
t2	C(1)	(0, 500)	0.5	0	-600
t3	C(0)	(-500, 0)	0.4	450	0
t4	C(0)	(0, -500)	0.5	0	-400

表选项

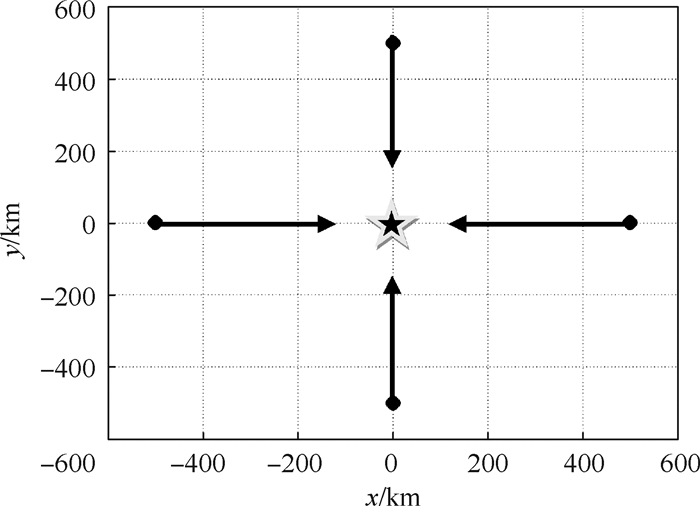图 4 作战态势 Fig. 4 Combat situation

图选项

3.1 目标识别过程仿真 当用传感器s¹对目标t¹跟踪识别时，取前30 s，其过程如图 5所示。当用传感器s²对目标t³跟踪识别时，取前30 s，其过程如图 6所示。

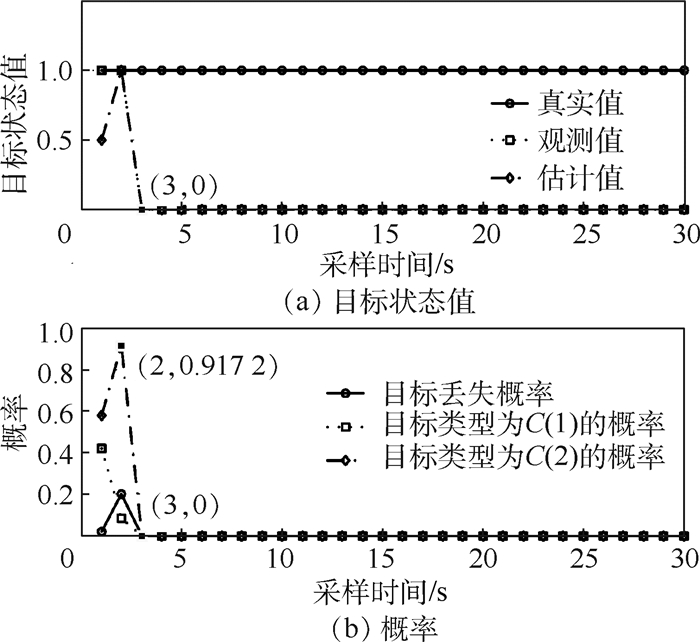图 5 传感器s1对目标t1的目标识别过程 Fig. 5 Process of target identification of sensor s1 to target t1

图选项

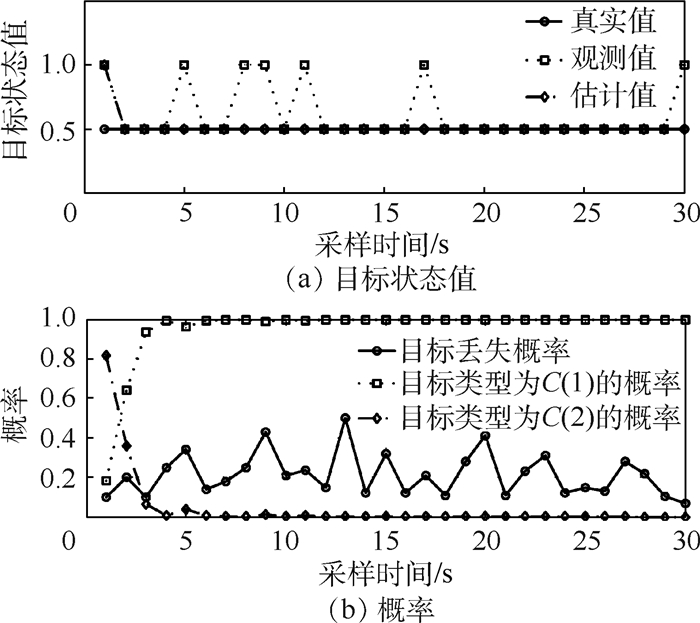图 6 传感器s2对目标t3的目标识别过程 Fig. 6 Process of target identification of sensor s2 to target t3

图选项

由图 5、图 6对比可知，对于类型为C(1)的真实目标t¹，传感器在整个过程中均保持对该目标跟踪；由于设置了阈值Δ，对于类型为C(2)的目标t³，一旦，将不再对该目标进行跟踪。
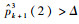
3.2 多传感器-多目标分配 在k=0时刻，生成k=1时刻的传感器-目标分配方案，以便后续时刻对目标进行跟踪。在仿真过程中，将本文提出的分布式算法与贪婪算法、拍卖算法作对比，如图 7所示。

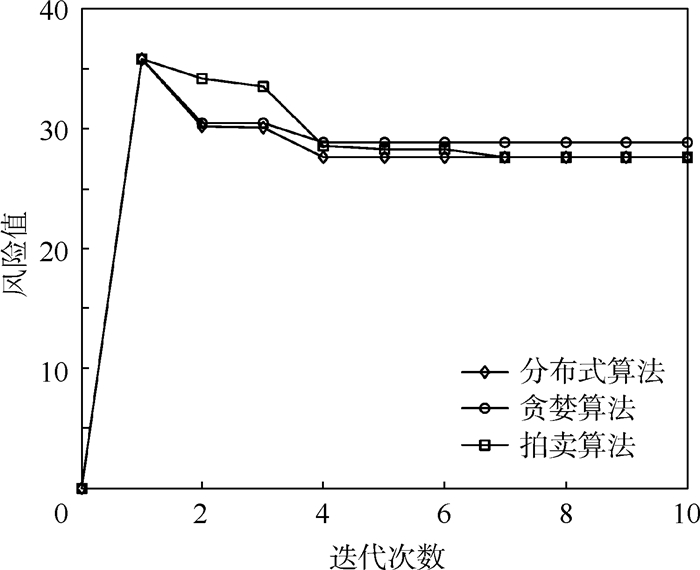图 7 算法对比 Fig. 7 Comparison of algorithms

图选项

由图 7可知，与贪婪算法相比，本文算法求解质量较高; 与拍卖算法相比，本文算法求解速度较快，说明本文算法具有良好性能。
3.3 本文方法与其他经典传感器管理方法对比 比较经典的传感器管理方法为基于协方差矩阵的传感器管理方法与基于信息论的传感器管理方法，本文分别选取基于跟踪精度控制的传感器管理方法^[16](简称跟踪精度控制)和基于Rényi矩阵的传感器管理方法^[17](简称信息增量控制)与本文方法作对比。分别计算3种传感器管理方法生成的传感器管理方案对应的风险值以及目标跟踪精度，其过程如图 8所示。由图 8(a)可以看出，风险值整体呈下降的趋势，由此可见，随着对目标的跟踪探测，对目标的识别风险和跟踪风险降低。在风险值方面，传感器管理方法的优劣依次为：本文方法>跟踪精度控制>信息增量控制。由图 8(b)可以看出，虽然本文方法尚未采取跟踪精度控制的方法，但其获得的目标跟踪精度值最低，原因为在k=5时刻后，传感器不再对虚假目标t³、t⁴跟踪，节省出传感器资源对真目标t¹、t²跟踪，由此避免了传感器资源浪费。而采用跟踪精度控制和信息增量控制的传感器管理方法，未考虑到跟踪目标的种类，一味追求对包括虚假目标在内的所有目标提高跟踪精度，由此造成了传感器资源浪费。该分析在图 8(c)~图 8(f)中得到证实。

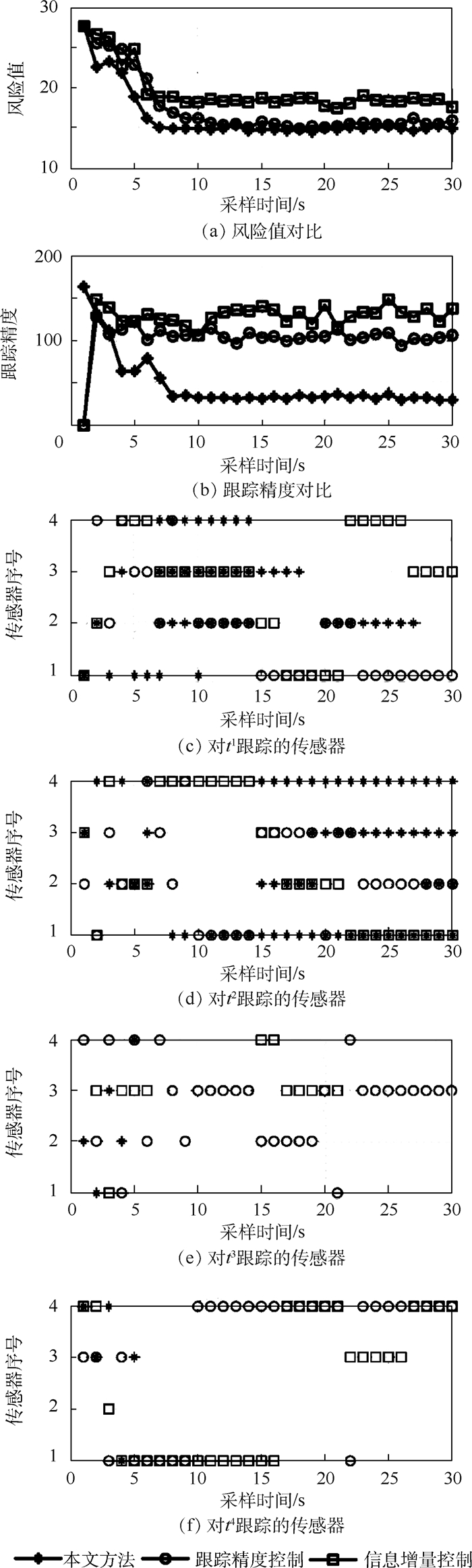图 8 传感器管理方法对比 Fig. 8 Comparison of sensor management methods

图选项

4 结论 本文研究多传感器协同跟踪多目标作战背景的传感器管理问题，建立同时考虑目标跟踪和目标识别任务的传感器管理模型，并针对模型的求解提出基于多Agent分布计算理论的分布式算法，通过仿真验证了模型和算法的有效性，仿真结果表明，本文方法不但能够得到最低的风险值，还能及时停止对虚假目标跟踪，从而避免传感器资源浪费。在多目标跟踪情况下，伴随着已有目标的消失与新目标的出现，若在对目标数目估计不准确情况下对传感器进行管理，得到的传感器管理方案可能欠准确，下一步将研究此种情况下的传感器风险管理问题。

参考文献

[1]	SUBEDI S, ZHANG Y D, AMIN M G, et al. Cramer-Rao type bounds for sparsity-aware multi-sensor multi-target tracking[J]. Signal Processing, 2018, 145: 68-77.
[2]	ASGHAR A B, JAWAID S T, SMITH S L. A complete greedy algorithm for infinite-horizon sensor scheduling[J]. Automatica, 2017, 81: 335-341. DOI:10.1016/j.automatica.2017.04.018
[3]	GOSTAR A, HOSEINNEZHAD R, WEIFEBG L, et al. Sensor-management for multi-target filters via minimization of posterior dispersion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2877-2884. DOI:10.1109/TAES.2017.2718280
[4]	HONG H G, BA-NBGU T, MAULE R. The Cauchy-Schwarz divergence for poisson point process[J]. IEEE Transactions on Information Theory, 2015, 61(8): 4475-4485. DOI:10.1109/TIT.2015.2441709
[5]	BUKAL M, MARKOVI I, PETROVI I.Score matching based assumed density filtering with the von Mises-Fisher distribution[C]//Proceedings of 20th International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2017: 433-438. https://lamor.fer.hr/images/50020776/Bukal2017.pdf
[6]	SAYIN M O, LIN C W, SHIRAISH S, et al. Information-driven autonomous intersection control via incentive compatible mechanisms[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 99(1): 1-13.
[7]	MARTIN S.Risk-based sensor resource management for field of view constraint sensor[C]//Proceedings of 18th International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2015: 2041-2048. https://c4i.gmu.edu/~pcosta/F15/data/fileserver/file/472057/filename/Paper_1570103675.pdf
[8]	BORGES M E G, MALTESE D, VANHEEGHE P, et al.Sensor management using expected risk reduction approach[C]//Proceedings of 19th International Conference on Information Fusion, Piscataway, NJ: IEEE Press, 2016: 2050-2058. https://www.researchgate.net/publication/308697816_Sensor_Management_using_Expected_Risk_Reduction_approach
[9]	BORGES M E G, MALTESE D, VANHEEGHE P, et al.http://html.rhhz.net/BJHKHTDXXBZRB/A%20risk-based%20sensor%20management%20using%20random%20finite%20sets%20and%20POMDP[C]//Proceedings of 20th International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2017: 1588-1596. http://html.rhhz.net/BJHKHTDXXBZRB/A%20risk-based%20sensor%20management%20using%20random%20finite%20sets%20and%20POMDP
[10]	童俊, 单甘霖. 基于修正Riccati方程和Kuhn-Munkres算法的多传感器跟踪资源分配[J]. 控制与决策, 2012, 27(5): 747-751. TONG J, SHAN G L. Study of multi-sensor allocation based on modified Riccati equation and Kuhn-Munkres algorithm[J]. Control and Decision, 2012, 27(5): 747-751. (in Chinese)
[11]	HEGARAT-MASCLE S L, BLOCH I, VIDAL-MADJAR D. Application of Dempster-Shafer evidence theory to unsupervised classification in multisource remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(4): 1018-1031. DOI:10.1109/36.602544
[12]	HARE J Z, GUPTA S, WETTERGREN T A. POSE:Prediction-based opportunistic sensing for energy efficiency in sensor networks using distributed supervisors[J]. IEEE Transactions on Cybernetics, 2017, 48(7): 2114-2127.
[13]	李志汇, 刘昌云, 倪鹏. 反导多传感器协同任务规划综述[J]. 宇航学报, 2016, 37(1): 29-38. LI Z H, LIU C Y, NI P. Review on multisensor cooperative mission planning in anti-TBM system[J]. Journal of Astronautics, 2016, 37(1): 29-38. DOI:10.3873/j.issn.1000-1328.2016.01.004 (in Chinese)
[14]	OZTURK O, BEGEN M A, ZARIC G S. A branch and bound algorithm for scheduling unit size jobs on parallel batching machines to minimize makespan[J]. International Journal of Production Research, 2017, 55(6): 1815-1831. DOI:10.1080/00207543.2016.1253889
[15]	SHI C G, SALOUS S, WANG F, et al. Power allocation for target detection in radar networks based on low probability of intercept:A cooperative game theoretical strategy[J]. Radio Science, 2017, 52(8): 1030-1045. DOI:10.1002/2017RS006332
[16]	ODEJIDE O O, BENTLEY E S, KONDI L P, et al. Effective resource management in visual sensor networks with MPSK[J]. IEEE Signal Processing Letters, 2013, 20(8): 739-742. DOI:10.1109/LSP.2013.2265912
[17]	LIU Y, WANG H. UKF based nonlinear filtering using minimum entropy criterion[J]. IEEE Transactions on Signal Processing Journal of Astronautics, 2013, 61(20): 4988-4999. DOI:10.1109/TSP.2013.2274956