随着新型装备不断向复杂化、集成化方向发展,面向实装的故障注入出现许多新问题:①装备物理封装严密或模块不可拆卸,导致故障注入器的访问深度无法满足部分故障模式的注入需求;②对装备实施直接故障注入时,容易对一些模块造成不可修复的损坏,比如后驱动故障注入中电流大小可能会对集成电路物理结构造成破坏,电源的短路故障会引起电源电路的永久性损坏等[6];③装备各功能单元间传递耦合关系比较复杂,部分故障模式进行物理注入后导致装备很难恢复至正常状态[7],比如高频高集成雷达装备,以及光电装备等精密度要求较高的装备。上述问题的存在制约了测试性验证试验的开展,降低了评估结果置信度,而等效故障注入可以依托现有故障注入手段,实现对所选故障样本的有效注入[8]。目前,关于等效故障注入的相关研究较少,文献[8]提出了基于故障传递特性的等效故障注入方法,解决了位置不可访问的故障注入问题,但需要等效故障与原故障的状态空间完全一致,降低了该方法的应用范围;文献[9]通过故障传播分析选择等效故障注入样本,但不能反映故障的行为状态特性;文献[10]研究了针对外场可更换模块的等效故障注入方法,但没有给出具体建模分析方法,也缺乏对不确定性信息的考虑。上述等效方法大都没有研究故障行为关系,相关性矩阵获取困难。由于装备故障之间普遍存在耦合现象,某一故障的发生会引起其他单元模块也出现相同的故障现象[11],这种传播关系与装备自身结构紧密相关,而故障行为模型[12]能够描述故障传播关系和故障行为状态,因此可以通过建立故障行为模型分析等效故障模式。
针对以上分析,提出一种基于“故障模式-功能-状态”(Failure mode-Function-State,FFS)故障行为模型的等效故障注入方法。首先,通过融合装备的结构信息、不确定性信息和层次性信息,建立FFS故障行为模型,在此基础上,由故障模式-故障模式相关矩阵、故障模式-功能相关矩阵和功能-状态相关矩阵计算得到故障模式-状态相关矩阵;然后,基于故障模式-状态相关矩阵进行故障模式等效性分析,获得等效故障模式;最后,将该方法应用于某装备发射控制系统,验证方法的有效性。
1 基于多元信息的FFS故障行为层次化建模 1.1 故障行为总体建模思路 故障行为建模采用定性分析、功能描述或者数学建模的方法对复杂装备故障发生时的行为状态进行准确描述[13],良好的故障行为模型应既能准确反映装备结构信息[14],又能描述建模要素间的关联关系。
故障行为总体建模思路如图 1所示。装备复杂的关联关系造成很难直接求解故障模式-状态相关关系,而由于测试性设计中一般根据功能设置测试点,使得故障模式-功能、功能-状态关联关系更易于求解,因此提出将“功能”作为FFS基本建模要素,通过功能与故障模式和状态的关系计算故障模式-状态相关矩阵。故障模式-功能-状态之间又存在2种不确定性信息:一是故障模式对功能的一定影响、可能影响、不影响3种关系[15],二是工作环境或测试设备引起状态检测不确定性,因此要求FFS模型能够表征不确定信息。同时,复杂装备的故障行为模型应考虑层次化信息,通过逐层细化的建模方法对系统各层次故障行为进行描述,既可以降低建模难度,又便于模型的删减和修改。另外,装备确定的结构连接关系是故障行为建模的确定性信息,是保证模型的准确性关键,故障行为建模必须以装备功能结构为基础。
 |
| 图 1 故障行为总体建模思路 Fig. 1 General idea of failure behavior modeling |
| 图选项 |
由图 1可知,故障行为模型的多元信息包括确定性信息、不确定性信息和层次性信息。确定性信息可用有向图DC={C, EC}描述,其中:C={c1, c2, …, cn}为系统单元组件,ci为约定建模层次的组成单元;EC=[eij]n×n为系统的功能结构连接矩阵,eij表示模型节点间的有向连接关系。故障模式与状态之间的不确定性关系可用Bayes网络[16]表示为BFmS={Fm, S, EB,


1.2 FFS故障行为模型 基于多元信息的FFS故障行为建模流程如图 2所示。
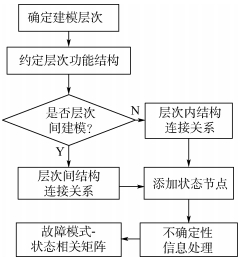 |
| 图 2 FFS故障行为建模流程 Fig. 2 FFS failure behavior modeling process |
| 图选项 |
首先,明确进行故障行为建模的装备层次,根据该层次对象的功能结构和故障模式影响分析结果,确定对象中的单元模块组成及相互连接关系,并用有向边连接起来。然后,根据装备的测试性设计定义的信号集确定信号流向,并将状态节点添加到相应的单元模块,状态节点的添加需要熟悉掌握装备的物理结构和原理特性。最后,处理故障模式、功能和状态不确定性信息,进而获得故障模式-状态相关矩阵。
融合多元信息的FFS模型用有向图表示为DFBM={C, Fm, Fu, S, E, P, L},构成模型的基本要素定义如下:功能集Fu={F1u, F2u, …, Fku},Fiu表示故障模式影响的功能;有向边矩阵E表示模型节点间的有向关联关系;概率集P=[(pijmu, pijus)],pijmu为故障模式与功能之间的关联概率,pijus为故障模式关联的功能异常时,状态也异常的概率;约定层次信息L=lr,lr为约定建模层次。
2 基于FFS模型的故障行为特性分析 首先,定义表征故障行为特性的有关概念。
定义1??故障模式-故障模式相关矩阵Rmm=[rijmm]m×m。其中:rijmm表示故障模式Fim与故障模式Fjm之间的相关关系。
定义2??故障模式-功能相关矩阵Rmu=[rijmu]m×k。其中:rijmu表示故障模式Fim与功能Fju的相关关系。
定义3??功能-状态相关矩阵Rus=[rijus]k×w。其中:rijus表示功能Fiu与状态sj的相关关系。
定义4??故障模式-状态相关矩阵Rms=[rijms]m×w。其中:rijms表示故障模式Fim与状态sj的相关关系。
定义5??故障模式层次相关矩阵Rmr=[rijmr]u×m。其中:rijmr表示紧邻上一层次故障模式与约定层次故障模式的关联关系。
定义6??Fim的行为状态向量Vis定义为矩阵Rms=[rijms]m×w中第i行所有为1的元素构成的向量,即故障模式Fim发生时状态空间的异常变化。
首先计算故障模式-故障模式相关矩阵,故障模式之间的邻接矩阵为Amm=[aij]m×m,如果故障模式Fim与Fjm有直接关联关系,则aij=1,根据矩阵乘法,设Amm2=(aij(2)),且
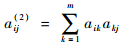 | (1) |
aij(2)=1的充要条件是:

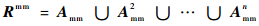 | (2) |
为计算故障模式与功能之间的关联概率,定义以下规则:
规则1??故障模式与功能的关系为一定影响,则pijmu=P(FjuFim)=1。
规则2??故障模式与功能的关系为可能影响,则
 | (3) |
式中:hik=1表示故障模式与功能有关联关系;P(Fim)为组件ci的故障模式故障概率,由故障模式影响及危害性分析(Failure Mode Effect and Critically Analysis, FMECA)得到;P(Fju)为组件ci的功能故障率,新装备的功能可靠性等数据匮乏,很难直接获得功能故障率,根据式(4)和式(5)可得到故障模式关联的功能故障率:
 | (4) |
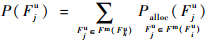 | (5) |
式中: Palloc(Fju)为故障模式Fim平均分配到关联的功能上的故障概率;Fm(Fiu)为故障模式与功能有关联关系的功能集。
规则3??故障模式与功能的关系为不影响,则pijmu=P(FjuFim)=0。
由上述计算规则可得故障模式与功能的邻接矩阵为

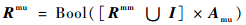 | (6) |
式中:Bool()为布尔变换;I为单位矩阵。
为计算功能-状态相关矩阵Rus=[rijus]k×w,首先需要确定状态的检测概率。为方便表述,设p=pijus,采用Beta分布Be(p; α, β)作为检测概率的先验分布[17],表示为
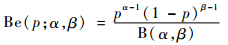 | (7) |
式中:B(α, β)为Beta函数:p为节点条件概率;α、β为分布超参数。
均值和方差分别为
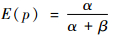 | (8) |
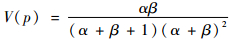 | (9) |
装备在研制过程中的测试性试验相关数据较少,首先基于专家评判确定先验分布,为降低专家评判的主观性,采用梯形模糊数描述专家经验信息,第i个专家给出的包含置信度δi的梯形模糊数为
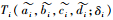
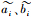
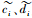
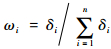 | (10) |
则节点概率的梯形模糊数为
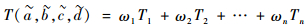 | (11) |
根据梯形模糊数可得节点概率的先验分布一阶矩和二阶矩分别为
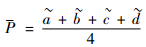 | (12) |
 | (13) |
联合式(8)、式(9)、式(12)、式(13),根据式(14)的约束优化模型即可得先验分布超参数α, β:
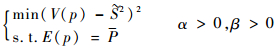 | (14) |
然后,将先验分布和研制阶段的试验信息通过Bayes融合得到节点概率的验后分布[18-19]。对于任意一个状态si执行Ni次测试,成功次数为ni,失败次数为Ni-ni,则根据试验样本Xi确定的节点概率密度函数为
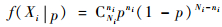 | (15) |
将先验分布Be(p; α, β)和节点概率密度函数f(Xi|p)代入Bayes融合公式,可得状态检测概率的验后分布为
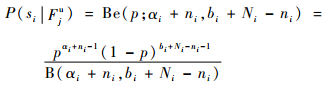 | (16) |
因此,功能-状态相关矩阵Rus=[rijus]k×w为
 | (17) |
故障行为模型中各节点不是一一对应的关系,节点间可能存在重边,由以下规则去除节点间的重边。
规则4??对于节点Fim到sk间的路径pathijk,基于式(18)合并重边:
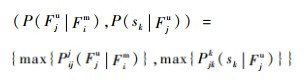 | (18) |
基于有向图的传递特性,设定合理相似度,将去除重边的相关矩阵代入式(19)可得约定层次故障模式-状态相关矩阵Rms。
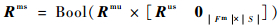 | (19) |
则紧邻上一层次故障模式-状态相关矩阵可表示为
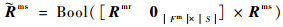 | (20) |
3 基于FFS故障行为模型的故障等效分析 等效故障模式是指故障发生后具有相同行为状态空间的2个或2个以上的故障模式[20]。结合故障模式-状态相关矩阵给出等效故障的定义,即在约定层次lr上,对于故障模式Fim和Fjm,若其对应的行为状态向量满足Vis=Vjs,则故障模式Fjm为故障模式Fim的等效故障模式。
一般来说,在结构简单、故障间耦合性较强的试验对象中比较容易出现行为状态向量相同的故障模式,但对于功能结构复杂的装备,其行为状态空间较大,找到2个行为状态向量完全相同的故障模式的概率较小,因此定义等效故障模式集,通过故障模式集对故障模式进行等效。
定义7??等效故障模式集。在约定层次lr上,若行为状态向量满足如下关系:
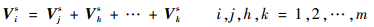 | (21) |
则称故障模式集{Fjm, Fhm, …, Fkm}为故障模式Fim的等效故障模式集,即Fim发生的行为状态与{Fjm, Fhm, …, Fkm}同时发生时的行为状态相同。
一般来说,在约定层次内即可找到等效故障模式,对于在约定层次不存在等效故障模式的不可注入故障,则根据层次化模型,在紧邻下一层次寻找等效故障或等效故障集。依据GJB/Z 1391—2006[21],低层次故障模式是紧邻上一层次的故障原因,低层次产品故障模式对高一层次的影响是紧邻上一层次产品的故障模式。假设lr层存在故障模式Fim不可注入,由层次化模型可得其包含的lr+1层的故障模式集为{F1m, F2m, …, Fnm},通过式(19)和式(20)获得lr层和lr+1层的故障模式-状态关联关系,然后按照上述等效分析方法分析其不同层次间的等效故障或等效故障集。
根据以上分析,基于FFS故障行为模型的等效故障注入流程如图 3所示。
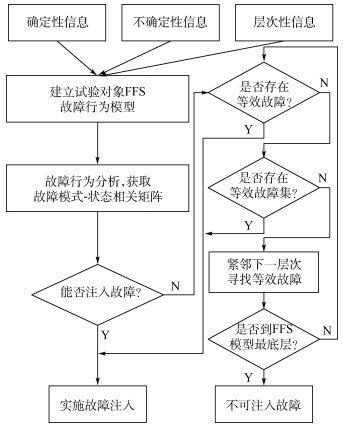 |
| 图 3 基于FFS故障行为模型的等效故障注入流程 Fig. 3 Equivalent fault injection process based on FFS failure behavior model |
| 图选项 |
4 实例分析 如图 4所示,某装备发射控制系统由主控模块、同步通信模块、通信管理模块、直流电源模块等7个模块单元组成,主要完成与各互联单元的信息交互、数据处理和状态控制等功能。
 |
| 图 4 发射控制系统功能结构 Fig. 4 Functional structure of launch control system |
| 图选项 |
根据生产方和使用方最终确定的FMECA,该系统共有47个故障模式,根据GJB 2072—94[22]确定实施故障注入的样本量为67个。按照测试性验证试验流程分别进行故障样本分配和样本抽取后进行故障注入,发现共有包含9个故障模式的13个故障样本由于注入点受限或注入后会造成不可修复的损坏而无法进行故障注入,不可注入率约为19%。
根据系统的层次结构和FMECA信息,建立发射控制系统FFS故障行为模型如图 5所示,不失问题一般性,这里仅给出同步通信模块和模数转换模块的l2层模型信息。由于底层模块间关联度较低,故l2的层次行为模型不考虑不同模块间关联故障。
 |
| 图 5 发射控制系统FFS故障行为模型 Fig. 5 FFS failure behavior model of launch control system |
| 图选项 |
以同步通信模块为例对等效故障注入进行详细分析。试验过程中,发现译码控制故障(F1mSC)和信号外回路干扰(F4mSC)2个故障模式无法注入。由图 5可得同步通信模块的故障模式邻接矩阵为
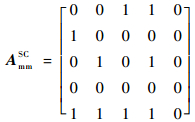 | (22) |
代入式(1)和式(2)可得故障模式-故障模式相关矩阵为
 | (23) |
同步通信模块中故障模式与功能之间的关系均为一定影响,则根据规则1可得
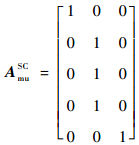 | (24) |
将式(23)、式(24)代入式(6)可得故障模式-功能相关矩阵为
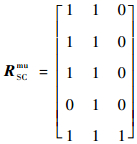 | (25) |
将由梯形模糊数得到的节点概率先验分布一阶矩和二阶矩代入式(14)可得状态概率先验分布矩阵为
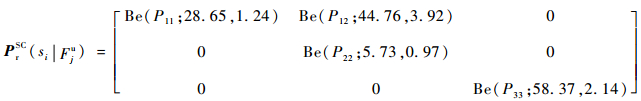 | (26) |
研制阶段针对设计功能对状态进行的测试数据如表 1所示。
表 1 功能-状态测试数据 Table 1 Test data of function-state
| 功能 | 状态 | 测试次数 | 成功次数 |
| F1uSC | s1 | 23 | 22 |
| s2 | 18 | 13 | |
| F2uSC | s2 | 27 | 22 |
| F3uSC | s3 | 12 | 11 |
表选项
将先验分布和状态测试数据代入式(15)、式(16),进行Bayes融合可得行为状态概率验后分布矩阵为
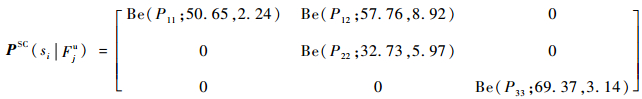 | (27) |
因此,功能-状态相关矩阵为
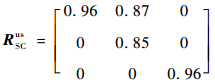 | (28) |
将式(25)和式(28)代入式(19)可得同步通信模块故障模式-状态相关矩阵为
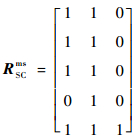 | (29) |
根据故障模式等效定义可得F1mSC、F2mSC、F3mSC互为等效故障模式。因此,不可注入故障模式F1mSC可由F2mSC或F3mSC进行等效注入,试验中选择F3mSC进行等效,通过故障注入系统进行故障注入,假设故障注入器是完全可靠的,启动机内测试(Built-in Test, BIT),采用测试性设计规定的检测方法发现同步通信协议故障指示灯亮(s1),测试Testloop1:recv全0(s2),与建模分析结果一致。由于l2层为模型的最低层,因此F4mSC无法等效,需进行不可注入故障审查。
同理,可得模数转换模块故障模式-状态相关矩阵为
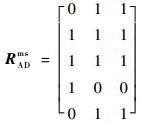 | (30) |
因此,F1mAD与F5mAD,F2mAD与F3mAD为等效故障模式,根据式(21)可得F2mAD和F3mAD的等效故障模式集为{F1mAD, F4mAD}、{F4mAD, F5mAD},则对于不可注入故障模式F2mAD,可由F3mAD等效,也可由故障模式集{F1mAD, F4mAD}或{F4mAD, F5mAD}等效,试验中选择采用F3mAD进行等效,启动BIT,采用测试性设计规定的检测方法发现自检Test Fail(s1)、测试通道AD X:Test Error(s2)、模数转换故障指示灯亮(s3),与建模分析结果一致。
采用相同方法对发射控制系统其他模块进行故障行为特性和故障模式等效性分析,等效故障注入后的试验结果如表 2所示。
表 2 发射控制系统故障注入结果 Table 2 Fault injection results of launch control system
| 模块 | 分配样本数 | 直接注入样本数 | 等效注入后样本数 |
| 直流电源模块 | 14 | 14 | 14 |
| 主控模块 | 7 | 4 | 6 |
| 通信管理模块 | 8 | 6 | 8 |
| 输入输出模块 | 9 | 8 | 9 |
| 同步通信模块 | 8 | 6 | 7 |
| 发射控制模块 | 14 | 11 | 12 |
| 模数转换模块 | 7 | 5 | 7 |
表选项
由上述分析过程及等效故障注入结果可知:
1) 装备的复杂性导致很难直接获得故障模式与状态的关联关系,而通过图 1可以看出,基于多元信息构建的FFS故障行为模型将试验对象的功能作为建模要素,有效解决了故障模式-状态相关矩阵获取难的问题。
2) FFS故障行为模型以装备结构信息为基础,融合了故障模式、功能和状态之间的不确定性信息,使得故障行为模型具备表征不确定性知识的能力,相比于传统的确定性建模,考虑因素更加全面,获得的行为状态关系更加准确。
3) 由同步通信模块的详细分析可知,对于不可注入故障模式F1mSC,可以通过故障行为模型进行等效故障注入,等效后的行为状态与建模分析结果一致。如表 2所示,采用基于FFS故障行为模型的方法进行等效注入后,发射控制系统的可注入样本由54个提高到63个,故障注入率提高约16.7%,有效增加了测试性验证试验的故障注入样本。
5 结论 1) 本文方法能够基于故障行为建模,通过求解故障模式与状态的关联关系进行等效故障注入。
2) FFS故障行为模型将“功能”作为基本建模要素,通过获取故障模式-功能和功能-状态相关矩阵,能够求解出准确的故障模式-状态相关矩阵。
3) FFS故障行为模型综合了不确定性、确定性和层次化结构等复杂装备的多元信息,能够更加准确地描述故障模式与状态的关联关系,而且层次化的结构也保证模型具有较好的扩展性。
4) 本文方法能够获得不可注入故障的等效故障模式或等效故障模式集,有效增加了故障注入样本,例如,某发射控制系统在进行故障等效后,故障注入率提高约16.7%。
本文方法通过邻接矩阵分析故障模式的等效性,对于复杂系统在较高约定层次的故障模式等效性分析,计算复杂度较高,如何降低计算复杂度,提高分析效率有待进一步研究。另外,若要进一步提高故障注入率,还需要深入研究更加有效的故障注入方法。
致谢 感谢北京电子工程总体研究所王承红高级工程师和刘丹丹高级工程师提供的试验验证对象,感谢中国航天科工集团有限公司潘国庆高级工程师提供的部分试验设备。
参考文献
| [1] | ZENG L, WANG X L. Research on the FMECA method suitable for testability test[J]. Electronic Product Reliability and Environment Testing, 2016, 34(3): 54-60. |
| [2] | ZHANG Y, QIU J, LIU G J, et al. Environmental stress-fault grey relation analysis for helicopter gyroscope[J]. The Journal of Grey System, 2012, 24(1): 29-38. |
| [3] | 邓露, 许爱强, 吴忠德. 基于遗传算法的故障样本优化选取方法[J]. 系统工程与电子技术, 2015, 37(7): 1703-1708. DENG L, XU A Q, WU Z D. Method of failure sample optimization selection based on genetic algorithm[J]. Systems Engineering and Electronics, 2015, 37(7): 1703-1708. (in Chinese) |
| [4] | WANG C, QIU J, LIU G J, et al. Testability evaluation using prior information of multiple sources[J]. Chinese Journal of Aeronautics, 2014, 27(4): 867-874. DOI:10.1016/j.cja.2014.03.029 |
| [5] | 田仲, 石君友. 系统测试性设计分析与验证[M]. 北京: 北京航空航天大学出版社, 2003: 363-384. TIAN Z, SHI J Y. Analysis and verification of system testability design[M]. Beijing: Beihang University Press, 2003: 363-384. (in Chinese) |
| [6] | 李华康.测试性试验中等效故障注入技术及应用[D].长沙: 国防科技大学, 2015: 5-6. LI H K.Study on the equivalent fault injection technique and its application in testability test[D].Changsha: National University of Defense Technology, 2015: 5-6(in Chinese). |
| [7] | ZHANG R S, XIAO L Y, LI J, et al. A fast fault injection platform of multiple SEUs for SRAM-based FPGAs[J]. Microelectronics Reliability, 2018, 82: 147-152. DOI:10.1016/j.microrel.2018.01.014 |
| [8] | 李天梅, 胡昌华, 周鑫. 基于故障传递特性的位置不可访问故障注入方法[J]. 航空学报, 2011, 32(12): 2277-2286. LI T M, HU C H, ZHOU X. Fault injection method resulting from inaccessible location fault based on fault propagation characteristics[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(12): 2277-2286. (in Chinese) |
| [9] | 张雷, 梁德潜. 基于多信号流图模型的等效故障注入样本选取[J]. 计算机测量与控制, 2017, 25(9): 28-31. ZHANG L, LIANG D Q. Selection of equivalent fault injection sample based on multi-signal flow graph model[J]. Computer Measurement & Control, 2017, 25(9): 28-31. (in Chinese) |
| [10] | 陈然, 连光耀, 陈子龙, 等. 基于层次模型的外场可更换模块故障注入方法[J]. 浙江大学学报(工学版), 2017, 51(7): 1390-1396. CHEN R, LIAN G Y, CHEN Z L, et al. Fault injection approach for line replaceable module based on hierarchical model[J]. Journal of Zhejiang University(Engineering Science), 2017, 51(7): 1390-1396. (in Chinese) |
| [11] | CHEN G, LIU F, MOHAMMAD S. Fault propagation analysis with uncertain parallel reasoning for process safety[J]. Frontiers in Artificial Intelligence and Applications, 2016, 281: 428-435. |
| [12] | ZENG Z G, CHEN Y X, KANG R. Failure behavior modeling:Towards a better characterization of product failures[J]. Chemical Engineering Transactions, 2013, 33(2): 571-576. |
| [13] | 查国清, 井海龙, 陈云霞, 等. 基于故障行为模型的产品寿命分析方法[J]. 北京航空航天大学学报, 2016, 42(11): 2371-2377. ZHA G Q, JING H L, CHEN Y X, et al. Life analysis method for products based on failure behavior models[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(11): 2371-2377. (in Chinese) |
| [14] | 尹园威, 尚朝轩, 马彦恒, 等. 层次测试性模型的评估方法[J]. 北京航空航天大学学报, 2015, 41(1): 90-95. YIN Y W, SHANG C X, MA Y H, et al. Method of testability evaluation using hierarchical testability model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 90-95. (in Chinese) |
| [15] | ERIC G.Modeling it both ways: Hybrid diagnostic modeling and its application to hierarchical system designs[C]//IEEE Autotestcon.Piscataway, NJ: IEEE Press, 2004: 576-582. |
| [16] | ZHANG X S, HUANG K L, YAN P C, et al. Hierarchical hybrid testability modeling and evaluation method based on information fusion[J]. Journal of System Engineering and Electronics, 2015, 26(3): 523-532. DOI:10.1109/JSEE.2015.00060 |
| [17] | 雷华军, 秦开宇. 确定测试性验证试验方案的贝叶斯方法[J]. 系统工程与电子技术, 2012, 34(12): 2612-2616. LEI H J, QIN K Y. Bayesian method for determination of testability demonstration test scheme[J]. Systems Engineering and Electronics, 2012, 34(12): 2612-2616. DOI:10.3969/j.issn.1001-506X.2012.12.36 (in Chinese) |
| [18] | 张西山, 黄考利, 闫鹏程, 等. 基于验前信息的测试性验证试验方案确定方法[J]. 北京航空航天大学学报, 2015, 41(8): 1505-1512. ZHANG X S, HUANG K L, YAN P C, et al. Method of confirming testability verification test scheme based on prior information[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1505-1512. (in Chinese) |
| [19] | SAVIC R M, KARLSSON M O. Importance of shrinkage in empirical bayes estimates for diagnostics:problems and solutions[J]. The AAPS Journal, 2009, 11(3): 558-569. DOI:10.1208/s12248-009-9133-0 |
| [20] | 中国人民解放军总装备部.测试与诊断术语: GJB 3385-98[S].北京: 中国人民解放军总装备部, 1998: 4. The General Armament Deparment of PLA.Terms for testing and diagnostics: GJB 3385-98[S].Beijing: The General Armament Department of PLA, 1998: 4(in Chinese). |
| [21] | 中国人民解放军总装备部.故障模式、影响及危害性分析指南: GJB/Z 1391-2006[S].北京: 中国人民解放军总装备部, 2006: 12. The General Armament Department of PLA.Guide to failure mode, effects and critically analysis: GJB/Z 1391-2006[S].Beijing: The General Armament Department of PLA, 2006: 12(in Chinese). |
| [22] | 国防科学技术工业委员会.维修性试验与评定: GJB 2072-94[S].北京: 国防科学技术工业委员会, 1994: 22. Commission of Science, Technology and Industry for National Defense.Maintainability test and evaluation: GJB 2072-94[S].Beijing: Commission of Science, Technology and Industry for National Defense, 1994: 22(in Chinese). |
