目前,最常见的激光稳频技术是直接将激光频率锁定于原子参考谱线,如饱和吸收法[10]和二向色原子蒸气激光锁定[11]等。这些稳频方法所实现的短期频率稳定性可以达到kHz量级。但是在没有合适的原子谱线与所需激光频率对应的情况下,比如在SERF陀螺仪、磁强计的研究中,通常需要将激光频率锁定于远共振线位置(超过一倍多普勒线宽)[12],上述稳频方法便不再适用。
失谐激光稳频经常利用声光调制器(Acousto-Optic Modulator, AOM)或者电光调制器(Electro-Optic Modulator, EOM)进行稳频[13]。然而,考虑到SERF原子磁强计的原子气室所充入的惰性气体气压的影响,原子磁强计的泵浦光的频率应该锁定在远离共振频率GHz量级的位置,而探测光为了避免与碱金属原子产生共振而产生超高光学厚度,进一步影响检测信噪比,往往需要高达100 GHz的失谐[14-15]。而传统的AOM和EOM等方法难以实现如此大范围的失谐。因此,找到一种可以实现大失谐激光频率稳定的方法对于工程技术和科学研究的发展都有重要意义。
本文提出了一种利用法布里-珀罗(Fabry-Perot,F-P)腔传递激光频率稳定性的方法,可以实现大失谐激光频率的锁定。本文将锁定于87Rb原子D2线饱和吸收峰的780 nm激光器作为参考光源。基于参考激光经过F-P腔形成的失谐功率谱,通过伺服反馈调节压电传感器(Piezoelectric sensor,PZT)来稳定F-P谐振腔长度,使其成为2个激光器频率无损传递的“桥梁”。767 nm外腔二极管激光器(External Cavity Diode Laser,ECDL)作为待锁定目标激光器,通过高频电流调制和锁相放大算法得到F-P谐振腔失稳信号,从而把激光器波长锁定于767.001 nm。实验结果验证了该方法的有效性,频率漂移为1 MHz/h,达到了SERF原子自旋系统对激光漂移的要求。该方法具有通用、对实验环境要求低的特点,可以广泛应用在量子光学、原子物理等精密测量实验中。
1 F-P腔频率稳定传递原理 鉴于原子自旋能级是天然的稳定参考源,在光频移、碰撞频移一定的条件下,其稳定度达到了目前最精准的原子钟[16](稳定度可达10-18/天)的参考标准。因此,为了获得高稳定的参考激光频率,使用原子饱和吸收光谱(Saturated Absorption Spectrum,SAS)锁定参考激光器的频率。使用两束频率一致、方向相反、光路重叠的激光穿过原子气室以获得碱金属原子的SAS。单色可调谐的激光可以将速度为零的原子从具有多普勒速度分布的原子气体中选出,使其吸收光子形成饱和,产生饱和吸收光谱[2]。理论上,饱和吸收谱线都具有相似的线型,为佛克脱轮廓背景谱线f(ω)和超精细能级的跃迁成分g(ω)的叠加,则整体的谱线G(ω)可以表示为[17]
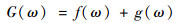 | (1) |
式中:ω为频率;f(ω)和g(ω)的表达式分别为[18]
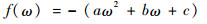 | (2) |
 | (3) |
其中:ω0为原子共振频率;γ为旋磁比,与原子种类有关;a、b、c和K为由原子种类决定的常数。对于碱金属原子而言,其饱和吸收谱线中的佛克脱轮廓强度远小于其超精细能级的跃迁成分[18],可忽略不计。如式(3)所示,超精细能级的跃迁成分为洛伦兹线型,曲线关于原子共振频率点对称分布,其饱和吸收峰的中心位置与原子共振频率重合,也是跃迁线的最大值位置。利用高频正弦调制信号Asin(Ωt)(A为振幅,Ω为频率)可以改变激光器的参数,实现频率调谐。经调制,频率为ω的激光变为ω′=ω+Asin(Ωt),可以得到参考激光器的饱和吸收谱线。对调制后的信号在ω处做泰勒展开可得[18]
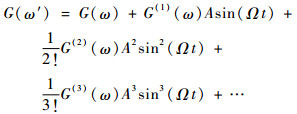 | (4) |
式中:G(m)(ω)为G(ω)的m阶导函数。本文使用一次谐波稳频,使调制后的光谱信号和参考信号Asin(Ω t)共同进入锁相放大电路,经过乘法器、傅里叶变换和低通滤波,得到的直流输出信号Vo为[19]
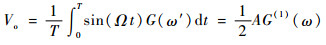 | (5) |
式中:T为扫描信号的周期。Vo正比于光谱信号的一次微分信号,其过零点位置为饱和吸收峰的中心。因此,将其作为误差信号送入比例-积分(PI)电路,根据齐格勒-尼柯尔斯整定规则[20],调节PI参数,即可锁定参考激光器于饱和吸收峰。
高稳定的参考激光频率可以作为稳定F-P腔长度的标准。激光频率和F-P腔长度产生谐振的条件为
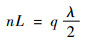 | (6) |
式中:L为F-P腔的长度;n为谐振腔介质的折射率;λ为激光波长,与L单位保持一致;q为正整数[21]。使用PZT驱动器线性扫描F-P腔的腔长,所得到的F-P腔失谐功率谱被光电探测器采集。类似地,利用调制、解调算法和先期稳定的参考激光频率,可以得到稳频所需的误差信号。通过调节PI控制的参数,可以锁定F-P腔长度,稳定度高达10-10[22],为目标激光器稳频奠定了基础。
利用F-P腔长度这个稳定的参考点,原则上可以实现大失谐激光频率的锁定。对目标激光器的外腔长度线性扫描,同时对其电流驱动源加入调制信号,得到待稳定激光经过F-P腔之后的失谐信号功率谱。同样使用锁相放大电路进行解调得到误差信号,并经过PI调节,反馈至激光器控制器的输入端,从而将激光频率精准地锁定于F-P腔失谐功率谱的峰值位置。
2 实验系统设计 利用F-P腔进行激光频率稳定传递,实现大失谐激光频率稳定的实验系统框图如图 1所示。在没有合适的原子参考谱线且失谐频率较大的情况下,使用一个稳定的激光器作为参考,F-P腔作为2个激光器之间传递的纽带,可以锁定目标激光器的频率。实验采用780 nm的激光器作为参考激光器,其频率稳定度必须达到或者高于MHz量级。780 nm的参考激光器和控制器使用北京优立光太科技有限公司生产的FSS801外腔半导体激光器综合系统,控制部分集成了激光器电流驱动器、激光器温度控制器、PZT驱动器、稳频模块。其中,PZT驱动器和稳频模块可以分别产生可调的扫描和调制信号,是激光频率调谐的前提。光路中的λ/2、λ/4波片和偏振分光棱镜(Polarization Beam Splitter,PBS)用于实现相位匹配,调节激光的偏振态和分光比。使用长度为50 mm、直径为25 mm的87Rb原子气室作为吸收池,光电探测器(Photo Detector,PD)将光功率信号转换为电压信号,产生87Rb的原子D2线SAS。通过稳频电路将控制信号反馈至激光器控制器,从而实现了参考激光器频率的稳定。
 |
| 图 1 稳频实验系统框图 Fig. 1 Block diagram of frequency stabilization experimental system |
| 图选项 |
图 1中,两部分光路之间加入的λ/2波片,使得参考激光和目标激光进入F-P腔之前的偏振方向垂直,在经过F-P腔之后能够被PBS4分离,分别被PD2和PD3探测。使用任意波形信号发生器(Agilent,33220A)输出的扫描信号和调制信号,经过自制加法器电路输入至PZT驱动器(Thorlabs,MDT694B),调节F-P腔的长度。被锁定的参考激光通过F-P腔之后被PD2转为电压信号,依靠稳频模块中的锁相放大模块和PI控制器,锁定F-P腔(Thorlabs,SA200-5B)的长度,为激光稳频提供一个超高稳定度的参考点。
稳定之后的F-P腔作为2个激光器频率稳定的桥梁,是767 nm的激光器(北京优立光太科技有限公司,FSS801)稳频的前提。调节λ/2波片改变进入F-P腔的光强,并利用光电探测器采集F-P腔失谐信号功率谱,同样利用稳频模块产生反馈信号给激光器控制器。反馈信号实现了对767 nm激光器外腔长度的精密调节,使目标激光器的频率锁定于F-P腔共振频率点。
3 实验及结果分析 在以上理论分析的基础上,2个激光器都工作在驱动电流为140 mA,温度为26℃的控制条件下。搭建光路,使780 nm激光器的电路控制系统输出10 Hz三角波信号和2.5 kHz的正弦波信号。调节并观测两者的幅度,并分别输送给PZT驱动器和激光器电流驱动器。同时,为了满足饱和吸收光谱观测对光功率的要求,本文采用遗传算法(Genetic Algorithm,GA)对激光器控制信号和激光器功率进行建模和跟踪,保证信号稳定。参考激光经过饱和吸收光路,被PD1采集到的SAS信号和调制信号共同输入至稳频模块的输入端,产生误差信号。实验中,扫描信号、87Rb的D2线SAS和经过锁相放大模块产生的误差信号如图 2所示。
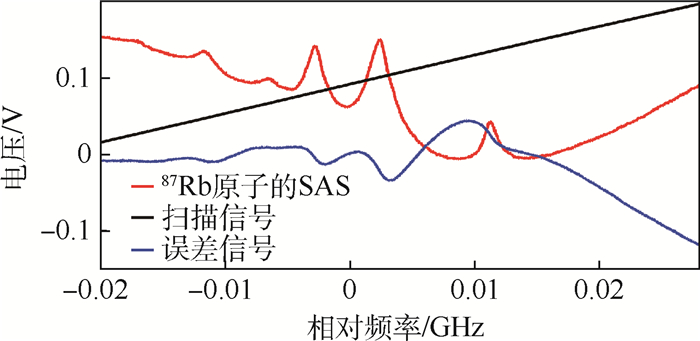 |
| 图 2 扫描信号、87Rb的D2线SAS和误差信号 Fig. 2 Scanning signal, SAS of 87Rb and error signal |
| 图选项 |
将图 2中的误差信号输入至PI控制器,在积分时间常数无穷大的前提下,调节比例放大倍数至光谱信号出现临界振荡,根据齐格勒-尼柯尔斯整定规则确定的比例放大倍数和积分时间分别为10 s和0.5 s,从而实现了参考激光的锁定。
为了产生稳定腔长的误差信号,实验采用了5 V、10 Hz的扫描信号和1 mV、30 kHz的调制参考信号实现了对780 nm的激光器频率的调谐。对激光经过PD2输出的F-P腔失谐信号功率谱进行解调,得到了误差信号。经过PI控制(比例放大倍数为10.3,积分时间为0.52 s)的信号输入给PZT驱动器,实现了F-P腔的高精度锁定。基于此,待锁定的767 nm的激光器受到分别为10 Hz的三角波扫描和2.5 kHz的正弦信号调制后,光束通过高品质因数的F-P腔得到的失谐功率谱、稳频所需的误差信号如图 3所示。
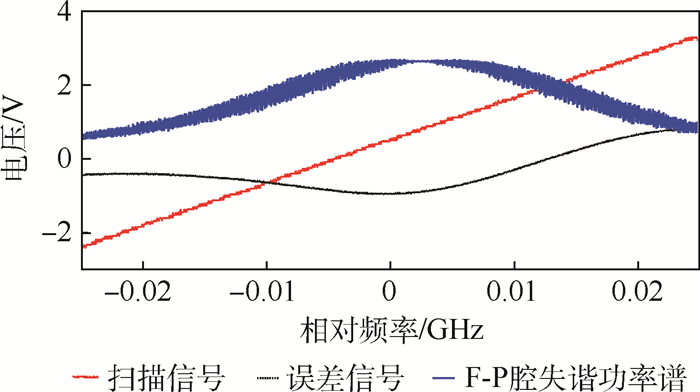 |
| 图 3 扫描信号、F-P腔失谐功率谱和误差信号 Fig. 3 Scanning signal, detuning power spectrum of F-P cavity and error signal |
| 图选项 |
调节PI参数(放大倍数为10.5,积分时间为0.45 s)和误差信号的相位,锁定目标激光器后,使用PD探测1 h内通过F-P腔的光强得到的电压变化如图 4所示。实验表明,目标激光器波长被精准地锁定在了767.001 nm,实现了150 GHz的大失谐,激光器被锁定之后的频率漂移可以达到1 MHz/h。
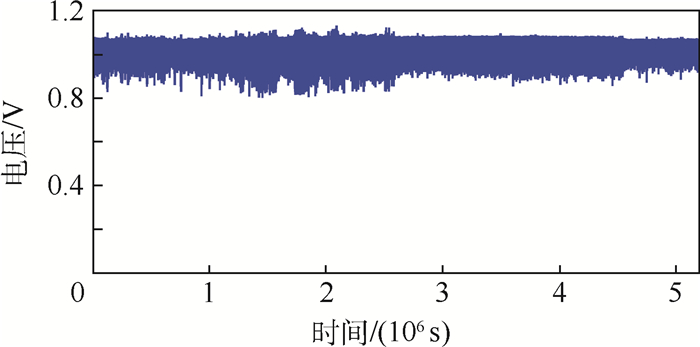 |
| 图 4 目标激光器锁定之后1 h通过F-P腔的光强 Fig. 4 Light intensity drift through F-P cavity during 1 h after target laser is locked |
| 图选项 |
实验证明利用高Q值F-P腔作为传递激光频率稳定的工具是可行的,但是考虑到F-P腔的长度对机械振动十分敏感,研究此方法对外界机械干扰的响应是推广该方法的必要前提。实验中,本文在F-P腔0.5 m范围内,人为给出了一个冲击噪声干扰,稳频后的目标激光经过F-P腔、稳频模块产生的误差信号和PD3的输出信号如图 5所示。在冲击噪声发出后,稳频系统经过大约0.5 s的自动调节,可以恢复至先前的锁频状态。可见,该稳频方法能够抵抗一定的外界机械干扰,实现大失谐激光频率的精准锁定。
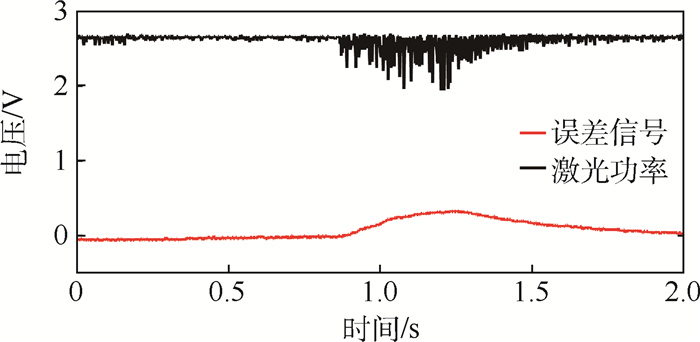 |
| 图 5 频率稳定后的冲击响应特性 Fig. 5 Impulse response characteristics after frequency stabilization |
| 图选项 |
4 结论 本文分析了激光器稳频的常用方法,针对SERF量子传感系统通常需要大失谐激光频率稳定的问题,提出了一种基于F-P腔实现频率稳定性传递的稳频技术。本文将锁定在87Rb原子D2线饱和吸收峰上的激光作为参考。根据激光的调制、解调算法,利用参考激光的F-P腔失谐功率谱提供一个超稳定腔长,作为目标激光器的稳频参考基准。对于目标激光器,可以通过伺服控制系统,将激光器波长锁定于767.001 nm。实验结果验证了该方法的有效性,实现了150 GHz的大失谐稳频,锁频后激光频率漂移为1 MHz/h。原则上,可以通过多普勒冷却、光晶格装载、磁场屏蔽等方法提高碱金属原子能级稳定度,从而进一步降低本方法稳频的长期漂移。该方法对参考激光器和待稳定激光器波长没有特殊要求,解决了大失谐频率激光稳频的问题,具有普适性,对工程实践和科学研究有重要意义。
参考文献
| [1] | KOBAYASHI K, UCHIKAWA Y. Development of a high spatial resolution SQUID magnetometer for biomagnetic measurement[J]. IEEE Transactions on Magnetics, 2003, 39(5): 3378-3380. DOI:10.1109/TMAG.2003.816156 |
| [2] | 王路威. 半导体激光器的发展及其应用[J]. 成都大学学报, 2003, 22(3): 34-38. WANG L W. Development of semicondutor lasers and their applications[J]. Journal of Chengdu University, 2003, 22(3): 34-38. (in Chinese) |
| [3] | 秦杰.基于129Xe-Cs的SERF原子自旋陀螺仪原理实验研究[D].北京: 北京航空航天大学, 2012. QIN J.Experimental study on the principle of SERF atomic spin gyroscope based on 129Xe-Cs[D].Beijing: Beihang University, 2012(in Chinese). |
| [4] | 万双爱.SERF原子自旋陀螺仪的误差分析及其抑制方法实验研究[D].北京: 北京航空航天大学, 2014. WAN S A.Experimental study on error analysis and suppression methods of SERF atomic spin gyroscope[D].Beijing: Beihang University, 2014(in Chinese). |
| [5] | ZHAI Y Y, YUE X G, WU Y J, et al. Effective preparation and collisional decay of atomic condensates in excited bands of anoptical lattice[J]. Physics Review A, 2013, 87: 063638. DOI:10.1103/PhysRevA.87.063638 |
| [6] | 陈熙, 全伟. 基于PD的半导体激光器温度控制系统设计方法[J]. 北京航空航天大学学报, 2015, 41(12): 2391-2396. CHEN X, QUAN W. Design method of a PD-based temperature control system for laser diode[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(12): 2391-2396. (in Chinese) |
| [7] | WASIK G, GAWLK W, ZACHOROWSKI J, et al. Laser frequency stabilization by Doppler-free magnetic dichroism[J]. Applied Physics B, 2002, 75(6-7): 613-619. DOI:10.1007/s00340-002-1041-2 |
| [8] | 李茹杰.SERF原子陀螺仪零偏稳定性理论分析与实验研究[D].北京: 北京航空航天大学, 2018. LI R J.Theoretical and experimental study on the bias stability of atomic gyroscope operated in the SERF regime[D].Beijing: Beihang University, 2018(in Chinese). |
| [9] | QUAN W, LI G H, FANG Z S, et al. Locking distributed feedback laser diode frequency to gas absorption lines based on genetic programming[J]. Optical Engineering, 2017, 56(1): 016106. DOI:10.1117/1.OE.56.1.016106 |
| [10] | DEMTORDER W. Laser spectroscopy:Basic concepts and instrumentation[M]. Berlin: Springer-Verlag, 1988. |
| [11] | CORWIN K L, LU Z T, HAND C F, et al. Frequency-stabilized diode laser with the Zeeman shift in an atomic vapor[J]. Applied Optics, 1998, 37(15): 3295. DOI:10.1364/AO.37.003295 |
| [12] | 张辉.铯原子喷泉钟NTSC-01光学系统的研制[D].西安: 西北大学, 2012. ZHANG H.Development of the NTSC-01 optical system of the helium fountain clock[D].Xi'an: Northwest University, 2012(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10697-1012444223.htm |
| [13] | MARCHANT A L, HANDEL S, WILES T P, et al. Off-resonance laser frequency stabilization using the Faraday effect[J]. Optics Letters, 2011, 36(1): 64-66. DOI:10.1364/OL.36.000064 |
| [14] | QUAN W, LI Y, LI R, et al. Far off-resonance laser frequency stabilization using multipass cells in Faraday rotation spectroscopy[J]. Applied Optics, 2016, 55(10): 2503-2507. DOI:10.1364/AO.55.002503 |
| [15] | DANG H B, MALOOF A C, ROMALIS M V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer[J]. Applied Physics Letters, 2010, 97(15): 151110. DOI:10.1063/1.3491215 |
| [16] | 杨红萍. 自旋压缩态及其在原子钟中的应用前景[J]. 时间频率学报, 2013, 36(1): 16-27. YANG H P. Spin-squeezing state of atomic ensembles and its application prospect in atomic clocks[J]. Journal of Time and Frequency, 2013, 36(1): 16-27. DOI:10.3969/j.issn.1674-0637.2013.01.003 (in Chinese) |
| [17] | 张庆国, 贺健, 尤景汉, 等. 氦辐射线吸收谱等效宽度的理论分析[J]. 激光与红外, 2012, 42(4): 372-376. ZHANG Q G, HE J, YOU J H, et al. Theoretical analysis of the equivalent width of the helium emission lines' absorption spectrum[J]. Laser & Infrared, 2012, 42(4): 372-376. DOI:10.3969/j.issn.1001-5078.2012.04.004 (in Chinese) |
| [18] | CHI H T, WANG X L, QUAN W. Pressure measurement of each gas in alkali-metal vapor cell with a mixed gas based on saturated absorption spectrum[J]. Spectroscopy & Spectral Analysis, 2018, 38(3): 948-952. |
| [19] | AYAT M, KARAMI M A, MIRZAKUCHAKI S, et al. Design of multiple modulated frequency lock-in amplifier for tapping-mode atomic force microscopy systems[J]. IEEE Transactions on Instrumentation & Measurement, 2016, 65(10): 2284-2292. |
| [20] | LIPKA M, PARNIAK M, WASILEWSKI W. Optical frequency locked loop for long-term stabilization of broad-line DFB laser frequency difference[J]. Applied Physics B, 2017, 123(9): 238. DOI:10.1007/s00340-017-6808-6 |
| [21] | TAO J, CHEN Y, LU J, et al. Method of the cavity length demodulation for optical fiber F-P sensors based on sparse fast Fourier transform[J]. Chinese Journal of Lasers, 2018, 45(5): 0510001. DOI:10.3788/CJL |
| [22] | BOHLOULI Z P, AFROUSHEH K, MARTIN J D D. Optical transfer cavity stabilization using current-modulated injection-locked diode lasers[J]. Review of Scientific Instruments, 2006, 77(9): 093105. DOI:10.1063/1.2337094 |
