虽然PSA性能优良,但极大的成本制约了其在实际雷达中的应用,主要包含:①天线体积限制,极化敏感阵元结构相对复杂,体积相对较大,且多出的信号通路也会占用一定体积;②成本限制,相比于普通阵列,PSA复杂的天线结构和信号通道数量使其成本翻倍提高,而获得的性能改善却有限,性能价格比有限;③大量已研制完成的单极化雷达无法对天线进行大规模全极化改造或改造成本极高,PSA无法使数量巨大的单极化雷达拥有极化信息处理能力。针对这个问题,本文提出了一种极化敏感辅助阵列(Auxiliary Polarization Sensitive Array,APSA)。在传统阵列的基础上,只对部分极化阵元进行双极化改造以最大限度节省成本,通过性能仿真证实改造模型的性能,设计空域-极化域导向矢量和优化极化滤波算法,完成对阵列接收信号的联合滤波。该阵列特殊的流型结构使信号无法完全用四元数[4-6]形式表示,因此考虑设计一种更适合该阵列的波束形成方法。
当前大多数自适应滤波算法都假定目标信号导向矢量已知或有一定的误差,而实际上在复杂的电磁环境下,目标信号导向矢量很可能是未知的。文献[13]介绍了根据高阶积累量对导向矢量进行盲辨识的显式方法和根据信号特征调整权矢量的隐式方法。非圆特征是某些人工调制的信号具有的一种特殊属性,例如BPSK(Binary Phase Shift Keying)、UQPSK(Unbalanced Quadrature Phase Shift Keying)等,都具有较强的非圆特征。文献[14-15]提出恢复信号非圆特征的波束形成算法,该算法不需要导向矢量先验信息,但是仅适用于单目标情况,未讨论多目标和干扰情况。
事实上,与BPSK类似,在雷达中广泛使用的二相编码信号同样具有很好的非圆特征。大多数情况下,雷达缺少准确的目标导向矢量的先验信息,因此考虑将基于非圆特征恢复的波束形成理论应用于雷达信号处理领域,以根据尽可能少的先验信息获得最佳的极化域-空域联合滤波性能。
本文提出了APSA天线模型及其极化域-空域导向矢量表示方法,对阵列性能进行了理论分析,并结合干扰情况进行了仿真实验;根据阵列的特殊流型结构,讨论了最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)[16]和特征子空间投影(Eigen-Subspace Projection,EP)[17]等算法,提出了在APSA基础上,针对二相编码信号进行非圆特征恢复的波束形成算法,该算法不需要目标信号导向矢量的先验信息,在干扰环境下有很强的适应性。
1 APSA模型 假设线阵由如图 1所示方式放置的阵元组成,阵元间距为半个信号波长,第1至i-1和i+L至N个阵元指向x轴,第i至i+L-1个阵元由交叉偶极子组成,分别指向x轴和y轴,其中:N为天线主极化阵元个数,L为辅助阵元个数。对于线阵,二维波达角度为(φf=90°, θ),φ为信号方位角,θ为信号入射角,极化参量为(γ, η),其空域导向矢量为
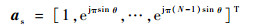 | (1) |
 |
| 图 1 APSA模型 Fig. 1 Model of APSA |
| 图选项 |
根据φf=90°,可以得到极化域导向矢量
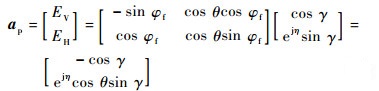 | (2) |
式中:EV和EH分别为天线在垂直和水平极化方向的导向矢量分量。
天线的所有阵元都能够接收到水平极化的信号,而第i至i+L-1个阵元能够接收到垂直极化的信号,构造其空域-极化域导向矢量为
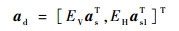 | (3) |
式中:交叉偶极子阵元的空域导向矢量as1=[ejπ(i-1)sin θ, ejπisin θ, …, ejπ(i+L-2)sin θ]T。
阵列的接收信号为
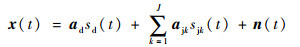 | (4) |
式中:sd(t)为入射的目标信号;J为干扰源数量;sjk(t)为第k个入射的干扰;ajk与ad形式类似,为第k个干扰在本阵列模型下的空域-极化域导向矢量;n(t)为加性高斯白噪声矢量。
与常规的PSA模型不同,本模型在传统单极化阵列的基础上,改造部分阵元,使阵列具有了一定的极化信号接收能力。与PSA相比,改造方法简单,成本相对低廉,其抗干扰性能有待进一步分析。
2 阵列性能分析 以J=1为例分析阵列模型的性能。理想情况下,阵列模型通过最优波束形成器的输出信干噪比(Signal to Interference plus Noise Ratio, SINR)ζSINR为[18]
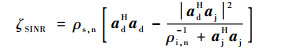 | (5) |
式中:aj为干扰导向矢量;ρs, n为接收信噪比(Signal to Noise Ratio, SNR);ρi, n为接收到的干噪比(Interference to Noise Ratio, INR)。
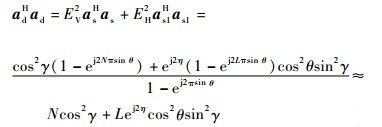 | (6) |
同理可得
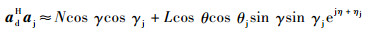 | (7) |
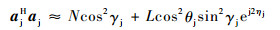 | (8) |
式中:γj、θj和ηj均为干扰参量,与目标信号参量相对应。
将式(6)~式(8)代入式(5)可知,阵列模型的输出SINR诸多条件有关:SNR越高,干扰与目标极化参量差异越大,INR越低,同极化和阵元越多,则输出SINR越高。
下面考虑4种特殊情况:
1) 不存在干扰,即ρi, n=0,SINR等同于理想情况,约为ρs, n(Ncos2γ+ej2ηLcos2θsin2γ),与阵列中主极化方向和交叉极化方向的阵元数量以及回波信号的极化方式有关系。
2) 存在干扰且干扰与目标空间方向吻合,有极化差异,此时adHaj相对增大;对单极化雷达,其L=0,仅通过空域滤波无法将目标与干扰区分开,输出SINR较低,不能满足探测目标的需要;而APSA模型中,L≠0, 输出SINR仅有所削减,在一定条件下仍然能满足探测目标的需要。事实上,很多针对雷达的自卫式干扰就属于这种情况。
3) 干扰极化与目标极化相同,有空间方向上的差异。此时APSA性能退化为单极化阵列天线模型,与单极化雷达滤波能力相当。
4) INR无穷大,只有在干扰与目标的空间角度和极化方式,即干扰与目标的导向矢量,线性相关时,输出SINR恒为零。
3 滤波算法描述 3.1 MVDR算法和EP算法 波束形成器的输出为权矢量w与各阵元输出矢量x的乘积,即y(t)=wHx(t),其中w=[w1, w2, …, wN+L]T。
根据MVDR,权矢量按照以下准则进行设计:
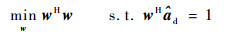 | (9) |
式中:ad为导向矢量的估计。
利用拉格朗日乘子法可得最优权值矢量为
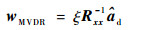 | (10) |
式中:Rxx=E[x(t)xH(t)],E[·]表示均值函数;ξ=(adHRxx-1ad)-1。
在信号通道数多的情况下,对Rxx直接求逆运算复杂且结果存在不确定性,为了防止奇异值且减小计算量,考虑对其进行特征值分解,结果为
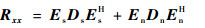 | (11) |
式中:Ds为由M个大特征值作为主对角线元素构成的对角矩阵;Es为Ds对应的主特征矢量矩阵;同理,Dn为由(N+L-M)个小特征值作为主对角线元素构成的对角矩阵;En为Dn对应的特征矢量矩阵。构成噪声子空间,只保留主特征空间进行处理,可得权矢量为
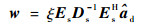 | (12) |
事实上,信号导向矢量的估计ad是存在估计误差的,而MVDR算法要求ad具有比较高的估计精度,否则可能在信号处形成零陷。
采取对ad向信号的特征子空间投影(EP)的方法以获得精度更高的导向矢量,即ad=EsEsHad,更新后的权矢量为
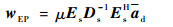 | (13) |
式中:μ为拉格朗日乘子。
3.2 二相编码信号非圆特征恢复算法 对于零均值复随机信号s(t),有
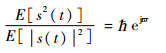 | (14) |
式中:0≤ ? ≤1为信号的二阶非圆率(Noncircularity Rate, NCR);?为信号的二阶非圆相位。?的物理意义为信号s(t)与其共轭s*(t)的相关程度,?值越高,则其非圆特性越强。
雷达常用的二相编码信号具有截获概率低、抗干扰能力强等特点,其数学表示为sd(t)=ejφ(t),φ(t)={0, π},根据式(14),其非圆率? =1,而理想情况下高斯白噪声的非圆率? =0。
波束形成器的输出信号非圆率为
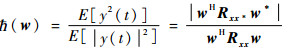 | (15) |
按照非圆率最大准则(Noncircularity Rate Maximization, NCRM)确定权矢量:
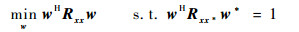 | (16) |
通过拉格朗日乘子法求问题的最优解:
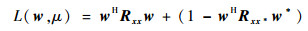 | (17) |
求w*的偏导得
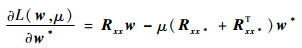 | (18) |
令式(18)等于0,得
 | (19) |
进而可得
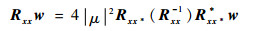 | (20) |
令?=Rxx-1Rxx(Rxx-1)*Rxx**,则
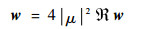 | (21) |
对?进行特征值分解,得到?=EwDwEwH,Dw=diag(λ1, λ2, …, λN+L)为由特征值构成的对角矩阵,Ew=[u1, u2, …, uN+L]为对应的特征矢量矩阵。
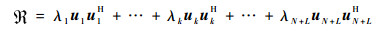 | (22) |
不考虑干扰和噪声的影响,理论上uk与其余的特征矢量正交,可得λkukukHui=0, i≠k,因此
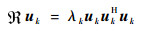 | (23) |
相当于将uk向ukukH构成的特征空间进行投影,因此可以得到? uk=εuk,ε是一个实数。结合式(21),在理想情况下可以得到w=uk。
为了减小干扰和噪声的影响,将分解得到的大特征值对应的特征向量作为目标信号对应的最优权值矢量。如果存在多个目标信号,可以先根据分解得到的主特征值或者通过其他改进方法判定信号源个数,再根据对应的权值矢量分步或同时进行波束形成。完成第k个目标信号波束形成的权值矢量为
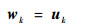 | (24) |
对第k个目标信号的滤波器输出为
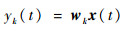 | (25) |
该过程可以利用有源相控阵的优势,在信号处理过程中串行或并行处理,即通过数字多波束[19]实现。
为研究各滤波算法的性能差异,可用式(26)计算不同权值矢量下的输出SINR[15]:
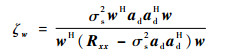 | (26) |
式中:σs2为信号功率。值得注意的是,式(26)与式(5)在导向矢量无误差的理想情况下是等价的,而式(26)更适用于一般情况。
4 仿真实验和分析 本节通过计算机仿真验证天线模型的适用性和算法的有效性。通过设计3个仿真实验,分别对算法的性能,辅助阵元个数对结果的影响,以及特殊环境下阵列的抗干扰性能进行分析。
4.1 实验1 阵列包含20个阵元,其中5个交叉偶极子组成的极化辅助阵元;信号形式为二相编码信号,其估计出的导向矢量有一定的空间角度误差和极化误差;存在2个干扰,其形式为高斯白噪声,在空域和极化域与目标信号有一定的区分。信号SNR为10 dB,信号导向矢量误差Δθ=1.5°,Δγ=4°。干扰1和干扰2的INR均为30 dB,其余的仿真参数设置见表 1。
表 1 实验1详细参数设置 Table 1 Detailed parameter setting in Experiment 1
| 参数 | 信号 | 干扰1 | 干扰2 |
| θ/(°) | 15 | 14 | 17 |
| γ/(°) | 78 | 30 | 45 |
| η/(°) | 45 | 75 | 25 |
表选项
3种算法在该仿真条件下的输出SINR与信号采样快拍数的关系见图 2。其中,理论SINR由式(27)求得,为完全排除干扰影响的结果,只与输入信噪比ρs, n和信号导向矢量有关[20]。
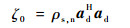 | (27) |
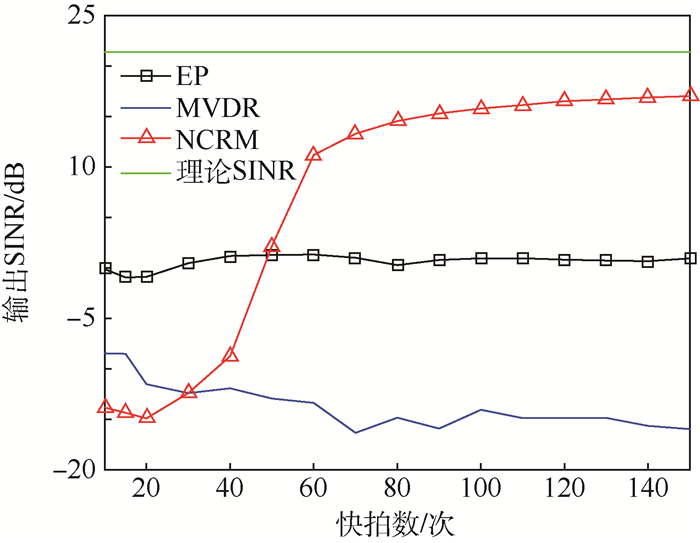 |
| 图 2 快拍数对输出SINR的影响 Fig. 2 Influence of snapshots on output SINR |
| 图选项 |
根据仿真结果,得以得出以下结论:
1) 当信号导向矢量估计存在较大误差时,基于该导向矢量进行波束形成的MVDR算法和EP算法基本失效;而基于信号非圆特性的NCRM算法在快拍数>60时输出SINR>10 dB,在较大干扰环境中也能最大程度地接近理论SINR,基本能够满足抗干扰需要。
2) 在导向矢量存在误差的情况下,常规的MVDR算法误将信号当干扰加以滤除,从而在信号处形成零陷,该结果与其他阵列结果基本一致。
3) 基于二相编码非圆特征恢复的波束形成算法不需要预先知道信号的导向矢量,因此在导向矢量存在较大误差的情况下依然能够较好地完成滤波;但是其对信号的二阶统计特性依赖大,因此在低快拍条件下表现一般,只有满足一定的快拍数时其性能才会迅速提高。本文仿真环境中,快拍数为40~60之间时该算法性能提升明显。固定采样点数为150,输入SNR从1~20 dB变化,其他参数不变,得到输出SINR曲线见图 3。
 |
| 图 3 输入SNR对输出SINR的影响 Fig. 3 Influence of input SNR on output SINR |
| 图选项 |
SNR大于5 dB时,NCRM算法的性能就要优于其他2种算法,且随着SNR的提升,呈上升趋势;常规的MVDR在导向矢量失真的情况下性能恶化;随着输入SNR的提高,EP算法也在错误的导向矢量的牵引下将一部分信号误当成干扰加以滤除。
从图 2和图 3可知,导向矢量失真对算法有效性影响极大,为了分析其对系统的影响,将导向矢量估计中空间角度误差从0°~6°进行变化,以分析其对输出SINR的影响(采样快拍数为100,输入SNR为15 dB),仿真结果见图 4。
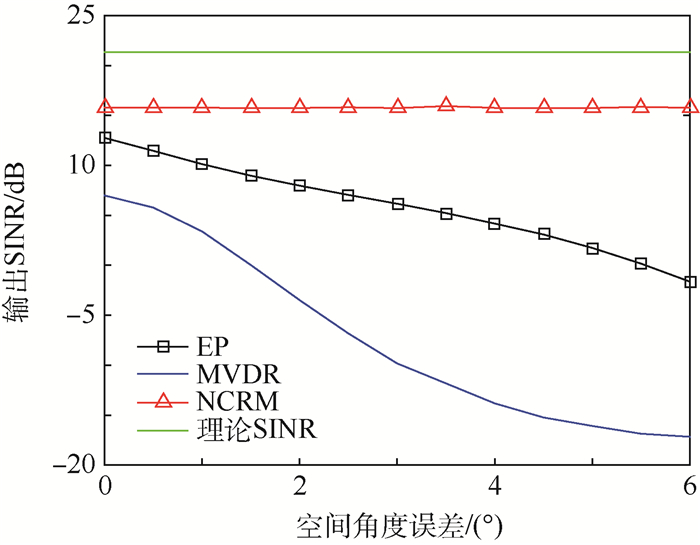 |
| 图 4 导向矢量空间角度误差对输出SINR的影响 Fig. 4 Influence of steering vector angle error in space on output SINR |
| 图选项 |
空间角度误差为0°时,NCRM与EP算法结果基本一致;随着空间角度误差增大,EP算法的输出SINR明显下降,而NCRM算法由于不需要导向矢量作为先验信息,其结果保持稳定。MVDR算法由于需要对多维矩阵进行求逆运算,其运算结果存在不稳定性,算法性能较差。
4.2 实验2 在本文提出的阵列模型中,极化辅助阵元的个数是影响滤波器结果输出的关键因素之一。采样点数为100,其他仿真条件不变,仅改变辅助阵元个数,其对输出SINR的影响见图 5。
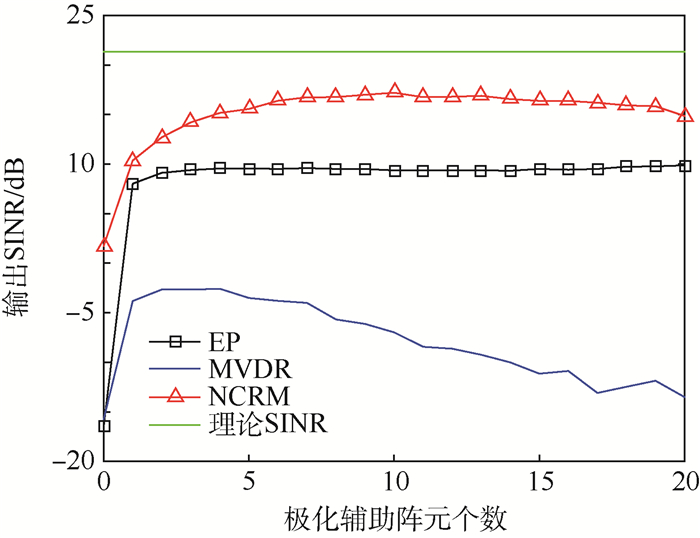 |
| 图 5 极化辅助阵元个数对输出SINR的影响 Fig. 5 Influence of auxiliary polarization array element number on output SINR |
| 图选项 |
讨论以下几种情况:
1) 当极化辅助阵元个数L=0时,即阵列模型为单极化阵列,在干扰角度与目标角度相差不大的情况下(干扰1与目标信号空间角相差1°,干扰2与其相差2°),3种算法的滤波性能都表现一般;由于导向矢量误差的存在,EP算法和MVDR算法直接将目标信号误当成干扰加以滤除。
2) 当L=1时,由于极化信息的引入,3种算法的性能均有大幅改善。可见对雷达天线的部分极化改造可以在控制成本的前提下迅速提高系统性能。
3) 当1 < L≤N时,随着极化辅助阵元个数的增加,系统的性能也在不断优化,同时也伴随着信号通路的增加,成本的上升,噪声的增加以及算法复杂度的增加。当L=N时,阵列模型等同于PSA,对NCRM算法来说,L的值增大并不一定就意味着系统性能的提升,过多的通道数量和噪声同样影响系统的性能,因此NCRM算法更适用于APSA模型。
4.3 实验3 下面讨论一种特殊情况,即目标与干扰的空间位置相同,通常讲的雷达主瓣干扰就属于该类情形,其原因是雷达的空间分辨力有限,无法将目标信号与干扰区分开。常规的单极化雷达无法通过纯空间滤波完成对此类干扰的排除,而拥有极化信息处理能力的APSA则能够通过极化域滤波进行处理。令干扰1的空间角度为15°,其干扰极化参量γ从0°~90°变化,干扰2置零,取100个采样点,其他条件不变。其输出结果见图 6。
 |
| 图 6 干扰与目标极化差异对输出SINR的影响 Fig. 6 Influence of interference polarization and target difference on output SINR |
| 图选项 |
在空间角度相同的情况下,系统为纯极化域滤波,当目标与干扰的极化参量γ差异足够大时(γ>30°),系统的输出SINR可以达到10 dB以上,基本满足抗干扰需求,干扰与目标极化差异越大,滤波性能越好。
与此同时,系统存在一定的局限性,即如果干扰与目标的空间位置相同且极化差异极小,或者在同一位置出现多个不同极化的干扰,单纯依靠极化滤波无法达到抗干扰效果,这与PSA是一致的。
5 结论 1) 二相编码信号的NCRM算法不需要导向矢量作为先验条件,对接收信号快拍数有一定要求,大于60快拍时其性能凸显出来。
2) 空间角度先验信息的误差严重影响基于导向矢量估计的滤波算法,但对NCRM算法没有影响。
3) 在干扰与目标信号存在极化差异的情况下,APSA由于添加了极化辅助阵元,其抗干扰效果获得极大改善,在辅助阵元个数仿真实验中,输出SINR比单极化阵列提高了15~30 dB。
4) 假设天线模型配合二相编码的NCRM算法具有一定的抗主瓣干扰能力。目标与干扰的极化参量γ>30°,系统的输出SINR可以达到10 dB以上(一个主瓣干扰情况)。
参考文献
| [1] | WEN D, MING D, GAO L, et al. A low-complexity DOA and polarization method of polarization-sensitive array[J]. Sensors, 2017, 17(5): 1170. DOI:10.3390/s17051170 |
| [2] | COMPTON R. On the performance of a polarization sensitive adaptive array[J]. IEEE Transactions on Antennas and Propagation, 1981, 29(5): 718-725. DOI:10.1109/TAP.1981.1142651 |
| [3] | WU D, XU Z, ZHANG L. Performance analysis of polarization-space-time three-domain joint processing for clutter suppression in airborne radar[J]. Progress in Electromagnetics Research, 2012, 129: 579-601. DOI:10.2528/PIER12052103 |
| [4] | LIU Z W, WANG Y X, ZHANG X R, et al. Spatially smoothed quaternion-Capon beamforming in the presence of coherent interferences[J]. Transactions of Beijing Institute of Technology, 2016, 25(2): 225-230. |
| [5] | LAN X, LIU W. Fully quaternion-valued adaptive beamforming based on crossed-dipole arrays[J]. Electronics, 2017, 6(2): 34. DOI:10.3390/electronics6020034 |
| [6] | JIANG M D, LIU W, LI Y. Adaptive beamforming for vector-sensor arrays based on a reweighted zero-attracting quaternion-valued LMS algorithm[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2016, 63(3): 274-278. DOI:10.1109/TCSII.2015.2482464 |
| [7] | DU L, LI J, STOICA P. Fully automatic computation of diagonal loading levels for robust adaptive beamforming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 449-458. DOI:10.1109/TAES.2010.5417174 |
| [8] | LU L, LIAO Y.Improved algorithm of mainlobe interference suppression based on eigen-subspace[C]//International Conference on Communication and Signal Processing.Piscataway, NJ: IEEE Press, 2016: 133-137. |
| [9] | ZHANG X, LIU W, XU Y, et al. Quaternion-valued robust adaptive beamformer for electromagnetic vector-sensor arrays with worst-case constraint[J]. Signal Processing, 2014, 104: 274-283. DOI:10.1016/j.sigpro.2014.04.006 |
| [10] | 虞翔, 李旦, 张建秋. 鲁棒成形极化敏感阵列波束的方法及极化估计[J]. 航空学报, 2017, 38(6): 320752. YU X, LI D, ZHANG J Q, et al. A robust beamformer with a polarization sensitive array and polarization estimation[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(6): 320752. (in Chinese) |
| [11] | SHERSON T, KLEIJN W B, HEUSDENS R.A distributed algorithm for robust LCMV beamforming[C]//IEEE International Conference on Acoustics, Speech and Signal Processing.Piscataway, NJ: IEEE Press, 2016: 101-105. |
| [12] | ZHANG X R, LIU Z W, XU Y G, et al. Adaptive tensorial beamformer based on electromagnetic vector-sensor arrays with coherent interferences[J]. Multidimensional Systems and Signal Processing, 2015, 26(3): 803-821. DOI:10.1007/s11045-014-0281-8 |
| [13] | 张贤达, 保铮. 通信信号处理[M]. 北京: 国防工业出版社, 2000: 98-101. ZHANG X D, BAO Z. Communication signal processing[M]. Beijing: National Defense Industry Press, 2000: 98-101. (in Chinese) |
| [14] | XU Y, MA J, LIU Z, et al. A class of diagonally loaded robust Capon beamformers for noncircular signals of interest[J]. Signal Processing, 2014, 94: 670-680. DOI:10.1016/j.sigpro.2013.07.013 |
| [15] | XU Y, YIN B, MA J, et al.High order noncircularity restoral diagonal loading robust adaptive beamforming: HNRDL[C]//Proceedings of 2015 International Radar Conference.Stevenage: IET, 2016: 3-8. |
| [16] | XIAO Y, YIN J, QI H, et al. MVDR algorithm based on estimated diagonal loading for beamforming[J]. Mathematical Problems in Engineering, 2017, 2017: 7904356. |
| [17] | HE Y, HONG Q, XIE H, et al.Energy error estimates of subspace method and multigrid algorithm for eigenvalue problems[J/OL].2017: 03038.http://arxiv.org/pdf/1705.03038.pdf. |
| [18] | XU Y G, LIU T, LIU Z W.Output SINR of MV beamformer with one EM vector sensor of and magnetic noise power[C]//Proceedings of the International Conference on Signal Processing.Piscataway, NJ: IEEE Press, 2004: 419-422. |
| [19] | WANG W C, LIU C J, LIU F, et al.A new multi-beamforming method for large array[C]//2009 IEEE Radar Conference.Piscataway, NJ: IEEE Press, 2009: 1-4. |
| [20] | TAO J W. Performance analysis for interference and noise canceller based on hypercomplex and spatio-temporal-polarisation processes[J]. IET Radar, Sonar and Navigation, 2013, 7(3): 277-286. DOI:10.1049/iet-rsn.2012.0151 |
