为充分发挥MEMS陀螺的优势,进一步扩展其应用领域,如何在当前的工艺和技术水平条件下提高MEMS陀螺使用精度一直是研究的重要方向[3]。MEMS陀螺具有体积小、成本低、易于集成的特点,随着多传感器融合技术的蓬勃发展,陀螺阵列技术逐渐受到了人们的重视。该技术首次由Bayard和Ploen提出[4],他们同时使用多个MEMS陀螺测量同一速率信号,然后利用信息融合技术得到载体速率的最优估计值。由于其最终的输出信号与单个真实陀螺的实际信号不同,所以在这种技术也被称为“虚拟陀螺”技术。陀螺阵列技术是MEMS陀螺的精度得到了有效的提高,且具有良好的可操作性,所以近来成为了惯性技术的一个研究热点。国内外很多科研机构都对这项技术进行了相关研究,并进行了试验验证[5-10]。
陀螺阵列技术的核心是多传感器融合估计方法。上述研究中采用的多是Kalman滤波及其扩展算法,这类方法在一定程度上提高了MEMS陀螺的输出精度。但是这种基于随机噪声假设的估计方法要求噪声的统计特性已知,噪声和未建模误差的概率化模型信息的缺失会影响其估计精度。而在MEMS陀螺的实际应用中,由于动态条件、温度等因素的影响,噪声的统计特性会产生一定的不确定性,甚至噪声本身可能包含部分难以用统计方法描述的非白噪声,这必然会影响Kalman滤波器的效果,甚至会造成滤波发散。与Kalman滤波不同的是,集员估计理论只要求噪声有界且已知,而无需知道噪声的分布以及均值和方差等统计特性[11-12]。这在实际应用中是容易实现的,而超出界限的往往被视作坏值剔除或作为故障诊断的依据。因此,本文研究了集员估计在MEMS陀螺阵列信号中的应用。
集员估计所得结果是一个包含状态真实值的可行集,而可行集形状往往十分复杂,难以确定,所以一般采用包含可行集的近似可行集来描述,其中最常用的是椭球集合,这种方法被称作最优定界椭球(OBE)算法[13-15],也是本文的主要研究内容。OBE算法通常将椭球中心作为真实值的点估计。实际上椭球中心并没有理论上的最优特性,而Chebyshev中心是使可行集worst-case误差最优的点[16],更适合作为真实值的点估计。但可行集的Cheyshev中心很难确定,所以本文采用松弛Chebyshev中心(RCC)作为真实值的角速率估计值。以此为基础,设计了新的参数优化准则,提出了基于RCC的OBE(RCC-OBE)算法,并将该算法用于陀螺阵列数据的融合,得到了MEMS陀螺阵列的RCC-OBE估计融合方法。
1 MEMS陀螺数学模型 陀螺的误差主要由确定性误差和随机误差构成,确定性误差可通过标定补偿,这里仅考虑随机误差,随机误差主要包括零偏不稳定性、角度随机游走(ARW)和角速率随机游走(RRW),因而对角速率ω的带噪声测量通常采用下面的模型[7]:
 | (1) |
 | (2) |
式中:y为陀螺输出; n为角度随机游走; b为受噪声w驱动的角速率随机游走。但具体模型还要由陀螺真实误差特性来决定。
2 MEMS陀螺阵列模型 采用式(1)描述的随机误差模型来建立陀螺阵列的系统模型。静态条件下,陀螺的真实角速率ω理论上等于0,但实际上由于外界环境的影响,陀螺的输入角速率不可能绝对等于0,而是表现为由噪声nω驱动的随机游走。选取6个陀螺组成阵列,则阵列系统的离散方程通常可以表示为[7]
 | (3) |
式中: xk=[b1(k), b2(k), …, b6(k), ω(k)]为状态向量,b1(k)~b6(k)为各陀螺的角速率随机游走,ω(k)为真实角速率;zk=[z1(k), z2(k), …, z6(k)]T为量测向量,z1(k)~z6(k)为各陀螺的输出值;状态转移矩阵Φk-1=I7,I7为7维单位矩阵;量测矩阵Γk-1=TI7,T为陀螺采样周期;量测矩阵Hk=[I616×1],16×1为所有元素均为1的6×1矩阵;过程噪声向量wk-1=[w1(k-1), w2(k-1), …, w6(k-1), nω(k-1)]T,w1(k-1)~w6(k-1)为各陀螺角速率随机游走的驱动噪声,nω(k-1)为真实角速率的驱动噪声;量测噪声向量vk-1=[v1(k-1), v2(k-1), …, v6(k-1)]T,v1(k-1)~v6(k-1)为各陀螺的输出噪声。
但是,在实际应用中,陀螺通常工作在动态条件下。此时,真实角速率跟被测对象的动态特性相关,而上述随机游走过程难以充分跟踪对象的动态特性。为提高陀螺阵列的动态性能,对角速率进行如下的建模:
 | (4) |
式中:a(k)为角加速度; j(k-1)为角加加速度,可以看作分布未知的噪声。则状态变量、过程噪声和阵列离散方程中的相关矩阵修改如下:
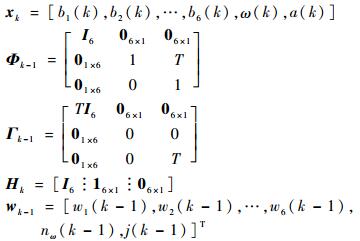 |
而量测变量和量测噪声保持不变。
另外,wk-1和vk分别为过程噪声和量测噪声。为满足Kalman滤波及其衍生算法的条件,它们通常被假设为高斯噪声。但是,这种条件有时难以满足。本文将其假设为一种更为广泛而且容易满足的情况,分布未知但有界(UBB),并假设其属于如下椭球:
 | (5) |
 | (6) |
式中:Qk、Rk为已知的正定矩阵。
相应的,初始状态假设属于如下椭球:
 | (7) |
式中:

3 RCC-OBE算法 RCC-OBE算法是在OBE算法的基础上改进而来,以UBB假设为前提,同样由时间更新和量测更新2个过程组成。
3.1 时间更新 假设k-1时刻包含状态可行集的椭球为


根据式(3)及式(5)所示的UBB假设,一步预测状态xk|k-1属于


 | (8) |
一般情况下,2个椭球的Minkowski和是凸的但形状复杂,难以精确确定。为简化计算,实现算法的递推,本节将通过计算外包椭球来逼近状态预测集
 | (9) |
具体过程如下:
 | (10) |
 | (11) |
式中:参数pk可通过最小化椭球的迹得到
 | (12) |
3.2 量测更新 根据式(3),k时刻状态xk必定属于量测椭球集
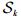

 | (13) |
式中:量测椭球可描述为
 | (14) |
同样的,笔者通过计算外包椭球来逼近这个交集:
 | (15) |
椭球中心和形状矩阵可按式(16)和式(17)计算:
 | (16) |
 | (17) |
式中:qk为用来优化椭球的参数。
 | (18) |
 | (19) |
 | (20) |
根据算法的几何意义可知,OBE算法的结果是椭球内的状态可行集,所以椭球内所有点均可作为状态的点估计。实际应用中,会将椭球的中心

假设x位于l个椭球的交集
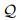
 | (21) |
这里椭球采用多项式表达,以便于后面的处理。则状态可行集
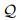

 | (22) |
不过,求解一个凸集的Chebyshev中心极其困难,因为式(22)中内部的极大化过程是一个非凸二次优化问题。为此,将式(22)内部的非凸最大化过程用其半定松弛(SDR)代替,并解决由此导致的凸凹极大极小问题,从而得到RCC。
式(22)中的极大化过程可以描述为
 | (23) |
令Δ=xxT,则式(23)等价于
 | (24) |
式中:
 | (25) |
并定义
 | (26) |
式(24)描述的目标函数对于(Δ, x)是凹的,但集合是非凸的。为实现式(24)的松弛,采用如下的凸集


 | (27) |
式中:Δ≥xxT表示Δ-xxT半正定。
所以RCC可以通过求解式(28)的极大极小问题解决
 | (28) |
式(28)描述的目标函数对于(Δ, x)是凹的,对于


 | (29) |
而式(29)内部的极小化是简单的二次型问题,其最优值为

 | (30) |
这是一个带有线性矩阵不等式约束和凹目标的凸优化问题,式(30)的解即为可行集的RCC。另外,由于

量测更新过程中,RCC位于

 | (31) |
经过式(27)~式(30)的松弛和转化过程,最终状态可行集的RCC可通过如下过程求得:

 | (32) |
 | (33) |
取



则k时刻状态可行集的RCC为
 | (34) |
式中:参数(α1, k, α2, k)可通过求解半定规划(SDP)问题得到:
 | (35) |
对于量测更新中参数的优化, 通常从外包椭球的大小考虑,通过最小容积或最小迹准则来选择最优参数。这有利于在更新中减小状态估计值的不确定范围,但并不能显著减小点估计的估计误差。为进一步提高本方法实际应用中的估计精度,本文提出了一种新的优化准则:
 | (36) |
式中:||·||表示2范数。该准则的几何意义是使k时刻的椭球中心与RCC的距离最小。这样可以使每步更新得到的外包椭球尽可能地包围在状态可行集的RCC周围,从而提高算法的稳定性和点估计的精确性。
那么,RCC-OBE算法的具体步骤可以总结如下:
步骤1??初始化。设置k=0,给定初始值:初始椭球中心


步骤2??时间更新。通过式(10)和式(11)计算状态预测椭球


步骤3??量测更新。通过式(16)~式(20)计算状态估计椭球


步骤4??令k=k+1,并回到步骤2。
4 试验与分析 本文试验采用六陀螺方案,将6个ADXRS300微机械振动陀螺焊接在同一电路板上,并对周围电路进行了设计。通过PXI4070 DMM板卡和PXI6502继电器板卡建立高精度测量系统,对同一轴向进行角速度测量。陀螺阵列系统如图 1所示。
 |
| 图 1 陀螺阵列系统 Fig. 1 System of gyro array |
| 图选项 |
试验中所用陀螺设定的带宽为40 Hz,为满足奈奎斯特定律,以200 Hz的频率进行陀螺输出数据的测量。试验过程中将陀螺阵列置于安装在隔离地基上的温控转台上,转台精度完全能够满足MEMS陀螺测试的要求。
为验证陀螺阵列和融合方法的性能,进行了陀螺阵列的摇摆试验。将陀螺阵列上电预热10min,然后设置转台参数使其做幅度为10°,周期为2 s的摇摆运动,所以陀螺的输入速率为ω=10π·sin(πt)(°)/s。然后按照以上要求采集10 s的陀螺阵列数据,单个陀螺(以陀螺5为例)的输出及输出误差如图 2所示。
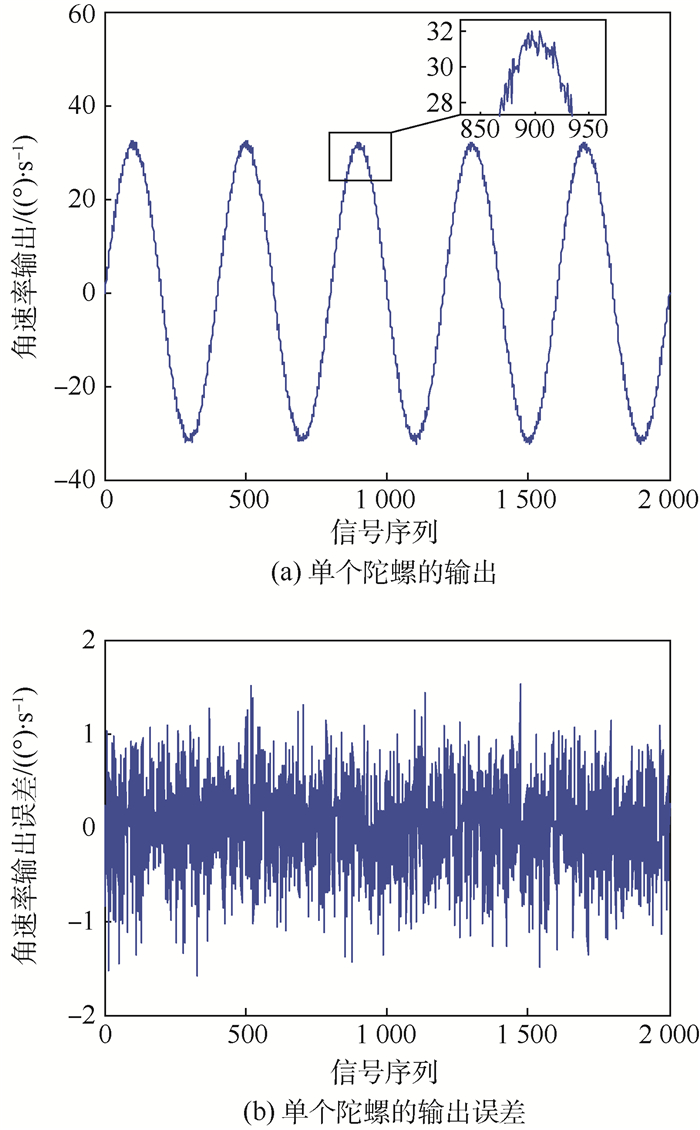 |
| 图 2 单个陀螺的输出及输出误差 Fig. 2 Output and output error of single gyro |
| 图选项 |
得到陀螺阵列的输出数据之后,采用第2节所述的方法对陀螺阵列进行建模,在此基础上,利用第3节推导的RCC-OBE算法对阵列数据进行融合。同时,采用了Kalman滤波和OBE算法作为对比融合方法。融合输出及输出误差见图 3。
 |
| 图 3 陀螺阵列的融合输出及输出误差 Fig. 3 Fusion output and output error of gyro array |
| 图选项 |
为了定量分析几种方法的性能,选择均方根误差(RMSE)和信噪比(SNR)2项指标来衡量其去噪效果。由均方根误差和信噪比的定义可知,同一信号去噪处理后,均方根误差越小,信噪比越大则去噪效果越好。
同时,为检验算法的有效性,笔者进行了多次试验,不同摇摆幅度(A)和周期(T)下的处理结果见表 1~表 3。
表 1 A=10°,T=2 s条件下处理结果 Table 1 Results of signal processed with A=10° and T=2 s
| 指标 | 单个陀螺 | Kalman滤波 | OBE | RCC-OBE |
| SNR/dB | 31.903 4 | 42.008 7 | 40.953 4 | 43.690 4 |
| RMSE/((°)·s-1) | 0.564 2 | 0.176 3 | 0.199 1 | 0.145 3 |
表选项
表 2 A=10°,T=4 s条件下处理结果 Table 2 Results of signal processed with A=10° and T=4 s
| 指标 | 单个陀螺 | Kalman滤波 | OBE | RCC-OBE |
| SNR/dB | 33.246 1 | 43.224 3 | 42.655 7 | 45.274 6 |
| RMSE/((°)·s-1) | 0.532 8 | 0.135 4 | 0.150 1 | 0.113 2 |
表选项
表 3 A=20°,T=2 s条件下处理结果 Table 3 Results of signal processed with A=20° and T=2 s
| 指标 | 单个陀螺 | Kalman滤波 | OBE | RCC-OBE |
| SNR/dB | 27.215 2 | 39.854 2 | 39.002 5 | 43.011 2 |
| RMSE/((°)·s-1) | 0.602 5 | 0.195 2 | 0.213 4 | 0.151 6 |
表选项
从图 2、图 3和表 1~表 3可以看出,试验中的3种方法均有效提高了MEMS陀螺的精度,这首先验证了陀螺阵列技术的有效性。
从计算结果来看,无论是信噪比还是均方根误差,RCC-OBE算法融合的效果都优于其他2种方法,特别是与同类型的OBE算法相比优势比较明显。另外,Kalman滤波等传统的融合方法只能得到一个估计值,而本文所提出的算法不仅可以实现高精度的点估计,同时能够得到估计的上边界值和下边界值,如图 4所示,图中虚线和点划线指的是算法估计边界。可以看到,当设定的噪声边界值不小于实际噪声边界时,陀螺输出的角速率的估计值也在一个硬边界内,这对于载体的姿态控制和制导都具有重要的意义。
 |
| 图 4 算法的边界估计结果 Fig. 4 Estimated bounds by different algorithms |
| 图选项 |
同时,需要指出的是,在边界估计方面,RCC-OBE与OBE相比并无优势,这是由它们的优化准则决定的。RCC-OBE的主要特点是在保证边界估计的基础上提高点估计性能。
5 结论 为降低MEMS陀螺的输出噪声,本文提出了一种基于RCC-OBE算法的陀螺阵列信号融合方法:
1) 在对陀螺阵列系统进行静态和动态建模的基础上,引入椭球定界算法对陀螺阵列信号进行融合。
2) 以OBE算法为代表的集员估计方法的优势是可以得到包含真实值的状态可行集,从而实现状态的保证边界估计,但是试验表明其在点估计方面表现偏弱。因此本文利用松弛的Chebyshev中心来改善估计精度,提出RCC-OBE算法,在保持集员估计优势,得到保证边界的基础上,进一步提高了点估计方面的性能。
3) 将6个MEMS陀螺芯片焊接在同一PCB板上,并设计了周围电路和测量系统进行陀螺阵列的融合试验,试验结果表明,该建模方法和融合方法能够有效地提高MEMS陀螺的使用精度。
另外,集员估计方法的特点决定了其具有检测传感器故障的能力,这一点笔者将在下一步的工作中深入研究。
参考文献
| [1] | KIM D, M'CLOSKEY R T. Spectral analysis of vibratory gyro noise[J]. IEEE Sensors Journal, 2013, 13(11): 4361-4374. DOI:10.1109/JSEN.2013.2269797 |
| [2] | 王鼎杰, 王广才, 吴杰. 微惯性/卫星组合导航高精度事后基准确定方法[J]. 中国惯性技术学报, 2017, 25(1): 97-102. WANG D J, WANG G C, WU J. Fixed-interval smoothing post-processing algorithm for low-cost MEMS-based integrated navigation system[J]. Journal of Chinese Intertial Technology, 2017, 25(1): 97-102. (in Chinese) |
| [3] | 郝燕玲, 刘博, 史宏洋. 新型反相位驱动双解耦微机械陀螺设计[J]. 哈尔滨工业大学学报, 2014, 46(9): 105-110. HAO Y L, LIU B, SHI H Y. The novel design of anti-phase double-decoupled micromachined gyroscope[J]. Journal of Harbin Institute of Technology, 2014, 46(9): 105-110. (in Chinese) |
| [4] | BAYARD D S, PLOEN S R.High accuracy inertial sensors from inexpensive components: US patent, 6882964[P].2005-04-19. |
| [5] | CHANG H L, XUE L, QIN W, et al. An integrated MEMS gyroscope array with higher accuracy output[J]. Sensors, 2008, 8(4): 2886-2899. DOI:10.3390/s8042886 |
| [6] | 吉训生, 王寿荣. 硅微陀螺阵列信号处理技术研究[J]. 宇航学报, 2009, 30(1): 235-239. JI X S, WANG S R. Research on signal procession of silicon micro-gyroscope array[J]. Journal of Astronautics, 2009, 30(1): 235-239. DOI:10.3873/j.issn.1000-1328.2009.00.041 (in Chinese) |
| [7] | XUE L, JIANG C Y, CHANG H L, et al. A novel Kalman filter for combining outputs of MEMS gyroscope array[J]. Measurement, 2012, 12(1): 745-754. |
| [8] | XUE L, JIANG C Y, WANG L X, et al. Noise reduction of MEMS gyroscope based on direct modeling for an angular rate signal[J]. Micromachines, 2015, 6(2): 266-280. DOI:10.3390/mi6020266 |
| [9] | LIU J Y, SHEN Q, QIN W W. Signal processing technique for combining numerous MEMS gyroscopes based on dynamic conditional correlation[J]. Micromachines, 2015, 6(6): 684-698. DOI:10.3390/mi6060684 |
| [10] | VACCARO R J, ZAKI A S. Reduced-drift virtual gyro from an array of low-cost gyros[J]. Sensors, 2017, 17(2): 352. DOI:10.3390/s17020352 |
| [11] | LE B F, SLIWKA J, JAULIN L, et al. Set-membership state estimation with fleeting data[J]. Automatica, 2012, 48(2): 381-387. DOI:10.1016/j.automatica.2011.11.004 |
| [12] | 周波, 樊帅权, 戴先中. 基于集员滤波的移动机器人动态环境建模[J]. 东南大学学报(自然科学版), 2011, 41(1): 107-112. ZHOU B, FAN S Q, DAI X Z. Dynamic environment modeling of mobile robots based on set membership filter[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(1): 107-112. DOI:10.3969/j.issn.1001-0505.2011.01.021 (in Chinese) |
| [13] | LIU Y, ZHAO Y, WU F. Ellipsoidal state-bounding-based set-membership estimation for linear system with unknown-but-bounded disturbances[J]. IET Control Theory and Applications, 2016, 10(4): 431-442. DOI:10.1049/iet-cta.2015.0654 |
| [14] | 周波, 钱堃, 马旭东, 等. 一种新的基于保证定界椭球算法的非线性集员滤波器[J]. 自动化学报, 2013, 39(2): 150-158. ZHOU B, QIAN K, MA X D, et al. A new nonlinear set membership filter based on guaranteed bounding ellipsoid algorithm[J]. Acta Automatica Sinica, 2013, 39(2): 150-158. (in Chinese) |
| [15] | 刘玉双, 赵剡, 吴发林. 基于外定界椭球集员估计的纯方位目标跟踪[J]. 北京航空航天大学学报, 2017, 43(3): 497-505. LIU Y S, ZHAO Y, WU F L. Bearing-only target tracking based on ellipsoidal outer-bounding set-membership estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 497-505. (in Chinese) |
| [16] | ELDAR C Y, BECK A, TEBOULLE M. A minimax Chebyshev estimator for bounded error estimation[J]. IEEE Transactions on Signal Processing, 2008, 56(4): 1388-1397. DOI:10.1109/TSP.2007.908945 |
